Как найти производную если есть степень

Как считать производную степенной функции

3 февраля 2015

Этим видео я начинаю длинную серию уроков, посвященную производным. Этот урок состоит из нескольких частей.

В первую очередь, я расскажу вам, что вообще такое производные и как их считать, но не мудреным академическим языком, а так, как я сам это понимаю и как объясняю своим ученикам. Во-вторых, мы рассмотрим простейшее правило для решения задач, в которых будем искать производные суммы, производные разности и производные степенной функции.

Мы рассмотрим более сложные комбинированные примеры, из которых вы, в частности, узнаете, что подобные задачи, содержащие корни и даже дроби, могут быть решены при использовании формулы производной степенной функции. Кроме того, конечно, будет множество задач и примеров решений самого разного уровня сложности.

Вообще, изначально я собирался записать коротенький 5-минутный ролик, но сами видите, что из этого получилось. Поэтому хватит лирики — приступаем к делу.

Что такое производная?

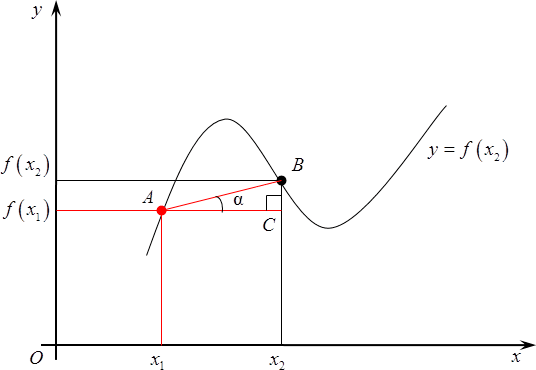
Итак, начнем издалека. Много лет назад, когда деревья были зеленее, а жизнь была веселее, математики задумались вот над чем: рассмотрим простую функцию, заданную своим графиком, назовем ее $y=fleft( x right)$. Разумеется, график существует не сам по себе, поэтому нужно провести оси $x$, а также ось $y$. А теперь давайте выберем любую точку на этом графике, абсолютно любую. Абсциссу назовем ${{x}_{1}}$, ордината, как не трудно догадаться, будет $fleft( {{x}_{1}} right)$.

Рассмотрим на том же графике еще одну точку. Не важно, какую, главное, чтобы она отличалась от первоначальной. У нее, опять же, есть абсцисса, назовем ее ${{x}_{2}}$, а также ордината — $fleft( {{x}_{2}} right)$.

Итак, мы получили две точки: у них разные абсциссы и, следовательно, разные значения функции, хотя последнее — необязательно. А вот что действительно важно, так это что, что из курса планиметрии нам известно: через две точки можно провести прямую и, причем, только одну. Вот давайте ее и проведем.

А теперь проведем через самую первую из них прямую, параллельную оси абсцисс. Получим прямоугольный треугольник. Давайте его обозначим $ABC$, прямой угол $C$. У этого треугольника возникает одно очень интересное свойство: дело в том, что угол$alpha $, на самом деле, равен углу, под которым пересекается прямая $AB$ с продолжением оси абсцисс. Судите сами:

1. прямая $AC$параллельна оси $Ox$ по построению,
2. прямая $AB$ пересекает $AC$ под $alpha $,
3. следовательно, $AB$ пересекает $Ox$под тем же самым $alpha $.

Что мы можем сказать об $text{ }!!alpha!!text{ }$? Ничего конкретного, разве что в треугольнике $ABC$отношение катета $BC$ к катету $AC$ равно тангенсу этого самого угла. Так и запишем:

[tg=frac{BC}{AC}]

Разумеется, $AC$ в данном случае легко считается:

[AC={{x}_{2}}-{{x}_{1}}]

Точно также и $BC$:

[BC=fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)]

Другими словами, мы можем записать следующее:

[operatorname{tg}text{ }!!alpha!!text{ }=frac{fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)}{{{x}_{2}}-{{x}_{1}}}]

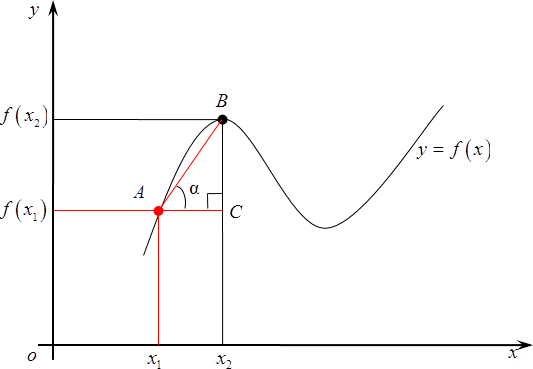
Теперь, когда мы все это выяснили, давайте вернемся к нашему графику и рассмотрим новую точку $B$. Сотрем старые значения и возьмем и возьмем $B$ где-нибудь поближе к ${{x}_{1}}$. Вновь обозначим ее абсциссу за ${{x}_{2}}$, а ординату — $fleft( {{x}_{2}} right)$.

Вновь рассмотрим наш маленький треугольник $ABC$и $text{ }!!alpha!!text{ }$ внутри него. Совершенно очевидно, что это будет уже совсем другой угол, тангенс будет также другим потому, что длины отрезков $AC$ и $BC$ существенно изменились, а формула для тангенса угла нисколько не поменялась — это по-прежнему соотношение между изменением функции и изменением аргумента.

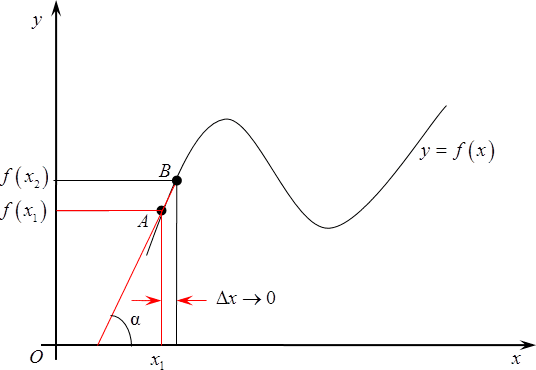
Наконец, продолжаем двигать $B$ все ближе к изначальной точке $A$, в результате треугольник еще уменьшится, а прямая, содержащая отрезок $AB$, все больше будет походить на касательную к графику функции.

 

В итоге, если продолжать сближение точек, т. е., уменьшать расстояние до нуля, то прямая $AB$, действительно, превратится в касательную к графику в данной точке, а $text{ }!!alpha!!text{ }$превратится из обычного элемента треугольника в угол между касательной к графику и положительным направлением оси $Ox$.

И вот тут мы плавно переходим к определению$f$, а именно, производной функции в точке ${{x}_{1}}$ называется тангенс угла $alpha $ между касательной к графику в точке ${{x}_{1}}$ и положительным направлением оси $Ox$:

[{f}’left( {{x}_{1}} right)=operatorname{tg}text{ }!!alpha!!text{ }]

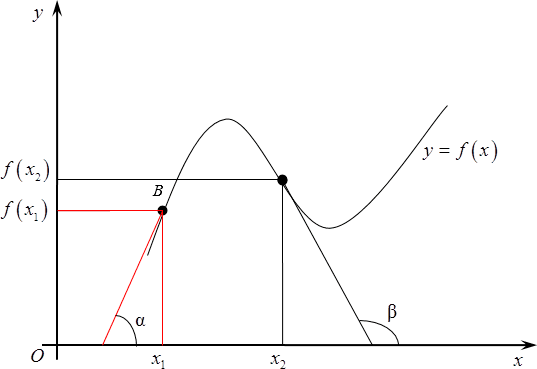
Возвращаясь к нашему графику, следует отметить, что в качестве ${{x}_{1}}$ можно выбрать любую точку на графике. Например, с тем же успехом мы могли снять штрих в точке, показанной на рисунке. 

Угол между касательной и положительным направлением оси назовем $beta $. Соответственно, $f$ в ${{x}_{2}}$ будет равна тангенсу этого угла $beta $.

[{f}’left( {{x}_{2}} right)=tgtext{ }!!beta!!text{ }]

В каждой точке графика будет своя касательная, а, следовательно, свое значение функции. В каждом из этих случаев помимо точки, в которой мы ищем производную разности или суммы, или производную степенной функции, необходимо взять другую точку, находящуюся на некотором расстоянии от нее, а затем устремить эту точку к исходной и, разумеется, выяснить, как в процессе такого движения будет меняться тангенс угла наклона.

Производная степенной функции

К сожалению, подобное определение нас совершено не устраивает. Все эти формулы, картинки, углы не дают нам ни малейшего представления о том, как считать реальную производную в реальных задачах. Поэтому давайте немного отвлечемся от формального определения и рассмотрим более действенные формулы и приемы, с помощью которых уже можно решать настоящие задачи.

Начнем с самых простых конструкций, а именно, функций вида $y={{x}^{n}}$, т.е. степенных функций. В этом случае мы можем записать следующее: ${y}’=ncdot {{x}^{n-1}}$. Другими словами, степень, которая стояла в показателе, показывается в множителе спереди, а сам показатель уменьшается на единицу. Например:

[begin{align}& y={{x}^{2}} \& {y}’=2cdot {{x}^{2-1}}=2x \end{align}]

А вот другой вариант:

[begin{align}& y={{x}^{1}} \& {y}’={{left( x right)}^{prime }}=1cdot {{x}^{0}}=1cdot 1=1 \& {{left( x right)}^{prime }}=1 \end{align}]

Пользуясь этими простыми правилами, давайте попробуем снять штрих следующих примеров:

[fleft( x right)={{x}^{6}}]

Итак, мы получаем:

[{{left( {{x}^{6}} right)}^{prime }}=6cdot {{x}^{5}}=6{{x}^{5}}]

Теперь решим второе выражение:

[begin{align}& fleft( x right)={{x}^{100}} \& {{left( {{x}^{100}} right)}^{prime }}=100cdot {{x}^{99}}=100{{x}^{99}} \end{align}]

Разумеется, это были очень простые задачи. Однако реальные задачи более сложные и они не ограничиваются одними лишь степенями функции.

Итак, правило № 1 – если функция представлена в виде других двух, то производная этой суммы равна сумме производных:

[{{left( f+g right)}^{prime }}={f}’+{g}’]

Аналогично, производная разности двух функций равна разности производных:

[{{left( f-g right)}^{prime }}={f}’-{g}’]

Пример:

[{{left( {{x}^{2}}+x right)}^{prime }}={{left( {{x}^{2}} right)}^{prime }}+{{left( x right)}^{prime }}=2x+1]

Кроме того, есть еще одно важное правило: если перед некоторой $f$ стоит константа $c$, на которую эта функция умножается, то $f$ всей этой конструкции считается так:

[{{left( ccdot f right)}^{prime }}=ccdot {f}’]

Пример:

[{{left( 3{{x}^{3}} right)}^{prime }}=3{{left( {{x}^{3}} right)}^{prime }}=3cdot 3{{x}^{2}}=9{{x}^{2}}]

Наконец, еще одно очень важное правило: в задачах часто встречается отдельное слагаемое, которое вообще не содержит $x$. Например, мы можем наблюдать это в наших сегодняшних выражениях. Производная константы, т. е., числа, никак не зависящего от $x$, всегда равна нулю, причем совершенно неважно, чему равна константа $c$:

[{{left( c right)}^{prime }}=0]

Пример решения:

[{{left( 1001 right)}^{prime }}={{left( frac{1}{1000} right)}^{prime }}=0]

Еще раз ключевые моменты:

1. Производная суммы двух функций всегда равна сумме производных: ${{left( f+g right)}^{prime }}={f}’+{g}’$;
2. По аналогичным причинам производная разности двух функций равна разности двух производных: ${{left( f-g right)}^{prime }}={f}’-{g}’$;
3. Если у функции присутствует множитель константа, то эту константу можно выносить за знак производной: ${{left( ccdot f right)}^{prime }}=ccdot {f}’$;
4. Если вся функция представляет собой константу, то ее производная всегда ноль: ${{left( c right)}^{prime }}=0$.

Давайте посмотрим, как все это работает на реальных примерах. Итак:

[y={{x}^{5}}-3{{x}^{2}}+7]

Записываем:

[begin{align}& {{left( {{x}^{5}}-3{{x}^{2}}+7 right)}^{prime }}={{left( {{x}^{5}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{7}’= \& =5{{x}^{4}}-3{{left( {{x}^{2}} right)}^{prime }}+0=5{{x}^{4}}-6x \end{align}]

В этом примере мы видим и производную суммы, и производную разности. Итого, производная равна $5{{x}^{4}}-6x$.

Переходим ко второй функции:

[fleft( x right)=3{{x}^{2}}-2x+2]

Записываем решение:

[begin{align}& {{left( 3{{x}^{2}}-2x+2 right)}^{prime }}={{left( 3{{x}^{2}} right)}^{prime }}-{{left( 2x right)}^{prime }}+{2}’= \& =3{{left( {{x}^{2}} right)}^{prime }}-2{x}’+0=3cdot 2x-2cdot 1=6x-2 \end{align}]

Вот мы и нашли ответ.

Переходим к третьей функции — она уже посерьезней:

[y=2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5]

Решаем:

[begin{align}& {{left( 2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5 right)}^{prime }}={{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{{left( frac{1}{2}x right)}^{prime }}-{5}’= \& =2{{left( {{x}^{3}} right)}^{prime }}-3{{left( {{x}^{2}} right)}^{prime }}+frac{1}{2}cdot {x}’=2cdot 3{{x}^{2}}-3cdot 2x+frac{1}{2}cdot 1=6{{x}^{2}}-6x+frac{1}{2} \end{align}]

Ответ мы нашли.

Переходим к последнему выражению — самому сложному и самому длинному:

[y=6{{x}^{7}}-14{{x}^{3}}+4x+5,{{x}_{0}}=-1]

Итак, считаем:

[begin{align}& {{left( 6{{x}^{7}}-14{{x}^{3}}+4x+5 right)}^{prime }}={{left( 6{{x}^{7}} right)}^{prime }}-{{left( 14{{x}^{3}} right)}^{prime }}+{{left( 4x right)}^{prime }}+{5}’= \& =6cdot 7cdot {{x}^{6}}-14cdot 3{{x}^{2}}+4cdot 1+0=42{{x}^{6}}-42{{x}^{2}}+4 \end{align}]

Но на этом решение не заканчивается, потому что нас просят не просто снять штрих, а посчитать ее значение в конкретной точке, поэтому подставляем в выражение −1 вместо $x$:

[{y}’left( -1 right)=42cdot 1-42cdot 1+4=4]

Идем далее и переходим к еще более сложным и интересным примерам. Дело в том, что формула решения степенной производной ${{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}$ имеет еще более широкую область применения, чем обычно принято считать. С ее помощью можно решать примеры с дробями, корнями и т. д. Именно этим мы сейчас и займемся.

Для начала еще раз запишем формулу, которая поможет нам найти производную степенной функции:

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

А теперь внимание: до сих пор мы рассматривали в качестве $n$ лишь натуральные числа, однако ничего не мешаем рассмотреть дроби и даже отрицательные числа. Например, мы можем записать следующее:

[begin{align}& sqrt{x}={{x}^{frac{1}{2}}} \& {{left( sqrt{x} right)}^{prime }}={{left( {{x}^{frac{1}{2}}} right)}^{prime }}=frac{1}{2}cdot {{x}^{-frac{1}{2}}}=frac{1}{2}cdot frac{1}{sqrt{x}}=frac{1}{2sqrt{x}} \end{align}]

Ничего сложного, поэтому посмотрим, как эта формула поможет нам при решении более сложных задач. Итак, пример:

[y=sqrt{x}+sqrt[3]{x}+sqrt[4]{x}]

Записываем решение:

[begin{align}& left( sqrt{x}+sqrt[3]{x}+sqrt[4]{x} right)={{left( sqrt{x} right)}^{prime }}+{{left( sqrt[3]{x} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }} \& {{left( sqrt{x} right)}^{prime }}=frac{1}{2sqrt{x}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot {{x}^{-frac{2}{3}}}=frac{1}{3}cdot frac{1}{sqrt[3]{{{x}^{2}}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}{{x}^{-frac{3}{4}}}=frac{1}{4}cdot frac{1}{sqrt[4]{{{x}^{3}}}} \end{align}]

Возвращаемся к нашему примеру и записываем:

[{y}’=frac{1}{2sqrt{x}}+frac{1}{3sqrt[3]{{{x}^{2}}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}]

Вот такое сложное решение.

Переходим ко второму примеру — здесь всего два слагаемых, но каждое из них содержит как классическую степень, так и корни.

[y={{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x}]

Сейчас мы узнаем, как найти производную степенной функции, которая, кроме того, содержит и корень:

[begin{align}& {{left( {{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}}cdot sqrt[3]{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{3}}cdot {{x}^{frac{2}{3}}} right)}^{prime }}= \& ={{left( {{x}^{3+frac{2}{3}}} right)}^{prime }}={{left( {{x}^{frac{11}{3}}} right)}^{prime }}=frac{11}{3}cdot {{x}^{frac{8}{3}}}=frac{11}{3}cdot {{x}^{2frac{2}{3}}}=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}} \& {{left( {{x}^{7}}cdot sqrt[3]{x} right)}^{prime }}={{left( {{x}^{7}}cdot {{x}^{frac{1}{3}}} right)}^{prime }}={{left( {{x}^{7frac{1}{3}}} right)}^{prime }}=7frac{1}{3}cdot {{x}^{6frac{1}{3}}}=frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x} \end{align}]

Оба слагаемых посчитаны, осталось записать окончательный ответ:

[{y}’=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}}+frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x}]

Мы нашли ответ.

Производная дроби через степенную функцию

Но и на этом возможности формулы для решения производной степенной функции не заканчиваются. Дело в том, что с ее помощью можно считать не только примеры с корнями, но также и с дробями. Это как раз та редкая возможность, которая значительно упрощает решение таких примеров, но при этом зачастую игнорируется не только учениками, но и учителями.

Итак, сейчас мы попытаемся совместить сразу две формулы. С одной стороны, классическая производная степенной функции

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

С другой стороны мы знаем, что выражение вида $frac{1}{{{x}^{n}}}$ представимо в виде ${{x}^{-n}}$. Следовательно,

[left( frac{1}{{{x}^{n}}} right)’={{left( {{x}^{-n}} right)}^{prime }}=-ncdot {{x}^{-n-1}}=-frac{n}{{{x}^{n+1}}}]

Пример:

[{{left( frac{1}{x} right)}^{prime }}=left( {{x}^{-1}} right)=-1cdot {{x}^{-2}}=-frac{1}{{{x}^{2}}}]

Таким образом, производные простых дробей, где в числителе стоит константа, а в знаменателе — степень, также считаются с помощью классической формулы. Посмотрим, как это работает на практике.

Итак, первая функция:

[fleft( x right)=frac{1}{{{x}^{2}}}]

Считаем:

[{{left( frac{1}{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{-2}} right)}^{prime }}=-2cdot {{x}^{-3}}=-frac{2}{{{x}^{3}}}]

Первый пример решен, переходим ко второму:

[y=frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}}]

Решаем:

[begin{align}& {{left( frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}} right)}^{prime }}= \& ={{left( frac{7}{4{{x}^{4}}} right)}^{prime }}-{{left( frac{2}{3{{x}^{3}}} right)}^{prime }}+{{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{4}} right)}^{prime }} \& {{left( frac{7}{4{{x}^{4}}} right)}^{prime }}=frac{7}{4}{{left( frac{1}{{{x}^{4}}} right)}^{prime }}=frac{7}{4}cdot {{left( {{x}^{-4}} right)}^{prime }}=frac{7}{4}cdot left( -4 right)cdot {{x}^{-5}}=frac{-7}{{{x}^{5}}} \& {{left( frac{2}{3{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( frac{1}{{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( {{x}^{-3}} right)}^{prime }}=frac{2}{3}cdot left( -3 right)cdot {{x}^{-4}}=frac{-2}{{{x}^{4}}} \& {{left( frac{5}{2}{{x}^{2}} right)}^{prime }}=frac{5}{2}cdot 2x=5x \& {{left( 2{{x}^{3}} right)}^{prime }}=2cdot 3{{x}^{2}}=6{{x}^{2}} \& {{left( 3{{x}^{4}} right)}^{prime }}=3cdot 4{{x}^{3}}=12{{x}^{3}} \end{align}]…

Теперь собираем все эти слагаемые в единую формулу:

[{y}’=-frac{7}{{{x}^{5}}}+frac{2}{{{x}^{4}}}+5x+6{{x}^{2}}-12{{x}^{3}}]

Мы получили ответ.

Однако прежде чем двигаться дальше, хотел бы обратить ваше внимание на форму записи самих исходных выражений: в первом выражении мы записали $fleft( x right)=…$, во втором: $y=…$ Многие ученики теряются, когда видят разные формы записи. Чем отличаются $fleft( x right)$ и $y$? На самом деле, ничем. Это просто разные записи с одним и тем же смыслом. Просто когда мы говорим $fleft( x right)$, то речь идет, прежде всего, о функции, а когда речь идет об $y$, то чаще всего подразумевается график функции. В остальном же это одно и то же, т. е., производная в обоих случаях считается одинаково.

Сложные задачи с производными

В заключение хотелось бы рассмотреть пару сложных комбинированных задач, в которых используется сразу все то, что мы сегодня рассмотрели. В них нас ждут и корни, и дроби, и суммы. Однако сложными эти примеры будут лишь в рамках сегодняшнего видеоурока, потому что по-настоящему сложные функции производных будут ждать вас впереди.

Итак, заключительная часть сегодняшнего видеоурока, состоящая из двух комбинированных задач. Начнем с первой из них:

[y={{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x}]

Считаем:

[begin{align}& {{left( {{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}} right)}^{prime }}-{{left( frac{1}{{{x}^{3}}} right)}^{prime }}+left( sqrt[3]{x} right) \& {{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}} \& {{left( frac{1}{{{x}^{3}}} right)}^{prime }}={{left( {{x}^{-3}} right)}^{prime }}=-3cdot {{x}^{-4}}=-frac{3}{{{x}^{4}}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot frac{1}{{{x}^{frac{2}{3}}}}=frac{1}{3sqrt[3]{{{x}^{2}}}} \end{align}]

Производная функции равна:

[{y}’=3{{x}^{2}}-frac{3}{{{x}^{4}}}+frac{1}{3sqrt[3]{{{x}^{2}}}}]

Первый пример решен. Рассмотрим вторую задачу:

[y=-frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}}]

Во втором примере действуем аналогично:

[{{left( -frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( -frac{2}{{{x}^{4}}} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }}+{{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}]

Посчитаем каждое слагаемое отдельно:

[begin{align}& {{left( -frac{2}{{{x}^{4}}} right)}^{prime }}=-2cdot {{left( {{x}^{-4}} right)}^{prime }}=-2cdot left( -4 right)cdot {{x}^{-5}}=frac{8}{{{x}^{5}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}cdot {{x}^{-frac{3}{4}}}=frac{1}{4cdot {{x}^{frac{3}{4}}}}=frac{1}{4sqrt[4]{{{x}^{3}}}} \& {{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( frac{4}{xcdot {{x}^{frac{3}{4}}}} right)}^{prime }}={{left( frac{4}{{{x}^{1frac{3}{4}}}} right)}^{prime }}=4cdot {{left( {{x}^{-1frac{3}{4}}} right)}^{prime }}= \& =4cdot left( -1frac{3}{4} right)cdot {{x}^{-2frac{3}{4}}}=4cdot left( -frac{7}{4} right)cdot frac{1}{{{x}^{2frac{3}{4}}}}=frac{-7}{{{x}^{2}}cdot {{x}^{frac{3}{4}}}}=-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}} \end{align}]

Все слагаемые посчитаны. Теперь возвращаемся к исходной формуле и складываем вместе все три слагаемых. Получаем, что окончательный ответ будет таким:

[{y}’=frac{8}{{{x}^{5}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}}]

И на этом все. Это был первый наш урок. В следующих уроках мы рассмотрим более сложные конструкции, а также выясним, зачем вообще нужны производные. 

Смотрите также:

1. Производная произведения и частного
2. Правила вычисления производных
3. Теорема Виета
4. Преобразование уравнений
5. Тест по методу интервалов для строгих неравенств
6. Тест по задачам B14: средний уровень, 2 вариант

Содержание:

• Формула
• Примеры вычисления производной степенной функции

Формула

Производная степенной функции равна произведению показателя степени и основания в степени на единицу меньше.

Заметим, что в качестве степени может быть как
натуральное число,
то есть 1, 2, 3, …; так и любое отрицательное число: — 1, — 2 и т.д., а также и любое дробное, например, 2,34; — 4,1 или $frac{3}{4}$ , $-frac{5}{6}$ .

Заметим, что если аргумент у степенной функции есть сложная функция (то есть там стоит более сложное выражение, чем просто $x$, то производную нужно находить по следующей формуле:

$$left(u^{n}right)^{prime}=n u^{n-1} cdot u^{prime}$$

Примеры вычисления производной степенной функции

Читать дальше: производная обратной функции (1/x)’.

Производная степени встречается в большинстве примеров на дифференцирование. Само правило нахождения производной степени простое. При дифференцировании степени с натуральным показателем проблем, как правило, не возникает. А вот найти производную степени с отрицательным или дробным показателями несколько сложнее. Легче всего понять, как найти производную степени, на примерах.

Открываем таблицу производных и правила дифференцирования.

Основная формула, по которой  может быть найдена производная любой степени —

   

Примеры. Найти производную степени:

   

   

Поскольку при дифференцировании число выносится за знак производной, то множитель, стоящий перед степенью, при нахождении производной просто переписываем:

   

   

Нахождение производной степени, стоящей в знаменателе дроби, немного сложнее. Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель. Получившуюся в результате вычислений степень с отрицательным показателем снова преобразовываем.

   

   

   

   

   

   

Производная степени используется и для дифференцирования корней. Предварительно корень приводится к степени, а в найденной производной снова возвращаемся к корню.

Например,

   

   

   

   

   

   

Если корень в знаменателе, сначала преобразовываем его в степень, затем — поднимаем наверх с отрицательным показателем, а  далее — как обычно, производная степени.

Например,

   

   

   

   

   

   

   

   

Примеры для самопроверки. Найти производную степени:

   

Показать решение

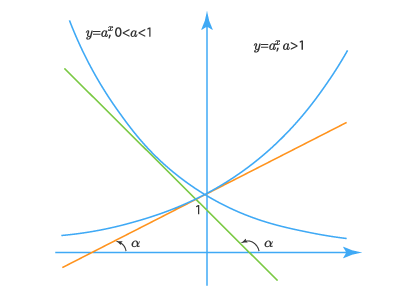
Найдем производную функции f(x)=ax,a>0,a≠0f(x)=a^x, a>0, a ne 0 и приведем некоторые ее свойства и практические примеры использования.

Производная функции f(x)=a в степени x

Как известно, производной функции f(x)f(x), определенной в точке x0x_0 и в некотором интервале, содержащем x0x_0, называют предел следующего вида:

f′(x0)=dfdx∣x=x0=lim⁡Δx→0f(x0+Δx)−f(x0)Δxf^{‘}(x_0)=dfrac{df}{dx}Bigr|_{x=x_0}=limlimits_{Delta x to 0}dfrac{ f(x_0+ Delta x)-f(x_0 )}{ Delta x}

если только такой предел существует.

Таким образом, для вычисления производной функции f(x)f(x) необходимо последовательно:

1. Записать выражение для приращения функции:

Δf(x0)=f(x0+Δx)−f(x0)Delta f(x_0 )=f(x_0+Delta x)-f(x_0 )

1. Упростить, по возможности, дробь

Δf(x0)Δx=f(x0+Δx)−f(x0)Δxdfrac {Delta f(x_0)}{Delta x}=dfrac {f(x_0+Delta x)-f(x_0)}{Delta x}

1. Вычислить предел дроби при Δx→0Delta x to 0 и записать полученное выражение для производной.

Применим этот алгоритм к вычислению производной показательной функции:

• Записываем приращение функции:

Δf(x0)=f(x0+Δx)−f(x0)=ax0+Δx−ax0=ax0(aΔx−1)Delta f(x_0)= f(x_0+Delta x)-f(x_0)= a^{x_0+Delta x}-a^{x_0}=a^{x_0} (a^{Delta x}-1)

• Получаем дробь:

Δf(x0)Δx=ax0aΔx−1Δxdfrac {Delta f(x_0)}{Delta x}= a^{x_0} dfrac {a^{Delta x}-1}{Delta x}

• Вычисляем производную:

f′(x0)=lim⁡Δx→0ax0aΔx−1Δx=ax0lim⁡Δx→0aΔx−1Δxf'(x_0 )= limlimits_{Delta x to 0} {a^{x_0} dfrac {a^{Delta x}-1}{Delta x}}= a^{x_0}limlimits_{Delta x to 0} {dfrac {a^{Delta x}-1}{Delta x}}

Используем далее представление показательной функции с помощью экспоненты:

ax=eln⁡a⋅xa^x=e^{ln {a} cdot x}

Тогда:

f′(x0)=ax0lim⁡Δx→0eln⁡a⋅Δx−1Δx=ln⁡a⋅ax0lim⁡t→0et−1tf'(x_0 )= a^{x_0}limlimits_{Delta x to 0} {dfrac {e^{ln {a} cdot Delta x}-1}{Delta x}}= ln {a} cdot a^{x_0}limlimits_{t to 0} {dfrac {e^{t}-1} {t}}

где t=ln⁡a⋅Δxt = ln {a} cdot Delta {x}

Для преобразования ete^{t} используем представление числа e≈2,71828e approx 2,71828 (числа Непера или числа Эйлера) в виде предела:

e=lim⁡n→∞(1+1n)ne=limlimits_{ntoinfty} Bigl( {1+dfrac {1}{n}} Bigr) ^n

Следовательно:

et=lim⁡n→∞(1+tn)ne^{t} =limlimits_{ntoinfty} Bigl( {1+dfrac {t}{n}} Bigr) ^n

Используем для выражения под знаком предела бином Ньютона:

(1+tn)n=1+Cn1tn+Cn2(tn)2+…+Cnn(tn)nBigl( {1+dfrac {t}{n}} Bigr) ^n=1+C_n^1 dfrac{t}{n}+ C_n^2 Bigl( {dfrac{t}{n}}Bigr)^2+ ldots + C_n^n Bigl( {dfrac{t}{n}}Bigr)^n

Тогда:

f′(x0)=ln⁡a⋅ax0lim⁡t→0lim⁡n→∞(1+Cn1tn+Cn2(tn)2+…+Cnn(tn)n)−1t=ln⁡a⋅ax0lim⁡t→0(lim⁡n→∞Cn1tn+Cn2(tn)2+…+Cnn(tn)nt)=ln⁡a⋅ax0lim⁡t→0lim⁡n→∞(Cn11n+Cn2t2−1n2+…+Cnntn−1nn)=ln⁡a⋅ax0lim⁡n→∞lim⁡t→0(n1n+Cn2t2−1n2+…+Cnntn−1nn)=ln⁡a⋅ax0(1+lim⁡n→∞lim⁡t→0(Cn2t2−1n2+…+Cnntn−1nn))f'(x_0 )= ln {a} cdot a^{x_0}limlimits_{t to 0}dfrac {limlimits_{ntoinfty} Bigl( {1+C_n^1 dfrac{t}{n}+ C_n^2 Bigl( {dfrac{t}{n}}Bigr)^2+ ldots + C_n^n Bigl( {dfrac{t}{n}}Bigr)^n }Bigr)-1}{t} = ln {a} cdot a^{x_0}limlimits_{t to 0}Bigl( limlimits_{ntoinfty} dfrac {C_n^1 dfrac{t}{n}+ C_n^2 Bigl( {dfrac{t}{n}}Bigr)^2+ ldots + C_n^n Bigl( {dfrac{t}{n}}Bigr)^n }{t}Bigr)= ln {a} cdot a^{x_0}limlimits_{t to 0} limlimits_{ntoinfty} Bigl( {C_n^1 dfrac{1}{n}+ C_n^2 dfrac{t^{2-1} }{n^2}+ ldots + C_n^n dfrac{t^{n-1} }{n^n}}Bigr)= ln {a} cdot a^{x_0}limlimits_{ ntoinfty } limlimits_{t to 0} Bigl( {n dfrac{1}{n}+ C_n^2 dfrac{t^{2-1} }{n^2}+ ldots + C_n^n dfrac{t^{n-1} }{n^n}}Bigr)=ln {a} cdot a^{x_0} Bigl( 1+ limlimits_{ ntoinfty } limlimits_{t to 0} Bigl( { C_n^2 dfrac{t^{2-1} }{n^2}+ ldots + C_n^n dfrac{t^{n-1} }{n^n}}Bigr) Bigr)

Учитывая, что:

lim⁡t→0(Cn2t2−1n2+…+Cnntn−1nn)=0limlimits_{t to 0} Bigl( { C_n^2 dfrac{t^{2-1} }{n^2}+ ldots + C_n^n dfrac{t^{n-1} }{n^n}}Bigr)=0

получаем:

f′(x0)=ln⁡a⋅ax0(1+0)f'(x_0 )= ln {a} cdot a^{x_0}(1+0)

Таким образом:

f′(x)=(ax)′=axln⁡af'(x)= (a^{x})^{‘}= a^{x} ln {a}

Как и следовало ожидать, при a=ea=e производная экспоненциальной функции f(x)=exf(x)=e^x равна этой же функции:

(ex)′=exln⁡e=ex(e^x )’=e^x ln {e}=e^x

Некоторые свойства и практические примеры

• Угол наклона αalpha касательной к графику функции y=axy=a^x в точке x=x0x=x_0 определяется соотношением:

tg⁡α=y′(x0)=axln⁡atg alpha =y^{‘} (x_0 )= a^{x} ln {a}

Здесь угол αalpha это угол между касательной и осью OxOx отсчитываемый от положительного направления OxOx против часовой стрелки.

Производная функции f(x)=axf(x)=a^x в точке x0=0x_0=0 равна:

f′(x0)=(ax)x0=0′=a0ln⁡a=ln⁡af’ (x_0 )=(a^x )_{x_0=0}’=a^0 ln {a}=ln {a}

• Производная сложной функции

y=ag(x)y=a^{g(x)}

согласно правил дифференцирования, равна:

y′=g′(x)ag(x)ln⁡ay’=g'(x) a^{g(x)} ln {a}

• Производная сложной функции

y=u(v),y=u(v), где v=axv=a^x

равна:

y′=uv′⋅v′=uv′⋅axln⁡ay’=u’_v cdot v’=u’_v cdot a^x ln {a}

Пример 1

Зная производную экспоненты и используя правило для дифференцирования сложной функции, найти производную показательной функции.

Решение

Воспользуемся формулой для производной экспоненты:

(ex)′=ex(e^x )’=e^x

Тогда:

(eg(x))′=g′(x)eg(x)(e^{g(x)})’=g'(x)e^{g(x)}

Полагая:

g(x)=xln⁡ag(x)= x ln {a}

находим:

(exln⁡a)′=(xln⁡a)′exln⁡a=ln⁡a⋅exln⁡a(e^{x ln {a}})’=(x ln {a} )’ e^{x ln {a}}= ln {a} cdot e^{x ln {a}}

Учитывая, что

exln⁡a=axe^{x ln {a}}=a^{x}

получаем:

(ax)′=axln⁡a(a^x )’=a^x ln {a}

Как и следовало ожидать, результат совпадает с полученным ранее.

Пример 2

Найти производную функции

f(x)=23×2−2xf(x)=2^{3x^2-2x}

Решение

f′(x)=(23×2−2x)′=(3×2−2x)′⋅23×2−2xln⁡2=(6x−2)⋅23×2−2xln⁡2f'(x)= Bigl( 2^{3x^2-2x} Bigr)’=(3x^2-2x)’ cdot 2^{3x^2-2x} ln {2}=(6x-2) cdot 2^{3x^2-2x} ln {2}

Пример 3

Найти производную функции

f(x)=sin⁡x2xf(x)= sin {x^{2x}}

Решение

Полагаем x2x=vx^{2x}=v

Тогда

f′(x)=(sin⁡v)v′⋅v′=cos⁡v⋅(x2x)′=cos⁡(x2x)⋅(e2xln⁡x)′=cos⁡(x2x)⋅(2xln⁡x)′⋅e2xln⁡x=e2xln⁡xcos⁡(x2x)⋅(2ln⁡x+2)=x2xcos⁡(x2x)⋅(2ln⁡x+2)f'(x) = (sin v)_v’ cdot v’ = cos v cdot (x^{2x} )’=cos (x^{2x}) cdot (e^{2x ln {x}})’= cos (x^{2x}) cdot (2x ln {x})’ cdot e^{2x ln {x}}= e^{2x ln {x}} cos (x^{2x}) cdot (2 ln {x}+2) = x^{2x}cos (x^{2x}) cdot (2 ln {x}+2)

В данной публикации мы рассмотрим, чему равна производная степенной функций (в т.ч. сложной), а также разберем примеры решения задач для закрепления изложенного материала.

Формула производной степенной функции

Для функции f(x) = x ⁿ, где n – действительное число, справедливо следующее выражение:

f ‘(x) = (x ⁿ)‘ = nx ^n-1

Т.е. производная степенной функции равняется произведению показателя степени на основание в степени, уменьшенной на единицу.

n – может быть как положительным, так и отрицательным числом (в т.ч. дробным):

Производная сложной степенной функции

В сложной функции вместо x представлено более сложное выражение. Производная такой функции определяется по формуле:

(y ⁿ)‘ = ny ^n-1 ⋅ y ‘

Примеры задач

Задание 1:
Вычислите производную функцию f(x) = x³/5.

Решение:
Согласно правилам дифференцирования константу в виде дроби можно вынести за знак производной:

Применив формулу производной, рассмотренную выше, получаем:

Задание 2:
Найдите производную функции f(x) = x² + √x – 6.

Решение:
Первоначальный вид производной функции:
f ‘(x) = (x² + √x – 6)‘.

С учетом правила дифференцирования суммы получаем:
f ‘(x) = (x²)‘ + (√x)‘ – (6)‘.

Остается только вычислить производные по отдельности:

(x²)‘ = 2x^2-1 = 2x

(-6)‘ = 0 (производная константы равна нулю)

Таким образом получаем: