Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Пример:
Решение:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Алгебра и начала математического анализа, 11 класс
Урок №10. Определение производной. Физический смысл производной.
Перечень вопросов, рассматриваемых в теме
1) Определение производной;
2) Физический смысл производной;
2) Приращение функции;
3) Скорость материальной точки в заданный момент времени по данному закону движения.
Глоссарий по теме
Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Изучая поведение функции y=f(x) около конкретной точки x0, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.
Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.
Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита «дельта»; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.
Итак, x1-x0=Δx, значит, x1=x0+Δx.
f(x1)-f(x0)=Δy, значит,
Δy=f(x0+Δx)-f(x0). (1)
Нельзя истолковывать термин «приращение» как «прирост».
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=1,9
Решение:
Δx= x1−x0=1,9-2=-0,1
Δf= f(1,9) –f(2)=1,92-22=-0,39
Ответ: Δx=-0,1; Δf =-0,39
Пример 2.
Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=2,1
Решение:
Δx= x1−x0=2,1-2=0,1
Δf= f(1,9) –f(2)=2,12-22=0,41
Ответ: Δx=0,1; Δf =0,41
Пример 3.
Найдем приращение Δf функции 
Решение:
по формуле (1) находим:

Ответ: 
С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t0; t0+∆t]. Если точка движется по прямой и известна ее координата x(t), то
Эта формула верна и для ∆t<0 (для промежутка [t0+∆t; t0]).
Аналогично выражение 
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Обозначение: y’ или f’(x)
Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.
Схема вычисления производной функции
- Найти приращение функции на отрезке [x; x+Δx]:
∆y=y(x+∆x)-y(x)
- Разделить приращение функции на приращение аргумента:
- Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Пример 4.
Вычислить производную функции y=x2
Решение: Используем схему вычисления производной по действиям:
- ∆y=y(x+∆x)-y(x)= (х+∆х)²-х²= х²+2х·∆х+ ∆х²-х²= 2х·∆х+ ∆х²
Ответ: y’=2x.
Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).
Таким образом, скорость – есть производная от пути по времени.
Пример 5.
Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.
Решение:
найдем ∆t= 1-0,8=0,2
S(0,8)= 1-2·0,8= -0,6=S(t)
S(1)= 1-2·1= -1=S(t+∆t)

Ответ: 
Необходимое и достаточное условие дифференцируемости
Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.
Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx.
На этой странице вы узнаете
- Почему функции похожи на американские горки?
- Как с помощью производной оценить рост популярности видео в соцсети?
- Какие фокусы творят тригонометрия и геометрия вместе?
Она спешит на помощь быстрее, чем Чип и Дейл. Она наш спасательный круг в океане математики. Давайте посмотрим, как производная способна на такие чудеса.
Производная
Функции достаточно часто встречаются при решении задач. Они могут быть как составными частями какого-то задания, так и отдельным номером. Разумеется, встречаются не только простые функции. Если открыть банк заданий, то мы удивимся, насколько сложными они бывают. Так что делать с такими сложными и непонятными функциями?
Производная — одно из самых важных понятий математического анализа. С ее помощью можно описать поведение любой функции.
Предположим, мы хотим прокатиться на американских горках. Представим их вид сбоку: это череда подъемов и резких спусков. Мы можем с легкостью описать их: на каких участках будет подъем, а на каких спуск, насколько крутыми они будут, сколько раз вагончик преодолеет границу между подъемом и спуском или спуском или подъемом. Мы даже можем предположить, на каких участках вагончик разгоняется сильнее. Точно так же можно описать и любую функцию.
Представим наши американские горки в виде функции.
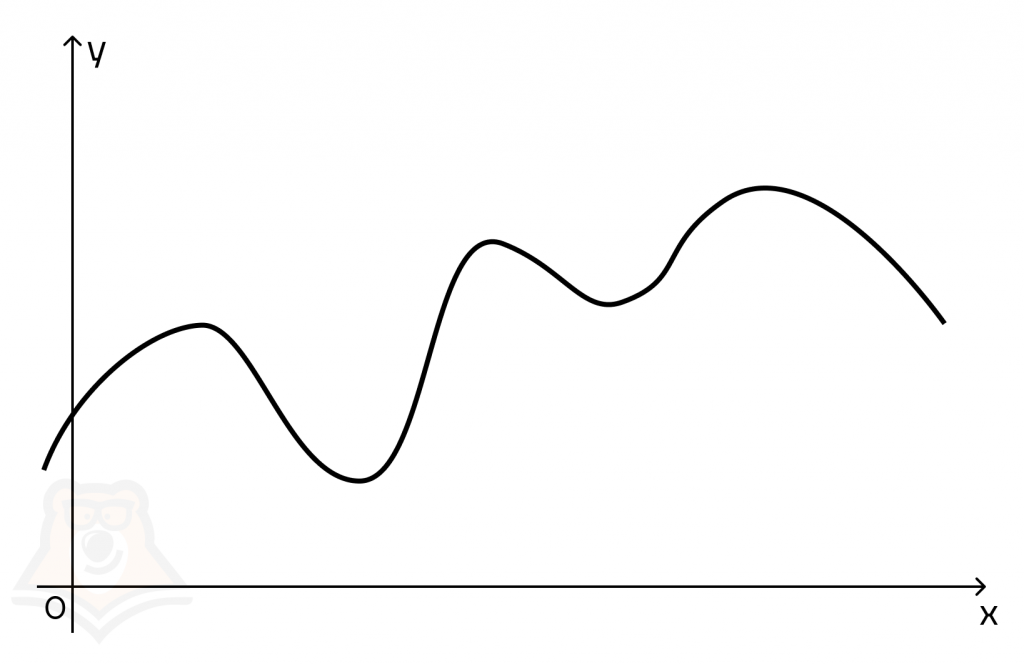
Функция будет на некоторых участках возрастать, а на некоторых убывать. Скорость ее изменения на разных участках будет разной.
Скорость изменения функции показывает, насколько сильно будет изменяться значение функции (то есть значение у) при небольшом изменении переменной функции (то есть значения х).
Отложим на нашем графике две точки: х и х1 и поднимем из них прямые, которые пересекут график в точках А и В. Тогда точка А будет иметь координаты (х;у), а точка В — (х1;у1).
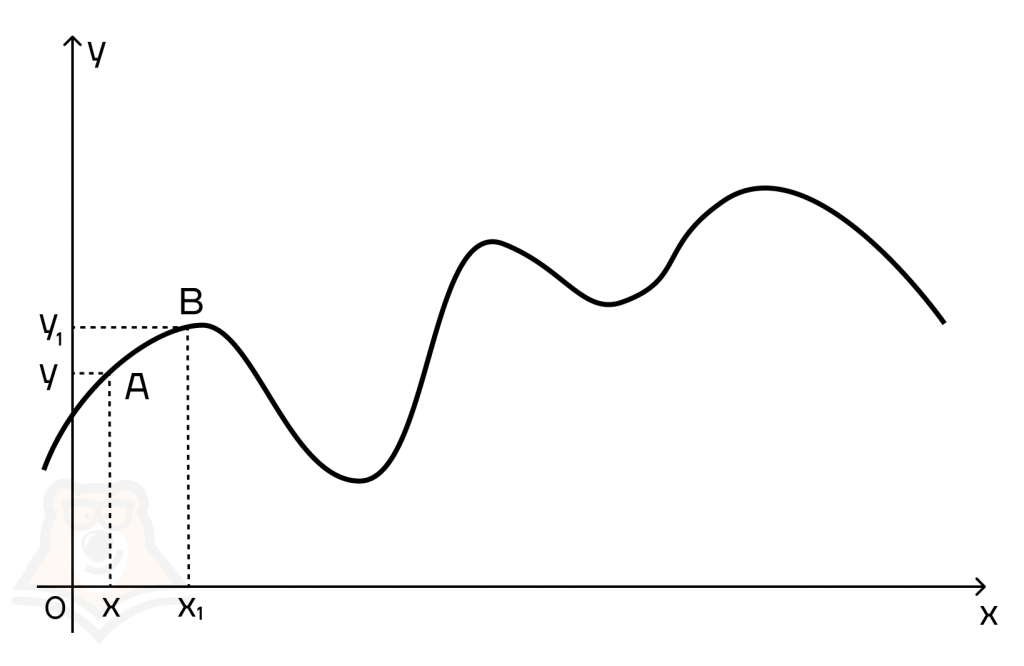
Представим, что наш вагончик проехал из точки А в точку В. Расстояние, которое он проехал по горизонтали, будет равно х1 — х, а поднялся он на высоту у1 — у. Для удобства дальнейших рассуждений примем эти расстояния за х и у.
Знак Δ “дельта” — означает изменение величины, то есть разность между тем, что было в точке А и стало в точке В.
Теперь мы можем ввести определение приращения.
Приращение функции — это разность между двумя значениями функции, то есть у.
Приращение аргумента — это разность между двумя значениями аргумента, то есть х.
Скорость изменения функции будет равна отношению приращения функции к приращению аргумента. При этом чем меньше будет приращение аргумента, тем точнее мы приблизимся к верному значению.
Отсюда мы получаем определение производной функции.
Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции.
Производную функции обозначают как f'(x).
(f'(x) = frac{Delta y}{Delta x}: при: Delta x rightarrow 0)
Если мы применим одинаковое приращение аргумента к разным участкам функции, то заметим, что приращение функции также будет разное. Где-то значение у изменится больше, где-то меньше. Именно так изменяется скорость функции на разных ее участках.
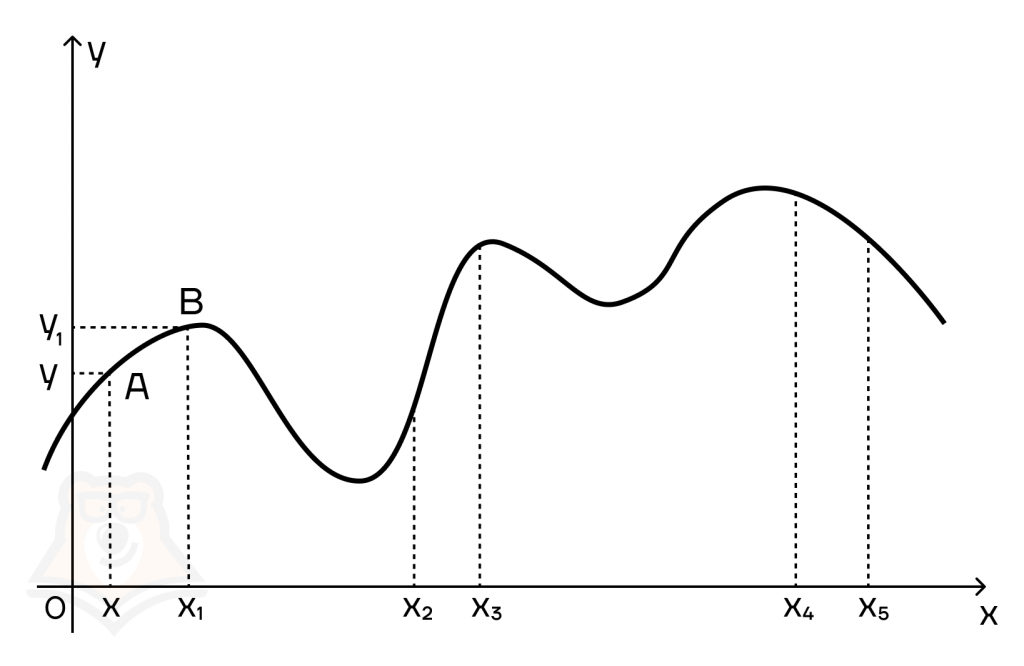
Нахождение производной называется дифференцированием.
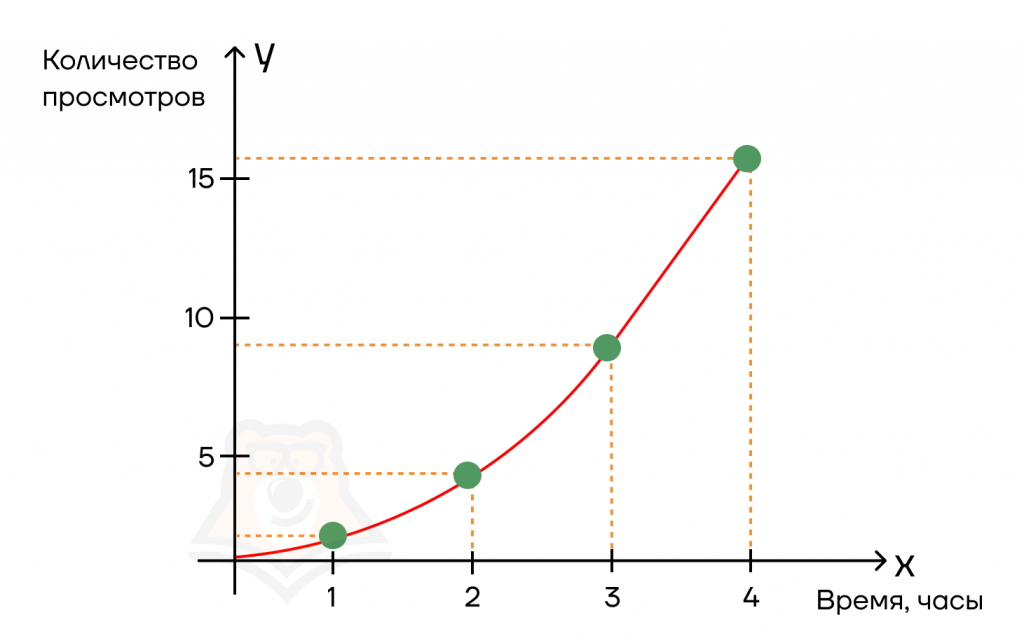
Допустим, мы выложили видео в соцсеть. Сначала было совсем невесело: за первый час всего один просмотр. За второй час ситуация сильно не изменилась — добавилось лишь 3 просмотра. Мы скинули ссылку на видео в чат друзей, и за третий час количество просмотров дошло до 9, а за четвертый час — до шестнадцати.
Возможно, ситуация не очень похожа на правду, и мы бы сразу попали в топ. Но пусть будет так для удобства цифр.
В результате мы имеем функцию, которая показывает, как количество просмотров менялось во времени.
Теперь зададимся вопросом: как быстро росла популярность у нашего ролика?
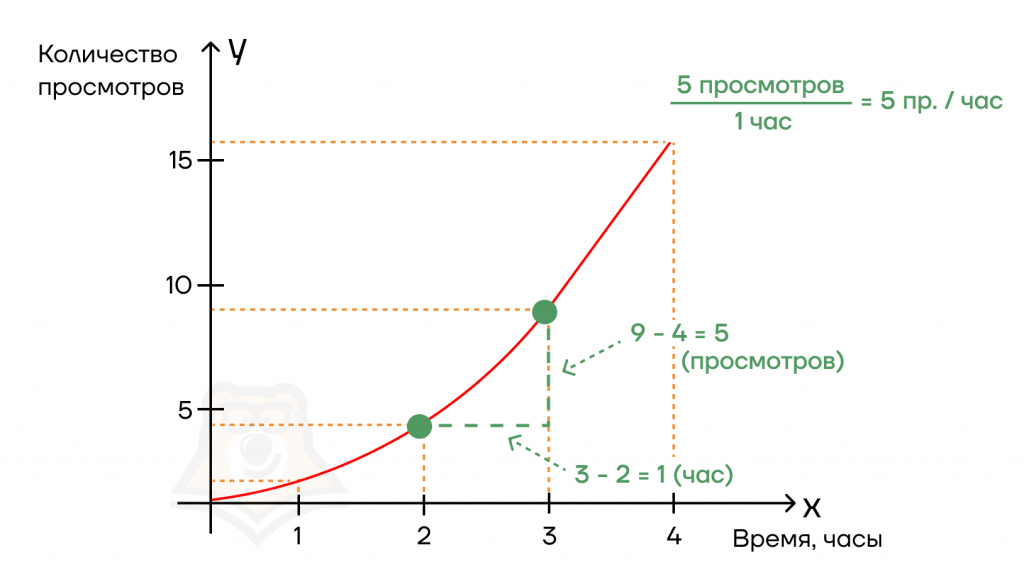
Чтобы это выяснить, мы возьмем две соседние точки на графике и посчитаем:
1) как изменилось количество просмотров между этими точкам (Δ количества просмотров);
2) как изменилось время между этими точками (Δ времени);
3) затем разделим Δ просмотров на Δ времени.
Получается, что “производительность” нашего видео была 5 просмотров в час.
Таким нехитрым образом, мы нашли производную от функции, показывающую рост популярности нашего ролика в сети за определенный промежуток времени:
(f'(x) = frac{Delta y}{Delta x} = frac{5}{1} = 5)(просмотров в час)
Геометрический смысл производной
Достроим прямоугольный треугольник АВС. Заметим, что отношение (frac{Delta x}{Delta y} = tg(BAC)), то есть равняется отношению противолежащего катета к прилежащему катету. Иначе это отношение можно записать как (tg(BAC) = frac{BC}{AC}).
Поскольку в этом примере мы взяли достаточно большое расстояние между значениями х, то АВ — секущая. Если мы будем сокращать расстояние между значениями аргумента, то две точки на графике будут ближе друг к другу, а секущая будет стремиться к касательной.

Следовательно, мы можем описать скорость изменения функции через тангенс угла наклона касательной, проведенной к графику функции в некоторой точке.
Из этих рассуждений мы можем вывести геометрический смысл производной:
Если провести касательную к функции в некоторой точке, то производная в этой точке будет равна тангенсу угла ее наклона.
Рассмотрим касательную отдельно. Это прямая, которая имеет уравнение y = kx+b, где к — коэффициент наклона.
Тогда мы получаем следующее уравнение:
f'(x) = k = tg(a)
Геометрический смысл производной — главный совместный номер. Производная равняется тангенсу угла наклона касательной, проведенной к функции в определенной точке.
Знак производной
Построим графики двух прямых с разным углом наклона. Пусть в первом случае k = 1, а во втором k = -1. Тогда получаем графики функций у = х и у = -х.
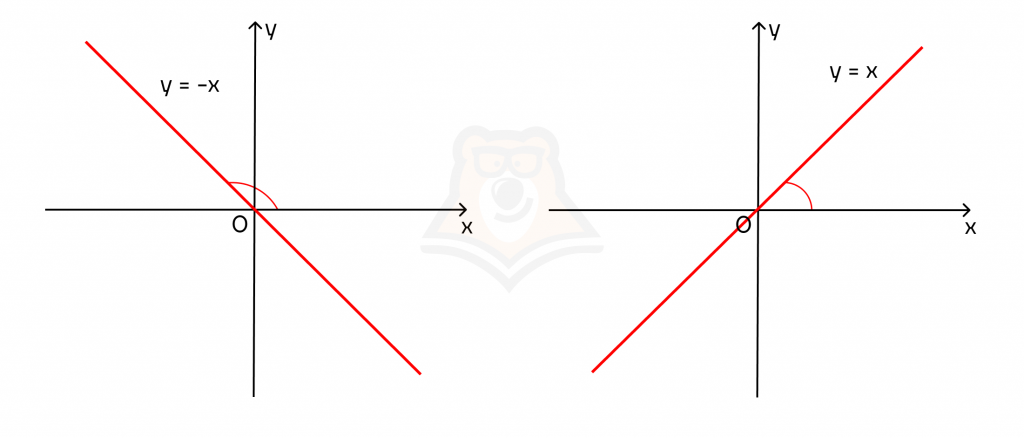
Заметим, что тангенс угла наклона имеет разные значения в этих случаях: tg(a) = -1 и tg(a) = 1.
Теперь достроим к касательным графики функций. В первом случае точка, к которой проведена касательная, будет лежать на участке функции, на котором она убывает. Во втором случае точка касания будет лежать на возрастающем участке функции.
Чтобы определить, убывает или возрастает функция, нужно посмотреть на ее наклон на участке.
Вспомним американские горки: пусть по функции будет слева направо ехать вагончик. В участках, где вагончик будет подниматься на гору, функция возрастает, а где вагончик съезжает с горки — функция убывает.
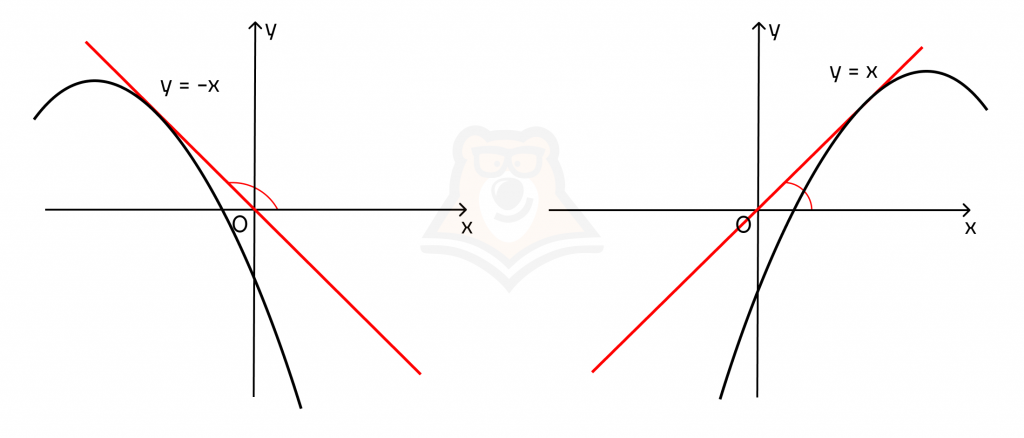
Из этих рассуждений мы можем вывести зависимость знака функции и знака производной.
1. Функция возрастает в точке тогда и только тогда, когда производная в данной точке положительна.
В этом случае касательная к функции также будет возрастать.
f'(x) = tg(a). Если tg(a) > 0, то и f'(x) > 0.
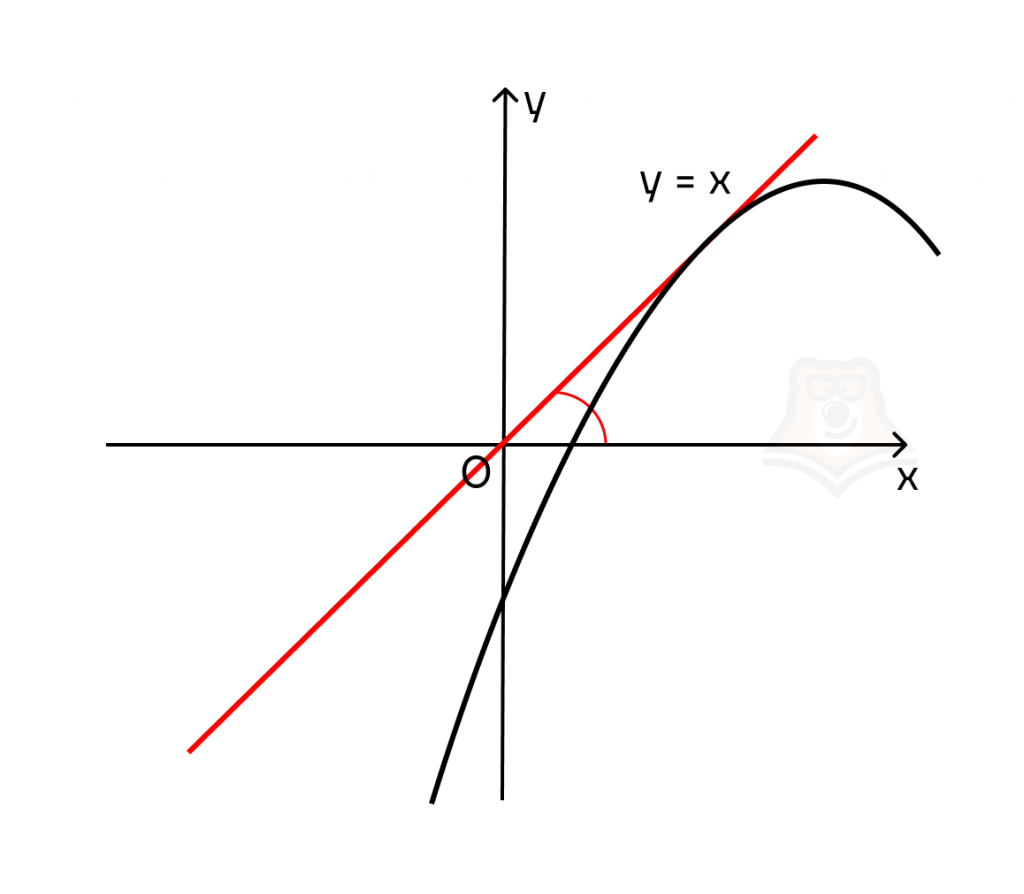
2. Функция убывает в точке тогда и только тогда, когда производная в данной точке отрицательна.
В этом случае касательная к функции будет убывать.
f'(x) = tg(a). Если tg(a) < 0, то и f'(x) < 0.

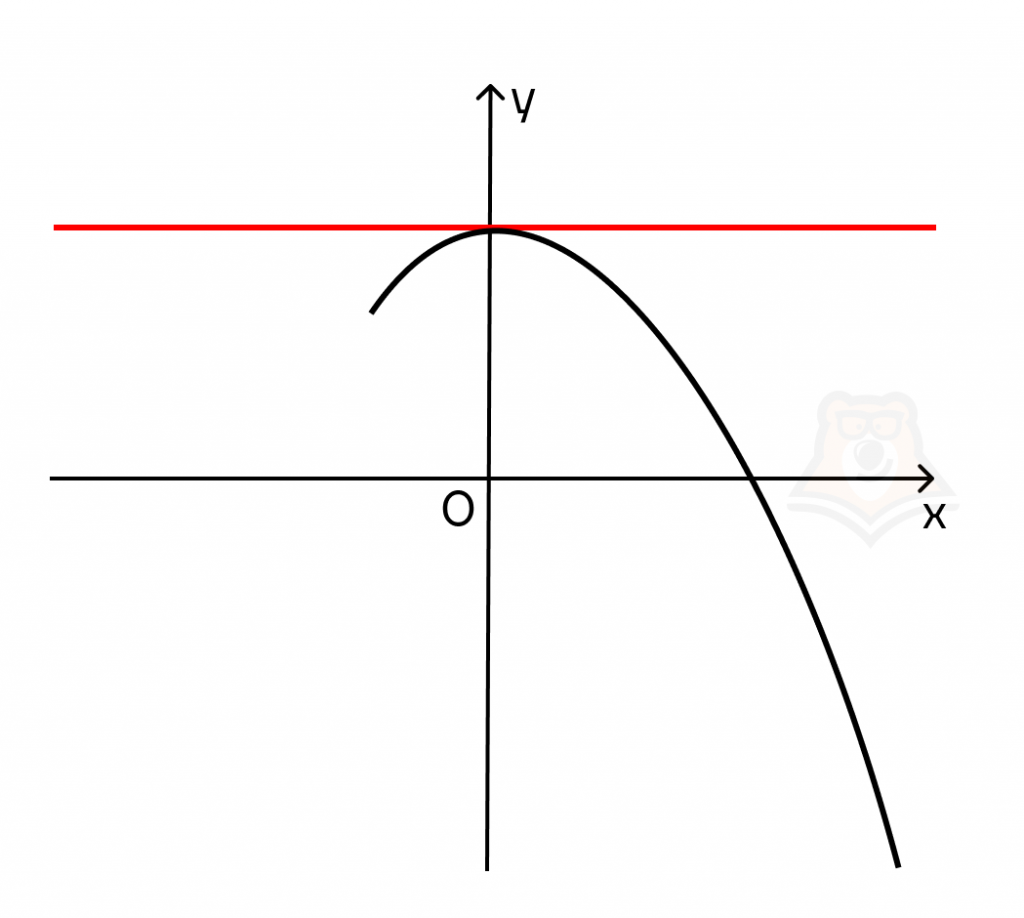
3. Если касательная к функции параллельна оси абсцисс, то производная в этой точке равна 0.
Поскольку прямая будет параллельна оси абсцисс, то у нее не будет угла наклона, а следовательно: k = tg(a) = 0 = f'(x).
Такие точки называются стационарными, это точки экстремума или седловые точки.
Подведем итог.
Знак производной определяется по изначальной функции:
- если функция возрастает, то производная положительна;
- если функция убывает, то производная отрицательна;
- в точках, где функция не возрастает и не убывает (стационарные точки), производная равна 0.
Точки экстремума
Как уже было сказано ранее, производная функции может равняться 0. Она принимает такое значение в точках экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.
Точки экстремума — точки, в которых достигается экстремум.
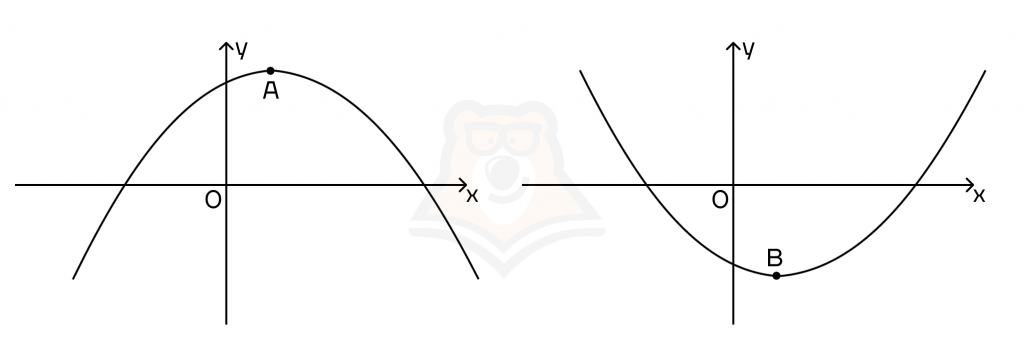
На рисунке видно, что точки А и В являются экстремумами. Например, до точки А функция будет возрастать, а после нее уже убывать, то есть наибольшее значение эта функция достигнет именно в точке экстремума.
Если вспомнить наш вагончик, то в точке А он достигнет наибольшую высоту над землей.
Во втором случае аналогичные рассуждения, но функция достигает уже наименьшее значение в точке В.
В теме производной есть такие термины, как “точка минимума” и “точка максимума”.
Точка минимума — это точка, в которой достигается минимальное значение функции.
В этой точке знак функции меняется с отрицательного на положительный (то есть сначала функция убывала, а потом начала возрастать). Это точка В.
Точка максимума — это точка, в которой достигается максимальное значение функции на отрезке.
В этой точке знак функции меняется с положительного на отрицательный (то есть сначала функция возрастала, а потом стала убывать). Это точка А.
Также с точками экстремума связаны наибольшее и наименьшее значение функции.
Важно!
Следует вспомнить, что когда мы говорим о значении функции, то имеем в виду значение ординаты, то есть у (или f(x)).
Наибольшее значение функции — точка на оси ординат, в которой достигается наибольшее значение функции на заданном отрезке.
Например, в точке А будет достигаться наибольшее значение функции.
Наименьшее значение функции — точка на оси ординат, в которой достигается наименьшее значение функции на заданном отрезке.
В точке В будет достигаться наименьшее значение функции.
Физический смысл производной
Предположим, что некоторая точка движется прямолинейно, и ее путь можно описать по закону х(t). То есть за определенное время t точка пройдет расстояние х.
А теперь вспомним формулу скорости: (v = frac{x}{t}).
Чтобы найти среднюю скорость на каком-то участке пути точки, нужно разделить весь путь на все время, или (v_{ср.} = frac{Delta x}{Delta t}). Таким образом, мы пришли к определению производной.
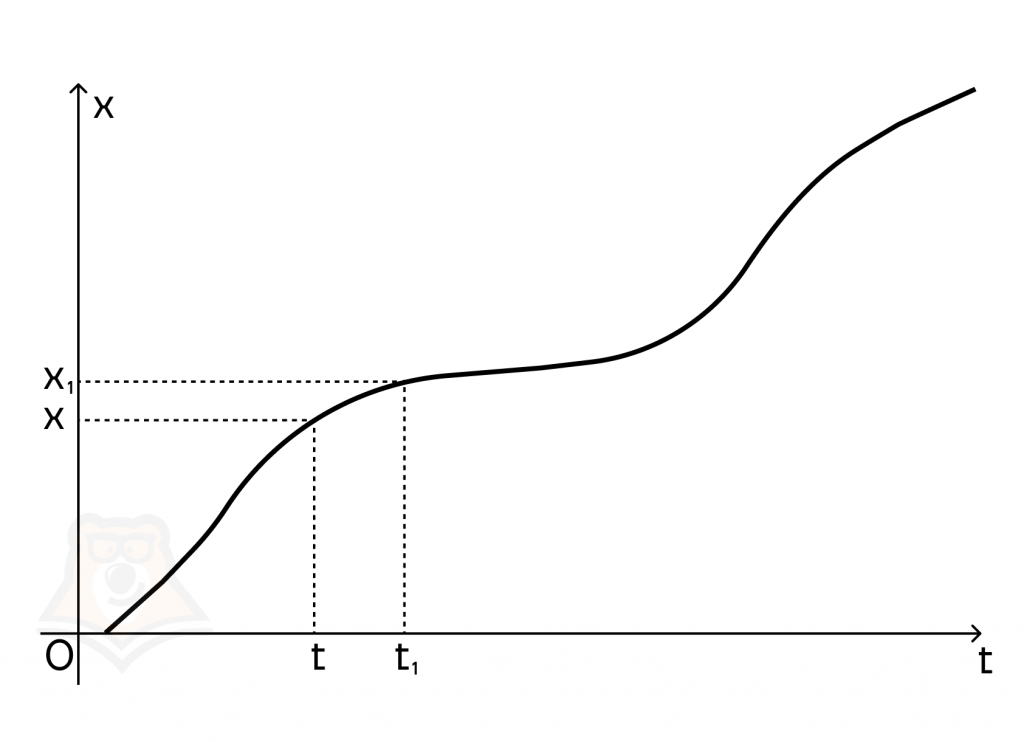
Физический (механический) смысл производной состоит в том, что производная от функции равняется скорости движения некоторого тела по траектории x(t) в момент времени t. x'(t) = v
Также вспомним, что скорость тела зависит от его ускорения. Тогда, применяя аналогичные рассуждения, получаем:
v'(t) = a
Производную можно брать несколько раз. Например, если мы дважды возьмем производную от x(t), то получим ускорение точки:
(x^{primeprime} (t) = v'(t) = a).
Как найти скорость и ускорение точки с помощью производной?
Для этого необходимо воспользоваться физическим смыслом производной: производная от функции равна скорости движения некоторого тела. Производная от скорости равна ускорению тела.
Фактчек
- Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции. Скорость изменения функции равняется отношению приращения функции к приращению аргумента. Нахождение производной называется дифференцированием.
- Если провести касательную к функции в некоторой функции, то производная в этой точке будет равна тангенсу угла ее наклона. Это геометрический смысл производной.
- Производная будет положительна на участках возрастания функции и отрицательна на участках убывания. В стационарных точках (точки экстремума и седловые точки) производная будет равна 0.
- Точка минимума — точка, в которой достигается минимальное значение на заданном отрезке, точка максимума — точка, в которой достигается максимальное значение.
- Физический (механический) смысл производной состоит в том, что производная от функции равняется скорости движения некоторого тела по траектории x(t) в момент времени t.
Термины
Абсцисса — координата определенной точки на оси Х.
Ордината — координата определенной точки на оси У.
Проверь себя
Задание 1.
Что такое приращение функции?
- Разность между значениями у;
- Разность между значениями х;
- Сумма значений у;
- Сумма значений х.
Задание 2.
Чему равна производная?
- Котангенсу угла наклона касательной;
- Тангенсу угла наклона касательной;
- Синусу угла наклона касательной;
- Косинусу угла наклона касательной.
Задание 3.
Как меняется знак производной в точке максимума?
- Знак производной не меняется;
- Производная всегда равна 0 и не имеет знака;
- Знак меняется с положительного на отрицательный;
- Знак меняется с отрицательного на положительный.
Задание 4.
В каком случае функция будет возрастать?
- Если производная положительна;
- Если производная отрицательна;
- Если производная равна 0;
- Ни один из вышеперечисленных случаев.
Задание 5.
Какая величина получится, если дважды взять производную у функции?
- Скорость;
- Ускорение;
- Путь;
- Время
Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 1
Заказать задачи по любым предметам можно здесь от 10 минут
Физический смысл производной
| Определение |
|
Физический смысл производной заключается в том, что мгновенная скорость материальной точки в определенный момент времени $ t_0 $ равна производной закона движения $ s(t_0) $ этой точки в момент времени $ t_0 $: $$ v(t_0) = s'(t_0) $$ |
Примеры решения
| Пример 1 |
| Найти мгновенную скорость движения материальной точки в момент времени $ t_0 = 2 c $, если точка движется по закону $ s(t) = 4t^2+2t+1 $ |
| Решение |
|
Скорость точки равна производной пути по времени: $$ v(t) = s'(t) = (4t^2+2t+1)’ = 8t + 2 $$ Мгновенная скорость в момент времени $ t_0 = 2 $: $$ v(t_0) = v(2) = 8 cdot 2 + 2 = 16 + 2 = 18 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ v = 18 text{м/с} $$ |
| Пример 2 |
| Пусть точка движется прямолинейно по закону $ s(t) = 3t^2-3t — 5 $. В какой момент времени скорость точки будет $ v = 3 $ м/с? |
| Решение |
|
Используя физический смысл производной, находим закон изменения скорости материальной точки: $$ v(t) = s'(t) = (3t^2-3t-5)’ = 6t — 3 $$ Чтобы найти момент времени $ t_0 $, в который скорость будет равной трём, нужно составить и решить уравнение $ v(t_0) = 3 $: $$ 6t_0 — 3 = 3 $$ $$ 6t_0 = 6 $$ $$ t_0 = 1 $$ |
| Ответ |
| $$ t_0 = 1 c $$ |
15 мая 2014
Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.
На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.
Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.
Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:
[v={S}’={x}’left( t right)]
Точно так же мы можем посчитать и ускорение:
[a={v}’={{S}’}’={{x}’}’left( t right)]
Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.
Давайте посмотрим, как это работает при решении реальных задач.
Пример № 1
Материальная точка движется по закону:
[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.
Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.
[v={S}’={x}’left( 2 right)]
Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.
Давайте решать. В первую очередь, посчитаем производную:
[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
Нам требуется найти производную в точке 2. Давайте подставим:
[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]
[=-16+32-12+5=9]
Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.
Пример № 2
Материальная точка движется по закону:
[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?
Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.
В первую очередь, вновь ищем производную:
[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]
[{x}’left( t right)={{t}^{2}}-8t+19]
От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:
[{{t}^{2}}-8t+19=3]
[{{t}^{2}}-8t+16=0]
[{{left( t-4 right)}^{2}}=0]
[t-4=0]
[t=4]
Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.
Ключевые моменты
В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.
Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.
Смотрите также:
- Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
- ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
- Схема Бернулли. Примеры решения задач
- Комбинаторика в задаче B6: средний тест
- Как решать задачи про летающие камни?
- B4: счетчики на электричество