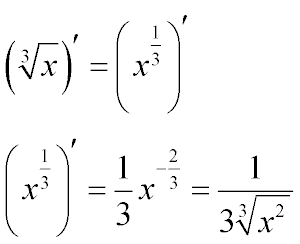Как найти производную функции кубический корень

Производная корня

Опубликовано 10.07.2021

Производная корня из x – это формула определения производной функции, выраженной корнем из x или производной корня из выражения относительно x. Все производные смотрите в таблице производных.

Формула производной квадратного корня

Давайте выведем с вами формулу для производной корня для простой функции, опираясь на формулу производной степени $(x^n)'=n cdot x^{n-1}$ :

$displaystyle (sqrt{x})'=(x^{frac{1}{2}})'= frac{1}{2}x^{frac{1}{2}-1}=frac{1}{2}=x^{-frac{1}{2}}=frac{1}{2 sqrt{x}}$ ,

То есть, получается, что формула производной корня: $displaystyle (sqrt{x})'=frac{1}{2 sqrt{x}}$ , где

Производная корня любой степени

Аналогично определим производную корня любой степени. Например, пусть нам нужно определить производную кубического корня иначе находим производную корня третьей степени из x.

Формула производной корня

Производная кубического корня

Определим производную корня кубического: $sqrt[3]{x^2}$ . Запишем этот корень как степень от . Получим $x^{frac{2}{3}}$ .

Находим производную:

$displaystyle (sqrt[3]{x^2})'=(x^{frac{2}{3}})'=frac{2}{3} cdot x^{frac{2}{3}-1}=frac{2}{3} cdot x^{-frac{1}{3}}$ или

$displaystyle (sqrt[3]{x^2})'=frac{2}{3 sqrt[3]{x}}$

Примеры нахождения производной корня

Пример 1

Найдите производную функции: при

Решение: находим производную функции: $displaystyle y'=frac{1}{2sqrt{x}}$ , теперь подставим данное значение . Получим $displaystyle y'(4)=frac{1}{2sqrt{4}}=frac{1}{4}$

Пример 2

Найдите производную функции . То есть нам нужно узнать, какова будет производная корня четвертой степени из x.

Решение: представим корень в виде степени. Получим $displaystyle sqrt[4]{x}=x^{frac{1}{4}}$ . Теперь легко можно найти производную, зная формулу производной степени.

$displaystyle f'(x)=(x^{frac{1}{4}})'=frac{1}{4} x^{frac{1}{4}-1}=frac{1}{4}x^{frac{-3}{4}}=frac{1}{4x^{frac{3}{4}}}=frac{1}{4 sqrt[4]{x^3}}$

Таким образом, теперь легко определять производную корня любой степени, просто представляя сам корень в виде степени и зная формулу производной степени.

( 5 оценок, среднее 4.2 из 5 )

Источник

См. также:

таблица производных простых функций

таблица производных логарифмических функций

таблица производных тригонометрических функций

Производная корня. Формулы для нахождения производной корня

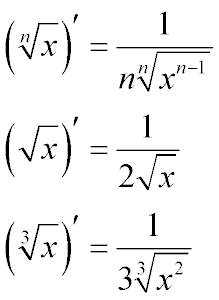
Общий случай формулы производной корня произвольной степени — дробь, в числителе которой единица, а в знаменателе число, равное степени корня, для которого вычислялась производная, умноженная на корень такой же степени, подкоренное выражение которого — переменная в степени корня, для которого вычислялась производная, уменьшенной на единицу
Производная квадратного корня — является частным случаем предыдущей формулы. Производная квадратного корня из x — это дробь, числитель которого равен единице, а знаменатель — двойка, умноженная на квадратный корень х
Производная кубического корня, также частный случай общей формулы. Производная кубического корня — это единица, деленная на три кубических корня из икс квадрат.

Ниже приведены преобразования, поясняющие, почему формулы нахождения производной квадратного и кубического корня именно такие, как приведены на рисунке.

Разумеется, данные формулы можно вообще не запоминать, если принять во внимание, что извлечение корня производной степени — это то же самое, что возведение в степень дроби, знаменатель которой равен той же степени. Тогда нахождение производной корня сводится к применению формулы нахождения производной степени соответствующей дроби.

Производная переменной под квадратным корнем

( √x )’ = 1 / ( 2√x ) или 1/2 х^-1/2

Пояснение:

( √x )’ = ( х^1/2 )’

Квадратный корень — это точно то же самое действие, что и возведение в степень 1/2, значит для нахождения производной корня можно применить формулу из правила нахождения производной от переменной в произвольной степени:

( х^1/2 )’ = 1/2 х^-1/2 = 1 / (2√х)

Производная кубического корня (производная корня третьей степени)

Производная кубического корня находится точно по такому же принципу, что и квадратного.

Представим себе кубический корень как степень 1/3 и найдем производную по общим правилам дифференцирования. Краткую формулу можно посмотреть на картинке выше, а ниже расписано пояснение, почему именно так.

Степень -2/3 получается в следствие вычитания единицы из 1/3

Производная переменной под корнем произвольной степени

Данная формула пригодна для нахождения производной корня любой степени:

( ⁿ√x )’ = 1 / ( n ⁿ√x^n-1 )

В более удобном для глаза виде она представлена на картинке выше.

Здесь:

n — степень корня, для которой находится производная

x — переменная, для которой находится производная

2080.1947

Производная дроби |

Описание курса

| Нахождение экстремума функции

Источник

Производная кубического корня равна 1 в трехкратном увеличении основания, возведенного в степень 2/3. Это на случай, если база неизвестна.

Чтобы продемонстрировать вышесказанное, мы должны помнить, что кубический корень эквивалентен экспоненциальной функции, показатель степени которой равен 1/3. Итак, мы помним, что производная степени равна показателю степени, умноженному на основание, возведенное в степень минус 1.

С математической точки зрения это можно объяснить следующим образом:

Мы могли бы даже обобщить вышеизложенное для всех корней:

Возвращаясь к корню куба, если он повлияет на функцию, производная будет вычислена, следуя цепному правилу, следующим образом: f ‘(x) = ny^п-1Y ‘. То есть мы должны добавить к предыдущему вычислению производную функции, на которую влияет кубический корень.

Примеры производных кубического корня

Давайте посмотрим на несколько примеров того, как вычислить производную кубического корня:

Теперь давайте посмотрим на пример, который немного сложнее:

Вы поможете развитию сайта, поделившись страницей с друзьями

Источник

Как найти производную корня

В задачах по математическому анализу иногда требуется найти производную корня. В зависимости от условий задачи, производная от функции «корень квадратный» (кубический) находится непосредственно или путем преобразования «корня» в степенную функцию с дробным показателем.

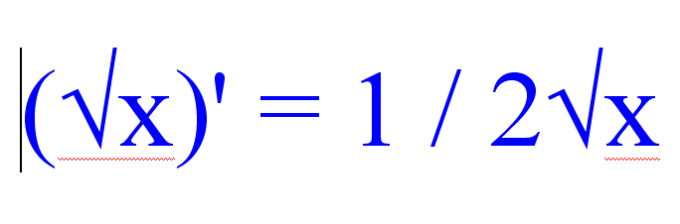
Вам понадобится

— карандаш;
— бумага.

Инструкция

Перед тем как находить производную корня, обратите внимание на остальные функции, присутствующие в решаемом примере. Если в задаче имеется много подкоренных выражений, то воспользуйтесь следующим правилом нахождения производной квадратного корня:

(√х)’ = 1 / 2√х.

А для нахождения производной кубического корня примените формулу:

(³√х)’ = 1 / 3(³√х)²,

где через ³√х обозначен кубический корень из х.

Если в примере, предназначенном для дифференцирования, встречается переменная в дробных степенях, то переведите обозначение корня в степенную функцию с соответствующим показателем. Для квадратного корня это будет степень ½, а для кубического корня – ⅓:

√х = х ^ ½,
³√х = x ^ ⅓,

где символ ^ обозначает возведение в степень.

Для нахождения производной степенной функции вообще и х^½, x^⅓, в частности, воспользуйтесь следующим правилом:

(х ^ n)’ = n * x^(n-1).

Для производной корня из этого соотношения вытекает:

(х^½)’ = ½ x ^ (-½) и
(x^⅓)’ = ⅓ x ^ (-⅔).

Продифференцировав все корни, внимательно посмотрите на остальные части примера. Если в ответе у вас получилось очень громоздкое выражение, то наверняка его можно упростить. Большинство школьных примеров составлено таким образом, чтобы в итоге получилось небольшое число или компактное выражение.

Во многих задачах на нахождение производной, корни (квадратные и кубические) встречаются вместе с другими функциями. Чтобы найти производную корня в этом случае, применяйте следующие правила:
• производная константы (постоянного числа, C) равняется нулю: C’ = 0;
• постоянный множитель выносится за знак производной: (k*f)’ = k * (f)’ (f – произвольная функция) ;
• производная суммы нескольких функций равняется сумме производных: (f + g)’ = (f)’ + (g)’;
• производная произведения двух функций равняется… нет, не произведению производных, а следующему выражению: (fg)’ = (f)’g + f (g)’;
• производная частного также равняется не частному производных, а находится согласно следующего правила: (f/g)’ = ((f)’g – f(g)’) / g².

Обратите внимание

На этой странице вы сможете вычислять производную функции онлайн с получением подробного решения задачи. Решение производных функции производится с использованием тех правил дифференцирования, которые студенты изучают в курсе математического анализа в институте. Для того, чтобы найти производную функции нужно в поле «Функция» ввести функцию для дифференцирования согласно правил ввода данных.

Полезный совет

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю: Математический смысл этого определения понять не очень просто, поскольку в школьном курсе алгебры понятие предела функции либо не изучают совсем, либо изучают очень поверхностно. Но для того, чтобы научиться находить производные различных функций, это и не обязательно.

Источники:

производная корень из икс

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

a	f(x)	f'(x)	Название исходной функции
−2	x⁻² = 1/x²	−2x⁻³ = −2/x³	обратный квадрат
−1	x⁻¹ = 1/x	−x⁻² = −1/x²	обратная пропорциональность
0	x⁰ = 1	0	константа
1/3	x^1/3 = ³√x	(1/3)x^−2/3 = 1/(3·³√(x²))	кубический корень
1/2	x^1/2 = √x	(1/2)x^−1/2 = 1/(2√x)	квадратный корень
1	x¹ = x	1	прямая пропорциональность
2	x²	2x	квадрат
3	x³	3x²	куб
4	x⁴	4x²	четвертая степень

Производная корня

Формула производной квадратного корня