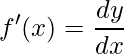Как найти производную функции матлаб

diff

Differentiate symbolic expression or function

Syntax

Description

example

Df = diff(f)
differentiates f with respect to the symbolic scalar
variable determined by symvar(f,1).

example

Df = diff(f,n)
computes the nth derivative of f with
respect to the symbolic scalar variable determined by
symvar.

example

Df = diff(f,var)
differentiates f with respect to the differentiation
parameter var. var can be a symbolic
scalar variable, such as x, a symbolic function, such as
f(x), or a derivative function, such as
diff(f(t),t).

example

Df = diff(f,var,n)
computes the nth derivative of f with
respect to var.

example

Df = diff(f,var1,...,varN)
differentiates f with respect to the parameters
var1,...,varN.

example

Df = diff(f,mvar)
differentiates f with respect to the symbolic matrix
variable mvar of type symmatrix.

Examples

collapse all

Differentiate Function

Find the derivative of the function sin(x^2).

syms f(x)
f(x) = sin(x^2);
Df = diff(f,x)

Find the value of the derivative at x = 2. Convert the value to double.

Differentiate with Respect to Particular Variable

Find the first derivative of this expression.

syms x t
Df = diff(sin(x*t^2))

Because you did not specify the differentiation variable, diff uses the default variable defined by symvar. For this expression, the default variable is x.

var = symvar(sin(x*t^2),1)

Now, find the derivative of this expression with respect to the variable t.

Higher-Order Derivatives of Univariate Expression

Find the 4th, 5th, and 6th derivatives of t6.

Higher-Order Derivatives of Multivariate Expression with Respect to Particular Variable

Find the second derivative of this expression with respect to the variable y.

syms x y
Df = diff(x*cos(x*y), y, 2)

Higher-Order Derivatives of Multivariate Expression with Respect to Default Variable

Compute the second derivative of the expression x*y. If you do not specify the differentiation variable, diff uses the variable determined by symvar. For this expression, symvar(x*y,1) returns x. Therefore, diff computes the second derivative of x*y with respect to x.

syms x y
Df = diff(x*y,2)

If you use nested diff calls and do not specify the differentiation variable, diff determines the differentiation variable for each call. For example, differentiate the expression x*y by calling the diff function twice.

In the first call, diff differentiates x*y with respect to x, and returns y. In the second call, diff differentiates y with respect to y, and returns 1.

Thus, diff(x*y,2) is equivalent to diff(x*y,x,x), and diff(diff(x*y)) is equivalent to diff(x*y,x,y).

Mixed Derivatives

Differentiate this expression with respect to the variables x and y.

syms x y
Df = diff(x*sin(x*y),x,y)
Df = 2 x cos(x y)-x2 y sin(x y)

You also can compute mixed higher-order derivatives by providing all differentiation variables.

syms x y
Df = diff(x*sin(x*y),x,x,x,y)
Df = x2 y3 sin(x y)-6 x y2 cos(x y)-6 y sin(x y)

Differentiate with Respect to Function and Derivative

Find the derivative of the function y=f(x)2dfdx with respect to f(x).

syms f(x) y
y = f(x)^2*diff(f(x),x);
Dy = diff(y,f(x))

Find the 2nd derivative of the function y=f(x)2dfdx with respect to f(x).

Find the mixed derivative of the function y=f(x)2dfdx with respect to f(x) and dfdx.

Dy3 = diff(y,f(x),diff(f(x)))

Euler–Lagrange Equation

Find the Euler–Lagrange equation that describes the motion of a mass-spring system. Define the kinetic and potential energy of the system.

syms x(t) m k
T = m/2*diff(x(t),t)^2;
V = k/2*x(t)^2;

Define the Lagrangian.

L = 

m ∂∂t x(t)22-k x(t)22

The Euler–Lagrange equation is given by

0=ddt∂L(t,x,x˙)∂x˙-∂L(t,x,x˙)∂x

Evaluate the term ∂L/∂x˙.

D1 = diff(L,diff(x(t),t))

Evaluate the second term ∂L/∂x.

Find the Euler–Lagrange equation of motion of the mass-spring system.

ans(t) = 

m ∂2∂t2 x(t)+k x(t)=0

Differentiate with Respect to Vectors

To evaluate derivatives with respect to vectors, you can use symbolic matrix variables. For example, find the derivatives ∂α/∂x and ∂α/∂y for the expression α=yTAx, where y is a 3-by-1 vector, A is a 3-by-4 matrix, and x is a 4-by-1 vector.

Create three symbolic matrix variables x, y, and A, of the appropriate sizes, and use them to define alpha.

syms x [4 1] matrix
syms y [3 1] matrix
syms A [3 4] matrix
alpha = y.'*A*x

Find the derivative of alpha with respect to the vectors x and y.

Differentiate with Respect to Matrix

To evaluate a derivative with respect to a matrix, you can use symbolic matrix variables. For example, find the derivative ∂Y/∂A for the expression Y=XTAX, where X is a 3-by-1 vector, and A is a 3-by-3 matrix. Here, Y is a scalar that is a function of the vector X and the matrix A.

Create two symbolic matrix variables to represent X and A. Define Y.

syms X [3 1] matrix
syms A [3 3] matrix
Y = X.'*A*X

Find the derivative of Y with respect to the matrix A.

The result is a Kronecker tensor product between XT and X, which is a 3-by-3 matrix.

Differentiate Symbolic Matrix Function

Differentiate a symbolic matrix function with respect to its matrix argument.

Find the derivative of the function t(X)=A⋅sin(B⋅X), where A is a 1-by-3 matrix, B is a 3-by-2 matrix, and X is a 2-by-1 matrix. Create A, B, and X as symbolic matrix variables and t(X) as a symbolic matrix function.

syms A [1 3] matrix
syms B [3 2] matrix
syms X [2 1] matrix
syms t(X) [1 1] matrix keepargs
t(X) = A*sin(B*X)

Differentiate the function with respect to X using diff.

Input Arguments

collapse all

f — Expression or function to differentiate
symbolic expression | symbolic function | symbolic vector | symbolic matrix | symbolic matrix variable | symbolic matrix function

Expression or function to differentiate, specified as one of these values:

  • a symbolic expression

  • a symbolic function

  • a symbolic vector or a symbolic matrix (a vector or a matrix
    of symbolic expressions or functions)

  • a symbolic matrix variable

  • a symbolic matrix function

If f is a symbolic vector or matrix,
diff differentiates each element of
f and returns a vector or a matrix of the same size
as f.

Data Types: single | double | sym | symfun | symmatrix | symfunmatrix

n — Order of derivative
nonnegative integer

Order of derivative, specified as a nonnegative integer.

var — Differentiation parameter
symbolic scalar variable | symbolic function | derivative function

Differentiation parameter, specified as a symbolic scalar variable,
symbolic function, or a derivative function created using the
diff function.

If you specify differentiation with respect to the symbolic function
var = f(x) or the derivative function var =
diff(f(x),x), then the first argument f
must not contain any of these:

  • Integral transforms, such as fourier,
    ifourier, laplace,
    ilaplace, htrans,
    ihtrans, ztrans, and
    iztrans

  • Unevaluated symbolic expressions that include
    limit or int

  • Symbolic functions evaluated at a specific point, such as
    f(3) or g(0)

Data Types: single | double | sym | symfun

var1,...,varN — Differentiation parameters
symbolic scalar variables | symbolic functions | derivative functions

Differentiation parameters, specified as symbolic scalar variables,
symbolic functions, or derivative functions created using the
diff function.

Data Types: single | double | sym | symfun

mvar — Differentiation parameter
symbolic matrix variable

Differentiation parameter, specified as a symbolic matrix variable.

When using a symbolic matrix variable as the differentiation parameter,
f must be a differentiable scalar function, where
mvar can represent a scalar, vector, or matrix. The
derivative of f cannot be a tensor or a matrix in terms
of tensors. For example, see Differentiate with Respect to Vectors and
Differentiate with Respect to Matrix.

Data Types: symmatrix

Limitations

  • The diff function does not support tensor derivatives when
    using a symbolic matrix variable as the differentiation parameter. If the
    derivative is a tensor, or the derivative is a matrix in terms of tensors, then
    the diff function will error.

Tips

  • When computing mixed higher-order derivatives with more than one variable, do
    not use n to specify the order of derivative. Instead,
    specify all differentiation variables explicitly.

  • To improve performance, diff assumes
    that all mixed derivatives commute. For example,

    This assumption suffices for most engineering and
    scientific problems.

  • If you differentiate a multivariate expression or function
    f without specifying the differentiation variable, then a
    nested call to diff and diff(f,n) can
    return different results. The reason is that in a nested call, each
    differentiation step determines and uses its own differentiation variable. In
    calls like diff(f,n), the differentiation variable is
    determined once by symvar(f,1) and used for all
    differentiation steps.

  • If you differentiate an expression or function containing
    abs or sign, the arguments must be
    real values. For complex arguments of abs and
    sign, the diff function formally
    computes the derivative, but this result is not generally valid because
    abs and sign are not
    differentiable over complex numbers.

Version History

Introduced before R2006a

Источник

Improve Article

Save Article

Like Article

  • Read
  • Discuss

    • Improve Article

    Save Article

    Like Article

    Differentiation of a function y = f(x) tells us how the value of y changes with respect to change in x. It can also be termed as the slope of a function.

    Derivative of a function f(x) wrt to x is represented as  {displaystyle f'(x)= frac {dy}{dx}}

    MATLAB allows users to calculate the derivative of a function using diff() method. Different syntax of diff() method are:

    • f’ = diff(f)
    • f’ = diff(f, a)
    • f’ = diff(f, b, 2)

    f’ = diff(f)

    It returns the derivative of function f(x) wrt variable x.

    Example 1:

    Matlab

    syms x

    f = cos(x);

    disp("f(x) :");

    disp(f);

    d = diff(f);

    disp("Derivative of f(x) :");

    disp(d);

    Output :

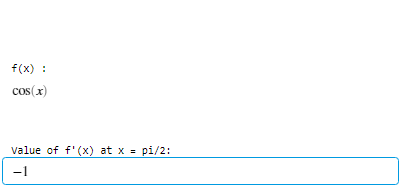
    Example 2: Evaluating the derivative of a function at a specified value using subs(y,x,k).

    • subs(y,x,k), it gives the value of function y at x = k.

    Matlab

    # variable x

    syms x

    f = cos(x);

    disp("f(x) :");

    disp(f);

    d = diff(f);

    val = subs(d,x,pi/2);

    disp("Value of f'(x) at x = pi/2:");

    disp(val);

    Output :

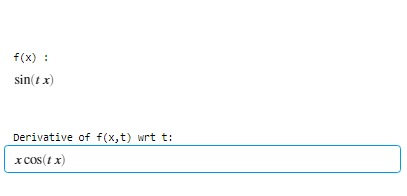
    f’ = diff(f, a)

    • It returns the derivative of function f with respect to variable a.

    Matlab

    syms x t;

    f = sin(x*t);

    disp("f(x) :");

    disp(f);

    d = diff(f,t);

    disp("Derivative of f(x,t) wrt t:");

    disp(d);

    Output :

    f’ = diff(f, b, 2)

    It returns the double derivative of function f with respect to variable b.

    Example 1:

    Matlab

    syms x n;

    f = x^n;

    disp("f(x,n) :");

    disp(f);

    d = diff(f,x,2);

    disp("Double Derivative of f(x,n) wrt x:");

    disp(d);

    Output :

    In the same way, you can also calculate the k-order derivative of function f using diff(f,x,k).

    Example 2: 

    Calculating the partial derivative 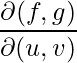 {displaystyle {frac {partial (f,g)}{partial (u,v)}}} } using Jacobian matrix and determinant.

    Matlab

    syms u v;

    f = u^2;

    g = sin(v)*(3*u);

    disp("f(u,v) :");

    disp(f);

    disp("g(u,v) :");

    disp(g);

    J = jacobian([f; g], [u v]);

    disp("Jacobian matrix :");

    disp(J);

    d = det(J);

    disp("Determinant of Jacobian matrix:");

    disp(d);

    Output :

    Last Updated :
    23 Aug, 2021

    Like Article

    Save Article

    Источник

    Дифференцируйте символьное выражение или функцию

    Синтаксис

    Описание

    пример

    Df = diff(f) дифференцирует f относительно символьной переменной, определенной symvar(f,1).

    пример

    Df = diff(f,n) вычисляет nпроизводная th f относительно символьной переменной, определенной symvar.

    пример

    Df = diff(f,var) дифференцирует f относительно параметра дифференцирования varvar может быть символьная скалярная переменная, такая как x, символьная функция, такая как f(x), или производная функция, такая как diff(f(t),t).

    пример

    Df = diff(f,var,n) вычисляет nпроизводная th f относительно var.

    пример

    Df = diff(f,var1,...,varN) дифференцирует f относительно параметров var1,...,varN.

    пример

    Df = diff(f,mvar) дифференцирует f относительно переменной mvar символьной матрицы из типа symmatrix. (начиная с R2021a)

    Примеры

    свернуть все

    Дифференцируйте функцию

    Найдите производную функции sin(x^2).

    syms f(x)
f(x) = sin(x^2);
Df = diff(f,x)

    Найдите значение производной в x = 2Конвертируйте полученное значение в числовое двойной точности.

    Дифференцирование относительно конкретной переменной

    Найдите первую производную этого выражения.

    syms x t
Df = diff(sin(x*t^2))

    Поскольку вы не задавали переменную дифференцирования, diff использует переменную по умолчанию, заданную symvar. Для этого выражения переменной по умолчанию является x.

    var = symvar(sin(x*t^2),1)

    Теперь найдите производную этого выражения относительно переменной t.

    Производные высшего порядка одномерного выражения

    Найдите 4-е, 5-е, и 6-е производные t6.

    Производные высшего порядка многомерного выражения относительно конкретной переменной

    Найдите вторую производную этого выражения относительно переменной y.

    syms x y
Df = diff(x*cos(x*y), y, 2)

    Производные высшего порядка многомерного выражения относительно переменной по умолчанию

    Вычислите вторую производную выражения x*y. Если вы не задаете переменную дифференцирования, diff использует переменную, определенную symvar. Для этого выражения, symvar(x*y,1) возвращает x. Поэтому diff вычисляет вторую производную x*y относительно x.

    syms x y
Df = diff(x*y,2)

    Если вы используете, вложил diff вызовы и не задают переменную дифференцирования, diff определяет переменную дифференцирования для каждого вызова. Например, дифференцируйте выражение x*y путем вызова diff функционируйте дважды.

    В первом вызове, diff дифференцирует x*y относительно x, и возвращает y. Во втором вызове, diff дифференцирует y относительно y, и возвращает 1.

    Таким образом, diff(x*y,2) эквивалентно diff(x*y,x,x), и diff(diff(x*y)) эквивалентно diff(x*y,x,y).

    Смешанные производные

    Дифференцируйте это выражение относительно переменных x и y.

    syms x y
Df = diff(x*sin(x*y),x,y)
    Df = 2 x cos(x y)-x2 y sin(x y)

    Также можно вычислить смешанные производные высшего порядка путем обеспечения всех переменных дифференцирования.

    syms x y
Df = diff(x*sin(x*y),x,x,x,y)
    Df = x2 y3 sin(x y)-6 x y2 cos(x y)-6 y sin(x y)

    Дифференцирование относительно функции и производной

    Найдите производную функции y=f(x)2dfdx относительно f(x).

    syms f(x) y
y = f(x)^2*diff(f(x),x);
Dy = diff(y,f(x))

    Найдите 2-ю производную функции y=f(x)2dfdx относительно f(x).

    Найдите смешанную производную функции y=f(x)2dfdx относительно f(x) и dfdx.

    Dy3 = diff(y,f(x),diff(f(x)))

    Уравнение Эйлера-Лагранжа

    Найдите уравнение Euler–Lagrange, которое описывает движение массово-пружинной системы. Задайте кинетическую и потенциальную энергию системы.

    syms x(t) m k
T = m/2*diff(x(t),t)^2;
V = k/2*x(t)^2;

    Задайте функцию Лагранжа.

    L = 

    m ∂∂t x(t)22-k x(t)22

    Уравнением Euler–Lagrange дают

    0=ddt∂L(t,x,x˙)∂x˙-∂L(t,x,x˙)∂x

    Оцените термин ∂L/∂x˙.

    D1 = diff(L,diff(x(t),t))

    Оцените второй термин ∂L/∂x.

    Найдите уравнение Euler–Lagrange движения массово-пружинной системы.

    ans(t) = 

    m ∂2∂t2 x(t)+k x(t)=0

    Дифференцируйтесь относительно векторов

    Начиная с R2021a

    Чтобы оценить производные относительно векторов, можно использовать переменные символьной матрицы. Например, найдите производные ∂α/∂x и ∂α/∂y для выражения α=yTAx, где y вектор 3 на 1, A матрица 3 на 4, и x 4 1 вектор.

    Создайте три переменные x символьной матрицыY, и A, из соответствующих размеров, и используют их, чтобы задать alpha.

    syms x [4 1] matrix
syms y [3 1] matrix
syms A [3 4] matrix
alpha = y.'*A*x

    Найдите производную alpha относительно векторов x и y.

    Дифференцируйтесь относительно матрицы

    Начиная с R2021a

    Чтобы оценить дифференциал относительно матрицы, можно использовать переменные символьной матрицы. Например, найдите дифференциал ∂Y/∂A для выражения Y=XTAX, где X вектор 3 на 1, и A 3х3 матрица. Здесь, Y скаляр, который является функцией вектора X и матрица A.

    Создайте две переменные символьной матрицы, чтобы представлять X и ADefine Y.

    syms X [3 1] matrix
syms A [3 3] matrix
Y = X.'*A*X

    Найдите дифференциал Y относительно матрицы A.

    Результатом является продукт тензора Кронекера между XT и X, который является 3х3 матрицей.

    Входные параметры

    свернуть все

    f — Выражение или функция, чтобы дифференцироваться
    символьное выражение | символьная функция | символьный вектор | символьная матрица | переменная символьной матрицы

    Выражение или функция, чтобы дифференцироваться в виде

    • символьное выражение

    • символьная функция

    • вектор или матрица символьных выражений или функций (символьный вектор или символьная матрица)

    • переменная символьной матрицы (начиная с R2021a)

    Если f символьный вектор или матрица, diff дифференцирует каждый элемент f и возвращает вектор или матрицу одного размера с f.

    Типы данных: single | double | sym | symfun | symmatrix

    var — Параметр дифференцирования
    символьная скалярная переменная | символьная функция | производная функция

    Параметр дифференцирования в виде символьной скалярной переменной, символьной функции или производной функции создал использование diff функция.

    Если вы задаете дифференцирование относительно символьного функционального var = f(x) или производный функциональный var = diff(f(x),x), затем первый аргумент f не должен содержать ни один из них:

    • Интеграл преобразовывает, такие как fourier, ifourier, laplace, ilaplace, htrans, ihtrans, ztrans, и iztrans

    • Неоцененные символьные выражения, которые включают limit или int

    • Символьные функции выполнены в отдельном моменте, такие как f(3) или g(0)

    Типы данных: single | double | sym | symfun

    var1,...,varN — Параметры дифференцирования
    символьные скалярные переменные | символьные функции | производные функции

    Параметры дифференцирования в виде символьных скалярных переменных, символьных функций или производной функции создали использование diff функция.

    Типы данных: single | double | sym | symfun

    mvar — Параметр дифференцирования
    переменная символьной матрицы

    Начиная с R2021a

    Параметр дифференцирования в виде переменной символьной матрицы.

    diff функция в настоящее время не поддерживает производные тензора. Если производная является тензором, или производная является матрицей в терминах тензоров, то diff функция будет ошибка. Если f дифференцируемая скалярная функция, mvar может быть скаляр, вектор или матрица. Для дальнейших примеров смотрите, Дифференцируются Относительно Векторов и Дифференцируются Относительно Матрицы.

    Типы данных: symmatrix

    n — Порядок дифференцирования
    неотрицательное целое число

    Порядок дифференцирования в виде неотрицательного целого числа.

    Советы

    • Когда вычисление смешало производные высшего порядка больше чем с одной переменной, не используйте n задавать порядок дифференцирования. Вместо этого задайте все переменные дифференцирования явным образом.

    • Улучшать производительность, diff принимает, что все смешанные производные коммутируются. Например,

      Это предположение достаточно для большинства технических и научных проблем.

    • Если вы дифференцируете многомерное выражение или функциональный f не задавая переменную дифференцирования, затем вложенный вызов diff и diff(f,n) может возвратить различные результаты. Это вызвано тем, что во вложенном вызове, каждый шаг дифференцирования определяет и использует свою собственную переменную дифференцирования. В вызовах как diff(f,n), переменная дифференцирования определяется однажды symvar(f,1) и используемый для всех шагов дифференцирования.

    • Если вы дифференцируете выражение или функциональный содержащий abs или sign, гарантируйте, что аргументы являются вещественными значениями. Для сложных аргументов abs и sign, diff функция официально вычисляет производную, но этот результат не обычно допустим потому что abs и sign не дифференцируемы по комплексным числам.

    Представлено до R2006a

    Источник

    Вычисление производной

    Нахождение производной функции, заданной
    в символьном виде в Matlab
    осуществляется с помощью функции diff(F
    [,     x, n]),
    где F – имя символьной
    функции или ее символьная запись, x
    – переменная дифференцирования, n
    – порядок производной, номер которой
    необходимо найти (по умолчанию n
    = 1).

    Для вычисления числового значения
    производной в некоторой точке в Matlab
    используют функцию subs(expr,
    var1, var2).
    Она заменяет var1
    на var2 в символьном
    выражении expr.

    Пример 3-19. Требуется найти первую
    производную функции

    и вычислить ее значение в точке х =
    16

    Инструкции

    Результат

    >> syms x

    >> f=sym(‘(x^(1/2)-2)^2’);

    >>% первая производная
    от f

    >> F=diff(f)

    >>% значение первой производной в
    точке х = 16

    >>
    subs(F,x,16)

    F =

    (x^(1/2)-2)/x^(1/2)

    ans =

    0.5000

    Пример 3-20. Требуется найти первую
    производную функции

    по х и по у.

    Инструкции

    Результат

    >> syms x,
    у

    >>% дифференцируем по х

    >> diff(‘(x^(1/2)-2)^2’, х)

    >>% дифференцируем по у

    >> diff(‘(x^(1/2)-2*y)^2’,y)

    ans =

    (x^(1/2)-2)/x^(1/2)

    ans =

    -4*x^(1/2)+8*y

    Задание 3- 7.

    а) Найдите первые производные следующих
    функций

    1.

    2.

    b) Найдите первые производные
    следующих функций по х и по у.

    1.

    2.

    Вопросы для повторения

    1. Что такое М-файл?

    2. Как создать новый М-файл?

    3. Как создать М–функцию?

    4. Поясните, как вводятся массивы (вектора
      или матрицы) в Matlab?

    5. Какую роль при работе с матрицами играет
      знак двоеточия?

    6. Перечислите основные матричные операции.

    7. Перечислите основные функции для работы
      с векторами и матрицами в Matlab.

    8. Поясните, как происходит построение
      двумерных графиков в Matlab.

    9. Поясните, как можно построить нескольких
      графиков в одной системе координат в
      Matlab.

    10. Какие возможности имеются в Matlab
      для оформления графиков?

    11. Перечислите основные операторы М-языка.

    12. Какой оператор используется для
      программирования условий в М-языке
      Matlab?

    13. Назовите две разновидности оператора
      If. Какой синтаксис имеет
      обычная форма If? Какой
      синтаксис имеет расширенная форма If?

    14. В каких случаях применяют цикл for
      … end? Какой синтаксис
      имеет оператора for …
      end?

    15. В каких случаях используется цикл
      while? Какой синтаксис имеет
      оператора while?

    16. Назовите основные средства отладки
      М-программ в Matlab.

    17. Какова технология решения алгебраических
      уравнений в Matlab?

    18. Поясните метод трапеций для вычисления
      определенного интеграла в Matlab.

    19. Как можно объявить символьную переменную
      в Matlab?

    20. Какая функция предназначена в Matlab
      для решения уравнений и систем в
      символьном виде?

    21. Какова технология вычисления пределов
      в Matlab?

    22. Какова технология вычисления производной
      в Matlab?

    Список используемой литературы

    1. Ануфриев И.Е., Смирнов А.Б., Смирнова
    Е.Н. MATLAB 7. – СПб.:
    БХВ-Петербург, 2005. – 1104 с.

    2. Алексеев Е.Р., Чеснокова О.В. MATLAB
    7. Самоучитель. М.: НТ Пресс, 2006. – 464 с.

    3. Сборник задач по курсу математики /
    Под ред. А.С. Солодовникова, А.В. Браилова.
    М.: Финансовая академия, 2001. 508 с.

    30

    Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    Источник

    Доброго времени суток! Сегодня мы продолжаем говорить об обработке статических данных (ранее разбирали апроксимацию и интерполяцию в Matlab).

    Процесс дифференцирования подразумевает нахождение производной. Для получения разных порядков производной, можно провести операцию дифференцирования несколько раз. Более детально, о смысле и значение производной, предлагаю ознакомиться здесь. Численное дифференцирование строится на использовании аппарата конечных разностей и соответствующего многообразия аппроксимаций.

    Нахождение первой производной в Matlab

    Сперва скажу, что есть стандартные средства дифференцирования в Matlab и именно методы (своего рода алгоритмы). К стандартным относится такой инструмент как diff(x). Она принимает аргумент x, который является массивом. Подробнее о diff() читайте здесь.

    Методы численного дифференцирования применяются, если исходную функцию y(x) трудно или невозможно продифференцировать аналитически. Методы имеют разную погрешность при расчётах. Рассмотрим основные из них и оценим погрешность помощью Matlab:
    Сравним результаты, дифференцируя функцию sin(x).

    h=0.2; %определим шаг сетки
x=0:h:pi; %интервал значений х
n=length(x); %число необходимых итераций
dy=cos(x); %производная y = sin(x) => y' = cos(x), так будем судить об отклонении и погрешности.
dz=sin(x); % для сравнения

    • Метод нахождения производной правой конечной разностью

      • Формула:Правая конечная разность

      for i=1:(n-1)
 dy1(i)=(sin(x(i+1))-sin(x(i)))/h;
 er1(i)=abs(dy(i)-dy1(i));
end

    • Метод нахождения производной левой конечной разностью

      • Формула: левая конечная разность

      for i=2:n
 dy2(i)=(sin(x(i))-sin(x(i-1)))/h;
 er2(i)=abs(dy(i)-dy2(i));
end

    • Метод нахождения производной центральной конечной разностью

      • Формула: центральная конечная разность

      for i=2:(n-1)
 dy3(i)=(sin(x(i+1))-sin(x(i-1)))/(2*h);
 er3(i)=abs(dy(i)-dy3(i));
end

    • Метод нахождения производной четвертого порядка точности

      • Формула для 4-го порядка точности и 4 переменных ( в нашем случае переменных больше )4 порядок точности для 4-ёх переменных

      for i=3:(n-1)
 dy4(i)=(-sin(x(i+1))+27*sin(x(i))-...
 27*sin(x(i-1))+sin(x(i-2)))/(24*h);
 er4(i)=abs(cos(x(i)-0.5*h)-dy4(i)); % абсолютную погрешность, которая вычисляется в точке x(i)-0.5*h
end

    %рисуем все на графиках
 plot(x([1:(n-1)]),er1([1:(n-1)]),'-o',...
             x([2:n]),er2([2:n]),'-p',...
     x([2:(n-1)]),er3([2:(n-1)]),'-h',...
     x([3:(n-1)]),er4([3:(n-1)]),'-*');
 title('Погрешность ("разность" анлитического и численного решения)');
 legend('Правая', ' Левая', 'Центральная', '4-ый порядок')
 grid on;
figure; plot(x([1:(n-1)]),dy([1:(n-1)]),'-d',...
                x([1:(n-1)]),dz([1:(n-1)]),'-<',...
                x([1:(n-1)]),dy1([1:(n-1)]),'-o',...
     x([3:(n-1)]),dy4([3:(n-1)]) - 0.5*h,'-*');
 legend('cos(x)', ' sin(x)', 'производная по правой конечной разности', 'производная по 4-ому порядоку')
 grid on

    Наши выводы:
    Погрешность (абсолютная ошибка)Сравнение (графики производных)

    Нахождение второй производной в Matlab

    Теперь провернём похожие фокусы с использование формулы для центральной конечной разности и формулы 4-го порядка точности для второй производной.
    Сравним результаты, дифференцируя функцию sin(x).

    h=0.2;  %определим шаг сетки
x=0:h:pi;  %определим сетку
n=length(x);  %число итераций
d2y=-sin(x);   %точное значение второй производной d2y=-sin(x)

    • Метод нахождения производной центральной конечной разностью для второй производной

      • Формула:Центральные разности для второй производной

      for i=2:(n-1)
    d2y1(i)=(sin(x(i+1))-2*sin(x(i))+sin(x(i-1)))/h^2;
    er1(i)=abs(d2y(i)-d2y1(i));<18pan>
end

    • Метод нахождения производной четвертого порядка точности для второй производной

      • Формула:4-ый порядок вторая производная

      for i=3:(n-2)
    d2y2(i)=(-sin(x(i+2))+16*sin(x(i+1))-30*sin(x(i))+...
                    16*sin(x(i-1))-sin(x(i-2)))/(12*h^2);
    er2(i)=abs(d2y(i)-d2y2(i));
end

    Наши выводы:
    погрешность, вторая производнаяГграфик вторых производных

    Метод Рунге: уточнения формул численного дифференцирования

    Я выделил в отдельности данный метод, так как он служит только для уточнения результатов. Быстренько пробежимся по примеру программы:

    %Теория и практика в среде MATLAB
%Программа иллюстрирующая метод Рунге по повышению точности численного
%дифференцирования путем комбинирования пары расчетов на двух равномерных сетках,
%причем вторая содержит вдвое большее количество узлов
d=sin(x);
h=0.1;  %определяем шаг исходной сетки
x=0:h:pi;  %формируем исходную сетку
n=length(x);  %количество итераций
hm=h/2; %определяем шаг более подробной сетки
xm=0:hm:pi;  %создаем сетку вдвое более подробную
m=length(xm); %количество итераций для подробной
%рассчитываем производную с помощью правой разности на исходной сетке и оцениваем
for i=1:(n-1)
    dy(i)=(sin(x(i+1))-sin(x(i)))/h;
    er1(i)=abs(cos(x(i))-dy(i));  %соответствующую абсолютную ошибку 
end
%рассчитываем производную с помощью правой разности на более частой сетке и оцениваем
for i=1:(m-1)
    dym(i)=(sin(xm(i+1))-sin(xm(i)))/hm;
    er2(i)=abs(cos(xm(i))-dym(i));
end
%уточняем значение производной с помощью метода Рунге
for i=1:(n-1)
    dyrunge(i)=dy(i)-2*(dy(i)-dym(2*i-1));
    er3(i)=abs(cos(x(i))-dyrunge(i));
end
%строим общий график со всеми тремя кривыми ошибок
plot(x([1:(n-1)]),er1([1:(n-1)]),'-o',...
     xm([1:2:(m-1)]),er2([1:2:(m-1)]),'-p',...
     x([1:(n-1)]),er3([1:(n-1)]),'-h');
  title('Погрешность ("разность" анлитического и численного решения)');
 legend( 'Правая конечная на исходной', 'Правая конечная на частой', 'уточнение Рунге')
 grid on;
 figure;plot(x([1:(n-1)]),d([1:(n-1)]),'-d',...
     x([1:(n-1)]),dy([1:(n-1)]),'-o',...
     xm([1:2:(m-1)]),dym([1:2:(m-1)]),'-p',...
     x([1:(n-1)]),dyrunge([1:(n-1)]),'-h');
 legend('sin(x)', 'Правая конечная на исходной', 'Правая конечная на частой', 'уточнение Рунге')
 grid on;

    И наш вывод:
    погрешность Рунге
    производные Рунге

    Численное дифференцирование в Matlab. Пример задачи

    Теперь рассмотрим задачу.
    1. Найти 1-ую и 2-ую производные функции, заданной таблично.

    xi	-3	-2	-1	0	1	2	3
yi	-0,71	-0,01	0,51	0,82	0,88	0,51	0,49

    2. Найти 1-ую и 2-ую производные функции y = ln(cos(x)) в точке х= 0,5 различными методами, а именно рассмотреть формулы простые и многоточечные. Оценить точность аппроксимации (это разница между значением производной, вычисленным по точной формуле, полученной аналитически, и её значением, вычисленным по конечно-разностным формулам).
    Исследовать влияние величины шага на точность вычисления производных по различным формулам.

    Решаем первый пункт.
    Нам не дана сама функция, а только точки через которые она проходит. Это значит, что мы должны найти такую функцию, которая приближенна к данным точкам. Найдём её с помощью апроксимации. Тему апроксимации в Matlab мы разбирали ранее. Выглядеть решение будет так:

    x=[-3 -2 -1 0 1 2 3];
y=[-0.71  -0.01  0.51  0.82  0.88  0.51	0.49];

nm=4;   %задаем степень аппроксимирующего полинома 
p=polyfit(x,y,nm);   %полиномизируем данные
y1=polyval(p,x);   %%расчитываем значения y1 в зависимости от коэффициентов полинома
dyt = polyder(p);  %берём производную по полиному
dyt2 = polyder(dyt);  %берём вторую производную
dy = polyval(dyt,x);   
dy2 = polyval(dyt2,x);
plot(x,y,'-*'); %строим точки
hold on
plot(x,y1,'-<');  %апроксимация
plot(x,dy,'-or');  %производная первого порядка
plot(x,dy2,'-og');  %производная второго порядка
grid on
legend('данные точки', 'апроксимирующая функция', 'производная первого порядка', 'производная второго порядка');

    Наш вывод:
    графики производных для задачи
    Если вам необходимо вывести значение переменных в процессе решения, достаточно просто убрать «;» в конце строчки кода.

    Решаем второй пункт.

    h = 0.2;
x = 0:h:pi;
n = length(x);
y = log(cos(x));
dy = -tan(x);  %аналитическое диф уравнение  
for i=1:(n-1)  % производная по правой конечной разности
    dy1(i) = (log(cos(x(i + 1))) - log(cos(x(i))))/h;
    er1(i) = abs(dy(i) - dy1(i));
end
for i=2:n  % производная по левой конечной разности
    dy2(i) = (log(cos(x(i))) - log(cos(x(i - 1))))/h;
    er2(i) = abs(dy(i) - dy2(i));
end
for i = 2:(n-1) % производная по центральной разности
    dy3(i) = (log(cos(x(i+1)))-log(cos(x(i-1))))/(2*h);
    er3(i) = abs(dy(i)-dy3(i));
end
x(i) - 0.5 * h;
for i = 3:(n-1)  % производная по 4ому порядку
    dy4(i) = (-log(cos(x(i+1)))+27*log(cos(x(i)))-27*log(cos(x(i-1)))...
        +log(cos((x(i-2)))))/(24*h);
    er4(i) = abs(-tan(x(i)-0.5*h)-dy4(i));
end
plot(x(1:(n-1)),er1(1:(n-1)),'-o',...
             x(2:n),er2(2:n),'-p',...
     x(2:(n-1)),er3(2:(n-1)),'-h',...
     x(3:(n-1)),er4(3:(n-1)),'-*');
  legend('Правая', ' Левая', 'Центральная', '4-ый порядок')
 %вторая производная 
 grid on;
 figure;
 d2y = 1(cos(x).^2);
for i = 2:(n-1)  % производная по центральной разности для второй производной
    d2y1(i) = (log(cos(x(i+1)))-2*log(cos(x(i)))+log(cos(x(i-1))))/(h.^2);
    er1(i) = abs(d2y(i)-d2y1(i));
end
for i = 3:(n-2)  % производная по 4ому порядку
    d2y2(i) = (log(cos(x(i+2)))+16*log(cos(x(i+1)))-30*log(cos(x(i)))+...
        16*log(cos(x(i-1)))-log(cos(x(i-2))))/(12*h.^2);
    er2(i) = abs(d2y(i)-d2y2(i));
end
plot(x(2:(n-1)),er1(2:(n-1)),'-o',...
     x(3:(n-2)),er2(3:(n-2)),'-p');
 legend( 'производная по центральной конечной разности', 'производная по 4-ому порядоку')
 grid on;

    В теории такие алгоритмы мы уже подробно разобрали. Этот момент «Исследовать влияние величины шага на точность вычисления производных по различным формулам.» я не расписывал в решении, так как его мы разобрали в теории в Методе Рунге.
    Наш вывод:
    погрешность первой производнойпогрешность второй производной

    На этом мы закончим. Если остались вопросы, задавайте их в комментариях. Также вы можете скачать исходники чтобы лучше понять тему: «Численное дифференцирование Matlab».

    Скачать исходник первого примера
    Скачать исходник второго примера
    Скачать исходник третьего примера
    Скачать исходник первого пункта
    Скачать исходник второго пункта

    Источник

    Понравилась статья? Поделить с друзьями:
  • Видео как найти пароль от аккаунта
  • Как найти настроить скайп
  • Как исправить неверный imei на мтс без компа
  • Наименьшее общее кратное как найти примеры
  • Не получился майонез без яиц как исправить