| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Показать Этапы
Номер Строки
Примеры
-
производная:с:использованием:определения:sqrt{x}
-
производная:с:использованием:определения:f(x)=2x^{2}−16x+35
-
производная:с:использованием:определения:frac{t}{t+1}
-
производная:с:использованием:определения:frac{1}{x}
- Показать больше
Описание
Найдите производную, используя определение шаг за шагом
derivative-using-definition-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
High School Math Solutions – Derivative Calculator, Trigonometric Functions
In the previous posts we covered the basic algebraic derivative rules (click here to see previous post). But how…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Описание метода вычисления значения производной можно найти под калькулятором.
Вычисление производной по ее определению
Начальное приращение аргумента
Параметр изменения приращения
Точность вычисления
Знаков после запятой: 4
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Вычисление производной по ее определению
Задача численного дифференцирования возникает когда функция задана таблично, или когда прямое дифференцирование затруднено (например, при сложном аналитическом виде функции). Если функция задана аналитически, то можно применить вычисление значения производной по ее определению.
В этом случае у нас есть некоторая функция , для которой нам надо вычислить значение производной в точке x₀. Мы предполагаем, что эта функция определена в окрестности точки x₀ и имеет производную в этой точке. Исходя из определения производной
существует предел отношения приращения функции Δy к приращению аргумента Δx при Δx→0, где
Значение производной можно получить переходя к пределу со все более уменьшающимся шагом, пока не будет достигнута требуемая точность. Для этого на каждом шаге последовательности n приращение аргумента вычисляется по следующей формуле
,
где
Δx₀ — начальное приращение аргумента, например, 0.1
a — некоторое число, большее 1, например, 10
n = 0, 1, …
Тогда
Последовательность останавливается при выполнении следующего условия
Производная функции
Производной функции y=f(x) в точке x0 называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).
Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
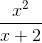
cos2(2x+π) ≡ (cos(2*x+pi))^2
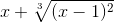
Правила ввода функции, заданной в неявном виде
Примеры
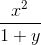
cos2(2x+y) ≡ (cos(2*x+y))^2
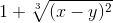
Если функция задана в виде y2-x=cos(y), то ее необходимо записать так: y^2-x-cos(y).
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
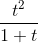
cos2(t) ≡ cos(t)^2
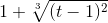
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
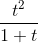
cos2(t) ≡ cos(t)^2
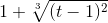
Как найти производную, исходяя из ее определения?
Правила нахождения производных
Пример 1. Найти производную функции y=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
.

В некоторых случаях, если, например, нужно найти производную функции y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции

Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию
Учитывая, что 
Но 

Пример 4. Найти производную функции y=xex
Решение.


Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Определение производной
Определение. Пусть функция ( y = f(x) ) определена в некотором интервале, содержащем внутри себя точку ( x_0 ).
Дадим аргументу приращение ( Delta x ) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
( Delta y ) (при переходе от точки ( x_0 ) к точке ( x_0 + Delta x ) ) и составим отношение
( frac{Delta y}{Delta x} ). Если существует предел этого отношения при ( Delta x rightarrow 0 ), то
указанный предел называют производной функции ( y=f(x) ) в точке ( x_0 ) и обозначают ( f'(x_0) ).
$$ lim_{Delta x to 0} frac{Delta y}{Delta x} = f'(x_0) $$
Для обозначения производной часто используют символ ( y’ ).
Отметим, что ( y’ = f(x) ) — это новая функция, но, естественно, связанная с функцией ( y = f(x) ), определенная во всех точках (x), в которых
существует указанный выше предел. Эту функцию называют так: производная функции ( y = f(x) ).
Геометрический смысл производной состоит в следующем. Если к графику функции ( y = f(x) ) в точке с абсциссой ( x=a ) можно
провести касательную, непараллельную оси (y), то ( f(a) ) выражает угловой коэффициент касательной:
( k = f'(a) )
Поскольку ( k = tg(a) ), то верно равенство ( f'(a) = tg(a) ) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция ( y = f(x) ) имеет
производную в конкретной точке ( x ):
$$ lim_{Delta x to 0} frac{Delta y}{Delta x} = f'(x) $$
Это означает, что около точки (x) выполняется приближенное равенство ( frac{Delta y}{Delta x} approx f'(x) ), т.е.
( Delta y approx f'(x) cdot Delta x ).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально»
приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке (x).
Например, для функции ( y = x^2 ) справедливо приближенное равенство ( Delta y approx 2x cdot Delta x ).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение ( x ), найти ( f(x) )
2. Дать аргументу ( x ) приращение ( Delta x ), перейти в новую точку ( x+ Delta x ), найти ( f(x+ Delta x) )
3. Найти приращение функции: ( Delta y = f(x + Delta x) — f(x) )
4. Составить отношение ( frac{Delta y}{Delta x} )
5. Вычислить $$ lim_{Delta x to 0} frac{Delta y}{Delta x} $$
Этот предел и есть производная функции в точке (x).
Если функция (y=f(x)) имеет производную в точке (x), то ее называют дифференцируемой в точке (x). Процедуру нахождения производной
функции (y=f(x)) называют дифференцированием функции (y=f(x)).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция (y=f(x)) дифференцируема в точке (x). Тогда к графику функции в точке ( M(x; ; f(x)) ) можно провести касательную,
причем, напомним, угловой коэффициент касательной равен ( f'(x) ). Такой график не может «разрываться» в точке (M), т. е. функция
обязана быть непрерывной в точке (x).
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция (y=f(x)) дифференцируема в точке (x), то
выполняется приближенное равенство ( Delta y approx f'(x) cdot Delta x ). Если в этом равенстве ( Delta x ) устремить к
нулю, то и ( Delta y ) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция ( y=|x|) непрерывна везде, в частности в точке (x=0), но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция ( y=sqrt[3]{x} ) непрерывна на всей числовой прямой, в том числе в точке (x=0).
И касательная к графику функции существует в любой точке, в том числе в точке (x=0). Но в этой точке касательная совпадает с осью (y),
т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид (x=0). Углового коэффициента у такой прямой нет, значит, не существует и
( f'(0) )
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее
дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси
абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она
перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием.
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если (C) — постоянное число и ( f=f(x), ; g=g(x) ) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
$$ C’=0 $$
$$ x’=1 $$
$$ ( f+g)’=f’+g’ $$
$$ (fg)’=f’g + fg’ $$
$$ (Cf)’=Cf’ $$
$$ left(frac{f}{g} right) ‘ = frac{f’g-fg’}{g^2} $$
$$ left(frac{C}{g} right) ‘ = -frac{Cg’}{g^2} $$
Производная сложной функции:
$$ f’_x(g(x)) = f’_g cdot g’_x $$
Таблица производных некоторых функций
$$ left( frac{1}{x} right) ‘ = -frac{1}{x^2} $$
$$ ( sqrt{x} ) ‘ = frac{1}{2sqrt{x}} $$
$$ left( x^a right) ‘ = a x^{a-1} $$
$$ left( a^x right) ‘ = a^x cdot ln a $$
$$ left( e^x right) ‘ = e^x $$
$$ ( ln x )’ = frac{1}{x} $$
$$ ( log_a x )’ = frac{1}{xln a} $$
$$ ( sin x )’ = cos x $$
$$ ( cos x )’ = -sin x $$
$$ ( text{tg} x )’ = frac{1}{cos^2 x} $$
$$ ( text{ctg} x )’ = -frac{1}{sin^2 x} $$
$$ ( arcsin x )’ = frac{1}{sqrt{1-x^2}} $$
$$ ( arccos x )’ = frac{-1}{sqrt{1-x^2}} $$
$$ ( text{arctg} x )’ = frac{1}{1+x^2} $$
$$ ( text{arcctg} x )’ = frac{-1}{1+x^2} $$
Данный онлайн калькулятор вычисляет производную функции. Программа не только вычисляет ответ, она производит пошаговое решение. Выбирается порядок дифференцирования.
Как пользоваться калькулятором для нахождения производных онлайн:
1. Введите математическое выражение с переменной x, в выражении используйте стандартные операции: + сложение, —
вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции.
2. Выберите порядок дифференцирования (решения производных от первого до пятого порядка включительно).
3. Нажмите кнопку — Вычислить производную.
4. Через несколько секунд внизу отобразится пошаговое решение производной с подробными комментариями.
При помощи нашего калькулятора вы можете найти производную онлайн как от элементарной функции, так и от сложной, не имеющей решения в аналитическом виде.
Калькулятор поможет найти производную функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
: x^a
модуль x: abs(x)
Для того, чтобы найти производную функции
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции 
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где 
Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.
- Примеры
- x*E^x, x;
- x^3*E^x, {x,17};
- x^3*y^2*Sin[x+y], x;
- x^3*y^2*Sin[x+y], y,
- x/(x+y^4), {x,6}.




 : x^a
: x^a