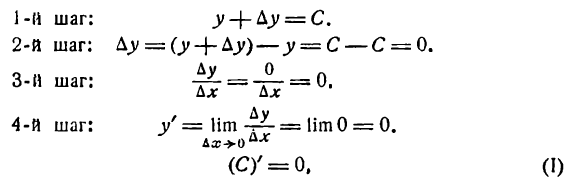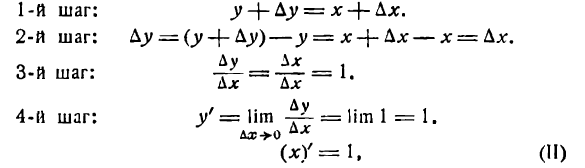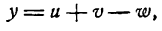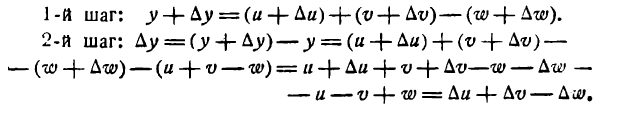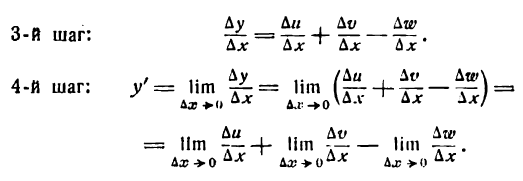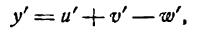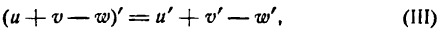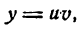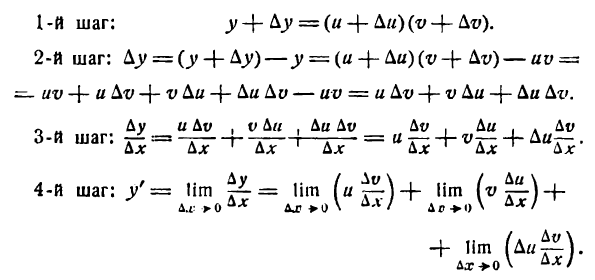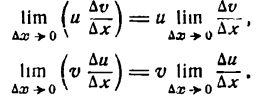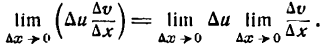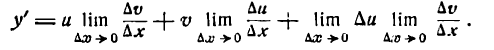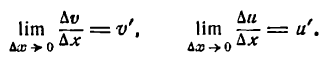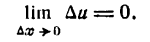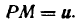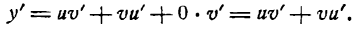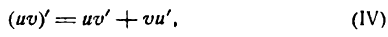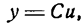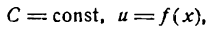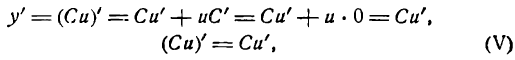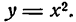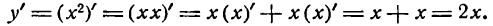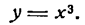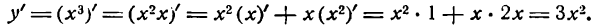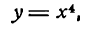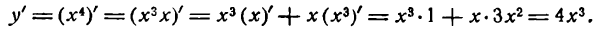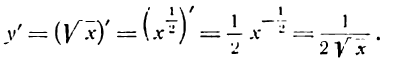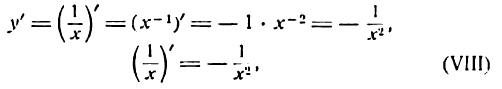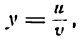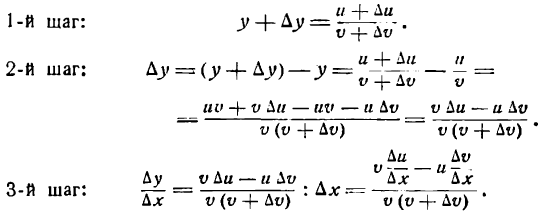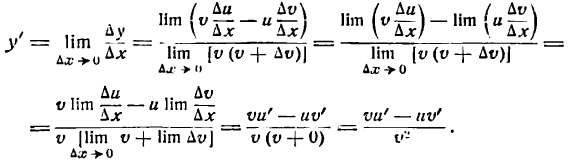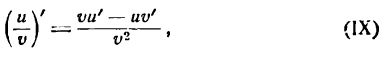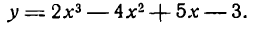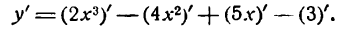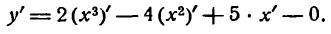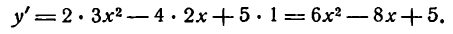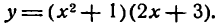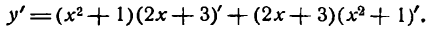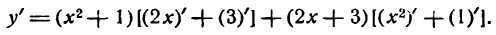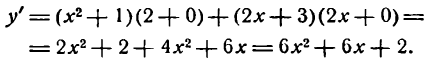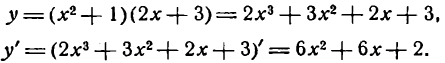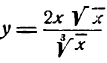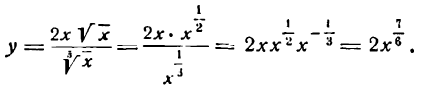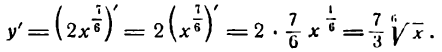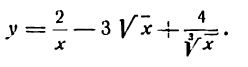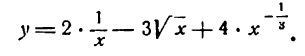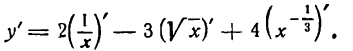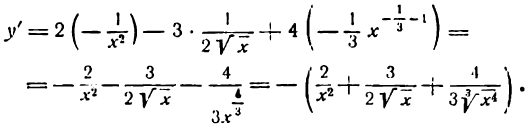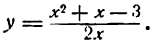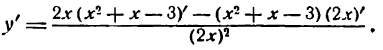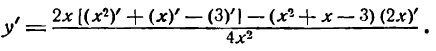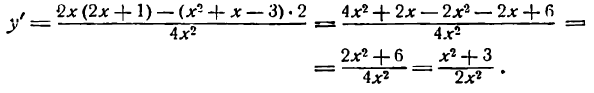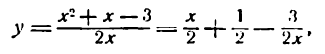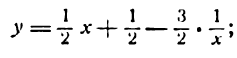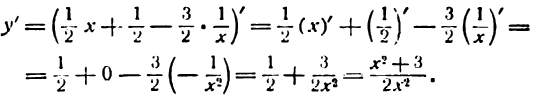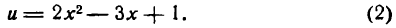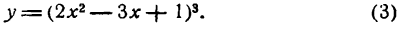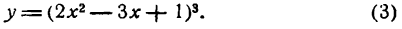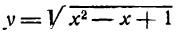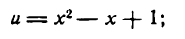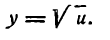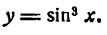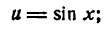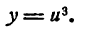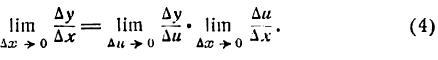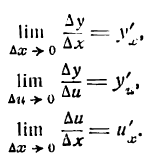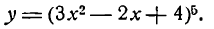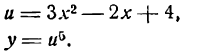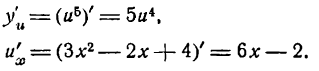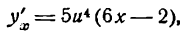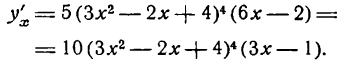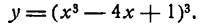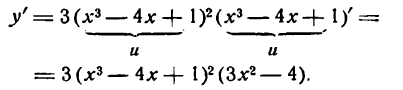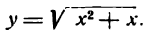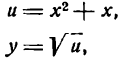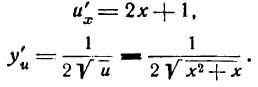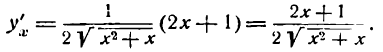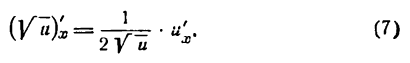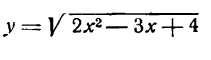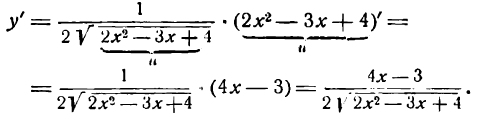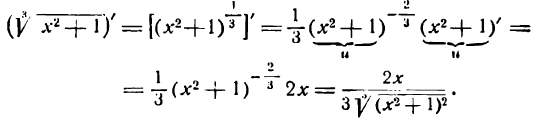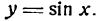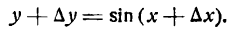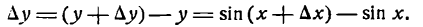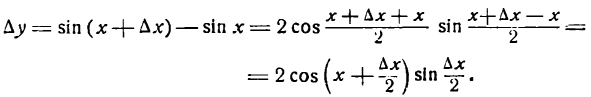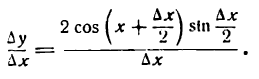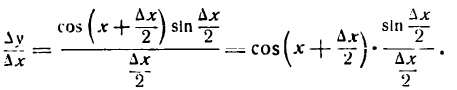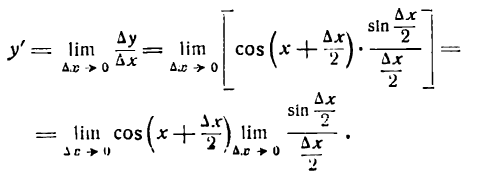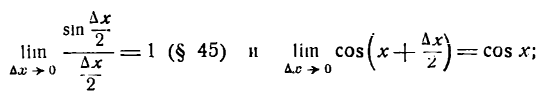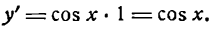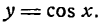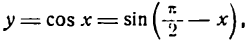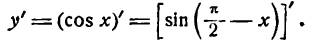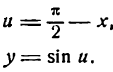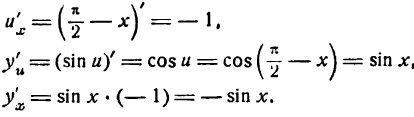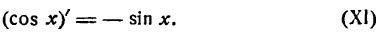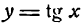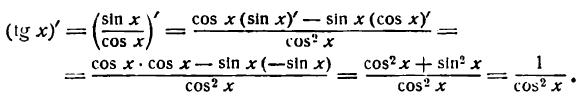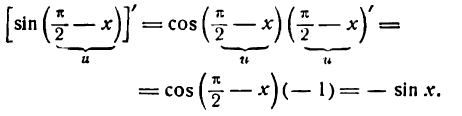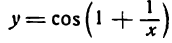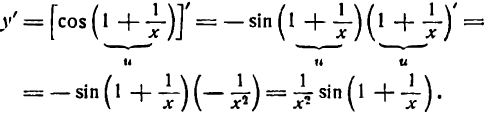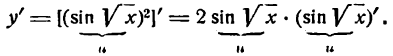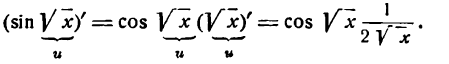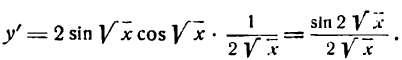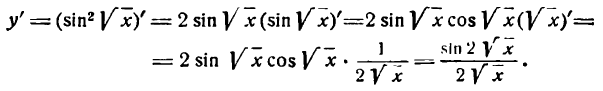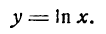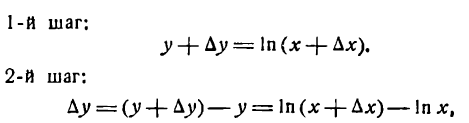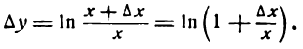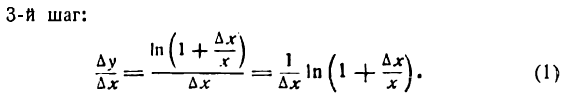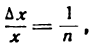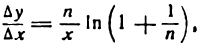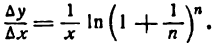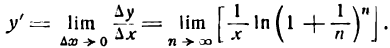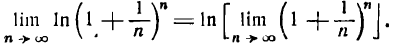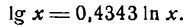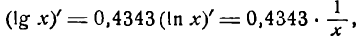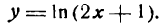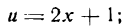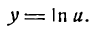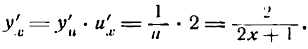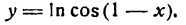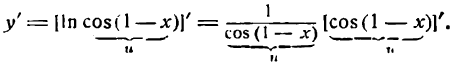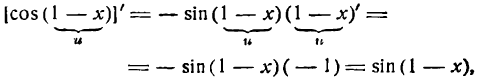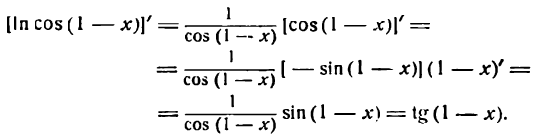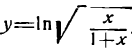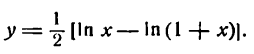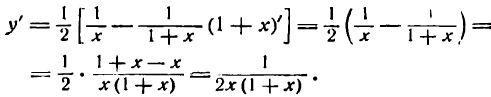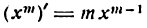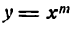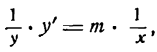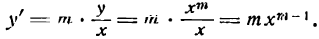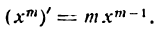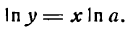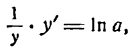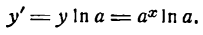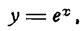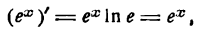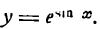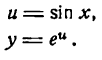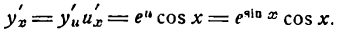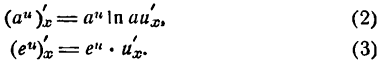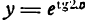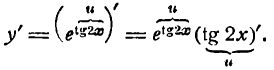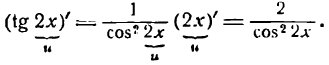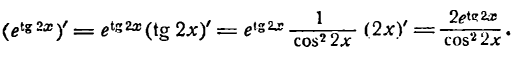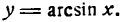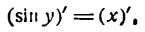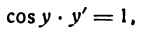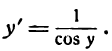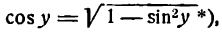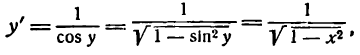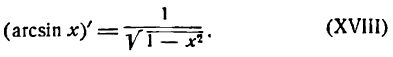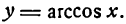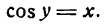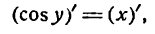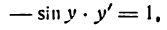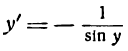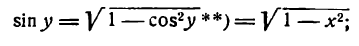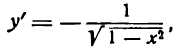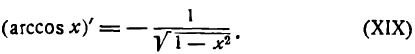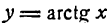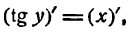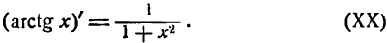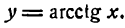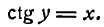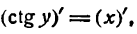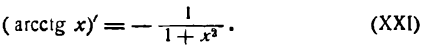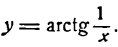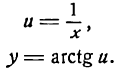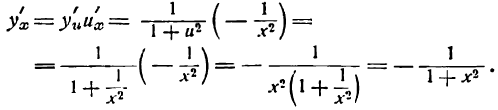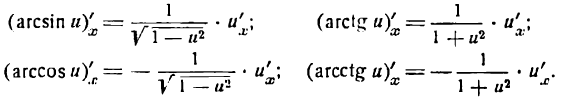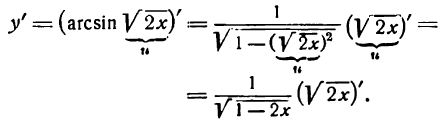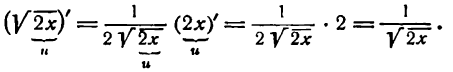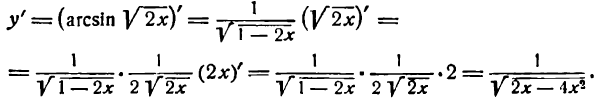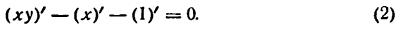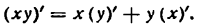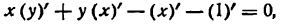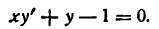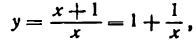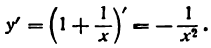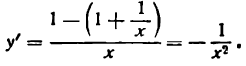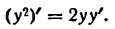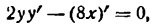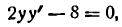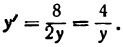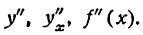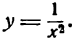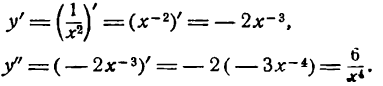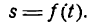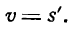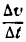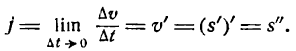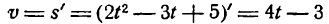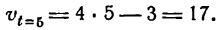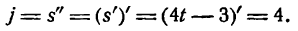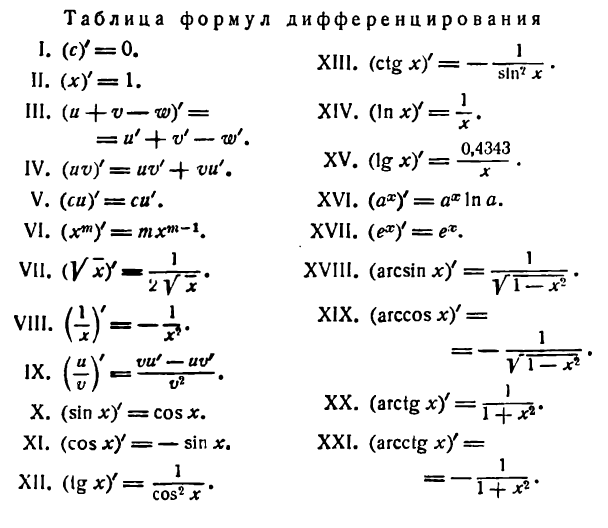Как найти производную функции при значении аргумента

Формулы дифференцирования

Выгодно иметь такие правила, которые позволяли бы находить производные проще, с минимальной затратой времени. Действительно, такие правила имеются, причем они выводятся из основного правила дифференцирования.

Производная постоянной

Пусть С — постоянная величина; тогда равенство

у = С

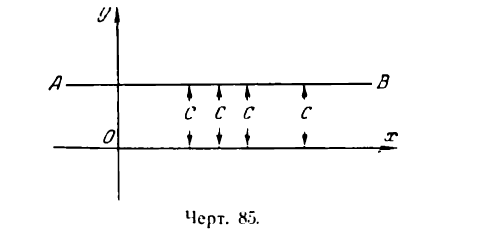
можно рассматривать как выражение функции, не меняющей своего значения с изменением аргумента. В справедливости этого можно убедиться, представив это равенство графически, т. е. в виде прямой линии АВ, параллельной оси Ох (рис. 85).

Действительно, с изменением абсциссы точек этой прямой ординаты их остаются постоянными.

Для нахождения производной функции у = С применим основное правило дифференцирования:

т. е. производная постоянной равна нулю.

Не следует производную постоянной смешивать с пределом постоянной, который, как известно, равен самой постоянной.

Производная функции у = х

Применяя основное правило дифференцирования, получим:

т. е. производная функции у = х равна единице, или: производная независимой переменной равна единице.

Производная алгебраической суммы функций

Возьмем функцию

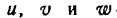
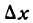
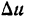
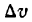
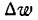
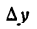
где — функции от х и имеющие производные по х. Если аргументу х дать приращение то и функции и, v и w получат приращения, соответственно равные , и , а потому у также получит приращение . По основному правилу находим:

Слагаемые правой части последнего равенства являются производными функций 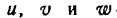. Указанное равенство можно переписать:

или

т. e. производная алгебраической суммы конечного числа функций равна алгебраической сумме производных каждой из них.

Производная произведения двух функций

Пусть дана функция

где и и v — функции от х имеющие производные по x. Дадим аргументу х приращение 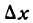тогда согласно основному правилу будем иметь:

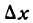
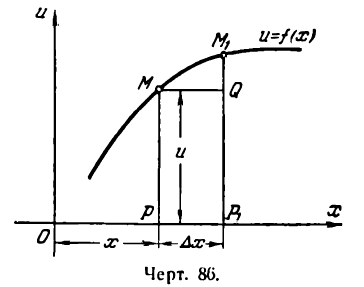
Но и и v не зависят от , а потому их нужно считать постоянными *)

*) Это можно иллюстрировать на рис. 86. Здесь

при 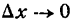; согласно следствию 1 теоремы IV можем написать:

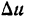
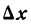
Приращение же функции и меняется с изменением , поэтому согласно теореме IV имеем:

Таким образом,

Но

Далее, так как и дифференцируема, то она непрерывна, следовательно.

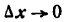
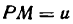
Если то не меняется.

Поэтому

Итак,

т. е. производная произведения двух функций равна сумме произведений первой функции на производную второй и второй функции на производную первой.

Производная произведения постоянной на функцию

Возьмем функцию

где

причем функция и имеет производную по х. Применяя правило (IV), получим:

т. е. производная произведения постоянной на функцию равна произведению постоянной на производную функции.

Производная степени с целым положительным показателем

Возьмем сначала функцию

Представив ее в виде произведения и применяя правило (IV), получим:

Найдем производную новой функции:

Заменив ее произведением 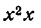и опять применяя то же правило (IV), найдем:

Поступив точно так же с функцией

найдем:

Если продолжать дифференцирование функций 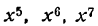и т. д. этим способом, то получим результаты, подчиняющиеся одной и той же формуле:

Таким образом, производная степени 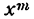, где т— целое положительное число, равна произведению показателя степени на основание х в степени, на единицу меньшей чем данная.

Однако выведенное правило справедливо для любого показателя т, что мы и докажем.

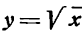
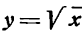
Производная функции . Представив функцию в виде степени с дробным показателем и применяя правило (VI), получим:

Таким образом,

т. е. производная функции 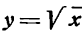равна единице, деленной на удвоенную функцию.

Производная функции .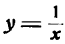

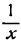
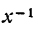
Заменив на и дифференцируя по правилу (VI), получим:

т. е. производная дроби 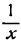равна отрицательной дроби, равной единице, деленной на квадрат знаменателя.

Производная частного

Возьмем функцию

где и и v — функции от х, имеющие производные по x, причем 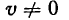при значении х, при котором находится производная. Применим основное правило дифференцирования.

4-й шаг: применяя теоремы V, III, II и следствие 1 теоремы IV , находим:

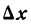
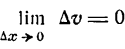
Здесь, как и при выводе формулы (IV), нужно считать и и v не зависящими от , а .

Итак,

т. е. производная частного равна дроби, знаменатель которой есть квадрат делителя, л числитель есть разность между произведением делителя на производную делимого и произведением делимого на производную делителя.

Применение формул дифференцирования

Рассмотрим несколько примеров на применение выведенных правил.

Пример:

Продифференцировать функцию

Решение:

По правилу (III) имеем:

Применяя к первым трем слагаемым правило (V), а к последнему— правило (I), получим:

Согласно правилам (VI) и (II) будем иметь:

Пример:

Продифференцировать функцию

Решение:

По правилу (IV) имеем:

По правилу (III):

По правилам (V), (II). (I) и (VI):

Этот пример можно решить иначе: сначала перемножить выражения в скобках, а затем продифференцировать полученную сумму:

Пример:

Продифференцировать функцию

Решение:

Преобразуем данную функцию следующим образом:

Применяя правила (V) и (VI), будем иметь:

Пример:

Продифференцировать функцию

Решение:

Представим данную функцию в следующем виде:

Применяя правила (III) и (V), получим:

По правилам (VIII), (VII) и (VI) имеем:

По правилам (VIII), (VII) и (VI) имеем:

Пример:

Продифференцировать функцию

Решение:

По правилу (IX) имеем:

Дифференцируя сумму по правилу (III), получим:

Наконец, по правилам (VI), (II), (I) и (V) найдем:

Можно иначе продифференцировать данную функцию, разделив в правой части данного уравнения почленно числитель на знаменатель, получим:

или

отсюда

Функция от функции (сложная функция)

Пусть нам даны две функции:

и

Если в (1) заменить и его выражением из (2), то получим:

Из уравнений (1) и (2) видно, что у есть функция от и, но и в свою очередь функция от х таким образом, функция у зависит от функции

Функцию (3) называют функцией от функции или слоэюной функцией.

Всякую сложную функцию можно представить в виде нескольких простых. Разберем примеры.

Пример:

Представить функцию

в виде двух простых.

Решение:

Положим

тогда

Мы получили две функции и и у более простого вида, чем данная.

Пример:

То же для функции

Решение:

Положим

тогда

Производная сложной функции

Возьмем функцию

причем

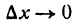
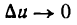
Пусть функция (2) имеет производную при данном х; тогда при и , Пусть также и функция (1) имеет производную при значении и, соответствующем тому же значению х. Напишем тождество

Применяя к правой части тождества (3) теорему о пределе произведения, получим:

Но, как известно,

Поэтому равенство (4) можно переписать:

Формула (5) служит для дифференцирования сложной функции, составленной из двух простых.

Пример:

Продифференцировать функцию

Решение:

Представим данную функцию в виде следующих двух:

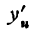
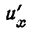
Найдем сначала (т. е. производную функции у по аргументу и), а затем и (т. е. производную функции и по аргументу х):

Искомая производная будет:

или, заменяя и его значением,

Как видно из формулы (5), производная сложной функции выражается произведением производных простых функций и, конечно, перестановка сомножителей не изменит результата. Однако удобней находить эти сомножители в одной определенно выбранной последовательности, которую полезно запомнить как правило. Так, например, для разобранного случая степенной функции это правило можно высказать следующим образом:

для дифференцирования сложной степенной функции*) нужно взять производную сначала от степени по основанию (принимая основание за аргумент), а потом от выражения, стоящего в основании, по независимой переменной и результаты перемножить.

*) Под сложной степенной функцией будем разуметь степень, основание которой есть функция от х.

Если 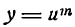— сложная степенная функция, то ее производная согласно этому правилу запишется так:

Пусть, например, требуется найти производную функции

Положив

и, применяя правило (6), будем иметь:

В дальнейшем для каждого особого случая будут даваться аналогичные правила, устанавливающие свою последовательность дифференцирования.

Разберем еще пример. Пусть требуется найти производную функции

Разбив ее на две простые функции, получим:

отсюда

Следовательно,

И здесь можно установить последовательность в нахождении производной, которая выразится следующим правилом: для дифференцирования сложной функции 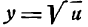нужно сначала взять производную от этой функции по подкоренному выражению и (считая и аргументом), а потом от подкоренного выражения по независимой переменной и результаты перемножить; таким образом, считая и функцией от x получаем:

Так, например, производная функции

но вышеуказанному правилу найдется так:

Если дан корень другой степени, то его нужно предварительно преобразовать в степень с дробным показателем и применить правило для дифференцирования сложной степенной функции. Например,

Производные тригонометрических функций

1. 

По общему правилу дифференцирования находим:

1-й шаг:

2-й шаг:

Преобразуя разность синусов, будем иметь:

3-й шаг:

После деления числителя и знаменателя дроби на 2 получим:

4-й шаг:

Но

поэтому

Следовательно

2.

По формуле приведения можно написать:

отсюда

Для дифференцирования сложной функции 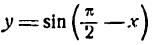представим ее в виде двух простых:

Согласно формуле (5) имеем:

Следовательно,

3.

Заменив tg x отношением 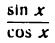и применяя правило дифференцирования частного, получим:

Итак, имеем:

4.

Как и в случае 3, имеем:

Таким образом,

В п. 2 настоящей лекции мы дифференцировали сложную функцию 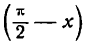, пользуясь формулой (5) .

Однако эту операцию можно произвести и по следующему правилу:

для дифференцирования сложной тригонометрической функции *) нужно сначала взять производную от тригонометрической функции по выражению, стоящему под ее знаком (принимая его за аргумент), а потом от этого выражения по независимой переменной и результаты перемножить;

*) Под сложной тригонометрической функцией будем понимать тригонометрическую функцию сложного аргумента.

поэтому, считая и функцией от х, получаем:

Пользуясь правилом (1), процесс дифференцирования функции sin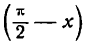 можно записать таким образом:

Пример:

Продифференцировать функцию

Решение:

Согласно правилу (2) настоящей лекции найдем:

Пример:

Продифференцировать функцию

Решение:

Переписав функцию в виде 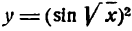найдем по правилу (6)

Но 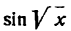сложная тригонометрическая функция, а потому согласно правилу (1) настоящей лекции имеем:

Следовательно,

Процесс дифференцирования данной функции можно записать следующим образом:

Производная логарифмической функции

Пусть дана функция

Для ее дифференцирования применим общее правило.

или

Положим

отсюда

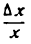
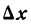
Подставив значения и в равенство (1), получим:

или, после потенцирования

Из равенства (2) следует, что, если

4-й шаг. Принимая во внимание условие (3), напишем:

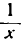
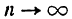
Множитель не зависит от n поэтому его можно считать постоянным при ; следовательно,

В подробных курсах анализа доказывается теорема: предел логарифма переменной величины равен логарифму предела этой же переменной величины; поэтому

Но, согласно,

Равенство (4) будет иметь вид

Следовательно,

т. е. производная натурального логарифма равна единице, деленной на аргумент.

Если дан десятичный логарифм, то его нужно предварительно выразить через натуральный. Мы знаем, что

Дифференцируя обе части последнего равенства, получим:

или

т. е. производная десятинного логарифма равна произведению производной натурального логарифма на постоянный множитель 0,4343.

Пример:

Продифференцировать функцию

Решение:

Данная функция сложная; положим

тогда

Отсюда согласно формуле (5) имеем:

Производную сложной логарифмической функции *) можно найти и по следующему правилу:

для дифференцирования сложной логарифмической функции нужно сначала взять производную от логарифма по выражению, стоящему под знаком логарифма (принимая его за аргумент), а потом от выражения, стоящего под знаком логарифма, по независимой переменной и результаты перемножить;

*) То-есть логарифмической функции сложного аргумента.

поэтому, считая и функцией х получаем:

Пример:

Продифференцировать функцию

Решение:

Согласно правилу (5) найдем:

Но cos ( 1—х) — сложная тригонометрическая функция; применяя к ней правило (2) , получим:

или

Пример:

Продифференцировать функцию

Решение:

Преобразуем сначала данную функцию, применив правила логарифмирования корня и дроби:

Продифференцировав полученную функцию [ln х по правилу (XIV), а ln (1 + x) по правилу (5)], найдем:

Производная степени при любом показателе

Мы вывели формулу

для m целого положительного. Докажем теперь справедливость этой формулы для любого показателя. Положим, что в равенстве

m имеет любое постоянное значение; логарифмируя это равенство по основанию е, получим:

Приняв во внимание, что ln у — сложная функция ( ln у зависит от у, а у зависит от x), дифференцируем обе части равенства (1) по х:

отсюда

Следовательно,

Производная показательной функции

Дана показательная функция

Прологарифмировав равенство (1) по основанию е, получим:

Дифференцируем это равенство по х, считая )ln у сложной функцией:

отсюда

Следовательно,

т. е. производная показательной функции 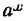равна произведению самой функции на натуральный логарифм основания.

Если дана показательная функция

где е — основание натурального логарифма, то производная ее найдется по формуле (XVI):

или

т. е. производная показательной функции равна самой функции.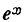

Пример:

Продифференцировать функцию

Решение:

Заменив данную сложную функцию двумя простыми, получим:

Согласно формуле (5) имеем:

Данную функцию можно дифференцировать и по следующему правилу:

для дифференцирования сложной показательной функции *) нужно сначала взять производную от показательной функции по выражению, стоящему в показателе (считая его аргументом), а потом от выражения, стоящего в показателе, по независимой переменной и результаты перемножить;

*) То-есть показательной функции сложного аргумента.

поэтому, считая и функцией от х, получаем:

Пример:

Продифференцировать функцию

Решение:

По правилу (3) настоящей лекции

Но согласно правилу (3)

Следовательно,

Производные обратных тригонометрических функций

1.

В силу определения арксинуса получаем:

Здесь sin у представляет сложную функцию (sin y зависит от у, а у зависит от х; дифференцируя обе части этого равенства по х, напишем):

или

откуда

Приняв во внимание, что

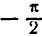
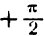
*) Здесь радикал берется с плюсом, так как значения arcsin х заключены между и , а в этом промежутке cos у имеет положительные значения.

а также равенство (1), получим:

или

2.

Согласно определению арккосинуса имеем:

Дифференцируя обе части этого равенства по x, считая cos у сложной функцией, найдем:

или

отсюда

Но

**) И здесь радикал берется с плюсом, так как значения arccos х заключены между 0 и 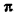; в этом же промежутке sin у имеет положительные значения.

поэтому

или

*) Здесь радикал берется с плюсом, так как значения arcsin х

К . TZ

заключены между — у и +у,ав этом промежутке cos у имеет

положительные значения.
**) И здесь радикал берется с плюсом, так как значения arccos х заключены между 0 и я; в этом же промежутке sin у имеет положительные значения.

3.

Согласно определению арктангенса имеем:

Дифференцируя обе части этого равенства по х, как и в предыдущих случаях, получим:

или

отсюда

Но

Приняв во внимание равенство (2), получим:

Следовательно,

4.

Для данной функции имеем:

После дифференцирования этого равенства получим:

или

отсюда

Но

Следовательно,

т. е.

Пример:

Продифференцировать функцию

Решение:

Заменим данную сложную функцию двумя простыми:

Согласно формуле (5) имеем:

Для дифференцирования этой функции можно воспользоваться и следующим правилом:

для дифференцирования сложной обратной тригонометрической функции*) нужно сначала взять производную от обратной тригонометрической функции по выражению, стоящему под ее знаком (принимая его за аргумент), а потом от этого же выражения по независимой переменной и результаты перемножить;

*) То-есть обратной тригонометрической функции сложного аргумента.

таким образом, считая и функцией от х, получаем:

Пример:

Продифференцировать функцию .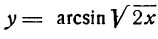

Решение:

Данная функция — обратная тригонометрическая и притом сложная; применяя вышеуказанное правило для производной аrсsin u, найдем:

Но 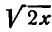тоже сложная функция; согласно правилу (7) имеем:

Следовательно,

Производная неявной функции

Пусть неявная функция у задана уравнением

Найдем производную у’, полагая, что она существует. Для этого дифференцируем обе части уравнения (1), применяя правило для производной алгебраической суммы, получим:

Так как ху — произведение переменных величин, то:

Таким образом, равенство (2) примет вид

или

Решая последнее уравнение относительно у’, найдем

Для дифференцирования данной функции можно было бы сначала выразить у через х, а потом уже найти производную от явной функции. В самом деле, из уравнения (1) имеем:

откуда

По внешнему виду этот результат отличается от найденного ранее, но если мы в равенстве (3) подставим значение у, то получим:

Таким образом, результаты дифференцирования в обоих случаях оказались одинаковыми. Однако переход от неявной к явной функции можно делать только в простейших случаях. Встречаются неявные функции, которые обратить в явные очень трудно и даже невозможно. Например, функцию у, заданную уравнением

ху + х = sin у, явно выразить нельзя. Поэтому приходится дифференцировать такие функции как неявные.

Разберем другой пример. Пусть требуется найти производную неявной функции у, заданной уравнением

Применяя правило дифференцирования алгебраической суммы, имеем:

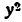
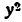
Но сложная функция ( зависит от у, а у зависит от х). По правилу дифференцирования сложной степенной функции имеем:

Следовательно, равенство (4) примет вид

или

откуда

Производная второго порядка

Пусть функция у = f(x) имеет производную у’ = f'(x). Производная от f'(x) по x , если она существует, называется второй производной или производной второго порядка.

Вторую производную функции у = f(x) принято обозначать так:

Пример:

Найти вторую производную функции

Решение:

Механический смысл второй производной

Пусть тело движется прямолинейно по закону

Мы установили, что скорость v движения тела в данный момент t определяется как производная пути по времени, т. е.

Если тело движется неравномерно, то скорость v с течением времени изменяется и за промежуток времени ät получает приращение . В этом случае величина отношения показывающая изменение скорости в единицу времени, называется средним ускорением в промежутке времени от t до t + .

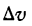
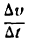
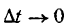
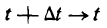
Положим, что , тогда среднее ускорение

стремится к величине, которая называется ускорением в данный момент времени t. Обозначив это ускорение через j, будем иметь:

Таким образом, ускорение прямолинейного движения тела в данный момент равно второй производной пути по времени, вычисленной для данного момента.

Пример:

Точка движется прямолинейно по закону

Найти скорость и ускорение точки в момент t = 5.

Решение:

Для определения скорости нужно найти первую производную данной функции при t = 5. Таким образом:

и

Ускорение j равно второй производной функции при t = 5, т. е.

Величина ускорения оказалась постоянной для любого значения t, значит, движение точки по заданному закону происходит с постоянным ускорением.

Дополнение к формулам дифференцирования

Смотрите также:

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Дифференциальное исчисление
45. Дифференциальные уравнения
46. Дифференциальные уравнения первого порядка
47. Дифференциальные уравнения высших порядков
48. Дифференциальные уравнения в частных производных
49. Тригонометрические функции
50. Тригонометрические уравнения и неравенства
51. Показательная функция
52. Показательные уравнения
53. Обобщенная степень
54. Взаимно обратные функции
55. Логарифмическая функция
56. Уравнения и неравенства
57. Положительные и отрицательные числа
58. Алгебраические выражения
59. Иррациональные алгебраические выражения
60. Преобразование алгебраических выражений
61. Преобразование дробных алгебраических выражений
62. Разложение многочленов на множители
63. Многочлены от одного переменного
64. Алгебраические дроби
65. Пропорции
66. Уравнения
67. Системы уравнений
68. Системы уравнений высших степеней
69. Системы алгебраических уравнений
70. Системы линейных уравнений
71. Системы дифференциальных уравнений
72. Арифметический квадратный корень
73. Квадратные и кубические корни
74. Извлечение квадратного корня
75. Рациональные числа
76. Иррациональные числа
77. Арифметический корень
78. Квадратные уравнения
79. Иррациональные уравнения
80. Последовательность
81. Ряды сходящиеся и расходящиеся
82. Тригонометрические функции произвольного угла
83. Тригонометрические формулы
84. Обратные тригонометрические функции
85. Теорема Безу
86. Математическая индукция
87. Показатель степени
88. Показательные функции и логарифмы
89. Множество
90. Множество действительных чисел
91. Числовые множества
92. Преобразование рациональных выражений
93. Преобразование иррациональных выражений
94. Геометрия
95. Действительные числа
96. Степени и корни
97. Степень с рациональным показателем
98. Тригонометрические функции угла
99. Тригонометрические функции числового аргумента
100. Тригонометрические выражения и их преобразования
101. Преобразование тригонометрических выражений
102. Комбинаторика
103. Вычислительная математика
104. Прямая линия на плоскости и ее уравнения
105. Прямая и плоскость
106. Линии и уравнения
107. Прямая линия
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат