Производная экспоненты
| Определение |
| Производная экспоненты равна самой же себе: $$ (e^x)’ = e^x $$ |
Если вместо $ x $ в экспоненте стоит сложная функция, то тогда производная экспоненты сложной функции находится по формуле: $$ (e^{f(x)})’ = e^{f(x)} cdot (f(x))’ = e^{f(x)} cdot f'(x) $$
То есть оставляем изначальную функцию неизменной и умножаем на производную степени, стоящей в экспоненте.
Примеры решения
| Пример 1 |
| Найти производную экпоненты в степени $ 2x $: $$ y = e^{2x} $$ |
| Решение |
|
Так как дана сложная функция, то находим производную по правилу: $$ (e^{f(x)})’ = e^{f(x)} cdot $$(x))’ = e^{f(x)} cdot f'(x) $$ Для этого считаем $ f(x) = 2x $ и $ f'(x) = (2x)’ = 2 $. Подставляем всё в формулу: $$ y’=(e^{2x})’ = e^{2x} cdot (2x)’ = e^{2x} cdot 2 = 2e^{2x} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y’ = 2e^{2x} $$ |
| Пример 2 |
| Найти производную экспоненты сложной функции: $$ y = cos e^x $$ |
| Решение |
|
Такая функция является сложной и взять от неё производную нужно по соответствующему правилу: $$ y’ = ( f(g(x)) )’ = f'(g(x)) cdot g'(x) $$ Записываем: $$ y’ = (cos e^x)’ = -sin e^x cdot (e^x)’ = -sin e^x cdot e^x = -e^x sin e^x $$ |
| Ответ |
| $$ y’ = -e^x sin e^x $$ |
Обратите внимание на то, что экспонента является единственной функцией на которую не оказывает влияния производная!
Содержание:
- Формула
- Примеры вычисления производной экспоненты
Формула
$$left(e^{x}right)^{prime}=e^{x}$$
Производная от экспоненты равна этой же экспоненте.
Заметим, что если степень экспоненты есть сложная функция, то
при нахождении производной экспоненту надо еще умножить на производную степени, то есть
$$left(e^{u}right)^{prime}=e^{u} cdot u^{prime}$$
Примеры вычисления производной экспоненты
Пример
Задание. Найти производную функции $y(x)=2 e^{x}$
Решение. Искомая производная
$$y^{prime}(x)=left(2 e^{x}right)^{prime}$$
По правилу дифференцирования константу можно выносить за знак производной, тогда будем иметь:
$$y^{prime}(x)=2 cdotleft(e^{x}right)^{prime}=2 cdot e^{x}=2 e^{x}$$
Ответ. $y^{prime}(x)=2 e^{x}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить производную функции $y(x)=e^{2x}$
Решение. Искомая производная
$$y^{prime}(x)=left(e^{2 x}right)^{prime}$$
Так как степень у экспоненты есть сложная функция, то производную от экспоненты умножим на производную от степени:
$$y^{prime}(x)=e^{2 x} cdot(2 x)^{prime}$$
Константу выносим за знак производной:
$$y^{prime}(x)=e^{2 x} cdot 2 cdot(x)^{prime}=2 e^{2 x} cdot 1=2 e^{2 x}$$
Ответ. $y^{prime}(x)=2 e^{2 x}$
Читать дальше: производная показательной функции (a^x)’.
Найдем производную функции f(x)=exf(x)=e^x и приведем некоторые ее свойства и практические примеры использования.
Производная экспоненты
Как известно, производной функции f(x)f(x), определенной в точке x0x_0 и в некотором интервале, содержащем x0x_0, называют предел следующего вида:
f′(x0)=dfdx∣x=x0=limΔx→0f(x0+Δx)−f(x0)Δxf^{‘}(x_0)=dfrac{df}{dx}Bigr|_{x=x_0}=limlimits_{Delta x to 0}dfrac{ f(x_0+ Delta x)-f(x_0 )}{ Delta x},
если только такой предел существует.
Таким образом, для вычисления производной функции f(x)f(x) необходимо последовательно:
- Записать выражение для приращения функции:
Δf(x0)=f(x0+Δx)−f(x0)Delta f(x_0 )=f(x_0+Delta x)-f(x_0 )
- Упростить, по возможности, дробь
Δf(x0)Δx=f(x0+Δx)−f(x0)Δxdfrac {Delta f(x_0)}{Delta x}=dfrac {f(x_0+Delta x)-f(x_0)}{Delta x}
- Вычислить предел дроби при Δx→0Delta x to 0 и записать полученное выражение для производной.
Применим этот алгоритм к вычислению производной экспоненты:
- Записываем приращение функции:
Δf(x0)=f(x0+Δx)−f(x0)=ex0+Δx−ex0=ex0(eΔx−1)Delta f(x_0)= f(x_0+Delta x)-f(x_0)= e^{x_0+Delta x}-e^{x_0}=e^{x_0} (e^{Delta x}-1)
- Получаем дробь:
Δf(x0)Δx=ex0eΔx−1Δxdfrac {Delta f(x_0)}{Delta x}= e^{x_0} dfrac {e^{Delta x}-1}{Delta x}
- Вычисляем производную:
f′(x0)=limΔx→0ex0eΔx−1Δx=ex0limΔx→0eΔx−1Δxf'(x_0 )= limlimits_{Delta x to 0} {e^{x_0} dfrac {e^{Delta x}-1}{Delta x}}= e^{x_0}limlimits_{Delta x to 0} {dfrac {e^{Delta x}-1}{Delta x}}
Для преобразования eΔxe^{Delta x} используем представление числа e≈2,71828e approx2,71828 (числа Непера или числа Эйлера) в виде предела:
e=limn→∞(1+1n)ne=limlimits_{ntoinfty} Bigl( {1+dfrac {1}{n}} Bigr) ^n
Следовательно:
eΔx=limn→∞(1+Δxn)ne^{Delta x} =limlimits_{ntoinfty} Bigl( {1+dfrac {Delta x }{n}} Bigr) ^n
Используем для выражения под знаком предела бином Ньютона:
(1+Δxn)n=1+Cn1Δxn+Cn2(Δxn)2+…+Cnn(Δxn)nBigl( {1+dfrac {Delta x }{n}} Bigr) ^n=1+C_n^1 dfrac{Delta x }{n}+ C_n^2 Bigl( {dfrac{Delta x }{n}}Bigr)^2+ ldots + C_n^n Bigl( {dfrac{Delta x }{n}}Bigr)^n
Тогда:
f′(x0)=ex0limΔx→0limn→∞(1+Cn1Δxn+Cn2(Δxn)2+…+Cnn(Δxn)n)−1Δx=f'(x_0 )= e^{x_0}limlimits_{Delta x to 0}dfrac {limlimits_{ntoinfty} Bigl( {1+C_n^1 dfrac{Delta x }{n}+ C_n^2 Bigl( {dfrac{Delta x }{n}}Bigr)^2+ ldots + C_n^n Bigl( {dfrac{Delta x }{n}}Bigr)^n }Bigr)-1}{Delta x } =
=ex0limΔx→0(limn→∞Cn1Δxn+Cn2(Δxn)2+…+Cnn(Δxn)nΔx)==e^{x_0}limlimits_{Delta x to 0}Bigl( limlimits_{ntoinfty} dfrac {C_n^1 dfrac{Delta x }{n}+ C_n^2 Bigl( {dfrac{Delta x }{n}}Bigr)^2+ ldots + C_n^n Bigl( {dfrac{Delta x }{n}}Bigr)^n }{Delta x } Bigr)=
=ex0limΔx→0limn→∞(Cn11n+Cn2(Δx)2−1n2+…+Cnn(Δx)n−1nn)==e^{x_0}limlimits_{Delta x to 0} limlimits_{ntoinfty} Bigl( {C_n^1 dfrac{1}{n}+ C_n^2 dfrac{(Delta x)^{2-1} }{n^2}+ ldots + C_n^n dfrac{(Delta x)^{n-1} }{n^n}}Bigr)=
=ex0limn→∞limΔx→0(n1n+Cn2(Δx)2−1n2+…+Cnn(Δx)n−1nn)== e^{x_0}limlimits_{ ntoinfty } limlimits_{Delta x to 0} Bigl( {n dfrac{1}{n}+ C_n^2 dfrac{(Delta x)^{2-1} }{n^2}+ ldots + C_n^n dfrac{(Delta x)^{n-1} }{n^n}}Bigr)=
=ex0(1+limn→∞limΔx→0(Cn2(Δx)2−1n2+…+Cnn(Δx)n−1nn))= e^{x_0} Bigl( 1+ limlimits_{ ntoinfty } limlimits_{Delta x to 0} Bigl( { C_n^2 dfrac{(Delta x)^{2-1} }{n^2}+ ldots + C_n^n dfrac{(Delta x)^{n-1} }{n^n}}Bigr) Bigr)
Учитывая, что:
limΔx→0(Cn2(Δx)2−1n2+…+Cnn(Δx)n−1nn)=0limlimits_{Delta x to 0} Bigl( { C_n^2 dfrac{(Delta x)^{2-1} }{n^2}+ ldots + C_n^n dfrac{(Delta x)^{n-1} }{n^n}}Bigr)=0,
получаем:
f′(x0)=ex0(1+0)f'(x_0 )= e^{x_0}(1+0)
Таким образом:
f′(x)=(ex)′=exf'(x)= (e^{x})^{‘}=e^{x}
Как видно, производная экспоненциальной функции f(x)=exf(x)=e^x равна этой же функции.
Некоторые свойства и практические примеры
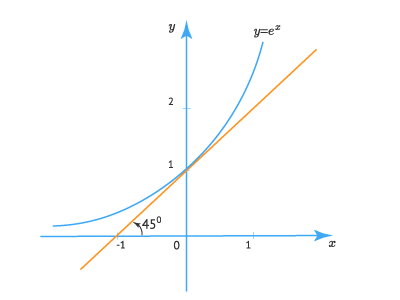
Угол наклона αalpha касательной к графику функции y=exy=e^x в точке x=x0x=x_0 определяется соотношением:
tgα=y′(x0)=ex0tg alpha =y^{‘} (x_0 )=e^{x_0}
Здесь угол αalpha это угол между касательной и осью OxOx, отсчитываемый от положительного направления OxOx против часовой стрелки.
Производная функции f(x)=exf(x)=e^x в точке x=0x=0 равна 11:
f′(0)=(ex)x=0′=e0=1f^{‘}(0)=(e^x )_{x=0}^{‘}=e^0=1
Это означает, что касательная к графику в точке M(0;1)M(0;1) с координатами: x0=0,y0=e0=1x_0=0, y_0=e^0=1 составляют с осью OxOx угол 45∘(tg45∘=1)45^{circ} (tg {45^{circ}}=1)
Производная сложной функции y=eg(x)y=e^{g(x)} согласно правил дифференцирования, равна:
y′=g′(x)eg(x)y’=g'(x) e^{g(x)}
Производная сложной функции y=u(v)y=u(v), где v=exv=e^x равна:
y′=uv′⋅v′=uv′⋅exy’=u’_v cdot v’=u’_v cdot e^x
Найти производную функции
f(x)=ex2+2xf(x)=e^{x^2+2x}
Решение
f′(x)=(ex2+2x)′=(x2+2x)′⋅ex2+2x=(2x+2)ex2+2xf'(x)= Bigl( e^{x^2+2x} Bigr)’=(x^2+2x)’ cdot e^{x^2+2x}=(2x+2) e^{x^2+2x}
Найти производную функции
f(x)=sine2xf(x)=sin{e^{2x}}
Решение
Полагаем: e2x=ve^{2x}=v
Тогда:
f′(x)=(sinv)v′⋅v′=cosv⋅(e2x)′=cos(e2x)⋅(2x)′e2x=2e2xcos(e2x)f'(x) = (sin v)_v’ cdot v’ = cos v cdot (e^{2x} )’ = cos (e^{2x}) cdot (2x)’ e^{2x}= 2e^{2x} cos(e^{2x})
Найти точку M(x0;y0)M(x_0; y_0) на графике функции y=exy=e^x в которой касательная к этому графику составляет с осью OxOx угол в 60∘60^{circ}.
Решение
Используя соотношение для угла наклона αalpha касательной:
tgα=f′(x)tg alpha =f’ (x)
для α=60∘alpha =60^{circ} получаем:
tg60∘=f′(x)=ex0tg 60^{circ}= f’ (x)=e^{x_0}
Отсюда находим координату x0x_0 точки MM:
ex0=3⇒x0=ln3e^{x_0}= sqrt 3 Rightarrow x_0=ln sqrt 3
Далее:
y0=ex0=eln3=3y_0=e^{x_0}=e^{ln sqrt 3}=sqrt 3
Искомая точка: M(ln3;3)M(ln sqrt 3; sqrt 3)
Тест по теме «Производная экспоненты»
Download Article
Download Article
Exponential functions are a special category of functions that involve exponents that are variables or functions. Using some of the basic rules of calculus, you can begin by finding the derivative of a basic functions like 
. This then provides a form that you can use for any numerical base raised to a variable exponent. Expanding this work, you can also find the derivative of functions where the exponent is itself a function. Finally, you will see how to differentiate the “power tower,” a special function in which the exponent matches the base.
-
1
Begin with a general exponential function. Begin with a basic exponential function using a variable as the base. By calculating the derivative of the general function in this way, you can use the solution as model for a full family of similar functions.[1]
-
2
Take the natural logarithm of both sides. You need to manipulate the function to help find a standard derivative in terms of the variable
. This begins by taking the natural logarithm of both sides, as follows:
Advertisement
-
3
Eliminate the exponent. Using the rules of logarithms, this equation can be simplified to eliminate the exponent. The exponent within the logarithm function can be removed as a multiple in front of the logarithm, as follows:
-
4
-
5
-
6
Advertisement
-
1
Choose the special example. The prior section showed how to differentiate the general case of an exponential function with any constant as the base. Next, select the special case where the base is the exponential constant
.[2]
-
2
-
3
Simplify the result. Recall that the natural logarithm is based on the special constant
. Therefore, the natural logarithm of is just 1. This simplifies the derivative result as follows:[4]
-
4
Interpret the final result. This proof leads to the special case that the derivative of the function
is that very function itself. Thus:[5]
Advertisement
-
1
-
2
-
3
Apply the chain rule. The chain rule requires you to find the derivatives of both functions
and . The resulting derivative is then the product of those two.[8]
-
4
Practice another example of
with a functional exponent. Select another example, .[9]
Advertisement
-
1
Define the function. For this special example, sometimes called the “power tower,” choose the function such that:[10]
-
2
Find the natural logarithm of each side. As before, the solution here begins with the natural logarithm of each side of the equation:[11]
-
3
Take the derivative of each side of the equation. On the right side of this equation, you will need to apply the product rule of derivatives. Recall that the product rule states that if
, then .[12]
-
4
Multiply each side by y. Isolate the derivative term on the right by multiplying both sides of the equation by y.[13]
-
5
Replace the original value of y. Recall from the first step that the function is
. Replacing this term in place of is the last step to find the derivative.[14]
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Advertisement
About This Article
Thanks to all authors for creating a page that has been read 141,863 times.
Did this article help you?
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Основные понятия
Прежде чем разобрать вопрос о производной от экспоненты в степени $x$, напомним определения
- функции;
- предела последовательности;
- производной;
- экспоненты.
Это необходимо для ясного понимания производной от экспоненты в степени $x$.
Определение 1
Функцией называют зависимость между двумя переменными величинами.
Возьмём $y=f(x)$, где $x$ и $y$ являются переменными величинами. Здесь $x$ называется аргументом, а $y$ — функцией. Аргумент может принимать произвольные значения. В свою очередь, переменная $y$ изменяется по определённому закону в зависимости от аргумента. То есть аргумент $x$ — это независимая переменная, а функция $y$ — это зависимая переменная. Любому значению $x$ соответствует единственное значение $y$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Если каждому натуральному числу $n=1, 2, 3, …$ поставить в соответствие в силу некоторого закона число $x_n$, то говорят, что определена последовательность чисел $x_1,x_2,…,x_n$. Иначе такая последовательность записывается как ${x_n}$. Все числа $x_n$ называют членами или элементами последовательности.
Определение 2
Пределом последовательности называют конечную или бесконечно удалённую точку числовой прямой. Предел записывают так: $lim x_n = limlimits_{ntoinfty}x_n = a$. Эта запись означает, что переменная $x_n$ стремится к $a$ $x_nto a$.
Производной функции $f$ в точке $x_0$ называется следующий предел:
$limlimits_{xto x_0}frac{f(x) — f(x_o)}{x-x_o}$. Он обозначается $f'(x_0)$.
Число $e$ равно следующему пределу:
$e=limlimits_{xtoinfty} (1+frac{1}{n})approx2,718281828459045…$
В данном пределе $n$ это натуральное или действительное число.
Владея понятиями о пределе, производной и экспоненте, можем приступить к доказательству формулы $(e^x)’=e^x$.
«Производная от экспоненты в степени х» 👇
Вывод производной от экспоненты в степени $x$
Имеем $e^x$, где $x: -infty
$y’=limlimits_{Delta xto 0} frac{e^{x+Delta x}-e^x}{Delta x}$.
По свойству экспоненты $e^{a+bx}=e^a*e^b$ можем преобразовать числитель предела:
$e^{x+Delta x}-e^x = e^x*e^{Delta x}-e^x = e^x(e^{Delta x}-1)$.
То есть $y’=limlimits_{Delta xto 0} frac{e^{x+Delta x}-e^x}{Delta x}=limlimits_{Delta xto 0} frac{e^x(e^{Delta x}-1)}{Delta x}$.
Обозначим $t=e^{Delta x}-1$. Получим $e^{Delta x}=t+1$, а по свойству логарифма выходит, что $Delta x = ln(t+1)$.
Так как экспонента непрерывна, имеем $limlimits_{Delta xto 0} e^{Delta x}=e^0=1.$ Поэтому если $Delta xto 0$, то и $t to 0$.
В результате покажем преобразование:
$y’=limlimits_{Delta xto 0} frac{e^{Delta x}-1}{Delta x}=e^xlimlimits_{tto 0}frac{t}{ln(t+1)}$.
Обозначим $n=frac {1}{t}$, тогда $t=frac{1}{n}$. Получается, что если $tto 0$, то $ntoinfty$.
Преобразуем наш предел:
$y’=e^xlimlimits_{tto 0}frac{t}{ln(t+1)}=e^xlimlimits_{ntoinfty}frac{1}{ncdot ln(frac{1}{n}+1)^n}$.
По свойству логарифма $bcdot ln c=ln c^b$ имеем
$ncdot ln (frac{1}{n}+1)=ln(frac{1}{n}+1)^n=ln(1+frac{1}{n})^n$.
Предел преобразуется следующим образом:
$y’=e^xlimlimits_{ntoinfty}frac{1}{ncdot ln(frac{1}{n}+1)} = e^xlimlimits_{ntoinfty}frac{1}{ln(frac{1}{n}+1)^n}= e^xfrac{1}{limlimits_{ntoinfty} ln(frac{1}{n}+1)^n}$.
Согласно свойству непрерывности логарифма и свойства пределов для непрерывной функции: $limlimits_{xto x_0}ln(f(x))=ln(limlimits_f(x))$, где $f(x)$ имеет положительный предел $limlimits_{xto x_0}f(x)$. Итак, в связи с тем, что логарифм непрерывен и существует положительный предел $limlimits_{ntoinfty}(frac{1}{n}+1)^n$, то можем вывести:
$limlimits_{ntoinfty}ln(1+frac{1}{n})^n=lnlimlimits_{ntoinfty}ln(1+frac{1}{n})^n=ln e=1$.
Воспользуемся значением второго замечательного предела $limlimits_{ntoinfty}(1+frac{1}{n})^n=e$. Получаем:
$y’= e^xfrac{1}{limlimits_{ntoinfty} ln(frac{1}{n}+1)^n} = e^xcdotfrac{1}{ln e} = e^xcdotfrac{1}{1}=e^x$.
Таким образом, мы вывели формулу производной экспоненты и можем утверждать, что производная от экспоненты в степени $x$ эквивалентна экспоненте в степени $x$:
$(e^x)’=e^x$.
Существуют также другие способы вывода этой формулы с использованием другим формул и правил.
Пример 1
Рассмотрим пример нахождения производной функции.
Условие: Найти производную функции $y=2^x + 3^x + 10^x + e^x$.
Решение: К слагаемым $2^x, 3^x$ и $10^x$ применяем формулу $(a^x)’=a^xcdot ln a$. Согласно выведенной формуле $(e^x)’=e^x$ четвертое слагаемое $e^x$ не изменяется.
Ответ: $y’ = 2^xcdot ln 2 + 3^xcdot ln 3 + 10^xcdot ln 10 + e^x$.
Таким образом, мы вывели формулу $(e^x)’=e^x$, при этом дав определения основным понятиям, разобрали пример нахождения производной функции с экспонентой в качестве одного из слагаемых.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме