Все предметы
Биология
География
Физика
Химия
История
Обществознание
Русский язык
Литература
Экономика
Право
Математика
Алгебра
Геометрия
Информатика
Английский язык
Українська мова
Українська література
Другие предметы
Беларуская мова
Қазақ тiлi
Немецкий язык
Окружающий мир
Французский язык
Музыка
МХК
ОБЖ
Психология
Оʻzbek tili
Кыргыз тили
Астрономия
Физкультура и спорт


termitprofiq
+10
Ответ дан
6 лет назад
Алгебра
10 — 11 классы
Найдите производную функции y = 4x^3
1) 12x^2
2)12x
3)4x^2
4)12x^3
рассчитать
Ответ проверен экспертом
1/5
(4 оценки)
7

Uiplomb
6 лет назад
Светило науки — 2 ответа — 0 раз оказано помощи
f′(x)=(4⋅x3)′==4⋅(x3)′==12⋅x2
Оцените пользу ответа

Мозг
Отвечающий
Остались вопросы?
Задать вопрос
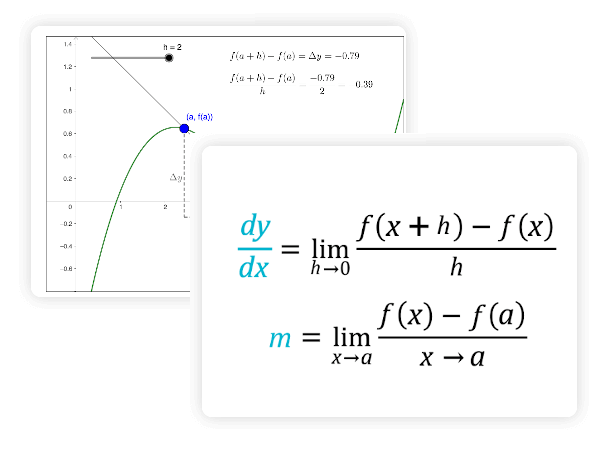
Определение производной
Определение. Пусть функция ( y = f(x) ) определена в некотором интервале, содержащем внутри себя точку ( x_0 ).
Дадим аргументу приращение ( Delta x ) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
( Delta y ) (при переходе от точки ( x_0 ) к точке ( x_0 + Delta x ) ) и составим отношение
( frac{Delta y}{Delta x} ). Если существует предел этого отношения при ( Delta x rightarrow 0 ), то
указанный предел называют производной функции ( y=f(x) ) в точке ( x_0 ) и обозначают ( f'(x_0) ).
$$ lim_{Delta x to 0} frac{Delta y}{Delta x} = f'(x_0) $$
Для обозначения производной часто используют символ ( y’ ).
Отметим, что ( y’ = f(x) ) — это новая функция, но, естественно, связанная с функцией ( y = f(x) ), определенная во всех точках (x), в которых
существует указанный выше предел. Эту функцию называют так: производная функции ( y = f(x) ).
Геометрический смысл производной состоит в следующем. Если к графику функции ( y = f(x) ) в точке с абсциссой ( x=a ) можно
провести касательную, непараллельную оси (y), то ( f(a) ) выражает угловой коэффициент касательной:
( k = f'(a) )
Поскольку ( k = tg(a) ), то верно равенство ( f'(a) = tg(a) ) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция ( y = f(x) ) имеет
производную в конкретной точке ( x ):
$$ lim_{Delta x to 0} frac{Delta y}{Delta x} = f'(x) $$
Это означает, что около точки (x) выполняется приближенное равенство ( frac{Delta y}{Delta x} approx f'(x) ), т.е.
( Delta y approx f'(x) cdot Delta x ).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально»
приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке (x).
Например, для функции ( y = x^2 ) справедливо приближенное равенство ( Delta y approx 2x cdot Delta x ).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение ( x ), найти ( f(x) )
2. Дать аргументу ( x ) приращение ( Delta x ), перейти в новую точку ( x+ Delta x ), найти ( f(x+ Delta x) )
3. Найти приращение функции: ( Delta y = f(x + Delta x) — f(x) )
4. Составить отношение ( frac{Delta y}{Delta x} )
5. Вычислить $$ lim_{Delta x to 0} frac{Delta y}{Delta x} $$
Этот предел и есть производная функции в точке (x).
Если функция (y=f(x)) имеет производную в точке (x), то ее называют дифференцируемой в точке (x). Процедуру нахождения производной
функции (y=f(x)) называют дифференцированием функции (y=f(x)).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция (y=f(x)) дифференцируема в точке (x). Тогда к графику функции в точке ( M(x; ; f(x)) ) можно провести касательную,
причем, напомним, угловой коэффициент касательной равен ( f'(x) ). Такой график не может «разрываться» в точке (M), т. е. функция
обязана быть непрерывной в точке (x).
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция (y=f(x)) дифференцируема в точке (x), то
выполняется приближенное равенство ( Delta y approx f'(x) cdot Delta x ). Если в этом равенстве ( Delta x ) устремить к
нулю, то и ( Delta y ) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция ( y=|x|) непрерывна везде, в частности в точке (x=0), но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция ( y=sqrt[3]{x} ) непрерывна на всей числовой прямой, в том числе в точке (x=0).
И касательная к графику функции существует в любой точке, в том числе в точке (x=0). Но в этой точке касательная совпадает с осью (y),
т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид (x=0). Углового коэффициента у такой прямой нет, значит, не существует и
( f'(0) )
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее
дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси
абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она
перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием.
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если (C) — постоянное число и ( f=f(x), ; g=g(x) ) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
$$ C’=0 $$
$$ x’=1 $$
$$ ( f+g)’=f’+g’ $$
$$ (fg)’=f’g + fg’ $$
$$ (Cf)’=Cf’ $$
$$ left(frac{f}{g} right) ‘ = frac{f’g-fg’}{g^2} $$
$$ left(frac{C}{g} right) ‘ = -frac{Cg’}{g^2} $$
Производная сложной функции:
$$ f’_x(g(x)) = f’_g cdot g’_x $$
Таблица производных некоторых функций
$$ left( frac{1}{x} right) ‘ = -frac{1}{x^2} $$
$$ ( sqrt{x} ) ‘ = frac{1}{2sqrt{x}} $$
$$ left( x^a right) ‘ = a x^{a-1} $$
$$ left( a^x right) ‘ = a^x cdot ln a $$
$$ left( e^x right) ‘ = e^x $$
$$ ( ln x )’ = frac{1}{x} $$
$$ ( log_a x )’ = frac{1}{xln a} $$
$$ ( sin x )’ = cos x $$
$$ ( cos x )’ = -sin x $$
$$ ( text{tg} x )’ = frac{1}{cos^2 x} $$
$$ ( text{ctg} x )’ = -frac{1}{sin^2 x} $$
$$ ( arcsin x )’ = frac{1}{sqrt{1-x^2}} $$
$$ ( arccos x )’ = frac{-1}{sqrt{1-x^2}} $$
$$ ( text{arctg} x )’ = frac{1}{1+x^2} $$
$$ ( text{arcctg} x )’ = frac{-1}{1+x^2} $$
Что такое производная в математике
Производная функции — это понятие дифференциального исчисления, которое характеризует скорость изменения функции в данной точке. Он определяется как предел отношения приращения функции к приращению ее аргумента, когда приращение аргумента стремится к нулю, если такой предел существует. Функция, имеющая конечную производную (в некоторой точке), называется дифференцируемой (в этой точке).
Процесс вычисления производной называется дифференцированием. Обратный процесс — поиск оригинала — интеграция.
Почему вам может понадобиться рассчитать производную
На первый взгляд производные нужны, чтобы набить головы уже перегруженным школьникам, но это не так. Рассмотрим машину, которая ездит по городу. Иногда стоит, иногда едет, иногда тормозит, иногда ускоряется.
Допустим, он ехал 3 часа и проехал 60 километров. Затем, используя формулу из начальной школы, мы делим 60 на 3 и говорим, что она ехала со скоростью 20 км / ч. Мы правы? Что ж, отчасти верно. Получили «среднюю скорость». Но что от этого толку? На этой скорости машина может ехать 5 минут, а в остальное время ехать медленнее или быстрее. Что я должен делать?
А зачем нам знать скорость на все 3 часа маршрута? Разделим маршрут на 3 части по часу и рассчитаем скорость на каждом участке. Давайте. Допустим, у вас скорость 10, 20 и 30 км/ч. Вот. Ситуация уже более ясная — в последний час машина ехала быстрее, чем в предыдущие.
Но это опять же в среднем. Что, если он просто ехал медленно полчаса за последний час, а затем внезапно ускорился и начал быстро двигаться? Да, может быть так.
Как мы видим, чем больше мы разбиваем наш 3-часовой интервал, тем точнее мы получим результат. Но нам не нужен «более точный» результат — нам нужен совершенно точный результат. Это означает, что время нужно делить на бесконечное количество частей. А сама деталь — значит, будет бесконечно маленькой.
Если мы разделим на это время расстояние, которое машина преодолела за бесконечно малый период времени, мы также получим скорость. Но уже не средний, а «моментальный». И таких мгновенных скоростей тоже будет бесконечно много.
Если вы понимаете все вышеперечисленное, тогда вы понимаете значение производной. Производная — это скорость, с которой что-то меняется. Например, в нашем случае скорость — это скорость, с которой «пройденное расстояние» изменяется во времени. А может быть «скорость изменения температуры при изменении долготы к северу». Или «скорость исчезновения конфет из вазы на кухне». В общем, если есть что-то, определенное значение «Y», которое зависит от некоторого значения «X», то, скорее всего, есть является производной, которая записывается как dy / dx. И это просто показывает, как значение y изменяется при бесконечно малом изменении значения x — как наше расстояние изменилось при бесконечно малом изменении во времени.

Данный калькулятор вычисляет производную функции и затем упрощает ее.
В поле функция введите математическое выражение с переменной x, в выражении используйте стандартные операции + сложение, — вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции. Полный синтаксис смотрите ниже.
Упрощение полученной производной может занять некоторое время, для сложных функций — весьма продолжительное. Если ждать до конца нет сил — нажмите кнопку остановить. У меня получался достаточно простой вариант уже после 10-15 секунд работы алгоритма упрощения.
Калькулятор производных
Производная функции
Допустимые операции: + — / * ^
Константы: pi
Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Показать детали вычисления
Показать шаги вычисления производной и упрощения формулы
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Синтаксис описания формул
В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, — — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.
Таблица синтаксиса математических выражений
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Вычисление производной
Вычисление производной — дело нехитрое, достаточно знать несколько простых правил и формулы дифференцирования простых функций; сложнее в этом онлайн калькуляторе было сделать интерпретатор математических выражений и алгоритм упрощения полученного результата, но об этом как-нибудь в другой раз…
Правила дифференцирования
1) производная суммы:
2) производная произведения:
3) производная частного:
4) производная сложной функции равна произведению производных:
Таблица производных
Производная степенной функции:
Производная показательной функции:
Производная экспонециальной функции:
Производная логарифмической функции:
Производные тригонометрических функций:
,
,
,
Производные обратных тригонометрических функций:
,
,
,
Производные гиперболических функций:
калькулятор производных онлайн помогает найти производную функции онлайн по заданной переменной и показывает пошаговое дифференцирование. Для лучшего понимания вы можете взглянуть на приведенные примеры, чтобы различать функцию. Вы можете использовать этот калькулятор производной для упрощения первой, второй, третьей или до 5 производных.
Без сомнения, онлайн калькулятор производных – лучший способ получить производные в любой момент и даже поможет вам решить частные производные. Что ж, этот контекст предоставляет вам правила производной, как найти производную онлайн (шаг за шагом) и с онлайн калькулятор.
В математике «производная» измеряет чувствительность к изменению выходного значения по отношению к изменению входного значения, но в расчетах производные являются центральными инструментами.
В случае движущегося объекта по времени производной является изменение скорости за определенное время. Проще говоря, он измеряет, насколько быстро движущийся объект меняет свое положение с течением времени. Следовательно, производная – это «мгновенная скорость изменения» зависимой переменной по отношению к независимой переменной.
Процесс поиска производной известен как дифференциация. Следовательно, калькулятор производных будет большим подспорьем для быстрой идентификации производных.
производная калькулятор функции f представлена как d / dx * f. «D» обозначает оператор производной, а x – переменную. Калькулятор деривативов позволяет вам находить деривативы без каких-либо затрат и ручных усилий. Однако производная от «производной функции» известна как вторая производная и может быть вычислена с помощью калькулятор производной второй производной. всякий раз, когда вам нужно обрабатывать до 5 деривативов вместе с последствиями правил дифференциации, просто попробуйте поискать деривативы, чтобы избежать риска ошибок.
Есть определенные правила, по которым можно узнать производные. Эти полезные правила помогут вам вычислить деривативы. Следуя им, вы можете добавить вычитание и понять, как брать производную. Посмотрите ниже, чтобы узнать о них:
| Общие функции | Функция | Производная |
|---|---|---|
| Постоянный | c | 0 |
| Линия | x | 1 |
| ax | a | |
| Квадрат | x2 | 2x |
| Квадратный корень | √x | (½)x-½ |
| Экспоненциальный | ex | ex |
| ax | ln(a) ax | |
| Логарифмы | ln(x) | 1/x |
| loga(x) | 1 / (x ln(a)) | |
| Тригонометрия (x в радианах) | sin(x) | cos(x) |
| cos(x) | −sin(x) | |
| tan(x) | sec2(x) | |
| Обратная тригонометрия | sin-1(x) | 1/√(1−x2) |
| cos-1(x) | −1/√(1−x2) | |
| tan-1(x) | 1/(1+x2) | |
| Правила | Функция | Производная |
|---|---|---|
| Умножение на константу | cf | cf’ |
| Правило власти | xn | nxn−1 |
| Правило суммы | f + g | f’ + g’ |
| Правило различия | f – g | f’ − g’ |
| Правило продукта | fg | f g’ + f’ g |
| Правило частного | f/g | (f’ g − g’ f )/g2 |
| Взаимное правило | 1/f | −f’/f2 |
| Правило цепи (как «Состав функций») |
f º g | (f’ º g) × g’ |
| Правило цепи (с помощью ‘ ) |
f(g(x)) | f’(g(x))g’(x) |
| Правило цепи (используя ( frac {dy} {dx} )) |
( frac{dy}{dx} = frac{dy}{du} frac{du}{dx}) |
Как найти производную (решенные примеры)?
Здесь мы поможем вам решить производные задачи в соответствии с вышеупомянутыми правилами дифференциации. Итак, начнем!
Пример:
Какая производная от (cos (x) )?
Помимо ручных вычислений, вы можете посмотреть на приведенную выше таблицу, чтобы найти производную онлайн функции онлайн от (cos (x) )
$$ frac {d} {dx} cos (x) $$
Мы можем написать так:
$$ = -sin (x) $$
Следовательно
$$ cos (x) ‘= – sin (x) $$
Правило власти:
Пример:
Что такое ( frac {d} {dx} x ^ 2 )?
Мы используем правило мощности, где (n = 2 ):
$$ frac {d} {dx} x ^ n = nx ^ {n-1} $$
После помещения (n = 2 ) в формулу правила мощности
$$ frac {d} {dx} x ^ 2 = 2x ^ {2-1} $$
$$ = 2x $$
( frac {2} {x} ) также (2x ^ {- 1} )
$$ frac {d} {dx} 2x ^ {- 1} = 2 frac {d} {dx} x ^ {- 1} $$
$$ = 2 (-1) x ^ {- 1-1} $$
Так;
$$ = -2x ^ {- 2} $$
$$ = frac {-2} {x ^ 2} $$
Умножение на константу:
Пример:
Что такое ( frac {d} {dx} 3x ^ 4 )?
$$ frac {d} {dx} 3x ^ 4 $$
Взятие из правила власти
$$ frac {d} {dx} x ^ 4 = 4x ^ {4-1} = 4x ^ 3 $$
$$ frac {d} {dx} 3x ^ 4 = 3 frac {d} {dx} x ^ 4 = 3 * 4x ^ 3 = 12x ^ 3 $$
Правило суммы:
Согласно правилу суммы:
Производная от (x + y = x ‘+ y’ )
Пример:
Какая производная от (x ^ 3 + 13 x ^ 2 )?
Каждую производную берем отдельно, после чего складываем.
$$ x ^ 3 + 13 x ^ 2 $$
Используя правило силы
$$ frac {d} {dx} (x ^ 3 = 13x ^ 2) = frac {d} {dx} x ^ 3 + frac {d} {dx} 13x ^ 2 $$
Следовательно
$$ = 3x ^ {3-1} + 13 * 2x ^ {2-1} = 3x ^ 2 + 26x $$
Правило различия:
Согласно правилу различий:
Производная от (x – y = x ‘- y’ )
Пример:
Что такое ( frac {d} {dy} (y ^ 2 – 3y ^ 4) )?
Каждую производную берем отдельно, после чего складываем.
Используя правило мощности
$$ frac {d} {dy} (y ^ 2 – 3y ^ 4) = frac {d} {dy} y ^ 2 – frac {d} {dy} 3y ^ 4 $$
$$ = 2y ^ {2-1} – 3 * 4y ^ {4-1} $$
Следовательно
$$ = 2–12 лет ^ 3 $$
Сумма, разность, константа, умножение и правило мощности:
Пример:
Что такое ( frac {d} {dx} (3x ^ 3 + x ^ 2 -7x) )?
Используя правило мощности
$$ frac {d} {dx} (3x ^ 3 + x ^ 2 -7x) $$
$$ = frac {d} {dx} 3x ^ 3 + frac {d} {dx} x ^ 2 – frac {d} {dx} 7x $$
$$ = 3 * 3x ^ {2-1} + 2x ^ {2-1} – 7 * 1 $$
Следовательно
$$ = 9x ^ 2 + 2x – 7 $$
Правило продукта:
Согласно правилу продукта:
Производная от (xy = xy ‘+ x’y )
Пример:
Какая производная от (sin (x) cos (x) )?
Если мы поместим значения в Правило продукта:
$$ x = грех $$
$$ y = cos $$
После прочтения таблицы выше:
$$ frac {d} {dz} (sin (z) cos (z)) $$
$$ = sin (z) frac {d} {dz} cos (z) + cos (z) frac {d} {dz} sin (z) $$
Так
$$ = sin (z) (- sin (z)) + cos (z). cos (z) $$
$$ = – грех ^ 2 (z) + cos ^ 2 (z) $$
Правило частного:
Согласно правилу частных:
$$ ( frac {x} {y}) ‘= frac {xy’ – x’y} {y ^ 2} $$
Пример:
Какая производная от ( frac {sin (z)} {z} )?
$$ frac {d} {dz} ( frac {sin (z)} {z}) $$
$$ = frac {z frac {d} {dz} (sin (z)) – sin (z) frac {d} {dz} z} {z ^ 2} $$
Следовательно
$$ = frac {zcos (z) – sin (z)} {z ^ 2} $$
Взаимное правило:
Согласно взаимному правилу:
Производная от ( frac {1} {w} = frac {-fw ‘} {w ^ 2} )
Пример:
Что такое ( frac {d} {dw} ( frac {1} {w}) )?
$$ frac {1} {w} $$
Используя (f (w) = w ), мы видим, что (f ’(w) = 1 )
$$ frac {d} {dw} ( frac {1} {w}) $$
Следовательно
$$ = frac {-1} {w ^ 2} $$
Правило цепи:
Согласно правилу цепочки:
Вывод (f (g (x)) = f ‘(g (x)) g’ (x) )
Пример:
Что такое ( frac {d} {dx} (cos (x ^ 3)) )?
$$ frac {dy} {dx} = frac {dy} {du}. frac {du} {dx} $$
Различайте каждое значение:
$$ frac {d} {dx} (cos (x ^ 3)) $$
$$ f (h) = cos (h) $$
Значение (h (x) )
$$ h (x) = x ^ 3 $$
$$ f ‘(h) = -sin (x) $$
$$ h ‘(x) = 3x ^ 2 $$
Согласно приведенной выше таблице производная от (cos (x) )
$$ frac {d} {dx} (cos (x ^ 3)) = -sin (h (x)) (3x ^ 2) $$
$$ = – 3x ^ 2 sin (x ^ 3) $$
по аналогии
$$ frac {d} {dx} (cos (x ^ 3)) = frac {d} {du} cos (u) frac {d} {x} x ^ 3 $$
$$ = -sin (u) 3x ^ 2 $$
Следовательно
$$ = -3x ^ 2 sin (x ^ 3) $$
Как работает онлайн-калькулятор производных финансовых инструментов?
Чтобы вычислить производную, вам необходимо выполнить простую пошаговую процедуру:
Вход:
- Прежде всего, вы введете уравнение с помощью вспомогательных функций, таких как sqrt, log, sin, cos, tan и т. Д. Вы можете получить помощь при загрузке уравнения, загрузив примеры в раскрывающемся меню. Он также будет предварительно
- просматривать ваше уравнение.
- Теперь выберите производную по (a, b, c, x, y, z или n ).
- Выберите количество раз, чтобы различать. Вы можете выбрать до 5 раз
- Нажмите кнопку “Рассчитать”
Выход:
- Прежде всего, он покажет ваш ввод
- Во-вторых, он найдет производную функции
- В-третьих, это упростит ваш ответ
- Он также покажет вам все расчеты вместе с применяемыми правилами дифференциации.
- Калькулятор дифференцирования поможет дифференцировать функцию по первой, второй, третьей, четвертой и пятой производной.
Часто задаваемые вопросы:
Как отличить функцию от двух переменных?
Прежде всего, вы должны взять частную производную z по x. Однако вскоре вы должны снова принять производную по y. x должен оставаться постоянным. Теперь обратите внимание на феномен перекрестного партиала как меры того, каким образом изменяется наклон при изменении переменной y. Для пояснения вы можете воспользоваться помощью калькулятора первой производной, решив задачу о производной.
Что вам говорит вторая производная?
Вторая производная калькулятор измеряет скорость изменения первой производной. Вторая производная покажет увеличение или уменьшение наклона касательной. Следовательно, с помощью калькулятор производных онлайн двойной производной можно отслеживать скорость изменения исходной функции.
Имеет ли значение порядок деривативов?
Порядок дифференцирования или производной совершенно не имеет значения. Вы можете сначала дифференцировать по второй производной, а затем по первой производной или наоборот. Для удобства вы можете использовать бесплатный калькулятор производной второй, который шаг за шагом вычисляет первое, второе или до 5 дифференциалов.
Как узнать, когда использовать логарифмическое дифференцирование?
Логарифмическое дифференцирование может использоваться для выражения формы (y = f (x) g (x) ), переменной в степени переменной. В такой ситуации вы не можете применить правило мощности и правило экспоненты. Вы можете попробовать калькулятор логарифмического дифференцирования, который поможет поэтапно решать ваши задачи логарифмического дифференцирования.
Что происходит, когда вы берете производную функции?
Всякий раз, когда будет производная функции, вы получите другую функцию, которая предоставит наклон исходной функции. Для производной функции должен быть такой же предел слева направо, чтобы она могла быть дифференцируемой в этой точке.
Подведение итогов:
Этот калькулятор производных онлайн демонстрирует пошаговую помощь по нахождению производных и производной функции. Он следует различным правилам дифференцирования, и любой может выполнять простые и сложные вычисления производных с помощью этого средства поиска производных. Это отличный помощник в академических и учебных целях и в равной степени поддерживает как студентов, так и профессионалов. Кроме того, этот производная калькулятор может при необходимости оценивать производные в заданной точке.
Other Languages: Derivative Calculator, Türev Hesaplama, Kalkulator Pochodnych, Kalkulator Turunan Online, 微分 計算 方法, 미분계산기, Derivace Kalkulačka, Calculadora De Derivada, Calculateur De Dérivée, Calculadora De Derivadas, Calcolatore Derivate.
