| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Показать Этапы
Номер Строки
Примеры
-
производное:от:f(x)=3-4x^2,:x=5
-
производное:от:f(x)=4^xln(x),:x=4
-
производное:от:f(x)=4sin(x)+2x^{x},:x=2
-
производное:от:f(x)=ln(x),:x=17
- Показать больше
Описание
Найти производную функции в заданной точке
derivative-point-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Advanced Math Solutions – Derivative Calculator, Implicit Differentiation
We’ve covered methods and rules to differentiate functions of the form y=f(x), where y is explicitly defined as…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Значение производной в точке
0 =
Изучаем производные
Что такое производная?
Геометрический смысл производной
Физический смысл производной
Обобщённая таблица производных
Как найти производную?
Производная сложной функции
Что такое дифференциал функции?
Решение
$$0$$
$$frac{d}{d x} 0$$
Подробное решение
-
Производная постоянной равна нулю.
Ответ:
Первая производная
[src]
$$0$$
Вторая производная
[src]
$$0$$
Третья производная
[src]
$$0$$
Описание метода вычисления значения производной можно найти под калькулятором.
Вычисление производной по ее определению
Начальное приращение аргумента
Параметр изменения приращения
Точность вычисления
Знаков после запятой: 4
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Вычисление производной по ее определению
Задача численного дифференцирования возникает когда функция задана таблично, или когда прямое дифференцирование затруднено (например, при сложном аналитическом виде функции). Если функция задана аналитически, то можно применить вычисление значения производной по ее определению.
В этом случае у нас есть некоторая функция , для которой нам надо вычислить значение производной в точке x₀. Мы предполагаем, что эта функция определена в окрестности точки x₀ и имеет производную в этой точке. Исходя из определения производной
существует предел отношения приращения функции Δy к приращению аргумента Δx при Δx→0, где
Значение производной можно получить переходя к пределу со все более уменьшающимся шагом, пока не будет достигнута требуемая точность. Для этого на каждом шаге последовательности n приращение аргумента вычисляется по следующей формуле
,
где
Δx₀ — начальное приращение аргумента, например, 0.1
a — некоторое число, большее 1, например, 10
n = 0, 1, …
Тогда
Последовательность останавливается при выполнении следующего условия
Производная функции
Производной функции y=f(x) в точке x0 называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).
Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
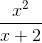
cos2(2x+π) ≡ (cos(2*x+pi))^2
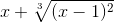
Правила ввода функции, заданной в неявном виде
Примеры
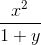
cos2(2x+y) ≡ (cos(2*x+y))^2
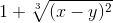
Если функция задана в виде y2-x=cos(y), то ее необходимо записать так: y^2-x-cos(y).
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
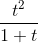
cos2(t) ≡ cos(t)^2
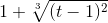
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
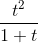
cos2(t) ≡ cos(t)^2
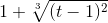
Как найти производную, исходяя из ее определения?
Правила нахождения производных
Пример 1. Найти производную функции y=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
.

В некоторых случаях, если, например, нужно найти производную функции y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции

Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию
Учитывая, что 
Но 

Пример 4. Найти производную функции y=xex
Решение.


Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).


