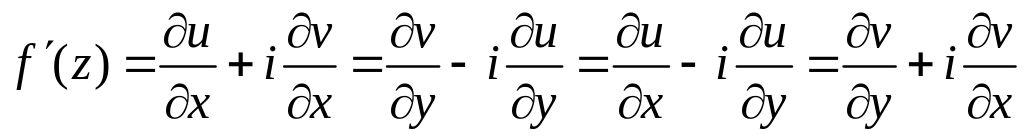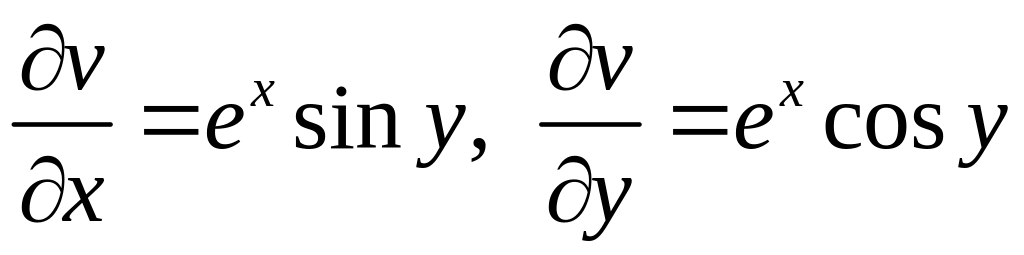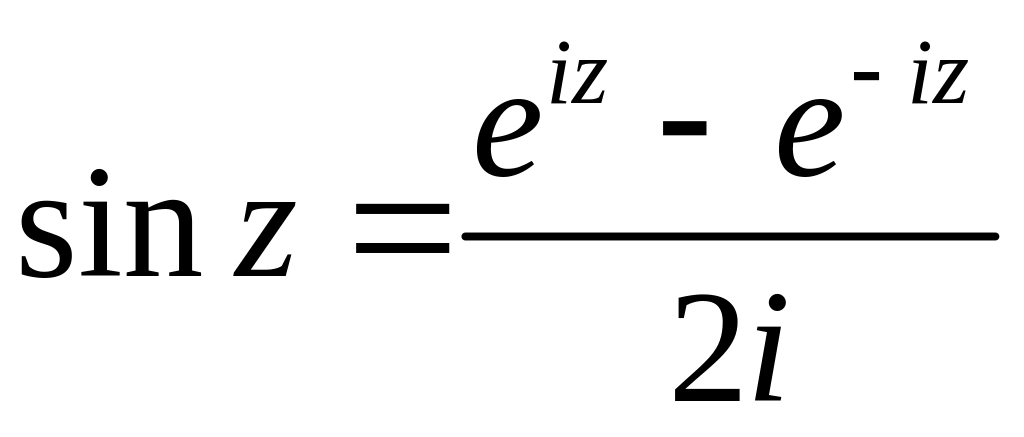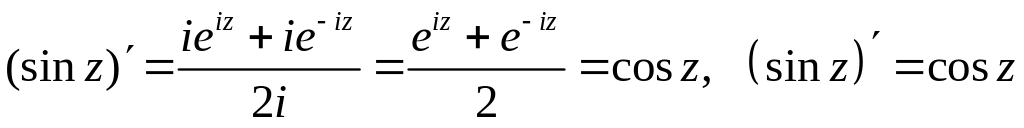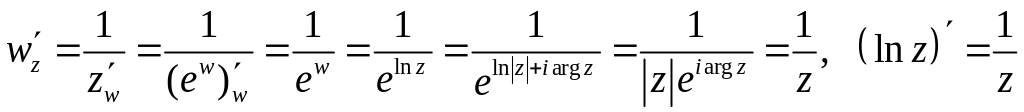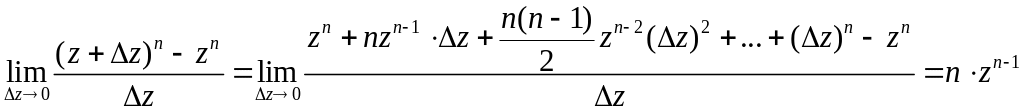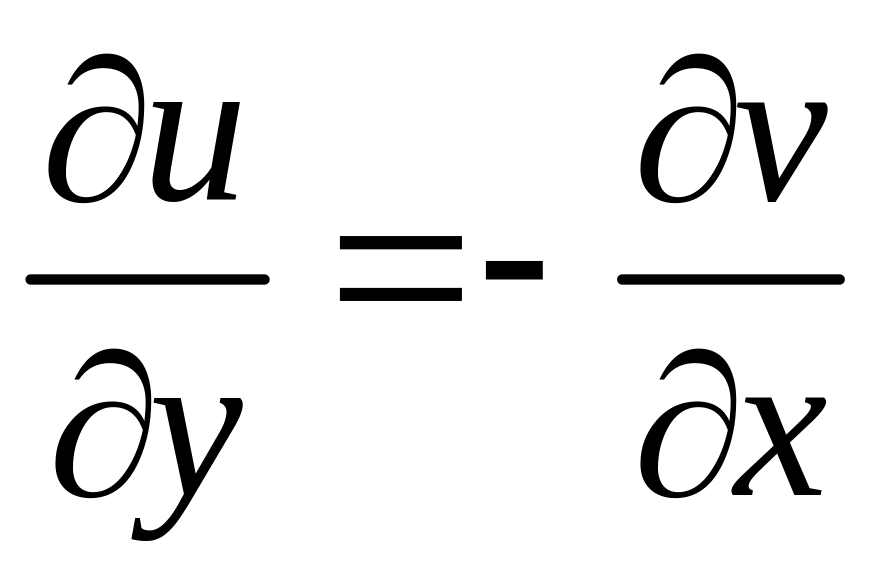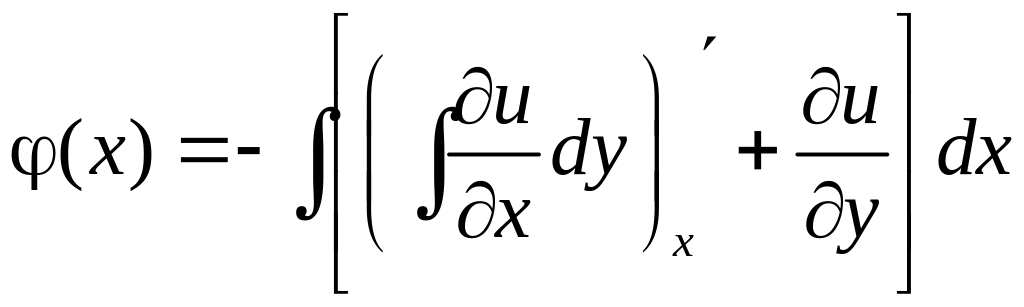Как найти производную комплексного числа - Исправление недочетов и поиск решений вместе с Examum.ru

Дифференцирование функций комплексного переменного

Правила дифференцирования

Так как производная функции комплексного переменного определяется, как и в действительной области, т.е. в виде предела $f'(z_0)= lim_{Delta zto0}frac{Delta f(z_0)}{Delta z}$ , то, используя это определение и свойства пределов, несложно убедиться в справедливости правил дифференцирования, известных из математического анализа. А именно имеет место следующее утверждение.

Утверждение 2.5

1. Сумма, произведение функций, дифференцируемых в точке, есть функция, дифференцируемая в этой точке, и справедливы равенства:

$begin{aligned}bigl(f_1(z)+f_2(z)bigr)'&= f'_1(z)+ f'_2(z),\ bigl(f_1(z)cdot f_2(z)bigr)'&= f'_1(z)cdot f_2(z)+ f_1(z)cdot f'_2(z). end{aligned}$

Из этого свойства и очевидного равенства c'=0~(c=text{const}) следует

$left(sum_{k=1}^{n}c_kf_k(z)right)'= sum_{k=1}^{n}bigl(c_kcdot f'_k(z)bigr).$

2. Частное функций, дифференцируемых в точке, есть функция, дифференцируемая в этой точке, при условии, что знаменатель в точке не равен нулю:

$left(frac{f_1(z)}{f_2(z)}right)'= frac{f'_1(z)cdot f_2(z)-f_1(z)cdot f'_2(z)}{f_2^2(z)},.$

3. Сложная функция комплексного переменного f(varphi(z)) дифференцируема в точке z_0 , если в этой точке дифференцируема функция , а функция f(u) дифференцируема в точке u_0 , где u_0=varphi(z_0) и u=varphi(z) . При этом в точке z_0 имеет место формула

bigl(f(varphi(z))bigr)'= f'(varphi(z))cdot varphi'(z).

▼ Примеры 2.29-2.31

Пример 2.29. Доказать дифференцируемость во всей плоскости функций: a) w=z ; б) w=z^n . Найти их производные.

Решение

а) По определению производной для любой точки zin mathbb{C} записываем $lim_{Delta zto0}frac{(z+Delta z)-z}{Delta z}=1$ ; предел существует для любой точки zinmathbb{C} и z'=1 .

б) Для любой точки $z_0inmathbb{C}$ и любого приращения Delta z рассмотрим

$lim_{Delta zto0}frac{Delta w}{Delta z}= lim_{Delta zto0}frac{(z_0+Delta z)^n-z_0^n}{Delta z},.$

Выражение (z_0+Delta z)^n раскрываем по формуле бинома Ньютона:

$(z_0+Delta z)^n= z_0^n+ ncdot z_0^{n-1}+ frac{n(n-1)}{2!}cdot (Delta z)^2cdot z_0^{n-2}+ ldots+ (Delta z)^n,$

в результате получаем

$begin{aligned}lim_{Delta zto0}frac{(z_0+Delta z)^n-z_0^n}{Delta z}&= lim_{Delta zto0}frac{Delta z left(nz_0^{n-1}+ frac{n(n-1)}{2!}Delta zcdot z_0^{n-2}+ ldots+ (Delta z)^{n-1}right)}{Delta z }=\ &=lim_{Delta zto0}! left(nz_0^{n-1}+ frac{n(n-1)}{2!}Delta zcdot z_0^{n-2}+ ldots+ (Delta z)^{n-1}right)= nz_0^{n-1}.end{aligned}$

Предел существует, следовательно, функция дифференцируема в точке z_0 . Так как z_0 — произвольная точка плоскости, то доказана дифференцируемость z^n ( — натуральное) при любом и получена формула $(z^n)'=nz^{n-1}$ .

Пример 2.30. Исследовать дифференцируемость функций комплексного переменного:

а) P_n(z) — многочлен степени ; б) R(z) — рациональная функция.

Решение

а) Дифференцируемость многочлена в любой точке zin mathbb{C} следует из дифференцируемости функции z^n (пример 2.29) и п. 1 утверждения 2.5.

б) Дифференцируемость рациональной функции $R(z)=frac{P_n(z)}{Q_n(z)}$ отношения двух многочленов в любой точке из области определения, т.е. за исключением нулей знаменателя, получается из результата п. «а» и п. 2 утверждения 2.5.

Пример 2.31. Найти модуль и аргумент производной f'(z) в точке z_0 , если

а) f(z)=2iz-3i ; б) $f(z)=frac{z-4i}{z+2i},~z_0=1-i$ ; в) f(z)=z^2 .

Решение

а) Используя правила дифференцирования, находим f'(z)=2i . Поэтому f'(z_0)=2i для любой точки z_0 и $|f'(z_0)|=2,~ arg f'(z_0)= frac{pi}{2}$ .

б) Используя правила дифференцирования частного, находим

$f'(z)= frac{z+2i-(z-4i)}{(z+2i)^2}= frac{6i}{(z+2i)^2},quad f'(z_0)= frac{6i}{(z_0+2i)^2}= f'(1-i)= frac{6i}{(1+i)^2}= frac{6i}{2i}=3.$

Поэтому в результате имеем |f'(1-i)|=3,~ arg f'(1-i)=0 .

в) Используя результат примера 2.29, находим (z^2)'=2z , поэтому f'(z_0)= 2z_0 и |f'(z_0)|=2|z_0|,~ arg f'(z_0)= 2arg z_0 .

Условия Коши-Римана дифференцируемости функции

Очевидно, между свойствами дифференцируемости функции комплексного переменного как функции точки плоскости и дифференцируемостью ее действительной и мнимой частей как функций двух действительных переменных существует тесная связь.

Утверждение 2.6

1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной u(x,y) и мнимой v(x,y) частей и выполняются условия Коши-Римана:

$begin{cases}dfrac{partial u}{partial x}= dfrac{partial v}{partial y},\[9pt] dfrac{partial u}{partial y}= -dfrac{partial v}{partial x}.end{cases}$

(2.19)

2. Если u(x,y) и v(x,y) дифференцируемы в точке (x_0,y_0) и в этой точке выполняются условия (2.19), то функция f(z)=u+iv дифференцируема в точке z_0=x_0+iy_0 .

3. Производная дифференцируемой функции может быть записана по одной из формул:

$begin{array}{ll}f'(z)=dfrac{partial u}{partial x}+ i,dfrac{partial v}{partial x},&quad f'(z)= dfrac{partial v}{partial y}- i,dfrac{partial u}{partial y},\[10pt] f'(z)=dfrac{partial u}{partial x}- i,dfrac{partial u}{partial y},&quad f'(z)= dfrac{partial v}{partial y}+ i,dfrac{partial v}{partial x}. end{array}$

(2.20)

Доказательство этих утверждений не представляет трудностей и опирается только на определения дифференцируемости функций f(z),~ u(x,y),~ v(x,y) .

Анализ утверждения 2.6 позволяет сделать следующие полезные для исследования функций на дифференцируемость замечания.

Замечания 2.7

1. Выполнение условий (2.19) является необходимым условием дифференцируемости функции f(z) в точке. Следовательно, их невыполнения достаточно для утверждения о том, что функция не является дифференцируемой в соответствующей точке.

2. Условия (2.19) не являются достаточными. Согласно п.2 утверждения 2.6 в соответствующей точке должны быть дифференцируемы функции u(x,y) и v(x,y) . Напомним, что условием дифференцируемости функции двух действительных переменных в точке является существование и непрерывность частных производных в этой точке.

Из утверждения 2.6 и замечаний 2.7 следует правило исследования функции на дифференцируемость.

Правило 2.1. Для исследования функции на дифференцируемость и нахождения ее производной следует выполнить следующие операции.

1. Для заданной функции f(z) найти действительную и мнимую части:

u=operatorname{Re}f(z),quad v=operatorname{Im}f(z),qquad u=u(x,y),quad v=v(x,y).

2. Найти частные производные функций u(x,y),~v(x,y) .

3. Проверить выполнение условий Коши-Римана. Точки, в которых эти условия не выполняются, являются точками, где функция не дифференцируема. Точки, в которых условия (2.19) выполняются и частные производные являются непрерывными, принадлежат области, где функция дифференцируема.

4. Записать выражение производной в точках дифференцируемости по одной из формул (2.20).

▼ Примеры 2.32-2.34

Пример 2.32. Исследовать на дифференцируемость функцию f(z)= sqrt{|xcdot y|} .

Решение

Для решения выделим два случая.

Первый случай. Рассмотрим произвольную точку zne0 . Исследование проводим по правилу 2.1.

1. По условию u(x,y)=sqrt{|x|}cdotsqrt{|y|},~ v(x,y)equiv0 .

2. Очевидно, $dfrac{partial v}{partial x}=0,~ dfrac{partial v}{partial y}=0$ для любой точки. Находим частные производные функции u(x,y) . Для нахождения $dfrac{partial u}{partial x}$ положим y=text{const} и, учитывая определение модуля, рассмотрим два случая: x>0 (тогда |x|=x ) и x<0 (тогда |x|=-x ). Получаем

$dfrac{partial u}{partial x}= sqrt{|y|}cdot frac{1}{2sqrt{x}}$ при x>0 и $dfrac{partial u}{partial x}= sqrt{|y|}cdot frac{-1}{2sqrt{-x}}$ при x<0 .

Аналогично при любом x=text{const} имеем

$dfrac{partial u}{partial y}= sqrt{|x|}cdot frac{1}{2sqrt{y}}$ при y>0 и $dfrac{partial u}{partial y}= sqrt{|x|}cdot frac{-1}{2sqrt{-y}}$ при y<0 .

3. Проверяем условие (2.19). Условие $dfrac{partial u}{partial x}= dfrac{partial v}{partial y}$ выполняется в точках прямой y=0 при любом xne0 . Условие $dfrac{partial u}{partial y}=-dfrac{partial v}{partial x}$ выполняется в точках прямой x=0 при любом yne0 . Вместе эти условия не выполняются ни в одной точке. Согласно п.2 замечаний 2.7 функция не является дифференцируемой.

Второй случай. Рассмотрим точку z=0 .

1,2. Найдем частные производные функции u=sqrt{|xcdot y|} в точке M_0(0;0) , используя определение:

$left.{dfrac{partial u}{partial x}}right|_{M_0}= lim_{Delta xto0} frac{u(Delta x,0)-u(0;0)}{Delta x}= lim_{xto0} frac{u(x,0)-u(0;0)}{x}= 0$ , так как u(x,0)=0 при любом .

Аналогично $left.{dfrac{partial u}{partial y}}right|_{M_0}= 0$ , так как v(x,y)=0 , то $dfrac{partial v}{partial x}=0$ и $dfrac{partial v}{partial y}=0$ .

3. Условие Коши-Римана (2.19) в точке M_0 (то есть z=0 ) выполняется.

Согласно п.2 замечаний 2.7 следует проверить дифференцируемость функций u(x,y),~ v(x,y) в точке M_0 . Это можно сделать, установив непрерывность частных производных в точке z=0 , для чего следует рассмотреть пределы всех найденных в п. «а» производных при zto 0 , то есть xto0,~ yto0 .

В данном случае удобнее проверить дифференцируемость f(z) в точке z=0 по определению производной. В точке z_0=0 рассмотрим произвольное приращение Delta z и составим приращение функции Delta f(0)= f(Delta z)-f(0)= f(Delta z) . Далее записываем предел

$lim_{Delta zto 0}frac{Delta f(0)}{Delta z}= lim_{Delta zto 0}frac{f(Delta z)}{Delta z}= lim_{zto0}frac{f(z)}{z}= lim_{zto0}frac{sqrt{|xcdot y|}}{x+iy},.$

Производная в точке z=0 существует, если этот предел имеет одно и то же значение при любом стремлении к 0, при этом нельзя ограничиться никаким специальным классом путей.

Выберем сначала в качестве пути простейший — прямую y=kx или в комплексной форме z=x(1+ki) . Тогда выражение для предела принимает вид

$lim_{zto0}frac{sqrt{kx^2}}{x(1+ik)}= lim_{zto0}frac{|x|cdot sqrt{|k|}}{x(1+ik)},,$

из чего следует, что значение предела зависит от , от наклона прямой — т.е. от выбранного пути. В частности, при k=1 , т.е. для прямой y=x , можно записать

$lim_{Delta zto0}frac{Delta f(0)}{Delta z}= lim_{xto0}frac{sqrt{x^2}}{x(1+i)}= lim_{xto0} frac{|x|}{x(1+i)},$

поэтому

при $x>0~~ lim_{Delta zto0} frac{Delta f(0)}{Delta z}= frac{1}{1+i}$ , а при $x<0~~ lim_{Delta zto0} frac{Delta f(0)}{Delta z}= -frac{1}{1+i}$ .

По определению $lim_{Delta zto0} frac{Delta f(0)}{Delta z}$ не существует и функция f(z)= sqrt{|xcdot y|} не дифференцируема в точке z=0 .

Объединяя результаты пунктов «а» и «б» , получаем окончательный ответ: данная функция не дифференцируема всюду.

Пример 2.33. Исследовать на дифференцируемость функции: а) f(z)=|z|^2 ; б) f(z)=overline{z} .

Решение

а) Найдем решение, используя правило 2.1.

1. Находим $u=operatorname{Re}f(z),~ v=operatorname{Im}f(z),~ u=x^2+y^2,~ v=0$ .

2. Определяем частные производные: $frac{partial u}{partial x}=2x,~ frac{partial u}{partial y}=2y,~ frac{partial v}{partial x}= 0,~ frac{partial v}{partial y}= 0$ .

3. Условия Коши-Римана (2.19) выполняются только в точке z=0 , где x=0 и y=0 . Непрерывность частных производных очевидна. Следовательно, функция f(z)=|z|^2 дифференцируема только в одной точке z=0 .

б) Найдем решение, используя также правило 2.1.

1. Находим operatorname{Re}overline{z} и operatorname{Im} overline{z} , то есть u=x и v=-y .

2,3. Условия (2.19) не выполняются ни в одной точке, так как $frac{partial u}{partial x}=1,~ frac{partial v}{partial y}=-1$ . Следовательно, функция не дифференцируема всюду.

Пример 2.34. Исследовать на дифференцируемость функцию e^z . Найти производную.

Решение

1. Из равенства e^z=e^x(cos y+isin y) находим u=e^xcos y,~ v=e^xsin y .

2. Находим частные производные:

$frac{partial u}{partial x}= e^xcos y,quad frac{partial u}{partial y}= -e^xsin y,quad frac{partial v}{partial x}= e^xsin y,quad frac{partial v}{partial y}= e^xcos y.$

3. Условия (2.19) выполняются в любой точке zinmathbb{C} , и частные производные, очевидно, непрерывны всюду. Поэтому функция e^z дифференцируема всюду в .

4. Надо полагать, что (e^z)'=e^z . Действительно, записываем производную По формуле (2.20), используя найденные частные производные

$f'(z)= frac{partial u}{partial x}+ i,frac{partial v}{partial x}= e^x(cos y+isin y)= e^xcdot e^{iy}=e^z.$

Условия Коши-Римана в полярных координатах

Пример 2.35. Записать условия Коши-Римана в полярных координатах.

Решение. Пусть f(z)= u(x,y)+iv(x,y) дифференцируема в точке и $z=r,e^{ivarphi}$ . Находим частные производные сложных функций u=u(x,y),~ v=v(x,y) , где $begin{cases}x=rcosvarphi,\ y=rsinvarphi, end{cases}$

$begin{aligned}dfrac{partial u}{partial r}&= dfrac{partial u}{partial x}cdot dfrac{partial x}{partial r}+ dfrac{partial u}{partial y}cdot dfrac{partial y}{partial r}= dfrac{partial u}{partial x}cdot cosvarphi+ dfrac{partial u}{partial y}cdot sinvarphi,;\[5pt] dfrac{partial u}{partial varphi}&= dfrac{partial u}{partial x}cdot dfrac{partial x}{partial varphi}+ dfrac{partial u}{partial y}cdot dfrac{partial u}{partial varphi}= dfrac{partial u}{partial x}cdot(-rsinvarphi)+ dfrac{partial u}{partial y}cdot rcosvarphi,. end{aligned}$

или, в силу условий (2.19), $dfrac{partial u}{partial varphi}= -r left(dfrac{partial v}{partial y}cdot sinvarphi+ dfrac{partial v}{partial x}cdot cosvarphiright)$

$begin{aligned}dfrac{partial v}{partial r}& = dfrac{partial v}{partial x}cdot dfrac{partial x}{partial r}+ dfrac{partial v}{partial y}cdot dfrac{partial y}{partial r}= dfrac{partial v}{partial x}cdot cosvarphi+ dfrac{partial v}{partial y}cdot sinvarphi,;\[5pt] dfrac{partial v}{partial varphi}&= dfrac{partial v}{partial x}cdot dfrac{partial x}{partial varphi}+ dfrac{partial v}{partial y}cdot dfrac{partial y}{partial varphi}= dfrac{partial v}{partial x}cdot(-rsinvarphi)+ dfrac{partial v}{partial y}cdot rcosvarphi,. end{aligned}$

или, используя условия (2.19): $dfrac{partial v}{partial varphi}= r left(dfrac{partial u}{partial x}cdot cosvarphi+ dfrac{partial u}{partial y}cdot sinvarphiright)$

Сравнивая равенства для $dfrac{partial u}{partial r}$ и $dfrac{partial v}{partial varphi}$ , имеем $dfrac{partial v}{partial varphi}=rcdot dfrac{partial u}{partial r}$ , а из равенств для $dfrac{partial u}{partial varphi}$ и $dfrac{partial v}{partial r}$ получаем $dfrac{partial u}{partial varphi}=-rcdot dfrac{partial v}{partial r}$ . Выписываем результат:

$begin{cases}dfrac{partial u}{partial r}= dfrac{1}{r}cdot dfrac{partial v}{partial varphi},\[9pt] dfrac{partial u}{partial varphi}= -rcdot dfrac{partial v}{partial r}.end{cases}$

(2.21)

Это и есть искомые условия Коши-Римана в полярных координатах.

▼ Примеры 2.36-2.37

Пример 2.36. Записать производную функции f(z) для случая $z=r,e^{ivarphi}$ в полярных координатах.

Решение

Пусть f(z)=u+iv,~ u=u(r,varphi),~ v=v(r,varphi) и $r=sqrt{x^2+y^2},~ varphi= operatorname{arctg}frac{y}{x}$ . Запишем частные производные по правилу дифференцирования сложной функции:

$dfrac{partial u}{partial x}= dfrac{partial u}{partial r}cdot dfrac{partial r}{partial x}+ dfrac{partial u}{partial varphi}cdot dfrac{partial varphi}{partial x},qquad dfrac{partial u}{partial y}= dfrac{partial u}{partial r}cdot dfrac{partial r}{partial y}+ dfrac{partial u}{partial varphi}cdot dfrac{partial varphi}{partial y}.$

Используя условия (2.21), запишем выражение для $f'(z)colon, f'(z)= dfrac{partial u}{partial x}-i,dfrac{partial u}{partial y}$ . Получим

$f'(z)= dfrac{partial u}{partial r}left(dfrac{partial r}{partial x}- i,dfrac{partial r}{partial y}right)- r, dfrac{partial v}{partial r}left(dfrac{partial varphi}{partial x}-i,dfrac{partial varphi }{partial y}right)!.$

Далее находим производные функций $r(x,y)= sqrt{x^2+y^2},~ varphi(x,y)= operatorname{arctg}frac{y}{x}$ и выписываем выражения, стоящие в скобках:

$begin{aligned}dfrac{partial r}{partial x}- i,dfrac{partial r}{partial y}&= frac{x}{sqrt{x^2+y^2}}- i,frac{y}{sqrt{x^2+y^2}}= frac{overline{z}}{r};\[5pt] dfrac{partial varphi}{partial x}-i,dfrac{partial varphi }{partial y}&= frac{-y}{x^2+y^2}-i,frac{x}{x^2+y^2}= -frac{i(x-iy)}{x^2+y^2}= frac{-icdot overline{z}}{zcdot overline{z}}= -frac{icdot overline{z}}{r^2},.end{aligned}$

Для производной получаем выражение

$f'(z)= frac{overline{z}}{r} left(dfrac{partial u}{partial r}+ i,dfrac{partial v}{partial r}right)quad Leftrightarrowquad f'(z)= frac{r}{z} left(dfrac{partial u}{partial r}+ i,dfrac{partial v}{partial r}right)!.$

(2.22)

Пример 2.37. Исследовать на дифференцируемость функцию f(z)= ln z,~ 0<arg z<2pi . Найти производную.

Решение

В области Dcolon, 0<arg z<2pi — плоскости с разрезом по действительной положительной полуоси, функция однозначная (см. рис. 2.5). Исследуем ее на дифференцируемость по правилу 2.1, используя запись в полярных координатах.

1. Из равенства ln z= ln r+i,varphi имеем u(r,varphi)= ln r,~ v(r,varphi)=varphi .

2. Находим частные производные: $dfrac{partial u}{partial r}= frac{1}{r},~ dfrac{partial u}{partial varphi}=0,~ dfrac{partial v}{partial r}=0,~ dfrac{partial v}{partial varphi}=1$ .

3. Условия (2.21) выполняются в любой точке области , следовательно, функция дифференцируема в области . Заметим, что, очевидно, дифференцируемой в соответствующей области будет любая однозначная ветвь логарифма, ln z=ln r+i(arg z+2kpi),~ kinmathbb{Z} . Используя формулу (2.22), записываем производную

$(ln z)'= frac{r}{z}cdot! left(frac{1}{r}+icdot0right)= frac{1}{z},.$

Геометрический смысл модуля и аргумента производной

Производная f'(z) как функция комплексного переменного определяет отображение некоторой области — области дифференцируемости функции f(z) на область . В каждой точке z_0in D определено комплексное число f'(z_0) , следовательно, определены |f'(z_0)| и arg f'(z_0) , если f'(z_0)ne0 . Геометрически число — длина радиуса-вектора точки f'(z_0) , a — угол наклона этого радиуса-вектора к действительной оси.

Возникает вопрос, как характеризуют эти величины само отображение w=f(z) в точке z_0 . Как известно, для функции действительной переменной аналогичный вопрос решается просто: производная f'(x_0) определяет угловой коэффициент касательной, проведенной к кривой y=f(x) в точке (x_0,f(x_0)) .

Рассмотрим геометрические свойства величин k=|f'(z_0)| и alpha= arg f'(z_0) , полагая f'(z_0)ne0 , а функцию f(z) дифференцируемой в окрестности точки z_0 . Так как по определению производной $f'(z_0)= lim_{Delta zto0} frac{Delta w}{Delta z}$ предел в точке не зависит от направления и способа стремления Delta z к нулю, то можно взять произвольную гладкую кривую gamma , проходящую через точку z_0 , и на ней любую точку из окрестности точки z_0 .

Образ кривой gamma при отображении w=f(z) обозначим Gamma , образы точек z_0 и через w_0 и соответственно; из непрерывности отображения очевидно, что w_0inGamma и winGamma . Приращения переменных Delta z=z-z_0 и Delta w=w-w_0 геометрически есть векторы (рис. 2.13,а), их длины — |Delta z|,~|Delta w| .

Из определения производной и свойства предела $lim_{Delta zto0}frac{Delta w}{Delta z}= f'(z)$ имеем $frac{Delta w}{Delta z}=f'(z_0)+alpha$ , следовательно,

$left|frac{Delta w}{Delta z}right|= bigl|f'(z_0)+alphabigr|leqslant bigl|f'(z_0)bigr|+ |alpha|$ , или $left|left|frac{Delta w}{Delta z}right|-bigl|f'(z_0)bigr|right|leqslant |alpha|< varepsilon$ для z_0in O(z_0) .

Последнее неравенство, согласно определению, означает $|f'(z_0)|= lim_{Delta zto0}left|frac{Delta w}{Delta z}right|$ . Перепишем его следующим образом:

$bigl|f'(z_0)bigr|= lim_{Delta zto0}left|frac{Delta w}{Delta z}right|= lim_{Delta zto0}frac{Delta l_{Gamma}}{Delta l_{gamma}}= frac{d,l_{Gamma}}{d,l_{gamma}},$

где $Delta l_{Gamma}$ и $Delta l_{gamma}$ — длины соответствующих дуг кривых Gamma и gamma , как известно, эквивалентных при |Delta z|to0 стягивающим их хордам |Delta w| и ; $d,l_{Gamma}$ и $d,l_{gamma}$ — элементы длин дуг Gamma и gamma в точках w_0 и z_0 соответственно.

Производная на комплексной плоскости

Отношение $frac{d,l_{Gamma}}{d,l_{gamma}}$ определяет изменение масштаба (растяжение, сжатие) в точке z_0 при отображении w=f(z) . В этом заключается геометрический смысл модуля производной.

Величина |f'(z_0)| не зависит от вида кривой gamma , поэтому отмеченное свойство имеет место и для любой другой гладкой кривой, проходящей через точку z_0 .

Следовательно, величина k=|f'(z_0)| модуля производной есть величина постоянная для данной функции f(z) и данной точки z_0 .

Для аргумента производной имеет место равенство arg f'(z_0)=theta-varphi , где theta и varphi — углы между действительными осями в плоскостях (w) и (z) соответственно и касательными, проведенными к кривым Gamma в точке w_0 и gamma в точке z_0 (рис. 2.13,а).

Если точки w_0 и z_0 совместить, то alpha=arg f'(z_0)= theta-varphi — угол поворота кривой gamma в точке z_0 при отображении w=f(z) (рис. 2.13,б).

В этом заключается геометрический смысл аргумента производной аналитической функции.

Это свойство, очевидно, имеет место и для любой другой гладкой i кривых gamma_1 и Gamma_1 проходящих через точки z_0 и w_0 соответственно, alpha=theta_1-varphi_1 . Из равенств alpha=theta-varphi и получаем theta_1-theta= varphi_1-varphi . Это означает, что угол beta между кривыми Gamma_1 и Gamma,~ beta=theta_1-theta — в равен углу между кривым gamma_1 и gamma,~ beta=varphi_1-varphi (рис. 2.14). Следовательно, при отображении сохраняются углы между кривыми.

Отображение, сохраняющее углы между кривыми, называется конформным.

Кривые, проходящие через точку, на комплексной

Полученные результаты сформулируем в виде утверждения.

Утверждение 2.7

1. Модуль |f'(z_0)| производной функции f(z) , дифференцируемой в окрестности точки z_0 , есть коэффициент линейного растяжения кривой в точке z_0 при отображении w=f(z) .

2. Аргумент производной в точке есть угол поворота кривой в этой точке при отображении w=f(z) .

3. Отображение с помощью дифференцируемой в окрестности точки z_0 функции f(z) , удовлетворяющее условию f'(z_0)ne0 , является конформным в точке z_0 . Оно обладает свойством постоянства растяжения и сохранения углов. Причем углы сохраняются как по величине, так и по направлению отсчета.

▼ Примеры 2.38-2.40

Пример 2.38. Найти коэффициент растяжения и угол поворота в точке z=2i при отображении $w=frac{z+1}{z+i}$ .

Решение

Находим производную $w'=frac{z+i-z-1}{(z+i)^2}$ , ее значение в точке $2icolon, w'(2i)= frac{1-i}{9}$ . Коэффициент растяжения равен модулю производной, $k=|w'(2i)|= frac{1}{9}sqrt{2}$ , угол поворота — аргументу производной $arg w'(2i)=-frac{pi}{4}$ .

Пример 2.39. Определить, какая часть плоскости при отображении w=z^2 растягивается, а какая — сжимается.

Решение

Находим производную w'=2z , коэффициент растяжения в любой точке равен |w'(z_0)=2|z_0|,~ k=2|z_0| . Множество точек z_0 , для которых k>1 , то есть $2|z_0|>1Rightarrow |z_0|>frac{1}{2}$ , очевидно, образует часть плоскости, которая при отображении растягивается. Следовательно, при отображении w=z^2 внешность круга $|z|>frac{1}{2}$ растягивается, а внутренняя часть $|z|<frac{1}{2}$ сжимается.

Пример 2.40. Показать, что при отображении w=z^2 координатная сетка плоскости (w) соответствует двум ортогональным семействам кривых плоскости (z) .

Решение

Так как f'(z)=2z , то отображение w=z^2 конформно всюду, кроме точки z=0 . Координатная сетка плоскости (w) — это совокупность линий u=text{const},~ v=text{const} . Очевидно, любая пара таких линий в точках пересечения образует прямой угол (рис. 2.15,а). Прообразами этих линий в плоскости (г) будут два семейства гипербол: x^2-y^2=c,~ cne0 и 2xy=c,~ cne0 (рис. 2.15,б). Они получаются из равенства w=z^2 , то есть u+iv=(x+iy)^2 или u=x^2-y^2,~ v=2xy . Линии рассматриваются при любых значениях cne0 . Заметим, что при c=0 линии y=pm x,~ y=0,~ x=0 проходят через точку z=0 , где f'(0)=0 .

Покажем, что гиперболы x^2-y^2=c_2 и 2xy=c_1 при любых c_1,c_2~(c_1ne0,,c_2ne0) пересекаются под прямым углом, т.е. прямой угол образуют касательные к этим кривым в точке пересечения кривых (например, точка на рис. 2.15,б). Угловой коэффициент кривой первого семейства — производную точке A(x_0, y_0) — находим по правилу дифференцирования неявной функции $y'_1(x_0)=-frac{2x_0}{-2y_0}= frac{x_0}{y_0}$ для кривой второго семейства $y'_2(x_0)=-frac{c_1}{2x_0^2}$ . Но в точке пересечения (x_0,y_0) верно равенство 2x_0y_0=c_1 , поэтому $y'_2(x_0)=-frac{2x_0y_0}{x_0^2}=-frac{y_0}{x_0}$ .

Условие ортогональности касательных выполнено: y'_1(x_0)cdot y'_2(x_0)=-1 .

Семейства прямых и гипербол на комплексной плоскости

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

1.3.1. Определение производной

Пусть
задана однозначная функция

на области D
(открытом связном множестве) комплексной
плоскости.

Определение.
Производной
функции

в точке z
называется предел отношения приращения
функции к приращению аргумента при
стремлении приращения аргумента к нулю

Если
этот предел существует, то функция

называется дифференцируемой
в точке

Если
функция

является дифференцируемой в каждой
точке области

,
то говорят, что она аналитическая
в области

Поскольку
определение производной функции
комплексного переменного полностью
аналогично определению производной
функции действительной переменной, то
в случае дифференцируемости функции

,
все известные правила дифференцирования
остаются в силе.

1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного

Теорема
1 (Условия
Коши – Римана).
Для того,
чтобы функция

,
определенная в некоторой области

,
была дифференцируема в точке

этой области, как функция комплексного
переменного, необходимо и достаточно,
чтобы функции

были дифференцируемы в той же точке
(как функции действительных переменных)
и, чтобы, кроме того, выполнялись условия:

При
выполнении условий теоремы, производная
функции

может быть представлена в виде:

1.3.3. Производные основных элементарных функций

Показательная
функция

.

Имеем

Действительная
и мнимая части

будут, соответственно,

Находим
частные производные:

.
Следовательно,

,
т.е. условия Коши-Римана выполнены,
значит, функция

аналитическая, и ее производная:

Функция

.

По
определению:

.
Т.е. является аналитической функцией,
тогда, пользуясь правилами дифференцирования,
получим:

Функция

.

Аналогично
предыдущему:

Функция
.

Функция

.

Функция
.

Логарифмическая
функция является обратной к показательной
функции, а значит – аналитической.
Воспользуемся правилом дифференцирования
обратной функции.

Имеем:

,
тогда

Функция

.

Производную
степенной функции вычислим непосредственно
по определению:

.
Предел
существует, следовательно,
функция

аналитическая, и ее производная:

Таким
образом, мы показали, что основные
элементарные функции комплексного
переменного являются аналитическими
функциями. Следовательно, всякая функция
комплексного переменного, являющаяся
композицией конечного числа основных
элементарных функций, будет аналитической
или дифференцируемой в области своего
определения.

Пример.
Вычислить
производную функции

.

Решение.
Имеем:

=

=

.

1.3.4. Восстановление аналитической функции по известной действительной или мнимой части

Условия,
при которых функция комплексного
переменного дифференцируема, достаточно
жесткие. Поэтому, аналитическая функция,
с точностью до постоянного слагаемого,
может быть задана свой действительной
или мнимой частью.

Действительная
и мнимая части функции

,
аналитической в некоторой области D,
связаны условиями Коши – Римана:

Пусть
известна одна из частей аналитической
функции, например

.
Из условия:

можно найти

(с точностью до неизвестной функции

).
Эту функцию

,
с точностью до постоянного слагаемого,
найдем из второго условия

.

А
именно,

или

.

Пример.
Найти
аналитическую функцию

,
если известна её мнимая часть

.

Решение.
Так как

,
то из условия

находим:

.
Следовательно,

,
где функция

пока
неизвестна. Для нахождения функции

дифференцируем
это равенство по y
и приравниваем
к известной производной, используя
условие

,
откуда

Следовательно,

Окончательно получаем

=
.

Ответ.

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Лекция 2
§11. Производная функции комплексного переменного
Далее будут рассматриваться функции, определенные на открытых и связных множествах, собственно и называемых областью. Открытость области означает, что в нее не
в входит граница (обычно одна или несколько замкнутых линий). Область называют связной, если две любые ее точки можно соединить непрерывной линией (траекторией), целиком состоящей из точек этой области. Если любая замкнутая самонепересекающаяся траектория L, находящаяся в области D, ограничивает некоторую область G  D , то область
называют односвязной (рис. 5а). Если же область D содержит внутри себя одну, две, …,
n – 1 областей, состоящих из точек, не принадлежащих D (вырезанных из D), то область
называется (по общему количеству границ) соответственно двусвязной, трехсвязной, … ,
n-связной (рис. 5б, 5в).
iy
б) двусвязная область
(кольцо r < ǀz – z0ǀ < R)
а) односвязная область
y0
r
в) пятисвязная область
R
z0
x
x0
Рис. 5. Связные области.
Производная функции f(z), заданной в области D, определяется как
f ( z  z )  f ( z )  0 
f
    lim
  ( z) ,

z

z
z
0
если этот предел существует. Здесь Δf = f(z + Δz) – f(z) – приращение функции;
приращением аргумента условие ǀΔzǀ → 0 можно заменить на Δz → 0 +0·i.
f z  lim
z  0
(11.1)
связанное с
Пример. Найти производную функции f(z) = z.
Решение. Применим определение (10.1). Здесь приращение Δf = (z + Δz) –z = Δz, поэтому
f
z
 lim
 lim 1  1 и, следовательно, zz  1 . ◄
z  0 z
z  0 z
z  0
f z  lim
f
 f z   (z ) ,
z
где  (z ) : lim  (z )  0 (здесь z считается параметром). Умножив обе части на Δz, получим
Из определения (11.1) следует, что если f(z) имеет производную, то
z  0
f  f z  z   (z)  z (где Δz → 0), причем  ( z)  z является бесконечно малой более высо-
кого порядка, чем Δz:  (z)  z  o(z) . Поэтому полное приращение функции f(z) в точке z
имеет такую структуру:
(11.2)
f  f z  z  о(z) .
При f z  0 слагаемое f z  z
будет главной, линейной, частью
iy
ρ = f z
iv
L
этого приращения. По аналогии с

φ
=
arg
f
z
z + Δz
функцией действительной переменρ
L1
ной, эта часть называется диффеθ
ω +Δω
z
ренциалом и обозначается df:
rρ
φ+θ
df  d[ f ( z)]  f z  z .
(11.3)
ω
Учитывая, что для случая
x
имеем f z  1 , можно видеть,
f
(
z
)

z
u
что dz = 1·Δz = Δz, и поэтому оконРис. 6. К геометрическому смыслу производной.
чательно можно записать:
1
df  d[ f ( z)]  f z  dz .
Отсюда получаем еще одно выражение для производной: f z 
(11.4)
d [ f ( z )] df

.
dz
dz
Выясним геометрический смысл производной функции комплексного переменного
(рис. 6). Из (11.2) имеем f  f z  z . Записывая сомножители в показательной форме, получаем f    rei z  ei  rei (  ) , где   r    f z  z , Arg ( )  Arg(z )  arg( f z ) . Это
означает, что точка z + Δz исходной комплексной плоскости переходит, посредством отображения ω = f(z), переходит в точку, полученную поворотом на угол   arg( f z) исходного
радиуса   z , измененного в f z раз. Полученное положение точки – приблизительное
за счет наличия слагаемого  (z)  z , проигнорированного при наших выкладках. Сами же
выкладки справедливы для любого положения точки z + Δz внутри открытого круга радиуса δ → 0+, описанного около точки z.
Пусть Г1 и Г2 – две гладкие
γ1
кривые, исходящие из точки z.
iv
γ2
Тогда можно говорить об угле
Г1
α
между этими кривыми как об угле
z
между касательными к ним, проα = θ 1 – θ2 =
веденными в точке z (рис. 7).
= (θ1 + φ) – (θ2 + φ)
Если выполнить отобраθ1
α
жение
ω = f(z), то обе касательω
θ2
x
u
ные повернутся на один и тот же
Г2
угол   arg( f z) , а это означает,
Рис. 7. К конформности отображения.
что сохранится и угол между касательными. Отображение, сохраняющее, с точностью до бесконечно малых высших порядков (по сравнению с Δz → 0),
углы вместе направлением их отсчета и обладающее свойством постоянства растяжений,
называется конформным отображением.
Функция, имеющая непрерывную производную в любой точке области D, называется аналитической на этой области. Отображение с помощью аналитической функции
является, очевидно, конформным во всех точках, в которых f z  0 .
Можно доказать, что если отображение f(z) конформно в любой точке области D,
то и множество значений E{f(z)} также является областью.
Можно также доказать, что если функция f(z) имеет на области D, т.е. в каждой
точке этой области, производную f z , то эта производная непрерывна на всей области D,
т.е. сама функция f(z) является аналитической на D. Кроме того, из (11.2) следует, что
функция, имеющая производную в точке z, непрерывна в этой точке. Тогда нетрудно заключить, что всякая аналитическая на области D функция обладает на этой области непрерывными производными f z, f z, f z,… (любого порядка).
Основные свойства производных для функций действительной переменной и
функций комплексного переменного совпадают. К ним относятся следующие:
(11.5)
[k1 f ( z)  k2 g ( z)]z  k1  f z  k2  g z ,
(11.6)
[ f ( z)  g ( z)]z  f z  g  f  g z ,
iy
 f ( z )   f z  g  f  g z
,
 g ( z)  
g2

z
(11.7)
а также правило дифференцирования сложной функции ω = ω(g(z)):
 z  g  g z 
d d dg
,


dz dg dz
(11.8)
которое справедливо при существовании производных  g и g z .
Совпадают, за исключением логарифмической функции, и таблицы производных.
Используя свойства (11.5) и (11.6), получаем:
2
( z 2 )z  ( z  z )z  1  z  z  1  2 z ,
( z 3 )z  ( z 2  z )z  2 z  z  z 2  1  3 z 2 ,
( z 4 )z  ( z 3  z )z  3z 2  z  z 3  1  4 z 3 .
Этого
достаточно
того, чтобы предположить, что ( z n )z  nz n1 . Тогда
( z n1 )z  ( z n  z )z  nz n1  z  z n  1  (n  1) z n , что полностью соответствует нашей гипотезе. Итак,
( z n )z  nz n1 , n  N 0 .
Теперь почленным дифференцированием ряда (6.1) получаем (e z )z  e z , и тогда легко получить производные всех функций, построенных на функции e z . Так, например,
(cos z )z 
для
1 iz
1
i
e iz  e iz
(e  e  iz )z  (ieiz  ie iz )  (e iz  e  iz )  
  sin z .
2
2
2
2i
Аналогично можно получить:
(sin z)z  cos z ,
(chz)z  shz ,
Используя (11.7), получаем:
2
2
1
 sin z   cos z  sin z
( tgz )z  

 
2
2
cos
z
cos
z
cos
z

z
,
(shz)z  chz .
(ctgz )z  
1
,
sin 2 z
( thz )z 
1
ch 2 z
,
(cthz )z  
1
sh 2 z
.
Наконец, записав показательную функцию a z с действительным основанием a > 0
как   a z  е z ln a  е g , где g  z ln a , получаем
(a z )z  ( )z  g  g z  е g  ln a  a z  ln a .
§12. Необходимое и достаточное условие дифференцируемости
Рассмотрим определение производной, представленное формулой (11.1):
f z  lim
z 0
f
z
Напомним, что f(z) = u(x,y) + i·v(x,y) и, как было отмечено в §10, Δz = Δх + i·Δу. Это
значит, что если z принимает приращение Δz, то за счет приращений Δх и Δу функции
u(x,y) и v(x,y) принимают приращения Δu и Δv. Поэтому можно записать:
Δf = Δu + i·Δv,
и, следовательно, f z  lim
z  0
f
u  iv
 lim
z  x  0 x  iy
.

 y  0
Если производная f z существует, то указанный предел должен быть единственным. Это предоставляет нам возможность выбрать наиболее простые траектории приближения от точки z + Δz к точке z. Таковыми являются траектории, параллельные координатным осям. При приближении к z вдоль оси OX (с Δу = 0) имеем Δz = Δх, и тогда
f
u  iv
u
v
 lim
 lim
 i  lim
 u x  i  vx ,
x  0 x
z  0 z
x  0 x
 x  0
x
f z  lim
а при приближении к z вдоль оси OiY

 y  0
f
u  iv 1
u
v
 lim
 lim
 lim
 i  u y  vy .
(с Δх = 0) – Δz = i·Δу, что дает f z  lim
z  0
z
 x  0

 y  0
iy
i y  0 y
x  0
y
Тогда в силу единственности предела, определяющего f z , приходим к равенству:
ux  i  vx  i  uy  vy , которое означает, в силу (3.1), систему:
 u x  vy 
 

v x  u y 
 u x  vy
 
u y  vx
.
(12.1)
Очевидно, что производную f z функции f(z) = u(x,y) + i·v(x,y) можно представить в
четырех формах:
f z  ux  i  vx  vy  i  uy  ux  i  uy  vy  i  vx .
(12.2)
В работе [2, §II.7] показано, что при условии дифференцируемости функций u(x,y)
и v(x,y) (а это влечет за собой их непрерывность) выполнение условий (12.1) является до3
статочным для того, чтобы функция f(z) была дифференцируемой. Тем самым получено
НДУ дифференцируемости функции f(z), определенной в некоторой [достаточно малой]
окрестности точки z и в самой этой точке, известное как условие Коши – Римана (или
Даламбера – Эйлера):
для дифференцируемости функции f(z) = u(x,y) + i·v(x,y) в точке z = x + i·y
необходимо и достаточно, чтобы функции u(x,y) и v(x,y) имели непрерывные
 u   v
частные производные по обеим переменным, удовлетворяющие условиям  x y .
u y  v x
Учитывая определение аналитической функции, сформулируем НДУ аналитичности функции f(z):
для того чтобы функция f(z) = u(x,y) + i·v(x,y) была аналитической на области D,
необходимо и достаточно, чтобы частные производные функций u(x,y) и v(x,y)
были непрерывны на D и чтобы выполнялись условия (12.1) Коши – Римана.
Найдем смешанные производные действительной и мнимой частей дифференцируемой функции f(z) = u(x,y) + i·v(x,y), привлекая условие Коши – Римана. Непрерывность
частных производных, входящих в (12.1), обеспечивает, для функций u(x,y) и v(x,y), равенство их смешанных производных второго порядка, и поэтому
  uyx
  (uy )x  (vx )x  vxx
 ;
  (ux )y  (vy )y  vyy
 , или uxy
uxy
  (vx )y  (uy )y  uyy
 ,
vxy
или vxy  vyx  (vy )x  (ux )x  uxx ,
Это приводит к равенствам vxx  vyy  uxy  uxy  0 и uxx  uyy  vxy  vxy  0 .
Дифференциальное уравнение g xx  g yy  0 (в частных производных) относительно
функции g(x, y) называется уравнением Лапласа. Говорят также об операторе Лапласа
Δ=
2
2
2
2
 2 таком, что ( g ( x, y ))  2 ( g ( x, y ))  2 ( g ( x, y )) .
2
у
х
у
х
Функция g = g(x, y), удовлетворяющая уравнению Лапласа
  g yy
  0 , называется гармонической.
g  0  g xx
Согласно введенным выше определениям, действительная и мнимая части аналитической [на области D] функции f(z) = u(x,y) + i·v(x,y) являются гармоническими функциями. Функции u(x,y) и v(x,y) в данном контексте называют также сопряженными [на D].
Оказывается, что по одной из этих сопряженных функций можно найти другую,
т.е. восстановить аналитическую функцию. Это означает, что любая гармоническая на D
функция является составной частью некоторой аналитической на D функции.
Пусть дана часть u(x,y) аналитической [на области D] функции f(z) = u(x,y) + i·v(x,y).
Найдем часть v(x,y) по ее полному дифференциалу, пользуясь условиями Коши – Римана.
Имеем: dv  vx dx  vy dy  P( x, y)dx  Q( x, y)dy , где функции P  vx  uy и Q  vy  ux известны,
поскольку функция u(x,y) дана. Из аналитичности функции f(z) = u + iv и вытекающей отсюда непрерывности частных производных функций u и v следует, что Qx  vyx  vxy  Рy ,
т.е. что выражение uy dx  ux dy  vx dx  vy dy является полным дифференциалом функции
u(x,y) и может быть найдено его интегрированием по любому пути, принадлежащему области D:
iY
(x,y)
(x0,y)
( x, y )
( x0 , y 0 )
( x0 , y 0 )
 dv  C 
 (uy dx  ux dy) .
(12.3)
Аналогично, при заданной части v(x,y) имеем:
Q(x,y)
(x0,y0)
( x, y )
v ( x, y ) 
P(x,y)
u ( x, y ) 
(x,y0)
( x, y )
( x, y )
( x, y )
( x0 , y 0 )
( x0 , y 0 )
( x0 , y 0 )
 du  C 
 (ux dx  uy dy)  C 
 (vy dx  vx dy) .
(12.4)
X
Рис. 8. К выводу формулы (12.5).
4
( x, y )
 P( x, y)dx  Q( x, y)dy можно вычислить, двигаясь от точки (х0, у0) к
Напомним, что
( x0 , y 0 )
произвольной точке (х, у) параллельно координатным осям, как
y
x
x
y
y0
x0
x0
y0
 Q( x0 , y)dy   P( x, y)dx   P( x, y0 )dx   Q( x, y)dy .
(12.5)
В формулах (12.3) – (12.5) константа С – произвольное действительное слагаемое
( С  R ). Точка (х0,у0) выбирается так, чтобы в ней не нарушалась аналитичность функции
f(z). На всей траектории движения от (х0,у0) к (х,у) аналитичность f(z) также не должна
нарушаться. Чтобы избежать этих ограничений и самого интегрирования, весьма желательно знать полные дифференциалы некоторых функций двух переменных или уметь их
находить методом подбора.
Поскольку полный дифференциал du функции u(x, y) есть du  ux dx  uy dy , то, например, d ( xy)  ydx  xdy, d x 2  y 2 
x
x y
2
2
dx 
y
x y
2
2
dy, d ln( x 2  y 2 ) 
2x
2y
dx  2
dy, и т.п.
2
x y
x  y2
2
Известно также, что для функции u(t) одной переменной du  d  u(t )dt  .
§13. Интегрирование функции комплексного переменного
Рассмотрим непрерывную в односвязной области D функцию f(z)= u(x,y) + iv(x,y).
Пусть в этой области лежит некоторая, кривая L: z(t )  x(t )  iy(t ), t [t1; t2 ] , заданная параметрически (с действительным параметром t), или, что то же самое, L:  xy  xy((tt).), t  [t ; t ].
1 2

2
2
Если кривая L – гладкая (для нее xt и yt непрерывны, причем ( xt )  ( yt )  0 ), то это
позволяет нам определить, вдоль линии L, интеграл от f(z) как сумму, содержащую два
криволинейных интеграла второго рода:
(13.1)
 f ( z)dz   (u  iv)(dx  idy)   (udx  vdy)  i  (vdx  udy).
L
L
L
L
Учитывая параметрическое задание кривой, получаем:

t1
t1
f ( z )dz   {u[ x(t ), y (t )]xtdt  v[ x(t ), y (t )] ytdt}  i  {v[ x(t ), y (t )]xtdt  u[ x(t ), y (t )] ytdt} , или
L
t1
t1

t1
t1
t1
t1
f ( z )dz   {u~(t ) xt  v~(t ) yt}dt  i  {v~(t ) xtdt  u~(t )] yt}dt .
L
(13.2)
Более того, поскольку на линии L справедливо dz  ztdt  ( xt  iyt )dt, то

L
t1
f ( z )dz   f [( z (t )]ztdt .
(13.3)
t1
Рассмотрим криволинейные интегралы, входящие в (13.1), и проверим условия,
при которых подынтегральные выражения являются полными дифференциалами. Для
u dx 
v dy ) имеем Py  Qx  uy  vx , а для  (v dx  u dy ) – Qx  Py  u x  vy . Но получен( 

L P ( x, y )
Q ( x, y )
L P
Q
ные условия являются не чем иным как условиями (12.1) Коши – Римана, а само условие
Py  Qx обеспечивает независимость криволинейного интеграла второго рода от линии интегрирования, а для замкнутой кривой L = С – равенство этого интеграла нулю. Поэтому
можно утверждать: если функция f(z) является аналитической в односвязной области D и
гладкая кривая С целиком принадлежит этой области, то  f ( z )dz (для замкнутого контура
С
используется не символ  , а символ  ).
Основываясь на свойствах криволинейных интегралов, можно получить такие
свойства для интеграла от функции комплексного переменного:
1º. Для кусочно-гладкой кривой L, состоящей из n гладких частей Lk:
5
n
 f ( z )dz    f ( z )dz .
(13.4)
k 1 Lk
L
2º. Если L–– противоположно ориентированная по отношению к L кривая, то
 f ( z)dz   f ( z)dz .
L
(13.5)
L
3º. Интеграл от л.к. конечного числа n функций равен л.к. интегралов:


n
n





 Lk


    k f k ( z) dz    k   f k ( z)dz   .
L  k 1

k 1 

(13.6)
4º. Если 0 < ǀf(z)ǀ ≤ М на всей кривой L, т.е. если на L модуль функции f(z) ограничен, то
 f ( z )dz  M  l , где l – длина кривой L.
(13.7)
L
Действительно, при оговоренных условиях имеем:
 f ( z )dz
L

t1
t1
t1
t1
 f [( z (t )]  ztdt  
t1
t1
t1
t1
t1
f [( z (t )]zt dt   f ( z )  zt dt  M  xt  iyt dt  M   ( xt ) 2  ( yt ) 2 dt  M  l .



z t
t1
l
Все рассмотренное в этом параграфе позволяет сформулировать теорему Коши:
если функции f(z) аналитична в односвязной области D, то интеграл от f(z) по любому
замкнутому кусочно-гладкому контуру С, целиком лежащему в области D, равен нулю.
В силу этой теоремы и того, что известные нам функции f(z): zn, ez (и, как следствие, az), sinz, cosz, shz, chz являются аналитическими на всей комплексной плоскости,
интеграле от каждой из них по любому замкнутому кусочно-гладкому контуру С равны
нулю.
§14. Теорема Коши для многосвязного контура
Рассмотрим теперь двусвязную область, ограниченную положительно ориентированным [кусочно-гладким] контуром Γ+ (рис. 9). Как показано на левом рисунке, этот контур не является непрерывным,
Γ1+
Γ1+
а состоит из двух положительно ориентированных частей:
Γ2+
Γ2+
Γ+ = Γ1+ + Γ2+.
D
γ+
Сделав теперь дополнительный
разрез области по лиγ–
нии γ, мы получаем возможность пройти весь контур Γ в
положительном направлении
так, что сама область станоРис. 9. К теореме Коши для двусвязного контура.
вится односвязной и остается
слева от направления обхода. Дополнительная линия проходится дважды и в противоположных направлениях γ– и γ+, поэтому суммарный интеграл на этом участке равен нулю.
Теперь, если функция f(z) аналитична и на замыкании области D (т.е. внутри D и на ее
границе Γ), то получаем, по теореме Коши, что  f ( z )dz  0 .

Если ориентировать контур Γ2 в противоположном направлении, то получаем:
 f ( z )dz   f ( z )dz  0  

  
1
2

1
f ( z )dz  
 f ( z )dz  

2

1
f ( z )dz 
 f ( z )dz .

2
Обычно о контуре Γ 2 говорят как о контуре, проходимом против часовой стрелки:
это направление отрицательно по отношению к области D, но положительно по отношению к внутренности самого этого контура.
Совершенно аналогично можно рассуждать и в отношении (n + 1)-связного контура с n непересекающимися «дырками», находящимися внутри замкнутого контура Γ+ и
6
ограниченными контурами Γ i (проходимыми против часовой стрелки). Тогда при услоn
виях, оговоренных выше (аналитичность f(z) внутри D и на ее границе Γ+ +  Г i ) имеем:
i 1
n
 f ( z )dz .
 f ( z )dz  
i 1 

(14.1)

i
Из этой теоремы и теоремы Коши вытекает, что контуры Γ i можно заменять
окружностями бесконечно малых радиусов, т.е. попросту выколотыми точками, и наоборот. Результат интегрирования от этого не изменяется.
В заключение рассмотрим один очень важный интеграл – от функции
1
( z  z 0 )n
с
натуральным n, имеющей особенность в точке z0 – в ней сама функция и ее производная
не существуют, т.е. в точке z0 нарушена аналитичность функции. Интегрирование ведется
по окружности С+: ǀz – z0ǀ = R, ориентированной против часовой стрелки.
По теореме Коши (для двусвязного контура) имеем:

C  : z  z0  R
dz

( z  z0 ) n

C  : z  z 0  Re it
2
dz


( z  z0 ) n
 2
i  dt  2i, n  1
Rieit dt  0
w


2
e 2i
1
R n eitn

d (eit )
dw
dw
 R1n  it n  R1n  n   R1n  n  0, n  1.
w

0 (e )
1 w
e0
Итак, для любого R > 0 имеет место [основная] формула:

C  : z  z0  R
dz
 2i.
z  z0
§15. Формула Коши. Обобщенная формула Коши
Теорема 1. Пусть f(z)–аналитическая в односвязной области D и на ее границе С+,
исключая некоторую внутреннюю точку z0. Тогда справедлива формула (Коши):

f ( z)
C
dz
2i  f ( z 0 ) .
z  z0
(15.1)
Доказательство этой теоремы основано на том, что функция ( z ) 
f ( z)  f ( z 0 )
стаz  z0
новится непрерывной в точке области D, если ее доопределить в точке z = z0 значением
f ( z 0 ) . Заметим, что сама функция f(z) в этой точке определена и непрерывна в силу ее
аналитичности во всех точках области D.
Таким образом, мы имеем очень простой способ вычисления интегралов от функций вида φ(z) =
f(z) =
f ( z)
с аналитической частью f(z)
z  z0
или, в других обозначениях, вида
( z )
с аналитической частью f(z), по любому замкнутому контуру, содержащему
z  z0
внутри себя только одну особую точку z0 (точку бесконечного разрыва).
Наиболее общей формулой для вычисления интеграла по замкнутому контуру является обобщенная формула Коши:

C

f ( z)
dz
( z  z 0 ) n 1
2πi  n! f ( n ) ( z 0 ) ,
(15.2)
где f (n) ( z0 ) – производная порядка n от функции f(z), вычисленная в точке z0. Поскольку
производная нулевого порядка от f(z) есть сама функции f(z), то формула (15.1) есть следствие формулы (15.2) при n = 0.
7
§16. Ряд Лорана
Здесь мы приведем основные теоремы, связанные с разложением аналитических
функций в ряды по степеням (z – z0), т.е. в окрестности точки z0.
Теорема 2. Для функции f(z), аналитической в круге | z – z0| < R, справедливо разложение в ряд Тейлора:
f ( z)  c0 
где c n 
1
2i
f ( )
 (  z
C
0)
n 1
d 
f
(n)

 cn (z  z0 ) n ,
(16.1)
n 1
(z0 )
n!
, С+ — окружность |z – z0| < ρ произвольного ра-
диуса ρ < R с центром в точке z0 ,расположенная в круге | z – z0| < ρ < R.
Указанный ряд сходится к f(z) в любой внутренней точке указанного круга.
Теорема 3. Для функции f(z), аналитической в кольце 0 ≤ r < | z – z0| < R ≤ +∞, справедливо разложение в ряд Лорана, сходящийся к к f(z) в любой точке этого кольца:


c n
f ( z)  
  cn ( z  z0 ) n ,
n
n 1 ( z  z0 )
 0


 n
главная часть
где cn 
(16.2)
правильная часть
f ()
1
f ()
1
d , c n 
d С+ – окружность |z – z0| < ρ произвольно2i C (  z 0 )  n 1
2i C (  z 0 ) n 1
го радиуса ρ < R с центром в точке z0.
Искать коэффициенты cn и c-n прямым интегрированием крайне невыгодно, но целый класс функций, а именно рациональные дроби, позволяет найти разложение в ряд Лорана, используя сумму членов бесконечно убывающей геометрической прогрессии:
для любого х: |х| < 1 имеем 1  x  x 2  x 3  x 4  … 

1
  xn
1  x n 0
(16.3)
В этой формуле «спрятана» еще одна – для отрицательных х:
для любого х: –1 < х < 0 имеем 1  x  x 2  x 3  x 4  x 5 … 

1
  (1) n 1 x n
1  x n 0
(16.4)
На использовании формулы (16.3), собственно, основан и вывод формулы (16.2).
Приведем пример.
► Пример 1. Разложить f ( z ) 
1
в ряд Лорана в окрестности точек z = 0, z= –2, z = 1 и
2z  4
z = ∞.
Решение. Данную нам функцию мы перепишем
1 1
1
   ( z ) . Какой бы ряд теперь мы бы
2 z2 2
так: f ( z )  
iy
z -1| = 3
z| = 2
z=–2
1
x
2
z=1
Рис.10. К примеру 1.
ни получили для φ(z), он будет просто умножаться
(почленно) на ½.
Раскладываем дробь φ(z) в ряд и использованием (16.3). Для этого необходимо получить в знаменателе дроби единицу; это можно сделать за счет вынесения за скобки либо первого, либо второго слагаемого,
но только после формирования в знаменателе слагаемого вида (z – z0).
1) Для z0= 0 (разложение φ(z) по степеням z) имеем
два варианта:
1
1 1
1 1
.
 
 
2 2
z
z2 z
1
1
z
2
Теперь анализируем условие, т.е. поведение полученных в знаменателях слагаемых при единице, в окрестности заданной точки z0 = 0.
8
Разложения (16.3) или (16.4) будут применимы при условиях
представления дроби или
z
2
 1  z  2 для
2
1 z  2
z
для первого
второго из них.
Нас интересует такая окрестность точки z0, в которую не попадает ни одна особая
точка функции φ(z); в нашем случае это z  2 . Это соответствует представлению
1
2
1
4
Используем (6.1): f ( z )   ( z )  
f ( z) 
 ( 1) n 1
1 
z
  (1) n 1     n  2 z n , или
4 n 0
2
n 0 2
n
1
1
1 1
.

2 1 z
2
z
2

(1) n 1
1 1
1
1 3 1 4
 z  z2 
z 
z    n2 z n   , z  2
4 8
16
32
64
2
2) Для z0= –2 (разложение f(z) по степеням z + 2) разложением f(z) в ряд Лорана явля1 1
. Здесь имеем ряд с с-1 = 1/2 и всеми другими cn = 0; ряд схо2 z2
ется сама f(z): f ( z )  
дится к f(z) во всех точках комплексной плоскости, кроме z = –2.
3) Для z0= 1 (разложение f(z) по степеням z – 1) мы используем разложение
 ( z) 
которое дает ряд, сходящийся при
f ( z) 
1
1
 ( z)  
2
6
f ( z) 
1
1
1

 
z  2 ( z  1)  3 3
z 1
1,
3
1
,
z 1
1
3
т.е. в круге |z – 1| < 3. Поэтому получаем:
1
1 
1  (1) n 1
 z 1 
n
   (1) n 1 
    n 1 ( z  1)
z  1 6 n 0
3 
2 n 0 3

1
3
n
, или
(1) n 1
1 1
1
1
 ( z  1)  ( z  1) 2 
( z  1) 3   
( z  1) n   , z  1  3 .
6 18
54
162
2  3 n 1
4) Для z = ∞ (разложение f(z) по степеням z в окрестности бесконечно удаленной
точки).
Бесконечно удаленной точкой в общем случае считается внешность окружности
минимального радиуса, в которую не попадает ни одна особая точка; у нас это – внешность круга z  2 , т.е. множество z  2 
2
1.
z
Поэтому можно использовать ранее полу-
1 1
1
2
1
1
  ( z) 
, которое, через ряд по степеням ,

2
2 z2 2
z
2z
1
z
ченное представление f ( z )  
позволяет записать:
f ( z) 
1
1
1  2 4
8 16
 1


1   2  3  4    
2 2z  z z
2z
z
z
 2z
1
z

(1) n 1 2 n
n 0
zn


(1) n 1 2 n 1
n 0
z n 1

.◄
§17. Вычет функции f(z) в точке
Рассматривая ряд Лорана для аналитической функции f(z)в окрестности точки z0,
можно заметить, что c1 
1
2i
 f ( )d  2i  f ( z )dz . Выражение в правой части называют
1
C
C
вычетом Re s f ( z ) функции f(z) в точке z0:
z  z0
9
1
2i
Re s f ( z ) 
z  z0
 f ( z )dz .
(17.1)
C
Получив ряд Лорана для f(z) в окрестности точки z0 ≠ ∞, имеем Re s f ( z )  c 1 .
z  z0
Что касается вычета в окрестности бесконечно удаленной точки z0 = ∞, то здесь
надо иметь в виду следующее. По теореме Коши для многосвязной области мы имеn
ли  f ( z )dz    f ( z )dz . Тогда, если контур Γ+ есть окружность С+:|z| = R, внутри которой

i 1  
i
заключены все n особых точек zi ≠ ∞ функции f(z), то можно записать:
n
s
 f ( z)dz  i1 zRe
z
f ( z) .
(17.2)
i
C
Теперь, учитывая то, что для бесконечно удаленной точки положительное направление ее «обхода» есть та же окружность |z| = R, но ориентированная отрицательно, то
Re s f ( z )  c 1 , где с-1 – коэффициент ряда Лорана для функции f(z), полученного при ее
z
разложении в окрестности точки z = ∞. Отсюда же следует теорема о вычетах:
n
Re s f ( z )   Re s f ( z )  0 .
z
i 1 z
 zi
(17.3)
Естественно, что вычеты можно находить не только через разложение функции f(z)
в ряд Лорана, но и прямым интегрированием функции с использованием формул (15.2) и
(15.1).
10

Источник