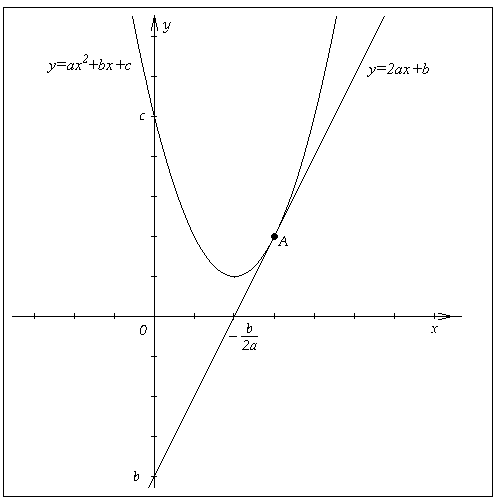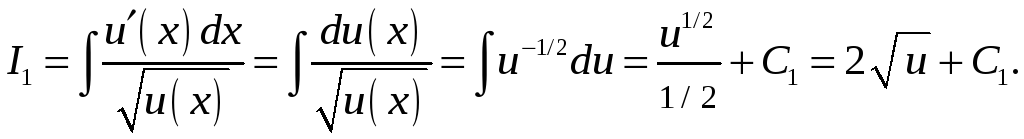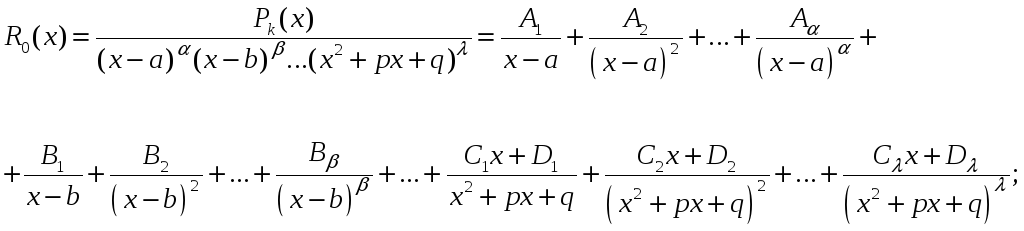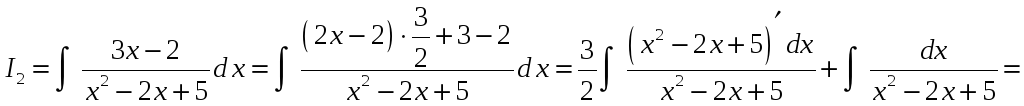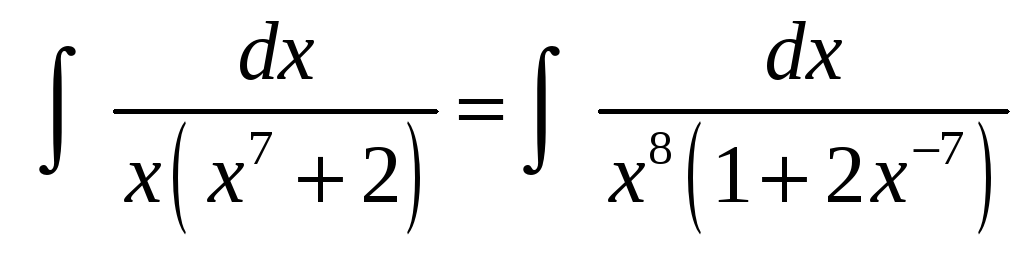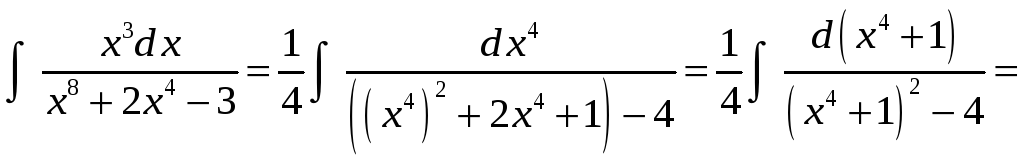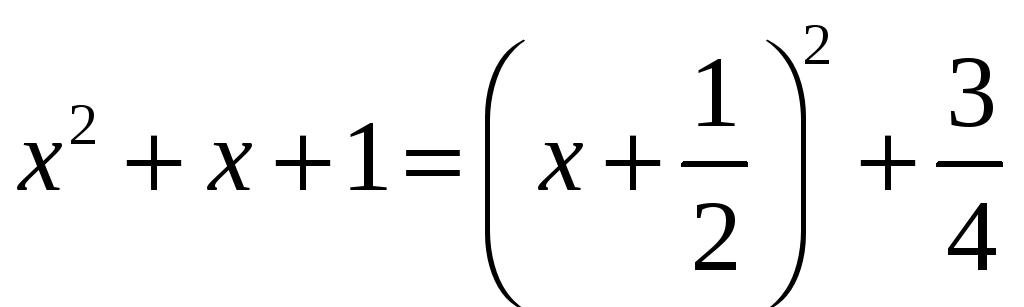Как найти производную квадратного трехчлена

Цели урока:

• Научить учащихся применять ранее полученные
  знания о квадратном трехчлене, линейной функции,
  производной, её геометрическом смысле в новой
  для них нестандартной ситуации;
• Показать учащимся при решении задач
  естественную неразрывную связь между алгеброй и
  геометрией.
• Формировать у учащихся навыки
  исследовательской работы.

Методы:

• лекция,
• практикум.

Пособия:

• слайды презентации PowerPoint с чертежами к уроку.

План урока:

• Организационный момент;
• Объявление темы урока, постановка целей урока;
• Лекционное изложение нового материала с
  элементами закрепления:
• Закрепление материала практическим решением
  нестандартных задач.
• Итоги урока, постановка домашнего задания.

Ход урока:

1. Организационный момент.

Приветствие учащихся. Сообщение темы, целей и
плана урока.

2. Повторение свойств линейной и квадратичной
функций;

По готовым слайдам презентации повторить
свойства линейной и квадратичной функции.

3. Лекционная часть урока “Квадратный трехчлен
и его производная”

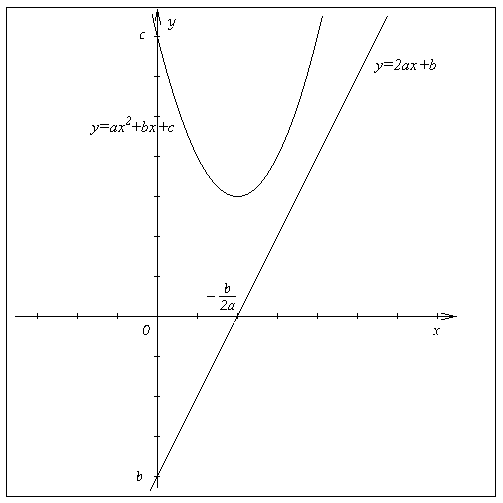
Рассмотрим две функции: квадратный трехчлен и его производную
, которая,
очевидно, является линейной функцией. На рисунке
1 изображены их графики – парабола и прямая , которые иллюстрируют
известный факт, что если на промежутке >0, то квадратный
трехчлен на этом промежутке возрастает, если на
промежутке <0,
то квадратный трехчлен на этом промежутке
убывает, а точка
является точкой экстремума.

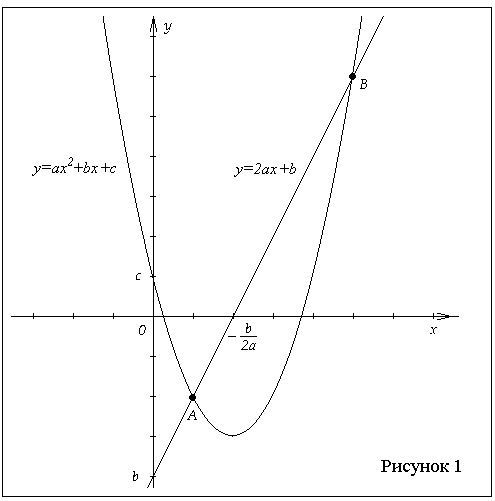
Как известно, прямая и парабола могут не
пересекаться или иметь одну или две общих точек.
Ясно, что это зависит от математических связей
между коэффициентами и .
Найдем эту связь.

Из курса алгебры и начал анализа известно
также, что существует бесконечно много
квадратных трехчленов, имеющих производную . Выясним, график
какого квадратного трехчлена касается графика
своей производной. В этом случае уравнение имеет
единственный корень, значит дискриминант
квадратного уравнения равен нулю, то есть .

 

Выразив из этого уравнения свободный член , получим, что при парабола
квадратного трехчлена касается графика своей производной.

Решая соответствующие неравенства нетрудно
выяснить, что

при :

1. если , то
   прямая не имеет
   общих точек с параболой квадратного трехчлена;
2. если , то
   прямая
   является касательной к параболе квадратного трехчлена;
3. если , то
   прямая
   пересекает параболу квадратного трехчлена .

при :

1. если , то
   прямая не имеет
   общих точек с параболой квадратного трехчлена;
2. если , то
   прямая
   является касательной к параболе квадратного трехчлена;
3. если , то
   прямая
   пересекает параболу квадратного трехчлена

В каждом из этих трех случае при решим по одной задаче.

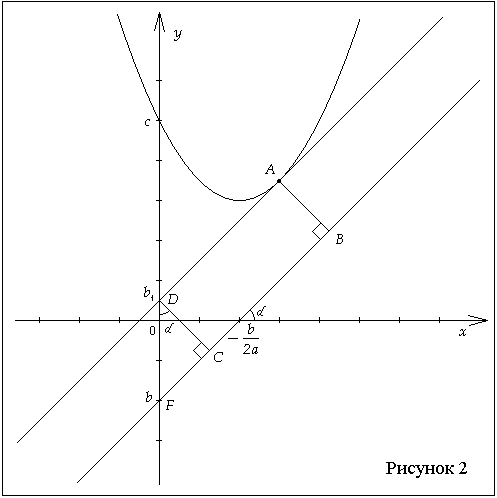
Задача 1. Найти расстояние от прямой до ближайшей точки
параболы , если
прямая и парабола не имеют общих точек.

Решение. Ясно, что искомое расстояние равно
расстоянию АВ между прямойи касательной к параболе , параллельной
прямой , где А –
точка касания и АВ^ .

Касательная имеет вид . Чтобы найти нужно вычислить координаты точки А
касания. Их нетрудно посчитать. Точка касания
имеет координаты A, где .
Составим уравнение касательной, зная угловой
коэффициент и
координаты точки касания, получим уравнение
касательной .
Это значит что .
Теперь можно вычислить DF=. В прямоугольном треугольнике DCF
острый угол равен углу между касательной и
положительным направлением оси абсцисс, поэтому . Решая
треугольник DCF находим СВ, а значит и искомое
расстояние .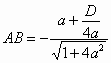

Задача 2. Как показано выше график
квадратного трехчлена касается графика своей
производной. Найдите координаты точки касания и
докажите, что эта точка касания расположена
всегда правее вершины параболы на одну единицу.

Решение. Координаты точки А касания посчитать
нетрудно, А.
Простой анализ координат точки А показывает, что
абсцисса точки касания на единицу больше, чем
абсцисса вершина параболы.

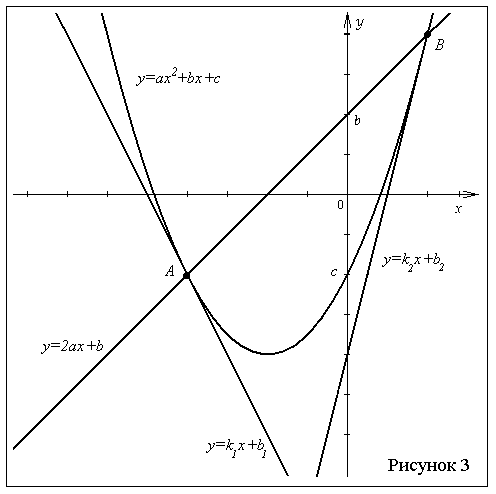
Задача 3. Парабола квадратного трехчлена и прямая , график его производной
пересекаются в двух точках А и В. К параболе через точки А и В
проведены две касательные с угловыми
коэффициентами
и. Докажите, что .

Решение. Абсциссы точек А и В пересечения
параболы и
прямой найдем
из уравнения , , , ,

Найдем угловые коэффициенты и касательных, проведенные через точки А и
В. Они равны значению функции в точках и , фактически эти значения совпадают
с ординатами точек А и В. Вычислим их: , . Теперь ясно, что .

Еще один интересный момент. Если угловой
коэффициент прямой АВ обозначить через , то учитывая, что , нетрудно
установить удивительно простую зависимость
между угловыми коэффициентами этих прямых: .

4. Практикум по решению задач.

1. Пусть
   некоторый квадратный трехчлен. Рассмотрим
   параболы и . Докажите, что
   вторая парабола получается из первой
   параллельным переносом на вектор .
2. Последовательность квадратных трехчленов,
   задана реккурентным соотношением , , .
   Докажите, что все параболы, являющиеся графиками
   функций из этой последовательности, имеют общую
   касательную.
3. Как продолжить последовательность функций из
   предыдущей задачи влево, если убрать ограничение
   , то есть
   найдите квадратный трехчлен, непосредственно
   предшествующий квадратному трехчлену.
4. Парабола
   пересекает ось

в двух точках. Через каждую из них проведены
касательные, которые пересекаются в точке С.
Найдите координаты точки С.

Ответы к задачам: 3. ; 4. .

5. Самостоятельная работа в двух вариантах.

Вариант 1. Решите задачу:

Парабола и
прямая
пересекаются в двух точках А и В. К параболе через
точки А и В проведены две касательные, которые
пересекаются в точке С. Докажите, что: медиана СМ
треугольника АВС параллельна оси ординат;

Вариант 2. Решите задачу:

Парабола и
прямая
пересекаются в двух точках А и В. К параболе через
точки А и В проведены две касательные, которые
пересекаются в точке С. Докажите, что одна из
средних линий треугольника АВС является
касательной к параболе .

6. Разбор задач самостоятельной работы

Разбор проводится по заранее подготовленным
слайдам презентации PowerPoint. Оба варианта
рассматриваются одновременно, потому что первая
часть решения задач обоих вариантов одинакова,
вторая же, различная часть, будет интересна
учащимся обоих вариантов.

7. Задание на дом:

1. Рассмотрим четыре параболы , , и , где – некоторый квадратный
   трехчлен. Докажите, что вершины этих парабол
   совпадают с вершинами некоторого квадрата.




2. Творческое задание (для желающих). Придумать
   свою задачу по теме “Квадратный трехчлен и его
   производная”

Рассмотрим интегралы следующих трех
типов:

где

или
.
Отметим, что интегралы 1-го и 2-го типа
при

возникают при интегрировании
дробно-рациональных функций.

Укажем общие рекомендации по отысканию
интегралов этих трех типов.

В интеграле

выделить из квадратного трехчлена
полный квадрат.

В интеграле

выделить в числителе производную
квадратного трехчлена.

В интеграле

вынести

из-под корня.

Пример 1. Найти интеграл
.

Имеем интеграл первого типа при
.
Выделим из квадратного трехчлена полный
квадрат:
.

Используя это равенство и формулу (13)
п.12.3, получим

Пример 2. Найти интеграл
.

Имеем интеграл второго типа при
.
Найдем производную квадратного трехчлена

и выделим ее в числителе следующим
образом:

.

Тогда

Второй интеграл в этой сумме был найден
в примере 1:

В первом интеграле воспользуемся тем,
что

Обозначив
,
окончательно получим:

Пример 3. Найти интеграл
.

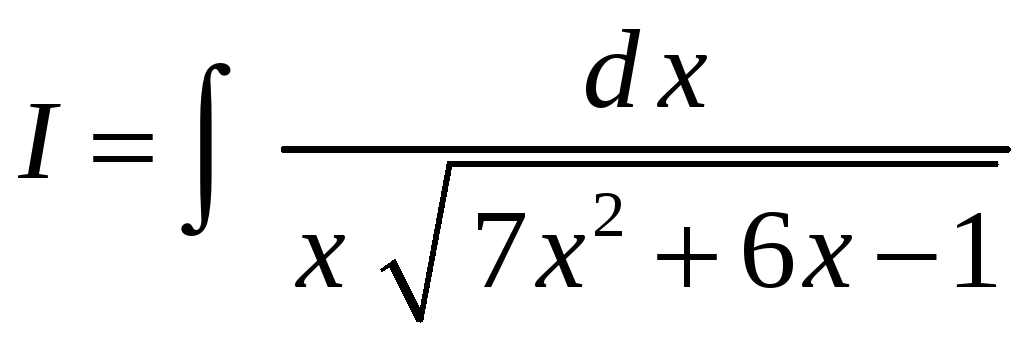
Имеем интеграл третьего типа. Вынесем

из-под корня:

.

Воспользуемся тем, что
,

.

Используя эти равенства и формулу (12)
п.12.3, получим

.

Интегрирование дробно-рациональных
функций

Дробно-рациональной функцией или
рациональной дробью

называется отношение двух многочленов:
.

Если степень многочлена в числителе
меньше степени многочлена в знаменателе,
т.е.
,
то рациональная дробь называется
правильной. В противном случае рациональная
дробь называется неправильной.

Интегрирование дробно-рациональной
функции проводится в несколько этапов.
Сначала мы перечислим эти этапы, а потом
подробно поясним каждый из них на
примере. Итак, для интегрирования
дробно-рациональной функции

следует:

1) если рациональная дробь неправильная,
то выделить из нее целую часть и правильную
рациональную дробь
:
;

2) знаменатель дроби

разложить на линейные множители

,
и квадратные множители
,
… с действительными коэффициентами;

3) правильную рациональную дробь разложить
методом неопределенных коэффициентов
на простейшие дроби

4) найти неопределенные (неизвестные
пока) коэффициенты

;

5) найти интегралы от целой части и
простейших дробей.

Поясним все сказанное на примерах.

Пример 4. Найти интеграл
.

Подынтегральная функция есть правильная
рациональная дробь, так как степень
многочлена в числителе меньше степени
многочлена в знаменателе. Кроме того,
знаменатель уже разложен на линейные
множители. Поэтому сразу переходим к
разложению рациональной дроби на
простейшие дроби с неопределенными
коэффициентами:

.

Умножив это равенство на
,
получим:

.

Подставив в это равенство последовательно
,
получим
,

,

.
Таким образом,

Мы нашли коэффициенты разложения

методом частных значений.

Теперь подставим найденные значения

в равенство:

.

Проинтегрируем полученные простейшие
дроби:

Пример 5. Найти интеграл
.

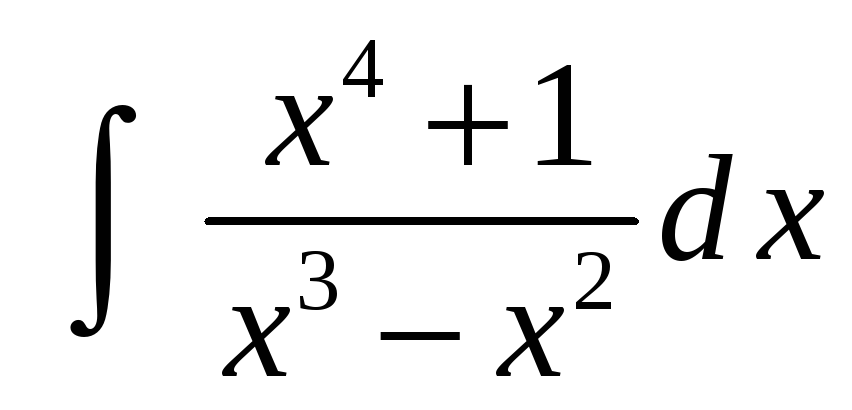
Подынтегральная функция есть неправильная
рациональная дробь, так как степень
многочлена в числителе больше степени
многочлена в знаменателе. Поэтому
выделим из неправильной дроби ее целую
часть, поделив числитель на знаменатель.
В результате деления получим

.

Теперь знаменатель получившейся
правильной дроби разложим на множители
,
а саму правильную дробь на простейшие
дроби:

.

Умножив это равенство на
,
получим:

.

Подставив в это равенство значения
,
получим

Для отыскания коэффициента

можно либо в равенстве (14.5) подставить
еще одно частное значение
,
либо в правой и левой частях равенства
(14.5) приравнять коэффициенты при
одинаковых степенях
,
например, при
:
.

Тогда

Подставляя найденные

в равенство (14.4) и используя равенство
(14.3), окончательно получим

Пример 6. Найти интеграл
.

Подынтегральная функция есть правильная
рациональная дробь, так как степень
многочлена в числителе меньше степени
многочлена в знаменателе. Квадратный
трехчлен в знаменателе

имеет отрицательный дискриминант,
следовательно, он не имеет действительных
корней и не разлагается на линейные
множители с действительными коэффициентами.
Поэтому перейдем к разложению рациональной
дроби на простейшие:

.

Умножив это равенство на
,
получим

.

Подставив в это равенство значения

получим:

или
.

Кроме того, в правой и левой частях
равенства сравним коэффициенты при
:

Итак,

Используя равенство, получим

.

Найдем первый интеграл:
.

Для отыскания второго интеграла выделим
в числителе производную квадратного
трехчлена, стоящего в знаменателе:

Складывая
,

и вводя
,
получим искомый интеграл:

Пример 7. Найти интеграл
.

Здесь разложение знаменателя на линейные
и квадратичные множители и разложение
дроби на простейшие требуют громоздких
выкладок. Значительно проще вынести из
скобки
:

и воспользоваться тем, что
.

Тогда

Пример 8. Найти интеграл
.

Решение. Как и в предыдущем примере,
разложение знаменателя на линейные и
квадратичные множители и разложение
дроби на простейшие требуют громоздких
выкладок. Удобнее воспользоваться тем,
что
.
Тогда

.

Интегрирование по справочникам

Для отыскания неопределенных интегралов
издаются обширные справочники (см. [5],
[6]). При пользовании такими справочниками
надо внимательно познакомиться с
принципами, по которым в них группируются
интегралы. Для успешного использования
справочников надо знать свойства
неопределенных интегралов и основные
методы интегрирования, так как многих
интегралов в справочниках нет, но их
легко можно привести к табличным
интегралам с помощью некоторых
преобразований.

Например, интеграл

отсутствует в справочниках. Прежде чем
использовать справочники, надо выделить
из квадратного трехчлена полный квадрат

и сделать замену переменной
,
.

Тогда

.

Каждый из трех получившихся интегралов
есть в справочниках. После их отыскания
надо подставить
.

Интегралы, не выражающиеся через
элементарные функции

Мы рассмотрели классы элементарных
функций, интегралы от которых выражаются
через элементарные функции.

На практике часто встречаются и такие
элементарные функции, интегралы от
которых нельзя выразить через элементарные
функции.

Отметим ряд интегралов, не выражающихся
через элементарные функции, но имеющих
большое прикладное значение:

С некоторыми из этих интегралов вы
позднее встретитесь, например с первым
интегралом – в теории вероятностей, со
вторым и третьим интегралами – в физике.

Оглавление

4.
Лекционное занятие. ИНТЕГРИРОВАНИЕ
ФУНКЦИЙ, СОДЕРЖАЩИХ КВАДРАТНЫЙ
ТРЕХЧЛЕН. 1

Интегрирование
дробно-рациональных функций 2

Интегрирование
по справочникам 6

Интегралы, не
выражающиеся через элементарные
функции 6

Оглавление 7

Квадратный трёхчлен в функции. Год назад опубликовал статью, в которой были рассмотрены  функции в составе которых имеется квадратный трёхчлен. Задания на нахождение точек максимума (минимума) или на вычисление наибольшего (наименьшего) значения функции.

Недавно меня попросили рассказать и показать каким образом такие задания можно решить по стандартному алгоритму, то есть через производную. Сразу скажу, что такой подход к решению нерационален, требует больше времени и он «неудобен». Привожу его для вас (чтобы знали).

Рекомендую посмотреть статью «Исследование функций. Это нужно знать!», также помните, что производные элементарных функций нужно знать наизусть, в теме производной без этого никак нельзя. Также необходимо понимание того, что такое сложная функция, в указанной выше статье имеется видео.

Рассмотрим задачи:

Найдите точку максимума функции

Сначала определим, при каких х функция имеет смысл (найдём область определения функции). Так как подкоренное выражение есть число неотрицательное, то решаем неравенство:

13 + 6х – х² ≥ 0

*Как решается квадратное неравенство подробно можно посмотреть здесь.

Данные корни разбивают ось х на три интервала.

Проверим при каких значениях х неравенство будет верным. Подставим из каждого интервала любое значение х в неравенство:

Значит решением неравенства будут являться все значения х принадлежащие интервалу (включая границы):

*Приближенно полученные выражения равны:   

Область определения данной функции найдена.

Вычислим производную функции. Это сложная функция:

Найдем нули производной:

Дробь равна нулю тогда, когда её числитель равен нулю, значит:

6 – 2х  = 0

х = 3

Полученное  значение х входит в область определения и разбивает её на два отрезка. Определим знаки производной на каждом из них (подставим выборочно любые значения в выражение производной), например 2 и 4:

Получили, что в точке х = 3 производная функции меняет свой знак с положительного на отрицательный, а это означает, что данная точка есть точка максимума.

Ответ: 3

Комментарий: представленное решение – это полное, математически грамотное решение, то есть такое как должно быть. О чем я? Дело в том, что для составления «полной картины», в первую очередь необходимо найти область определения. Конечно, можно поспорить. Дело в том, можно сразу находить  производную, затем её «нули» и далее установить имеет ли функция значение при этом х. Затем определить знаки в «соседних» точках и станет понятно является ли эта точка точкой максимума (или минимума). Да, можно и так.

Кто проанализировал все типы таких примеров из единого банка заданий ЕГЭ по математике, тот справедливо может сказать, что достаточно вообще найти нули производной, полученное (целое) значение х и будет являться искомым. Согласен! Но понимать суть всего процесса решения «от и до»  необходимо.

Если в подобном задании на ЕГЭ будет стоять вопрос о вычислении наибольшего (наименьшего) значения, то оно будет в точке х, полученной при решении f′(х) = 0, то есть в «нуле функции».

Найдите точку максимума функции у =log₇(–2 – 12х – х²) + 10. 

Вычислим производную функции, используем формулу производной логарифма и производной сложной функции:

Найдем нули производной:

Дробь равна нулю тогда и только тогда, когда её числитель равен нулю:

– 2х –12 = 0

х = – 6

Данное значение обращает подлогарифмическое выражение в положительное:

–2 – 12∙(–6) – (–6)² = 34

то есть оно принадлежит области определения функции.

Определим знаки производной в «соседних» точках, например возьмем точки  –7 и –5:

Получили, что в точке х = – 6 производная функции меняет свой знак с положительного на отрицательный, а это означает, что данная точка есть точка максимума функции.

Ответ: –6

Комментарий: здесь мы не стали находить область определения. Сразу вычислили производную и нашли х, при котором производная обращается в нуль. Затем определили знаки производной на интервалах полученных разбиением числовой оси точкой х =  – 6 и сделали вывод.

Если в подобном задании (с логарифмом) будет стоять вопрос о вычислении наибольшего (наименьшего) значения функции, то также вычисляйте его в точке х, полученной при решении f′(х) = 0.

Найдите точку максимума функции 

Вычислим производную функции, используем формулу производной показательной и производной сложной функции:

Найдем нули производной. Известно, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другие при этом не теряют смысла. В данном случае нулю равен только один множитель:

–2х + 12 = 0

х = 6

Определим знаки производной на интервалах, которые получаются разбиением числовой оси точкой х=6, возьмём точки 0 и10:

Получили, что в точке х = 6 производная функции меняет свой знак с положительного на отрицательный, а это означает, что данная точка есть точка максимума функции.

Ответ: 6

Комментарий: в данном случае область определения не имеет ограничений, то есть при всех х функция имеет значение.

Если будет стоять вопрос о нахождении максимального  (минимального) значения функции на определённом интервале, то тут действуйте по стандартному алгоритму (посмотрите задания на сайте, их достаточно).

В любом случае, свойства производной для исследования функции, табличные значения производных и алгоритм нахождения точек максимума (минимума) нужно знать обязательно.

Как вы убедились, данный подход к решению таких заданий (через производную) требует больше времени, знания теории и умственного напряжения. Показал его для того, чтобы знали и понимали, каким образом ещё можно решить подобные задания. Конечно же, этот способ намного проще.

Успеха вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Была ли эта статья полезной?

Квадратный трехчлен и его производная

Разделы: Математика

Класс: 11

Цели урока:

• Научить учащихся применять ранее полученные знания о квадратном трехчлене, линейной функции, производной, её геометрическом смысле в новой для них нестандартной ситуации;
• Показать учащимся при решении задач естественную неразрывную связь между алгеброй и геометрией.
• Формировать у учащихся навыки исследовательской работы.

Пособия:

• слайды презентации PowerPoint с чертежами к уроку.

План урока:

• Организационный момент;
• Объявление темы урока, постановка целей урока;
• Лекционное изложение нового материала с элементами закрепления:
• Закрепление материала практическим решением нестандартных задач.
• Итоги урока, постановка домашнего задания.

1. Организационный момент.

Приветствие учащихся. Сообщение темы, целей и плана урока.

2. Повторение свойств линейной и квадратичной функций;

По готовым слайдам презентации повторить свойства линейной и квадратичной функции.

3. Лекционная часть урока “Квадратный трехчлен и его производная”

Рассмотрим две функции: квадратный трехчлен и его производную , которая, очевидно, является линейной функцией. На рисунке 1 изображены их графики – парабола и прямая , которые иллюстрируют известный факт, что если на промежутке >0, то квадратный трехчлен на этом промежутке возрастает, если на промежутке ^ .

Касательная имеет вид . Чтобы найти нужно вычислить координаты точки А касания. Их нетрудно посчитать. Точка касания имеет координаты A, где . Составим уравнение касательной, зная угловой коэффициент и координаты точки касания, получим уравнение касательной . Это значит что . Теперь можно вычислить DF=. В прямоугольном треугольнике DCF острый угол равен углу между касательной и положительным направлением оси абсцисс, поэтому . Решая треугольник DCF находим СВ, а значит и искомое расстояние .

Задача 2. Как показано выше график квадратного трехчлена касается графика своей производной. Найдите координаты точки касания и докажите, что эта точка касания расположена всегда правее вершины параболы на одну единицу.

Решение. Координаты точки А касания посчитать нетрудно, А. Простой анализ координат точки А показывает, что абсцисса точки касания на единицу больше, чем абсцисса вершина параболы.

Задача 3. Парабола квадратного трехчлена и прямая , график его производной пересекаются в двух точках А и В. К параболе через точки А и В проведены две касательные с угловыми коэффициентами и. Докажите, что .

Решение. Абсциссы точек А и В пересечения параболы и прямой найдем из уравнения , , , ,

Найдем угловые коэффициенты и касательных, проведенные через точки А и В. Они равны значению функции в точках и , фактически эти значения совпадают с ординатами точек А и В. Вычислим их: , . Теперь ясно, что .

Еще один интересный момент. Если угловой коэффициент прямой АВ обозначить через , то учитывая, что , нетрудно установить удивительно простую зависимость между угловыми коэффициентами этих прямых: .

4. Практикум по решению задач.

Пусть некоторый квадратный трехчлен. Рассмотрим параболы и . Докажите, что вторая парабола получается из первой параллельным переносом на вектор .

Последовательность квадратных трехчленов, задана реккурентным соотношением , , . Докажите, что все параболы, являющиеся графиками функций из этой последовательности, имеют общую касательную.

Как продолжить последовательность функций из предыдущей задачи влево, если убрать ограничение , то есть найдите квадратный трехчлен, непосредственно предшествующий квадратному трехчлену.

Парабола пересекает ось

в двух точках. Через каждую из них проведены касательные, которые пересекаются в точке С. Найдите координаты точки С.

Ответы к задачам: 3. ; 4. .

5. Самостоятельная работа в двух вариантах.

Вариант 1. Решите задачу:

Парабола и прямая пересекаются в двух точках А и В. К параболе через точки А и В проведены две касательные, которые пересекаются в точке С. Докажите, что: медиана СМ треугольника АВС параллельна оси ординат;

Вариант 2. Решите задачу:

Парабола и прямая пересекаются в двух точках А и В. К параболе через точки А и В проведены две касательные, которые пересекаются в точке С. Докажите, что одна из средних линий треугольника АВС является касательной к параболе .

6. Разбор задач самостоятельной работы

Разбор проводится по заранее подготовленным слайдам презентации PowerPoint. Оба варианта рассматриваются одновременно, потому что первая часть решения задач обоих вариантов одинакова, вторая же, различная часть, будет интересна учащимся обоих вариантов.

7. Задание на дом:

Рассмотрим четыре параболы , , и , где – некоторый квадратный трехчлен. Докажите, что вершины этих парабол совпадают с вершинами некоторого квадрата.

Творческое задание (для желающих). Придумать свою задачу по теме “Квадратный трехчлен и его производная”

Производная квадратичной функции

На странице «Производная функции» мы выяснили, что предел отношения Δs/Δt получил название производной функции s(t).

Напомним, что величина Δs — это приращение расстояния; Δt — приращение времени.

Определение производной можно сформулировать в следующем виде:

Производной называется предел отношения приращения расстояния к приращению времени, при стремлении к нулю последнего.

Если уйти от конкретики, и не привязываться к расстоянию и времени, то определение производной будет звучать так:

Производная — это предел отношения приращения функции к приращению независимой переменной при стремлении к нулю приращения независимой переменной.

Смысл производной заключается в том, что она показывает скорость изменения функции при изменении её аргумента.

Напомним важные моменты производной для функции s(t):

• приращение независимой переменной может быть сколь угодно малым, но обязательно отличным от нуля;
• поскольку s есть функция t [s(t)], то и предел отношения Δs/Δt является также функцией t, которая называется мгновенной скоростью v(t);
• v зависит от значения t при котором берется производная s.

Обозначение производной через предел довольно громоздко и не совсем удобно, поэтому, чаще используют сокращенные варианты (в общем случае вместо переменной s используется перменная y, а вместо переменной t — переменная x — что вполне логично, поскольку расстояние мы откладывали по оси ординат, а время — по оси абсцисс):

Частенько вместо функции пишется ее выражение:

На странице Равноускоренное движение мы искали производную квадратичной функции «наощупь», пошагово уменьшая приращение времени, теперь сделаем это алгебраически.

Изначально составим соотношение:

Знаменатель не трогаем. В числителе делаем преобразования, чтобы избавиться от переменной y. Дэльта игрек — это разность между начальной точкой (y) и некой точкой (y₁), соответствующей величине приращения (y+Δy). После этого заменяем y на x 2 .

Раскрывая скобки в числителе, получаем выражение:

Теперь наше соотношение примет следующий вид:

Ищем предел квадратичной функции:

Последнее равенство требует пояснения. Предел двух слагаемых одно из которых независимо, а второе стремится к нулю, будет равен независимому слагаемому.

Алгебраическим путём мы нашли производную квадратичной функции (y=x 2 ):

Теперь ещё раз вернёмся на страницу Равноускоренного движения, на которой мы пошаговым путём нашли производную квадратичной функции для значений t=1 (s’=2) и t=2,5 (s’=5).

Подставляя эти же значения в нашу формулу, мы получим те же значения производных.

Если вам понравился сайт, будем благодарны за его популяризацию Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Примеры решения производных с ответами

Простое объяснение принципов решения производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения производных

Для вычисления производных вам потребуется таблица производных. Кроме того, существуют формулы для нахождения сложных производных.

Процесс нахождения производный называется дифференцированием.

10. 0, c neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»219″ style=»vertical-align: -5px;» />
11. 0, c neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»180″ style=»vertical-align: -5px;» />

– производная суммы (разницы).

– производная произведения.

– производная частного.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Примеры решений производных

Задача

Найти производную функции

Решение

Заданная функция является сложной и её производная равна произведению производной от косинуса на производную от его аргумента:

Ответ

Задание

Найти производную функции

Решение

Обозначим , где . Тогда, согласно правила вычисления производной сложной функции, получим:

Ответ

Задача

Найти производную функции при .

Решение

.
.

Ответ

.

Задача

Найти производную функции .

Решение

.
После приведения подобных членов получаем:
.

Ответ

Задача

Найти производную функции .

Решение

В этом примере квадратный корень извлекается из суммы . Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения:
.

Ответ

.

Задача

Найти производную функции .

Решение

Применяя правила дифференцирования дробей, получаем:

.
Применяя правила дифференцирования котангенса, получаем:
.
Учитывая, что и , после упрощения получим:
.

Ответ

.

Задача

Найти производную функции .

Решение

Применяя правила дифференцирования дробей, получаем:
.

Ответ

.

Задача

Найти производную функции .

Решение

Применяя правила дифференцирования дробей, получаем:
.

Ответ

.

Задача

Найти производную функции .

Решение

Дифференцирование можно произвести в два этапа: вначале продифференцировать степень функции арксинус, а затем произвести дифференцирование самого арксинуса, перемножив результаты:
.

Ответ

.

Задача

Найти производную функции .

Решение

По правилам дифференцирования показательной функции с основанием , производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени:
.

Ответ

.