Загрузить PDF
Загрузить PDF
Производная многочлена характеризует скорость изменения функции (в определенной точке). Для получения производной многочлена необходимо перемножить коэффициенты при переменных и степени соответствующих переменных, понизить степени на 1 и удалить свободные члены. Если Вы хотите узнать процесс, прочтите эту статью.
Шаги
-
1
Выделите члены с переменной и свободный член в многочлене. Члены с переменной – любые члены с переменной и коэффициентом при ней, свободный член – член без переменной, коэффициент (число). Например, дан многочлен: y = 5x3 + 9x2 + 7x + 3
- Члены с переменной: 5x3, 9x2, and 7x
- Свободный член: 3
-
2
Перемножьте коэффициенты при каждой переменной и их степени. Результат будет представлять собой новый коэффициент перед соответствующей переменной. После перемножения просто поставьте результат перед соответствующей переменной. Вот как это делается:
- 5x3 = 5 x 3 = 15
- 9x2 = 9 x 2 = 18
- 7x = 7 x 1 = 7
-
3
Понизьте каждую степень на 1. Для этого просто вычтите 1 из степени каждой переменной. Вот как это делается:
- 5x3 = 5x2
- 9x2 = 9x1
- 7x = 7
-
4
Замените старые коэффициенты и степени новыми. Для завершения нахождения производной замените старые коэффициенты на новые (результат перемножения) и степени на пониженные на единицу. Производная от свободного члена = 0, поэтому Вы можете убрать свободный член (3).
- 5x3 becomes 15x2
- 9x2 becomes 18x
- 7x becomes 7
- Производная многочлена y = 5x3 + 9x2 + 7x + 3 равна y = 15x2 + 18x + 7
-
5
Найдите значение производной в зависимости от данного значения «x». Для нахождения значения «y» с данным значением «x,» подставьте значение «x» в уравнение. Например, для вычисления у при x = 2, подставьте 2 вместо x в найденное производное уравнение. Вот так:
- 2 —> y = 15x2 + 18x+ 7 = 15 x 22 + 18 x 2 + 7 =
- y = 60 + 36 + 7 = 103
- Значение производной при x = 2: 103.
Реклама
Советы
- Общее правило дифференцирования: d/dx[axn]=naxn-1
- Вычисление неопределенных интегралов многочленов проводится по аналогичной схеме, только в обратном порядке.Например, дана производная 12x2 + 4x1 +5x0 + 0. Вы прибавляете 1 к каждой степени переменной и делите на полученное число каждый коэффициент. Результат: 4x3 + 2x2 + 5x1 + C, где C неизвестный свободный член (невозможно вычислить его точное значение).
- Запомните определение производной: lim [f(x+h)-f(x)]/h при h->0
- Работайте с отрицательными или дробными степенями по тем же правилам. Например, производная от x-1 будет -x-2, а от x1/3 будет (1/3)x-2/3.
- Запомните, что описанный процесс работает только при постоянных степенях (в степени стоит число). Например, d/dx x^x не будет x(x^(x-1)), а равно x^x(1+ln(x)). Общее правило дифференцирования работает с x^n при постоянной n.
Реклама
Об этой статье
Эту страницу просматривали 25 930 раз.
Была ли эта статья полезной?
Значение производной многочлена по методу Горнера
| Элементы многочлена |
| Переменная X при которой находим значения производной |
Рассмотрим одну из простых и незаслужено забытых на просторах интернета методики определения производной полинома, произвольной (положительной) степени.
До последнего был уверен, что если известен многочлен вида
и необходимо узнать значение производной например 5 порядка в какой либо точке, необходимо сначала вычислить эту производную (пятого порядка), а потом уже подставив значение, рассчитать производную.
Оказывается есть более простой и алгоритмически легкий способ, нахождения производной в точке.
Для этого нам понадобится методика описанная в материалах: Разложить многочлен по степеням и Метод Горнера. Деление многочлена.
Да, да, оказывается метод Горнера с успехом решает поставленную задачу.
Рассмотрим пример:
Вычислить производную третьего порядка при х=3 следующего многочлена
1. Разделим заданный многочлен на
Получим =2x^2+x+4)
Число 19 есть значение функции =2x^3-5x^2+x+7)
2. Разделим =2x^2+x+4)
Получим =2x+7)
Так как это первая проивзодная, то умножим полученный результат на 1!(один факториал)=1. Получили то же число 25
Число 25 это значение первой производной от заданной функции при x=3. То есть если мы вычислим первую производную
=6x^2-10x+1)
3. Разделим =2x+7)
получим =2)
Умножим это число на 2! (два факториал) =2 и мы получим значение производной функции второго порядка при х=3
Это число =26
4. Производная третьего порядка вычисляется в данном случае просто, так как =2)
И получим, что производная третьего порядка при заданном многочлене при x=3 равна 12.
Таким незамысловатым способом мы можем находить значения любой производной любого полинома.
Алгоритм прост, но при многочленах со степенями выше 10, мы сталкиваемся с необходимостью вычислять факториалы выше 10, что очень трудоемко, так как факториал от 10 равен 3628800, а факториал от 16 уже 20922789888000
Но нам на пользу приходит одно из свойств методики Горнера, которое гласит: Если мы умножим какую либо функцию на число то и остаток отделения возрастет во столько же раз.
Поэтому нам достаточно умножать полученные коэффиценты полинома от деления на числа 1,2,3,4,5 и т.д. в зависимости от того какую производную мы вычислем в данный момент и вычислить остаток.
Калькулятор работает и в поле комплексных чисел, поэтому решим вот такой пример.
Есть функция
Необходимо узнать все возможные производные этой функции при x=i
Несложно убедится что решая это вручную, можно допустить оплошность и пойти по неверному пути.
Намного проще воспользоватся ботом и через XMPP клиент написать
propol 2 1-5i 0 -7 i 2 -9 -1;i
и мы получим все результаты
Найдены значения производной полинома
0 производная. Значение функции -10-6i
1 производная. Значение функции 7+35i
2 производная. Значение функции 112-66i
3 производная. Значение функции -180-282i
4 производная. Значение функции -528+120i
5 производная. Значение функции -1440+720i
6 производная. Значение функции 720+6480i
7 производная. Значение функции 10080
Логичный вопрос — а что же такое нулевая производная?
Ответим — это исходная функция. А значение -10-6i получается если бы мы -i подставили в исходную функцию
Попробуем решить другое уравнение
знаем чему же равна четвертая производная функции
при х=2+i
Полином 17-ой степени.. это серъезно как и вычисление при комплексном аргументе.
Что ж попробуем
| Заданная функция | ||||||||||||||||||||||||||||||||||||||
=(7-i)*x^{17}+(2)*x^{11}+(-i)*x^{7}+(9)*x^{1}+(-5)*x^{0}) |
||||||||||||||||||||||||||||||||||||||
|
при значении x=2+i значение функции при взятии четвертой производной будет
| 4 | 13006113720-5465417040i |
Что еще можно заметить?
Что необходимо внимательно смотреть на расчеты.
В нашем примере при взятии 17 призводной получается число 24.898
хотя должно конечно же быть (17!))
Это небольшая недоработка (ошибка при вычислении больших производных) будет испарвлена в ближайшее время. Но вычисления производных не выше 10 порядка, бот осуществляет правильно.
Удачных расчетов!
урок 3. Математика ЕГЭ
Как найти производную от функции
Как считать производные?
Никто не использует определение производной, чтобы ее вычислить. Как же тогда ее посчитать?
Оказывается, существуют специальные формулы, с помощью которых производная от функции вычисляется достаточно просто.
Формулы производной
Выпишем теперь все формулы производной функции и порешаем примеры.
Производная от константы
Производная от любого числа всегда равна (0):
$$(const)^{/}=0;$$
Пример 1
$$(5)^{/}=0;$$
Производная от (x)
Производная просто от (x) равна (1):
$$x^{/}=1;$$
Производная от степени
$$(x^n)^{/}=n*x^{n-1};$$
Пример 2
$$(x^4)^{/}=4*x^{4-1}=4*x^{3};$$
$$(x^{10})^{/}=10*x^{10-1}=10*x^{9};$$
$$(x^{-3})^{/}=-3*x^{-3-1}=-3*x^{-4};$$
$$(x^{frac{1}{3}})^{/}=frac{1}{3}*x^{1-frac{1}{3}}=frac{1}{3}*x^{frac{2}{3}};$$
Производная от квадратного корня
$$(sqrt{x})^{/}=frac{1}{2sqrt{x}};$$
Тут полезно заметить, что формулу производной от квадратного корня можно не учить. Она сводится к формуле производной от степени:
$$(sqrt{x})^{/}=(x^{frac{1}{2}})^{/}=frac{1}{2}*x^{frac{1}{2}-1}=frac{1}{2}*x^{-frac{1}{2}}=frac{1}{2sqrt{x}};$$
Производная от синуса
$$sin(x)^{/}=cos(x);$$
Производная от косинуса
$$cos(x)^{/}=-sin(x);$$
Производная от тангенса
$$tg(x)^{/}=frac{1}{cos^{2}(x)};$$
Производная от котангенса
$$tg(x)^{/}=frac{-1}{sin^{2}(x)};$$
Производная от экспоненты
$$(e^x)^{/}=e^x;$$
Производная от показательной функции
$$(a^x)^{/}=a^x*ln(a);$$
Пример 3
$$(2^x)^{/}=2^{x}*ln(2);$$
Производная от натурального логарифма
$$(ln(x))^{/}=frac{1}{x};$$
Производная от логарифма
$$(log_{a}(x))^{/}=frac{1}{x*ln(a)};$$
Свойства производной
Помимо формул по вычислению производной еще есть свойства производной, их тоже надо выучить.
Вынесение константы за знак производной
$$(alpha*f(x))^{/}=alpha*(f(x))^{/};$$
Пример 4
$$(3*x^5)^{/}=3*(x^5)^{/}=3*5x^4=15x^4;$$
$$(10sin(x))^{/}==10*(sin(x))^{/}=10*cos(x);$$
Производная от суммы и разности двух функций
$$(f(x) pm g(x))^{/}=(f(x))^{/} pm (g(x))^{/};$$
Пример 5
$$(2x^4+x^3)^{/}=?$$
Тут (f(x)=2x^4), а (g(x)=x^3). Тогда по формуле производной от суммы:
$$(2x^4+x^3)^{/}=(2x^4)^{/}+(x^3)^{/}=2*(x^4)^{/}+(x^3)^{/}=2*4x^3+3x^2=8x^3+3x^2;$$
Пример 6
$$(ln(x)+cos(x))^{/}=(ln(x))^{/}+(cos(x))^{/}=frac{1}{x}-sin(x);$$
Пример 7
$$(x^6-e^x)^{/}=(x^6)^{/}-(e^x)^{/}=6x^5-e^x;$$
Производная от произведения двух функций
$$(f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/};$$
Пример 8
$$(x^2*sin(x))^{/}=?$$
$$(x^2*sin(x))^{/}=(x^2)^{/}*sin(x)+x^2*(sin(x))^{/}=2x*sin(x)+x^2*cos(x);$$
Пример 9
$$(ln(x)*e^x)^{/}=(ln(x))^{/}*e^x+ln(x)*(e^x)^{/}=frac{1}{x}*e^x+ln(x)*e^x;$$
Производная от частного двух функций
$$left(frac{f(x)}{g(x)}right)^{/}=frac{(f(x))^{/}*g(x)-f(x)*(g(x))^{/}}{(g(x))^2};$$
Пример 10
$$left(frac{x^3}{sin(x)}right)^{/}=frac{(x^3)^{/}*sin(x)-x^3*(sin(x))^{/}}{(sin(x))^2}=frac{3x^2*sin(x)-x^3*cos(x)}{(sin(x))^2};$$
Примеры нахождения производной
Рассмотрим несколько примеров нахождения производной, чтобы разобраться, как применяются свойства и формулы производной на практике.
Пример 11
$$(5x^3+2cos(x))^{/}=(5x^3)^{/}+(2cos(x))^{/}=$$
$$=5*(x^3)^{/}+2*(cos(x))^{/}=5*3*x^2+2*(-sin(x))=15x^2-2sin(x);$$
Пример 12
$$left(-frac{3x^2}{2x^4+5x}right)^{/}=-frac{(3x^2)^{/}*(2x^4+5x)-3x^2*(2x^4+5x)^{/}}{(2x^4+5x)^2}=$$
$$=-frac{6x*(2x^4+5x)-3x^2*(8x+5)}{(2x^4+5x)^2}=-frac{12x^5-24x^3+15x^2}{(2x^4+5x)^2};$$
Пример 13
$$(2xsqrt{x})^{/}=(2x)^{/}*sqrt{x}+2x*(sqrt{x})^{/}=$$
$$=2*sqrt{x}+2x*frac{1}{2sqrt{x}}=2*sqrt{x}+frac{2x}{2sqrt{x}}=2*sqrt{x}+sqrt{x}=3sqrt{x};$$
Производная сложной функции
Сложная функция — это функция не от аргумента (x), а от какой-то другой функции: (f(g(x))). Например, функция (sin(x^2)) будет сложной функцией: «внешняя» функция синуса берется от «внутренней» функции степени ((x^2)). Так как под синусом стоит аргумент не (x), а (x^2), то такая функция будет называться сложной.
Еще примеры сложных функций:
-
$$ln(3x^4);$$
Внешняя функция: натуральный логарифм; Внутренняя функция: ((3x^4)). -
$$cos(ln(x));$$
Внешняя функция: косинус; Внутренняя функция: ((ln(x))). -
$$e^{2x^2+3};$$
Внешняя функция: экспонента; Внутренняя функция: ((2x^2+3)). -
$$(sin(x))^3;$$
Внешняя функция: возведение в третью степень; Внутренняя функция: (sin(x)).
Чтобы посчитать производную от такой функции, нужно сначала найти производную внешней функции, а затем умножить результат на производную внутренней функции. В общем виде формула выглядит так:
$$f(g(x))^{/}=f^{/}(g(x))*g^{/}(x);$$
Скорее всего, выглядит непонятно, поэтому давайте разберем на примерах.
Пример 14
$$((cos(x))^4)^{/}=?$$
Внешней функцией тут будет возведение в четвертую степень, поэтому сначала считаем производную от степени по формуле ((x^n)^{/}=n*x^{n-1}). А потом умножаем результат на производную внутренней функции, у нас это функция косинуса, по формуле (cos(x)^{/}=-sin(x)):
$$((cos(x))^4)^{/}=underset{text{внешняя производная}}{underbrace{4*(cos(x))^3}}*underset{text{внутренняя производная}}{underbrace{(cos(x))^{/}}}=$$
$$=4*(cos(x))^3*(-sin(x))=-4*(cos(x))^3*sin(x);$$
Пример 15
$$(e^{2x^3+5})^{/}=?$$
Внешняя функция — это экспонента ((e^x)^{/}=e^x), а внутренняя функция — квадратный многочлен ((2x^3+5)):
$$(e^{2x^3+5})^{/}=e^{2x^3+5}*(2x^3+5)^{/}=e^{2x^3+5}*((2x^3)^{/}+5^{/})=e^{2x^3+5}*6x^2.$$
Пример 16
$$(ln((2x^2+3)^6))^{/}=?$$
Внешняя функция — это натуральной логарифм, берем производную от него по формуле ((ln(x))^{/}=frac{1}{x}), и умножаем на производную внутренней функции, у нас это шестая степень: ((x^n)^{/}=n*x^{n-1}). Но и на этом еще не все: под шестой степенью стоит не просто (x), а квадратный многочлен, значит еще нужно умножить на производную от этого квадратного многочлена:
$$ln((2x^2+3)^6)=frac{1}{(2x^2+3)^6}*((2x^2+3)^6)^{/}*(2x^2+3)^{/}=$$
$$=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*(4x+0)=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*4x=$$
$$=frac{6*(2x^2+3)^5*4x}{(2x^2+3)^6}=frac{24x*(2x^2+3)^5}{(2x^2+3)^6}=frac{24x}{(2x^2+3)^6}.$$
Вывод формул производной функции
Выведем некоторые из этих формул, чтобы было понимание, откуда они берутся. Но перед этим познакомимся с новыми обозначениями. Запись (f(x)) означает, что функция берется от аргумента (x). Например:
$$f(x)=x^3+sin(x);$$
На месте аргумента (x) может стоять все что угодно, например выражение (2x+3). Обозначение такой функции будет (f(2x+3)), а сама функция примет вид:
$$f(2x+3)=(2x+3)^3+sin(2x+3);$$
То есть, везде вместо аргумента (x) мы пишем (2x+3).
И несколько важных замечаний про (Delta f(x)) и (Delta x). Напомню, что значок (Delta) означает изменение некоторой величины. (Delta x) — изменения координаты (x) при переходе от одной точки на графике функции к другой; (Delta f(x)) — разница координат (y) между двумя точками на графике. Подробнее про это можно почитать в главе, где мы вводим понятие производной. Распишем (Delta x) для двух близких точек на графике функции (O) и (B):
$$Delta x=x_B-x_O;$$
Отсюда можно выразить (x_B):
$$x_B=x_O+Delta x;$$
Абсцисса (координата точки по оси (x)) точки (B) получается путем сложения абсциссы точки (O) и (Delta x).
Кстати, функцию (f(x)=x^3+sin(x)) от аргумента (x_B=x_O+Delta x) можно расписать:
$$f(x_B)=f(x_O+Delta x)=(x_O+Delta x)^3+sin(x_O+Delta x);$$
Рис.1. График произвольной функции
И распишем (Delta f):
$$Delta f(x)=f(x_B)-f(x_O)=f(x_O+Delta x)-f(x_O);$$
Тогда определение производной можно записать в виде:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x_O+Delta x)-f(x_O)}{Delta x} quad при quad Delta x to 0;$$
За (x_O) обычно обозначают точку, в окрестности которой берут производную. То есть, получается (x_O) — это абсцисса начальной точки, а (x_O+Delta x) — абсцисса конечной точки.
Нам это пригодится при выводе формул производной.
Производная квадратичной функции
Выведем теперь формулу производной от (f(x)=x^2), воспользовавшись определением производной:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
Распишем числитель (f(x+Delta x)-f(x)) с учетом, что (f(x)=x^2):
$$f(x+Delta x)-f(x)=(x+Delta x)^2-x^2=x^2+2xDelta x+(Delta x)^2-x^2=2xDelta x+(Delta x)^2;$$
Подставим в определение производной:
$$f^{/}(x)=frac{2xDelta x+(Delta x)^2}{Delta x}=frac{Delta x*(2x+Delta x)}{Delta x}=2x+Delta x;$$
Напоминаю, что (Delta x) это бесконечно малая величина:
$$(Delta x)^2 ll 0;$$
Поэтому этим слагаемым можно пренебречь. Вот мы и получили формулу для производной от квадратной функции:
$$f^{/}(x)=(x^2)^{/}=2x;$$
Производная от третьей степени
Аналогичные рассуждения можно провести для функции третьей степени:
$$f(x)=x^3;$$
Воспользуемся определением производной:
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
$$f(x+Delta x)-f(x)=(x+Delta x)^3-x^3=(x+Delta x-x)((x+Delta x)^2+(x+Delta x)*x+x^2)=$$
$$=Delta x*(x^2+2x*Delta x+(Delta x)^2+x^2+x*Delta x+x^2)=Delta x*(3x^2+3xDelta x);$$
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x}=frac{Delta x*(3x^2+3xDelta x)}{Delta x}=3x^2+3xDelta x;$$
Так как при умножении на бесконечно малую величину получается бесконечно малая величина, то слагаемым (3xDelta x) можно пренебречь:
$$f^{/}(x)=(x^3)^{/}=3x^2;$$
Точно таким же способом можно вывести формулы производных для любых степеней:
$$(x^4)^{/}=4x^3;$$
$$(x^5)^{/}=5x^4;$$
$$…$$
$$(x^n)^{/}=n*x^{n-1};$$
Кстати, эта формула справедлива и для дробных степеней.
Вывод остальных формул делается похожим образом, только там может понадобиться знание пределов. Вывод всех формул разбирается в университетском курсе математического анализа.
Что такое производная функции простыми словами? Для чего нужна производная? Определение производной
Как решать задания №7 из ЕГЭ по математике. Анализ графиков при помощи производной. Графики производной и графики функции
Исследуем функцию с помощью производной. Находим точки минимума и максимума, наибольшее и наименьшее значение функции. Точки экстремума. Промежутки возрастания и убывания.
Связь коэффициента наклона и тангенса угла наклона касательной к функции и производной функции в точке касания. Задание №7 в ЕГЭ по математике.
Download Article
Download Article
Differentiation is one of the fundamental processes in calculus. Differentiating a function (usually called f(x)) results in another function called the derivative, written as f'(x) («f prime of x»). This derivative has many uses in physics and mathematics. For instance, if we graph a polynomial f(x), the derivative f'(x) tells us the slope (the rate of change) of the original function at all its points. The first section of this article teaches you to differentiate each term of the polynomial, one at a time. The second section uses this approach to walk through a typical example problem, differentiating an entire polynomial. After some practice, differentiating 
-
1
Differentiate any constant to zero. A constant is any ordinary number, with no variable involved—for example, 3, -16, or
. These are freebies in any differentiation problem, because their derivative is always 0. Just cross out that term and move on.[1]
- Write this in the form
. This says «The derivative of 3 with respect to x is 0.»
- The derivative of a term is the «rate of change» of that term: how quickly that term changes inside a function. Since a constant never changes (3 will always stay 3), its rate of change is always zero.
- Write this in the form
-
2
Advertisement
-
3
-
4
-
5
Multiply by the coefficient from the original term. The coefficient in front of the variable doesn’t change when you differentiate the term. If you end up with more than one coefficient in your answer, multiply them together.[7]
Advertisement
-
1
Treat each term as a separate problem. Polynomials contain multiple terms, added or subtracted together. To differentiate the polynomial, differentiate each term separately. You can leave all of the addition and subtraction symbols alone.[8]
-
2
Get rid of the constant term. If there is a constant (a term without a variable), delete it. Differentiating always removes the constant term.[9]
- In our example, 6 is the constant.
, so we can get rid of it.
- Careful: only terms with no variables are constants. This rule does not affect numbers that are multiplied by x or any other variable.
- In our example, 6 is the constant.
-
3
Move each variable’s exponent to the front of the term. Remember, when we differentiate, each variable’s exponent becomes a coefficient. If there is already a coefficient in front of the term, multiply the two coefficients together.[10]
-
4
Lower each exponent by one degree. To do this, subtract 1 from each exponent in each variable term.[11]
-
5
Find the value of the new equation at a given «x» value. You’re already done with the differentiation, but there’s a common next step in test problems. If you’re asked to «evaluate the expression» for a value of x, all you need to do is replace each x in the new equation with the given value and solve.[12]
Advertisement
Add New Question
-
Question
How can I subtract and add polynomials?
Add or subtract «like» terms only, meaning you add or subtract their coefficients. Like terms are those having identical variables. For example, 5x²y³ and 10x²y³ are like terms, but 5x²y³ and 10x²y² are not.
-
Question
How can I go about finding the real roots of polynomial functions?
It depends on the degree of the polynomial. If it’s linear, simply divide. If it’s quadratic, use the formula x = (-b +/-√(b2 — 4ac))/2a. Cubic and quartic equations also have formulas to find the roots (although more complicated). However, it has been proven that there is no general, explicit formula for the roots of equations of degree 5 or higher (see Abel-Ruffini theorem). So you must try to factorize or use trial-and-error to find some roots. If they don’t work, then by the above theorem you’ll probably never find explicit solutions (unless you use elliptic functions). Of course, if you just want to analyze roots without getting actual values, just examine the graph with differentials.
-
Question
How do I evaluate 3^2 — 2^3 + 10x^0?
3² = 9. 2³ = 8. 10(x)^0 = 10(1) = 10. 9 — 8 + 10 = 11.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Advertisement
About This Article
Thanks to all authors for creating a page that has been read 211,991 times.
Did this article help you?
-
Формальная производная, ее свойства
Многочлен f(x+y)-f(x)
делится на y без остатка
(проверить по теореме Безу). Положим
.
Многочлен F(x,0)
называют производной многочлена f(x)
и обозначают
.
Теорема 2.19 (Свойства
производной)
Доказательство
следует из определения производной.
Говорят, что кратность
корня a
многочлена f(x)
равна k,
если f(x)
делится на
и не делится (без остатка) на
.
Теорема 2.20 (Кратность
корня)
Если a корень
многочлена f(x)
кратности k, то a
корень его производной кратности k—1.
Доказательство.
Пусть a
корень кратности k
многочлена f(x).
Тогда f(x)
представим в виде произведения
,
причём
.
Производная от f(x)
равна
,
где
.
Поскольку
,
то теорема доказана.
Следствие 2.6
Многочлен
не имеет кратных множителей.
Доказательство.
Перейдём к полю разложения f(x).
Многочлен
над этим полем имеет те же самые корни,
что и f(x),
только кратности 1. Вернёмся в исходное
поле P.
Многочлен
разлагается на те же неприводимые
множители что и f(x),
только кратности 1.
-
Производные высоких порядков
Производную порядка k от
многочлена f(x)
обозначим
.
При k=0 под
будем понимать исходный многочлен.
Лемма 2.1
.
Доказательство
проведём индукцией по j.
При j=1
получаем формулу дифференцирования
произведения. Пусть формула верна для
j-1.
Покажем её справедливость для j.
Имеют место равенства.
Взяв производную от каждого слагаемого,
приведя подобные, получим требуемое
равенство.
Следствие 2.7 Условие
при i=0,…,k-1
и
равносильно тому, что
— корень f(x)
кратности k.
Доказательство.
Пусть
— корень f(x)
кратности k,
тогда
,
причём
.
Производная порядка i
равна
.
Подставив
получим равенства
при i=0,…,k-1
и
.
Обратно, разложим f(x)
по степеням
,
т.е.
.
Легко проверить
и значит
— корень f(x)
кратности k.
-
Интерполяционный многочлен Лагранжа-Сильвестра
В ряде случаев необходимо найти многочлен
наименьшей степени, у которого на
некотором множестве заданы не только
его значения, но и значения производных
до определенных порядков. Пусть на
множестве точек
заданы значения функции и её производных
высших порядков. Под
будем понимать значение производной
порядка i в точке
.
Под производной порядка 0 будем понимать
саму функцию. Пусть заданы значения
,
где j=1,…,k
и
.
Теорема 2.21 (Интерполяционный
многочлен Лагранжа — Сильвестра)
Существует единственный многочлен
h(x) степени
меньше
,
удовлетворяющий равенствам
,
где j=1,…,k
и
.
Доказательство.
Положим
,
.
Для i=1,…,k
определим числа
и далее по индукции
,
где
.
Многочлен
удовлетворяет равенствам:
при
и
,
и
.
Что бы убедится в справедливости равенств
найдём производную j
порядка
.
Поскольку
при
и
,
то равенства
при
и
установлены. Подставим теперь
и получим
Подставив вместо
равное ему выражение, после приведения
подобных, получим равенство
.
Далее осталось написать интерполяционный
многочлен
.
Поскольку степень каждого слагаемого
меньше
,
то и степень суммы меньше
.
Единственность интерполяционного
многочлена покажем методом от противного.
Допустим, существует два интерполяционных
многочлена h(x)
и g(x).
Их разность имеет
корнем кратности не меньше
и значит, делится на w(x)
без остатка. Поскольку степень w(x)
заведомо больше чем степень h(x)-g(x),
то h(x)=g(x).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


=a_0x^{n}+a_1x^{n-1}+a_2x^{n-2}+.....+a_{n-1}x+a_n)
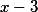
=2x^7+(1-5i)x^6%20-7x^4+x^3i+2x^2%20-9x-1)
=(7-i)x^{17}+2x^{11}%20-ix^7+9x-5)













