Производная неявной функции
Формула
Рассмотрим функцию y(x), которая записывается неявным способом в общем виде $ F(x,y(x)) = 0 $. Производная неявной функции находится двумя способами:
- Дифференцированием обеих частей уравнения
- С помощью использования готовой формулы $ y’ = — frac{F’_x}{F’_y} $
Как найти?
Способ 1
Не требуется приводить функцию к явному виду. Нужно сразу приступать к дифференцированию левой и правой части уравнения по $ x $. Стоит обратить внимание, что производная $ y’ $ вычисляется по правилу дифференцирования сложной функции. Например, $ (y^2)’_x = 2yy’ $. После нахождения производной необходимо выразить $ y’ $ из полученного уравнения и разместить $ y’ $ в левой части.
Способ 2
Можно воспользоваться формулой, в которой используются в числителе и знаменателе частные производные неявной функции $ F(x,y(x)) = 0 $. Для нахождения числителя берем производную по $ x $, а для знаменателя производную по $ y $.
Вторую производную неявной функции можно найти с помощью повторного дифференцирования первой производной неявной функции.
Примеры решений
Рассмотрим практические примеры решений на вычисление производной неявно заданной функции.
| Пример 1 |
|
Найти производную неявной функции $ 3x^2y^2 -5x = 3y — 1 $ |
| Решение |
|
Воспользуемся способом №1. А именно продифференцируем левую и правую часть уравнения: $$ (3x^2y^2 -5x)’_x = (3y — 1)’_x $$ Не забываем при дифференцировании использовать формулу производной произведения функций: $$ (3x^2)’_x y^2 + 3x^2 (y^2)’_x — (5x)’_x = (3y)’_x — (1)’_x $$ $$ 6x y^2 + 3x^2 2yy’ — 5 = 3y’ $$ Далее выражаем y’ из уравнения: $$ 6x y^2 — 5 = 3y’ — 6x^2 yy’ $$ $$ 6x y^2 — 5 = y'(3-6x^2 y) $$ $$ y’ = frac{6x y^2 — 5}{3 — 6x^2y } $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y’ = frac{6x y^2 — 5}{3 — 6x^2y } $$ |
| Пример 2 |
|
Функция задана неявно, найти производную $ 3x^4 y^5 + e^{7x-4y} -4x^5 -2y^4 = 0 $ |
| Решение |
|
Воспользуемся способом №2. Находим частные производные функции $ F(x,y) = 0 $ Положим $ y $ постоянной и продифференцируем по $ x $: $$ F’_x = 12x^3 y^5 + e^{7x-4y} cdot 7 — 20x^4 $$ $$ F’_x = 12x^3 y^5 + 7e^{7x-4y} — 20x^4 $$ Считаем теперь $ x $ константой и дифференцируем по $ y $: $$ F’_y = 15x^4 y^4 + e^{7x-4y} cdot (-4) — 8y^3 $$ $$ F’_y = 15x^4 y^4 — 4e^{7x-4y} — 8y^3 $$ Подставляем теперь в формулу $ y’ = -frac{F’_x}{F’_y} $ и получаем: $$ y’ = -frac{12x^3 y^5 + 7e^{7x-4y} — 20x^4}{15x^4 y^4 — 4e^{7x-4y} — 8y^3} $$ |
| Ответ |
| $$ y’ = -frac{12x^3 y^5 + 7e^{7x-4y} — 20x^4}{15x^4 y^4 — 4e^{7x-4y} — 8y^3} $$ |
Производная функции, заданной параметрически
4 января 2022
Сегодня мы научимся считать производную параметрической функции. Для этого разберём основную формулу, несколько примеров, но главное — одну из самых частых и глупых ошибок, которые допускают начинающие студенты.
План такой:
- Параметрическое задание функции — основные понятия
- Производная функции, заданной параметрически
- Типичные ошибки на примере второй производной
- Третья производная — разминка для мозгов
Начнём с ключевых определений и соображений.
1. Функция, заданная параметрически
Считая производные, мы привыкли работать с функциями, заданными аналитически, т.е. формулой $y=fleft( x right)$. Подставляя в эту формулу разные значения $x$, мы легко находим значение $y$.
Несколько примеров таких функций:
- Квадратичная функция: $y={{x}^{2}}$. График — парабола.
- Показательная функция: $y={{text{e}}^{x}}$. Она же «экспонента».
- Тригонометрическая функция: $y=sin x$. График — синусоида.
Но что если величины $y$ и $x$ зависят не друг от друга, а от некой третьей переменной? Скажем, от параметра $t$?
Пример 1. Функция, заданная параметрически:
[left{ begin{align} & x=cos t \ & y=sin t \ end{align} right.]
Перебирая разные $tin mathbb{R}$, мы будем получать точки с координатами $left( x;y right)$, которые в итоге превратятся в график:
Да это же тригонометрическая окружность! Она задаётся уравнением ${{x}^{2}}+{{y}^{2}}=1$.
График такого уравнения не является функцией (если забыли почему, гляньте урок про графики уравнений с двумя переменными). Но его можно «составить» из графиков двух функций:
[begin{align} & {{y}_{1}}=sqrt{1-{{x}^{2}}} \ & {{y}_{2}}=-sqrt{1-{{x}^{2}}} \ end{align}]
А вот это уже привычные нам аналитические функции, и для них можно посчитать производную!
К сожалению, далеко не всегда параметрическое уравнение вида
[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]
можно свести к привычными выражениям вида $y=fleft( x right)$. Но это ни в коем случае не означает, что для таких параметрических функций нельзя посчитать производную. Можно и даже нужно. И поможет нам в этом следующая формула.
2. Производная функции, заданной параметрически
Итак, основная теорема.
Теорема 1. Пусть функция $y=fleft( x right)$ задана параметрически:
[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]
Тогда производная этой функции считается по формуле
[{{{y}’}_{x}}left( x right)=frac{{{{{y}’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
Эту теорему очень легко доказать. В самом деле, если функция $x=varphi left( t right)$ рассматривается на интервале $tin left( a;b right)$ таком, что существует обратная функция $t={{varphi }^{-1}}left( x right)$, то можно определить сложную функцию
[yleft( x right)=psi left( {{varphi }^{-1}}left( x right) right)]
По теореме о производной сложной функции:
[{{{y}’}_{x}}left( x right)={{{psi }’}_{x}}left( {{varphi }^{-1}}left( x right) right)={{{psi }’}_{x}}left( t right)={{{psi }’}_{t}}left( t right)cdot {{{t}’}_{x}}left( x right)]
[begin{align} {{{{y}’}}_{x}}left( x right) & ={{{{psi }’}}_{x}}left( {{varphi }^{-1}}left( x right) right)= \ & ={{{{psi }’}}_{x}}left( t right)= \ & ={{{{psi }’}}_{t}}left( t right)cdot {{{{t}’}}_{x}}left( x right) end{align}]
Но по теореме об обратной функции ${{{t}’}_{x}}={1}/{{{{{x}’}}_{t}}};$, поэтому
[{{{y}’}_{x}}left( x right)=frac{{{{{psi }’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
Что и требовалось доказать.
Замечание. Когда выражение дифференцируется по разным переменным, целесообразно указывать в нижним индексе ту переменную, по которой выполняется дифференцирование: ${{{y}’}_{x}}$, ${{{y}’}_{t}}$, ${{{x}’}_{t}}$ и т.д.
Это поможет избежать недоразумений и глупых вычислительных ошибок. Кроме того, подобные обозначения активно используются в дифференциальном исчислении функций нескольких переменных.
Детальное руководство по работе с нижними индексами и переменными дифференцирования — см. урок «Производная сложной функции». Сейчас просто отметим, что мы привыкли считать производную по переменной $x$. Но с тем же успехом можно считать производную и по $t$, и по какому-нибудь $varphi $, и вообще по любой переменной, которую мы увидим в функции.
2.1. Примеры
Приведённые выше формулы могут показаться сложными и страшными. Но на деле это одна из самых лёгких тем в производных. Взгляните:
Пример 1. Найдите ${{{y}’}_{x}}$, если
[left{ begin{align} & x=2t \ & y=3{{t}^{2}}-5t \ end{align} right.]
Считаем производные ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( 2t right)}^{prime }}_{t}=2 \ & {{{{y}’}}_{t}}={{left( 3{{t}^{2}}-5t right)}^{prime }}_{t}=6t-5 end{align}]
Теперь считаем ${{{y}’}_{x}}$ по формуле производной параметрической функции:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{6t-5}{2}]
Вот и всё! Готовое выражение можно разбить на две дроби, а можно оставить и так.
Пример 2. Найдите ${{{y}’}_{x}}$, если
[left{ begin{align} & x={{2}^{-t}} \ & y={{2}^{2t}} \ end{align} right.]
Вместо многочленов видим показательные функции. Это ничего не меняет, снова считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( {{2}^{-t}} right)}^{prime }}_{t}={{2}^{-t}}cdot left( -ln 2 right) \ & {{{{y}’}}_{t}}={{left( {{2}^{2t}} right)}^{prime }}_{t}={{2}^{2t}}cdot 2ln 2 end{align}]
Теперь находим ${{{y}’}_{x}}$ по формуле:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{2}^{2t}}cdot 2ln 2}{{{2}^{-t}}cdot left( -ln 2 right)}=-{{2}^{3t+1}}]
Для решения этого задания пришлось вспомнить производную показательной функции и некоторые свойства степеней.:)
Пример 3. Найдите ${{{y}’}_{x}}$, если
[left{ begin{align} & x=acos varphi \ & y=bsin varphi \ end{align} right.]
Здесь переменной-параметром является $varphi $, а буквы $a$ и $b$ — просто числа, которые будут частью ответа. Считаем ${{{x}’}_{varphi }}$ и ${{{y}’}_{varphi }}$ — производные тригонометрических функций:
[begin{align} & {{{{x}’}}_{varphi }}={{left( acos varphi right)}^{prime }}_{varphi }=-asin varphi\ & {{{{y}’}}_{varphi }}={{left( bsin varphi right)}^{prime }}_{varphi }=bcos varphiend{align}]
Находим ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{varphi }}}{{{{{x}’}}_{varphi }}}=frac{bcos varphi }{-asin varphi }=-frac{b}{a}operatorname{ctg}varphi ]
2.2. Производная в точке
Понятно, что это были совсем простые задачи. Буквально через минуту мы рассмотрим примеры посерьёзнее, но сначала важное дополнение.
Часто нам требуется посчитать не производную функции вообще, а лишь в конкретной точке. Например, чтобы провести касательную или нормаль к кривой, заданной параметрически, в некой точке ${{M}_{0}}left( {{x}_{0}};{{y}_{0}} right)$, лежащей на этой кривой.
В этом случае задача ещё более упрощается.
Пример 4. Найдите ${{{y}’}_{x}}$ при $t={pi }/{4};$, если
[begin{align} & xleft( t right)=tcdot left( tcos t-2sin t right) \ & yleft( t right)=tcdot left( tsin t+2cos t right) \ end{align}]
Задача явно серьёзнее, чем все предыдущие. Считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( tcdot left( tcos t-2sin t right) right)}^{prime }}_{t}=-left( {{t}^{2}}+2 right)cdot sin t \ & {{{{y}’}}_{t}}={{left( tcdot left( tsin t+2cos t right) right)}^{prime }}_{t}=left( {{t}^{2}}+2 right)cdot cos t end{align}]
[begin{align} {{{{x}’}}_{t}} & ={{left( tcdot left( tcos t-2sin t right) right)}^{prime }}_{t}= \ & =-left( {{t}^{2}}+2 right)cdot sin t \ {{{{y}’}}_{t}} & ={{left( tcdot left( tsin t+2cos t right) right)}^{prime }}_{t}= \ & =left( {{t}^{2}}+2 right)cdot cos tend{align}]
И сразу подставляем $t={pi }/{4};$:
[begin{align} & {{{{x}’}}_{t}}left( frac{pi }{4} right)=-left( frac{{{pi }^{2}}}{16}+2 right)cdot frac{sqrt{2}}{2} \ & {{{{y}’}}_{t}}left( frac{pi }{4} right)=left( frac{{{pi }^{2}}}{16}+2 right)cdot frac{sqrt{2}}{2} end{align}]
Осталось найти ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=-frac{32+{{pi }^{2}}}{32+{{pi }^{2}}}=-1]
Разумеется, можно было сначала найти общую формулу для ${{{y}’}_{x}}$, а уже затем подставить в неё $t={pi }/{4};$ — результат получится точно такой же.
3. Типичные ошибки при вычислении производных
А теперь, пожалуй, ключевой момент, связанный с дифференцированием параметрических функций. Ошибка, которую я сам допустил много лет назад.
Давайте ещё раз взглянем на функцию, заданную параметрически:
[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]
И на производную этой функции:
[{{{y}’}_{x}}left( x right)=frac{{{{{y}’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
А теперь представьте, что надо посчитать вторую производную: ${{{y}»}_{xx}}$. И тут у многих проскакивает мысль: а что если взять формулу для первой производной и просто увеличить в ней количество «штрихов»?
Получится что-то типа вот этого:
[{{{y}»}_{xx}}left( x right)=frac{{{{{y}»}}_{tt}}left( t right)}{{{{{x}»}}_{tt}}left( t right)}]
Так вот: эта формула не верна!
Чтобы правильно найти вторую производную функции, заданной параметрически, достаточно вспомнить, что вторая производная — это просто производная от производной:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}]
Проще говоря, сначала мы находим ${{{y}’}_{x}}$ — это будет какая-то функция от $t$. Затем уже от этой функции вновь считаем производную — всё по той же формуле, которую мы сегодня уже много раз использовали. Получится так:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}]
Тут нас ждёт две новости:
- Хорошая: мы уже знаем ${{{x}’}_{t}}$. Это значит, что каждая последующая производная будет считаться чуть проще и быстрее;
- Плохая: можно легко запутаться во всех этих штрихах и переменных.
Чтобы разобраться с плохой новостью, достаточно просто небольшой практики. Поэтому сейчас мы разберём три примера. А точнее, три задачи из контрольных работ МГТУ им. Баумана. А там знают толк в производных.:)
Пример 5. Найдите ${{{y}»}_{xx}}$, если
[left{ begin{align} & x=cos 2t \ & y=sin t \ end{align} right.]
1. Сначала находим первую производную. Для этого считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}=-2sin 2t=-4sin tcos t \ & {{{{y}’}}_{t}}=cos t end{align}]
Откуда находим саму производную ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{cos t}{-4sin tcos t}=-frac{1}{4sin t}]
2. Теперь находим вторую производную. Для этого считаем ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}={{left( -frac{1}{4sin t} right)}^{prime }}_{t}=frac{cos t}{4{{sin }^{2}}t}]
Кроме того, мы уже знаем ${{{x}’}_{t}}$. Поэтому находим вторую производную ${{{y}»}_{xx}}$:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{cos t}{4{{sin }^{2}}t}cdot frac{1}{-4sin tcos t}=-frac{1}{16}cdot frac{1}{{{sin }^{3}}t}]
[begin{align} {{{{y}»}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =frac{cos t}{4{{sin }^{2}}t}cdot frac{1}{-4sin tcos t}= \ & =-frac{1}{16}cdot frac{1}{{{sin }^{3}}t} end{align}]
Вторая производная найдена.
Для сравнения посчитаем «производную» по неправильной формуле:
[frac{{{{{y}»}}_{tt}}}{{{{{x}»}}_{tt}}}=frac{{{left( {{{{y}’}}_{t}} right)}^{prime }}_{t}}{{{left( {{{{x}’}}_{t}} right)}^{prime }}_{t}}=frac{{{left( cos t right)}^{prime }}_{t}}{{{left( -2sin 2t right)}^{prime }}_{t}}=frac{-sin t}{-4cos 2t}=frac{1}{4}cdot frac{sin t}{cos 2t}]
[begin{align} frac{{{{{y}»}}_{tt}}}{{{{{x}»}}_{tt}}} & =frac{{{left( {{{{y}’}}_{t}} right)}^{prime }}_{t}}{{{left( {{{{x}’}}_{t}} right)}^{prime }}_{t}}=frac{{{left( cos t right)}^{prime }}_{t}}{{{left( -2sin 2t right)}^{prime }}_{t}}= \ & =frac{-sin t}{-4cos 2t}=frac{1}{4}cdot frac{sin t}{cos 2t} end{align}]
Получили совершенно другое выражение, которое не является второй производной.
Итак, вторая производная считается из первой ровно по той же формуле, по какой первая производная считается из исходной функции.
Пример 6. Найдите ${{{y}»}_{xx}}$, если
[left{ begin{align} & x={{text{e}}^{t}}+1 \ & y=left( {{t}^{2}}-2t+2 right)cdot {{text{e}}^{t}} \ end{align} right.]
Первая производная ${{{y}’}_{x}}$ через ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{text{e}}^{t}} \ & {{{{y}’}}_{t}}={{t}^{2}}cdot {{text{e}}^{t}} \ & {{{{y}’}}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{t}^{2}}cdot {{text{e}}^{t}}}{{{text{e}}^{t}}}={{t}^{2}} \ end{align}]
Вторая производная ${{{y}»}_{xx}}$ через ${{{x}’}_{t}}$ и ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[begin{align} & {{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}=2t \ & {{{{y}»}}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{2t}{{{text{e}}^{t}}} \ end{align}]
Замечание. Когда освоитесь с основной формулой, выкладки можно сократить буквально до двух строк:
[begin{align} & {{{{y}’}}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{t}^{2}}cdot {{text{e}}^{t}}}{{{text{e}}^{t}}}={{t}^{2}} \ & {{{{y}»}}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{2t}{{{text{e}}^{t}}} \ end{align}]
Впрочем, не стоит увлекаться сокращением выкладок, если у вас есть хоть малейшее сомнение или недопонимание на любом этапе вычислений.
Пара дополнительных минут — сомнительная экономия по сравнению с парой баллов на контрольной. И уж тем более по сравнению с недопониманием материала.
Пример 7. Найдите ${{{y}»}_{xx}}$, если
[left{ begin{align} & x={1}/{left( 1+{{t}^{2}} right)}; \ & y=2operatorname{arctg}t \ end{align} right.]
Дифференцирование арктангенса дробно-рациональной функции — довольно громоздкие действия. Тут в пару строк не уложиться.
1. Считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( frac{1}{1+{{t}^{2}}} right)}^{prime }}_{t}=frac{-2t}{{{left( 1+{{t}^{2}} right)}^{2}}} \ & {{{{y}’}}_{t}}={{left( 2operatorname{arctg}t right)}^{prime }}_{t}=frac{2}{1+{{t}^{2}}} \ end{align}]
Первая производная ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{2}{1+{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}=-frac{1+{{t}^{2}}}{t}]
2. Считаем ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}=-frac{2tcdot t-left( 1+{{t}^{2}} right)}{{{t}^{2}}}=frac{1-{{t}^{2}}}{{{t}^{2}}}]
Вторая производная ${{{y}»}_{xx}}$:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{1-{{t}^{2}}}{{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}=frac{{{left( 1+{{t}^{2}} right)}^{2}}left( {{t}^{2}}-1 right)}{2{{t}^{3}}}]
[begin{align} {{{{y}»}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =frac{1-{{t}^{2}}}{{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}= \ & =frac{{{left( 1+{{t}^{2}} right)}^{2}}left( {{t}^{2}}-1 right)}{2{{t}^{3}}} end{align}]
Замечание. При делении дробных выражений полезно заменять их умножением на обратное:
[frac{Aleft( x right)}{Bleft( x right)}:frac{Pleft( x right)}{Qleft( x right)}=frac{Aleft( x right)}{Bleft( x right)}cdot frac{Qleft( x right)}{Pleft( x right)}]
Именно так мы и поступили при вычислении ${{{y}’}_{x}}$ и ${{{y}»}_{xx}}$ в последнем примере. И не только в последнем.:)
4. Третья производная
Пример 8. Найдите производную третьего порядка ${{{y}»’}_{xxx}}$ для функции, заданной параметрически:
[left{ begin{align} & xleft( t right)={{text{e}}^{t}}left( cos t+sin t right) \ & yleft( t right)={{text{e}}^{t}}left( cos t-sin t right) \ end{align} right.]
Решение будет состоять из трёх шагов.
1. Найдём первую производную ${{{y}’}_{x}}$. Для этого считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} {{{{x}’}}_{t}} & =2cos tcdot {{text{e}}^{t}} \ {{{{y}’}}_{t}} & =-2sin tcdot {{text{e}}^{t}} \ end{align}]
Первая производная ${{{y}’}_{t}}$ равна
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{-2sin tcdot {{text{e}}^{t}}}{2cos tcdot {{text{e}}^{t}}}=-operatorname{tg}t]
2. Считаем вторую производную. При этом ${{{x}’}_{t}}$ уже посчитано, осталось найти ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}={{left( -operatorname{tg}t right)}^{prime }}_{t}=-frac{1}{{{cos }^{2}}t}]
Находим вторую производную по всё той же формуле:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=-frac{1}{{{cos }^{2}}t}cdot frac{1}{2cos tcdot {{text{e}}^{t}}}=-frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t}]
[begin{align} {{{{y}»}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =-frac{1}{{{cos }^{2}}t}cdot frac{1}{2cos tcdot {{text{e}}^{t}}}= \ & =-frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} end{align}]
3. Считаем третью производную. Вновь нужно лишь найти ${{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t}$:
[{{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t}={{left( -frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} right)}^{prime }}_{t}=frac{cos t-3sin t}{2{{text{e}}^{t}}{{cos }^{4}}t}]
[begin{align} {{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t} & ={{left( -frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} right)}^{prime }}_{t}= \ & =frac{cos t-3sin t}{2{{text{e}}^{t}}{{cos }^{4}}t} end{align}]
Для сокращения вычислений я сразу записал готовую формулу ${{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t}$ — проверьте её самостоятельно. А дальше вновь используем формулу производной для параметрической функции:
[{{{y}»’}_{xxx}}=frac{{{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{cos t-3sin t}{4{{text{e}}^{2t}}cdot {{cos }^{5}}t}]
Задача решена. Хотя вычислений получилось довольно много.
В любом случае помните главную формулу:
[{{{y}’}_{x}}left( x right)=frac{{{{{psi }’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
И помните, что вторая производная не равна частному вторых производных:
[{{{y}»}_{xx}}left( x right)ne frac{{{{{psi }»}}_{tt}}left( t right)}{{{{{x}»}}_{tt}}left( t right)}]
Попытка использовать эту формулу для нахождения производных высших порядков будет считаться грубой ошибкой.
Вот и вся теория. Теперь — за практику!:)
Смотрите также:
- Частные производные для функции нескольких переменных
- Формула полной вероятности
- Тест по теории вероятностей (1 вариант)
- Видеоурок по задачам C2: уравнение плоскости через определитель
- Процент: неизвестно начальное значение (метод пропорции)
- Производительность совместного труда
Производные различных порядков от неявных функций
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Как найти первую и вторую производные параметрической функции
Параметрическое представление функциональной зависимости y от x для функции y = f(x) имеет вид:
Пусть функции x = x(t) и y = y(t) определены и непрерывны на интервале изменения параметра t. Продифференцируем данные функции.
Для нахождения первой производной необходимо разделить второе уравнение на первое:
Для нахождения второй производной:
Пример 1
Найти вторую производную параметрической функции
[left{begin{array}{l} {x=ln t} \ {y=3t^{2} } end{array}right. ]
Решение.
- Найдем первую производную по формуле:
- Найдем вторую производную
[y’_{x} =frac{y’_{t} }{x’_{t} } ]
[y’_{t} =left(t^{3} right)^{{‘} } =6t x’_{t} =left(ln tright)^{{‘} } =frac{1}{t} ]
[y’_{x} =frac{6t}{frac{1}{t} } =6t^{2} ]
[y»_{xx} =left(6t^{2} right)^{{‘} } =12t]
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Что такое неявно заданная функция, и как ее найти
Определение
Если функция вида y=y(x) задана уравнением F(x;y(x)) = 0, то функция является неявно заданной.
Для нахождения дифференциала неявной функции необходимо выполнить следующие действия:
- Продифференцировать обе части уравнения по х.
- Поскольку у — дифференцируемая функция, для ее нахождения используется правило вычисления производной сложной функции.
- В правой части уравнения должно получится значение 0.
Примечание
Это значит перенести все слева направо и привести к уравнению вида F(x;y(x)) = 0
- Решить полученное уравнение относительно y`(x)
Пусть неявная функция у от x определяется равенством:
[frac{x^{2} }{a^{2} } +frac{y^{2} }{b^{2} } -1=0]
Дифференцируем по x все члены этого равенства:
[frac{2x}{a^{2} } +frac{2ydy}{b^{2} dx} =0]
[frac{dy}{dx} =-frac{b^{2} x}{a^{2} y} ]
Последнее равенство снова дифференцируем по х:
[frac{d^{2} y}{dx^{2} } =-frac{b^{2} (y-x)frac{dy}{dx} }{a^{2} y} ]
Заменим производную dy/dx ее выражением:
[frac{d^{2} y}{dx^{2} } =-frac{b^{2} (y+x)frac{b^{2} }{a^{2} } frac{x}{y} }{a^{2} y} ]
[frac{d^{2} y}{dx^{2} } =-frac{b^{2} left(a^{2} y^{2} +b^{2} x^{2} right)}{a^{4} y^{3} } ]
Поскольку $a^2y^2 + b^2x^2 = a^2b^2$, вторую производную можно представить в виде
[frac{d^{2} y}{dx^{2} } =frac{b^{4} }{a^{2} y^{3} } ]
Дифференцируя по х последнее равенство, найдем $frac{d^{3} y}{dx^{3} } $ и т. д.
«Производные различных порядков от неявных функций» 👇
Пример 2
Найти вторую производную неявно заданной функции
[2x^{3} -xy^{2} =4]
Решение.
- Перенесем все части выражения в левую часть, приравняем к нулю и продифференцируем:
- Выразим y`
- Повторно дифференцируем равенство
- Выполним замену y`
- Упростим
[left(2x^{3} -xy^{2} -4right)^{{‘} } =0]
[left(2x^{3} right)^{{‘} } -left(xy^{2} right)^{{‘} } -left(4right)^{{‘} } =0]
[6x^{2} -left(x’y^{2} +xleft(y^{2} right)^{{‘} } right)=0]
[6x^{2} -y^{2} -2xyy’=0]
[y’=frac{6x^{2} -y^{2} }{2xy} ]
[left(6x^{2} -y^{2} -2xyy’right)^{{‘} } =12x-2y-2left(xyright)^{{‘} } y’-2xyy’]
[12x-2y-2left(xyright)^{{‘} } y-2xyy’=12x-2y-2x’y’-2xy’-2xyy»]
[12x-2y-2x’y’-2xy’-2xyy»=12x-2y-2y’-2xy’-2xyy»]
[12x-2y-2frac{6x^{2} -y^{2} }{2xy} -2xfrac{6x^{2} -y^{2} }{2xy} -2xyy»=0]
[frac{12x^{2} y-2xy^{2} }{xy} -frac{6x^{2} -y^{2} }{xy} -frac{6x^{3} -y^{2} }{xy} -2xyy»=0]
[frac{12x^{2} y-2xy^{2} -6x^{2} +2y^{2} -6x^{3} }{xy} -2xyy»=0]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 15.12.2022
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
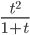
cos2(t) ≡ cos(t)^2
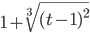
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
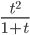
cos2(t) ≡ cos(t)^2
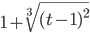
Пример 1. Найти производную функции y по x, заданной параметрически:
Решение.


Пример 2. Найти y’’xx функции
Решение. Найдем y’x по формуле (*): 
Производную y’x запишем в параметрической форме
К этой функции снова применим формулу (*):

Пример 3. Для функции 
Решение. 




Пусть
значения двух переменных x
и y
связаны между собой некоторым уравнением,
которое символически запишем так: F(x,
y) = 0(1)
Если
на некотором множестве D
каждому значению переменной x
соответствует единственное значение
y,
которое вместе с x
удовлетворяет уравнению (1), то будем
говорить, что это уравнение задает
неявную
функцию
y=f(x).
Из
определения следует, что для любой
неявной функции y=f(x),
заданной уравнением (1), имеет место
тождество F(x,
f(x)) ≡ 0,
справедливое при всех x
D.
Например,
уравнение x2
+ y2
– a2
= 0 неявно определяет две элементарные
функции
.
Действительно, после подстановки в
исходное уравнение этих значений получим
равенство x2+(a2–x2)
– a2
= 0.
Однако,
не всякую неявно заданную функцию можно
представить явно, т.е. в виде y=f(x).
Например,
функции, заданные уравнениями y2–
y
– x2=0
или
,
не выражаются через элементарные
функции, т.е. эти уравнения нельзя
разрешить относительно y.
Заметим,
что каждая явная функция y=f(x)
может быть представлена и как неявная
y–f(x)
= 0.
Таким
образом, неявная функция – это определенный
способ задания зависимости между
переменными x
и y.
Рассмотрим
правило нахождения производной неявной
функции, не преобразовывая ее в явную,
т.е. не представляя в виде y=f(x).
Чтобы
найти производную у‘
неявной функции F(x,
y)=0, нужно обе
части этого уравнения продифференцировать
по x,
рассматривая у
как функцию от x,
и из этого полученного уравнения найти
искомую производную y‘.
Чтобы найти y»,
нужно уравнение F(x,
y)=0 дважды
продифференцировать по x
и выразить y»
и т.д.
Примеры.
Найти производные функций заданных
неявно. . Найти
производные функций заданных неявно.
Итак,
производная неявной функции выражается,
как правило, не только через аргумент,
но и через функцию.
45. Производная параметрически заданной функции.
Пусть
Предположим,
что эти функции имеют производные и
функция x
= (t)
имеет обратную функцию t
= Ф(х).
Тогда
функция у = (t)
может быть рассмотрена как сложная
функция y
= [Ф(х)].
т.к.
Ф(х) – обратная функция, то
Окончательно
получаем:
Таким
образом, можно находить производную
функции, не находя непосредственной
зависимости у от х.
37 Производные высших порядков.
Понятие
производной произвольного порядка
задаётся рекуррентно.
Полагаем
Если
функция f
дифференцируема в x0,
то производная первого порядка
определяется соотношением
Пусть
теперь производная n-го
порядка f(n)
определена в некоторой окрестности
точки x0
и дифференцируема. Тогда
Если
функция
имеет
в некоторой области D частную
производную
по одной из переменных, то названная
производная, сама являясь функцией от
может иметь в некоторой точке
частные
производные по той же или по любой другой
переменной. Для исходной функции
эти
производные будут частными производными
второго порядка (или вторыми частными
производными).
или
или
Частная
производная второго или более высокого
порядка, взятая по различным переменным,
называется смешанной
частной производной.
Например,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #




