Как найти производную сложной функции обратной функции

ПРОИЗВОДНАЯ
ФУНКЦИИ

ОДНОЙ
ПЕРЕМЕННОЙ

1.     Определение
производной.

2.     Геометрический 
и экономический смысл производной.

3.     Зависимость
между непрерывностью и дифференцируемостью
функции.

4.     Основные
правила дифференцирования.

5.     Производная
сложной и обратной функции.

6. 
Таблица производных.

7. 
Производные высших порядков.

8. 
Дифференциал функции.

1. 
Определение производной.

Пусть y=f(x)
непрерывная функция от х. Дадим аргументу
х приращение,
тогда функция y получит
приращение.
Составим отношение.
Это отношение есть некоторая функция
от.
Может случиться, что эта функция имеет
предел при,
т.е. существует

.

Этот
предел называется производной
от данной функции y и
обычно обозначается через:

.

Производной функции называется
предел отношения приращения функции к
приращению аргумента, когда приращение
аргумента стремится к нулю, если этот
предел существует и конечен.

Действие
нахождения производной
называется дифференцированием,
а функция, имеющая конечную производную,
называется дифференцируемой.

1.      Геометрический 
и экономический смысл

производной.

Геометрический
смысл производной:
для данной функции y=f(x)
ее производная  для
каждого значения х равна угловому
коэффициенту касательной к графику
функции в соответствующей точке.

.

Экономический
смысл производной.

Пусть
предприятие выпускает однородную
продукцию. Тогда издержки производства y можно
считать функцией количества выпускаемой
продукции x,  y=f(x).
Предположим, что количество выпускаемой
продукции изменилось на,
тогда издержки производства изменяются
на:.

Разделим
приращение издержек производства на
приращение выпускаемой продукции:. 
Это равенство выражает среднее приращение
издержек производства на единицу
приращенной продукции, перейдем к
пределy,

.

Этот
предел в экономике называется предельными
издержками производства. Таким
образом, производная выражает
предельные издержки производства и
характеризует приближенно дополнительные
затраты на производство единицы
дополнительной продукции.

Аналогичным
образом могут быть определены предельная
выручка, предельный доход, предельный
продукт, предельная полезность и другие
предельные величины.

3. 
Зависимость между непрерывностью и
дифференцируемостью функции.

Функция y=f(x)
называется непрерывной в
точке, если               .
Функция y=f(x)
называется дифференцируемой  в точке,
если она имеет производную, т.е. 

Между
этими понятиями существует связь.

Теорема: Если
функция дифференцируема в некоторой
точке, то в этой точке функция непрерывна.
Обратное утверждение неверно: непрерывная
функция может не иметь производной.

Следствие: Если
функция не является непрерывной в
некоторой точке, то она не имеет
производной в этой точке.

4. 
Основные правила дифференцирования.

1.        Производная
постоянной  величины равна 0.

2.        Производная
алгебраической суммы  нескольких
дифференцируемых функций равна сумме
производных этих функций.

3.        Производная
произведения двух дифференцируемых
функций равна сумме произведения каждой
функции на производную другой функции.

Следствия:

а)
Постоянный множитель можно выносить
за знак производной.

б)
Производная произведения любого числа
дифференцируемых функций равна сумме
произведения производной каждой
функции на произведение всех остальных
функций.

;   

4.        Производная
частного равна производной числителя,
умноженной на знаменатель, минус
производная знаменателя, умноженная
на числитель, и все это деленное на
квадрат знаменателя.

Следствия: 1);        
2) .

5. 
Производная сложной и обратной функции.

1. Производная
сложной функции равна
произведению производных от функций,
составляющих данную функцию.

, —
дифференцируемые функции.  Тогда

.

2. Производная
обратной функции.
Пусть нам дана дифференцируемая
функция y= f(x).
Если y рассматривать
как аргумент, а x-
функцию, то новая функция называется
обратной по отношению к y. 
Зная производную функции   y= f(x)  ,
можно найти производную обратной
функции,
предполагая, что обратная функция
существует и непрерывна.

Теорема. Для
дифференцируемой функции с производной
не равной 0, производная обратной функции
равна обратной величине производной
данной функции  .

6. 
Таблица производных.

№       
Функция y                                       
Производная 

1                                                            
0

2                                                                
1

3                                                               

4                                                             

5                                                          

6                                                         

7                                                             

8                                                          

9                                                               

10                                                            

11                                                          

12                                                     

13                                                  

14                                                 

15                                                   

16                                                 

Примеры: Найти
производную функций:

а) 

Воспользуемся
формулами  а
также свойством производной, что
постоянный множитель можно выносить
за знак производной.

.

б) 

Это
сложная степенная функция.
Обозначим,         
тогда.
Воспользуемся производной сложной
функции.

7
. Производные высших порядков.

Производная у′ =f ′(x) 
называется производной первого порядка.
Если  f ′(x) дифференцируема,
то ее производная обозначается
символом      у″ =f ″(x)и
называется производной
второго порядка.

Производная
от производной первого порядка называется
производной второго порядка.

Если,
то вторая производная обозначается

.

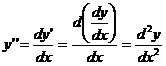
Производная n-го
порядка есть производная от производной
(n-1)
порядка.

8. 
Дифференциал функции.

Пусть
функция y=f(x) дифференцируема
при некотором значении х. Следовательно,
в точке х существует конечная
производная     По
определению предела  имеем   

Отсюда
находим .

y′
от не
зависит, она остается постоянной при 

Если то  —
является бесконечно малой величиной
того же порядка малости, что и. —
бесконечно  малая величина  более
высокого порядка малости, чем первое
слагаемое. Поэтому величину  ()
называют главной, линейной
относительно частью
приращения функции; чем меньше,
тем большую долю приращения составляет
это выражение. Поэтому при малых
значениях приращение
функции можно заменить,
т.е.

Эту
главную часть приращения функции
называют дифференциалом
функции в
точке х и
обозначают dy или df(x),
следовательно, 
или 

Дифференциал
равен произведению ее производной на
приращение независимой переменной.

Если   f(x)=x,  тогда   dx=x′=, т.е. .

Окончательно
можно записать: 

Из
изложенного выше следует, что,
т.е. приращение функции отличается
от дифференциала на
бесконечно малую величину более высокого
порядка, чем.
Поэтому при достаточно  малых
значениях  имеем,
т.е.,
откуда  получаем  формулу:

.

Чем
меньше значение,
тем точнее эта формула, и ее можно 
использовать для приближенных вычислений.

Пример.
Вычислить 

Решение:,

где 

Найдем,  .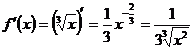           
Тогда  имеем:  

Соседние файлы в папке Матем

• #
• #
• #
• #
• #
• #

  26.02.2016104.31 Кб575.docx

• #
• #
• #
• #

Содержание:

1. Определение производной
2. Производная сложной и обратной функций
3. Производные высших порядков
4. Геометрический смысл производной
5. Экономическая интерпретация производной

Определение производной

Производной функции в точке называется предел отношения приращения функции к приращению аргумента при .

Производную функции в точке обозначают одним из символов или .

Итак, по определению

Операцию вычисления производной принято называть дифференцированием.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Пример №1

Исходя из определения производной, найти производную функции

Решение:

По формуле (11.1) находим:

Основные правила вычисления производной. Если С — постоянная величина и функции и имеют производные, то

1.

2.

3.

4.

5.

3° Таблица производных.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

Возможно вам будут полезны данные страницы:

Пример №2

Используя правила дифференцирования и таблицу производных, найти производную функции

Решение:

Производная сложной и обратной функций

Пусть функция имеет производную в точке, а функция — в соответствующей точке . Тогда сложная функция имеет производную в точке х, которая вычисляется по формуле

(11.2)

Пусть функция непрерывна, строго монотонна на отрезке и имеет конечную не равную нулю производную в некоторой точке . Тогда обратная функция также имеет производную в соответствующей точке, определяемую равенством

(11.3)

Пример №3

Найти производную функции .

Решение:

Функцию можно представить в виде , где , поэтому

Концепция дифференциальных вычислений, которая характеризует скорость изменения функции в определенной точке.

Производные высших порядков

Если функция имеет производную в точке , то эта производная называется второй производной или производной второго порядка функции в точке и обозначается через или или

Если производная -го порядка функции имеет производную в точке , то эта производная называется -й производной или производной -го порядка функции в точке и обозначается через или или

Итак,

Производные порядка выше первого называются производными высших порядков.

Пример №4

Вычислить производную n-го порядка функции .

Решение:

Первую производную этой функции можно записать в виде

Таким образом, при дифференцировании функции аргумент этой функции увеличивается на. Следовательно, справедлива формула

Геометрический смысл производной

Пусть существует касательная к графику функции в точке (рис. 11.1). Тогда существует производная функции в точке , которая равна угловому коэффициенту этой касательной: Верно и обратное: если существует производная функции в точке , то существует касательная к графику функции в точке , угловой коэффициент которой равен этой производной (геометрический смысл производной).

Геометрическая интерпретация производной позволяет записать уравнение касательной к графику функции в точке :

(11.4) Рис. 11.1 Прямая, проходящая через точку касания перпендикулярно к касательной, называется нормалью к графику функции в этой точке. Уравнение нормали:

(11.5)

Пример №5

Составить уравнение касательной к кривой

в точке с абсциссой

Решение:

По заданному значению находим

Значит, касательная проходит через точку . Найдем угловой коэффициент касательной:

Теперь составим уравнение касательной, согласно формуле (11.4):

или

Пример №6

На кривой найти точку, в которой

касательная параллельна прямой .

Решение:

Пусть искомая точка касания есть . Тогда угловой коэффициент касательной равен значению производной в точке касания:

Чтобы касательная была параллельна прямой , их угловые коэффициенты должны совпадать, то есть , откуда .

Подставляя найденное значение абсциссы искомой точки в уравнение кривой, найдем значение ее ординаты . Итак, искомая точка .

Экономическая интерпретация производной

Одним из примеров применения понятия производной в экономическом анализе служит расчет производительности труда в заданный момент времени. Рассмотрим количество произведенной продукции как функцию от времени, т.е. . Тогда приращение показывает количество произведенной продукции за период от доа отношение показывает среднюю производительность труда за этот период. Следовательно, производная показывает производительность труда в момент времени , то есть производительность труда — это скорость изменения количества произведенной продукции за единицу времени.

Аналогично определяются предельная выручка, предельный доход, предельные издержки производства и т.д. Например, предельные издержки производства определяются как производная функции издержек производства по количеству выпускаемой продукции.

Пример №7

Объем продукции, произведенной группой работников за восьмичасовую смену, описывается уравнением

где — рабочее время в часах . Вычислить производительность труда в начале и в конце рабочего дня.

Решение:

Производительность труда вычисляется по формуле

В начале рабочего дня производительность труда данной группы работников будет

В конце рабочего дня производительность труда данной группы работников будет равна Итак, мы наблюдаем спад производительности труда к концу рабочего дня.

Пусть функция удовлетворяет условиям теоремы о непрерывности сложной функции и функция является для нее Обратной.

Теорема (о производной обратной функции)

Пусть функция является непрерывной и строго монотонной в некоторой окрестности точки и имеет в этой точке производную Тогда Обратная функция также имеет в соответствующей точке производную, причем

(5.3.1)

Теорема (о производной сложной функции).

Пусть функция имеет производную в точке , а функция имеет производную в соответствующей точке . Тогда сложная функция имеет Производную в точке и справедлива следующая формула:

(5.3.2)

В данной теореме рассмотрена суперпозиция двух функций, где зависит от через промежуточную переменную . Возможна и более сложная зависимость с несколькими промежуточными переменными, однако правило дифференцирования сложной функции остается тем же. Например, если то производная вычисляется по формуле

(5.3.3)

Пример:

Найти производную функции

Решение

Эту функцию можно представить через промежуточную переменную как Тогда по формуле (5.3.2)

Производная неявной функции

Пусть дифференцируемая функция удовлетворяет уравнению , т. е. задана неявно. Чтобы найти производную функции , заданную неявно, необходимо продифференцировать обе части уравнения по переменной , рассматривая как сложную функцию от , а затем из полученного уравнения найти производную

Пример

Найти производную функции , заданную уравнением , и вычислить ее значение в точке (2;0).

Решение

Дифференцируя обе части равенства и учитывая, что есть функция от , получим , откуда

Значение производной при равно

Производная показательно–степенной функции (логарифмическая производная)

Пусть функция положительна и дифференцируема в точке . Вычислим производную функции . По правилу дифференцирования сложной функции получаем

.

(5.3.4)

Это выражение называется логарифмической производной функции . Найдем с помощью логарифмической производной производную показательно–степенной функции

(5.3.5)

Где и – некоторые функции от аргумента , имеющие в точке соответствующие производные. Поскольку то использование формулы (5.3.5) приводит к равенству

С учетом вида функции получаем следующую формулу для производной показательно–степенной функции:

(5.3.6)

< Предыдущая		Следующая >

Пусть у = f(и) и u = φ(х)— тогда у = f(φ{x)) — сложная функция с промежуточным аргументом и н независимым аргументом х.

По условию Отсюда, по теореме о связи функции, ее предела и бесконечно малой функции, имеем

или где .
Функция u = φ(х) имеет производную в точке х: , поэтому
Подставив значение Δи в равенство (20.6), получим
т.е. Разделив полученное равенство на Δх и перейдя к пределу при Δх→0, получим
Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько. Так, если у = f(u), u = φ(v), v = g{х), то Пусть у = f(x) и х = φ(y) — взаимно обратные функции.
Рассмотрим обратную функцию х = φ(y). Дадим аргументу у приращение Δу ≠ 0. Ему соответствует приращение Δх обратной функции, причем Δх ≠ 0 в силу строгой монотонности функции у = f(x). Поэтому можно записать    Если Δy→0, то в силу непрерывности обратной функции приращение Δх→0. И так как , то из (20.7) следуют равенства

Таким образом, производная обратной функции равна обратной величине производной данной функции.
Правило дифференцирования обратной функции записывают так:
Пример 1. Найти производную функции
Решение: Данная функция является сложной. Ее можно представить в виде цепочки «простых» функций: , где , где z = tg q, где q =. . По правилу дифференцирования сложной функции ( )получаем:
Пример 2. Пользуясь правилом дифференцирования обратной функции, найти производную для функции
Решение: Обратная функция имеет производную . Следовательно,

Инфоурок

›

Алгебра

›Презентации›Производная сложной и обратной функций (занятие №4-5)