По запросу пользователя Необходим калькулятор для вычисления производных создаем калькулятор, вычисляющий производную сложно-показательной функции, которая конструируется на основе заданной функции и мощности.
Заданная функция является одновременно основанием и степенью данной функции. Функция возводится в степень самой себя определенное мощностью количество раз.
Производная сложно-показательной функции
Допустимые операции: + — / * ^
Константы: pi
Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Производная функции
Производной функции y=f(x) в точке x0 называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).
Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
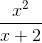
cos2(2x+π) ≡ (cos(2*x+pi))^2
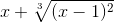
Правила ввода функции, заданной в неявном виде
Примеры
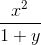
cos2(2x+y) ≡ (cos(2*x+y))^2
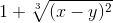
Если функция задана в виде y2-x=cos(y), то ее необходимо записать так: y^2-x-cos(y).
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
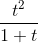
cos2(t) ≡ cos(t)^2
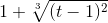
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
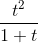
cos2(t) ≡ cos(t)^2
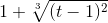
Как найти производную, исходяя из ее определения?
Правила нахождения производных
Пример 1. Найти производную функции y=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
.

В некоторых случаях, если, например, нужно найти производную функции y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции

Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию
Учитывая, что 
Но 

Пример 4. Найти производную функции y=xex
Решение.


Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Производная по-шагам

Примеры производных
- Производные от степенных функций
-
x^7/10
-
(x^2 - 1)/(x^a - 5)
- Производные от сложных функций
-
sin(ln(x))
-
ln(sin(x))
- Производные от показательных функций
-
e^(-x^2)
- Производные от логарифмов
-
1-log(x-5)
-
ln(a*x) / ln(x^3)
- Производные от обратных тригонометрических функций
-
arcsin(1-x)
-
arctan(a*x + b)
- Производная неявной функции
-
e^y/x = x*y + 1
- Частная производная функции
-
x^2*sin(-y) + y/x
-
x*y*cos(z)
Подробнее про Производная функции
.
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Показать Этапы
Номер Строки
Примеры
-
frac{d}{dx}(frac{3x+9}{2-x})
-
frac{d^2}{dx^2}(frac{3x+9}{2-x})
-
(sin^2(theta))»
-
производное:от:f(x)=3-4x^2,::x=5
-
неявная:производная:frac{dy}{dx},:(x-y)^2=x+y-1
-
frac{partial}{partial ypartial x}(sin (x^2y^2))
-
frac{partial }{partial x}(sin (x^2y^2))
- Показать больше
Описание
Поэтапное дифференцирование функций
derivative-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Advanced Math Solutions – Derivative Calculator, Implicit Differentiation
We’ve covered methods and rules to differentiate functions of the form y=f(x), where y is explicitly defined as…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Данный онлайн калькулятор вычисляет производную функции. Программа не только вычисляет ответ, она производит пошаговое решение. Выбирается порядок дифференцирования.
Как пользоваться калькулятором для нахождения производных онлайн:
1. Введите математическое выражение с переменной x, в выражении используйте стандартные операции: + сложение, —
вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции.
2. Выберите порядок дифференцирования (решения производных от первого до пятого порядка включительно).
3. Нажмите кнопку — Вычислить производную.
4. Через несколько секунд внизу отобразится пошаговое решение производной с подробными комментариями.
При помощи нашего калькулятора вы можете найти производную онлайн как от элементарной функции, так и от сложной, не имеющей решения в аналитическом виде.
Калькулятор поможет найти производную функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
: x^a
модуль x: abs(x)
Для того, чтобы найти производную функции
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции 
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где 
Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.
- Примеры
- x*E^x, x;
- x^3*E^x, {x,17};
- x^3*y^2*Sin[x+y], x;
- x^3*y^2*Sin[x+y], y,
- x/(x+y^4), {x,6}.




 : x^a
: x^a