Вступление
Бывало когда-нибудь такое, что вы хотите просуммировать какой-то бесконечный ряд, но не можете подобрать частичную сумму ряда? Вы все ещё не пользовались дискретной производной? Тогда мы идём к вам!
Определение
Дискретной производной последовательности
назовем такую последовательность
, что для любых натуральных
выполняется:
Рассмотрим примеры:
Ну, суть вы поняли. Чем-то напоминает производную функции, правда? Мы поняли как вычислять дискретные производные «простейших» последовательностей. Кхм, но что делать с суммой, разностью, произведением и частным последовательностей? У «обычной» производной есть некоторые правила дифференцирования. Давайте-ка придумаем для дискретной!
Сначала рассмотрим сумму. Логично, что сумма последовательностей это тоже какая-то последовательность. Попробуем найти производную по определению:
Феноменально! Мы получили, что производная суммы последовательностей есть сумма производных этих последовательностей!
спасибо, кэп
Попробуем доказать тоже самое с разностью
А мы переходим к произведению!
Аналогично, найдем по определению:
Круто, правда? Рассмотрим частное:
Cool…
Но это все производная. Может, есть и дискретная первообразная? Оказывается, есть!
Еще определения
Дискретной первообразной последовательности
называют такую последовательность
что для любых натуральных
выполняется:
С этим понятно. Го придумаем аналог Ньютона-Лейбница!
Да ладно! Вот это
прикол
совпадение! А теперь то же самое покрасивее:
И обобщим на множество натуральных чисел от
до
:
Применение
Кто помнит ту самую формулу для суммы ряда квадратов натуральных чисел от
до
? А вот и я не помню. Давайте-ка ее выведем!
Но для начала надо найти первообразную для последовательности
:
А теперь, собственно, сама сумма:
Как насчет суммы кубов?
Сначала вычислим
Первообразная для
:
Кхм, казалось бы, ничего сложного…
Для продвинутых
Не всегда так просто найти интеграл, правда? Что мы делаем в трудных случаях? Правильно, интегрируем по частям. Быть может, есть аналог? Не буду вас томить, он есть, и сейчас мы его выведем.
Допустим, надо вычислить сумму ряда
Что делать? Вряд ли вы сможете так просто подобрать дискрентную первообразную к последовательности. Давайте смотреть.
Мы уже знаем, что:
Тогда
А теперь один нетривиальный шаг:
Все внутренние слагаемые взаимно уничтожились.
Подставим в полученное до этого равенство:
Финита ля комедия.
Найдем ту самую сумму:
Кому-то может показаться, будто формула стала еще более громоздкой, и мы только усложнили себе работу. Но это не так. Пусть
, тогда:
Воу! Мы нашли явную формулу для частичной суммы ряда. Неплохо, правда?
Никто и не спорит, что было достаточно непросто. Но как говорил Александр Суворов: Тяжело в учении — легко в бою.
Так давайте же попробуем применить наши новые знания в боевых действиях!
Прикольная задачка
Предлагаю попрактиковаться с этим на примере задачки с отбора в Tinkoff Generation на курсы по Machine Learning. Вот сама задачка:
Вы устали решать задачки с отборов на курсы Tinkoff Generation и решили устроить перерыв, посмотрев несколько серий нового сериала, о котором все говорят.
Вы начинаете смотреть все серии, начиная с первой. Каждая серия длится один час. После просмотра очередной серии, вы с постоянной вероятностью ppp начинаете смотреть следующую, иначе ваш перерыв заканчивается, и вы возвращаетесь к работе.
Голод, сон и прочие нужды вас не останавливают, а в сериале бесконечное количество серий; в теории, ваш перерыв может длиться бесконечно.
Сколько в среднем будет длиться ваш перерыв?
Строго говоря, здесь нам нужно найти математическое ожидание. Давайте разбираться.
Решение
Вероятность того, что перерыв будет длиться 1 час, равна:
2 часа
n часов:
Тогда математическое ожидание равно:
Знакомо, правда?
Мы уже находили, что
тогда совсем очевиден нужный нам ряд:
И задача сводится к нахождению предела последовательности
где
, так как
— вероятность события.
Докажем теперь, что
Теперь легко понять, что
И
Some up
Фух… Это было
easy-peasy
жестко, даже для меня, дорогие читатели. Список достижений за сегодня:
- Мы поняли, что такое дискретная производная
- Вывели свойственные ей правила дифференцирования
- Мы поняли, что такое дискретная первообразная
- Мы вывели аналог формулы Ньютона-Лейбница
- Вывели аналог интегрирования по частям
- Решили сложную задачку с отбора на курс по Machine Learning в Tinkoff Generation
Неплохо для начала, а вы как считаете?
Комментарии приветствуются!
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Было полезно?
4.65%
Другое (напишу в комментах)
4
Проголосовали 86 пользователей.
Воздержались 17 пользователей.
Дифференцирование под знаком ряда(почленное дифференцирование).
Определение. Если для сходящегося
ряда
существует производная суммы, равная
ряду производных
,
то говорят, что возможно дифференцирование
под знаком ряда.
Теорема 4. Если на промежутке
определены гладкие функции
,
ряд
сходится к функции S(x),
ряд производных
сходится равномерно, то функция S(x)
– гладкая и возможно дифференцирование
под знаком ряда на этом промежутке.
Доказательство. Будем действовать
на отрезке [a, x],
содержащемся в данном промежутке.
Обозначим сумму
.
По теореме 2 эта функция – непрерывна.
По теореме 3 эту функцию можно интегрировать
почленно:
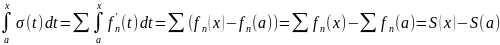
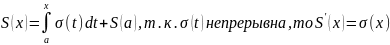
Итак, функция S(x)
– гладкая и ее производная равна сумме
ряда производных f ’n(x).
Степенные ряды.
Определение и теорема об области
сходимости.
Определение. Степенным рядом
называется функциональный ряд следующего
вида
.
Для краткости будем обозначать его
.
Введем величину
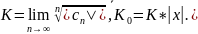
-
Если
К=0, К0<1, ряд абсолютно сходится
при всех х. -
Если
К=
,
ряд расходится при всех
. -
Если
,
то ряд абсолютно сходится при К0<1
и расходится при K0>1.
Введем величину R=1/K,
считая ее равной
или 0 в первом и втором случаях
соответственно. Эта величина называется
радиусом сходимости. Тем самым
доказана лемма, приведенная ниже.
Лемма. Существует такая величина
,
что:
— если
,
то ряд
абсолютно сходится всюду;
— если R=0, то ряд сходится
только при х=0;
— если 0<R<
,
то ряд абсолютно сходится при |x|<R
и расходится при |x|>R.
Интервал (-R;R)
называется интервалом сходимости.
Видно, что на его концах поведение ряда
может быть различным. Тем самым доказана
следующая теорема:
Теорема. Областью сходимости
степенного ряда степенного ряда
является один из промежутков: 0, (-R;R),
[-R;R], (-R;R],
[-R;R),
,
где радиус сходимости удовлетворяет
равенству
.
Ясно, что в общем случае, для ряда
областью сходимости является промежуток
(a-R,a+R).
Вычисление радиуса сходимости.
Метод Коши : R=1/K
,
(если существует этот самый предел).
По Даламберу
(также, если существует этот самый
предел).
Равномерная сходимость степенного
ряда.
Отрезок [a,b]
входящий (-R;R)
будем называть внутренним. Ясно, что
существует такое число r
: 0<r<R,
что [a, b]
входит в [-r,r]
который входит в (-R,R).
Теорема 1. На внутреннем отрезке
степенной ряд сходится равномерно.
Доказательство. Если
сходится абсолютно, так как точка r
находится в интервале сходимости. Итак,
по достаточному свойству Вейерштрасса,
ряд сходится равномерно на отрезке [-r
; r] и, следовательно, на
[a;b].
Почленное интегрирование и
дифференцирование степенного ряда.
Вначале заметим, что ряды
отличаются друг от друга только
сомножителем х, поэтому их поведение
одинаково и они имеют один и тот же
радиус сходимости. Кроме того, вспомним
утверждение о верхнем пределе числовой
последовательности :
.
Теорема 2. На интервале сходимости
степенной ряд можно дифференцировать
под знаком ряда
.
Радиусы сходимости этих рядов одинаковы.
Доказательство. Обозначим радиусы
сходимости этих рядов, соответственно,
как R, R1.
По Коши,
.
Пусть теперь точка х – произвольная
фиксированная точка интервала сходимости.
Ясно, что существует такая величина r,
что
.
По теореме 1, на внутреннем отрезке [-r
; r] степенные ряды
сходится равномерно. Члены степенного
ряда – гладкие функции. Тогда, по теореме
4 о дифференцирования функционального
ряда, можно дифференцировать под знаком
степенного ряда.
Кроме заключения, из теоремы 2 также
следует, что сумма степенного ряда имеет
производные любого порядка. Такие
функции называются бесконечно
дифференцируемыми или аналитическими.
Поскольку из дифференцируемости следует
непрерывность, то справедлива следующая
теорема. Теорема 3. Сумма степенного
ряда на интервале сходимости является
непрерывной функцией.
Теорема 4. На интервале сходимости
степенной ряд можно интегрировать под
знаком ряда:
Радиусы сходимости этих рядов одинаковы.
Доказательство. Возможность
интегрирования под знаком ряда следует
из непрерывности функций cntn
и равномерной сходимости степенного
ряда на внутреннем отрезке [0, x]
в силу теоремы 3 об интегрировании
функционального ряда. Обозначим радиус
сходимости ряда
Тогда,
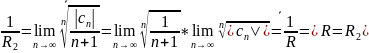
Разложение логарифма в степенной ряд.
Рассмотрим ln(1+x)
как интеграл с переменным верхним
пределом:
Поскольку подынтегральная дробь является
суммой степенного ряда с радиусом
сходимости R=1, то при |x|<1
переменная
находится в интервале сходимости ряда.
По теореме 4, возможно интегрирование
под знаком ряда, тогда
.
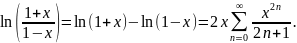
Этот ряд сходится быстрее ряда элементов
геометрической прогрессии.
Разложение арктангенса в степенной
ряд.
Аналогично предыдущему случаю имеем :
.
Обозначим z=t2,
ряд
сходится при
.
После интегрирования под знаком ряда,
получаем :
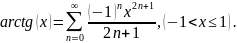
Для приближенного вычисления арктангенсов
при x>1, используют
формулу:
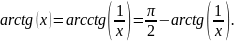
Разложение арксинуса в степенной ряд.
Степенной ряд для
.
Тогда представим
.
Поскольку
,
то возможно интегрирование под знаком
ряда:
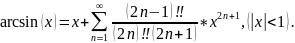
Ряд Тейлора.
Пусть функция f(x)
имеет производные любого порядка на
некотором промежутке, содержащем в себе
точку а.
Определение. Рядом Тейлора
функции f(x)
называется степенной ряд
Если ряд
сходится, то, как легко проверить, он
является рядом Тейлора своей суммы.
Рассмотрим обратную задачу. Пусть
задана бесконечно дифференцируемая
функция и составлен ее ряд Тейлора.
Сходится ли этот ряд, а если сходится,
то совпадает ли его сумма с заданной
функцией? Там в лекциях какая то магия
происходит, и делается вывод, что
бесконечной дифференцируемости функции
еще недостаточно для ее разложимости
в ряд Тейлора.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вступление
Бывало когда-нибудь такое, что вы хотите просуммировать какой-то бесконечный ряд, но не можете подобрать частичную сумму ряда? Вы все ещё не пользовались дискретной производной? Тогда мы идём к вам!
Определение
Дискретной производной последовательности 



Рассмотрим примеры:
Ну, суть вы поняли. Чем-то напоминает производную функции, правда? Мы поняли как вычислять дискретный производные «простейших» последовательностей. Кхм, но что делать с суммой, разностью, произведением и частным последовательностей? У «обычной» производной есть некоторые правила дифференцирования. Давайте-ка придумаем для дискретной!
Сначала рассмотрим сумму. Логично, что сумма последовательностей это тоже какая-то последовательность. Попробуем найти производную по определению:
Феноменально! Мы получили, что производная суммы последовательностей есть сумма производных этих последовательностей!спасибо, кэп
Попробуем доказать тоже самое с разностью
А мы переходим к произведению!
Аналогично, найдем по определению:

Круто, правда? Рассмотрим частное:
Cool…
Но это все производная. Может, есть и дискретная первообразная? Оказывается, есть!
Еще определения
Дискретной первообразной последовательности 


С этим понятно. Го придумаем аналог Ньютона-Лейбница!
Да ладно! Вот это прикол совпадение! А теперь то же самое покрасивее:
И обобщим на множество натуральных чисел от 

Применение
Кто помнит ту самую формулу для суммы ряда квадратов натуральных чисел от 

Но для начала надо найти первообразную для последовательности 
А теперь, собственно, сама сумма:
Как насчет суммы кубов?
Сначала вычислим
Первообразная для 
Кхм, казалось бы, ничего сложного…
Для продвинутых
Не всегда так просто найти интеграл, правда? Что мы делаем в трудных случаях? Правильно, интегрируем по частям. Быть может, есть аналог? Не буду вас томить, он есть, и сейчас мы его выведем.
Допустим, надо вычислить сумму ряда
Что делать? Вряд ли вы сможете так просто подобрать дискрентную первообразную к последовательности. Давайте смотреть.
Мы уже знаем, что:
Тогда
А теперь один нетривиальный шаг:
Подставим в полученное до этого равенство:
Финита ля комедия.
Найдем ту самую сумму:
Кому-то может показаться, будто формула стала еще более громоздкой, и мы только усложнили себе работу. Но это не так. Пусть 
Прикольная задачка
Предлагаю попрактиковаться с этим на примере задачки с отбора в Tinkoff Generation на курсы по Machine Learning. Вот сама задачка:
Вы устали решать задачки с отборов на курсы Tinkoff Generation и решили устроить перерыв, посмотрев несколько серий нового сериала, о котором все говорят.
Вы начинаете смотреть все серии, начиная с первой. Каждая серия длится один час. После просмотра очередной серии, вы с постоянной вероятностью ppp начинаете смотреть следующую, иначе ваш перерыв заканчивается, и вы возвращаетесь к работе.
Голод, сон и прочие нужды вас не останавливают, а в сериале бесконечное количество серий; в теории, ваш перерыв может длиться бесконечно.
Сколько в среднем будет длиться ваш перерыв?
Строго говоря, здесь нам нужно найти математическое ожидание. Давайте разбираться.
Решение
Вероятность того, что перерыв будет длиться 1 час, равна:
2 часа
n часов:
Тогда математическое ожидание равно:
Знакомо, правда?
Мы уже находили, что
тогда совсем очевиден нужный нам ряд:
И задача сводится к нахождению предела последовательности
где 

Докажем теперь, что
Теперь легко понять, что
И
Some up
Фух… Это было easy-peasy жестко, даже для меня, дорогие читатели. Список достижений за сегодня:
- Мы поняли, что такое дискретная производная
- Вывели свойственные ей правила дифференцирования
- Мы поняли, что такое дискретная первообразная
- Мы вывели аналог формулы Ньютона-Лейбница
- Вывели аналог интегрирования по частям
- Решили сложную задачку с отбора на Tinkoff Generation курсы по ML
Неплохо для начала, а вы как считаете?
Жду ваших замечаний в комментах, коршуны самые внимательные!
Автор: Левон Минасян
Источник
производная суммы равна сумме производных, следовательно, имеем
[math]frac{partial S}{partial a}=sumlimits_{i=1}^nfrac{partial((y_i-ae^{x_i}-bx^2_i-c)^2)}{partial a}=sumlimits_{i=1}^n 2(y_i-ae^{x_i}-bx^2_i-c)cdot(-e^{x_i})=-2sumlimits_{i=1}^n e^{x_i}(y_i-ae^{x_i}-bx^2_i-c)[/math]
[math]frac{partial^2 S}{partial a^2}=-2sumlimits_{i=1}^n frac{partial (e^{x_i}(y_i-ae^{x_i}-bx^2_i-c))}{partial a}=-2sumlimits_{i=1}^n -e^{x_i}cdot e^{x_i}=2sumlimits_{i=1}^n e^{2x_i}[/math]
[math]frac{partial^2 S}{partial apartial b}=-2sumlimits_{i=1}^n frac{partial (e^{x_i}(y_i-ae^{x_i}-bx^2_i-c))}{partial b}=-2sumlimits_{i=1}^n -e^{x_i}cdot x^2_i=2sumlimits_{i=1}^n x^2_i e^{x_i}[/math]
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Ряд, члены которого являются функциями одной илинескольких независимых переменных, определёнными на некотором множестве, называется функциональным рядом.
Рассмотрим функциональный ряд$sum limits _{n=1}^{infty }u_{n} (x)=u_{1} (x)+u_{2} (x)+u_{3} (x)+…$, члены которого являются функциями одной независимой переменной х. Сумма первых n членов ряда $S_{n} (x)=u_{1} (x)+u_{2} (x)+…+u_{n} (x)$ является частичной суммой данного функционального ряда. Общий член $u_{n} (x)$ есть функция от х, определённая в некоторой области. Рассмотрим функциональный ряд в точке $x=x_{0} $. Если соответствующий числовой ряд $sum limits _{n=1}^{infty }u_{n} (x_{0} )$сходится, т.е. существует предел частичных сумм этого ряда$mathop{lim }limits_{nto infty } S_{n} (x_{0} )=S(x_{0} )$(где $S(x_{0} )
Определение 2
Областью сходимости функционального ряда $sum limits _{n=1}^{infty }u_{n} (x)$ называется множество всех таких значений х, при которых функциональный ряд сходится. Область сходимости, состоящая из всех точек сходимости, обозначается $D(x)$. Отметим, что $D(x)subset $R.
Функциональный ряд сходится в области $D(x)$, если для любого $xin D(x)$ он сходится как числовой ряд, при этом его сумма будет некоторой функцией $S(x)$. Это так называемая предельная функция последовательности $left{S{}_{n} (x)right}$: $mathop{lim }limits_{nto infty } S_{n} (x)=S(x)$.
Как находить область сходимости функционального ряда $D(x)$? Можно использовать признак, аналогичный признаку Даламбера. Для ряда $sum limits _{n=1}^{infty }u_{n} (x)$ составляем $u_{n+1} (x)$ и рассматриваем предел при фиксированном х: $mathop{lim }limits_{nto infty } left|frac{u_{n+1} (x)}{u_{n} (x)} right|=left|l(x)right|$. Тогда $D(x)$ является решением неравенства $left|l(x)right|
«Интегрирование и дифференцирование рядов» 👇
Пример 1
Найти область сходимости ряда $sum limits _{n=1}^{infty }, frac{x^{n} }{n} , $.
Решение. Обозначим $u_{n} (x)=frac{x^{n} }{n} $, $u_{n+1} (x)=frac{x^{n+1} }{n+1} $. Составим и вычислим предел $mathop{lim }limits_{nto infty } left|frac{u_{n+1} (x)}{u_{n} (x)} right|=mathop{lim }limits_{nto infty } left|frac{x^{n+1} cdot n}{x^{n} cdot (n+1)} right|=left|xright|$, тогда область сходимости ряда определяется неравенством $left|xright|
-
если $x=1$, $u_{n} (1)=frac{1}{n} $, то получается расходящийся ряд $sum limits _{n=1}^{infty }, frac{1}{n} , $;
-
если $x=-1$, $u_{n} (-1)=frac{(-1)^{n} }{n} $, то ряд $sum limits _{n=1}^{infty }frac{(-1)^{n} }{n} , , $ сходится условно (по признаку Лейбница).
Таким образом, область сходимости $D(x)$ ряда $sum limits _{n=1}^{infty }, frac{x^{n} }{n} , $имеет вид:$-1le x
Свойства степенных рядов
Рассмотрим степенной ряд $sum limits _{n=0}^{infty }a_{n} x^{n} $, у которого интервал сходимости $(-R;, R)$, тогда сумма степенного ряда $S(x)$ определена для всех $xin (-R;R)$ и можно записать равенство $S(x)=sum limits _{n=0}^{infty }a_{n} x^{n} $.
Свойство 1. Степенной ряд $sum limits _{n=0}^{infty }a_{n} x^{n} $ сходится абсолютно в любом промежутке $[a;b], , subset , (-R;R)$, лежащем в интервале сходимости, причём сумма степенного ряда $S(x)$ является непрерывной функцией при всех $xin [a;b]$.
Свойство 2. Если отрезок $[a;b], , subset , (-R;R)$, то степенной ряд можнопочленно интегрировать от a до b, т.е. если
$S(x)=sum limits _{n=0}^{infty }a_{n} x^{n} =a_{0} +a_{1} x+a_{2} x^{2} +…$, то
$int limits _{a}^{b}S(x), {rm d}x =sum limits _{n=0}^{infty }int limits _{a}^{b}a_{n} x^{n} , {rm d}x=int limits _{a}^{b}a_{0} {rm d}x +int limits _{a}^{b}a_{1} x, {rm d}x +…+int limits _{a}^{b}a_{n} x^{n} , {rm d}x +…$.
При этом радиус сходимости не меняется:
где $a’_{n} =frac{a_{n} }{n+1} $ — коэффициенты проинтегрированного ряда.
Свойство 3. Сумма степенного ряда есть функция, имеющая внутри интервала сходимости производные любого порядка. Производные от суммы степенного ряда будут суммами рядов, полученных из данного степенного ряда почленным дифференцированием соответствующее число раз, причём радиусы сходимости таких рядов будут те же, что и у исходного ряда.
Если $S(x)=a_{0} +a_{1} x+a_{2} x^{2} +…+a_{n} x^{n} +…=sum limits _{n=0}^{infty }, a_{n} cdot x^{n} $,то $S'(x)=a_{1} +2a_{2} x+…+na_{n} x^{n-1} +…=sum limits _{n=1}^{infty }, ncdot a_{n} cdot x^{n-1} $,$S»(x)=2a_{2} +6a_{3} x+…+n(n-1)a_{n} x^{n-2} +…=sum limits _{n=2}^{infty }, ncdot (n-1)cdot a_{n} cdot x^{n-2} $, … , и т.д.
Примеры
-
Ряд $sum limits _{n=1}^{infty }n!; x^{n} $ сходится только в точке $x=0$, во всех остальных точках ряд расходится. $V:left{0right}.$
-
Ряд $sum limits _{n=1}^{infty }frac{x^{n} }{n!} $ сходится во всех точках оси, $V=R$.
-
Ряд $sum limits _{n=1}^{infty }frac{(-1)^{n} x^{n} }{n} $ сходится в области $V=(-1,, 1]$.
-
Ряд $sum limits _{n=1}^{infty }frac{1}{n+cos x} $ расходится во всех точках оси $V=$$emptyset$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

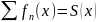
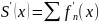
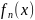
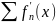

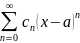
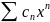
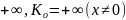
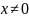
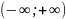
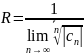
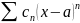
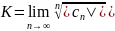
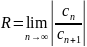
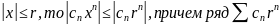
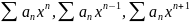
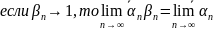
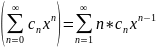
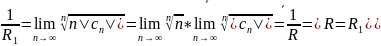
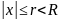
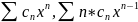
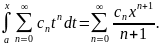
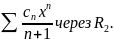
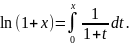
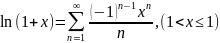
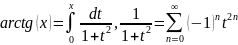
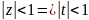
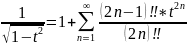
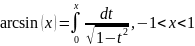
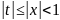
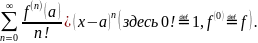




























![Дискретная производная или Коротко о том, как суммировать ряды - 44 $E[X]=limlimits_{n to infty}{sum_{i=1}^ni*P(i)}=limlimits_{n to infty}{sum_{i=1}^ni*(1-p)p^{i-1}}==(1-p)limlimits_{n to infty}{sum_{i=1}^ni*p^{i-1}}$](https://www.pvsm.ru/images/2019/09/28/diskretnaya-proizvodnaya-ili-korotko-o-tom-kak-summirovat-ryady-44.svg)







![Дискретная производная или Коротко о том, как суммировать ряды - 54 $E[X]=(1-p)limlimits_{ntoinfty}sum_{i=1}^n{ip^{i-1}}=(1-p)frac{1}{(p-1)^2}=frac{1}{1-p}$](https://www.pvsm.ru/images/2019/09/28/diskretnaya-proizvodnaya-ili-korotko-o-tom-kak-summirovat-ryady-54.svg)