Как найти производную третьего порядка калькулятор - Исправление недочетов и поиск решений вместе с Examum.ru

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Показать Этапы

Номер Строки

Примеры

frac{d^3}{dx^3}(frac{3x+9}{2-x})
(sin^2(theta))»’
frac{d^3}{dy^3}(a^y)
frac{d^3}{dx^3}(frac{sqrt{x}}{2x+3})
frac{d}{dx^3}(e^{x^n})
(xln(x))»’
Показать больше

Описание

Дифференцируйте функции шаг за шагом

third-derivative-calculator

Блог-сообщения, имеющие отношение к Symbolab

High School Math Solutions – Derivative Calculator, Products & Quotients

In the previous post we covered the basic derivative rules (click here to see previous post). We are now going…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Калькулятор

Инструкция

Примечание: π записывается как pi; корень квадратный как sqrt().

Шаг 1. Введите в ячейку калькулятора заданную функцию.

Шаг 2. Нажать кнопку “Найти”.

Шаг 3. Получите результат.

Третья производная функция

Вычисление производной функции третьего порядка – это довольно-таки частая задача по высшей математике. Понятие производной – ого порядка вычисляется последовательно, начиная с первого порядка. Переход производной к более высоким порядкам производится при помощи формулы:

$y^{(n)}(x) = (y^{n - 1}(x))`$

Важно! Чтобы порядок производной не путать с показателем степени, пишут или в круглых скобках, или римскими цифрами. Например, производная третьего порядка: $y^{(3)}$ или $y^{III}$ .

Источник

Данный калькулятор вычисляет первую вторую и другие производные заданной функции.
В поле функция введите математическое выражение с переменной x, в выражении используйте стандартные операции + сложение, — вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции. Полный синтаксис смотрите ниже. Для сложных функций калькулятор может работать довольно долго, так как используется не очень оптимальный алгоритм упрощения.

Калькулятор производных второго и более порядка

Производная заданного порядка

Допустимые операции: + — / * ^
Константы: pi
Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

Максимальное число производных

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Синтаксис описания формул

В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, — — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec — экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), log__p — логарифм по основанию p, например log7(x) — логарифм по основанию 7, root__p — корень степени p, например root3(x) — кубический корень.

Пошаговый алгоритм вычисления одной производной, а также правила вычисления производных можно найти тут Производная функции.

Источник

Калькулятор для вычисления производных от первого до пятого порядка включительно.
Пример. Найти производную третьего порядка функции

Решение. В калькулятор вставляем функцию в виде sin(x)cos(x),выбираем порядок производной «3», нажимаем кнопку «Ok», получаем ответ (решение бесплатно)

Калькулятор для нахождения частных производных.

Пример. Найти частные производные функции

z = x³-2xy+y²

Решение. Найдем частную производную по x первого порядка.
В калькулятор вводим функцию в виде x^3-2xy+y^2, переменную дифференцирования указываем x, порядок 1, нажимаем Ok, получаем ответ:

Источник

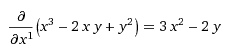
Данный онлайн калькулятор вычисляет производную функции. Программа не только вычисляет ответ, она производит пошаговое решение. Выбирается порядок дифференцирования.
Как пользоваться калькулятором для нахождения производных онлайн:
1. Введите математическое выражение с переменной x, в выражении используйте стандартные операции: + сложение, —
вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции.
2. Выберите порядок дифференцирования (решения производных от первого до пятого порядка включительно).
3. Нажмите кнопку — Вычислить производную.
4. Через несколько секунд внизу отобразится пошаговое решение производной с подробными комментариями.

При помощи нашего калькулятора вы можете найти производную онлайн как от элементарной функции, так и от сложной, не имеющей решения в аналитическом виде.
Калькулятор поможет найти производную функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.

Основные функции

$x^{a}$ : x^a

модуль x: abs(x)

Производные

Для того, чтобы найти производную функции f(x)
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции напишите в окне гаджета: f[x, y, z,…,t], j, где
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где означает тоже, что и Выше.

Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.

Примеры

x*E^x, x;
x^3*E^x, {x,17};
x^3*y^2*Sin[x+y], x;
x^3*y^2*Sin[x+y], y,
x/(x+y^4), {x,6}.

Источник