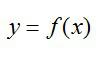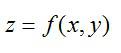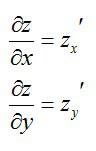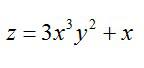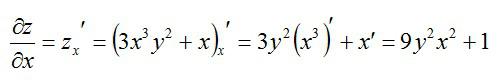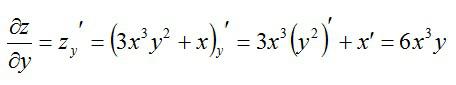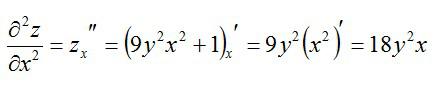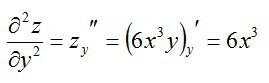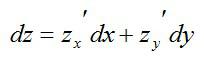Производные различных порядков
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Производные различных порядков — производные первого и высших порядков.
Дифференцируя производную первого порядка f`(x) мы получим производную от производной — производную второго порядка.
Определение
Производная от производной второго порядка называется производной третьего порядка, а производная n-го порядка называется производной от производной n-1го порядка.
Производная второго порядка обозначается y» или f»(x). Таким образом, дифференцируя функцию, n-раз получим производную вида f n(x).
Формула дифференцирования второго порядка
Формула дифференцирования второго порядка имеет вид:
[f»(x)=frac{d^{2} y}{dx^{2} } =mathop{lim }limits_{xto x0} frac{f'(x)-f'(x_{0} )}{x-x_{0} } =left(f'(x)right){{‘} } ]
Производная n-го порядка равна нулю, если степень меньше порядка производной. Например, пятая производная функции y = 5×2 равна нулю
Таблица производных высших порядков
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 1
- Найдем производную первого порядка сложной функции по формуле произведения:
- Найдем производную второго порядка для выражения
- Упростим выражение
[left[f(x)cdot g(x)right]{{‘} } =f(x)’cdot g(x)+f(x)cdot g(x)’]
[y’=left[xcdot ln (2x+1)right]{{‘} } =x’cdot ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =1cdot ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =]
[y’=ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =ln (2x+1)+xcdot frac{1}{2x+1} cdot (2x+1)’=]
[=ln (2x+1)+2xcdot frac{1}{2x+1} =ln (2x+1)+frac{2x}{2x+1} ]
[y»=left(ln (2x+1)+frac{2x}{2x+1} right){{‘} } =ln (2x+1)’+left(frac{2x}{2x+1} right){{‘} } =frac{1}{2x+1} cdot (2x+1)’+frac{2x’cdot (2x+1)-2xcdot (2x+1)’}{left(2x+1right)^{2} } =]
[y»=frac{2}{2x+1} +frac{2(2x+1)-2xcdot 2}{left(2x+1right)^{2} } =frac{2}{2x+1} +frac{2((2x+1)-2x)}{left(2x+1right)^{2} } =frac{2}{2x+1} +frac{2}{left(2x+1right)^{2} } =]
[y»=frac{2left(2x+1right)}{left(2x+1right)^{2} } +frac{2}{left(2x+1right)^{2} } =frac{2left(2x+1right)+2}{left(2x+1right)^{2} } =frac{4x+4}{left(2x+1right)^{2} } ]
«Производные различных порядков» 👇
Пример 2
Найти производную четвертого порядка
[y=x^{5} -x^{4} +3x^{3} ]
Решение.
- Найдем производную первого порядка
- Найдем производную второго порядка
- Найдем производную третьего порядка
- Найдем производную четвертого порядка
[y’=left(x^{5} -x^{4} +3x^{3} right){{‘} } =5x^{4} -4x^{3} +3cdot 3x^{2} =5x^{4} -4x^{3} +9x^{2} ]
[y»=left(5x^{4} -4x^{3} +9x^{2} right){{‘} } =20x^{3} -12x^{2} +18x]
[y»’=left(20x^{3} -12x^{2} +18xright){{‘} } =60x^{2} -24x+18]
[y»»=left(60x^{2} -24x+18right){{‘} } =120x-24]
Пример 3
Найти производную четвертого порядка функции
[y=frac{x^{2} +5x^{3} }{18} ]
Решение: Самая большая степень составного неизвестного равна 3, что меньше степени производной, а значит производная четвертого порядка равна 0.
Пример 4
Найти производную 13 порядка функции
[y=sin x]
Решение.
- Найдем производную первого порядка
- Найдем производную второго порядка
- Найдем производную третьего порядка
- Найдем производную четвертого порядка
- Найдем производную 13 порядка:
[y’=sin’x=cos x=sin (x+frac{pi }{2} )]
[y»=cos’x=-sin x=sin (x+2frac{pi }{2} )]
[y»’=-sin’x=-cos x=sin (x+3frac{pi }{2} )]
[y^{(4)} =-cos x’=sin x=sin (x+4frac{pi }{2} )]
Таким образом:
[y^{(n)} =sin (x+frac{ncdot pi }{2} ),nin N]
[y^{(13)} =sin (x+frac{13cdot pi }{2} )=cos x]
Пример 5
Вычислить производную четвертой степени функции $x^{8}$
Решение.
Вычисления производим по формуле нахождения производной высшего порядка
[left(x^{p} right)^{(n)} =p(p-1)(p-2)…(p-n+1)x^{p-n} ]
где p = 8, n = 4
[left(x^{8} right)^{(4)} =8(8-1)(8-2)(8-4+1)x^{8-4} =8cdot 7cdot 6cdot 5cdot x^{4} =1680x^{4} ]
[left(x^{8} right)^{(4)} =1680x^{4} ]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 15.12.2022
Содержание:
- Механический смысл второй производной
- Вычисления производной любого порядка, формула Лейбница
Если функция $y=f(x)$ имеет производную в каждой точке
$x$ своей области определения, то ее производная
$f^{prime}(x)$ есть функция от
$x$. Функция
$y=f^{prime}(x)$, в свою очередь, может иметь производную, которую
называют производной второго порядка функции $y=f(x)$ (или второй
производной) и обозначают символом $f^{prime prime}(x)$. Таким образом
$f^{prime prime}(x)=frac{mathrm{d}^{2} y}{mathrm{d} x^{2}}=lim _{x rightarrow x_{0}} frac{f^{prime}(x)-f^{prime}left(x_{0}right)}{x-x_{0}}=left(f^{prime}(x)right)^{prime}$
Пример
Задание. Найти вторую производную функции $y(x)=x ln (2 x+3)$
Решение. Для начала найдем первую производную:
$y^{prime}(x)=(x ln (2 x+3))^{prime}=(x)^{prime} cdot ln (2 x+3)+x cdot(ln (2 x+3))^{prime}=$
$=1 cdot ln (2 x+3)+x cdot frac{1}{2 x+3} cdot(2 x+3)^{prime}=ln (2 x+3)+$
$+frac{x}{2 x+3} cdotleft[(2 x)^{prime}+(3)^{prime}right]=ln (2 x+3)+frac{x}{2 x+3} cdotleft[2 cdot(x)^{prime}+0right]=$
$=ln (2 x+3)+frac{x}{2 x+3} cdot 2 cdot 1=ln (2 x+3)+frac{2 x}{2 x+3}$
Для нахождения второй производной продифференцируем выражение для первой производной еще раз:
$y^{prime prime}(x)=left(y^{prime}(x)right)^{prime}=left(ln (2 x+3)+frac{2 x}{2 x+3}right)^{prime}=$
$=(ln (2 x+3))^{prime}+left(frac{2 x}{2 x+3}right)^{prime}=$
$=frac{1}{2 x+3} cdot(2 x+3)^{prime}+frac{(2 x)^{prime} cdot(2 x+3)-2 x cdot(2 x+3)^{prime}}{(2 x+3)^{2}}=$
$=frac{1}{2 x+3}left[(2 x)^{prime}+(3)^{prime}right]+frac{2(x)^{prime} cdot(2 x+3)-2 x cdotleft[(2 x)^{prime}+(3)^{prime}right]}{(2 x+3)^{2}}=$
$=frac{1}{2 x+3}left[2 cdot(x)^{prime}+0right]+frac{2 cdot 1 cdot(2 x+3)-2 x cdotleft[2 cdot(x)^{prime}+0right]}{(2 x+3)^{2}}=$
$=frac{1}{2 x+3} cdot 2 cdot 1+frac{2(2 x+3)-2 x cdot 2 cdot 1}{(2 x+3)^{2}}=$
$=frac{2}{2 x+3}+frac{4 x+6-4 x}{(2 x+3)^{2}}=frac{2}{2 x+3}+frac{6}{(2 x+3)^{2}}=$
$=frac{2(2 x+3)+6}{(2 x+3)^{2}}=frac{4 x+6+6}{(2 x+3)^{2}}=frac{4 x+12}{(2 x+3)^{2}}=frac{4(x+3)}{(2 x+3)^{2}}$
Ответ. $y^{prime prime}(x)=frac{4(x+3)}{(2 x+3)^{2}}$
Производные более высоких порядков определяются аналогично. То есть производная
$n$-го порядка функции
$f(x)$ есть первая производная от производной
$(n-1)$-го порядка этой функции:
$f^{(n)}(x)=frac{mathrm{d}^{n} y}{mathrm{d} x^{n}}=left(f^{(n-1)}(x)right)^{prime}$
Замечание
Число $n$, указывающее порядок производной, заключается в скобки.
Механический смысл второй производной
Теорема
(Механический смысл второй производной)
Если точка движется прямолинейно и задан закон ее движения $s=f(t)$,
то ускорение точки равно второй производной от пути по времени:
$a(t)=s^{prime prime}(t)$
Замечание
Ускорение материального тела равно первой производной от скорости, то есть:
$a(t)=v^{prime}(t)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Материальная точка движется по закону
$s(t)=2 t^{3}+3 t$, где
$s$ измеряется в метрах, а
$t$ — в секундах. Найти значение
$t$, при котором ускорение точки равно 12.
Решение. Найдем ускорение материальной точки:
$a(t)=s^{prime prime}(t)=left(2 t^{3}+3 tright)^{prime prime}=left(left(2 t^{3}+3 tright)^{prime}right)^{prime}=left(left(2 t^{3}right)^{prime}+(3 t)^{prime}right)^{prime}=$
$=left(2 cdot 3 t^{2}+3 cdot 1right)^{prime}=left(6 t^{2}+3right)^{prime}=left(6 t^{2}right)^{prime}+(3)^{prime}=$
$=6 cdotleft(t^{2}right)^{prime}+0=6 cdot 2 t=12 t$
Искомое время $t$ найдем из уравнения:
$a(t)=12 Rightarrow 12 t=12 Rightarrow t=1 mathrm{c}$
Ответ. $t=1 c$
Вычисления производной любого порядка, формула Лейбница
Для вычисления производной любого порядка от произведения двух функций, минуя последовательное применение
формулы вычисления производной от произведения двух функций, применяется формула Лейбница:
$(u v)^{(n)}=u^{(n)} v+C_{n}^{1} u^{(n-1)} v^{prime}+C_{n}^{2} u^{(n-2)} v^{prime prime}+ldots+C_{n}^{n-1} u^{prime} v^{(n-1)}+u v^{(n)}$
где $C_{n}^{k}=frac{n !}{k !(n-k) !}$,
$n !=1 cdot 2 cdot ldots cdot n$ — факториал
натурального числа
$n$.
Пример
Задание. Найти $y^{(4)}(x)$, если
$y(x)=e^{4 x} sin 3 x$
Решение. Так как заданная функция представляет собой произведение двух функций
$u(x)=e^{4 x}$,
$v(x)=sin 3 x$, то для нахождения производной четвертого
порядка целесообразно будет применить формулу Лейбница:
$y^{(4)}(x)=left(e^{4 x}right)^{(4)} cdot sin 3 x+C_{4}^{1}left(e^{4 x}right)^{(3)} cdot(sin 3 x)^{prime}+$
$+C_{4}^{2}left(e^{4 x}right)^{prime prime} cdot(sin 3 x)^{prime prime}+C_{4}^{3}left(e^{4 x}right)^{prime} cdot(sin 3 x)^{(3)}+e^{4 x}(sin 3 x)^{(4)}$
Найдем все производные и посчитаем коэффициенты при слагаемых.
1) Посчитаем коэффициенты при слагаемых:
$C_{4}^{1}=frac{4 !}{1 ! cdot(4-1) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$
$C_{4}^{2}=frac{4 !}{2 ! cdot(4-2) !}=frac{4 !}{2 ! cdot 2 !}=frac{2 ! cdot 3 cdot 4}{2 ! cdot 2 !}=frac{3 cdot 4}{2}=6$
$C_{4}^{3}=frac{4 !}{3 ! cdot(4-3) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$
2) Найдем производные от функции $u(x)$:
$u(x)=e^{4 x}, u^{prime}(x)=left(e^{4 x}right)^{prime}=e^{4 x} cdot(4 x)^{prime}=e^{4 x} cdot 4 cdot(x)^{prime}=4 e^{4 x}$
$u^{prime prime}(x)=left(u^{prime}(x)right)^{prime}=left(4 e^{4 x}right)^{prime}=4 cdotleft(e^{4 x}right)^{prime}=16 e^{4 x}$
$u^{prime prime prime}(x)=left(u^{prime prime}(x)right)^{prime}=left(16 e^{4 x}right)^{prime}=64 e^{4 x}$
$u^{(4)}(x)=left(u^{prime prime prime}(x)right)^{prime}=left(64 e^{4 x}right)^{prime}=256 e^{4 x}$
3) Найдем производные от функции $v(x)$:
$v(x)=sin 3 x, v^{prime}(x)=(sin 3 x)^{prime}=cos 3 x cdot(3 x)^{prime}=3 cos 3 x$
$v^{prime prime}(x)=left(v^{prime}(x)right)^{prime}=(3 cos 3 x)^{prime}=3 cdot(cos 3 x)^{prime}=$
$=3 cdot(-sin 3 x) cdot(3 x)^{prime}=-9 sin 3 x$
$v^{prime prime prime}(x)=left(v^{prime prime}(x)right)^{prime}=-27 cos 3 x, v^{(4)}(x)=left(v^{prime prime prime}(x)right)^{prime}=81 sin 3 x$
Тогда
$y^{(4)}(x)=256 e^{4 x} cdot sin 3 x+4 cdot 64 e^{4 x} cdot 3 cos 3 x+$
$+6 cdot 16 e^{4 x} cdot(-9 sin 3 x)+4 cdot 4 e^{4 x} cdot(-27 cos 3 x)+e^{4 x} 81 sin 3 x=$
$=e^{4 x}(336 cos 3 x-527 sin 3 x)$
Ответ. $y^{(4)}(x)=e^{4 x}(336 cos 3 x-527 sin 3 x)$
Читать дальше: таблица производных высших порядков.
Производная
является также функцией от
и называется производной первого
порядка.
Если
функция
дифференцируема, то ее производная
называется производной второго порядка
и обозначается
.
Итак,
.
Производная
от производной второго порядка, если
она существует, называется производной
третьего порядка и обозначается
.
Итак,
.
Производной
n—го
порядка называется производная от
производной (n—1)
порядка:
.
Производные
порядка выше первого называются
производными
высших порядков.
Примеры.
1)
Найти производную 3-го порядка для
функции
.
Имеем:
;
;
.
2)
Найти производную
-го
порядка для функции
.
Имеем:
;
;
;
;
.
Таким образом,
.
§14. Дифференциал функции
14.1. Понятие дифференциала функции
Пусть
функция
имеет в точке
отличную от нуля производную
.
Тогда, по теореме о связи функции, ее
предела и бесконечно малой функции,
можно записать
,
где
при
,
или
.
Таким
образом, приращение функции представляет
собой сумму двух слагаемых
и
,
которые являются бесконечно малыми при
.
При этом первое слагаемое есть бесконечно
малая функция одного порядка с
,
а второе слагаемое есть бесконечно
малая функция более высокого порядка,
чем
.
Поэтому первое слагаемое
называют главной частью приращения
функции.
-
Дифференциалом
функциив точке
называется главная часть приращения
функции, равная произведению производной
функции на приращение аргумента и
обозначается
,
т.е.
.
Рассмотрим
функцию у=х.
В этом случае
,
то есть
.
Таким образом,
дифференциал функции равен произведению
производной этой функции на дифференциал
независимой переменной, т.е.
.
Тогда,
согласно данной формуле, производную
функции можно записать, как отношение
ее дифференциалов:
.
Отметим,
что дифференциал обладает инвариантностью
формы, то
есть та же формула применяется и для
вычисления дифференциала от сложной
функции:
если
,
то
.
14.2. Основные теоремы о дифференциалах
Теорема
14.1.
Дифференциал
суммы, произведения и частного двух
дифференцируемых функций определяются
следующими формулами:
,
,
.
Теорема
14.2.
Дифференциал
сложной функции равен произведению
производной этой функции по промежуточному
аргументу на дифференциал этого
промежуточного аргумента.
Это свойство
дифференциала называют инвариантностью
(неизменностью) формы первого дифференциала.
Пример.
Функция
является сложной. Здесь
,
где
.
Тогда
.
14.3. Применение дифференциала к приближенным вычислениям
Для
функции
приращение функции
состоит из двух слагаемых, одно из
которых является бесконечно малой
более высокого порядка чем
,
что дает нам право им пренебречь:
,
т.е.
или
.
Данные формулы
используются для приближенных вычислений.
Пример.
Вычислить
приближенно
.
Рассмотрим
функцию
.
По формуле
имеем:
,
т.е.
.
Так как
,
то при
и
,
получаем:
.
§15. Исследование функций при помощи производных
15.1. Правило Лопиталя
Для вычисления
пределов часто используют следующую
теорему.
Теорема
15.1.
(правило
Лопиталя).
Пусть
функции
и
дифференцируемы в некоторой окрестности
точки
(за исключением может быть самой точки),
и
(или
),
причем
в некоторой окрестности точки х0,
тогда
.
Так,
неопределенности вида
или
приводятся к неопределенностям вида
с помощью алгебраических преобразований.
Неопределенности вида
с помощью логарифмирования сводятся к
неопределенности вида
.
В некоторых случаях для решения задачи
требуется неоднократное применение
правила Лопиталя.
Примеры.
1)

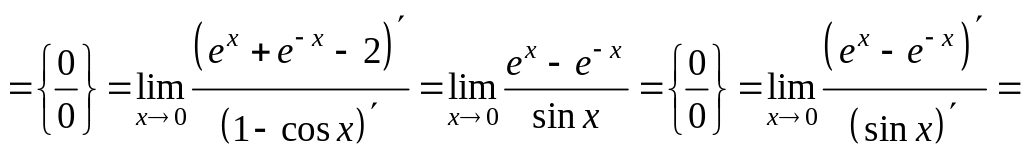
.
2)

=
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Под понятием производные различных порядков обычно понимаются производные первого или высших порядков.
Дифференцирование производной первого порядка [F^{prime}(x)] позволит вычислить производную от производной — именуемую производной второго порядка. Далее назовем определение производной.
Производная производной второго порядка именуется производной третьего порядка, в этой связи производная n-го
порядка определяется как производная от производной n-1го порядка.
Производная функции второго порядка обозначается записью [y^{prime prime}] или [F^{prime prime}(x)]. Дифференцировка функции [n] раз приводит к получению производной вида [f n(x)].
Дифференцирование второго порядка
Производные в математике всегда находятся по определенной формуле. Итак, формула дифференцирования второго порядка записывается следующим образом:
[f^{prime prime}(x)=frac{d^{2} y}{d x^{2}}=lim _{x rightarrow x_{0}}=frac{f^{prime}(x)-f^{prime}left(x_{0}right)}{x-x_{0}}=left(f^{prime}(x)right)^{prime}]
В случае, если степень меньше, чем порядок производной, производная n-го порядка будет равна нулю.
Таблица с формулами производных высших порядков
Формулы для нахождения производных высших порядков наиболее удобно представить в виде таблицы формул производных:
| Функция | Формула нахождения |
| [left(x^{p}right)^{(n)}] | [left(x^{p}right)^{(n)}=p(p-1)(p-1) ldots(p-n+1) x^{p-n}] |
| [left(a^{k x+b}right)^{(n)}] | [left(a^{k x+b}right)^{(n)}=k^{n} a^{k x+b} 1 n^{n} a] |
| [left(e^{k x+b}right)^{(n)}] | [left(e^{k x+b}right)^{(n)}=k^{n} e^{k x+b}] |
| [(sin a x)^{(n)}] | [(sin a x)^{(n)}=a^{n} sin left(a x+frac{п n}{2}right)] |
| [(cos a x)^{(n)}] | [(sin a x)^{(n)}=a^{n} cos left(a x+frac{п n}{2}right)] |
| [left((a x+b)^{p}right)^{n}] | [left((a x+b)^{p}right)^{n}=a^{n} p(p-1)(p-2) ldots(p-n+1)(a x+b)^{n-1}] |
| [left(log _{a}|x|right)^{(n)}] | [left(log _{a}|x|right)^{(n)}=frac{(-1)^{n-1}(n-1) !}{x^{n} ln a}] |
| [(ln |x|)^{n}] | [left(log _{a}|x|right)^{(n)}=frac{(-1)^{n-1}(n-1) !}{x^{n}}] |
| [(a u(x)+beta gamma(x))^{n}] | [(a u(x)+beta gamma(x))^{n}=a u^{n}(x)+beta^{n} gamma(x)] |
Нет времени решать самому?
Наши эксперты помогут!
Примеры нахождения производных
Примеры
Пример 1
Как найти производную первого порядка функции по формуле произведения:
[|f(x) cdot g(x)|^{prime}=f(x)^{prime} cdot g(x)+f(x) cdot g(x)^{prime}\y^{prime}=[x cdot ln (2
x+1)]^{prime}=x^{prime} cdot ln (2 x+1)+x cdot(ln (2 x+1))^{prime}\=1 cdot ln (2 x+1)+x cdot(ln
(2 x+1))^{prime}=y^{prime}\=ln (2 x+1)+x cdot(ln (2 x+1))^{prime}\=ln (2 x+1)+x frac{1}{2 x+1}
cdot(2 x+1)^{prime}=ln (2 x+1)+2 x cdot frac{1}{2 x+1}\=ln (2 x+1)+frac{2 x}{2 x+1}]
Как найти производную второго порядка в данном выражении:
[y^{prime prime}=left(ln (2 x+1)+frac{2 x}{2 x+1}right)^{prime}=ln (2 x+1)^{prime}+left(frac{2
x}{2 x+1}right)^{prime}\=left(frac{1}{2 x+1}right) cdot(2 x+1)^{prime}+frac{2 x^{prime} cdot(2
x+1)-2 x cdot(2 x+1)^{prime}}{(2 x+1)^{2}}\=y^{prime prime}=frac{2}{2 x+1}+frac{2(2 x+1)-2 x cdot
2}{(2 x+1)^{2}}=frac{2}{2 x+1}+frac{2((2 x+1)-2 x)}{(2 x+1)^{2}}\=frac{2}{2 x+1}+frac{2}{(2
x+1)^{2}}]
Упростим полученное решение:
[y^{prime prime}=frac{2(2 x+1)}{(2 x+1)^{2}}+frac{2}{(2 x+1)^{2}}=frac{2(2 x+1)+2}{(2 x+1)^{2}}=frac{4
x+4}{(2 x+1)^{2}}]
Пример 2
Задача на нахождение производной различных порядков на примере производной четвертого порядка:
[y=x^{5}-x^{4}+3 x^{3}]
Решение:
[y^{prime}=left(x^{5}-x^{4}+3 x^{3}right)^{prime}=5 x^{4}-4 x^{3}+3 cdot 3 x^{2}=5 x^{4}-4 x^{3}+9
x^{2}\y^{prime prime}=left(5 x^{4}-4 x^{3}+9 x^{2}right)^{prime}=20 x^{3}-12 x^{2}+18 x\y^{prime
prime prime}=left(20 x^{3}-12 x^{2}+18 xright)^{prime}=60 x^{2}-24 x+18\y^{4}=left(60 x^{2}-24
x+18right)^{prime}=120 x-24]
Пример 3
Нахождение производной различных порядков от функций на следующем частном примере:
[y=frac{x^{2}+5 x^{3}}{18}]
Ответ: решение не является сложным и не потребует онлайн-калькулятора. Наибольшая степень одной из переменных
равна 3, что меньше степени производной. Следовательно, производная четвертого порядка равна 0.
Пример 4
Необходимо найти производную 13 порядка для [y=sin x]
Решение: найдем производную первого порядка (и затем 2-4 порядков)
[y^{prime}=sin ^{prime} x=cos x=sin left(x+frac{pi}{2}right)\y^{prime prime}=cos ^{prime}
x=-sin x=sin left(x+2 frac{pi}{2}right)\y^{prime prime prime}=-sin ^{prime} x=-cos x=sin
left(x+3 frac{pi}{2}right)\y^{(4)}=-cos ^{prime} x=sin x=sin left(x+4 frac{pi}{2}right)]
Следовательно:
[y^{(n)} sin left(x+frac{n cdot pi}{2}right), n in N]
Итоговый результат:
[y^{(13)}=sin left(x+frac{13 cdot pi}{2}right)=cos x]
Пример 5
Подсчитайте производную четвертой степени функции [x^{8}]
Решение:
Используем формулу нахождения производной высшего порядка
[left(x^{p}right)^{(n)}=p(p-1)(p-1) ldots(p-n+1) x^{p-n}]
Учтем, что p=8, n=4
[left(x^{8}right)^{(4)}=8(8-1)(8-2)(8-4+1) x^{8-4}=8 cdot 7 cdot 6 cdot 5 cdot x^{4}=1680 x^{4}\left(x^{8}right)^{(4)}=1680 x^{4}]
Пример 6
Подсчитайте производную функции [y=2^{x}-operatorname{arctg} x].
Решение:
[y^{prime}=left(2^{x}-operatorname{arctg} xright)^{prime}=left(2^{x}right)^{prime}-(operatorname{arctg} x)^{prime}]
Используем формулы для обратной и тригонометрической функции [y^{prime}=2^{x} ln 2-frac{1}{1+x^{2}}]
Ответ: [y^{prime}=2^{x} ln 2-frac{1}{1+x^{2}}]
Чтобы понять частные производные, сначала нужно разобраться с обычными. И не нужно ничего искать: в нашей отдельной статье мы уже подготовили все для того, чтобы у вас это получилось. А сейчас речь пойдет о частных производных.
Добро пожаловать на наш телеграм-канал за полезной рассылкой и актуальными студенческими новостями.
Функция двух и более переменных
Прежде чем говорить о частных производных, нужно затронуть понятие функции нескольких переменных, без которого нет смысла в частной производной. В школе мы привыкли иметь дело с функциями одной переменной:
Производными таких функций мы и считали раньше. График функции одной переменной представляет собой линию на плоскости: прямую, параболу, гиперболу и т.д.
А что, если добавить еще одну переменную? Получится такая функция:
Это – функция двух независимых переменных x и y. График такой функции представляет собой поверхность в трехмерном пространстве: шар, гиперболоид, параболоид или еще какой-нибудь сферический конь в вакууме. Частные производные функции z по иксу и игреку соответственно записываются так:
Существуют также функции трех и более переменных. Правда, график такой функции нарисовать невозможно: для этого понадобилось бы как минимум четырехмерное пространство, которое невозможно изобразить.
Частная производная первого порядка
Запоминаем главное правило:
При вычислении частной производной по одной из переменных, вторая переменная принимается за константу. В остальном правила вычисления производной не меняются.
То есть, частная производная по сути ничем не отличается от обычной. Так что, держите перед глазами таблицу производных элементарных функций и правила вычисления обычных производных. Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции:
Сначала возьмем частную производную по иксу, считая игрек обычным числом:
Теперь считаем частную производную по игреку, принимая икс за константу:
Как видите, ничего сложного в этом нет, а успех с более сложными примерами – лишь дело практики.
Частная производная второго порядка
Как находится частная производная второго порядка? Так же, как и первого. Чтобы найти частные производные второго порядка, нужно просто взять производную от производной первого порядка. Вернемся к примеру выше и посчитаем частные производные второго порядка.
По иксу:
По игреку:
Частные производные третьего и высших порядков не отличаются по принципу вычисления. Систематизируем правила:
- При дифференцировании по одной независимой переменной, вторая принимается за константу.
- Производная второго порядка – это производная от производной первого порядка. Третьего порядка – производная от производной второго порядка и т.д.
Частные производные и полный дифференциал функции
Частый вопрос в практических заданиях – нахождение полного дифференциала функции. Для функции нескольких переменных полный дифференциал определяется, как главная линейная часть малого полного приращения функции относительно приращений аргументов.
Определение звучит громоздко, но с буквами все проще. Полный дифференциал первого порядка функции нескольких переменных выглядит так:
Зная, как считаются частные производные, нет никакой проблемы вычислить и полный дифференциал.
Частные производные – не такая уж и бесполезная тема. Например, дифференциальные уравнения в частных производных второго порядка широко используются для математического описания реальных физических процессов.
Здесь мы дали лишь общее, поверхностное представление о частных производных первого и второго порядка. Вас интересует эта тема или остались конкретные вопросы? Задавайте их в комментариях и обращайтесь к экспертам профессионального студенческого сервиса за квалифицированной и скорой помощью в учебе. С нами вы не останетесь один на один с проблемой!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.