Как найти производящую функцию моментов - Исправление недочетов и поиск решений вместе с Examum.ru

1. Начнем с главного — что такое “момент” в вероятности и статистике?

Скажем, нас интересует случайная переменная X.

Моменты — это ожидаемые значения X, например, E(X), E(X²), E(X³) и т.д.

 Первый момент — E(X),
 Второй момент — E(X²),
 Третий момент — E(X³),
 …
 n-й момент — E(X^n).

Нам очень хорошо знакомы первые два момента: математическое ожидание μ = E(X) и дисперсия E(X²) − μ². Это важные характеристики X.Математическое ожидание — это среднее значение случайной величины, дисперсия — мера разброса значений. Но должны быть и другие функции, также определяющие распределение. Например, третий момент указывает на асимметрию, четвертый — насколько тяжелы хвосты распределения.

Моменты говорят нам о свойствах распределения.

2. Что же такое производящая функция моментов?

Эта функция определяет распределение значений случайной величины— E(X), E(X²), E(X³), … , E(X^n).

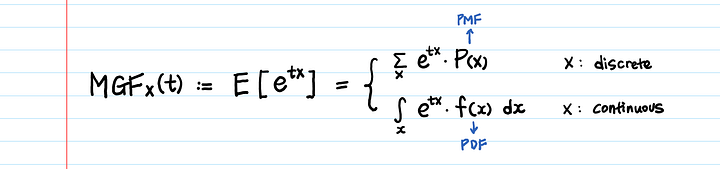
Определение производящей функции моментов

Глядя на определение, вы можете сказать:

“Меня не интересует E(e^tx). Мне нужно E(X^n).”

Возьмите производную от ПФМ n раз и подставьте t = 0. Так вы получите E(X^n).

Как получить моменты из ПФМ

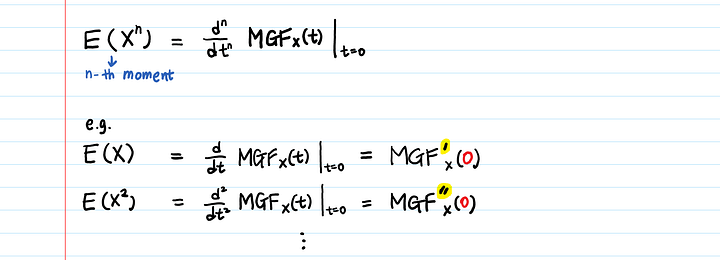
3. Почему n-й момент является n-й производной ПФМ?

Для доказательства используем ряды Тейлора:

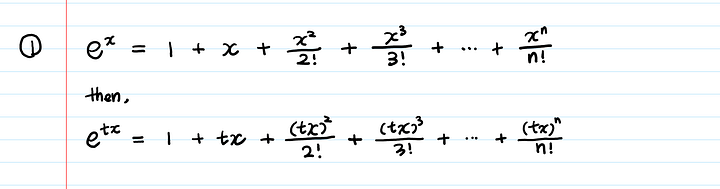
Затем берем ожидаемое значение:

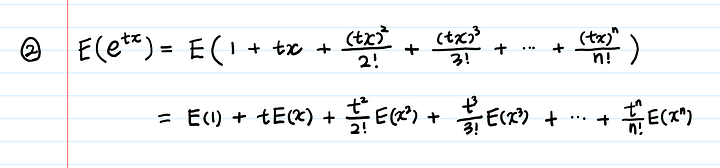
Теперь берем производную по t:

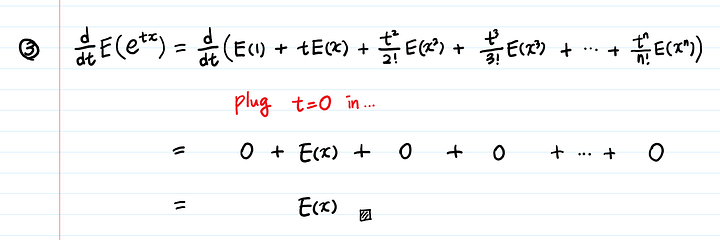
Если возьмем другую производную (то есть производную дважды), получим E(X²).
Снова возьмем производную (третью), получим E(X³), и так далее.

Когда я впервые увидела ПФМ, я не поняла роль t в функции, потому что t показалась произвольной переменной, которая не особенно меня интересовала. Между тем t является вспомогательной переменной — мы вводим t, чтобы использовать исчисление (производные) и обнулить значения (которые нас не интересуют).

Подождите… но мы можем вычислить моменты, используя определение ожидаемых значений. Зачем нам ПФМ?

4. Так зачем нам нужна ПФМ?

Для удобства.

Производящая функция моментов упрощает вычисление моментов.

Как?

В моем учебнике математики написано: “найдите производящую функцию момента биномиального (n, p), пуассонового (λ), экспоненциального (λ), нормального (0, 1) распределений и так далее”. Однако в нем никогда не объяснялось, почему ПФМ полезна и удобна.

Я думаю, пример ниже порадует вас — самый яркий пример, где есть простое использование ПФМ: ПФМ экспоненциального распределения. (Не знакомы с экспоненциальным распределением? ? Экспоненциальное распределение: восприятие, происхождение, применение)

Начнем с плотности вероятности:

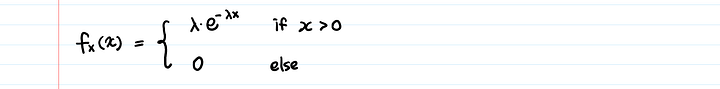
Плотность вероятности экспоненциального распределения

Продифференцируем экспоненциальную ПФМ:

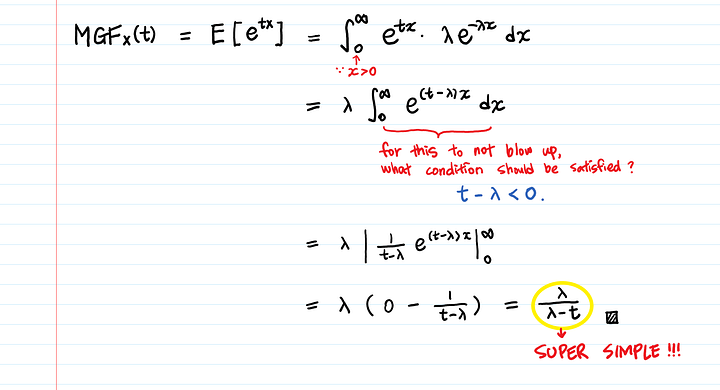
Чтобы ПФМ существовала, должно существовать ожидаемое значение E(e^tx).
Вот почему t — λ < 0 — важное условие: в противном случае интеграл не будет сходиться (это называется тестом на сходимость и проверяется первым делом, когда нужно определить, сходится интеграл или расходится).

Раз у нас есть ПФМ: λ/(λ-t), вычисление моментов становится просто вопросом взятия производных, что проще, чем использование интегралов для расчета ожидаемого значения напрямую.

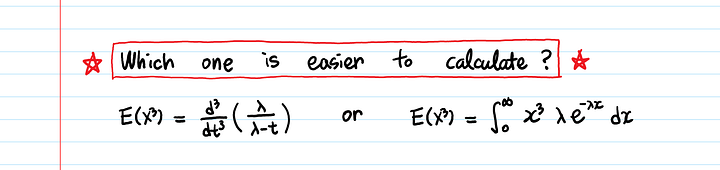
Используя ПФМ, можно находить моменты при помощи производных, а не интегралов!

Несколько замечаний:

Для любой действительной ПФМ M(0) = 1.
Всякий раз при вычислении ПФМ подставляйте t = 0 и смотрите, получите ли 1.
Моменты помогают подробнее описать распределение. Например, можно полностью описать нормальное распределение по первым двум моментам — математическому ожиданию и дисперсии. Чем больше моментов вы знаете, тем больше вы знаете о распределении. Если вы никогда не встречали человека, но знаете его рост, вес, цвет кожи, хобби и т.д., вы по-прежнему не знаете его полностью, но у вас есть много информации о нем.
Прелесть ПФМ в том, что, получив ПФМ (когда ожидаемое значение существует), вы можете получить любой n-й момент, так как ПФМ кодирует все моменты случайной переменной в одну функцию, из которой их легко снова извлечь.
Распределение вероятностей однозначно определяется его ПФМ. Если у двух случайных переменных одинаковая ПФМ, они должны иметь одинаковое распределение.
Одно из важнейших свойств распределения — насколько тяжелы его хвосты, особенно, в управлении финансовыми рисками. Если вспомнить финансовый кризис 2008 года, в основе которого по сути лежали неудачные определения вероятностей редких событий, управляющие рисками недооценили эксцесс (“выпуклость”) финансового обеспечения, лежащего в основе торговых позиций фонда. Иногда выглядящие случайными распределения с гипотетически гладкими кривыми риска могут содержать скрытые эксцессы. И мы можем найти их, используя ПФМ!

Производящая функция

Для случайной величины $xi$ производящая функция моментов (сокращенно ПФМ) определяется следующим образом:

$$
M_{xi}(t)=M[e^{txi}].
$$

Для дискретной случайной величины с законом вида $(x_i,p_i)$ ПФМ выражается как

$$M_{xi}(t)=M[e^{txi}]=sum_i e^{tx_i}cdot p_i.$$

Для непрерывной случайной величины с плотностью распределения $f(x)$:

$$M_{xi}(t)=M[e^{txi}]=int_{-infty}^{infty} e^{tx}cdot f(x),dx.$$

Производящая функция моментов — это двустороннее преобразование Лапласа от плотности распределения случайной
величины.

По известной ПФМ можно вычислять моменты случайной величины по формуле:

$$M[xi^n] = frac{d^n}{dx^n} M_{xi}(t)|_{t=0} $$

ПФМ однозначно определяет распределение случайной величины. ПФМ суммы независимых случайных величин равна произведению их проиводящих функций моментов. Производящая функция существует только в случае существования всех моментов, а характеристическая функция — всегда.

В этом разделе вы найдете примеры нахождения производящей функции для разных законов распределения, в том числе для заданных произвольно случайных величины (см. задачи 3 и 4), а также пример решения обратной задачи — по имеющейся производящей функции восстановить закон распределения случайной величины.

Понравилось? Добавьте в закладки

Примеры решений: производящая функция

Задача 1. Найти производящую функцию моментов для случайной величины, имеющей геометрическое распределение. Вычислить с помощью найденной функции математическое ожидание и дисперсию.

Задача 2. Найти производящую функцию моментов для случайной величины, имеющей распределение Пуассона с параметром $lambda$. Вычислить с помощью найденной функции математическое ожидание и дисперсию.

Задача 3. Дискретная случайная величина X имеет ряд распределения.
x=-2 x=0 x=2
1/4 1/2 1/4
Найти производящую функцию моментов случайной величины X и с ее помощью вычислить математическое ожидание и дисперсию.

Задача 4. Абсолютно непрерывная случайная величина имеет плотность распределения
$$
p(x)=
left{
begin{array}{l}
sin(x)/2, x in[0;pi],\
0, x notin[0;pi] \
end{array}
right.
$$
Найти производящую функцию моментов.

Задача 5. Задана производящая функция вероятностей $p(t)=t(pt+q)^n$. Найти ряд и функцию распределения соответствующей случайной величины.

Мы отлично умеем решать задачи по теории вероятностей

Источник

Привет, сегодня поговорим про производящая функция моментов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
производящая функция моментов, пфм , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

производящая функция моментов — способ задания вероятностных распределений. Используется чаще всего для вычисления моментов.

Определение

Пусть есть случайная величина с распределением . Тогда ее производящей функцией моментов называется функция, имеющая вид:

Пользуясь формулами для вычисления математического ожидания, определение производящей функции моментов можно переписать в виде:

то есть производящая функция моментов — это двустороннее преобразование Лапласа распределения случайной величины (с точностью до отражения).

Дискретные и абсолютно непрерывные случайные величины

Если случайная величина дискретна, то есть , то

Пример. Пусть имеет распределение Бернулли. Тогда

Если случайная величина абсолютно непрерывна, то есть она имеет плотность , то

Пример. Пусть имеет стандартное непрерывное равномерное распределение. Тогда

Свойства производящих функций моментов

Свойства производящих функций моментов во многом аналогичны свойствам характеристических функций в силу похожести их определений.

Вычисление моментов

Объясняем производящую функцию моментов

1. Начнем с главного — что такое “момент” в вероятности и статистике?

Скажем, нас интересует случайная переменная X.

Моменты — это ожидаемые значения X, например, E(X), E(X²), E(X³) и т.д.

Первый момент — E(X),

Второй момент — E(X²),

Третий момент — E(X³),

…

n-й момент — E(X^n).

Нам очень хорошо знакомы первые два момента: математическое ожидание μ = E(X) и дисперсия E(X²) − μ². Это важные характеристики X. Математическое ожидание — это среднее значение случайной величины, дисперсия — мера разброса значений. Но должны быть и другие функции, также определяющие распределение. Например, третий момент указывает на асимметрию, четвертый — насколько тяжелы хвосты распределения.

Моменты говорят нам о свойствах распределения.

2. Что же такое производящая функция моментов?

Эта функция определяет распределение значений случайной величины— E(X), E(X²), E(X³), … , E(X^n).

Определение производящей функции моментов

Глядя на определение, вы можете сказать:

“Меня не интересует E(e^tx). Мне нужно E(X^n).”

Возьмите производную от
пфм n раз и подставьте t = 0. Так вы получите E(X^n).

Как получить моменты из ПФМ

3. Почему n-й момент является n-й производной ПФМ?

Для доказательства используем ряды Тейлора:

Затем берем ожидаемое значение:

Теперь берем производную по t:

Подождите… но мы можем вычислить моменты, используя определение ожидаемых значений. Зачем нам ПФМ?

Определение ожидаемых значений (если вы хотите разобраться в разнице между X и x, почитайте ниже)

В чем отличие ? от ??

Это математические соглашения. ? — стохастическое, а ? — детерминированное. Допустим, ? —число, которое мы получили, бросив кубик. То есть ? может быть любым числом из множества {1,2,3,4,5,6}. Но как только кубик брошен, значение ? определено. ? = ? означает, что случайная величина ? принимает конкретное значение ?. Итак:

? — случайная величина, обозначаемая заглавной буквой.
? — определенное (фиксированное) значение, которое может принимать случайная величина. Например, ?1, ?2, …, ?n может быть выборкой, соответствующей случайной величине X.

Следовательно, совокупная вероятность P(? ≤ ?) означает, что диапазон функции ? меньше определенного значения ?

4. Так зачем нам нужна ПФМ?

Для удобства. Производящая функция моментов упрощает вычисление моментов.

Как?

В учебнике математики написано: “найдите производящую функцию момента биномиального (n, p), пуассонового (λ), экспоненциального (λ), нормального (0, 1) распределений и так далее”. Однако в нем никогда не объяснялось, почему ПФМ полезна и удобна.

Начнем с плотности вероятности:

Плотность вероятности экспоненциального распределения

Продифференцируем экспоненциальную ПФМ:

Чтобы ПФМ существовала, должно существовать ожидаемое значение E(e^tx).
Вот почему t — λ < 0 — важное условие: в противном случае интеграл не будет сходиться (это называется тестом на сходимость и проверяется первым делом, когда нужно определить, сходится интеграл или расходится).

Используя ПФМ, можно находить моменты при помощи производных, а не интегралов!

Несколько замечаний:

Для любой действительной ПФМ M(0) = 1.
Всякий раз при вычислении ПФМ подставляйте t = 0 и смотрите, получите ли 1.
Моменты помогают подробнее описать распределение. Например, можно полностью описать нормальное распределение по первым двум моментам — математическому ожиданию и дисперсии. Чем больше моментов вы знаете, тем больше вы знаете о распределении. Если вы никогда не встречали человека, но знаете его рост, вес, цвет кожи, хобби и т.д., вы по-прежнему не знаете его полностью, но у вас есть много информации о нем.
Прелесть ПФМ в том, что, получив ПФМ (когда ожидаемое значение существует), вы можете получить любой n-й момент, так как ПФМ кодирует все моменты случайной переменной в одну функцию, из которой их легко снова извлечь.
Распределение вероятностей однозначно определяется его ПФМ. Если у двух случайных переменных одинаковая ПФМ, они должны иметь одинаковое распределение.
Одно из важнейших свойств распределения — насколько тяжелы его хвосты, особенно, в управлении финансовыми рисками. Если вспомнить финансовый кризис 2008 года, в основе которого по сути лежали неудачные определения вероятностей редких событий, управляющие рисками недооценили эксцесс (“выпуклость”) финансового обеспечения, лежащего в основе торговых позиций фонда. Иногда выглядящие случайными распределения с гипотетически гладкими кривыми риска могут содержать скрытые эксцессы. И мы можем найти их, используя ПФМ!

Cм. также

понятие — производящая функция ,
производящая функция последовательности , генератриса ,
производящая функция канонического преобразования ,

Я хотел бы услышать твое мнение про производящая функция моментов Надеюсь, что теперь ты понял что такое производящая функция моментов, пфм
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория вероятностей. Математическая статистика и Стохастический анализ

Источник

Многоме́рное
норма́льное распределе́ние
(или многоме́рное
га́уссовское распределе́ние)
в теории
вероятностей— это обобщениеодномерного
нормального распределения.

Случайный
векторимеет
многомерное нормальное распределение,
если выполняется одно из следующих
эквивалентных условий:

1
Произвольная линейная
комбинациякомпонентов вектораимеет
нормальное распределение или является
константой.

2
Существует вектор независимых
стандартных
нормальных случайных
величин
,
вещественный векториматрицаА размерностиn*m,
такие что:
.

3
Существует вектор
инеотрицательно
определённаясимметричная матрицаразмерностиn*n,
такие что плотность
вероятностивектораX
имеет вид:

где
—
определитель матрицы,
а—
матрицаобратнаяк.

4
Существует вектор
и
неотрицательно определённая симметричная
матрицаразмерностиn*n,
такие что характеристическая
функциявектораX
имеет вид:

замечания:

1Если
одно из приведённых выше определений
принято в качестве основного, то другие
выводятся в качестве теорем.

2Вектор
является
векторомсредних
значенийX,
а
—
егоковариационная
матрица.

3В
случае n=1,
многомерное нормальное распределение
сводится к обычному нормальному
распределению.

4Если
случайный вектор X
имеет многомерное нормальное распределение,
то пишут
.

свойства многомерного
распределения:

—Если
вектор
имеет
многомерное нормальное распределение,
то его компонентыимеют
одномерное нормальное распределение.
Обратное, вообще говоря, неверно!

-Если
случайные величины
имеют
одномерное нормальное распределение
и совместнонезависимы,
то случайный векторимеет
многомерное нормальное распределение.
Матрица ковариацийтакого
вектора диагональна.

-Если
имеет
многомерное нормальное распределение,
и его компоненты попарнонекоррелированы,
то они независимы. Однако, если только
компонентыимеют
одномерное нормальное распределение
и попарно не коррелируют, то отсюдане
следует, что они независимы.

Контрпример.
Пусть
,
ас
равными вероятностями. Тогда если,
то корреляцияX
и Y
равна нулю. Однако, эти случайные величины
зависимы.

-Многомерное
нормальное распределение устойчивоотносительнолинейных
преобразований. Если,
а
A —
произвольная матрица размерности
m*n,
то

705.4Свойства производящих функций, примеры их вычисления.

Производящая
функция

Производящая
функция
— способ задания вероятностных
распределений. Используется чаще всего
для вычисления моментов.

Пусть
есть случайная величина X
с распределением .
Тогда её производящей функцией моментов
называется функция, имеющая вид

Пользуясь
формулами для вычисления математического
ожидания, определение производящей
функции моментов можно переписать в
виде:

то
есть производящая функция моментов —
это двустороннее преобразование Лапласа
распределения случайной величины (с
точностью до отражения).

Свойства
производящих функций моментов

Свойства
производящих функций моментов во многом
аналогичны свойствам характеристических
функций в силу похожести их определений.

Производящая
функция моментов однозначно определяет
распределение. Пусть X,Y
суть две случайные величины, и .
Тогда .
В частности, если обе величины абсолютно
непрерывны, то совпадение производящих
функций моментов влечёт совпадение
плотностей. Если обе случайные величины
дискретны, то совпадение производящих
функций моментов влечёт совпадение
функций вероятности.
Производящая
функция моментов как функция случайной
величины однородна:

Производящая
функция моментов суммы независимых
случайных величин равна произведению
их производящих функций моментов. Пусть

суть независимые случайные величины.
Обозначим .
Тогда

Пример: Производящая
функция чисел Белла.

Альтернативный
вариант ответа

Пусть
существует X-
случайная величина дискретного типа,
то есть принимает значения
гдеX
целочисленное 0,1,2,…,k
с вероятностями p₀,p₁,…p_k,
тогда производящей функцией мы называем
,

где
Z-
комплексная переменная, а X
– случайная величина.

Свойства
производящих функций:

3)Возьмем
—
разложим в ряд Тейлора в точке (0).сравним (1) и (2).

31//По
производящей функции можно восстановить
вероятности p_k.

Если
от
в
(1) брать производные так какприможно брать любые производные.

при
Z>1
тогда при Z=1

Необходимо,
чтобы правая часть была конечна.

Частный
случай:

5)
Если Y=aX+b
то
(следует
из определения)

6)
Если случайные величины X,Y
–независимы, то

где
независимы.

Пример:

Вычислить
производящую функцию распределения
Пуассона.

Случайная
величина принимает значения.

где
k=0,1,2,…

тогда

где

Следствие:

Пусть
-n
– независимых случайных величин, которые
имеют распределение Пуассона c
параметром
., тогдаY
тоже имеет распределение Пуассона с
параметром
.

Мы
получили

Пусть. Найти закон распределения, который
соответствует данной производящей
функции.

если
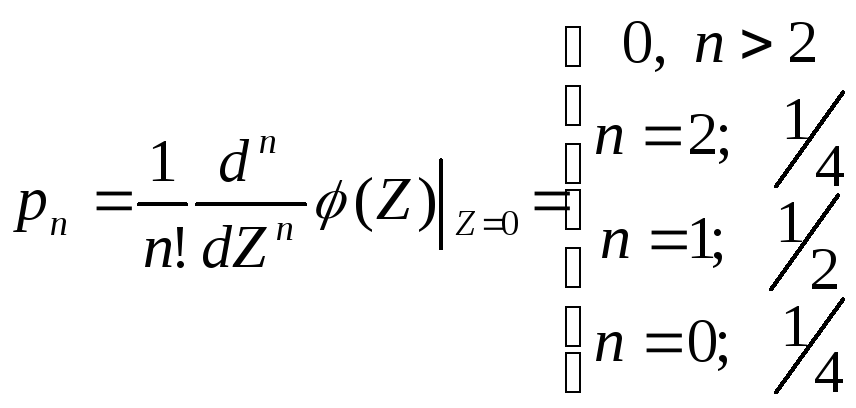
n>2;
то производная 0

Случайная
величина принимает значение 0, 1, 2, с
вероятностями

Производящая
функция называется производящей
функцией момента (т.к. м. вычислить
момент).

Вычислить
для распределения Пуассона с параметром.

Для
распределения Пуассона получим формулу.

Источник

Производя́щая фу́нкция моме́нтов — способ задания вероятностных распределений. Используется чаще всего для вычисления моментов.

Определение

Пусть есть случайная величина с распределением ${displaystyle mathbb {P} ^{X}}$ . Тогда её производящей функцией моментов называется функция, имеющая вид

${displaystyle M_{X}(t)=mathbb {E} left[e^{tX}right]}$

${displaystyle M_{X}(t)=int limits _{-infty }^{infty }e^{tx},mathbb {P} ^{X}(dx)}$

Дискретные и абсолютно непрерывные случайные величины

Если случайная величина дискретна, то есть ${displaystyle mathbb {P} (X=x_{i})=p_{i},;i=1,2,ldots }$ , то

${displaystyle M_{X}(t)=sum _{i=1}^{infty }e^{tx_{i}},p_{i}}$

Пример. Пусть имеет распределение Бернулли. Тогда

${displaystyle M_{X}(t)=e^{tcdot 1}cdot p+e^{tcdot 0}cdot q=pe^{t}+q}$

Если случайная величина абсолютно непрерывна, то есть она имеет плотность ${displaystyle f_{X}(x)}$ , то

${displaystyle M_{X}(t)=int limits _{-infty }^{infty }e^{tx},f_{X}(x),dx}$

Пример. Пусть имеет стандартное непрерывное равномерное распределение. Тогда

${displaystyle M_{X}(t)=int limits _{0}^{1}e^{tx}cdot 1,dx=left.{frac {e^{tx}}{t}}rightvert _{0}^{1}={frac {e^{t}-1}{t}}}$

Cвойства производящих функций моментов

${displaystyle M_{aX}(t)=M_{X}(at),;forall ain mathbb {R} }$

${displaystyle M_{S_{n}}(t)=prod limits _{i=1}^{n}M_{X_{i}}(t)}$

Вычисление моментов

${displaystyle mathbb {E} left[X^{n}right]=left.{frac {d^{n}}{dt^{n}}}M_{X}(t)rightvert _{t=0}}$

См. также

Моменты случайной величины;
Характеристическая функция случайной величины.

he:פונקציה יוצרת מומנטים
nl:Momentgenererende functie
pl:Funkcja tworząca momenty
su:Fungsi nu ngahasilkeun momen

Источник