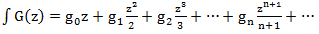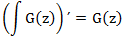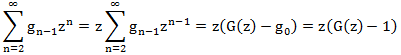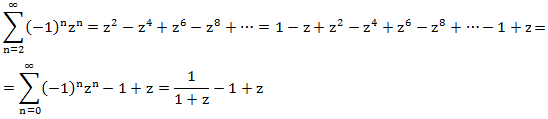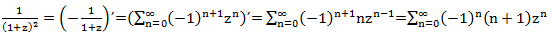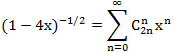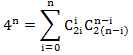Производящие функции — туда и обратно
Время на прочтение
9 мин
Количество просмотров 95K
«Производящая функция является устройством, отчасти напоминающим мешок. Вместо того чтобы нести отдельно много предметов, что могло бы оказаться затруднительным, мы собираем их вместе, и тогда нам нужно нести лишь один предмет — мешок».
Д. Пойа
Введение
Математика делится на два мира — дискретный и непрерывный. В реальном мире есть место и для того и для другого, и часто к изучению одного явления можно подойти с разных сторон. В этой статье мы рассмотрим метод решения задач с помощью производящих функций — мостика ведущего из дискретного мира в непрерывный, и наоборот.
Идея производящих функций достаточно проста: сопоставим некоторой последовательности <g0, g1, g2, …, gn> — дискретному объекту, степенной ряд g0 + g1z + g2z2 +… + gnzn +… — объект непрерывный, тем самым мы подключаем к решению задачи целый арсенал средств математического анализа. Обычно говорят, последовательность генерируется, порождается производящей функцией. Важно понимать, что это символьная конструкция, то есть вместо символа z может быть любой объект, для которого определены операции сложения и умножения.
История возникновения производящих функций
Известно, что начало методу производящих функций положил английский математик Абрахам де Муавр, а дальнейшему развитию и продолжению данного метода мы обязаны великому математику, имя которого Леонард Эйлер.
В 50-х годах XVIII века Эйлер решал следующую задачу: какие грузы можно взвесить с помощью гирь в 20, 21, 22,…, 2n грамм и сколькими способами? При решении этой задачи он использовал никому неизвестный на то время метод производящих функций, которому и посвящена данная статья. К этой задаче мы вернёмся немного позже, после того как разберёмся более подробно с устройством производящих функций.
Метод производящих функций
Изучение этого мощного механизма позволяющего решать многие задачи, мы начнём с простенькой задачи: сколькими способами можно расположить в линию чёрные и белые шары, общее количество которых равно n?
Обозначим белый шар символом ○, чёрный — ●, Tn — искомое количество расположений шаров. Символом Ø — обозначим нулевое количество шаров. Как и любое решение комбинаторной задачи начнём с тривиальных случаев:
Если n=1, то очевидно имеется 2 способа — взять либо белый шар ○, либо взять чёрный шар ●, таким образом, T2 = 2.
Если n=2, то имеется 4 способа расположений: ○○, ○●, ●○, ●●.
Рассмотрим случай для n=3. Мы можем начать белым шаром и продолжить 4-мя комбинациями, описанными выше ○○○, ○○●, ○●○, ○●●, или же мы можем начать чёрным шаром и аналогично продолжить 4-мя шарами ●○○, ●○●, ●●○, ●●●.
В итоге количество шаров удвоилось, то есть T3 = 2T2. Аналогично T4 = 2T3, то есть, обобщая для всех n, получаем рекуррентное уравнение Tn = 2Tn-1 которое и является решением для данной задачи. Решение такого уравнения можно легко угадать — Tn = 2n (так как 2⋅2n-1 = 2n).
А что если у нас плохо с угадыванием? И что делать, если уравнение будет сложнее? А вообще причём здесь производящие функции?
«Просуммируем» все возможные комбинации расположений шаров:
G = Ø + ○ + ● + ○○ + ○● + ●○ + ●● + ○○○ + ○○● + ○●○ + ○●● + ●○○ + ●○● + ●●○ + ●●● +…
Вопрос о допустимости такой нелепой на первый взгляд суммы опустим. Будем складывать и умножать последовательности шаров. Со сложением всё понятно, но что значит умножить одну последовательность шаров на другую? Перемножив ○● на ●○ мы получим не что иное как ○●●○. Заметим, однако, что произведение шаров в отличие от произведения чисел не является коммутативным, так как ○●⋅●○ ≠ ●○⋅○●. Символ Ø — в произведении играет роль мультипликативной единицы, то есть Ø ⋅ ○○● = ○○● ⋅ Ø = ○○● и коммутирует с любой последовательностью шаров.
Производя с рядом G последовательность манипуляций, а именно вынося за скобки левый белый и чёрный шары
G = Ø + ○ (Ø + ○ + ● + ○○ + ○● + ●○ + ●● + …) + ● (Ø + ○ + ● + ○○ + ○● + ●○ + ●● + …) = Ø + ○G +●G
получим уравнение G = Ø + ○G +●G.
Несмотря на то, что умножение некоммутативно, и мы фактически не различаем левое и правое деление, попробуем всё же «решить» это уравнение, на свой страх и риск. Получим,
Учитывая формулу суммы геометрической прогрессии 
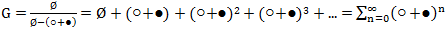
В этой сумме так же учтены все возможные варианты разбиения в точности по одному разу. Далее воспользуемся формулой бинома Ньютона: 

Коэффициент при ○k ●n-k равный числу сочетаний из n по k, показывает общее количество последовательностей из n шаров содержащих ○ шары в количеств k штук и ● шары в количестве n-k штук. Таким образом, общее количество расположений n шаров есть сумма по всем возможным значениям k. Как известно 
Эту формулу можно было получить непосредственно из 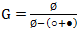
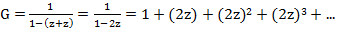
Обсуждение метода
Так что же позволяет данному методу быть работоспособным при решении различных задач?
Алгоритм решения задачи можно описать примерно следующим образом: рассматривается некоторая бесконечная сумма, которая в конечном итоге представляет собой формальный степенной ряд G(z) = g0 + g1z + g2z2 +… + gnzn +… причем коэффициенты gk (не заданные в явном виде) — являются ключом к решению исходной задачи. То, что ряд является формальным, говорит о том, что z — является просто символом, то есть вместо него может быть любой объект: число, шар, кость домино и т.д. В отличие от степенных рядов в анализе формальным степенным рядам не придается числовых значений и, соответственно, нет смысла говорить о сходимости таких рядов для числовых аргументов.
G(z) = g0 + g1z + g2z2 +… + gnzn +… — называется производящей функцией для последовательности <g0, g1, g2, …, gn>. Заметим, однако, что хотя G(z) — функция, это всё таки формальная запись, то есть мы не можем подставить вместо z любое значение z = z0, за исключением z = 0, так как G(0) = g0.
Затем производя различные преобразования с бесконечной суммой G(z) мы преобразуем её к замкнутому (компактному) виду. То есть у производящей функции есть 2 представления: бесконечное и замкнутое и, как правило, для решения задачи необходимо бесконечный вид преобразовать к замкнутому, а затем замкнутый вид разложить в степенной ряд, и тем самым получить значения для коэффициентов gk.
Отвечая на поставленный вначале вопрос можно сказать так: успех данного метода связан с возможностью записать производящую функцию в замкнутом виде. Так, например, производящая функция для последовательности <1, 1, 1, …, 1> в бесконечном виде представляется как 1 + x + x2 + x3 + …, а в замкнутом 
А теперь вооружившись знаниями, вернемся к задаче, которую решал Эйлер.
Итак, задача звучит следующим образом: какие грузы можно взвесить с помощью гирь в 20, 21, 22,…, 2n грамм и сколькими способам?
Я не знаю, как долго Эйлер придумывал решение для этой задачи, но оно поражает своей неожиданностью. Посудите сами. Эйлер рассматривает произведение G(z) = (1+z)(1+z2)(1+z4)… которое после раскрытия скобок представляется в виде бесконечного ряда G(z) = 1 + g1z + g2z2 + g3z3 +….
Что же из себя представляют коэффициенты gk? Каждый gk — это коэффициент при zk, а zk — получается как произведение каких-то одночленов z2m, то есть gk — это в точности число разных представлений числа k в виде суммы некоторых из чисел 1, 2, 22, 23,…, 2m,…. Другими словами gk — это число способов взвешивания груза в k грамм заданными гирями. Как раз то, что мы искали!
Следующий шаг Эйлера поражает не менее предыдущего. Он умножает обе части равенства на (1-z).
(1-z)G(z) = (1-z)(1+z)(1+z2)(1+z4)(1+z8)…
(1-z)G(z) = (1-z2)(1+z2)(1+z4)(1+z8)…
(1-z)G(z) = (1-z4)(1+z4)(1+z8)…
(1-z)G(z) = 1
С одной стороны G(z) = 1 + g1z + g2z2 + g3z3 +… с другой стороны мы только что получили 

Решение рекуррентных соотношений
Производящие функции подходят для решения не только комбинаторных задач. Оказывается, с их помощью можно решать рекуррентные соотношения.
Начнем со всеми знакомой последовательностью чисел Фибоначчи. Каждый из нас знает её рекуррентный вид: F0 = 0, F1 = 1, Fn = Fn-1 + Fn-2, n ≥ 2. Однако не каждый знает вид этой формулы в замкнутом виде и это не удивительно, ведь она содержит иррациональное число(«золотое сечение») в своём составе.
Итак, имеем
F0 = 0,
F1 = 1,
Fn = Fn-1 + Fn-2, n ≥ 2
Умножим каждую строчку на z0, z1, …, zn соответственно:
z0 ⋅ F0 = 0,
z1 ⋅ F1 = z,
zn ⋅ Fn = zn ⋅ Fn-1 + zn ⋅ Fn-2, n ≥ 2
Просуммируем эти равенства:
Обозначим левую часть
Рассмотрим каждое из слагаемых в правой части:
Имеем следующее уравнение G(z) = z + z G(z) + z2 G(z) решая которое относительно G(z) находим
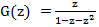
Разложим её на сумму простейших дробей, для этого найдем корни уравнения 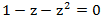
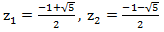
Следующим шагом является нахождение коэффициентов a и b. Для этого умножим дроби на общий знаменатель:
Подставляя в это уравнение значение z = z1 и z = z2, находим
Напоследок немного преобразуем выражение для производящей функции
Теперь каждая из дробей представляет собой сумму геометрической прогрессии.
По формуле 
Но ведь мы искали G(z) в виде 
Эту формулу можно переписать в другом виде не используя «золотое сечение»:
что достаточно трудно было ожидать, учитывая красивое рекуррентное уравнение.
Давайте запишем общий алгоритм решения рекуррентных уравнений, используя производящие функции. Он записывается в 4 шага:
- Запишите одно уравнение, выражающее gn через другие элементы последовательности. Это уравнение должно оставаться справедливым для всех целых n с учетом того, что g-1=g-2=….=0.
- Умножьте обе части уравнения на zn и просуммируйте по всем n. В левой части получится сумма
, которая равна производящей функции G(z). Правую часть следует преобразовать так, чтобы она превратилась в какое-то другое выражение, включающее G(z).
- Решите полученное уравнение, получив для G(z) выражение в замкнутом виде.
- Разложите G(z) в степенной ряд и прочитайте коэффициент при zn, это и будет замкнутый вид для gn.
Причина, по которой данный метод работает, заключается в том, что единая функция G(z) представляет всю последовательность gn и это представление допускает многие преобразования.
Прежде чем переходить к следующему примеру, рассмотрим 2 операции, совершаемые над производящими функциями, которые часто оказываются полезными.
Дифференцирование и интегрирование производящих функций
Для производящих функций обычное определение производной можно записать следующим образом.
Пусть G = G(z) – производящая функция. Производной этой функции называется функция 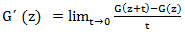
Тем самым, действие дифференцирования на произвольной производящей функции
G (z) = g0 + g1z + g2z2 + g3z3 +… дает G΄(z) = g1 + 2g2z + 3g3z2 + 4g4z3 +….
Интегралом называется функция
Операция дифференцирования обратна операции интегрирования:
Операция же интегрирования производной приводит к функции с нулевым свободным членом, и поэтому результат, отличается от исходной функции,
Нетрудно заметить, что для функций, представимых в виде степенных рядов, формула для производной соответствует обычной. Формула для интеграла соответствует значению интеграла с переменным верхним пределом
Используя только что полученные знания о дифференцировании и интегрировании производящих функций, попробуем решить следующее рекуррентное уравнение:
g0 = 1,
g1 = 1,
gn = gn-1 + 2gn-2 + (-1)n
Будем следовать вышеописанному алгоритму. Первое условие алгоритма выполнено. Умножим обе части всех равенств на z в соответствующей степени и просуммируем:
z0⋅ g0 = 1,
z1 ⋅ g1 = z,
zn ⋅ gn = zn ⋅ gn-1 + 2zn ⋅ gn-2 + (-1)n ⋅ zn
Левая часть 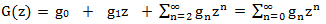
Попытаемся выразить правую часть через G(z). Рассмотрим каждое слагаемое:
Составляем уравнение:
Это и есть производящая функция для заданного рекуррентного уравнения. Раскладывая её на простейшие дроби (например, методом неопределенных коэффициентов или методом подстановки различных значений z), получаем:
Второе и третье слагаемые легко раскладываются в степенной ряд, а вот с первым придется чуть повозиться. Используя правило дифференцирования производящих функций имеем:
Собственно всё. Раскладываем каждое слагаемое в степенной ряд и получаем ответ:
С одной стороны мы искали G(z) в виде 
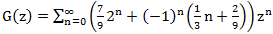
Значит, 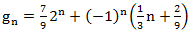
Вместо заключения
Производящие функции нашли большое применение в математике, поскольку являются мощным оружием при решении многих практических задач, связанных, например, с перечислением, распределением и разбиением множеств объектов различной природы. Кроме того применение производящих функций позволяет доказать некоторые комбинаторные формулы, которые иначе получить очень трудно. Например, разложение функции 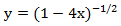

Возводя в квадрат обе части этого равенства получим
Приравнивая коэффициенты при xn в левой и правой частях, получаем
Эта формула имеет прозрачный комбинаторный смысл, но доказать её непросто. Еще в 80-е годы XX века появились публикации, посвященный этому вопросу.
| Определение: |
| Производящая функция (англ. generating function) — это формальный степенной ряд вида , порождающий (производящий) последовательность . |
Метод производящих функций был разработан Эйлером в 1750-х годах.
Содержание
- 1 Применение
- 2 Примеры производящих функций
- 3 Примеры решений задач методом производящих функций
- 3.1 Решение рекуррентных соотношений
- 3.2 Расчет дисперсии геометрического распределения
- 3.3 Пример задачи на нахождение производящей функции
- 4 Приложения
- 4.1 Примеры простых производящих функций
- 5 См. также
- 6 Примечания
- 7 Источники информации
Применение
Производящая функция используется для:
- Компактной записи информации о последовательности.
- Нахождения зависимости для последовательности , заданной рекуррентным соотношением. Например, для чисел Фибоначчи.
- Нахождения рекуррентного соотношения для последовательности — вид производящей функции может помочь найти формулу.
- Исследования асимптотического поведения последовательности.
- Доказательства тождеств с последовательностями.
- Решения задачи подсчета объектов в комбинаторике. Например, в доказательстве пентагональной теоремы или в задаче нахождения количества расстановок ладей на доске .
- Вычисления бесконечных сумм.
Примеры производящих функций
Рассмотрим производящие функции для различных комбинаторных последовательностей:
- — производящая функция для разности количества разбиений числа в четное и нечетное число различных слагаемых. Например, коэффициент при равен , потому что существует два разбиения на четное число различных слагаемых и одно на нечетное (). Правильность этого легко осознать, если понять, что каждая скобка представляет какое-то слагаемое и мы можем его взять (второе слагаемое — ) или не взять (первое — ). Эта производящая функция используется в комбинаторном доказательстве пентагональной теоремы.
- — производящая функция для последовательности , где — число разбиений числа на слагаемые.
- — производящая функция для последовательности , где — число разбиений на различные слагаемые.
- — производящая функция для последовательности , где — число разбиений на нечётные слагаемые. С помощью метода производящих функций можно доказать, что производящие функции последовательностей равны, соответственно :
Примеры решений задач методом производящих функций
Решение рекуррентных соотношений
Существует целый класс последовательностей, задаваемых рекуррентным соотношением, например, — числа Фибоначчи или —
числа Каталана. Метод производящих функций позволяет получить выражение для через номер элемента в последовательности в замкнутом виде, то есть в таком виде, что выражение можно вычислить, предполагая, что достаточно мало.
Пусть последовательность удовлетворяет некоторому рекуррентному соотношению. Мы хотим получить выражение для (при ) в замкнутом виде. Алгоритм получения замкнутого выражения для чисел , удовлетворяющих рекуррентному соотношению, с помощью производящих функций состоит из 4 шагов:
- Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен , то есть количество предшествующих элементов, требуемых для вычисления элемента с номером , равно ):
- Домножить каждую строчку на в соответствующей степени и просуммировать строчки для всех .
- В полученном уравнении привести все суммы к замкнутому виду. Получить уравнение для производящей функции.
- Выразить в явном виде (решить уравнение, полученное на предыдущем шаге) и разложить производящую функцию в ряд по степеням .
Для демонстрации универсальности метода рассмотрим довольно произвольное рекуррентное соотношение:
Запишем производящую функцию для этой последовательности и преобразуем правую часть:
Для того, чтобы замкнуть последнюю сумму воспользуемся очень важным приемом, который используется при преобразовании производящих функций. Фактически мы имеем дело с последовательностью (в нашем случае последовательность ). Такая последовательность получается путём дифференцирования функции , производящей для , с последующим умножением результата на :
Тогда замкнем последнее слагаемое следующим образом:
Таким образом, наше последнее слагаемое примет вид:
Это уравнение для производящей функции. Из него выражаем :
Разложим знаменатель на множители и разобьём дробь на сумму простых дробей [1]:
Разложим первое слагаемое в ряд, используя расширенные биномиальные коэффициенты [2]:
Расчет дисперсии геометрического распределения
Метод производящих функций также используется для нахождения математического ожидания и дисперсии различных распределений в теории вероятностей. Например, в геометрическом распределении [3] для нахождения дисперсии нужно найти два мат. ожидания:
которые фактически являются производящими функциями последовательностей и :
.
Тогда:
Пример задачи на нахождение производящей функции
| Задача: |
| Рассмотрим множество путей на прямой, состоящих из шагов длины вправо и влево. Найдите производящую функцию для числа таких путей из шагов, начинающихся в и оканчивающихся в . |
Заметим, что для того, чтобы закончить путь в , необходимо совершить равное число шагов вправо и влево. Тогда задача сводится к тому, чтобы выбрать позиций для, например, шагов вправо из всего шагов. Тогда ответом будет сумма от нуля до бесконечности по всех . То есть:
Рассмотрим , где — число Каталана. Тогда, заметим что . Так как , то справедливо равенство:
Мы знаем, что производящая функция для чисел Каталана равна . Найдем .
Соответственно, ответом будет производящая функция вида:
| Задача: |
| Рассмотрим множество путей на прямой, состоящих из шагов длины вправо и влево. Найдите производящую функцию для числа таких путей из шагов, начинающихся и оканчивающихся в и не заходящих в отрицательную полупрямую. |
Заметим, что задача аналогична Правильной скобочной последовательности. Тогда производящей функцией для нашей задачи будет производящая функция для правильной скобочной последовательности, а именно:
Приложения
Примеры простых производящих функций
На последнем шаге приведения производящей функции к замкнутому виду требуется разложить полученные слагаемые в ряд. Для этого можно воспользоваться таблицей основных производящих функций [4].
Все суммы выполняются по переменной от до . Элементы последовательности нумеруются от .
| Последовательность | Производящая функция в виде ряда | Производящая функция в замкнутом виде |
| ( нулей в начале) | ||
| (повторяется через ) | ||
См. также
- Производящая функция Дирихле
Примечания
- ↑ О разложении рациональной функции в ряд
- ↑ Расширенные биномиальные коэффициенты
- ↑ Геометрическое распределение
- ↑ Таблица производящих функций
Источники информации
- Вайнштейн Ф., Разбиение чисел. Журнал «Квант» № 11, 1988 год
- Производящие функции
- Wikipedia — Generating function
- Нахождение количества разбиений числа на слагаемые. Пентагональная теорема Эйлера
- Graham, Knuth, and Patashnik: Concrete Mathematics
Метод
рекуррентных соотношений позволяет
решать многие комбинаторные задачи. Но
в ряде случаев рекуррентные соотношения
трудно составить, а иногда ещё трудней
решить. Часто эти трудности удается
обойти, используя производящие функции.
Понятие производящей функции тесно
связано с понятием бесконечного
степенного ряда.
Здесь
необходимо знать: понятие ряда, сумма
ряда, степенной ряд, сходимость степенных
рядов, свойства сходящихся рядов,
операции над ними. Эти понятия изложены
в любом учебнике по математическому
анализу, и мы их опускаем.
Определение
1: Пусть
дана числовая последовательность:
.
Образуем степенной ряд с этими
коэффициентами:.
Если этот ряд сходится в некоторой
области к функции,
то эту функцию называютпроизводящей
для последовательности чисел
.
Примеры: 1)
Для степенного ряда
,
члены которого можно рассматривать как
геометрическую прогрессию, знаменатель.
Значит, степенной ряд при условиисходится к своей сумме
.
Таким образом, получаем:
,
если.
Значит,
функция
является производящей для последовательности
чисел(коэффициенты степенного ряда).
2) Аналогично
можно получить:
.
Значит,
функция
является производящей для последовательности
чисел.
3)
Из формулы бинома Ньютона следует:
,
т.е.
функция
является производящей для чисел вида
,
где.
С
помощью последней производящей функции
можно доказать некоторые свойства чисел
,
т. е. для биномиальных коэффициентов.
Например:
;
;
(здесь
обе суммы конечны и обрываются, когда
значения
и
станут больше
).
Кроме того:
,
,
.
В
последнем равенстве, если
,
то считают, что.
Поэтомуменяется от
до наименьшего из чисел
,
.
Последнее
равенство можно доказать следующим
образом:
,
.
Отсюда
следует: .
Применяя
в левой части формулу биному Ньютона и
раскрывая скобки в правой части,
приравниваем коэффициенты при одинаковых
степенях
,
получаем требуемую формулу.
В
частном случае, когда
,
получаем равенство:
,
.
Проиллюстрируем
на примерах применение производящих
функций к решению некоторых комбинаторных
задач.
1)
Рассмотрим разбиение числа
на слагаемые, каждое из которых равно
одному из чисел.
При этом слагаемые не повторяются и их
порядок не играет роли.
Для
решения задачи рассмотрим выражение
.
Раскрывая скобки, получим слагаемые
вида,
где– некоторые из чисел
.
Поэтому
встретится
в сумме столько раз, сколькими способами
можно разбить
на слагаемые требуемым образом.
Например,
если надо узнать, сколькими способами
можно заплатить 78 копеек, беря не более
одной монеты каждого достоинства, то
надо составить выражение:
,
раскрыть
скобки и найти коэффициент при слагаемом
.
2)
Если требуется разложить число
на слагаемые
,
каждое из которых может встречаться в
разложении один или несколько раз, тогда
количество слагаемых в скобках
увеличивается.
Например: 1)
Сколькими способами можно заплатить
29 коп., используя монеты по 2 и 5 коп?
Т.е.
надо найти число способов разбить число
29 на слагаемые, равные 2 и 5, причем порядок
слагаемых роли не играет, и каждое
слагаемое может повторяться несколько
раз. Для этого составим выражение:
.
Ясно,
что при раскрытии скобок выражение
войдет в разложение с коэффициентом,
равным числу решений уравнения
.
В частности, коэффициент при
дает ответ на вопрос задачи.
Вместо
раскрытия скобок можно поступить иначе:
составить производящую функцию. Эта
функция представляет собой произведение
двух дробей:
.
Разделив
«уголком» числитель на знаменатель,
находим коэффициент при выражении
.
2)
Поступающий в ВУЗ должен сдать 4 экзамена,
причем для поступления достаточно
набрать 17 балов. Сколькими способами
абитуриент может сдать экзамены, чтобы
поступить в ВУЗ?
Требуется
узнать, сколькими способами можно
представить число 17 в виде суммы 4-х
слагаемых, принимающих значения 3, 4, 5,
причем здесь порядок слагаемых имеет
значение.
Для
решения этой задачи можно взять
производящую функцию
.
При раскрытии скобок каждое слагаемоевстретится столько раз, сколькими
способами можноразбить на сумму 4-х слагаемых, принимающих
значения 3, 4 и 5. При этом встречаются
члены, получаемые друг из друга
перестановкой слагаемых.
В
выражении
можно раскрыть скобки по полиномиальной
теореме, а можно следующим образом:
.
Поэтому
.
.
Перемножая
почленно эти выражения, найдем, что
коэффициент при
равен 16. Значит, разложение можно сделать
16 способами.
Между
производящими функциями и рекуррентными
соотношениями существует тесная связь.
Пусть
— производящая функция для последовательности
чисел.
Это означает, чтоявляется суммой степенного ряда:
.
Пусть
– многочлены, причем
и
,
значит, дробь
– правильная (в противном случае можно
выделить целую часть). Раскладывая дробь
в ряд, получим:
.
Раскрывая
скобки справа и приравнивая коэффициенты
при одинаковых степенях
,
получаем:
При
считаем, что
.
А дальше все соотношения имеют вид:,
где,
т.к.не
имеет членов степени
,
,
…
Таким
образом, коэффициенты ряда
,
,…
удовлетворяют рассмотренному рекуррентному
соотношению. Коэффициенты этого
соотношения зависят только от знаменателя
дроби. Числитель нужен только для
нахождения первых членоврекуррентной
последовательности.
Обратно,
если задано рекуррентное соотношение
и заданы члены
,
то, вычисляя значения,
получим производящую функциюдля последовательности чисел
.
Полученную
алгебраическую дробь можно разлагать
на элементарные дроби и производить
алгебраические преобразования.
Соседние файлы в папке 26-03-2013_00-36-55
- #
- #
- #
- #
Таблица производящих функций
В таблице указаны основные производящие
функции, которые обычно требуются
для решения типичных задач.
Все суммы
∑
выполняются по переменной
n
от
0 до
∞, если
не указано иное.
Элементы последовательности нумеруются от
0.

Доказательство
Предлагаемые для рассмотрения
производящие функции являются своего рода
«азбукой», или, если угодно,
«таблицей умножения» для
теории производящий функций.
Понимание
этих производящих функций
позволит работать
с более сложными выражениями,
а знание таблицы ускорит
многие устные вычисления.
Первая и вторая производящие функции
выводятся непосредственно из определения
(см. «Введение»).
Третья последовательность
подробно разбирается в приложении
«О разложении 1/(1−z)».
Производящая функция последовательности №4
получается заменой
z на
−z
в функции для последовательности №3.
Аналогично получаются
производящие функции для последовательностей
№5, №7 и №8: нужно заменить
в третьей производящей функии
z на
zm,
2z и
rz соответственно.
Производящая функция последовательности №6
получается путём дифференцирования
функции №3:

Точно такой же результат получается, если
использовать биномиальный ряд
(см. «Расширенные биномиальные коэффициенты»):

Совершенно аналогично нужно поступить с
производящей функцией последовательностей
№10 и №11:

если теперь заменить m на
m+1
и использовать тот факт,
что для целых положительных
n
справедливо тождество
,
то получим одиннадцатую строку таблицы:

Последовательность №9
и производящая функция для неё
следуют из биномиальной теоремы
(после замены a
на z,
а b на 1 ),
утверждение которой доказывается
в курсе комбинаторики:

Производящая функция для последовательности №12
получается интегрированием производящей
функции для последовательности №3
(полагаем, что константа интегрирования равна нулю,
чтобы выполнялось a0=0):

Последовательность №13 получается
аналогично, но c
дополнительной заменой
z на −z
и умножением результата на
−1.
Разложение в ряд экспоненты (строка №14 таблицы) известно
из курса математического анализа.
По формуле Тейлора коэффициент при
zn равен производной порядка
n,
вычисленной в нуле, поделённой на
n!:

Причём ряд для экспоненты сходится
для любого комплексного
z
(если, конечно, считать, что z — число).

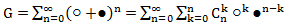

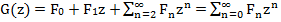
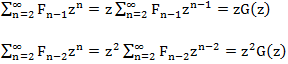

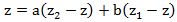

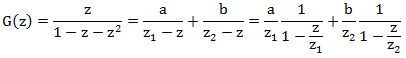
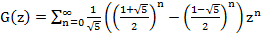

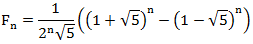
 , которая равна производящей функции G(z). Правую часть следует преобразовать так, чтобы она превратилась в какое-то другое выражение, включающее G(z).
, которая равна производящей функции G(z). Правую часть следует преобразовать так, чтобы она превратилась в какое-то другое выражение, включающее G(z).