Время, скорость, расстояние
О чем эта статья:
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Формула пути
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
В цилиндрических координатах длина пути может быть выражена как:
В сферических координатах формулу длины пути запишем:
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением. Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds, который называют элементарным. При этом:
где $bar$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути $Delta s$ на отрезке времени от $t$ до $t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении $langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
Примеры решения задач
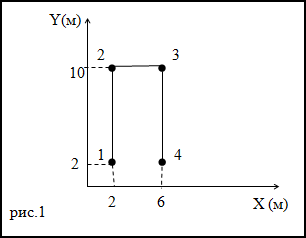
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой, чему равно перемещение, если точка двигалась 1-2-3-4.
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
Ответ. Путь равен 20 м, перемещение равно 4 м.
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией: x=-0,2t 2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения задачи примем формулу пути в виде:
Подставим в (2.1) функцию x=-0,2t 2 , учтем, что $0 c leq t leq 5 c$ имеем:
Как посчитать путь ускоряющегося тела не используя время
Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.
Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).
Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.
Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.
Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.
Выводим формулу пути без времени
Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.
В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону).
Сонаправленные или противоположно направленные векторы называют коллинеарными векторами. Прочитайте подробнее о коллинеарных векторах.
Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:
( large v_ <0>left( frac<text<м>> right)) – начальная скорость тела;
( large v left( frac<text<м>> right)) – конечная скорость;
( large a left( frac<text<м>>> right)) – ускорение тела;
( large S left( text <м>right)) – путь, пройденный телом;
(large t left( c right)) – время, за которое тело прошло этот путь.
В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.
Что сделать, чтобы получить формулу пути, в которой отсутствует время:
- сначала получить выражение для времени t из уравнения для скорости;
- затем в формулу пути подставить полученное выражение вместо времени t.
Выражаем время из формулы для скорости
Выпишем формулу, связывающую начальную и конечную скорость тела:
[ large v = v_ <0>+ a cdot t ]
Избавимся в правой части от начальной скорости, обозначенной символом ( v_<0>). Для этого из обеих частей уравнения вычтем число ( v_<0>). Получим такую запись:
[ large v — v_ <0>= a cdot t ]
Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». Для этого разделим обе части уравнения на «a»:
Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».
В формулу пути подставим выражение для времени
Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:
В первом уравнении системы будем заменять символ t дробью из второго уравнения. Тогда система из двух уравнений превратится в единственное уравнение. И в этом уравнении не будет символа t времени:
Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.
Упрощаем выражение, расположенное до знака «плюс» в правой части
Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:
Умножим числитель дроби на число (v_<0>).
- сначала числитель обособим скобками;
- затем запишем число (v_<0>) перед скобками;
- а потом внесем это число внутрь скобок.
В числитель дроби, обособленный с помощью скобок помещаем число (v_<0>):
Теперь необходимо умножить скобку на число (v_<0>). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.
Нужно к каждой скорости в скобках дописать число (v_<0>), умножая его на эти скорости. Получим такое выражение:
То есть, вместо первоначальной записи, мы получили такую запись:
Возводим в квадрат дробь
После знака «плюс» в правой части уравнения располагается дробь, которую нужно возвести в квадрат. Обратим внимание на эту дробь:
Правильно возвести дробь в степень поможет рисунок 3.
В результате возведения в квадрат дробь приобретет такой вид:
В числителе этой дроби находится выражение в скобках, которое нужно возвести в квадрат. И нам придется применить одну из формул сокращенного умножения. Запоминать формулы сокращенного умножения удобно в виде, приведенном на рисунке 4.
Используем для этого формулу сокращенного умножения, которая содержит знак «минус». Она называется «Квадрат разности». Тогда числитель дроби превратится в такую запись:
Теперь можем записать полученную дробь:
Упрощаем правую часть, записанную после знака «плюс»
Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:
Мы уже провели некоторые преобразования и можем теперь заменить дробь, возводимую в квадрат более подробной записью:
Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.
Итак, поменяем местами знаменатели дробей:
Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:
А перемножив числители и знаменатели двух дробей, получим такую запись:
Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:
Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».
Теперь, осталось сложить две дроби в правой части – дробь, записанную до знака «плюс» с дробью, записанной после знака «плюс». А чтобы эти дроби можно было сложить, нужно будет привести их к общему знаменателю.
Приводим к общему знаменателю дроби в правой части уравнения
Вернемся еще раз к первоначальному уравнению:
Заменим правую часть этого уравнения выражениями, которые мы получили:
Сравним знаменатели дробей.
Первая дробь обладает знаменателем «a», а вторая – «2a». Выберем число «2a» в качестве общего знаменателя обеих дробей.
Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:
Примечания:
- Нам известно, что если какое-либо число умножить на единицу, то после умножения это число не изменится. Значит, если какое-либо выражение умножить на единицу, то полученное выражение останется равным самому себе. На единицу можно умножать все, что угодно – дроби, выражения в скобках и т. п.
- Математики часто применяют прием умножения на единицу. А после этого единицу записывают в виде некоторой дроби. При этом используют правило: Единица – это дробь, у которой числитель и знаменатель равны (одинаковые).
Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:
Получим такую дробь:
Поместим ее в выражение для пути:
Дроби с одинаковыми знаменателями складываем
Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:
Раскроем скобки в числителе полученного выражения:
Примечание: Обратим внимание на то, что в числителе дважды встречается член (2v_ <0>v), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа (2v_<0>v) вычитается такое же число (2vv_<0>). В конце концов, это число покидает нашу запись и, она упрощается:
Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:
Вычтем подобные члены, содержащие ( v^<2>_<0>):
В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:
Примечания:
- Это формула, с помощью которой можно рассчитать путь тела, когда известны его начальная и конечная скорость, а, так же, ускорение.
- Видно, что время t в правой части этого выражения отсутствует.
- Мы выводили эту формулу для случая, когда тело увеличивало скорость.
Как выглядит формула пути без времени, когда скорость тела уменьшается
Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:
Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:
Выводы
Пусть нам известны начальная и конечная скорость тела и его ускорение. Тогда путь, пройденный телом, можно рассчитать так:
http://www.webmath.ru/poleznoe/formules_21_27_put.php
Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$
В цилиндрических координатах длина пути может быть выражена как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$
В сферических координатах формулу длины пути запишем:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением.
Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:
$$d s=|d bar{r}|=v d t$$
где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=vleft(t_{2}-t_{1}right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+frac{a t^{2}}{2}(7)$$
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 — 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:
$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$
Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c leq t leq 5 c$ имеем:
$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.
- Прямолинейное равномерное движение на координатной прямой
- Уравнение прямолинейного равномерного движения
- Удобная система отсчета для решения задачи о прямолинейном движении
- График движения x=x(t)
- Как найти уравнение движения по графику движения?
- График скорости vx=vx(t)
- Как найти путь и перемещение по графику скорости?
- Задачи
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.
Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin{gather*} x=x_0+s=x_0+vt\ x=20+10t end{gather*}
Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin{gather*} x=x_0-st=x_0-vt\ x=20-10t end{gather*} Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Основная задача механики – уметь определять положение тела в пространстве в любой момент времени.
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
Назовем проекцией вектора скорости (overrightarrow{x}) на параллельную ему ось координат OX величину (v_x=pm|overrightarrow{v}|=pm v).
Знак проекции определяется следующим правилом:
- если направление вектора (overrightarrow{v}) совпадает с направлением оси OX, то (v_x=vgt 0)
- если направление вектора (overrightarrow{v}) противоположно направлению оси OX, то (v_x=-vlt 0)
В любой момент времени t координата тела x(t) при прямолинейном равномерном движении описывается уравнением: $$ x(t)=x_0+v_x t $$ где (x_0) — координата в начальный момент времени, (v_x) — проекция вектора скорости движения.
Проекция перемещения (overrightarrow{r}) на параллельную ему ось координат OX в любой момент времени t определяется формулой: $$ triangle x=x(t)-x_0 $$ Знак (triangle x) указывает на направление совершенного перемещения:
- если (triangle xgt 0), перемещение (overrightarrow{r}) произошло в направлении оси OX;
- если (triangle xlt 0), перемещение (overrightarrow{r}) произошло противоположно направлению оси OX.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Прямолинейное движение описывается с помощью координатной прямой, параллельной направлению движения тела.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
В осях (t) и (x) график (x(t)=x_0+v_x t) является прямой.
Эта прямая:
- возрастает, если (v_xgt 0)
- убывает, если (v_xlt 0)
- постоянна (параллельна оси (t)), если (v_x= 0)
 |
Построим графики зависимости координаты от времени для нашего примера:
x=20+10t — машина движется вправо (в направлении оси OX) |
п.5. Как найти уравнение движения по графику движения?
Шаг 1. Выбрать на прямой любые две точки (A(t_1,x_1)) и (B(t_2,x_2)).
Шаг 2. Найти проекцию скорости как отношение: $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{triangle x}{triangle t} $$ Шаг 3. Найти начальную координату по одной из формул: $$ x_0=x_1-v_x t_1 text{или} x_0=x_2-v_x t_2 $$ Шаг 4. Записать найденное уравнение движения: $$ x(t)=x_0+v_x t $$
п.6. График скорости vx=vx(t)
В осях (t) и (x) график (v_x(t)=v_x=const) является прямой, параллельной оси (t).
Эта прямая:
- расположена над осью (t), если (v_xgt 0)
- расположена под осью (t), если (v_xlt 0)
- совпадает с осью (t), если (v_x=0)
Для рассмотренного примера:
Внимание!
В отличие от алгебры, в физике масштабы на осях, как правило, разные.
Поэтому обязательно нужно:
1) указывать обозначения и единицы измерения физических величин, которым соответствуют оси графика;
2) подбирать масштабы так, чтобы с графиком было удобно работать.
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:
На графике скорости путь, пройденный за промежуток времени (triangle t=t_2-t_1) равен площади прямоугольника, длина которого равна (triangle t), а ширина (triangle |v_x|): $$ s=|v_x|triangle t $$
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
На графике скорости проекция перемещения на ось OX за промежуток времени (triangle t=t_2-t_1) равна площади (v_xtriangle t), с учетом знака: $$ triangle x=v_xtriangle t $$
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin{gather*} x_1=x(5)=8cdot 5=40 text{(м)}\ x_2=x(10)=8cdot 10=80 text{(м)} end{gather*}
б) Скорость (v_x=8) м/с — постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text{(м)} $$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{56-38}{2-1}=18 (text{тыс.км/ч}) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text{тыс.км/ч}) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text{тыс.км}) $$
г) Переведем скорость в км/с: $$ 18000frac{text{км}}{text{ч}}=frac{18000 text{км}}{1 text{ч}}=frac{18000 text{км}}{3600 text{c}}=5 text{км/c} $$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в (XVI) веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путём. Формула выглядит следующим образом:
, где (а) — это ускорение.
Сравним графики равномерного и равноускоренного движения.
Графики прямолинейного равномерного движения
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость (a(t)) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график (v(t)) — прямая линия, параллельная оси времени.
Правило определения пути по графику (v(t)): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График (s(t)) — наклонная линия.
Рис. (1). График зависимости скорости от времени при равномерном прямолинейном движении
Рис. (2). График зависимости пути от времени при равномерном прямолинейном движении
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график (a(t)) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. Скорость изменяется согласно линейной зависимости.
Зависимость пути от времени. При равноускоренном движении путь изменяется согласно квадратной зависимости:
s=v0t+at22
. В координатах зависимость имеет вид:
x=x0+v0xt+axt22
.
Графиком является ветка параболы.
Рис. (3). График зависимости пути от времени при равноускоренном движении
Источники:
Рис. 1. График зависимости скорости от времени при равномерном прямолинейном движении. © ЯКласс.
Рис. 2. График зависимости пути от времени при равномерном прямолинейном движении. © ЯКласс.
Рис. 3. График зависимости пути от времени при равноускоренном движении. © ЯКласс.
Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.
Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).
Рис.1. Так выглядит формула, по которой можно вычислить путь тела, не зная, сколько времени занимало движение
Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.
Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.
Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.
Выводим формулу пути без времени
Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.
В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону).
Сонаправленные или противоположно направленные векторы называют коллинеарными векторами. Прочитайте подробнее о коллинеарных векторах.
Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:
[ large begin{cases} S = v_{0} cdot t + displaystylefrac{a}{2} cdot t^{2} \ v = v_{0} + a cdot t end{cases} ]
( large v_{0} left( frac{text{м}}{c} right)) – начальная скорость тела;
( large v left( frac{text{м}}{c} right)) – конечная скорость;
( large a left( frac{text{м}}{c^{2}} right)) – ускорение тела;
( large S left( text{м} right)) – путь, пройденный телом;
(large t left( c right)) – время, за которое тело прошло этот путь.
В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.
Что сделать, чтобы получить формулу пути, в которой отсутствует время:
- сначала получить выражение для времени t из уравнения для скорости;
- затем в формулу пути подставить полученное выражение вместо времени t.
Выражаем время из формулы для скорости
Выпишем формулу, связывающую начальную и конечную скорость тела:
[ large v = v_{0} + a cdot t ]
Избавимся в правой части от начальной скорости, обозначенной символом ( v_{0}). Для этого из обеих частей уравнения вычтем число ( v_{0}). Получим такую запись:
[ large v — v_{0} = a cdot t ]
Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». Для этого разделим обе части уравнения на «a»:
[ large frac{ v — v_{0}}{a} = t ]
Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».
В формулу пути подставим выражение для времени
Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:
[ large begin{cases} S = v_{0}cdot t + displaystyle frac{a}{2}cdot t^{2}\ displaystyle frac{v — v_{0}}{a} = t end{cases} ]
В первом уравнении системы будем заменять символ t дробью из второго уравнения. Тогда система из двух уравнений превратится в единственное уравнение. И в этом уравнении не будет символа t времени:
[large S = v_{0} cdot frac{ v — v_{0}}{a} + frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]
Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.
Упрощаем выражение, расположенное до знака «плюс» в правой части
Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:
[large v_{0} cdot frac{ v — v_{0}}{a} ]
Умножим числитель дроби на число (v_{0}).
Для этого:
- сначала числитель обособим скобками;
- затем запишем число (v_{0}) перед скобками;
- а потом внесем это число внутрь скобок.
В числитель дроби, обособленный с помощью скобок помещаем число (v_{0}):
[large v_{0} cdot frac{ (v — v_{0})}{a} = frac{ v_{0} cdot (v — v_{0})}{a} ]
Теперь необходимо умножить скобку на число (v_{0}). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.
Рис. 2. Чтобы умножить скобку на число, нужно умножить каждое слагаемое в скобке на это число
Нужно к каждой скорости в скобках дописать число (v_{0}), умножая его на эти скорости. Получим такое выражение:
[large frac{ v_{0} cdot (v — v_{0})}{a} = frac{ (v_{0} cdot v — v_{0} cdot v_{0})}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} ]
То есть, вместо первоначальной записи, мы получили такую запись:
[large v_{0} cdot frac{ (v — v_{0})}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} ]
Возводим в квадрат дробь
После знака «плюс» в правой части уравнения располагается дробь, которую нужно возвести в квадрат. Обратим внимание на эту дробь:
[large left( frac{ v — v_{0}}{a} right)^{2}]
Правильно возвести дробь в степень поможет рисунок 3.
Рис. 3. Дробь возводим в степень, отдельно возводя в эту степень ее числитель и знаменатель
В результате возведения в квадрат дробь приобретет такой вид:
[large left( frac{ v — v_{0}}{a} right)^{2} = frac{ (v — v_{0})^{2}}{a^{2}}]
В числителе этой дроби находится выражение в скобках, которое нужно возвести в квадрат. И нам придется применить одну из формул сокращенного умножения. Запоминать формулы сокращенного умножения удобно в виде, приведенном на рисунке 4.
Рис. 4. Удобный для запоминания вид формул сокращенного умножения
Используем для этого формулу сокращенного умножения, которая содержит знак «минус». Она называется «Квадрат разности». Тогда числитель дроби превратится в такую запись:
[large ( v — v_{0})^{2} = (v^{2} + v^{2}_{0} — 2vv_{0})]
Теперь можем записать полученную дробь:
[large frac{ (v — v_{0})^{2}}{a^{2}} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}} ]
Упрощаем правую часть, записанную после знака «плюс»
Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:
[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]
Мы уже провели некоторые преобразования и можем теперь заменить дробь, возводимую в квадрат более подробной записью:
[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2} = frac{a}{2} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}}]
Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.
Итак, поменяем местами знаменатели дробей:
[large frac{a}{2} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}} = frac{a}{a^{2}} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2}]
Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:
[large frac{a}{a^{2}} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2} = frac{1}{a} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2}]
А перемножив числители и знаменатели двух дробей, получим такую запись:
[large frac{1}{a} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:
[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».
Теперь, осталось сложить две дроби в правой части – дробь, записанную до знака «плюс» с дробью, записанной после знака «плюс». А чтобы эти дроби можно было сложить, нужно будет привести их к общему знаменателю.
Приводим к общему знаменателю дроби в правой части уравнения
Вернемся еще раз к первоначальному уравнению:
[large S = v_{0} cdot frac{ v — v_{0}}{a} + frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]
Заменим правую часть этого уравнения выражениями, которые мы получили:
[large S = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} + frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Сравним знаменатели дробей.
Первая дробь обладает знаменателем «a», а вторая – «2a». Выберем число «2a» в качестве общего знаменателя обеих дробей.
Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:
[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot 1]
Примечания:
- Нам известно, что если какое-либо число умножить на единицу, то после умножения это число не изменится. Значит, если какое-либо выражение умножить на единицу, то полученное выражение останется равным самому себе. На единицу можно умножать все, что угодно – дроби, выражения в скобках и т. п.
- Математики часто применяют прием умножения на единицу. А после этого единицу записывают в виде некоторой дроби. При этом используют правило: Единица – это дробь, у которой числитель и знаменатель равны (одинаковые).
Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:
[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot 1 = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot frac{2}{2}]
Получим такую дробь:
[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot frac{2}{2} = frac{ 2(v_{0} cdot v – v^{2}_{0} )}{2a} ]
Поместим ее в выражение для пути:
[large S = frac{ 2(v_{0} cdot v – v^{2}_{0} )}{2a} + frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Дроби с одинаковыми знаменателями складываем
Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:
[large S = frac{ 2(v_{0} cdot v – v^{2}_{0} ) + (v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]
Раскроем скобки в числителе полученного выражения:
[large S = frac{ 2v_{0} v – 2v^{2}_{0} + v^{2} + v^{2}_{0} — 2vv_{0}}{2a}]
Примечание: Обратим внимание на то, что в числителе дважды встречается член (2v_{0} v), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа (2v_{0}v) вычитается такое же число (2vv_{0}). В конце концов, это число покидает нашу запись и, она упрощается:
[large S = frac{ – 2v^{2}_{0} + v^{2} + v^{2}_{0}}{2a}]
Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:
[large S = frac{ v^{2} + v^{2}_{0} – 2v^{2}_{0}}{2a}]
Вычтем подобные члены, содержащие ( v^{2}_{0}):
[large v^{2}_{0} – 2v^{2}_{0} = – v^{2}_{0} ]
В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:
[large boxed{ S = frac{ v^{2} — v^{2}_{0}}{2a} }]
Примечания:
- Это формула, с помощью которой можно рассчитать путь тела, когда известны его начальная и конечная скорость, а, так же, ускорение.
- Видно, что время t в правой части этого выражения отсутствует.
- Мы выводили эту формулу для случая, когда тело увеличивало скорость.
Как выглядит формула пути без времени, когда скорость тела уменьшается
Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:
[large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]
Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:
[ large begin{cases} S = v_{0} cdot t — displaystyle frac{a}{2} cdot t^{2} \ v = v_{0} — a cdot t end{cases} ]
Выводы
Пусть нам известны начальная и конечная скорость тела и его ускорение. Тогда путь, пройденный телом, можно рассчитать так:
- Когда движение равноускоренное и скорость тела увеличивается: [large boxed{ S = frac{ v^{2} — v^{2}_{0}}{2a} }]
- А когда движение равнозамедленное и скорость уменьшается: [large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]