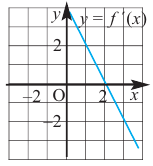
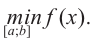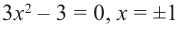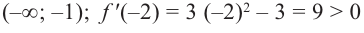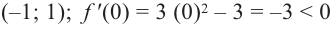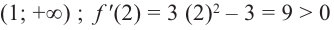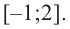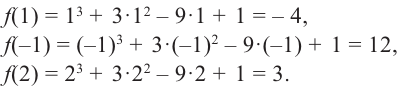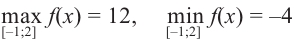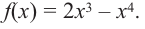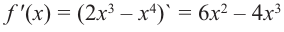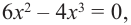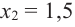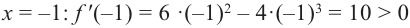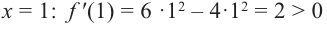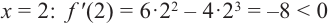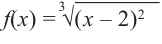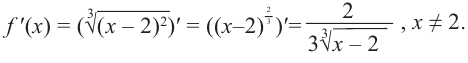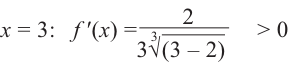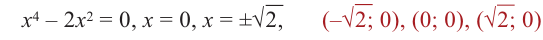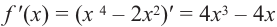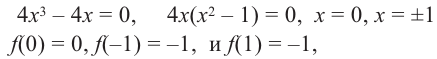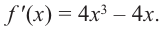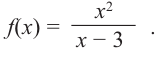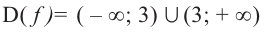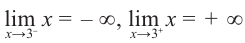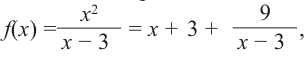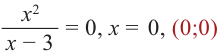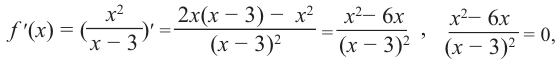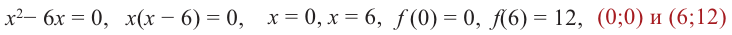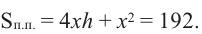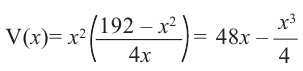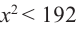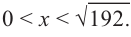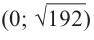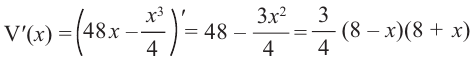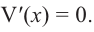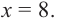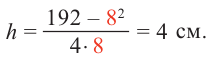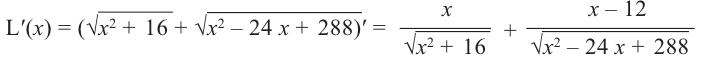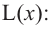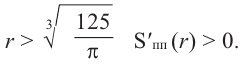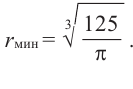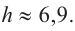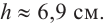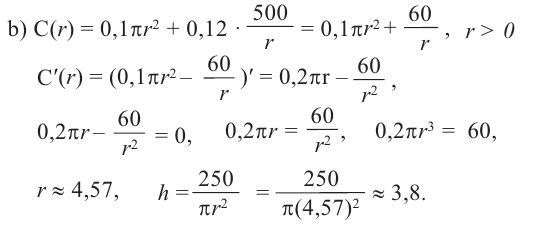Содержание:
- Монотонность функции, основные понятия и определения
- Связь монотонности функции с ее производной
Монотонность функции, основные понятия и определения
Определение
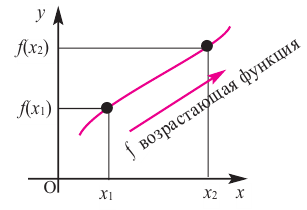
Функция $y=f(x)$ называется строго возрастающей на
промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е.
$f(x) uparrow : x_{1} lt x_{2} Rightarrow fleft(x_{1}right) lt fleft(x_{2}right)$
Пример
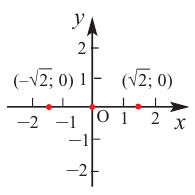
Функция $y=x^{2}$ является возрастающей на промежутке
$[0 ; 1]$, так как:
для $0 lt 1 : f(0)=0^{2}=0 lt f(1)=1^{2}=1$
Определение
Функция $f(x)$ называется строго убывающей на
промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е.
$f(x) downarrow : x_{1} lt x_{2} Rightarrow fleft(x_{1}right)>fleft(x_{2}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Функция $y=x^{2}$ является строго убывающей на
промежутке $[-1 ; 0]$, так как:
для $-1 lt 0 : f(-1)=(-1)^{2}=1>f(0)=0^{2}=0$
Функция $y=f(x)$ строго возрастающая или строго убывающая
на промежутке называется монотонной на этом промежутке.
Определение
Функция $y=f(x)$ называется неубывающей на промежутке,
если из неравенства $x_{1} lt x_{2}$ следует неравенство
$fleft(x_{1}right) leq fleft(x_{2}right)$.
Функция $y=f(x)$ называется невозрастающей на
промежутке, если из неравенства $x_{1} lt x_{2}$ следует
неравенство $fleft(x_{1}right) geq fleft(x_{2}right)$.
Связь монотонности функции с ее производной
Теорема
(Об условии возрастания/убывания монотонной функции)
Если производная функции $f^{prime}(x)>0$ на некотором
промежутке $X$, то функция
$y=f(x)$ возрастает на этом промежутке; если же
$f^{prime}(x) lt 0$ на промежутке
$X$, то функция
$y=f(x)$ убывает на этом промежутке.
Замечание
Обратное утверждение формулируется несколько иначе. Если функция возрастает на промежутке, то
$f^{prime}left(x_{0}right) geq 0$ или не существует.
Пример
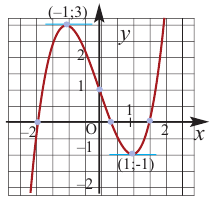
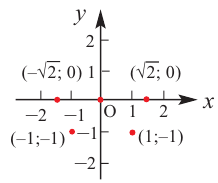
Задание. Исследовать функцию $y=x^{3}$ на монотонность на всей числовой прямой.
Решение. Найдем производную заданной функции:
$y^{prime}=left(x^{3}right)^{prime}=3 x^{2}$
Для любого действительного $x$:
$y^{prime}(x)=3 x^{2} geq 0$, а поэтому делаем вывод, что заданная функция
возрастает на всей действительной оси.
Ответ. Функция $y=x^{3}$ возрастает на всей действительной оси.
Читать дальше: понятие экстремума функции.
Применение
производной в исследовании функций.
§1. Возрастание
и убывание функций.
Теорема (критерий
монотонности дифференцируемой функции).
Пусть функция
непрерывна
на промежутке
и дифференцируема во всех его внутренних
точках. Тогда:
— для монотонного
возрастания функции необходимо и
достаточно, чтобы в
0;
— для монотонного
убывания функции необходимо и достаточно,
чтобы в (а,в)
0;
— для постоянности
функции необходимо и достаточно, чтобы
в (а,в)
=0.
Док-во.
Докажем достаточность для возрастающей
функции. Выберем произвольно точки
.
По теореме Лагранжа найдется точка
,
такая что
.
Т.к. оба множителя в правой части
неотрицательны, то
,
т.е.
.
Следовательно, функция является монотонно
возрастающей.
Докажем необходимость
для возрастающей функции. Пусть f(x)
– монотонно
возрастает. Тогда
,
следовательно
в (а,в).
Для убывающей
функции доказательства аналогичны.
Докажем необходимость
для постоянной функции. Если f(x)=const
в (а,в),
то
.
Докажем достаточность
для постоянной функции. Пусть
в (a,b).
Тогда тем более
в (a,b).
Тогда по доказанному выше функция
монотонно возрастает в (a,b),
т.е.
.
С другой стороны, если
в (a,b),
то тем более
в (a,b).
Тогда по доказанному выше функция
монотонно убывает в (a,b),
т.е.
.
Одновременное выполнение этих условий
возможно лишь при
.▲
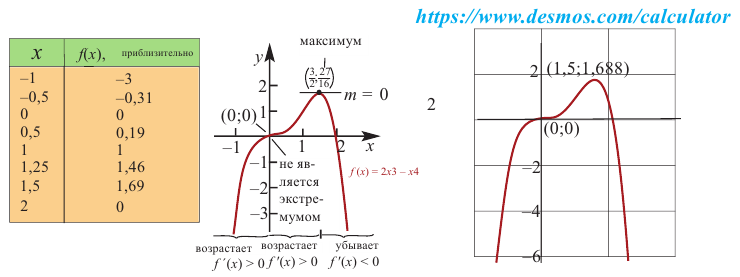
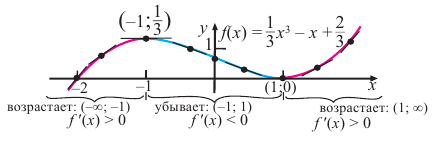
Пример.
Найти промежутки монотонности функции
.
Найдем производную
.
Очевидно, что при
производная
,
функция является возрастающей. При
производная
,
функция убывает.
§2.
Экстремумы функции.
Пусть функция
задана на интервале
.
Опр.
Точка
называется точкой локального максимума
функции f(x),
если в некоторой ее окрестности
выполняется условие:
.
Опр.
Точка
называется точкой локального минимума
функции f(x),
если в некоторой ее окрестности
выполняется условие:
.
Значения функции
в точках локального минимума и максимума
называют минимумом и максимумом функции.
Минимум и максимум функции объединяют
в понятие «экстремум функции»
(extr
f).
Отметить
отличия локального и глобального
экстремумов.
Теорема (необходимое
условие локального экстремума). Если
дифференцируемая
функция
имеет экстремум в точке
,
то ее производная в этой точке равна
нулю:.
Док-во. Если
— точка экстремума дифференцируемой
функции, то существует некоторая
окрестность этой точки, в которой
выполнены условия теоремы Ферма. Тогда
ее производная
.
Замечание.
Функция может иметь экстремум и в точках,
в которых она не дифференцируема (если
эти точки входят в область определения).
Например, функция
имеет экстремум в точке х=0,
но не дифференцируема в ней.
Точки, в которых
производная равна нулю или не существует,
называются стационарными
или критическими
точками. Из теоремы следует, что точки
локального экстремума функции являются
ее критическими точками. Обратное
утверждение неверно. Например, функция
имеет неотрицательную производную,
т.е. возрастает на всей числовой оси,
следовательно не имеет точек экстремума.
В то же время,
является ее критической точкой.
Теорема
(достаточное условие локального
экстремума). Если
при переходе через критическую точку
производная дифференцируемой функции
меняет знак с «+» на «-», то
— точка локального максимума, если с «-»
на «+», то
— точка локального минимума.
Док-во. В соответствии
с достаточным условием монотонности,
функция возрастает слева от
и убывает справа, тогда в силу непрерывности
функции,
является точкой максимума. Аналогичные
рассуждения для минимума.
Замечание.
Если при переходе через критическую
точку производная не меняет знак, то в
этой точке экстремума функции нет.
Теорема
(2 достаточное условие локального
экстремума).
Для того, чтобы функция имела локальный
максимум (минимум) в критической точке
,
достаточно, чтобы в некоторой окрестности
этой точки существовала непрерывная
вторая производная и
().
(без док-ва).
Пример. Найти
экстремумы функции;
Ее производная:.
Определим критические
точки:
,
— критические точки.
Определим знак
производной в окрестностях критических
точек.
— точка минимума,
— минимум функции;
— точка максимума,
— максимум функции.
§3. Наибольшее и
наименьшее значения функции на отрезке.
При решении
прикладных задач бывает нужно найти
глобальные экстремумы функции на
некотором промежутке. Если этот промежуток
является отрезком, то экстремумы функция
может достигать как в точках экстремума,
так и на концах отрезка.
Пример.
Найти наибольшее значение функции
на отрезке
.
Решение.
Данная функция является непрерывной
на данном отрезке (т.к. знаменатель не
обращается в нуль), а следовательно,
может принимать экстремальные значения
либо в точках экстремума, либо на концах
отрезка. Вычислим производную:
.
Тогда критическими точками являются
точки х=0 и
х=-2.
Данному отрезку принадлежит только
точка х=0.
Вычислим значения функции в точке
экстремума и на концах отрезка:
,
,
.
Сравнивая эти значения, заключаем, что
наибольшее значение функции достигается
в точке х=0.
§4. Выпуклость
функции. Точки перегиба.
Опр. Функция
называется выпуклой вверх (выпуклой)
на промежутке Х, если
.
График выпуклой на промежутке Х функции
расположен над любой ее секущей (и под
любой ее касательной) на этом промежутке.
Аналогично вводится
определение функции, выпуклой вниз
(вогнутой).
выпуклая
(вверх) вогнутая
(выпуклая вниз)
Теорема (критерий
выпуклости функции).
Пусть функция
дифференцируема в интервале (а,в).
Тогда для выпуклости функции вниз
необходимо и достаточно, чтобы
монотонно возрастала на этом интервале.
Для выпуклости функции вверх необходимо
и достаточно, чтобы
монотонно убывала на этом интервале.
Следствие
(достаточное условие выпуклости).
Если вторая производная дважды
дифференцируемой функции неотрицательна
(неположительна) внутри некоторого
промежутка, то функция выпукла вниз
(вверх) на этом промежутке.
Опр.
Точки, в которых график функции меняет
направление выпуклости, называются
точками перегиба графика функции.
Абсциссы точек
перегиба являются точками экстремума
первой производной.
Теорема (необходимое
условие точки перегиба).
Вторая производная дважды дифференцируемой
функции в точке перегиба равна нулю:
.
Абсциссы точек, в
которых выполняется необходимое условие,
называются критическими
точками второго рода.
Если перегиб графика есть, то только в
таких точках.
Теорема (достаточное
условие точки перегиба). Пусть
— дважды дифференцируема в интервале
(а,в).
Тогда если вторая производная при
переходе через критическую точку второго
рода
меняет знак, то точка
является
точкой перегиба графика функции.
Замечание.
Если смены знака второй производной не
происходит, то перегиба графика в точке
нет.
Пример.
,
;
— точка перегиба.
Итак, чтобы найти
интервалы выпуклости функции, нужно:
1. Найти вторую
производную функции.
2. Найти точки, в
которых
или не существует.
3. Исследовать знак
второй производной слева и справа от
найденных точек и сделать вывод о
направлении выпуклости и точках перегиба
на основании достаточных условий.
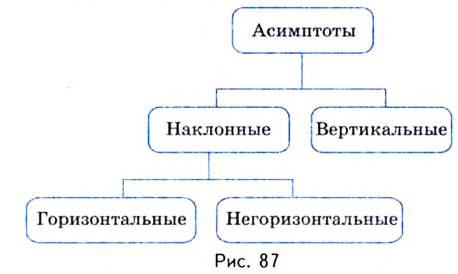
§5. Асимптоты
графика функции.
Графики некоторых
функций расположены на плоскости так,
что при неограниченном удалении от
начала координат они неограниченно
приближаются к некоторым прямым, но не
пересекают их. Такие прямые называются
асимптотами функции.
Асимптоты могут
быть горизонтальными, вертикальными,
наклонными.
Прямая y=a
называется
горизонтальной асимптотой к графику
функции y=f(x),
если существует конечный предел
.
Прямая x=b
называется вертикальной асимптотой к
графику функции y=f(x),
если существует конечный предел
.
Вертикальные
асимптоты следует искать в точках
разрыва функции или на концах области
определения.
Если у функции нет
горизонтальных асимптот, то, возможно,
есть наклонные.
Наклонная асимптота
к графику функции существует в том
случае, когда существуют конечные числа
к
и в,
вычисляемые по формулам:
,
.
Тогда наклонная асимптота задается
уравнением y=kx+b.
Если хотя бы одно из чисел к
и в
несобственное, то наклонных асимптот
у графика функции нет.
§6. Общая схема
исследования функции.
I.
1. Область определения.
2. Точки
пересечения с осями координат.
3. Четность.
4. Периодичность.
5. непрерывность.
6. Асимптоты.
II.
7. Монотонность.
8. Точки
экстремума, экстремумы.
III.
9. Направления выпуклости.
10. Точки перегиба
графика.
IV.11.
Дополнительные точки.
12. Построение
графика.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лекция 4. Применение производной к исследованию функций и построению графиков.
План
1. Возрастание и
убывание функции.
2. Экстремумы
функции.
3. Схема исследования функции и построения её
графика с помощью производной.
4. Решение задач
(Учебник: Ш.А.
Алимов Алгебра и начала математического анализа 10-11 класс глава IX §49, §50, §51, стр. 261-264, стр. 265-269, стр. 271-275)
1. Возрастание и
убывание функции.
Производная широко
используется для исследования функций, т.е. для изучения различных свойств
функций. Например, с помощью производной можно находить промежутки возрастания
и убывания функции, её наибольшее и наименьшее значения.
Рассмотрим применение
производной к нахождению промежутков возрастания и убывания функций.

производной функции положительны на некотором промежутке, т.е.
. Тогда угловой коэффициент касательной
к графику этой функции в каждой точке данного промежутка положителен.
Это означает, что касательная образует острый угол с осью Ox, и поэтому график функции на этом промежутке «поднимается», т.е.
функция возрастает (рис.120).
Если на некотором промежутке, то угловой коэффициент касательной
к графику функции
отрицателен.
Это означает, что
касательная образует тупой угол с осью Ox, и поэтому
график функции на этом промежутке «опускается», т.е. функция убывает (рис. 121).
Итак, если на промежутке, то функция
возрастает на этом промежутке.
Если на промежутке, то функция
убывает на этом промежутке.
При доказательстве
теорем о достаточных условиях возрастания или убывания функции используется теорема
Лагранжа.
Теорема Лагранжа. Если функция непрерывна на отрезке [a;b]
и дифференцируема на интервале (a;b),
то существует точка такая, что
. (1)
Доказательство
формулы (1) приводится в курсе высшей математики. Поясним геометрический смысл
этой формулы.
Проведём через
точки и
графика функции
прямую l и назовём эту прямую секущей. Угловой
коэффициент секущей равен .
Запишем формулу (1)
в виде . (2)
Согласно формуле
(2) угловой коэффициент касательной к графику функции в точке C с абсциссой c
(рис. 122) равен угловому коэффициенту секущей l, т.е. на
интервале (a;b) найдётся такая точка c, что в точке графика с абсциссой c касательная к
графику функции параллельна секущей. Сформулируем с помощью теоремы Лагранжа теорему
о достаточном условии возрастания функции.

функция дифференцируема на интервале (a;b) и
для всех
, то функция возрастает на интервале (a;b).
Пример 1.
Доказать, что
функция возрастает на промежутке
.
Доказательство:
Найдём производную:
.
Если , и поэтому данная функция возрастает на промежутке
.
Промежутки
возрастания и убывания функции часто называют промежутками монотонности
этой функции.
Правило
нахождения интервалов монотонности функции .
1. Находят
производную данной функции.
2. Находят точки, в
которых равна нулю или не существует, т.е. критические точки функции
.
3. Найденными
точками область определения функции разбивается на интервалы, на каждом из которых производная
сохраняет свой знак. Эти интервалы являются интервалами монотонности
(т.е. критические точки отмечаем на числовой прямой и определяем знак
производной в каждом интервале, подставив соответствующее значение xв формулу производной).
4. Исследуют знак на каждом из найденных интервалов.
Если на
рассматриваемом интервале , то на этом интервале
возрастает;
если же , то на таком интервале
убывает.
Пример 2.

интервалы монотонности функции .
Решение
Найдем производную:
.
Решая неравенство , т.е. неравенство
, находим интервалы возрастания:
.
Решая неравенство , т.е. неравенство
, находим интервал убывания
.
Ответ: возрастает;
убывает.
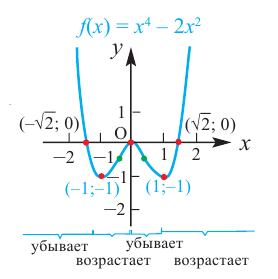
График функции изображен на рисунке 123. Из этого рисунка видно, что функция
возрастает не только на интервалах
, но и на промежутках
; убывает не только на интервале
, но и на отрезке
.
2. Экстремумы
функции.
На рисунке 123
изображён график функции . Рассмотрим окрестность точки x = 0, т.е.
некоторый интервал, содержащий эту точку. Как видно из рисунка, существует
такая окрестность точки x = 0, что наибольшее значение
функция в этой окрестности принимает в точке x = 0.
Например, на интервале (-1; 1) наибольшее значение, равное 0, функция принимает
в точке x = 0. Точку x = 0 называют
точкой максимума этой функции.
Аналогично точку x = 2 называют точкой минимума функции , так как функции в этой точке меньше её значения в любой точке
некоторой окрестности точки x = 2, например окрестности
(1,5; 2,5).
Точка называетсяточкой максимума функции
, если существует такая окрестность точки
, что для всех
из этой окрестности выполняется неравенство
.
 |
Например, точка является точкой максимума функции
, так как
и при всех значения
верно неравенство
(рис. 124).
Точка называетсяточкой минимума функции
, если существует такая окрестность точки
, что для всех
из этой окрестности выполняется неравенство
.
Например, точка является точкой минимума функции
, так как
при всех значениях
(рис. 125).
Точки минимума и
точки максимума называются точками экстремума. Экстремум –
значение функции в этих точках.
Рассмотрим функцию , которая определена в некоторой окрестности точки
и имеет производную в этой точке.
Теорема. Если — точка экстремума дифференцируемой функции
, то
.
Это утверждение
называют теоремой Ферма.
 |
Теорема Ферма имеет наглядный геометрический смысл: касательная к
графику функции в точке
, где
— точка экстремума функции
, параллельна оси абсцисс, и поэтому её угловой коэффициент
равен нулю (рис. 126).
Например, функция (рис.124) имеет в точке
максимум, её производная
. Функция
имеет минимум в точке
(рис. 125),
.
Отметим, что если , то этого недостаточно, чтобы утверждать, что
обязательно точка экстремума функции
.
Например, если . Однако точка x = 0 не является точкой
экстремума, так как функция возрастает на всей числовой оси (рис. 127).
Итак, точки
экстремума дифференцируемой функции нужно искать только среди корней уравнения , но не всегда корень этого уравнения является точкой экстремума.
Точки, в которых производная функции равна нулю, называют стационарными.
Заметим, что
функция может иметь экстремум и в точке, где эта функция не имеет производной.
Например, x = 0 – точка минимума функции не существует. Точки, в которых функция имеет производную, равную
нулю, или недифференцируема, называют критическими точками этой функции.
Таким образом, для
того чтобы точка была точкой экстремума функции
, необходимо, чтобы эта точка была критической точкой данной функции.
Приведём достаточные условия того, что стационарная точка является точкой
экстремума, т.е. условия, при выполнении которых стационарная точка есть точка
максимума или минимума функции.
 |
Теорема. Пусть функция дифференцируема на интервале (a; b),
, и
.
Тогда:
1) если при переходе через стационарную точку функции
её производная меняет знак с «плюса» на «минус», т.е.
слева от точки
и
справа от точки
, то
— точка максимума функции
(рис. 128);
2) если при переходе через стационарную точку функции
её производная меняет знак с «минуса» на «плюс», то
— точка минимума функции
(рис. 129);
Если же не меняет знак в окрестности точки
, то данная функция не имеет экстремума в точке
.
Правило
нахождения экстремумов функции .
1. Находят
производную данной функции.
2. Находят все
критические точки из области определения функции.
3. Устанавливают
знаки производной функции при переходе через критические точки и выписывают
точки экстремума.
4. Вычисляют
значения функции в каждой точке экстремума.
Пример 3
Найти точки
экстремума функции .
Решение
1. Найдём
производную:
2. Найдём все
критические точки из области определения функции. Решим уравнение .
.
3. Установим знаки производной функции при переходе через критические
точки и выпишем точки экстремума. Для этого отметим полученные
значения на числовой прямой. Точки и
разделили область определения функции
на три интервала. Вычислим знак производной в каждом из этих
интервалов:
;
;
.
Так как при
переходе через точку знак производной не меняется, то эта точка не является точкой
экстремума.
При переходе через
точку производная меняет знак с «-» на «+». Поэтому
— точка минимума.
Ответ: — точка минимума.
Пример 4
Найти точки
экстремума функции и значения функции в этих точках.
Решение
1. Найдём
производную: .
2. Найдём
критические точки.
или
– не существует
.
3. Установим знаки производной функции при переходе через критические
точки и выпишем точки экстремума. Для этого отметим
полученные значения на числовой прямой. Точки и
разделили область определения функции
на три интервала. Вычислим знак производной в каждом из этих
интервалов:
;
;
.
При переходе через
точку производная меняет знак с «+» на «-». Поэтому
— точка максимума. При переходе через точку
производная меняет знак с «-» на «+», поэтому
— точка минимума.
4. Вычислим значения функции в каждой точке экстремума.
Значение функции в
точке максимума равно , а в точке минимума
.
Ответ: — максимум,
. – минимум.
3. Схема
исследования функции и построения её графика с помощью производной.
Примерная
схема исследования функции:
1. Найти область
определения функции (если возможно, то множество значений).
2. Выяснить, не
является ли функция чётной, нечётной, периодической.
3. Найти точки
пересечения графика функции с осями координат (если это не вызывает
затруднений).
4. Найти асимптоты
графика функции (если это необходимо, только для функций, которые имеют точки
разрыва, т.е. не являются непрерывными).
5. Найти промежутки
монотонности функции и её экстремумы.
6*. Найти
промежутки выпуклости графика функции и точки перегиба (применение производной
второго порядка).
7. Вычислить
координаты дополнительных точек (если это необходимо).
В зависимости от
сложности функции некоторые пункты данной схемы могут быть пропущены.
Пример 5
Построить график
функции .
Решение
1.
2. Исследуем на
чётность: . Функция не является ни чётной, ни нечетной, т.е. общего вида.
3. Пересечение с
осью Ox: ,
. Таким образом, получили две точки
.
Пересечение с осью Oy: .
4. С помощью
производной найдём промежутки монотонности этой функции и её точки экстремума.
Производная равна . Найдем стационарные точки:
,
откуда .
Для определения
знака производной разложим квадратный трёхчлен на множители:
.
Производная
положительна на промежутках , следовательно, на этих промежутках функция возрастает.
При производная отрицательна, следовательно, на интервале
функция убывает.
Точка является точкой максимума, так как слева от этой точки функция
возрастает, а справа убывает. Значение функции в этой точке равно .
Точка является точкой минимума, так как слева от этой точки функция убывает,
а справа возрастает; её значение в точке минимума равняется .
Результаты
исследования представим в следующей таблице:
 |
5.
Для более точного построения графика найдём значения функции ещё в двух точках:

Используя
результаты исследования, построим график функции (рис. 132).
Пример 6. Исследуйте и постройте графики функций:
а) ;б)
.
|
№ |
План исследования |
Применение |
плана |
|
шага |
Функции |
а) |
б) |
|
1 |
Находим область |
|
|
|
2 |
Исследуем функцию |
|
|
|
3
|
Находим нули |
|
|
|
4 |
Находим производную |
|
|
|
5
|
Находим промежутки |
х=0 – не |
х=0 – точка |
|
6 |
Находим предел |
|
|
|
7
|
Строим эскиз |
4. Задания для
самостоятельного решения
Задача 1 (1 балл)
Найдите промежутки
убывания и возрастания функции: .
В ответе укажите
промежуток убывания.
Задача 2 (2 балла)
Найдите промежутки
убывания и возрастания функции: .
1. при убывает; при
возрастает
2. при убывает; при
возрастает
3. при убывает; при
возрастает
4. при возрастает
В ответе укажите
номер с правильным ответом.
Задача 3 (3 балла)
Найдите промежутки
убывания функции .
Задача 4 (2 балла)
Найдите точку
минимума функции .
Задача 5 (2 балла)
Найдите точку
максимума функции .
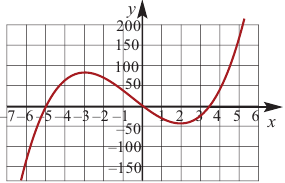
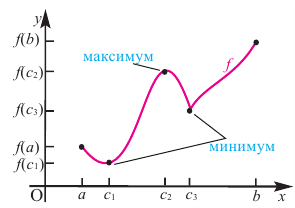
С помощью производной можно исследовать функцию на монотонность и найти точки экстремума, определить наибольшее и наименьшее значения функции на отрезке.
Чтобы определить промежутки монотонности и экстремумы функции f(x), нужно:
1. найти производнуюf′(x).
2. Определить стационарные и критические точки.
3. Нанести стационарные и критические точки на числовую прямую и определить знаки производной на каждом промежутке.
4. Определить промежутки монотонности функции и точки экстремума функции.
Подробнее:
- исследование функции на монотонность;
- отыскание точек экстремума.
Чтобы найти наибольшее (наименьшее) значение функции (f(x)) на промежутке [(a); (b)], нужно:
1. вычислить производную (f’(x)).
2. Решить уравнение (f’(x)=0).
3. Выбрать те корни уравнения, которые попали в промежуток [(a); (b)].
4. Подставить в исходную функцию эти корни, а также точки (a) и (b).
5. Выбрать из полученных чисел наибольшее (наименьшее).
Для решения таких задач необходимо знать формулы и правила дифференцирования, уметь находить производную сложной функции.
Полезно знать основные свойства некоторых функций, например квадратичной функции, так как некоторые задания можно решить без нахождения производной.
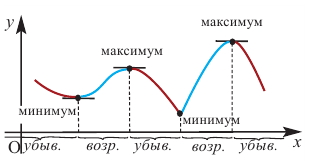
Исследовать функцию — это значит установить её свойства: указать её область определения и область значений; промежутки возрастания и убывания; промежутки, на которых функция приобретает положительные значения, на которых — отрицательные; выяснить, не является ли данная функция чётной или нечётной и т. д.
Содержание:
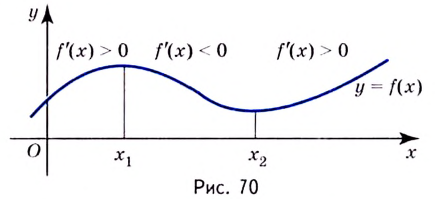
Что такое исследование функции
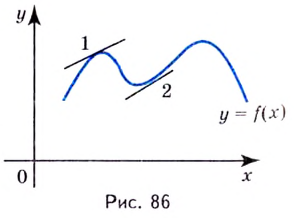
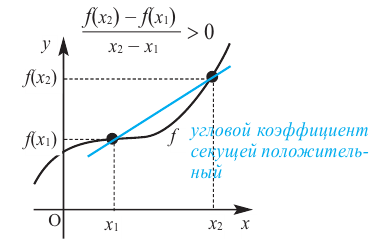
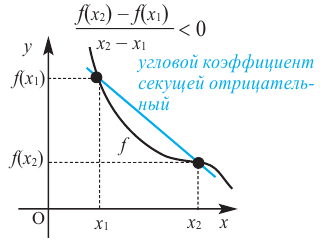
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис. 70).
Правильными будут следующие утверждения.
- Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
- Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
- Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
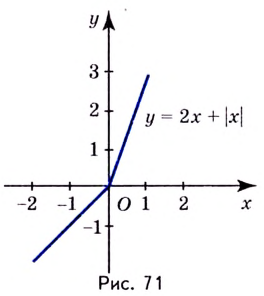
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция
Из сказанного следует, что два соседних промежутка, на одном из которых функция возрастает, а на другом — убывает, могут разделяться только такой точкой, в которой производная функции равна нулю или не существует.
Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называют критическими точками функции.
Следовательно, чтобы определить промежутки возрастания и убывания функции 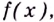
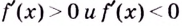
Пример:
Найдите промежутки возрастания и убывания функции
Решение:
Уравнение 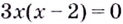
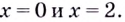
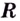
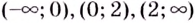
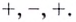
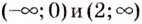
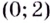
Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция 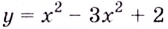
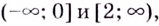
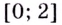
Пример:
Найдите промежутки убывания функции
Решение:
Критические точки: 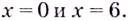
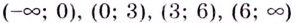
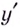
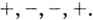
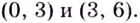
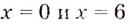
Пример:
Найдите критические точки функции 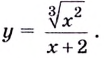
Решение:
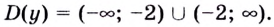
Найдём точки, в которых производная равна нулю или не существует: 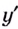
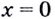
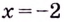

Ответ. 0 и 4.
Пример:
Докажите, что функция 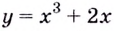
Решение:
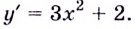
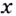
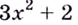
Пример:
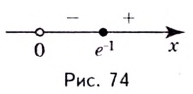
Установите, на каком промежутке функция 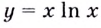
Решение:
Способ 1. 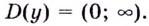
Найдём критические точки функции:
Эта точка разбивает область определения функции на два промежутка (рис. 74). Определим знак производной на каждом из них.
Следовательно, функция 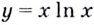
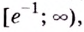
Способ 2. Решим неравенство 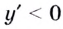
Ответ. Возрастает, если 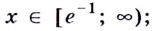
Применение второй производной к исследованию функций и построению их графиков
При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график. Оказывается, что поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Вспомним, что такое вторая производная.
Пусть функция 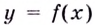
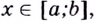
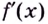
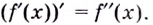
Например, найти производную 2-го порядка функции 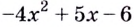
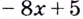
Кривая 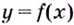
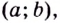
Кривая 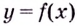
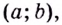
Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой.
Интервалы выпуклости и вогнутости находят при помощи такой теоремы.
Теорема. Если вторая производная дважды дифференцируемой функции 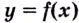
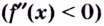
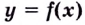
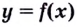
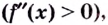
Из теоремы следует, что точками перегиба кривой 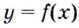
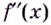
Установим до статочное условие существования точки перегиба.
Теорема. Пусть 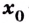
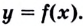
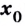
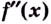
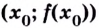
Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой:
- найти область определения функции;
- найти критические точки второго рода;
- определить знак второй производной на образованных интервалах. Если
то кривая выпуклая; если
— кривая вогнутая;
- если производная
меняет знак при переходе через точку
то точка
является точкой перегиба кривой
Пример №1
Найдите интервалы выпуклости, вогнутости и точки перегиба кривой
Решение:
1) Область определения функции:
2) Найдём вторую производную: 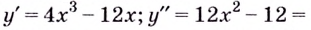
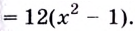
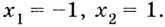
3) Разбиваем область определения на интервалы 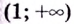
Если 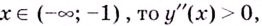
Если 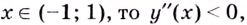
Если 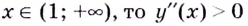
Следовательно, точки 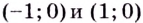
Напомним, что прямая 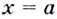
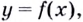
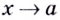
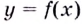
Уравнение наклонной асимптоты:
Если записанные пределы существуют, то существует наклонная асимптота; если хотя бы один из них не существует или равен 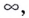
Если 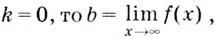
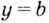
Замечание: Рассмотренные пределы могут быть односторонними, а под символом 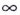
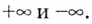
Пример №2
Найдите асимптоты кривых:
Решение:
а) 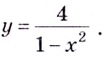
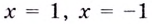
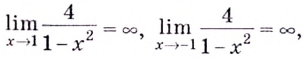
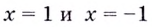
Найдём наклонную асимптоту: 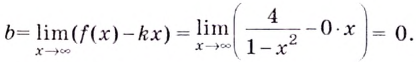
Следовательно, заданная кривая имеет три асимптоты:
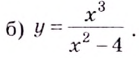
Поскольку функция не определена в точках 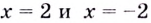
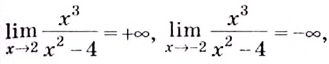
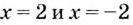
Для наклонной асимптоты
Значит прямая 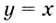
Итак, асимптоты кривой:
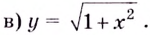
Следовательно, 
2) если 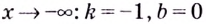

Следовательно, заданная кривая имеет две асимптоты:
Определение точек перегиба, интервалов выпуклости и асимптот существенно помогает в построении графиков различных функций.
Нахождение промежутков возрастания и убывания функции
Интервалы возрастания и убывания функции
возрастающая функция
Если для любых 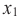
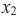
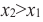
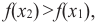
убывающая
Если для любых 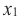
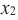
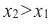
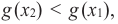
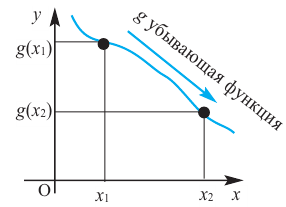
Связь промежутков возрастания и убывания функции с угловым коэффициентом секущей можно выразить следующим образом.
Если на заданном промежутке угловой коэффициент любой секущей положителен, то на этом промежутке функция 
Если на заданном промежутке угловой коэффициент любой секущей отрицателен, то на этом промежутке функция 
Промежутки возрастания и убывания функции
Пусть на определенном промежутке производная функции 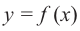
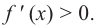
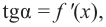
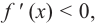
Теорема. Если функция 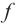
Примечание: если функция 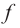
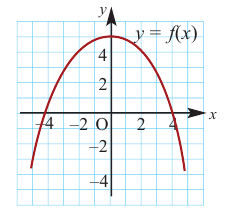
По графику функции 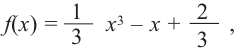
На интервалах 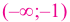
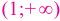
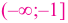
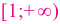
На интервале 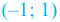
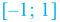
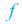
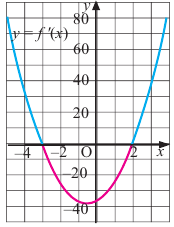
Пример №3
При помощи производной определите промежутки возрастания и убывания функции
Решение: 1. Алгебраический метод.
Найдем производную функции
Функция 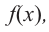
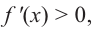
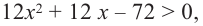
Для решения неравенства сначала надо решить соответствующее уравнение
Значит, при 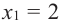
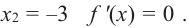
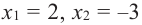
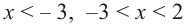
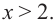
Из таблицы и непрерывности функции 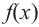
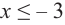
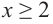
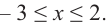
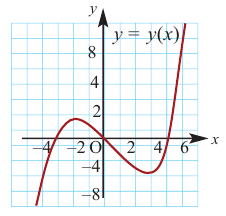
2. Промежутки возрастания и убывания функции можно определить но графику производной. На рисунке изображен график производной
График производной 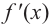
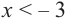
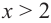
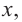
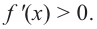
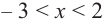
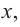
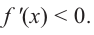
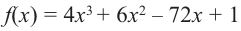
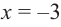
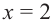
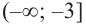
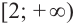
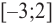
Пример №4
Изобразите схематично график непрерывной функции согласно еле дующим условиям:
a) при 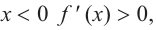
b) при 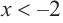
Решение:
а) при 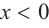
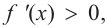
функция возрастает. При 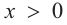
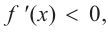
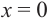
b) При 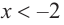
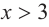
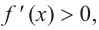
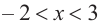
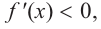
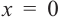
Критические точки и экстремумы функции
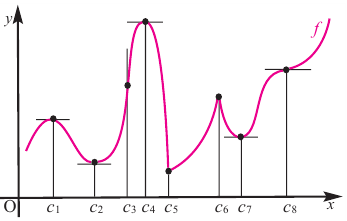
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 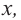
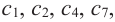
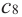
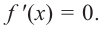
2. В точках 
3. Для рассматриваемой нами функции критические точки 
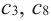
По графику видно, что в точках внутреннего экстремума(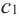
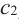
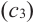
Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 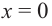
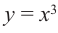
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т. е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.
Достаточное условие существования экстремума
Пусть функция 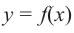
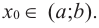
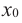
слева от точки
положительна, а справа — отрицательна, то точка
является точкой максимума.
слева от
отрицательна, а справа — положительна, то точка
является точкой минимума
с каждой стороны от точки
имеет одинаковые знаки, то точка
не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 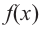
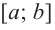
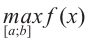
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
Пример №5
Для функции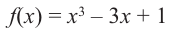
Решение: Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции:
2. Критические точки функции:
3. Точки 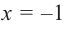
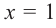
Проверим знак 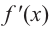
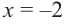
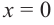
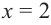

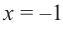
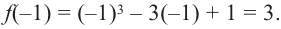
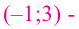
При 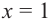
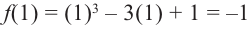
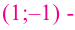
4. Используя полученные для функции 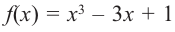
Пример №6
Найдите наибольшее и наименьшее значение функции 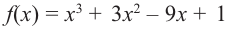
Решение: Сначала найдем критические точки.
Так как 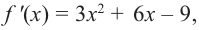
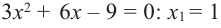
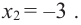
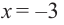
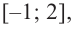
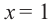
Из этих значений наименьшее — 4, наибольшее 12. Таким образом:
Пример №7
Найдите экстремумы функции
Решение: 1. Производная функции:
2. Критические точки:
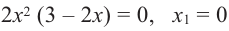
3. Интервалы, на которые критические точки делят область определения функции:
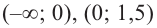
Проверим знак 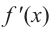
Для промежутка 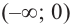
Для промежутка 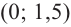
Для промежутка 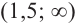
Используя полученную для функции 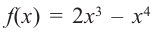
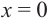
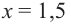
Пример №8
Найдите экстремумы функции
Решение: 1. Производная
2. Критические точки: для этого надо решить уравнение 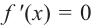
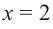
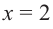
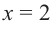
3. Промежутки, на которые критическая точка делит область определения функции: 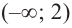
Определим знак 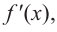
Для 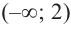
Для 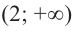
Пример №9
По графику функции производной 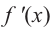
Решение:
Производная 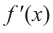
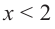
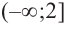
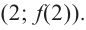
- Заказать решение задач по высшей математике
Построение графиков функции с помощью производной
Функция — многочлен определена и непрерывна на всей числовой оси.
Чтобы построить график функции- многочлен надо выполнить следующие шаги.
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания функции.
- Найдите максимумы и минимумы.
- Постройте график.
Пример:
Постройте график функции
1) Точки пересечения с осями координат :
2) Критические точки ( точки, в которых производная равна нулю):
значит, точки 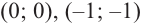
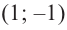
3) Промежутки возрастания и убывания. Экстремумы.
Критические точки 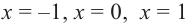
4) Используя полученную информацию, построим график функции.
Чтобы построить график рациональной функции надо выполнить следующие шаги.
- Найдите область определения.
- Найдите асимптоты (если они есть).
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания и экстремумы.
- Постройте график.
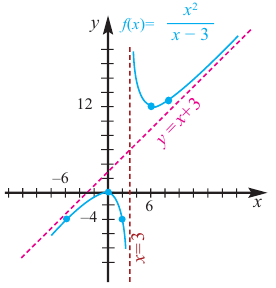
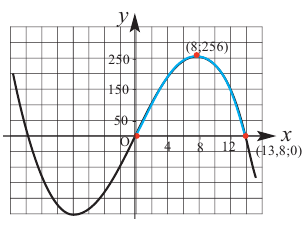
Пример:
Постройте график функции
1) Область определения функции:
2) Асимптоты:
Прямая 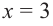
Так как степень многочлена в числителе больше степени многочлена в знаменателе, рациональная функция не имеет горизонтальной асимптоты. Однако, записав следующее:
условии 
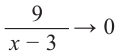
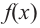
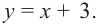
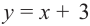
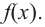
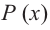
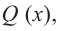
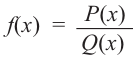
3) Точки пересечения с осями координат:
4) Критические точки:
5) Промежутки возрастания и убывания: в точке 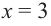
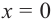
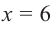
6) Построим график. Отметим на координатной плоскости точки 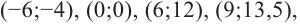
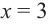
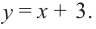
Обратите внимание! В области, близкой к точке 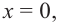
Задачи на экстремумы. Оптимизации
В реальной жизненной ситуации возникает необходимость выбора оптимального варианта и нахождения экстремумов определенной функции. Ежедневно, при решении проблем в различных областях, мы сталкиваемся с терминами наибольшая прибыль, наименьшие затраты, наибольшее напряжение, наибольший объем, наибольшая площадь и т.д. Большое экономическое значение в промышленности, при определении дизайна упаковки, имеет вопрос, как подобрать размеры упаковки с наименьшими затратами. Такого рода задания связаны с нахождением максимального или минимального значения величины. Задачи на нахождение максимального и минимального значения величины называются задачами на оптимизацию. Для решения данных задач применяется производная.
Замечание 1: На интервале 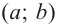
Замечание 2: В рассматриваемом интервале может быть одна стационарная точка: или точка максимума, или точка минимума. В этом случае, в точке максимума функция принимает наибольшее значение, а в точке минимума — наименьшее значение.
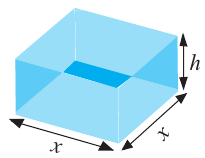
Пример 1. Максимальный объем. Фирма планирует выпуск коробки без крышки, с квадратным основанием и площадью поверхности 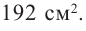
Решение:
Так как основанием коробки является квадрат, то ее объем можно вычислить по формуле 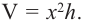
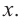
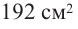
Тогда выразим 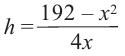
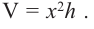
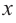
Теперь найдем область определения функции 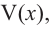
Понятно, что длина не может быть отрицательной, т. е. 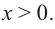
или 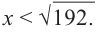
Найдем максимальное значение функции 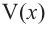
Для этого используем производную первого порядка:
При 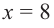
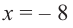
Однако. 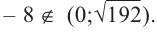
При 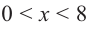
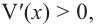
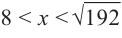
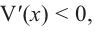
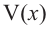
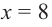
Если длина основания коробки будет 8 см, то высота будет равна
Значит, максимальный объем будет иметь коробка с размерами
Построив при помощи графкалькулятора график функции 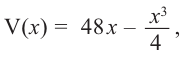
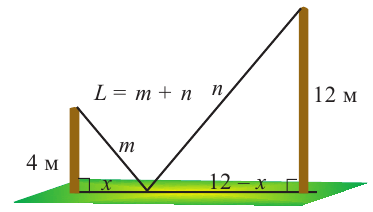
Пример 2. Минимальное потребление. Два столба высотой 4 м и 12 м находятся на расстоянии 12 м друг от друга. Самые высокие точки столбов соединены с металлической проволокой, каждая из которых, в свою очередь крепится на земле в одной точке. Выберите такую точку на земле, чтобы для крепления использовалось наименьшее количество проволоки.
Решение: 1) Изобразим рисунок, соответствующий условию задачи, и обозначим соответствующие данные на рисунке.
2) Аналитически выразим зависимость между переменными.
По теореме Пифагора:
зависимость функции 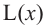
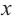
Производная функции
Найдем критические точки функции
Сравнивая значения функции 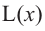
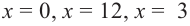
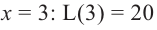
При решении задач на экстремумы обратите внимание на следующее!
1. Внимательно читайте условие. Сделайте соответствующий рисунок.
2. Задайте список соответствующих переменных и констант, которые менялись и оставались неизменными и какие единицы использовались. Если на рисунке есть размеры, обозначьте их.
3. Выберите соответствующий параметр 
4. Полученные значения объясните экспериментально.
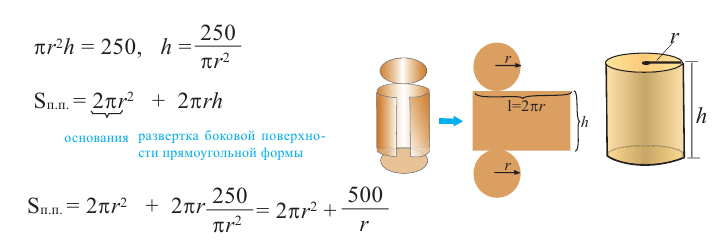
Пример: Минимальное потребление материала. Для мясных консервов планируется использовать банку в форме цилиндра объемом 250
a) Каких размеров должна быть банка, чтобы для ее изготовления использовалось как можно меньше материала?
b) Для круглого основания используется материал, цена 1 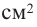
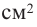
Решение: а) По условию задачи объем равен 250 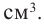
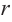
Для функции, выражающей площадь поверхности, область определения представляет собой незамкнутый интервал, и мы должны найти, при каком значении 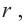
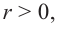
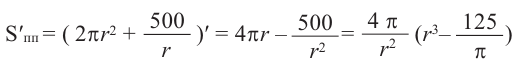
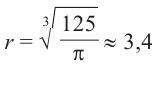
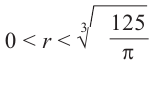
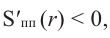
Значит,
Подставим значение 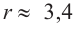
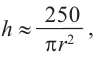
Итак, минимальные затраты на материал будет иметь банка цилиндрической формы с размерами 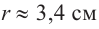
Размеры, при которых затраты на материал будут минимальными
- Приложения производной
- Производные высших порядков
- Дифференциал функции
- Дифференцируемые функции
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
















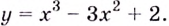
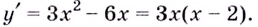
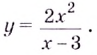
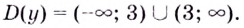
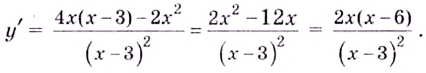
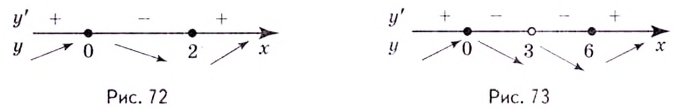
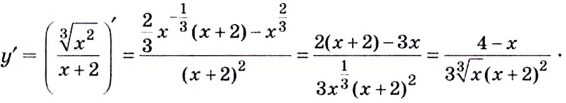
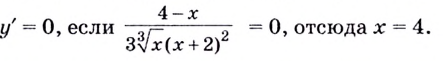
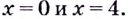
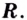
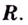
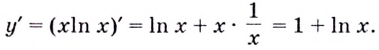
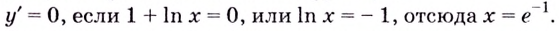
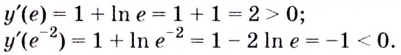
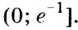
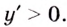
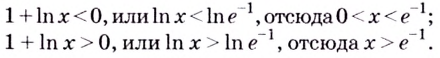
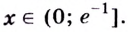
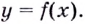
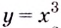
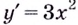
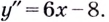
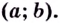
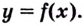
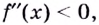 то кривая выпуклая; если
то кривая выпуклая; если 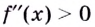 — кривая вогнутая;
— кривая вогнутая;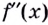 меняет знак при переходе через точку
меняет знак при переходе через точку 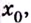 то точка
то точка 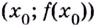 является точкой перегиба кривой
является точкой перегиба кривой 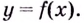
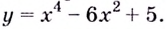
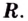
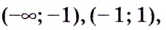
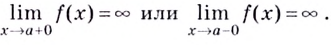
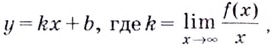
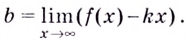
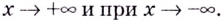
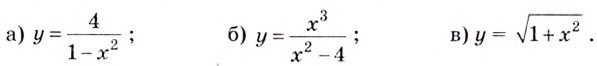
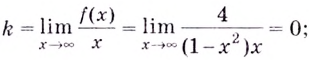
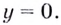
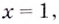
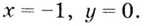
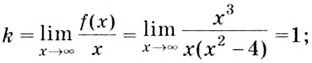
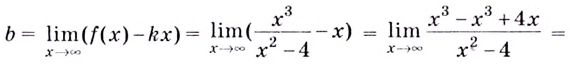
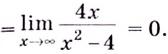
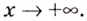
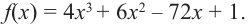
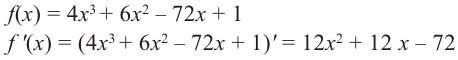
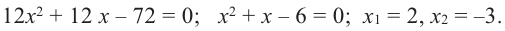

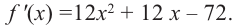
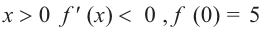
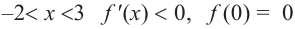
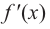 слева от точки
слева от точки 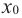 положительна, а справа — отрицательна, то точка
положительна, а справа — отрицательна, то точка 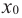 является точкой максимума.
является точкой максимума.