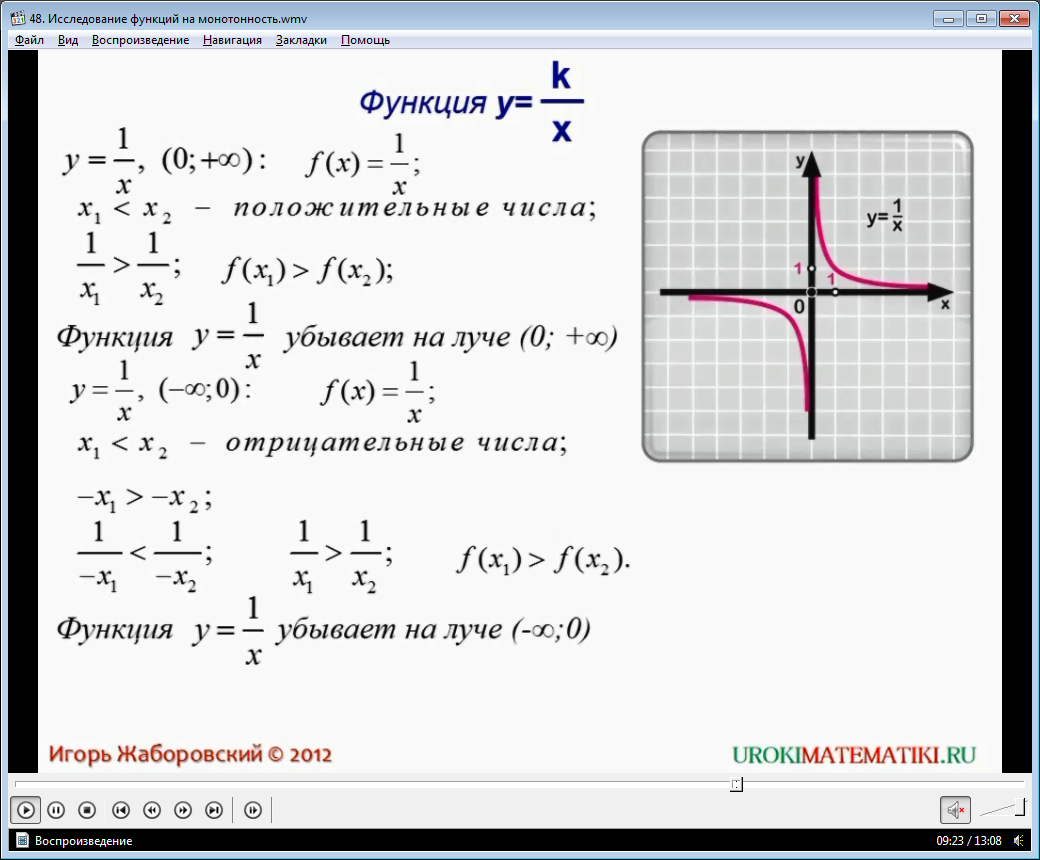
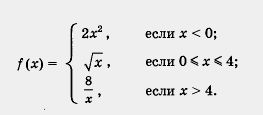Как найти промежутки монотонности гиперболы - Исправление недочетов и поиск решений вместе с Examum.ru

Свойства гиперболы

1) Область определения и область значений

По аналитическому заданию функции видно, что х ≠-a, поскольку знаменатель дроби не может ровняться нулю. Таким образом получим:

D(f)=(-∞;-а) U (-a;+∞)

Область значений

Е(f)=(-∞;+∞)

2) Нули функции

Если b=0, то график функции не пересекает ось ОХ;

Если b≠0, то гипербола имеет одну точку пересечения с ОХ:*

x=-(k+ab)/b

3) Промежутки знакопостоянства

Рассмотрим только 2 простых случая, остальные случаи вы можете рассмотреть аналитически самостоятельно по алгоритму из раздела Свойства функций -> Знакопостоянство

Случай 1: a=0, b=0, k>0

f(x)>0, при x ∈ (0; +∞)

f(x)<0, при x ∈ (-∞;0)

Случай 1: a=0, b=0, k<0

f(x)<0, при x ∈ (0; +∞)

f(x)>0, при x ∈ (-∞;0)

4) Промежутки монотонности

Аналогично с промежутками знакопостоянства рассмотрим только 2 случая

Случай 1: a=0, b=0, k>0

Функция убывает при

x ∈ (-∞;0) U (0; +∞)

Функция возрастает при

x ∈ (-∞;0) U (0; +∞)

5) Четность и нечетность

Функция является нечетной при a=0, b=0, то есть если имеет вид y=k/x

Источник

Дата публикации: 09 апреля 2017.

Урок и презентация на тему: «Исследование функции на монотонность. Определения возрастающей и убывающей функции»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Скачать:
Исследование функции на монотонность (PPTX)

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Алимов Ш.А.
Муравин Г.К.
Макарычев Ю.Н.

Определение возрастающей и убывающей функции

Определять, возрастает или убывает функция, мы уже пробовали и раньше. Для этого мы двигались по графику слева направо. Если функция двигалась снизу вверх мы говорили, что функция возрастает. Если же наоборот – сверху вниз, то функция убывает. Такое определение, с математической точки зрения, не корректно. График – это всего лишь иллюстрация зависимости функции от переменой.

Поиск промежутков возрастания и убывания функции называется исследованием функции на монотонность. Давайте введем строгие определения возрастающей и убывающей функции.

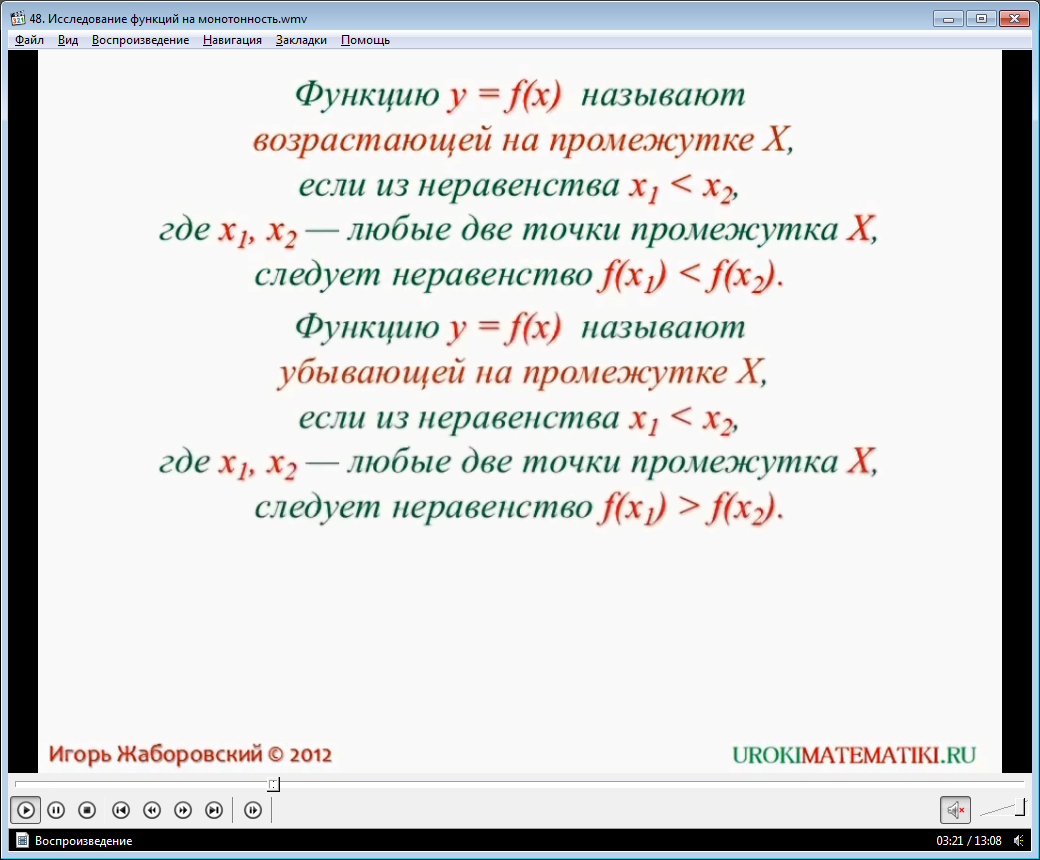
Определение. Функцию $y=f(x)$ называют возрастающей на промежутке $Х$, если из неравенства $x_1<x_2$ следует, что $f(x_1)<f(x_2)$. Здесь точки $х_1$ и $х_2$ любые из промежутка $Х$.
Другими словами, если всякому большему значению переменой из промежутка $Х$ соответствует большее значение функции, то такая функция будет возрастающей.

Определение. Функцию $y=f(x)$ называют убывающей на промежутке $Х$, если из неравенства $x_1<x_2$ следует, что $f(x_1)>f(x_2)$. Здесь точки $х_1$ и $х_2$ любые из промежутка $Х$.
Другими словами, если всякому большему значению переменой из промежутка $Х$ соответствует меньшее значение функции, то такая функция будет убывающей.

Давайте рассмотрим все изученные ранее функции и определим их промежутки возрастания и убывания.
1. Линейная функция $y=kx+m$.
Если $k>0$, то функция $y=kx+m$ возрастает на всей области определения.
Если $k<0$, то функция $y=kx+m$ убывает на всей области определения.
Давайте докажем наше утверждения, используя определения выше.

Для случая $k>0$. Рассмотрим два значения аргумента, такие что $x_1<x_2$. Тогда, согласно свойствам неравенств, $k*x_1<k*x_2$ (умножаем на положительное число, знак неравенства не меняется). Теперь воспользуемся другим свойством. Прибавим любое одинаковое число к левой и правой части, знак не меняется, то есть: $k*x_1+m<k*x_2+m$.
Это означает, что $f(x1)<f(x2)$, а значит функция возрастает.

Ребята, то, что функция $y=kx+m$ убывает на всей области определения для $k<0$, докажите самостоятельно!

Если функция возрастает на всей области определения, то такую функцию называют возрастающей. Если же она убывает на всей области определения, то – убывающей.

2. Функция $y=kx^2$.

Примеры функций

Рассмотрим конкретную функцию $y=x^2$.
Будем рассматривать ее на двух промежутках: $(-∞;0)$ и $(0;+∞)$.
Начнем с промежутка $(0;+∞)$.
Пусть $0<x_1<x_2$ – положительные числа. Тогда, возведя их в квадрат, получим неравенства того же смысла, то есть $0<x_1^2<x_2^2$. Но это означает, что $f(x_1)<f(x_2)$.
Значит на рассмотренном промежутке функция возрастает.

Теперь рассмотрим промежуток $(-∞;0)$.
Пусть $x_1<x_2<0$ – отрицательные числа. Перейдя к противоположному знаку, получим положительные числа и неравенства другого смысла $-x_1>-x_2>0$.
Мы можем опять возвести члены неравенства в квадрат, и получится неравенство того же смысла $0>x_1^2>x_2^2$. Это означает, что $f(x_1)>f(x_2)$, то есть меньшему значению переменой соответствует большее значение функции. Функция убывает на этом промежутке.

Из графика полученные свойства видны сразу. Но строгое доказательство гораздо ценней, чем иллюстрация. Ребята, самостоятельно исследуйте параболу на монотонность для $k<0$.

3. Функция $y=frac{k}{x}$.
Опять же давайте рассмотрим самый просто случай, при $k=1$.

Рассмотрим два промежутка: $хϵ(-∞;0)$ и $xϵ (0;+∞)$.

Начнем с промежутка $(0;+∞)$.
Пусть $0<x_1<x_2$ – положительные числа. Когда мы рассматривали неравенства, мы уточнили, что при делении единицы на положительные числа получится неравенство противоположного смысла, то есть $frac{1}{x_1}>frac{1}{x_2}$. Это означает,что $f(x_1)>f(x_2)$, то есть функция убывает на этом промежутке.

Рассмотрим промежуток $(-∞;0)$.
Пусть $x_1<x_2<0$ – отрицательные числа, перейдя к противоположному знаку получим положительные числа и неравенства другого смысла $-x_1>-x_2>0$. Тогда $frac{1}{-x_1}<frac{1}{-x_2}$ или $frac{1}{x_1}>frac{1}{x_2}$ – большему значению аргумента соответствует меньшее значение функции. Гипербола на рассмотренном промежутке убывает.
Для любых $k>0$ можно доказать, что гипербола на рассмотренных промежутках будет иметь те же промежутки монотонности.

4. Функция $y=sqrt{x}$.
В этот раз даже строить график не будем. Область определения функции корня: $D(y)=[0;+∞)$, то есть все числа из области определения положительные.
Рассмотрим $0<x_1<x_2$.
Давайте докажем, что $f(x_1)<f(x_2)$ или $sqrt{x_1}<sqrt{x_2}$.
Так как $х_1$ и $х_2$ – положительные числа, мы можем возводить их в квадрат, и неравенство будет того же смысла.
$(sqrt{x_1})^2<(sqrt{x_2})^2$ или $х_1<x_2$, что соответствует действительности. Таким образом, функция корня квадратного – возрастающая функция.

Пример.
Построить и прочитать график функции:
$f(x)=begin {cases} 3x^2, x<-1, \ sqrt{x+1}+3, -1≤x<3, \ frac{15}{x}, x≥3. end {cases}$
Решение.
Будем строить графики на соответствующих промежутках. Заметим, что график функции $y=sqrt{x+1}+3$ получается из графика $y=sqrt{x}$ сдвигом на одну единицу влево и три единицы вверх.

Осталось прочитать или найти свойства функции.
1. Область определения: множество действительных чисел.
2. $y>0$ при любых $x$. Равенства нулю нет.
3. Функция убывает на $(-∞;-1)$ и $[3;+∞)$.
Функция возрастает на $[-1;3)$.
4. Функция ограничена снизу, но неограничена сверху.
5. Наименьшего и наибольшего значения нет.
6. Функция непрерывна.
7. Область значений $(0;+∞)$.

Задачи для самостоятельного решения

1. Исследовать функцию $y=kx^2$ на монотонность, при $k<0$.
2. Исследовать функцию $y=frac{k}{x}$ на монотонность, при $k<0$.
3. Исследовать функцию $y=-sqrt{x}$ на монотонность.
4. Построить и прочитать график функции: $f(x)=begin {cases} -x^2+1, x<1, \ -sqrt{x-1}, 1≤x<5, \ -frac{10}{x}, x≥5. end {cases}$

Источник

Интервалы возрастания и убывания функции

С помощью данного сервиса можно найти интервалы возрастания и убывания функции в онлайн режиме с оформлением решения в Word.

Решение онлайн
Видеоинструкция

Исследование функции с помощью производной

Определение: Точка х₀ называется точкой локального максимума, если для любого х из окрестности точки х₀ выполняется неравенство: f(x₀)>f(x).

Определение: Точка х₀ называется точкой локального минимума, если для любого х из окрестности точки х₀ выполняется неравенство: f(x₀)<f(x).

Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.

Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.

Правило нахождения экстремумов функции y=f(x) с помощью первой производной

Найти производную функции f′(x).
Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
Вычислить значения функции в точках минимума и максимума.

С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.

Пример №1: Найти промежутки монотонности и экстремумы функции: f(x)=x³–3x².

Решение: Найдем первую производную функции f′(x)=3x²–6x.

Найдем критические точки по первой производной, решив уравнение 3x²–6x=0; 3x(x-2)=0 ;x = 0, x = 2

Исследуем поведение первой производной в критических точках и на промежутках между ними.

`x`	(-∞, 0)	0	(0, 2)	2	(2, +∞)
`f′(x)`	+	0	—	0	+
`f(x)`	возрастает	max	убывает	min	возрастает

f(0) = 0³ – 3*0² = 0

f(2) = 2³ – 3*2² = -4

Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);

точка минимума функции (2;-4); точка максимума функции (0;0).

Правило нахождения экстремумов функции y=f(x) с помощью второй производной

Найти производную f′(x).
Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
Найти вторую производную f″(x).
Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
Вычислить значения функции в точках экстремума.

Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f»(x) ≥ 0 при всех х [a, b].

Все вычисления можно проделать в онлайн режиме.

Пример №2. Исследовать на экстремум с помощью второй производной функцию: f(x) = x² – 2x — 3.

Решение: Находим производную: f′(x) = 2x — 2.

Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.

Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: f_min = f(1) = -4.

Ответ: Точка минимума имеет координаты (1; -4).

Источник

Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Исследование функций на монотонность

Исследование функций на монотонность

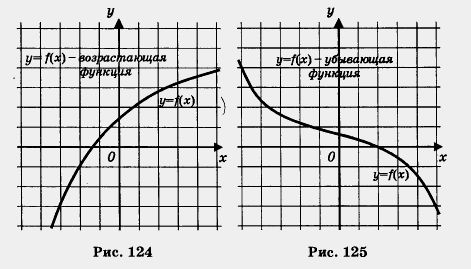
С понятиями возрастающей и убывающей функций мы впервые познакомились в курсе алгебры 7-го класса. Глядя на график функции, мы снимали соответствующую информацию: если двигаясь по графику слева направо мы в то же время движемся снизу вверх (как бы поднимаемся в горку), то мы объявляли функцию возрастающей (рис. 124); если же мы движемся сверху вниз (спускаемся с горки), то мы объявляли функцию убывающей (рис. 125).

Однако математики не очень жалуют такой способ исследования свойств функции. Они считают, что определения понятий не должны опираться на рисунок, — чертеж должен лишь иллюстрировать то или иное свойство функции на ее графике. Дадим строгие определения понятий возрастания и убывания функции.

Определение 1.Функцию у = f(x) называют возрастающей на промежутке X, если из неравенства х₁ < х₂— где хг и х2 — любые две точки промежутка X, следует неравенство f(x₁) < f(x₂).

Определение 2. Функцию у = f(x) называют убывающей на промежутке X, если из неравенства х₁ < х₂, где х₁ и х₂ — любые две точки промежутка X, следует неравенство f(x₁) > f(x₂).

На практике удобнее пользоваться следующими формулировками:

функция возрастает, если большему значению аргумента соответствует большее значение функции;
функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Используя эти определения и установленные в § 33 свойства числовых неравенств, мы сможем обосновать выводы о возрастании или убывании ранее изученных функций.

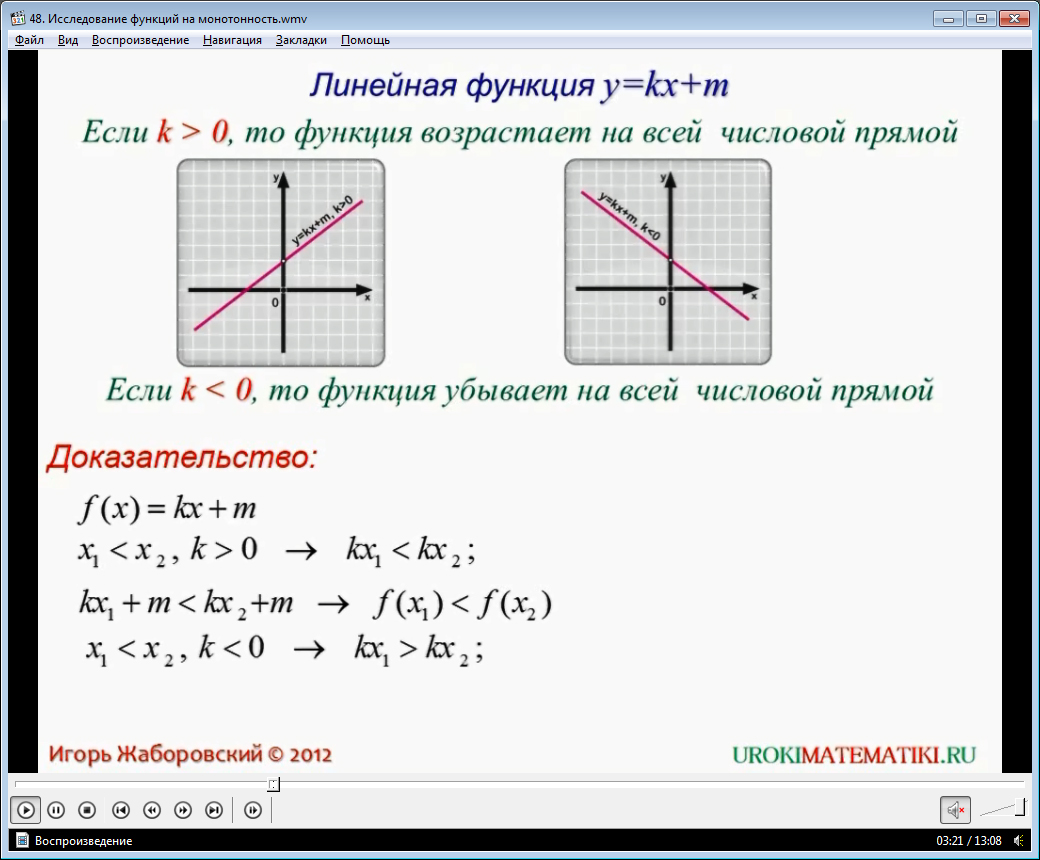
1. Линейная функция у = kx +m

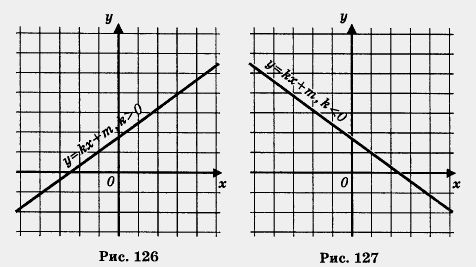
Если k > 0, то функция возрастает на всей числовой прямой (рис. 126); если k < 0, то функция убывает на всей числовой прямой (рис. 127).

Доказательство. Положим f(х) = kx +m. Если х₁ < х₂ и k > О, то, согласно свойству 3 числовых неравенств (см. § 33), kx₁ < kx₂. Далее, согласно свойству 2, из kx₁ < kx₂ следует, что kx₁ + m < kx₂ + m, т. е. f(х₁) < f(х₂).

Итак, из неравенства х₁ < х₂ следует, что f(х₁) < f(x₂). Это и означает возрастание функции у = f(х), т.е. линейной функции у = kx+ m.

Если же х₁ < х₂ и k < 0, то, согласно свойству 3 числовых неравенств, kx₁ > kx₂, а согласно свойству 2, из kx₁ > kx₂ следует, что kx₁ + m> kx₂ + т.

Итак, из неравенства х₁ < х₂ следует, что f(х₁) > f(х₂). Это и означает убывание функции у = f(x), т. е. линейной функции у = kx + m.

Если функция возрастает (убывает) во всей своей области определения, то ее можно называть возрастающей (убывающей), не указывая промежутка. Например, про функцию у = 2х — 3 можно сказать, что она возрастает на всей числовой прямой, но можно сказать и короче: у = 2х — 3 — возрастающая
функция.

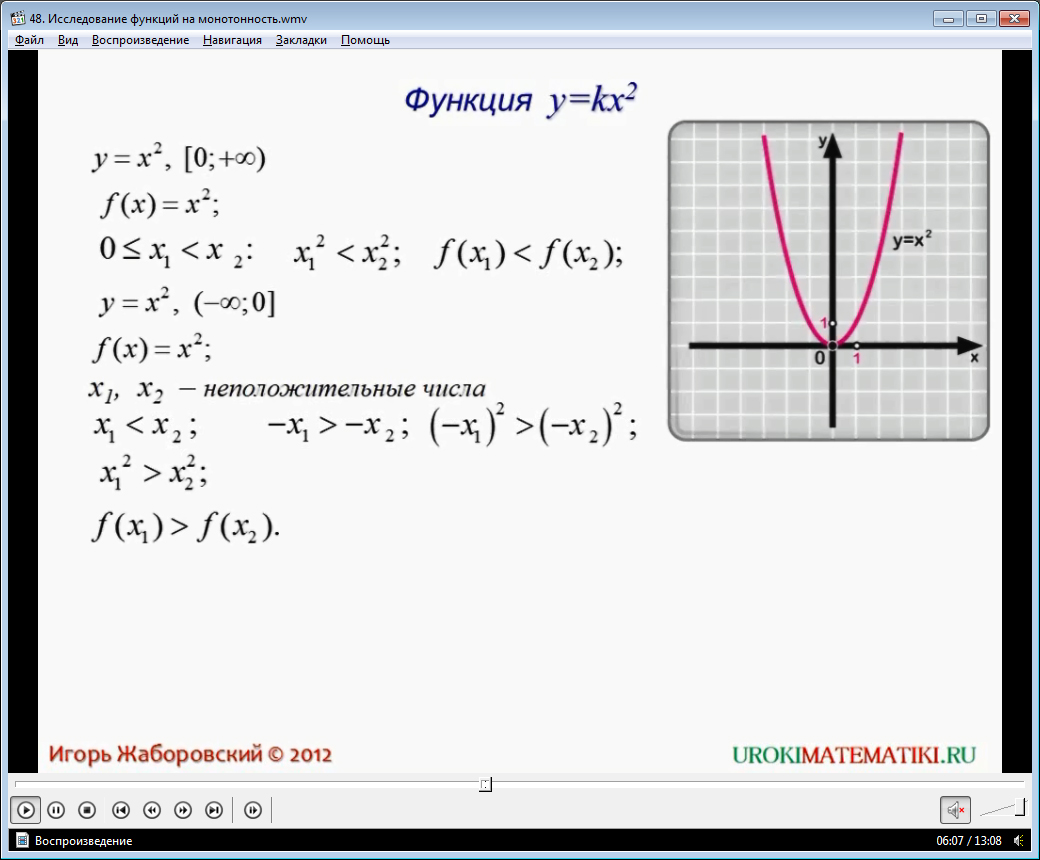
2. Функция у = х2

1. Рассмотрим функцию у = х² на луче [0, + ₀₀). Пусть 0 х₁ < х₂. Тогда, согласно свойству 6 числовых неравенств, , т. е.f(x₁) < f(x₂)- Итак, из х₁ < х₂ следует f(x₁) < f(x₂). Таким образом, функция у = х² возрастает на луче [0, + ₀₀) (рис. 128).

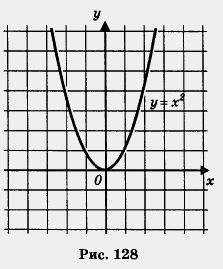
2. Рассмотрим функцию у = х² на луче (- со, 0]. Возьмем два неположительных числа х₁ и х₂, таких, что х₁ < х₂. Тогда, согласно свойству 3 числовых неравенств, выполняется неравенство — х₁ > — х₂. Так как числа — х₁ и — х₂ неотрицательны, то, возведя в квадрат обе части последнего неравенства, получим неравенство того же смысла (-х₁)² > (-х₂)², т.е. Это значит, что f(х₁) >f(х₂).

Итак, из неравенства х₁ < х₂ следует, что f(х₁) > f(х₂).

Поэтому функция у = х² убывает на луче (- ₀₀, 0] (рис. 128).
3. Функция у
1. Рассмотрим функцию на промежутке (0, + ₀₀).
Пусть х1 < х₂. Так как х₁ и х₂ — положительные числа, то из х₁< x₂ следует (см. пример 1 из § 33), т. е. f(x₁) > f(x₂).

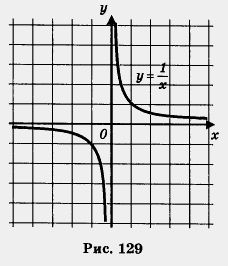
Итак, из неравенства х₁ < х₂ следует, что f(x₁) > f(x₂). Это значит, что функция убывает на открытом луче (0, + ₀₀) (рис. 129).

2. Рассмотрим функцию на промежутке (-оо, 0). Пусть х₁ < х₂, х₁ и х₂ — отрицательные числа. Тогда — х₁ > — х₂, причем обе части последнего неравенства — положительные числа, а потому (мы снова воспользовались неравенством, доказанным в примере 1 из § 33). Далее имеем , откуда получаем .

Итак, из неравенства х₁ < х₂ следует, что f(x₁) >f(x₂) т.е. функция убывает на открытом луче (-₀₀, 0)

Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание и убывание называют исследованием функции на монотонность.

Пример. Построить и прочитать график функции y = f{x), где

Решение.

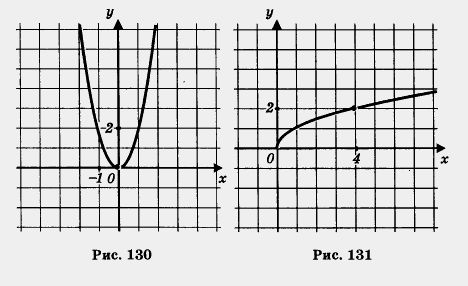
1) Построим график функции у = 2х² и возьмем ветвь этой параболы при х < 0 (рис. 130).

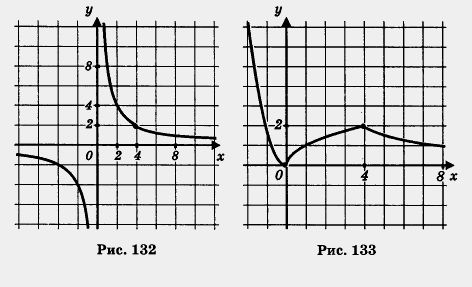
2) Построим график функции и выделим его часть на отрезке [0, 4] (рис. 131).

3) Построим гиперболу 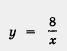и выделим ее часть на открытом луче (4, + ₀₀) (рис. 132).
4) Все три «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 133).

Прочитаем график функции у = f(x).

1. Область определения функции — вся числовая прямая.

2. у = 0 при х = 0; у > 0 при х > 0.

3. Функция убывает на луче (-оо, 0], возрастает на отрезке [0, 4], убывает на луче [4, + оо).

4. Функция ограничена снизу, но не ограничена сверху.

5. у_наим. = 0 (достигается при х = 0); Y_наиб— не существует.

6. Функция непрерывна.

7. Область значений функции — луч [0, + оо).

8. Функция выпукла вниз на луче (-оо, 0], выпукла вверх на отрезке [0, 4], выпукла вниз на луче [4, + оо).

Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.

_{Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:

Источник

В повседневной жизни часто приходится наблюдать множество процессов и явлений, при изучении которых нужно рассматривать самые разнообразные величины. Эти величины могут по-разному зависеть друг от друга. Закон, по которому одна величина зависит от другой, мы назвали функцией. Это одно из основных математических и общенаучных понятий, имеющее практическое применение во многих областях знаний и человеческой деятельности. Поэтому так важно уметь исследовать функции.

В данном видео уроке познакомимся с правилами исследования известных нам функций на монотонность.

Разглядывая графики, мы уже многое можем сказать об их функциях. Например, указать возрастает функция или убывает, как об этом говориться в видео уроке. Однако понятия возрастания и убывания функций в математике имеют свои точные определения, которые и приведены в предложенном нашему вниманию видеоматериале.

Так, чтобы судить о возрастании или убывании функции, зададим некоторый промежуток, на котором будем исследовать функцию. В видео уроке это промежуток Х. Выберем любые два числа, принадлежащие промежутку Х. Пусть это будут числа х₁ и х₂. Эти два числа являются двумя значениями аргумента, которым соответствуют два значения какой-либо функции f(x₁) и f(x₂). Если получается, что при х₁ > х₂ выполняется неравенство f(x₁) > f(x₂), то наша функция возрастает на промежутке Х.

Другими словами, можно сказать, что функция f(x) называется возрастающей на данном числовом промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Аналогично в видео уроке рассматривается понятие убывающей функции.

Далее в видеоматериале подробно проводится исследование линейной функции y = kx + m. Как известно, эта функция определена на всем множестве действительных чисел, то есть на всей числовой прямой. Даже если не проводить математических доказательств, а просто судить по графику этой функции, видно, что она ведет себя одинаково на всей области определения. Функция либо возрастает (график все время идет вверх), либо убывает (график все время идет вниз). В таких случаях можно не указывать промежуток, а просто сказать, что функция возрастающая или убывающая.

Возрастает или убывает функция y = kx + m, зависит от коэффициента k. Если коэффициент k положительный, то функция y = kx + m возрастает на всей области определения, то есть является возрастающей. Если коэффициент k отрицательный, то функция убывает. Доказательство возрастания или убывания функции y = kx + m основано на свойствах числовых неравенств и рассматривается в видео уроке.

Обычно, если функция только возрастает или только убывает на данном числовом промежутке, то ее называют монотонной на этом промежутке. Функция y = kx + m монотонна на всей своей области определения.

Следующая функция, которая рассматривается в видео уроке квадратичная y = kx². Как и в первом случае, областью ее определения являются все действительные числа x. По графику мы видим, что функция ведет себя неодинаково. К тому же коэффициент k может быть, как положительным, так и отрицательным. Пусть коэффициент k больше нуля. Тогда если аргумент принадлежит промежутку (-∞; 0], то функция убывает. А вот на числовом промежутке [0; +∞) функция возрастает. Доказательство возрастания и убывания функции на соответствующих числовых промежутках, основанное на свойствах числовых неравенств, и с учетом знака коэффициента k, приведено в видео уроке.

Переходим к рассмотрению функции y = k/x. Это график обратной пропорциональности. Он не является непрерывной линией. Действительно, x не может равняться нулю. Поэтому рассматриваем функцию на промежутках (-∞; 0) и (0; +∞). Графиком обратной пропорциональности является кривая, состоящая из двух ветвей, симметричных относительно начала координат. Она называется гиперболой. Расположение ветвей гиперболы, а также возрастание или убывание функции на соответствующих промежутках, зависит от знака коэффициентаk. Подробно и доказательно поведение гиперболы показано в видеоматериале.

Еще одна функция, которую рассматривают видео уроке это y = √x. Доказывается, что она является возрастающей.

Завершает видео урок пример построения графика и исследования функции, которая на разных участках числовой оси задается разными формулами.

Источник