Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Определение
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом.
Внимание!
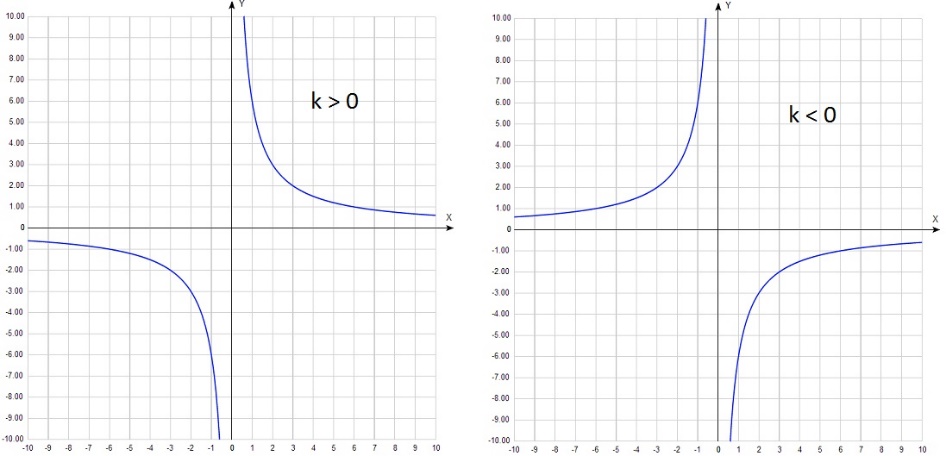
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом:
По данному рисунку видно, что нулей функции не существует.
Как найти нули функции?
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции.
Пример №1. Найти нули функции (если они существуют):
а) у= –11х +22
б) у= (х + 76)(х – 95)
в) у= – 46/х
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Получим х=2.
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Определение
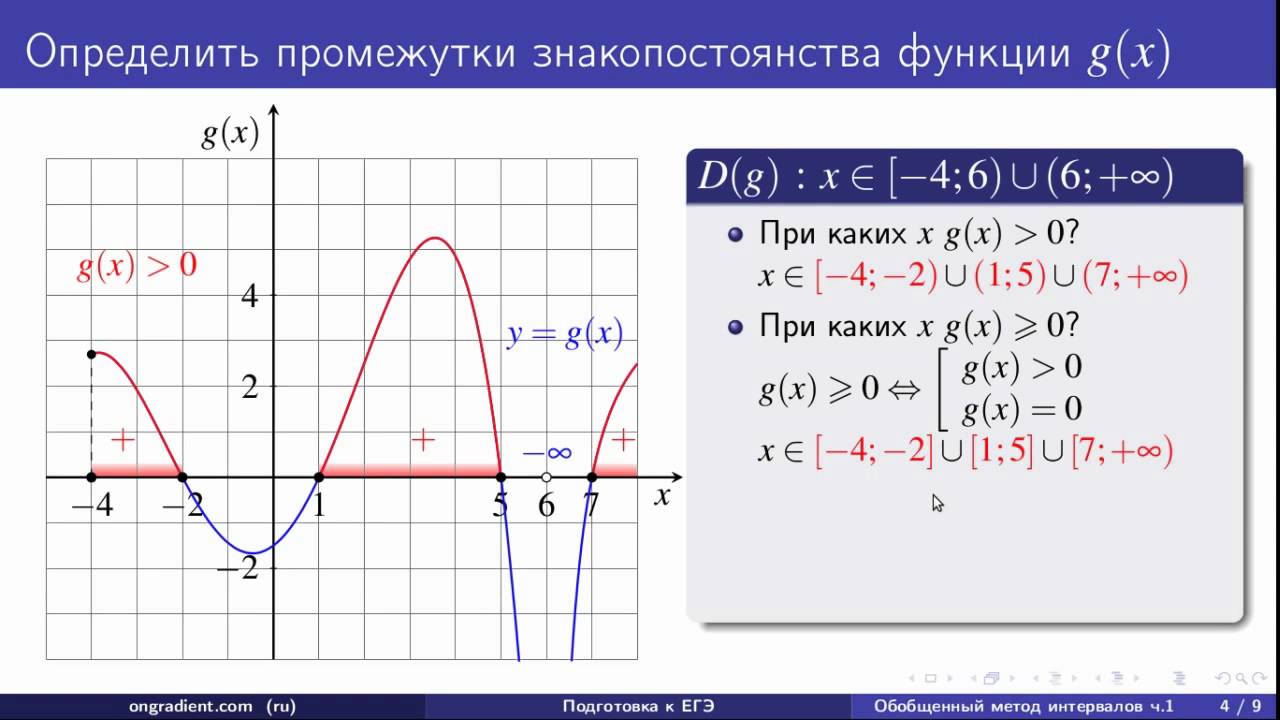
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Определение
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Даниил Романович | Просмотров: 16.1k
Промежутки знакопостоянства — такие промежутки на области определения, в которых значения функции сохраняют свой знак.
Для нахождения промежутков знакопостоянства функции y=f(x) надо решить неравенства f(x)>0, f(x)<0.
Пример:
Найдем промежутки знакопостоянства функции y=x2+x−2.
Решим неравенство: x2+x−2<0.
Сначала найдем нули функции f(x)=x2+x−2:
x2+x−2=0
D=1−4⋅(−2)=9
x=−1±32
x1=1,x2=−2
Таким образом, получились промежутки значений аргумента, в которых функция сохраняет знак:
(−∞;−2),(−2;1),(1;+∞)
Для того, чтобы определить знак функции на каждом из этих промежутков, найдем значение функции в произвольной точке из каждого промежутка. Точки выбираются из соображений удобства вычислений.
Возьмем значения аргумента: −3∈(−∞;−2), 0∈(−2;1) и 2∈(1;+∞) и найдем для них значения функции.
f(−3)=(−3)2+(−3)−2=9−3−2=4
f(0)=−2
f(2)=4
Значит, в промежутке (−∞;−2) функция принимает положительные значения, в промежутке (−2;1) — отрицательные и в промежутке (1;+∞) — положительные.
Это же можно наблюдать на графике функции:
На
прошлом уроке мы с вами изучили понятие функция. Изучили её график и научились
находить область определения и область значений функции.
Свойства
функций:
·
нули
функции;
·
промежутки
знакопостоянства функции;
·
промежутки
монотонности функции.
Нули
функции
Определение:
Нулями
функции называют такие значения аргумента, при которых
функция равна нулю.
В
данном случае функция задана графически и мы
определили нули функции по графику. Так же нули функции можно находить по
формуле, с помощью которой задана функция.
Решив
уравнение, мы найдём те значения х, при которых функция равна нулю.
Стоит
обратить внимание на то, что не каждая функция имеет нули.
График
не пересекает ось икс ни в одной точке.
Промежутки
знакопостоянства функции
Определение:
Промежутки
знакопостоянства функции
— это такие промежутки из области определения, на которых данная функция
принимает значения только одного знака, либо положительные, либо отрицательные.
Функция
принимает положительные значения:
И
отрицательные значения:
Запишите
промежутки знакопостоянства функции:
Положительные
и отрицательные значения функции:
Промежутки
монотонности функции
Определение:
Функция
называется возрастающей в некотором промежутке, если большему значению
аргумента из этого промежутка соответствует большее значение функции.
Определение:
Функция
называется убывающей в некотором промежутке, если большему значению
аргумента из этого промежутка соответствует меньшее значение функции.
Определение:
Промежутками
монотонности называют такие промежутки из области
определения, на которых функция либо возрастает, либо убывает.
Опишем
свойства функции:
Графиком
является прямая, поэтому для построения достаточно
двух точек:
Найдём
значения функции:
Областью
определения и областью значений будет множество всех действительных чисел. Ведь
х и у могут быть любыми числами.
Найдём
нули функции:
Запишем
промежутки знакопостоянства:
Запишем
промежутки монотонности:
Свойства функций.
Итак, мы познакомились с функцией, узнали, что такое область определения и область значений функции. Теперь рассмотрим свойства функций. Их существует много, однако, изучаются они постепенно. В 9 классе мы знакомимся с нулями функции, промежутками возрастания и убывания (монотонность) и промежутками знакопостоянства и чётностью (нечётностью) функции. Рассмотрим их подробно.
-
Нулями функции называются значения независимой переменной (аргумента), при которых значение функции равно нулю. В графической интерпретации нулями функции являются абсциссы точек пересечения графика с осью абсцисс (осью х).
На графике нули функции: .
Для того, чтобы найти нули функции, заданной аналитически, необходимо решить уравнение: . Корни этого уравнения являются нулями функции.
Например, найти нули функции .
или
Значит, нули функции: .
-
Промежутками знакопостоянства функции называются промежутки значений аргумента, на которых значения функции либо только положительны, либо только отрицательны. Другими словами, это те промежутки, на которых функция сохраняет свой знак.
Рассматривая график сверху, найдём промежутки знакопостоянства.
-
функция принимает только положительные значения на тех участках графика, где он находится выше оси Ох, т.е. при ;
-
функция принимает только отрицательные значения на тех участках графика, где он находится ниже оси Ох, т.е. при .
Для того, чтобы найти промежутки знакопостоянства функции, заданной аналитически, необходимо решить неравенства: и . Решения этих неравенств и будут промежутками знакопостоянства функции.
Например, найти промежутки знакопостоянства функции .
Это неравенство можно решить двумя способами: с помощью систем неравенств и методом интервалов. Метод интервалов будет рассмотрен нами чуть позже, поэтому воспользуемся системами неравенств. Произведение двух множителей положительно, если эти множители имеют одинаковый знак. Значит, получается совокупность двух систем:
или
Значит, при
Теперь находим промежутки, на которых функция принимает отрицательные значения.
Произведение двух множителей отрицательно, если эти множители имеют разные знаки, т.е.
или
Значит, при .
-
Чётной называется функция, если противоположным значениям аргумента соответствуют одинаковые значения функции, т.е. . График чётной функции симметричен относительно оси ординат (оси Оу).
Нечётной называется функция, если противоположным значениям аргумента соответствуют противоположные значения функции, т.е. . График нечётной функции симметричен относительно начала координат.
На рисунке слева график чётной функции, на рисунке справа – нечётной функции.
Для того, чтобы определить чётность функции, заданной аналитически, необходимо в заданную функцию вместо х подставить –х и произвести упрощение. Если в результате получится функция, равная заданной, то функция чётная; если получится функция, противоположная заданной, то она нечётная; если не получится ни один из предложенных вариантов, то функция не является ни чётной, ни нечётной.
Например, исследовать на чётность функцию .
Находим значение этой функции при противоположном значении х, т.е.
.
Полученное выражение не совпадает с заданным и не противоположно ему, значит, функция не является ни чётной, ни нечётной. Её график не симметричен относительно оси Оу и не симметричен относительно начала координат.
Приведём ещё один пример: .
.
После упрощения получили выражение, полностью совпадающее с заданным. Значит, функция является чётной и её график симметричен относительно начала координат.
-
Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции (или меньшему значению аргумента соответствует меньшее значение функции), т.е. если при , то функция возрастающая.
Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции (или меньшему значению аргумента соответствует большее значение функции), т.е. если при , то функция убывающая.
Для примера рассмотрим графики на рисунках выше.
Синий график: функция возрастает при
функция убывает при
Зелёный график: функция возрастает при
функция убывает при
Промежутки возрастания и убывания функции называются промежутками монотонности функции.
Если функция задана аналитически, то нахождение промежутков монотонности является более сложным процессом и он изучается в 11 классе. Мы ограничимся определением этих промежутков по графикам.
-
Наибольшим значением функции называется самое большое значение функции по сравнению со всеми остальными.
Наименьшим значением функции называется самое маленькое значение функции по сравнению со всеми остальными.
Строгое определение наибольшего и наименьшего значения функции будет дано в старших классах.
На синем графике наибольшего значения нет, т.к. график бесконечен в положительном направлении оси Оу. А наименьшее значение равно . Записывается это так: .
На зелёном графике нет ни наибольшего, ни наименьшего значения функции.
-
На рисунках изображены части графиков нечётных функций. Достройте эти графики.
-
Какая из данных функций является чётной, а какая – нечётной:
- Приведите необходимые обоснования.
-
Докажите, что – чётная функция, а – нечётная, если:
-
Является ли чётной или нечётной функция , если:
-
На рисунках изображены части графиков чётных функций. Достройте эти графики.
-
Постройте график функции , зная, что при её значения могут быть найдены по формуле:
-
-
Известно, что функция – чётная и она обращается в нуль при и . Укажите другие значения аргумента, при которых .
-
Известно, что функция – чётная и она принимает значения, равные нулю, при и . Укажите другие значения аргумента, при которых .
-
Известно, что уравнение , где – нечётная функция с областью определения , имеет положительные корни и . Найдите неположительные корни уравнения.
-
Известно, что уравнение , где – нечётная функция с областью определения , имеет положительные корни и . Найдите неположительные корни уравнения.
-
Линейная функция является нечётной. Найдите значение .
-
Функция , где – некоторое число, является чётной. Найдите значение .
-
Известно, что и – нечётные функции. Верно ли утверждение, что нечётной является функция , если:
Известно, что и – нечётные функции. Верно ли утверждение, что чётной является функция , если: Представьте каким-либо способом функцию в виде суммы чётной и нечётной функций, если:
-
-
Функция , область определения которой – промежуток , задана графиком на рисунке. Укажите промежутки, на которых эта функция возрастает и на которых убывает.
-
Функция , область определения которой – промежуток , задана графиком на рисунке. Укажите промежутки, на которых эта функция возрастает и на которых убывает.
-
Какая из линейных функций и является возрастающей, убывающей и почему?
-
Докажите, что функция является убывающей на промежутке и возрастающей на промежутке .
-
Докажите, что функция является возрастающей на промежутке и убывающей на промежутке .
-
Укажите промежутки возрастания и убывания функций .
-
Определите характер монотонности функций и . Докажите, что функция возрастающая, а функция — убывающая.
-
Известно, что функция является монотонной и что уравнение имеет корень, равный . Имеет ли это уравнение другие корни?
-
Известно, что уравнение , где – монотонная функция, имеет корень, равный . Имеет ли это уравнение другие корни?
-
Известно, что функция возрастает на промежутке . При каких значениях, принадлежащих этому промежутку, верно неравенство:
Известно, что функция убывает на промежутке . При каких значениях, принадлежащих этому промежутку, верно неравенство: Известно, что функции и – убывающие. Является ли убывающей функция , если: Известно, что функции и – возрастающие. Является ли возрастающей функция , если: Известно, что функция определена на множестве и возрастает на промежутке , где . Как изменяется эта функция на промежутке , если:
-
– функция нечётная?
-
-
Известно, что функция определена на множестве и убывает на промежутке , где . Как изменяется эта функция на промежутке , если:
-
– функция нечётная?
-
-
Найдите наибольшее и наименьшее значения функции:
-
;
-
Укажите значение аргумента, при котором функция принимает наименьшее значение. Существует ли наибольшее значение этой функции?
-
Укажите значение аргумента, при котором функция принимает наибольшее значение. Существует ли наименьшее значение этой функции?
-
Найдите область определения функции:
-
-
Найдите нули функции и области положительных и отрицательных значений, если:
-
-
Изобразите схематически график функции , зная результаты исследования функции:
-
функция является непрерывной и нечётной;
-
при
-
функция возрастает на промежутке .
-
Изобразите схематически график функции , зная результаты исследования функции:
-
функция является непрерывной и чётной;
-
при при
-
функция возрастает на промежутке .
-
С помощью графика определите свойства функции:
-
область определения функции;
-
область значений функции;
-
нули функции;
-
промежутки знакопостоянства;
-
чётность функции;
-
монотонность функции (промежутки возрастания и убывания);
-
наибольшее и наименьшее значение функции.
-
Определить свойства функций, заданных формулами:
-
-
С помощью графика определите свойства функции:
-
область определения функции;
-
область значений функции;
-
нули функции;
-
промежутки знакопостоянства;
-
чётность функции;
-
монотонность функции (промежутки возрастания и убывания);
-
наибольшее и наименьшее значение функции.
-
Найдите нули функции (если они существуют):
-
С помощью графика определите свойства функции:
-
область определения функции;
-
область значений функции;
-
нули функции;
-
промежутки знакопостоянства;
-
чётность функции;
-
монотонность функции (промежутки возрастания и убывания);
-
наибольшее и наименьшее значение функции.
-
Постройте график функции и опишите её свойства.
-
Постройте график функции и опишите её свойства.
-
Выясните свойства функции
-
Выясните свойства функции
-
С помощью графика определите свойства функции:
-
область определения функции;
-
область значений функции;
-
нули функции;
-
промежутки знакопостоянства;
-
чётность функции;
-
монотонность функции (промежутки возрастания и убывания);
-
наибольшее и наименьшее значение функции.
-
Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?
-
Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?
-
Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?
-
Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?
12
-
-
-
-
-
-
-
-
На прошлых уроках мы изучили понятия функция, график функции, область определения и область значений функции.
По графику функции можно определять и другие свойства функции. Рассмотрим их.
Нули функции.
Не трудно догадаться что мы будем рассматривать при каких значениях икс функция обращается в нуль. То есть, нулями функции называют значения аргумента, при которых функция обращается в нуль.
Рассмотрим на примере.
На экране изображен график функции. Он пересекает ось абсцисс в четырех точках. Найдем координаты этих точек. Первая точка имеет координаты минус два нуль, вторая – один нуль, третья – четыре нуль и четвертая – семь нуль. То есть у всех этих точек ордината равна нулю, а абсциссы имеют разные значения.
Можем записать, что наша функция равна нулю при икс равном минус двум, икс равном одному, икс равном четырем и икс равном семи. То есть, нулями нашей функции являются числа минус два, один, четыре и семь.
Также нули функции можно находить по формуле, с помощью которой задана функция.
Найдем нули функции, заданной формулой.
Для этого составим соответствующее уравнение игрек равен нулю. Решив его, мы найдем значения икс, при которых функция равна нулю, то есть нули функции. Получаем икс равен нулю или двум. Нулями данной функции являются числа нуль и два.
Любая ли функция будет иметь нули?
Для ответа на этот вопрос рассмотрим функцию игрек равен икс в квадрате плюс два. Квадрат любого числа есть число неотрицательное. Прибавляя к неотрицательному числу два, получим число положительное. Значит, график этой функции не пересекает ось абсцисс ни в одной точке.
Таким образом, не любая функция имеет нули функции.
Вернемся к первому примеру. По графику видно, что аргумент икс принимает значения от минус пяти до восьми. Значит областью определения функции является промежуток от минус пяти до восьми.
Нули функции разбивают область определения функции на несколько промежутков. Определите, какой знак имеют значения функции на каждом из промежутков.
На промежутках от минус пяти до минус двух, от одного до четырех и от семи до восьми график функции расположен выше оси абсцисс, значит, функция принимает на этих промежутках положительные значения. Запишем это следующим образом: игрек принимает положительные значения при икс, принадлежащем объединению промежутков от минус пяти до минус двух, от одного до четырех и от семи до восьми, включая минус пять и восемь. На промежутках от минус двух до одного и от четырех до семи график функции расположен ниже оси абсцисс, следовательно, функция на этих промежутках принимает отрицательные значения. Запишем это так: игрек принимает отрицательные значения при икс, принадлежащем объединению промежутков от минус двух до одного и от четырех до семи.
Таким образом, промежутки в которых функция принимает значения только одного знака, называют промежутками знакопостоянства функции.
Выясним теперь, как изменяются (увеличиваются или уменьшаются) значения данной функции с изменением икс от минус пяти до восьми.
На графике видно, что с возрастанием икс от минус пяти до нуля и от двух целых пяти десятых до пяти значения игрек уменьшаются. А с возрастанием икс от нуля до двух целых пяти десятых и от пяти до восьми значения игрек увеличиваются.
Говорят, что в промежутках от минус пяти до нуля и от двух целых пяти десятых до пяти функция является убывающей, а на промежутках от нуля до двух целых пяти десятых и от пяти до восьми – возрастающей.
Запишем определения.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции. Другими словами, функцию игрек равен эф от икс называют возрастающей, если для любых икс один и икс два из этого промежутка, таких что икс два больше икс один, выполняется неравенство эф от икс два больше чем эф от икс один. Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. Другими словами, функцию игрек равен эф от икс называют убывающей, если для любых икс один и икс два из этого промежутка, таких что икс два больше икс один, выполняется неравенство эф от икс два меньше чем эф от икс один.
Если функция возрастает на всей области определения, то ее называют возрастающей функцией, а если убывает, то убывающей функцией.
Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция
На рисунке изображен график функции игрек равен эф от икс, где икс принимает значения из промежутка от минус семи до пяти, включая минус семь и пять. Укажите промежутки, в которых функция возрастает, и промежутки, в которых она убывает.
Таким образом, сегодня мы рассмотрели следующие свойства функций: нули функции, промежутки знакопостоянства функции, промежутки монотонности функции. Давайте ещё раз вспомним эти понятия.
Нули функции это значения аргумента, при которых функция обращается в нуль. Промежутки знакопостоянства функции это промежутки из области определения, на которых функция сохраняет знак (либо положительна, либо отрицательна). Промежутки монотонности функции это такие промежутки из области определения, на которых функция либо возрастает, либо убывает.
Опишите свойства функции игрек равен минус два икс плюс три. Удобнее определять свойства функции по графику. Поэтому построим график заданной функции.
Нам дана линейная функция, графиком которой является прямая. Для построения прямой достаточно знать координаты двух точек. Определим их. Значение функции при икс равном нулю равно трем. При икс равном двум значений функции равно минус одному. Проведем прямую через эти точки.
Опишем свойства заданной функции. Областью определения функции является множество всех действительных чисел. Областью значений функции также является множество всех действительных чисел. Найдем нули функции. При определении их по графику мы можем получить неточные значения. Поэтому найдем их по формуле, задающей данную функцию. Находим нули функции из линейного уравнения. Решив его, получаем значение икс, равное одной целой пяти десятым. То есть функция равна нулю при икс равном одной целой пяти десятым.
Запишем промежутки знакопостоянства. Функция принимает положительные значения на промежутке от минус бесконечности до одной целой пяти десятых, не включая концы. И отрицательные значения на промежутке от одной целой пяти десятых до плюс бесконечности, не включая концы.
Что касается промежутков монотонности функции, то по графику видно, что функция убывает на всей области определения. Так и запишем.