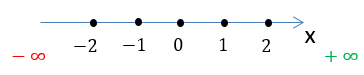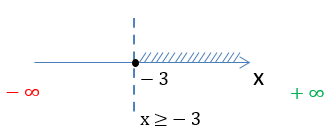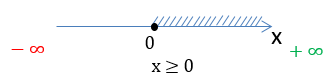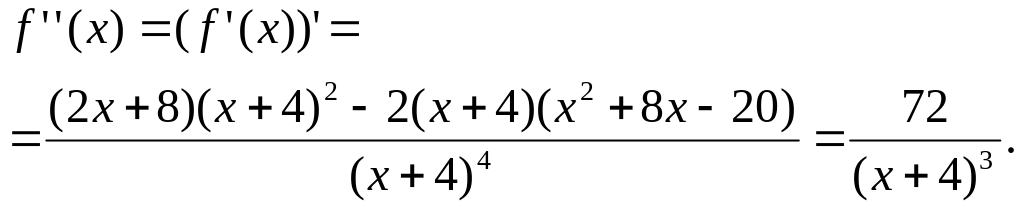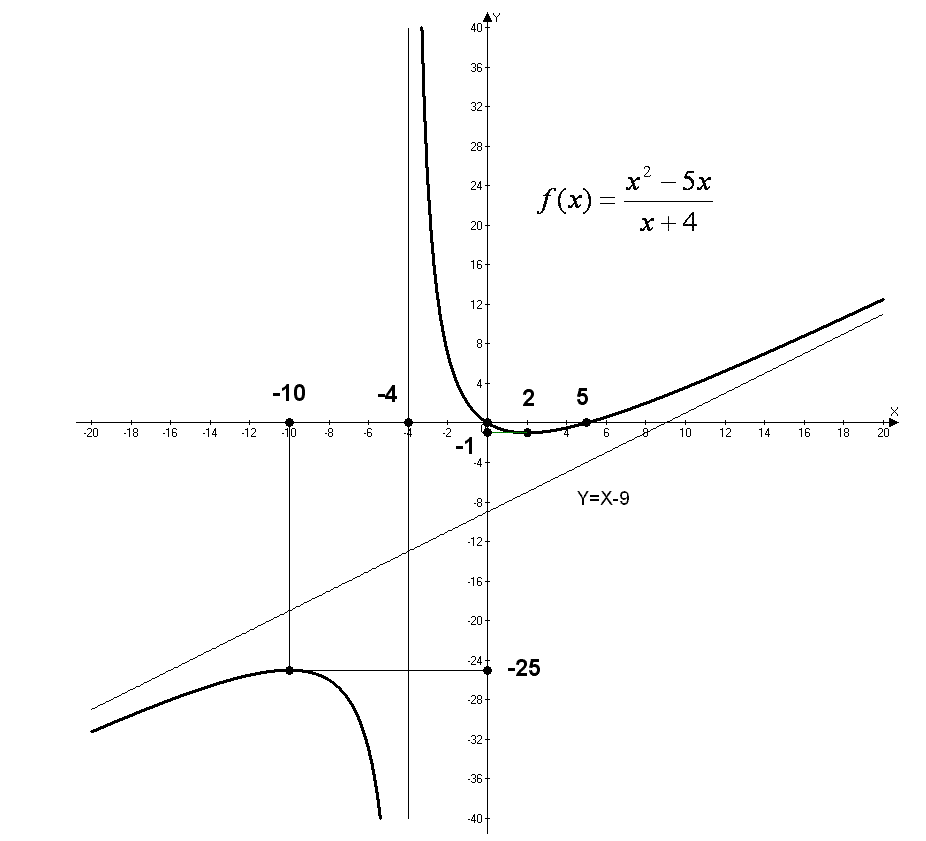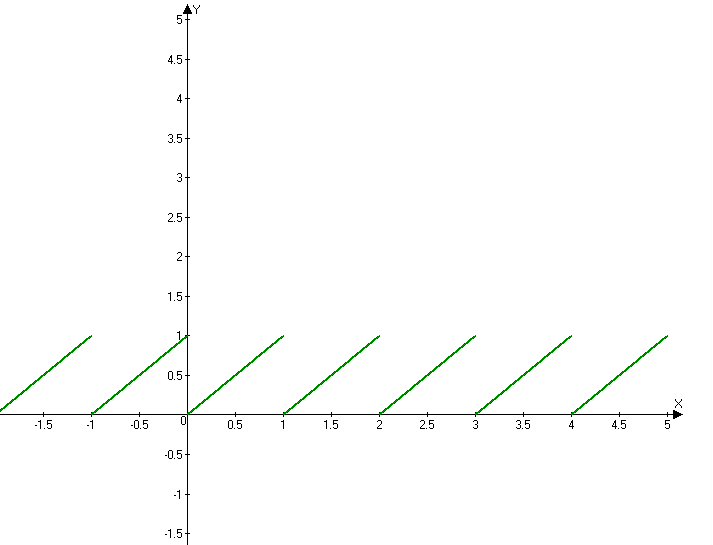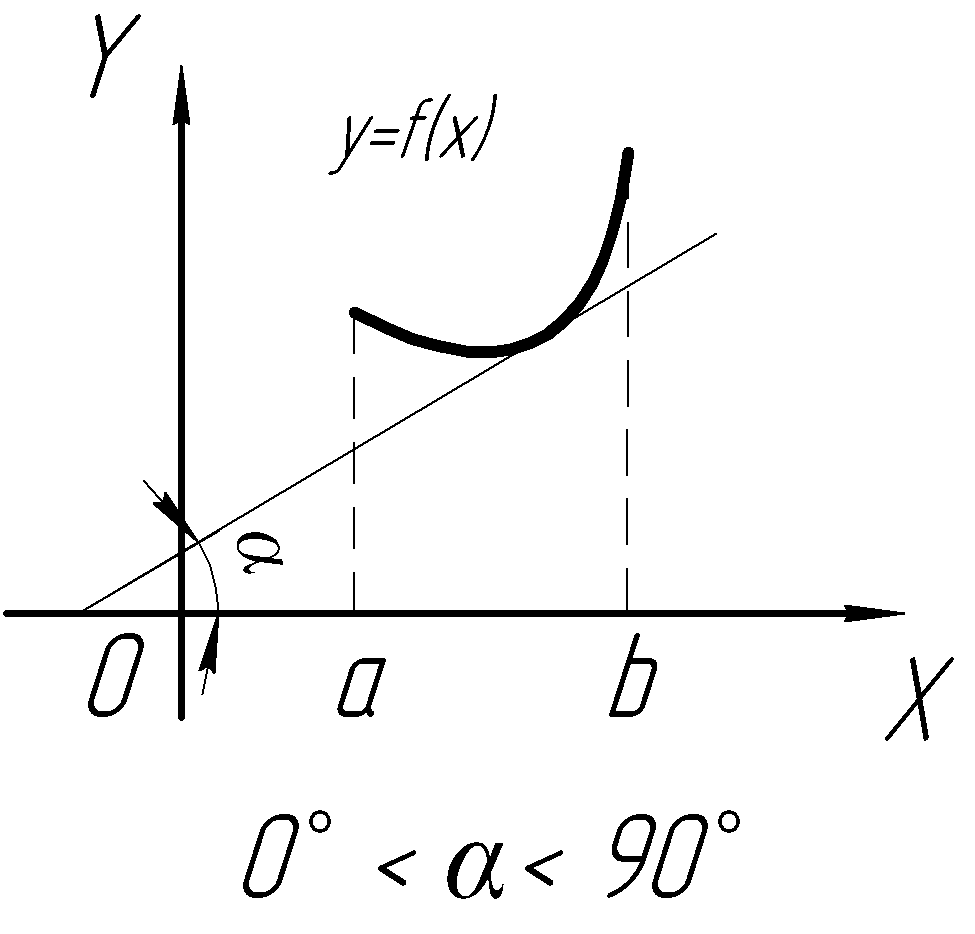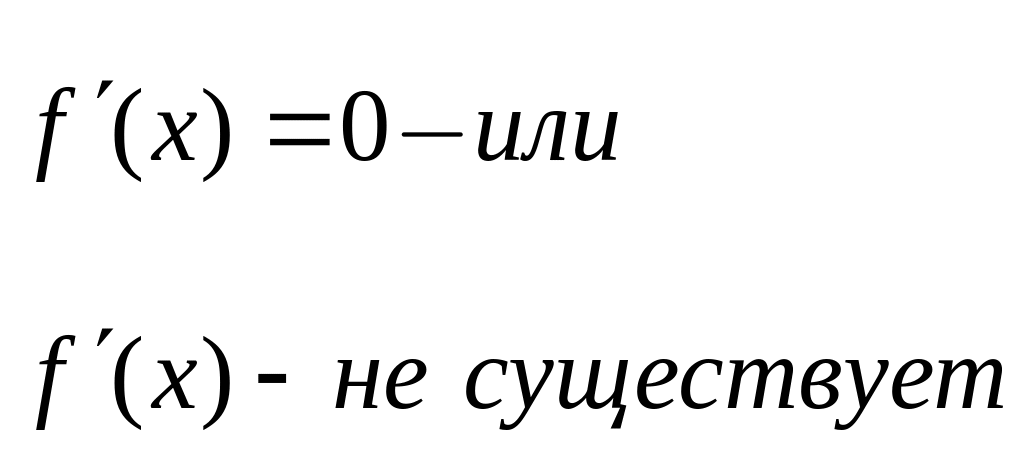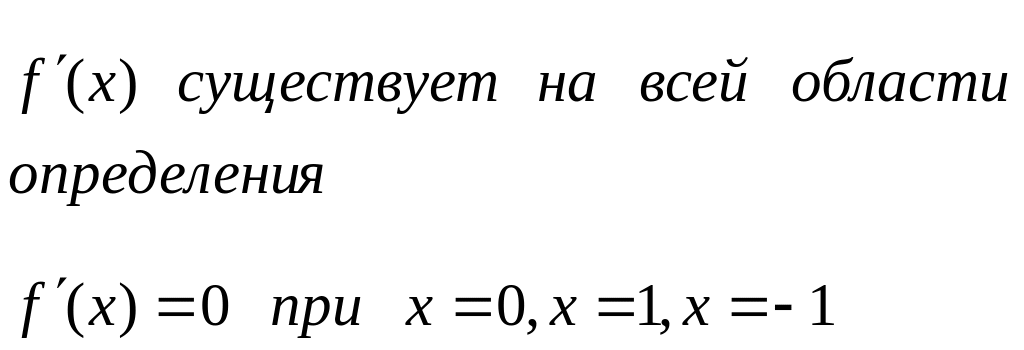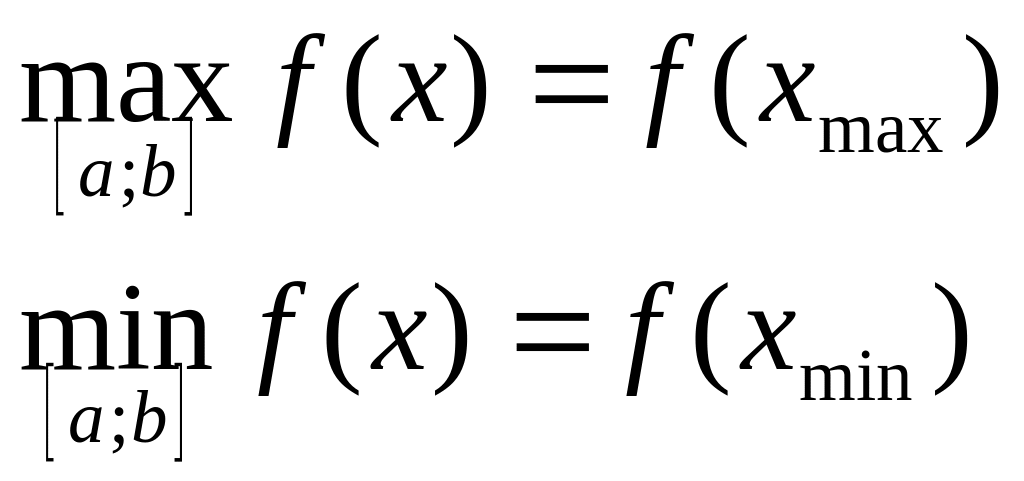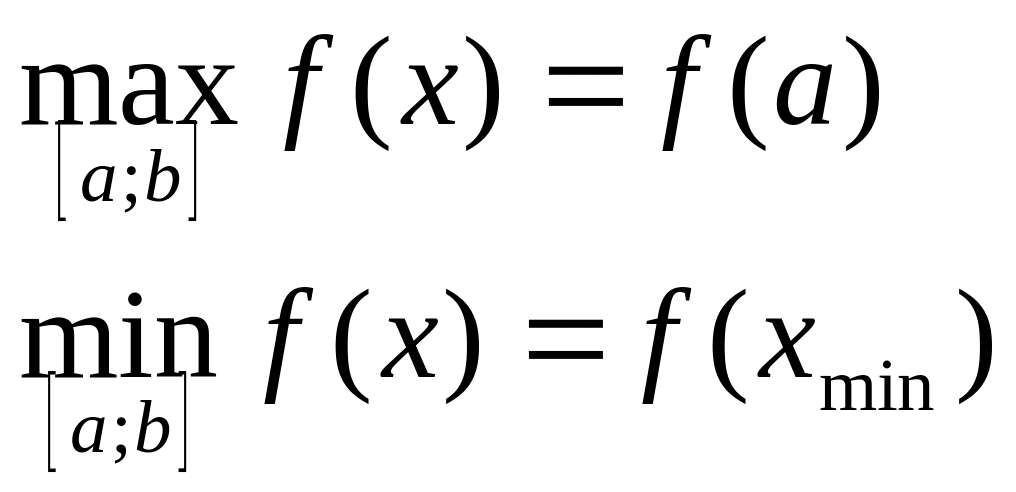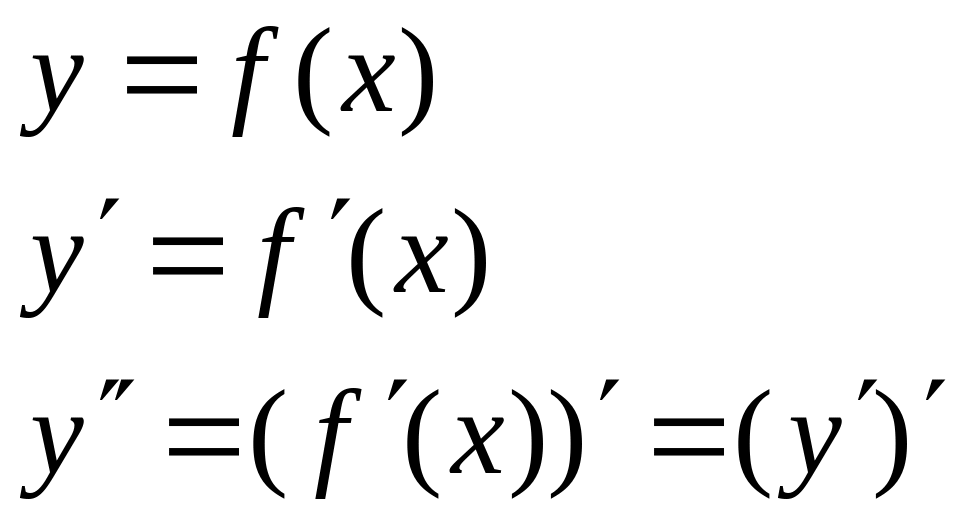Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
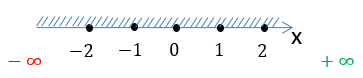
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
Запишем результат по правилам записи неравенств.
D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
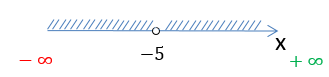
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
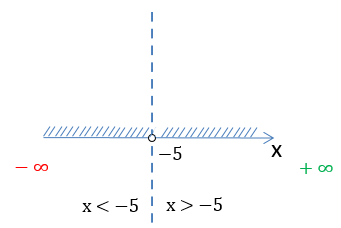
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».
x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
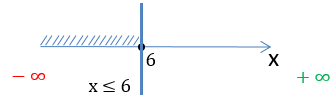
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
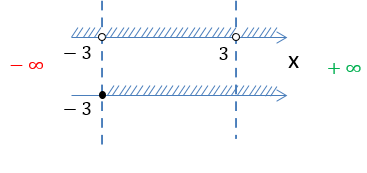
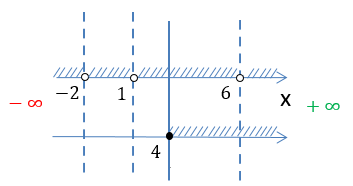
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
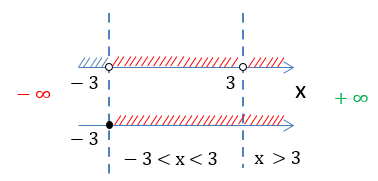
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
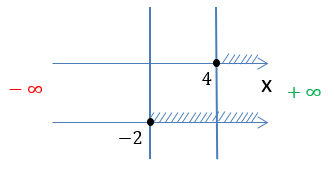
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции
0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить
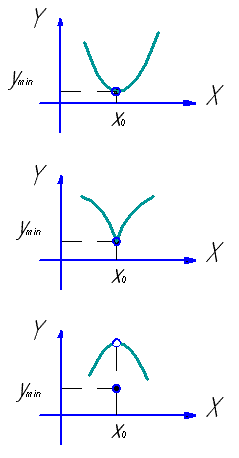
1. Область определения функции.
2. Четность, нечетность, периодичность.
3. Точки пересечения с осями координат.
4. Производная и критические точки.
5. Промежутки возрастания, убывания и
точки экстремума и значение функции в
этих точках.
6. Поведение функции на концах области
определения и асимптоты графика функции
(вертикальные, горизонтальные, и
наклонные)
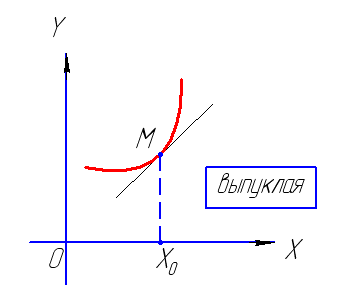
7. Вторая производная и исследование
функции на выпуклость и вогнутость, и
нахождение точек перегиба.
8. Нахождение контрольных точек.
9. Построение графика по результатам
исследования.
Приложения.
Таблица
1. Как найти область определения функции.
Таблица
2. Четные и нечетные функции.
Таблица
3. Периодические функции.
Таблица
4. Применение производной к исследованию
функции.
Таблица
5. Асимптоты графика функции.
Таблица
6. Вторая производная и точки перегиба.
Примеры.
Пример
1. Исследовать
функцию
и построить график функции.
Пример
2. Исследовать
функцию
и построить график функции.
Пример
3. Исследовать
функцию
и построить график функции.
|
Схема исследования эскиза |
|||||||
|
Схема |
Пример |
||||||
|
1. Область определения функции (см. |
Область определения:
|
||||||
|
2. Четность, нечетность (табл. периодичность |
Функция ни четная, ни нечетная и не |
||||||
|
3. Точки пересечения с осями координат |
x = 0; y = 0 |
||||||
|
y = 0;
|
|||||||
|
4. Производная и критические точки |
|
||||||
|
|
|||||||
|
5. Промежутки возрастания, убывания |
|
||||||
|
6. Поведение функции на концах (табл. 5) |
П слева
При справа x
Так как
то при тогда
т.е. y |
||||||
|
7. Вторая производная и исследование |
П оскольку |
||||||
|
|
||||||
|
|
|
Как найти |
|||
|
№ |
Вид функции |
Ограничения
(f(x) существуют!) |
Формулировка |
|
1 |
|
|
Знаменатель дроби не равен нулю |
|
2 |
|
|
Под знаком корня четной степени может |
|
3 |
|
|
Под знаком логарифма может стоять |
|
4 |
(a |
|
В основании логарифма может стоять |
|
5 |
|
|
Под знаком котангенса может стоять (k – целое) |
|
6 |
|
|
Под знаком котангенса может стоять (k – целое) |
|
7 |
|
|
Под знаком арксинуса и арккосинуса |
|
8 |
|
||
|
9 |
|
||
|
а) |
x – любое число |
||
|
б) — |
|
||
|
в) — положитель-ное не целое число |
|
||
|
г) — отрицатель-ное не целое число |
|
Таблица 1
Таблица 2
|
Четные и нечетные |
|
|
Четная функция |
Нечетная функция |
|
Определение. Функция f
|
Определение. Функция f
|
|
Свойства |
Свойства |
|
График четной функции |
График нечетной функции |
|
Примеры четных функций |
Примеры нечетных функций |
|
|
|
|
|
|
Таблица 3
|
Периодические |
|||
|
Определение. |
|||
|
Свойства |
|||
|
1. Если число Т период функции f k*T |
|||
|
2. Если функция y=f(x) (A, b, k |
|||
|
3. Если функция y=f(x) |
|||
|
4. Для построения графика периодической влево и вправо |
|||
|
Примеры периодических функций |
|||
|
y=sin(x) T=2π
|
y=cos(x) T=2π
|
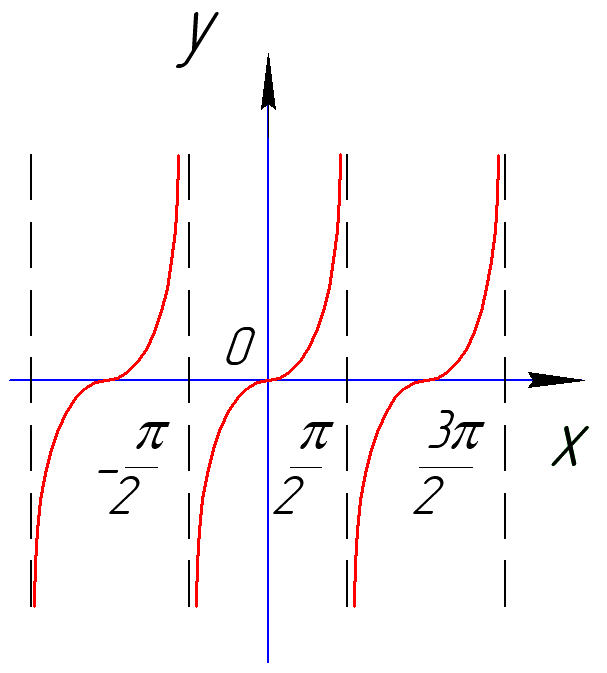
y=tg(x) T=π
|
y=ctg(x) T=π
|
|
y=sin(3x)
T=
|
y={x}- дробная часть х T=1
|
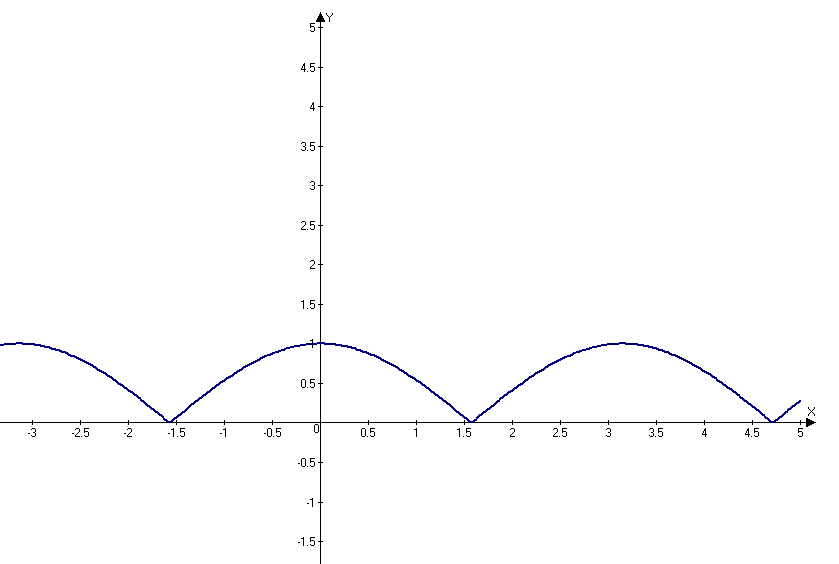
y=|cos(x)| T=π
|
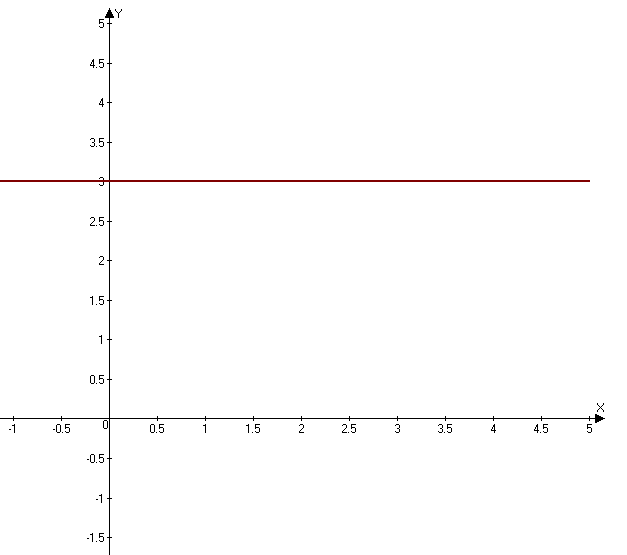
y=3 T-любое число (Т≠0)
|
|
Практические приемы нахождения |
|||
|
1. Найти период каждой составляющей 2. Подобрать Пример: |
Таблица 4
|
Применение |
|||
|
Монотонность и постоянство функции |
|||
|
Достаточное возрастания |
Достаточное возрастания |
||
|
Если в каждой то функция ƒ(x) возрастает на |
|
Если в каждой то функция ƒ(x) убывает на |
|
|
З но возрастания Например, — возрастающая на
ее производная равна нулю. |
|||
|
Необходимое и достаточное условие |
|||
|
Функция |
|
Экстремумы (максимум и минимум) |
|
|
Точка максимума |
Точка минимума |
|
Определение Точка из области определения называется для найдется
( , т из этой окрестности выполняется
|
Определение Точка из области определения называется для найдется
— ( ) , такая, из этой окрестности выполняется
|
|
— точка максимума |
— точка минимума |
|
Точки максимума
Значения функции экстремумами |
|
|
-максимум |
-минимум |
|
Критические точки |
|
|
Определение. в |
|
|
Необходимое |
Достаточное |
|
В точках экстремума равна — точка экстремума |
Если функция непрерывна и , то — точка экстремума функции в знак меняется с «+» на «-» — точка максимума в знак меняется с «-» на «+» точка минимума |
|
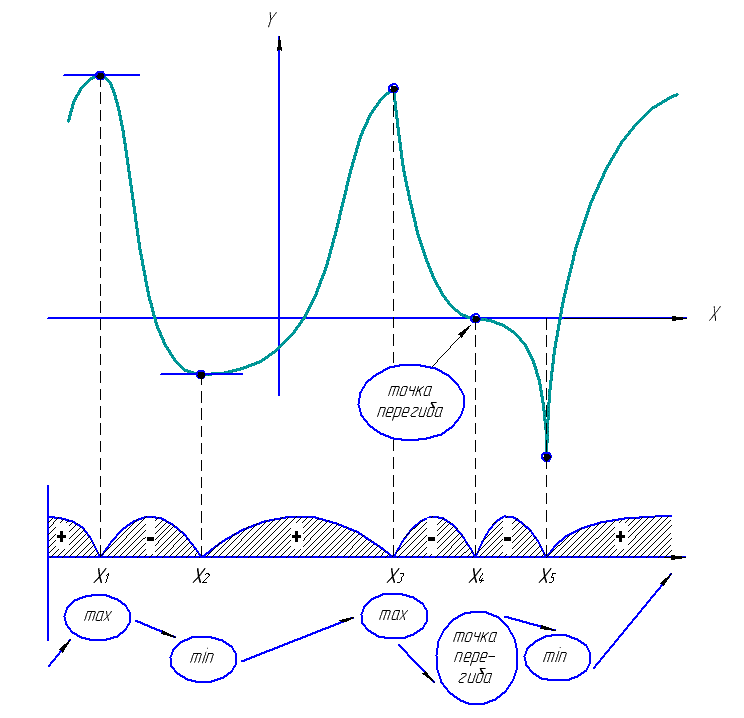
Пример графика функции , ( |
|
|
|
|
|
Исследование функции на монотонность и экстремумы |
|
|
Схема |
Пример |
|
1. Найти область |
Область определения: Функция |
|
2. Найти производную |
|
|
3. Найти критические или не существует |
|
|
4. Отметить |
|
|
5. Относительно |
|
6. Записать |
возрастает при |
|
убывает |
|
|
Точки экстремума: Экстремумы: |
|
Наибольшее и наименьшее значение |
|||
|
Свойства |
|||
|
Если функция непрерывна |
|||
|
Примеры |
|||
|
|
|
|
|
|
|
|
|
|
|
Нахождение наибольшего и наименьшего непрерывной |
|||
|
Схема |
Пример Найти при |
||
|
1. Найти производную |
|
||
|
2. Найти критические ( |
|
||
|
3. Выбрать |
Заданному отрезку |
||
|
4. Вычислить |
|
||
|
5. Сравнить |
|
|
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ |
||
|
Определение. к при |
||
|
Вертикальные асимптоты (х = а) |
||
|
асимптота Вертикальная |
||
|
Примеры |
||
|
|
|
|
|
О.О. При При X
|
О.О. При X
|
О.О. При (слева) y→+∞ При (справа) y→-∞ X —
|
Таблица 5.
|
Наклонные и |
|
|
1. |
|
|
Пример 1 |
Пример 2 |
|
При т.е.
— наклонная вертикальная |
При т.е.
— горизонтальная
вертикальная |
|
|
|
|
2. |
|
|
|
|
|
Для примера 1 |
Для примера 2 |
|
— наклонная |
— горизонтальная |
Таблица 6.
|
ВТОРАЯ ПРОИЗВОДНАЯ И ТОЧКИ ПЕРЕГИБА |
|
|
Понятие второй |
|
|
|
Пусть функция дифференцируема, то ее производную и (или |
|
Пример. |
|
|
Понятия |
|
|
Пусть функция определена Тогда |
|
|
|
Если в некоторой (кроме направлен |
|
|
Если в некоторой (кроме направлен |
|
|
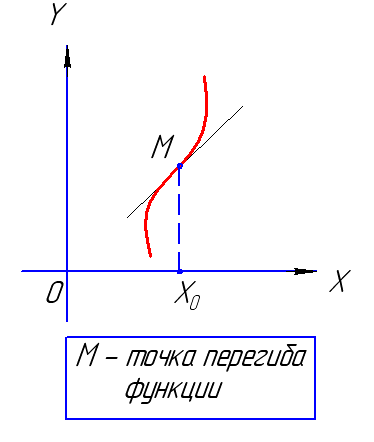
Если точка оси абсцисс обладает тем свойством, переходит с одной стороны касательной называется точкой перегиба функции , — — точка В : кривая ниже касательной, а при |
|
Достаточные которая |
|||
|
Условие |
Условие |
||
|
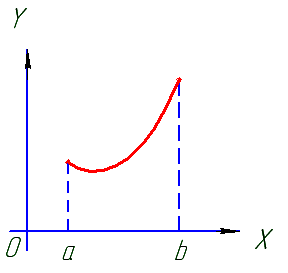
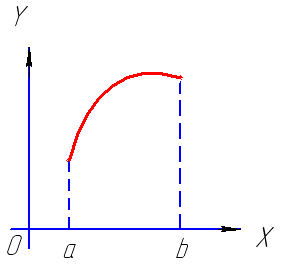
Если в каждой |
|
Если в каждой график направлен |
|
|
Замечание:
Эти условия
Например, график хотя ее вторая производная |
|
||
|
Нахождение |
|||
|
Необходимое |
Достаточное |
||
|
В ее |
Если имеет и , |
||
|
Исследование на выпуклость, вогнутость и точки |
|||
|
Схема |
Пример. |
||
|
1. Найти область |
Область определения: Функция |
||
|
2. Найти вторую |
|
||
|
3. Найти внутренние или не |
|
||
|
|
|||
|
4. Отметить |
|
||
|
5. Записать |
В интервале направлен направлен Точки |
Пример 1:
Исследовать
функцию
и построить график функции.
Т.к. знаменатель
заданной функции не должен быть равен
нулю, то можем записать:
Функция определена
на трех указанных участках.
2.
Функция четная,
график функции симметричен оси OY.
Функция не
периодическая.
3. Точки пересечения с осями координат.
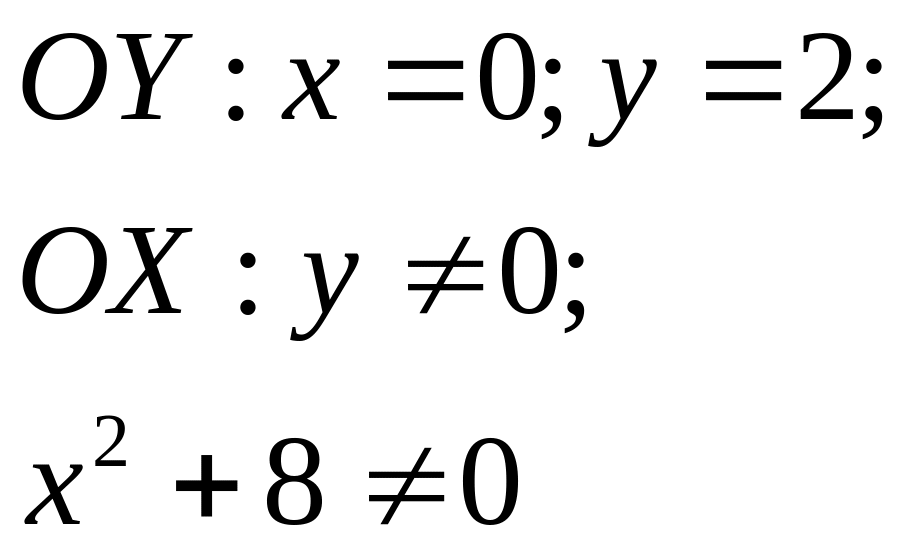
Точка пересечения
с осью OY
(0;2), точек пересечения с осью OX
нет.
4. Производная и критические точки.

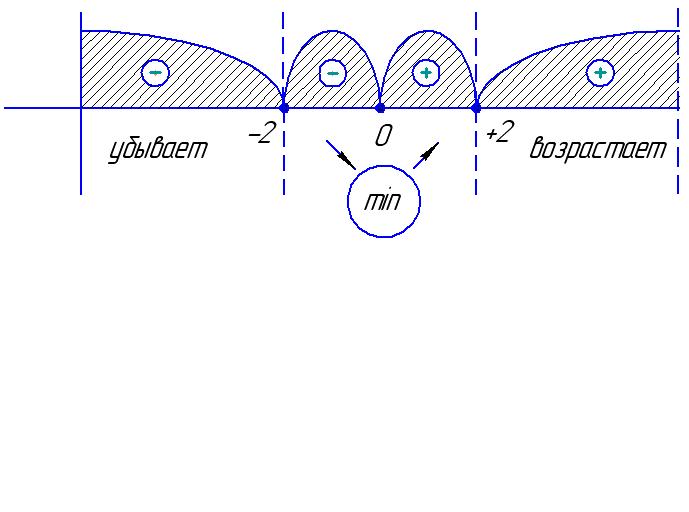
5. Промежутки
возрастания, убывания, точки экстремума.
На рисунке
представлено изменение знака первой
производной и поведение функции на
участках области определения.
Точка Х0(0;2)
– точка минимума функции.
6. Поведение
функции на концах области определения
и асимптоты.
При :
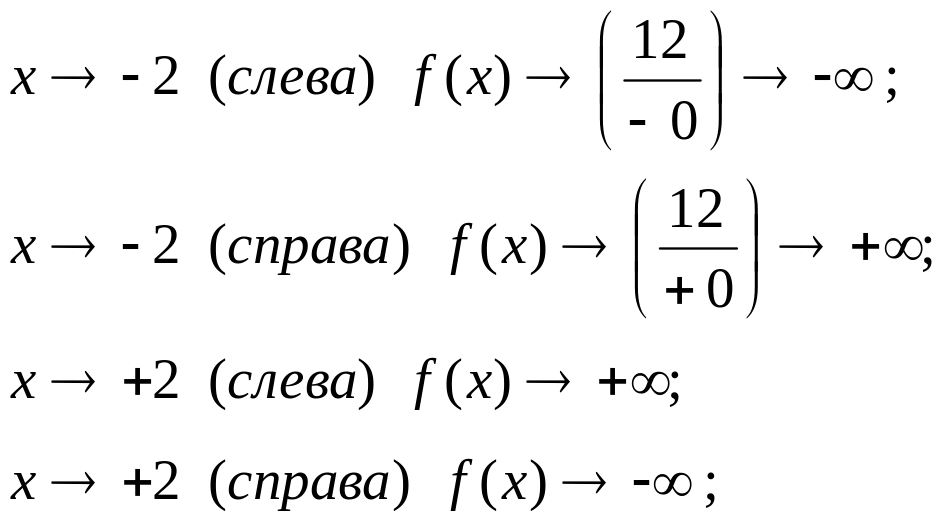
Следовательно, мы
имеем две вертикальные асимптоты
Наклонные и
горизонтальные асимптоты типа: y=kx+b
находим по формулам:

Уравнение асимптоты
примет вид: y=0*x-1=-1.
Горизонтальная
асимптота: Y=-1.
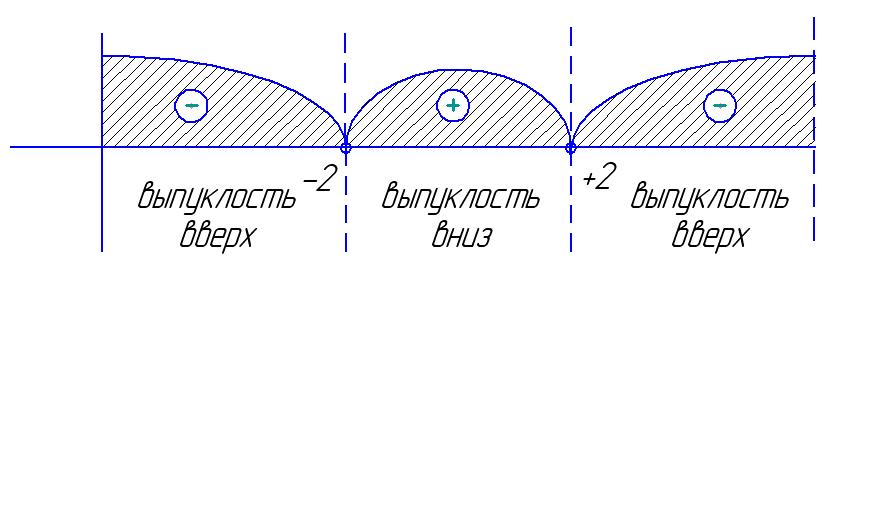
7. Вторая производная
и исследование функции на выпуклость
и вогнутость.

— не существует в
точках +2 и -2.
Знак производной
меняется в указанных точках.
На рисунке
представлено изменение знака второй
производной и поведение функции на
участках области определения.
8. Контрольные
точки.
Для более наглядного
представления поведения графика функции
определим значение функции в точках:

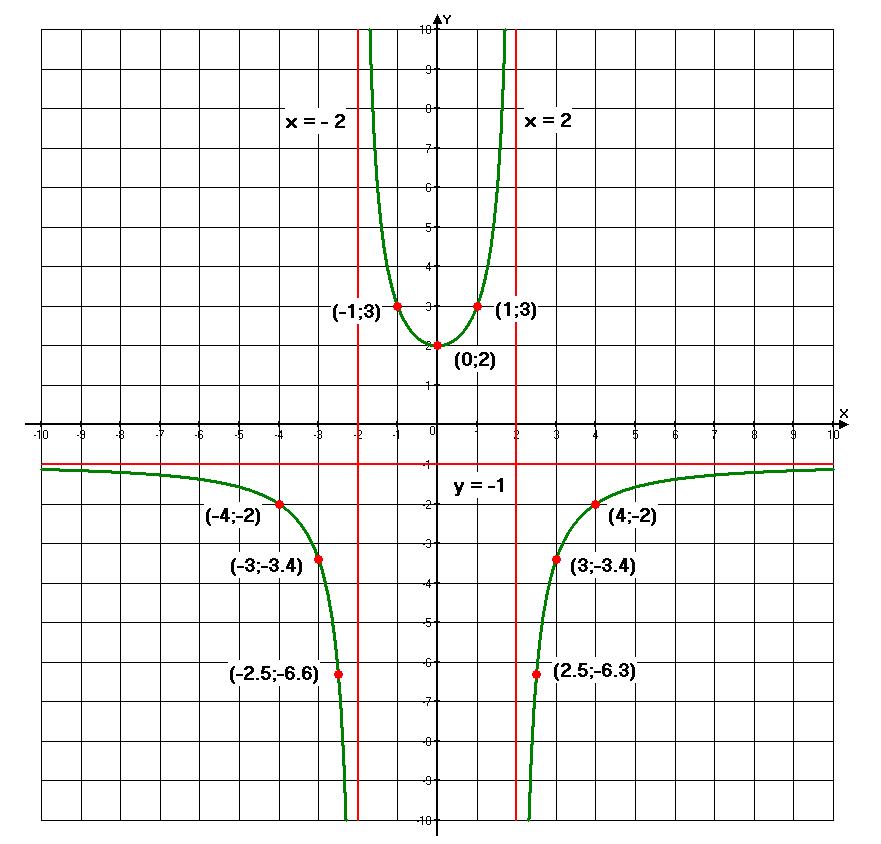
9. График функции
представлен на рисунке.
Красным цветом
отмечены асимптоты графика и найденные
по результатам исследования точки.
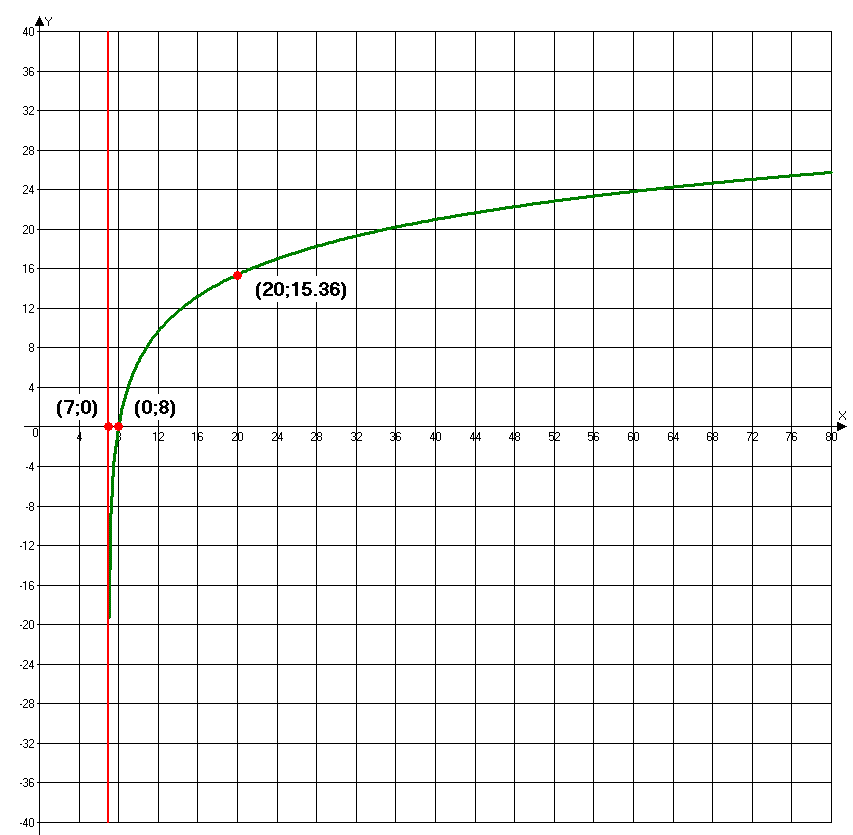
Пример 2:
Исследовать
функцию
и построить график функции.
1. Область определения функции:
Т.к. под знаком
логарифма может стоять только положительное
выражение, то можем записать следующее:
Функция определена
на указанном участке.
2.
Функция ни нечетная,
ни четная, не периодическая.
3. Точки пересечения с осями координат.
Точек пересечения
с осью OY
нет. Точка пересечения с осью ОХ: х=8.
4. Производная и критические точки.
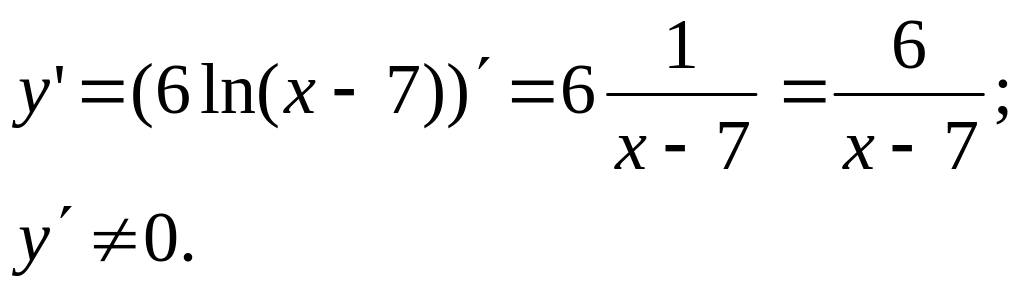
5. Промежутки
возрастания, убывания, точки экстремума.
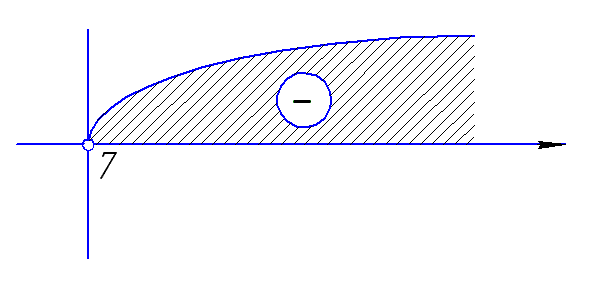
На рисунке
представлено изменение знака первой
производной и поведение функции на
участках области определения.
точек экстремума
нет.
возрастает
на всей области определения
6. Поведение
функции на концах области определения
и асимптоты.
При :
Следовательно, мы
имеем вертикальную асимптоту
Наклонные и
горизонтальные асимптоты типа: y=kx+b
находим по формулам:

наклонных и
горизонтальных асимптот нет.
7. Вторая производная
и исследование функции на выпуклость
и вогнутость.

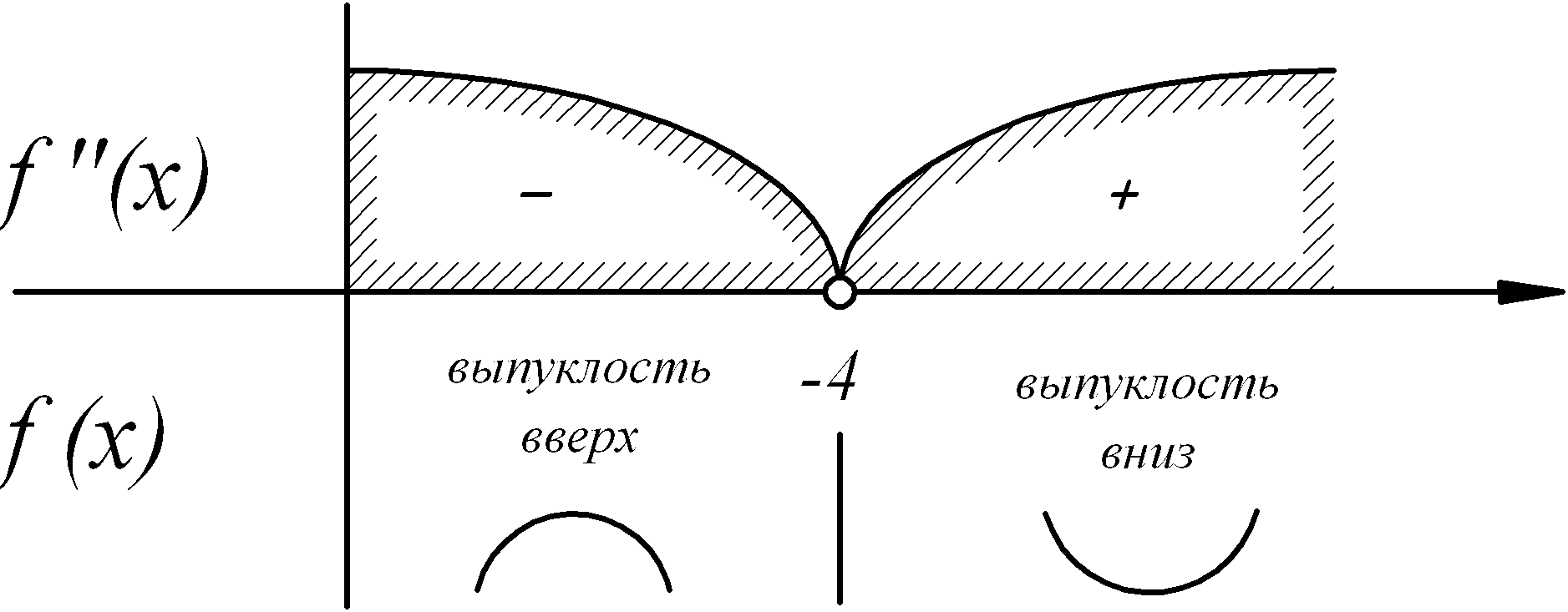
Вторая производная
не меняет знак на всей области определения.
выпуклость
вверх
8. Контрольные
точки.
Для более наглядного
представления поведения графика функции
определим значение функции в точках:
9. График функции
представлен на рисунке.
Красным цветом
отмечены асимптоты графика и найденные
по результатам исследования точи.
Пример 3:
Исследовать
функцию
и построить график функции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
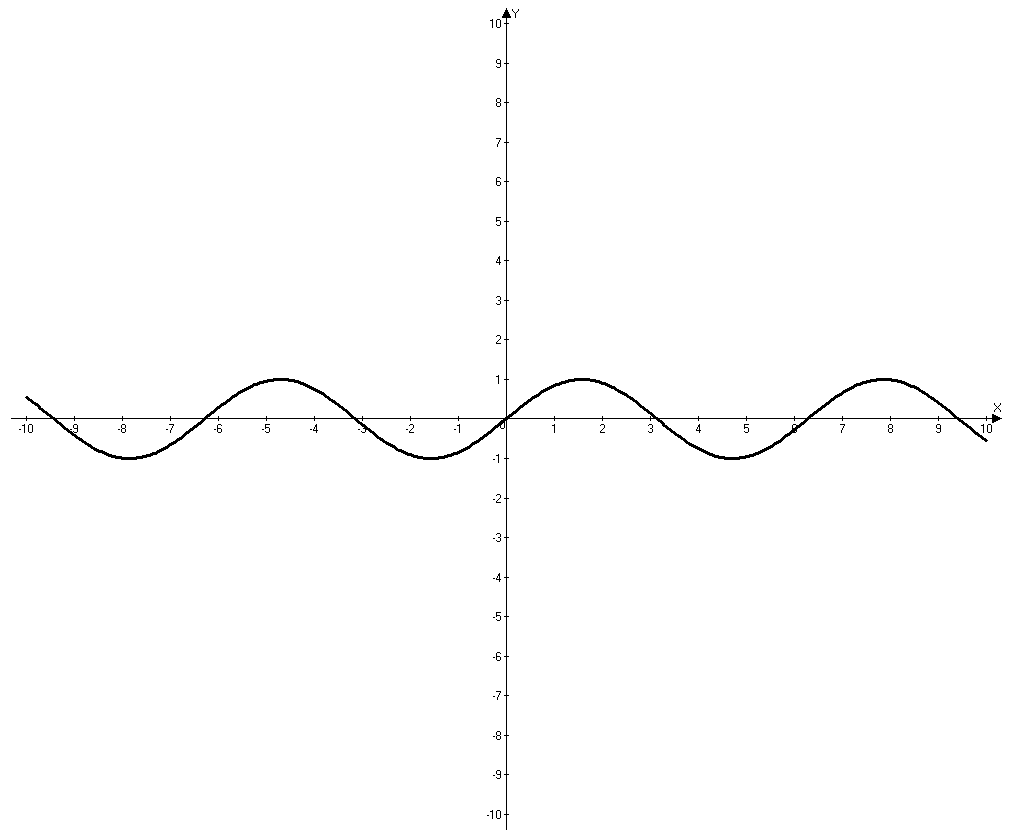
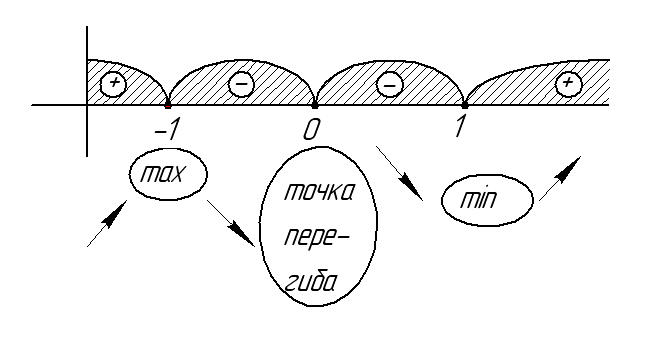
Исследование графика функции
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции;
- область значений функции;
- нули функции;
- промежутки возрастания и убывания;
- точки максимума и минимума;
- наибольшее и наименьшее значение функции на отрезке.
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.
Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).
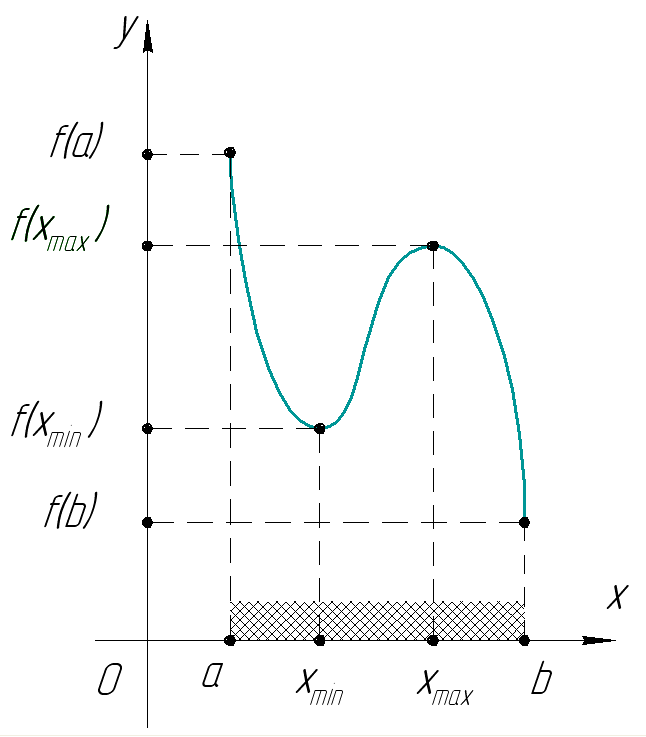
На нашем рисунке область определения функции — это отрезок
. Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок
— от самого нижнего до самого верхнего значения
.
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки
и
.
Значения функции положительны там, где . На нашем рисунке это промежутки
и
.
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от
до
.
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества
можно взять отрезок
, интервал
, объединение промежутков или всю числовую прямую.
Функция возрастает на множестве
, если для любых
и
, принадлежащих множеству
, из неравенства
следует неравенство
.
Иными словами, чем больше , тем больше
, то есть график идет вправо и вверх.
Функция убывает на множестве
, если для любых
и
, принадлежащих множеству
, из неравенства
следует неравенство
.
Для убывающей функции большему значению соответствует меньшее значение
. График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке
и убывает на промежутках
и
.
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и
на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и
.
А что делать, если нужно найти, например, минимум функции на отрезке
? В данном случае ответ:
. Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке
.
Можно сказать, что экстремумы функции равны и
.
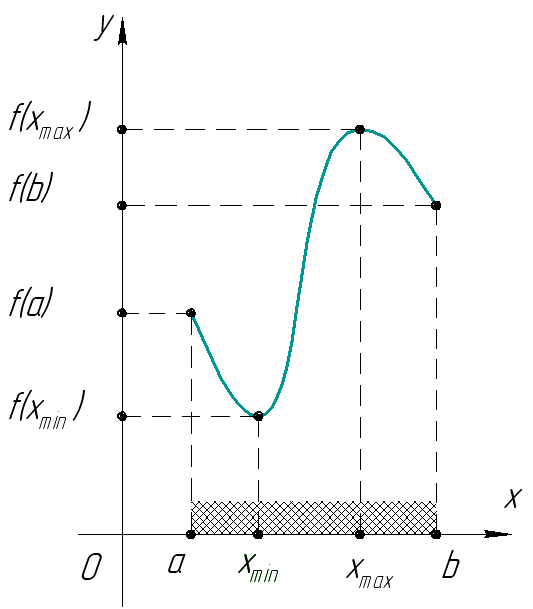
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно
и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно
. Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Исследование графика функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
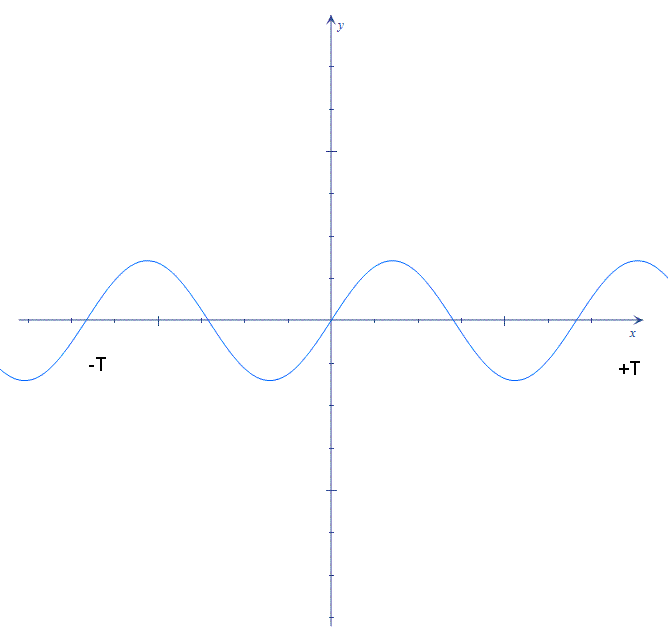
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Определение
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом.
Внимание!
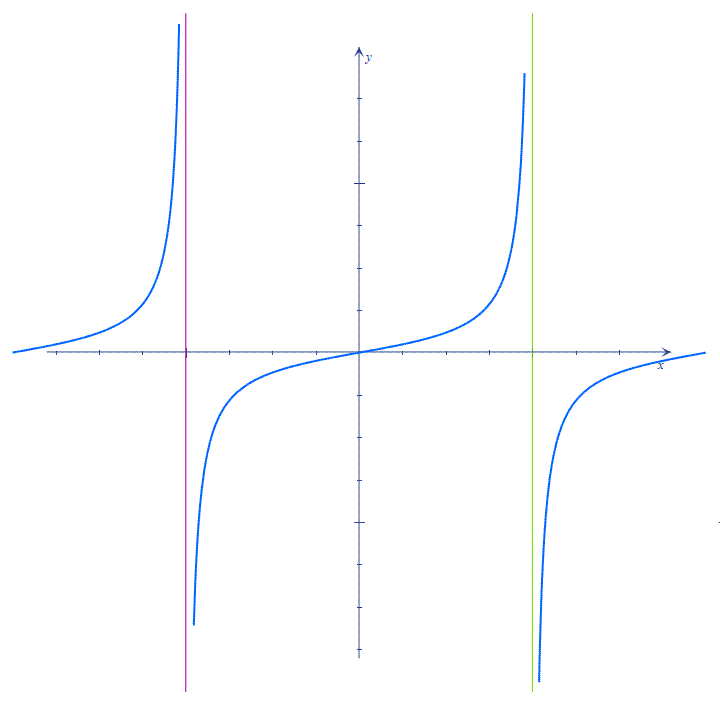
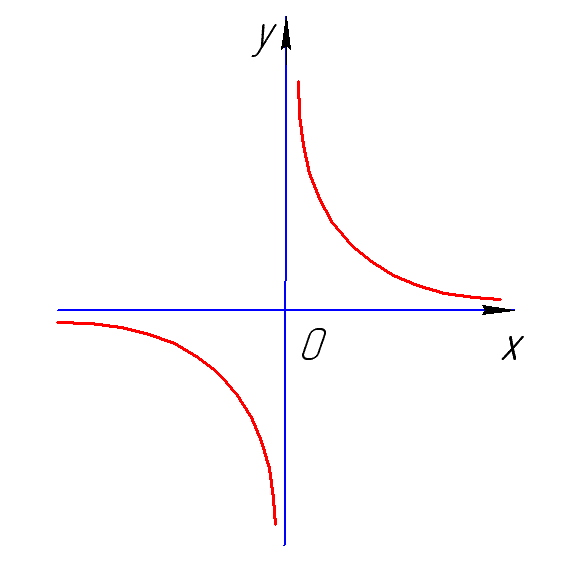
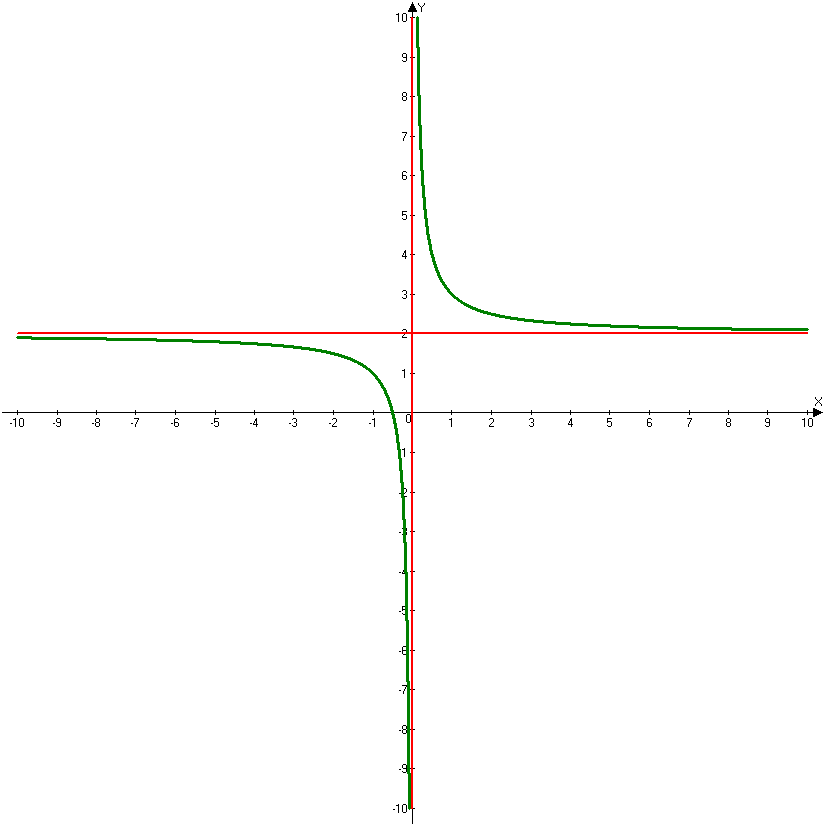
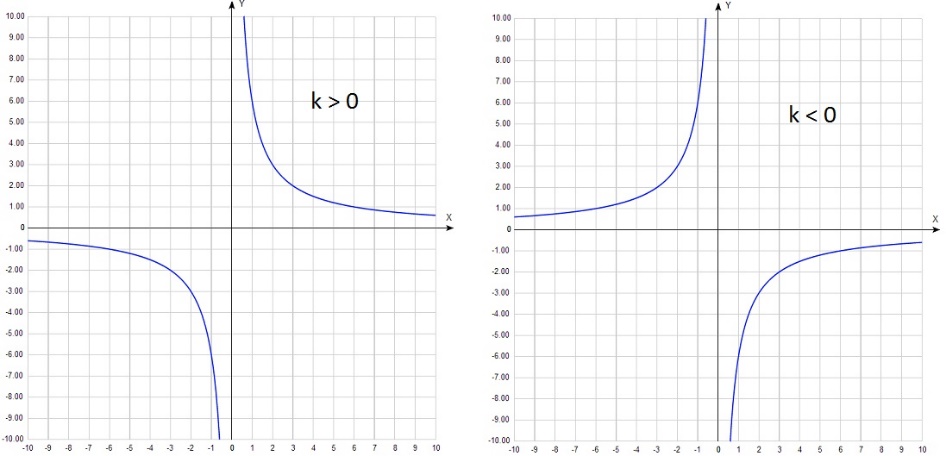
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом:
По данному рисунку видно, что нулей функции не существует.
Как найти нули функции?
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции.
Пример №1. Найти нули функции (если они существуют):
а) у= –11х +22
б) у= (х + 76)(х – 95)
в) у= – 46/х
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Получим х=2.
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Определение
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
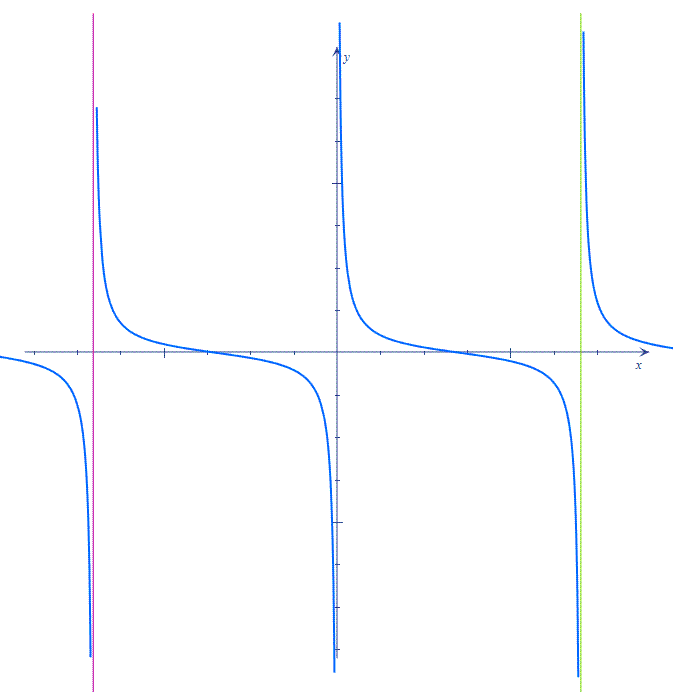
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Определение
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Даниил Романович | Просмотров: 16.1k