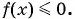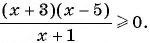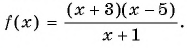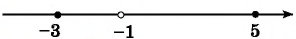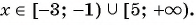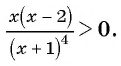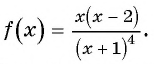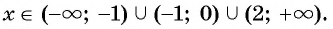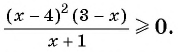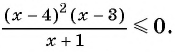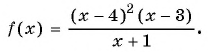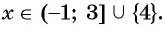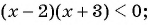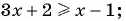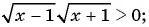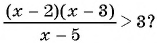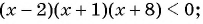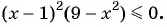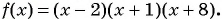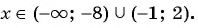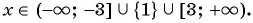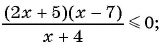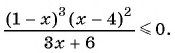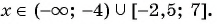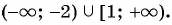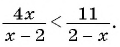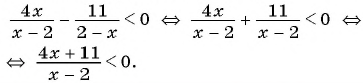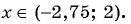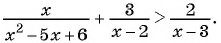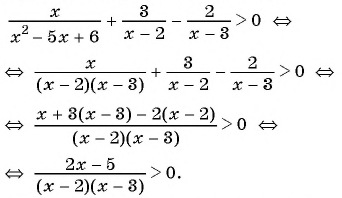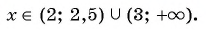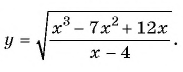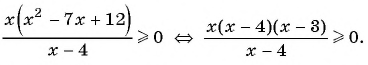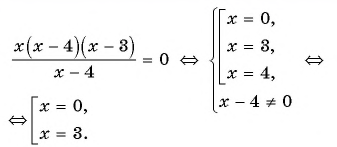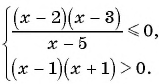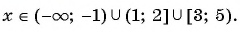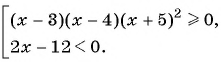Метод интервалов
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
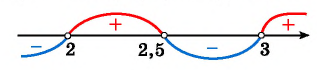
1. Рассмотрим неравенство:
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .
, где
и
— корни квадратного уравнения
.
Получим:
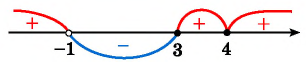
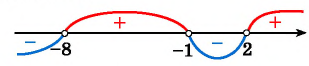
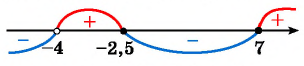
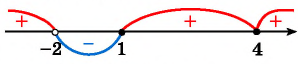
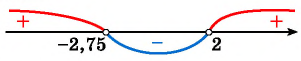
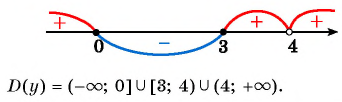
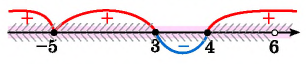
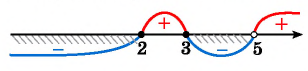
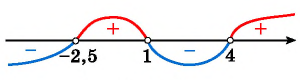
Рисуем ось X и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
Нули знаменателя и
— выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя).
Напомним, что мы изображаем точку на числовой прямой выколотой (пустой), если соответствующее значение переменной никак не может быть решением неравенства. В нашем примере точки и
выколотые, потому что в них знаменатель обращается в ноль.
Нули числителя и
— закрашены, так как неравенство нестрогое. При
и
наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось X на 5 промежутков.
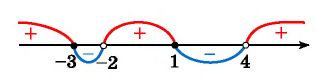
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например,
и проверим знак выражения
в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак
.
Следующий промежуток:
. Проверим знак при
. Получаем, что левая часть поменяла знак на
.
. Возьмем
. При
выражение положительно — следовательно, оно положительно на всем промежутке от
до
.
При
левая часть неравенства отрицательна.
И, наконец,
. Подставим
и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак
.
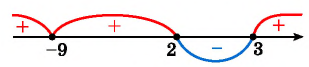
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: .
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
, или
, или
, или
(в левой части — дробно-рациональная функция, в правой — нуль).
Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
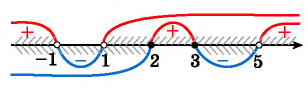
2. Рассмотрим еще одно неравенство:
Решение:
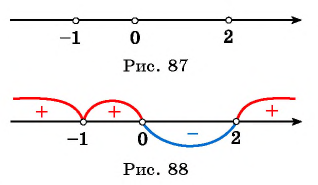
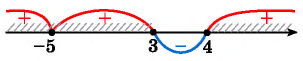
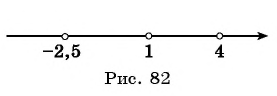
Снова расставляем точки на оси X. Точки и
— выколотые, поскольку это нули знаменателя. Точка
— тоже выколота, поскольку неравенство строгое, и значение переменной
не может быть решением неравенства.
При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например,
. Левая часть имеет знак
:
При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак
:
При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак
:
Наконец, при все множители положительны, и левая часть имеет знак
:
Ответ: .
Почему нарушилось чередование знаков? Потому что при переходе через точку 2 «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку
знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
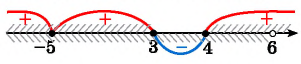
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Решение:
Левая часть та же, что и в предыдущем примере. Та же будет и картина знаков:
Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при
и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
Ответ: .
В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
Решение:
Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения
при всех
одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех
.
Придём к равносильному неравенству:
Решим неравенство методом интервалов. Действуем по алгоритму: числитель левой части равен нулю при а знаменатель обращается в ноль при
. Отметим эти точки на координатной прямой. Точки выколоты, потому что неравенство строгое. Эти точки разбивают числовую ось на три интервала. Найдем знаки на каждом из интервалов. На крайнем правом знак положителен, а дальше знаки чередуются.
Нам нужен «интервал со знаком минус», то есть такой, где Выпишем ответ.
Ответ:
Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Решение:
Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь
может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
Мы поступим по-другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
Применим метод интервалов.
Действуем по алгоритму. Отметим на координатной прямой точки и
. Они выколотые, потому что неравенство строгое. Эти точки разбивают ось Х на три интервала. Расставим знаки на каждом из них.
Ответ:
6. Решите неравенство:
Решение:
Приведем левую часть неравенства к общему знаменателю и преобразуем числитель:
Применим метод интервалов:
Числитель равен нулю при Знаменатель обращается в ноль при
или
. Неравенство строгое, поэтому все эти точки на числовой оси отмечаем как пустые.
Если , то
. Далее знаки чередуются.
Нам нужны «интервалы со знаком минус». Выпишем их и получим ответ.
Ответ:
7. Решите неравенство
Решение:
Приведем неравенство к виду:
Для этого все перенесем в левую часть, приведем к общему знаменателю и разложим числитель и знаменатель на множители. Применяем формулу разности квадратов и формулу разложения квадратного трехчлена на множители
Получим:
Найдем нули числителя и знаменателя и отметим их на числовой оси:
Выпишем интервалы, где неравенство выполняется, и получим ответ.
Ответ:
8. Решите неравенство:
Решение:
Разложим левую часть неравенства на множители.
Для этого вынесем общий множитель за скобки, а затем воспользуемся формулой:
Получим:
Применим метод интервалов.
Левая часть неравенства обращается в ноль, если ,
или
. Нанесем эти точки на координатную прямую. Все точки закрашенные, так как неравенство нестрогое, в нем присутствует знак «меньше или равно».
Ответ:
9. Решите неравенство:
Решение:
Разложим числитель на множители с помощью группировки:
Знаменатель тоже разложим на множители:
Неравенство примет вид:
Мы видим, что числитель равен нулю при
Знаменатель равен нулю при . Множитель
стоит в числителе и в знаменателе, и он не может равняться нулю.
Отметим полученные точки на координатной прямой. Две из них закрашены (это 3 и 1), а две нет (это -1 и -2). Найдем знаки на каждом промежутке.
При переходе через точку знак не меняется, так как множитель
присутствует и в числителе, и в знаменателе.
Выпишем ответ.
Ответ:
10. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Напомним, что выражение мы разложили на множители, решив квадратное уравнение:
Неравенство примет вид:
Воспользуемся методом интервалов.
Числитель дроби в левой части неравенства равен нулю, если Знаменатель обращается в ноль, если
или
. Отметим эти точки на координатной прямой и определим знаки на интервалах.
Ответ:
11. Решите неравенство:
Решение:
Можно сразу применить метод интервалов.
Но лучше, чтобы не запутаться со знаками, умножить обе части неравенства на (-1) и не забыть поменять знак неравенства на противоположный.
Теперь применим метод интервалов.
Отметим на координатной прямой нули числителя и знаменателя и определим знаки на интервалах.
Обратите внимание, что знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени.
Ответ:
12. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Сократим на множитель при условии, что
.
Здесь мы действуем чуть иначе, чем в задаче 9.
Неравенство равносильно системе:
Решаем второе неравенство системы методом интервалов:
Второму неравенству удовлетворяют точки .
Точка в этот промежуток не входит.
Ответ:
13. Решите неравенство:
Решение:
Разложив числитель на множители, получим:
Применим метод интервалов.
Отметим на числовой оси точки, в которых числитель и знаменатель обращаются в ноль. Обратите внимание, что точки -1 и 5 закрашены, а точки 2 и 4 пустые.
Определим знаки на интервалах.
Знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени. При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.
В ответе запишем интервалы, на которых неравенство выполняется.
Ответ:
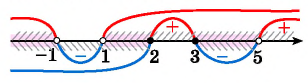
14. Решите неравенство:
Разложим числитель и знаменатель на множители, используя формулы сокращенного умножения: суммы и разности кубов, разности квадратов.
Кажется, что неравенство сложное. Попробуем разложить на множители выражения и
Оказывается, что дискриминанты соответствующих квадратных уравнений отрицательны, поэтому и
при всех х.
Разделим обе части неравенства на эти положительные выражения.
Получим:
Неравенство равносильно системе:
Решим первое неравенство системы методом интервалов:
Его решением является промежуток [1;4], причем точка в этот промежуток не входит.
Ответ:
Мы показали на различных примерах, как применяется метод интервалов.
Сделаем вывод:
Метод интервалов помогает решать дробно-рациональные неравенства по алгоритму. Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Метод интервалов» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Свойства функции
В этой статье мы коротко суммируем сведения, которые касаются такого важного математического понятия, как функция. Мы поговорим о том, что такое числовая функция и какие свойства функции необходимо знать и уметь исследовать.
Что такое числовая функция? Пусть у нас есть два числовых множества: Х и Y, и между этими множествами есть определенная зависимость. То есть каждому элементу х из множества Х по определенному правилу ставится в соответствие единственный элемент y из множества Y.
Важно, что каждому элементу х из множества Х соответствует один и только один элемент y из множества Y.
Правило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией.
Множество Х называется областью определения функции.
Множество Y называется множеством значений значений функции.
Равенство называется уравнением функции. В этом уравнении — независимая переменная, или аргумент функции. — зависимая переменная.
Если мы возьмем все пары и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции — это графической изображение зависимости между множествами Х и Y.
Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.
Основные свойства функций.
1. Область определения функции.
Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции имеет смысл. Другими словами, это область допустимых значений выражения .
Чтобы по графику функции найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
2. Множество значений функции.
Множество значений функции Е(y)— это множество всех значений, которые может принимать зависимая переменная y.
Чтобы по графику функции найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
Нули функции — это те значения аргумента х, при которых значение функции (y) равно нулю.
Чтобы найти нули функции , нужно решить уравнение . Корни этого уравнения и будут нулями функции .
Чтобы найти нули функции по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции .
4. Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции — это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть или .
Чтобы найти промежутки знакопостоянства функции , нужно решить неравенства и .
Чтобы найти промежутки знакопостоянства функции по ее графику, нужно
- найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ — при этих значениях аргумента ,
- найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ — при этих значениях аргумента .
5. Промежутки монотонности функции.
Промежутки монотонности функции — это такие промежутки значений аргумента х, при которых функция возрастает или убывает.
Говорят, что функция возрастает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: .
Другими словами, функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Чтобы по графику функции определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.
Говорят, что функция убывает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: .
Другими словами, функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Чтобы по графику функции определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.
6. Точки максимума и минимума функции.
Точка называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
.
Графически это означает что точка с абсциссой x_0 лежит выше других точек из окрестности I графика функции y=f(x).
Точка называется точкой минимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
Графически это означает что точка с абсциссой лежит ниже других точек из окрестности I графика функции .
Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.
7. Четность (нечетность) функции.
Функция называется четной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.
Другими словами, область определения четной функции симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .
Функция называется нечетной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.
Другими словами, область определения нечетной функции симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .
Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.
Чтобы определить четность функции, нужно:
а). Найти область определения функции , и определить, является ли она симметричным множеством.
Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция — функция общего вида.
Если область определения функции — симметричное множество, то проверяем п. б)
б). В уравнение функции нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду или .
Если , то функция четная.
Если , то функция нечетная.
Если не удалось привести ни к тому ни к другому, то наша функция — общего вида.
График четной функции симметричен относительно оси ординат ( прямой OY ).
График нечетной функции симметричен относительно начала координат ( точки (0,0) ).
8. Периодичность функции.
Функция называется периодической, если существует такое положительное число Т, что
- для любого значения х из области определения функции, х+Т также принадлежит D(x)
В программе средней школы из числа периодических функций изучают только тригонометрические функции.
Предлагаю вам посмотреть ВИДЕОУРОК, в котором я рассказываю, как определить свойства функции по ее графику.
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!
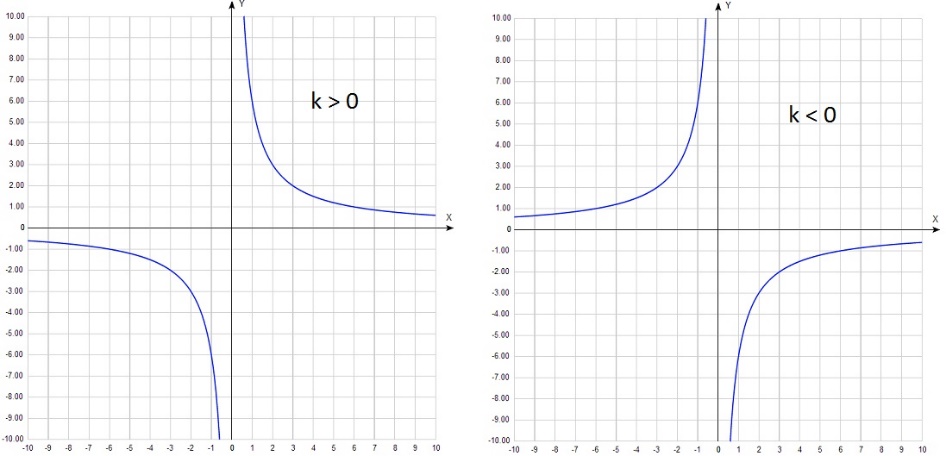
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
График функции у=k/x выглядит следующим образом: По данному рисунку видно, что нулей функции не существует. Как найти нули функции?
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
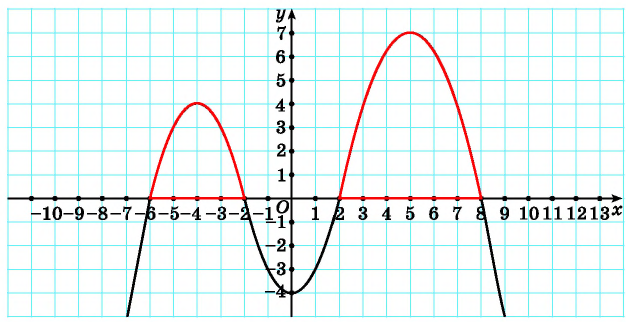
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Построение графиков функций
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
при х ≠ -1.
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Определение
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом.
Внимание!
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом:
По данному рисунку видно, что нулей функции не существует.
Как найти нули функции?
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции.
Пример №1. Найти нули функции (если они существуют):
а) у= –11х +22
б) у= (х + 76)(х – 95)
в) у= – 46/х
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Получим х=2.
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Определение
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Определение
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Даниил Романович | Просмотров: 16.1k
Рациональным называется неравенство, в левой и правой частях которого — рациональные выражения.
Содержание:
Задача:
Лодка прошла по течению реки 5 км и вернулась обратно, затратив на весь путь не больше 1 ч. Какова наименьшая возможная скорость лодки, если скорость течения реки равна
Решение:
Обозначим через
По условию задачи на весь путь лодка затратила не больше 1 ч. Составим математическую модель:
Полученное в ходе решения задачи неравенство 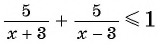
Метод интервалов для решения дробно-рациональных неравенств
Рассмотрим один из методов решения рациональных неравенств — метод интервалов. Этот метод основан на использовании графика функции.
Предположим, что нужно решить неравенство 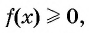
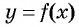
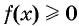
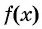
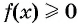
Рис. 80
Рис. 81
значения переменной 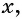
Заметим, что такие же решения имеет неравенство 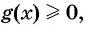
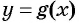
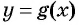
Таким образом, для применения метода интервалов к решению неравенства достаточно построить схему графика функции, на которой отражены только некоторые (необходимые для решения неравенства) свойства функции, а именно ее область определения, нули и промежутки знакопостоянства.
Примеры с решением
Пример №1
Решите неравенство
Решение:
Рассмотрим функцию 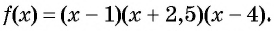
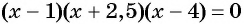
Отметим нули функции на оси абсцисс (рис. 82). Так как данное неравенство строгое, то нули функции отметим на оси пустыми точками.
Нули функции разбили ось на четыре промежутка. Определим, выше или ниже оси абсцисс расположен график функции в каждом из полученных промежутков.
Поскольку правее точки 4 каждый из трех множителей произведения 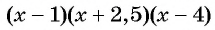
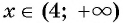
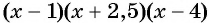
При переходе через каждую из отмеченных точек знак функции 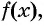
Построим схему графика функции 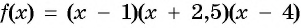
Рис. 83
При 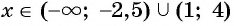
Ответ:
Пример №2
Решите неравенство
Решение:
Рассмотрим функцию 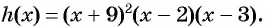
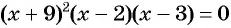
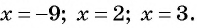
Затем определим положение графика функции в каждом из четырех полученных промежутков. Правее точки 3 каждый из трех множителей произведения 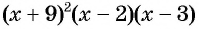
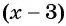
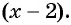
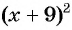
Рис. 84
Построим схему графика функции (см. рис. 84) и запишем решение неравенства в соответствии с его знаком:
Ответ:
Если во множителе число 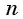
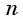
Пример №3
Решите неравенство
Решение:
Рассмотрим функцию
Отметим на оси абсцисс нули этой функции (числа -3 и 1) и те значения переменной, которые не входят в область определения функции 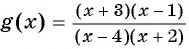
Рис. 85
Рис. 86
Так как неравенство нестрогое, то нули функции являются решениями неравенства (на оси абсцисс — закрашенные точки -3 и 1). Нули знаменателя не являются решениями неравенства (на оси абсцисс — пустые точки -2 и 4).
Построим схему графика (рис. 86). Положение графика относительно оси абсцисс меняется при переходе через каждую точку. По схеме графика в соответствии со знаком неравенства запишем его решение:
Ответ:
Для того чтобы решить рациональное неравенство методом интервалов, нужно:
- Привести неравенство к виду
или
- Найти и отметить на оси абсцисс нули функции и те значения переменной, при которых значения функции не существуют (нули знаменателя).
- Построить схему графика функции.
- Записать ответ в соответствии со знаком неравенства.
Решите неравенство
Решение:
(1) Неравенство имеет вид 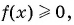
(2)
(3)
(4) Ответ:
Пример №4
Решите неравенство
Решение:
(1) Неравенство имеет вид 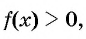
(2) Найдем нули функции (числа 0; 2) и, поскольку знак неравенства строгий, отметим их на оси абсцисс пустыми точками. Найдем значение переменной, при котором значения функции не существуют, — нуль знаменателя (число -1) и отметим его на оси абсцисс пустой точкой (рис. 87).
(3) Построим схему графика функции, при этом учтем, что при переходе через точку -1 положение графика относительно оси не меняется, а при переходе через точки 0 и 2 меняется (рис. 88).
(4) Ответ:
Для того чтобы положение графика в первом правом промежутке было выше оси абсцисс, нужно умножением обеих частей неравенства на -1 добиться положительных коэффициентов перед переменной в линейных множителях.
- Заказать решение задач по высшей математике
Пример №5
Решите неравенство
Решение:
Для того чтобы все коэффициенты перед переменными в линейных множителях были положительными, умножим обе части неравенства 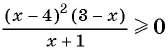
(1) Неравенство имеем вид 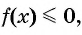
(2) Найдем нули функции (числа 3 и 4) и, поскольку знак неравенства нестрогий, отметим их на оси абсцисс закрашенными точками. Найдем значение переменной, при котором значение функции не существует (число -1), и отметим его на оси абсцисс пустой точкой (рис. 89).
Рис. 89
Рис. 90
(3) Построим схему графика функции, при этом учтем, что при переходе через точку 4 положение графика относительно оси не меняется, а при переходе через точки -1 и 3 меняется (рис. 90).
(4) Ответ:
Пример №6
Какие из следующих неравенств являются рациональными:
а)
б)
в)
г)
Решение:
Неравенства а), б), г) — рациональные, так как в левой и правой частях этих неравенств — рациональные выражения. Неравенство в) не является рациональным, так как содержит иррациональные выражения с переменной.
Пример №7
Решите неравенство:
а)
б)
Решение:
а) (1) Неравенство имеет вид 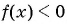
(2) Нулями функции являются числа -8; —1 и 2. Поскольку знак неравенства строгий, отметим их на оси абсцисс пустыми точками.
(3) Построим схему графика функции. При переходе через каждую из точек -8; -1 и 2 положение графика относительно оси меняется.
(4) Ответ:
б) Умножим обе части данного неравенства на -1 и получим неравенство 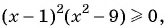
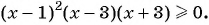
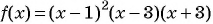
При переходе через точку 1 положение графика относительно оси не меняется, а при переходе через точки -3 и 3 — меняется.
Ответ:
Пример №8
Решите неравенство:
а)
б)
Решение:
а) Нулями функции 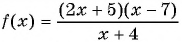
Ответ:
б) Умножим обе части неравенства на 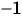
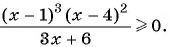
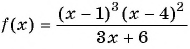
Ответ:
Пример №9
Решите неравенство
Решение:
Запишем неравенство в виде:
Нулем функции 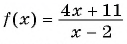
Ответ:
Пример №10
Решите неравенство
Решение:
Приведем неравенство к виду:
Отметим на оси абсцисс нуль функции
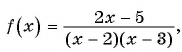
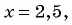
Ответ:
Пример №11
Найдите область определения функции
Решение:
Так как функция 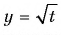
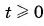
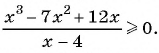
Для нахождения нулей функции 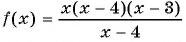
При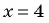
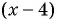
Пример №12
Решите систему неравенств
Решение:
Отметим на оси абсцисс множество решений первого неравенства системы.
Ответ:
Пример №13
Найдите решение совокупности неравенств
Решение:
Отметим на оси абсцисс множество решений первого неравенства совокупности.
Отметим на этой же оси множество решений второго неравенства совокупности.
Найдем объединение множеств решений.
Ответ:
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
3.4. Определите, при каком а функция является периодической.
3.5. Найдите если:
3.6. Определите, при каком значении аргумента значение функции равно –1.
3.7. Определите при каких значениях х график функции расположен выше графика функции
poznayka.org
Промежутки знакопостоянства функции. — КиберПедия
Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у.
Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом .
Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Типы ф-й
Сложная
Сложная функция — это функция от функции
Неявная
Неявные функции — это функции, заданные уравнением, не разрешенным относительно зависимой переменной.
Обратная
Если уравнение y=f(x) может быть однозначно разрешено относительного переменного x (т.е. сущ. Ф-я x=g(y) такая, что y=f[g(y)]), то ф-я x=g(y) – обратная по отношению к y=f(x).
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.
Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
Монотонность функции.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Четность (нечетность) функции.
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.
Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
Периодическость функции.
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Предел ф-ии
Предел ф-ии (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Последовательность an называется бесконечно малой, если
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Последовательность an называется бесконечно большой, если
Первый замечательный предел
Второй замечательный предел
Непрерывность ф-ии
Ф-яf(x) называется непрерывной при x = E, если
1) Эта ф-я определена в точке E, т.е. существует число f(E)
2) Существует конечный предел limf(x)
3) Этот предел равен значению ф-ии в точкеE, т.е. x -> E.
Точки разрыва
Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Производная сложной функции
Рассмотрим сложную функцию y = y(u(x))
Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y’u, u’x), тогда сложная функция y = y(u(x)) дифференцируема и y’x = y’u u’x.
Доказательство
Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем
Теорема доказана.
Доказательство
Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y).
Тогда получаем
Теорема доказана.
Производные высших порядков
Дифференцируемость функции
Функция y=f(x)называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Правило Лопиталя
Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например, найти . Этот предел существует . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.
Монотонность ф-ии
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Экстремумы
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках — ее экстремумами.
Первое достаточное условие.
Пусть xо — критическая точка. Если f ‘ (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе достаточное условие. Пусть функция f(x) имеет производную
f ‘ (x) в окрестности точки xо и вторую производную f»(xo) в самой точке xо. Если f ‘(xо) = 0, f»(xo)>0 (f»(xo)<0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же f»(xo)=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Точки перегиба
Точка графика непрерывной функции, отделяющая его выпуклую часть отвогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Определим достаточные условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется уравнением y = f(x). Если f »(x0) = 0 или f »(x0) не существует и при переходе через значениеx = x0 производная f »(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть f »(x) < 0 при x < x0 и f »(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f »(x) > 0 при x < x0 и f »(x) < 0 при x > x0.
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Асимптоты графика функции
Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Формула Тейлора
Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.
ФОРМУЛА ТЕЙЛОРА
, где Rn(x) — остаточный член формулы Тейлора.
Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у.
Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом .
Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Типы ф-й
Сложная
Сложная функция — это функция от функции
Неявная
Неявные функции — это функции, заданные уравнением, не разрешенным относительно зависимой переменной.
Обратная
Если уравнение y=f(x) может быть однозначно разрешено относительного переменного x (т.е. сущ. Ф-я x=g(y) такая, что y=f[g(y)]), то ф-я x=g(y) – обратная по отношению к y=f(x).
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.
Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
Монотонность функции.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
cyberpedia.su
Как найти интервалы знакопостоянства функции?
Алгоритм метода интервалов прост и бесхитростен:
1) Находим область определения функции.
2) Находим нули функции (точки пересечения графика с осью абсцисс).
3) В большинстве заданий потребуется чертёж. Чертим ось и откладываем на ней точки разрыва (если они есть), а также нули функции (если они есть). Определяем знаки функции на интервалах, которые входят в область определения.
Пункты можете законспектировать, впрочем, алгоритм очень быстро запомнит даже полный чайник. Тут всё прозрачно и логично.
Начнём с распространённой квадратичной функции:
Пример 1
Найти интервалы знакопостоянства функции.
Решение:
1) Функция определена и непрерывна на всей числовой прямой. Таким образом, точки разрыва и «нехорошие» промежутки отсутствуют.
2) Найдём нули функции. Для этого нужно решить уравнение . В данном случае:
Дискриминант положителен, значит, уравнение имеет два действительных корня:
3) Откладываем все найденные точки на числовой оси:
В статье Область определения функции я выполнял подобные чертежи схематически, но сейчас для бОльшей наглядности изложения буду их масштабировать (за исключением клинических случаев). На том же уроке мы узнали, как выяснить знаки функции на интервалах – можно проанализировать расположение параболы. В данном случае ветви параболы направлены вверх, следовательно, на интервалах функция будет положительна: . Попа параболы сидит на интервале ниже оси абсцисс, и функция здесь отрицательна: .
Хорошо, параболу многие читатели представляют. Но что делать, если функция более сложная? Например, . Заметная часть аудитории уже затруднится сказать, как принципиально выглядит график данной функции. И это, так скажем, ещё только минимальное усложнение.
Однако и в простых и в сложных случаях работает универсальный способ:
Рассмотрим функцию непрерывную на некотором интервале , график которой не пересекает ось на этом интервале. Тогда:
– если функция положительна в какой-либо точке интервала , то она положительна и ВО ВСЕХ точках данного интервала;
– если функция отрицательна в какой-либо точке интервала , то она отрицательна и ВО ВСЕХ точках данного интервала.
Включите немного воображения: если на интервале нет точек разрыва, и график не пересекает ось абсцисс, то он не может по мановению волшебной палочки перескочить из нижней полуплоскости в верхнюю полуплоскость (или наоборот). Поэтому знак функции на таком интервале легко определить по одной-единственной точке.
Проведём небольшой эксперимент. Представьте, что вы совсем не знаете, как выглядит график функции и вам необходимо найти её интервалы знакопостоянства (кстати, если действительно не знаете, таки начертите многострадальную примадонну =)).
1) Берём произвольную точку интервала . С вычислительной точки зрения проще всего взять . Подставляем её в нашу функцию:
Следовательно, функция положительна ив каждой точке интервала .
2) Берём произвольную точку интервала , здесь по удобству вне конкуренции ноль. Снова выполняем подстановку:
А, значит, функция отрицательна ив каждой точке интервала .
3) И, наконец, обрабатываем наиболее простую точку интервала :
Поэтому функция положительна в каждой точке интервала .
Выполненные подстановки, вычисления почти всегда нетрудно выполнить устно, но в крайнем случае существует и черновик.
Фиксируем полученные результаты на числовой оси:
Да, вы не имеете никаких представлений о параболе, но совершенно точно можете сказать, что на интервалах график функции расположен ВЫШЕ оси , а на интервале – НИЖЕ данной оси.
Ответ:
, если ;
, если .
Точно так же решается целый спектр задач-«сателлитов», вот некоторые из них:
Решить квадратичное неравенство .
Проводим аналогичные действия и даём ответ .
Решить квадратичное неравенство .
Проводим аналогичные действия и даём ответ .
Найтиобласть определенияфункции .
Проводим аналогичные действия, даём ответ .
И т.п.
Метод интервалов работает в самых примитивных случаях, например, для функции . Здесь прямая пересекает ось абсцисс в точке , при этом слева от данной точки (график ниже оси ), а справа (график выше оси ). Тем не менее, для тех, кто в танке, задача разрешима и методом интервалов.
Может ли функция быть положительно или отрицательной на всей числовой прямой? Конечно, в статье Область определения функции мы рассмотрели типовые примеры. В частности выяснили, что (парабола, полностью лежащая в верхней полуплоскости). Метод интервалов проходит и тут! Рассматриваем единственный интервал , берём из него самую удобную точку и выполняем подстановку: . А значит, функция положительна и в каждой точке интервала .
Перейдём к кубическим многочленам:
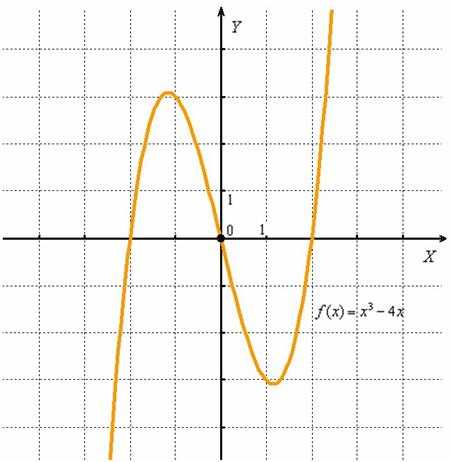
Пример 2
Найти интервалы знакопостоянства функции.
Решение: снова придерживаемся алгоритма:
1) Функция определена на всей числовой прямой.
2) Найдём нули функции, то есть решим уравнение . Для этого выполним разложение на множители:
Таким образом, нули функции: .
3) Откладываем найденные значения на числовой прямой:
Теперь в каждом из 4-х полученных интервалов берём наиболее простую точку и находим значения функции в данных точках:
Таким образом:
Ответ:
, если ;
, если .
Вы можете не знать, как выглядит график функции , но уже, по крайне мере, понятно, где он выше оси , а где ниже.
Кубическая функция настолько распространена, что не удержусь от полного чертежа «молнии»:
Казалось бы, решение можно упростить: взять левый интервал , выяснить, что на нём функция отрицательна, а дальше знаки будут чередоваться – «плюс», «минус», «плюс». Знакочередование бывает часто, но…
3-net.ru
Как найти знаки постоянства числовых функций и их промежутки???
Определить легко и просто. 1) если дан график функции, то — по рисунку. 2) Если дана функция ( формула, то решать неравенство) Если это №326, то надо построить график функции, затем любым «цветом» обвести часть графика, расположенную выше оси ОХ, найти для этих точек абсциссы ( то есть х) , получится промежуток на котором функция принимает значения положительные (у>0) , затем аналогично другим «цветом»….
Можно начать с точек пересечения графика функции и оси ОХ. . В них у=0, записать в ответ чему = х.
Название промежутка зависит от знака. Если знак ≥, то ставить надо квадратную скобку, в противном — круглую
В ответ надо писать значения переменной х.
Функция меняем свой знак при переходе через свои корни (нули) , или может поменять знак приперехрде через точки, в которых она не существует. Приравняйте функцию к 0 и найдите корни. Приравняйте знаменатель к 0 и найдите точки, в которых функция не определена. Нанесите все точки на числовую прямую и определите знак функции слева и справа от точек (возьмите любое число из промежутка и подставьте в функцию) . Этот метод наз. Методом интервалов
спроси что нибудь о литературе или географии:):)
touch.otvet.mail.ru
Как найти интервалы знакопостоянства функции?
⇐ ПредыдущаяСтр 6 из 12Следующая ⇒
Алгоритм метода интервалов прост и бесхитростен:
1) Находим область определения функции.
2) Находим нули функции (точки пересечения графика с осью абсцисс).
3) В большинстве заданий потребуется чертёж. Чертим ось и откладываем на ней точки разрыва (если они есть), а также нули функции (если они есть). Определяем знаки функции на интервалах, которые входят в область определения.
Пункты можете законспектировать, впрочем, алгоритм очень быстро запомнит даже полный чайник. Тут всё прозрачно и логично.
Начнём с распространённой квадратичной функции:
Пример 1
Найти интервалы знакопостоянства функции.
Решение:
1) Функция определена и непрерывна на всей числовой прямой. Таким образом, точки разрыва и «нехорошие» промежутки отсутствуют.
2) Найдём нули функции. Для этого нужно решить уравнение . В данном случае:
Дискриминант положителен, значит, уравнение имеет два действительных корня:
3) Откладываем все найденные точки на числовой оси:
В статье Область определения функции я выполнял подобные чертежи схематически, но сейчас для бОльшей наглядности изложения буду их масштабировать (за исключением клинических случаев). На том же уроке мы узнали, как выяснить знаки функции на интервалах – можно проанализировать расположение параболы. В данном случае ветви параболы направлены вверх, следовательно, на интервалах функция будет положительна: . Попа параболы сидит на интервале ниже оси абсцисс, и функция здесь отрицательна: .
Хорошо, параболу многие читатели представляют. Но что делать, если функция более сложная? Например, . Заметная часть аудитории уже затруднится сказать, как принципиально выглядит график данной функции. И это, так скажем, ещё только минимальное усложнение.
Однако и в простых и в сложных случаях работает универсальный способ:
Рассмотрим функцию непрерывную на некотором интервале , график которой не пересекает ось на этом интервале. Тогда:
– если функция положительна в какой-либо точке интервала , то она положительна и ВО ВСЕХ точках данного интервала;
– если функция отрицательна в какой-либо точке интервала , то она отрицательна и ВО ВСЕХ точках данного интервала.
Включите немного воображения: если на интервале нет точек разрыва, и график не пересекает ось абсцисс, то он не может по мановению волшебной палочки перескочить из нижней полуплоскости в верхнюю полуплоскость (или наоборот). Поэтому знак функции на таком интервале легко определить по одной-единственной точке.
Проведём небольшой эксперимент. Представьте, что вы совсем не знаете, как выглядит график функции и вам необходимо найти её интервалы знакопостоянства (кстати, если действительно не знаете, таки начертите многострадальную примадонну =)).
1) Берём произвольную точку интервала . С вычислительной точки зрения проще всего взять . Подставляем её в нашу функцию:
Следовательно, функция положительна ив каждой точке интервала .
2) Берём произвольную точку интервала , здесь по удобству вне конкуренции ноль. Снова выполняем подстановку:
А, значит, функция отрицательна ив каждой точке интервала .
3) И, наконец, обрабатываем наиболее простую точку интервала :
Поэтому функция положительна в каждой точке интервала .
Выполненные подстановки, вычисления почти всегда нетрудно выполнить устно, но в крайнем случае существует и черновик.
Фиксируем полученные результаты на числовой оси:
Да, вы не имеете никаких представлений о параболе, но совершенно точно можете сказать, что на интервалах график функции расположен ВЫШЕ оси , а на интервале – НИЖЕ данной оси.
Ответ:
, если ;
, если .
Точно так же решается целый спектр задач-«сателлитов», вот некоторые из них:
Решить квадратичное неравенство .
Проводим аналогичные действия и даём ответ .
Решить квадратичное неравенство .
Проводим аналогичные действия и даём ответ .
Найти область определения функции .
Проводим аналогичные действия, даём ответ .
И т.п.
Метод интервалов работает в самых примитивных случаях, например, для функции . Здесь прямая пересекает ось абсцисс в точке , при этом слева от данной точки (график ниже оси ), а справа (график выше оси ). Тем не менее, для тех, кто в танке, задача разрешима и методом интервалов.
Может ли функция быть положительно или отрицательной на всей числовой прямой? Конечно, в статье Область определения функции мы рассмотрели типовые примеры. В частности выяснили, что (парабола, полностью лежащая в верхней полуплоскости). Метод интервалов проходит и тут! Рассматриваем единственный интервал , берём из него самую удобную точку и выполняем подстановку: . А значит, функция положительна и в каждой точке интервала .
Перейдём к кубическим многочленам:
Пример 2
Найти интервалы знакопостоянства функции.
Решение: снова придерживаемся алгоритма:
1) Функция определена на всей числовой прямой.
2) Найдём нули функции, то есть решим уравнение . Для этого выполним разложение на множители:
Таким образом, нули функции: .
3) Откладываем найденные значения на числовой прямой:
Теперь в каждом из 4-х полученных интервалов берём наиболее простую точку и находим значения функции в данных точках:
Таким образом:
Ответ:
, если ;
, если .
Вы можете не знать, как выглядит график функции , но уже, по крайне мере, понятно, где он выше оси , а где ниже.
Кубическая функция настолько распространена, что не удержусь от полного чертежа «молнии»:
Казалось бы, решение можно упростить: взять левый интервал , выяснить, что на нём функция отрицательна, а дальше знаки будут чередоваться – «плюс», «минус», «плюс». Знакочередование бывает часто, но…
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
arhivinfo.ru






























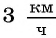
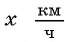

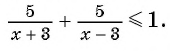
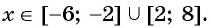
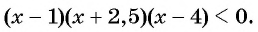
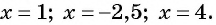
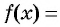
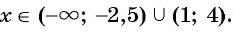
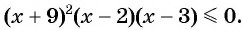
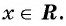
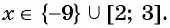
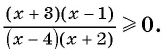
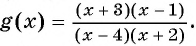
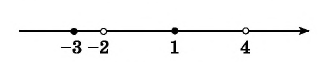
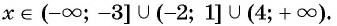
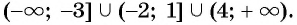
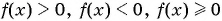 или
или