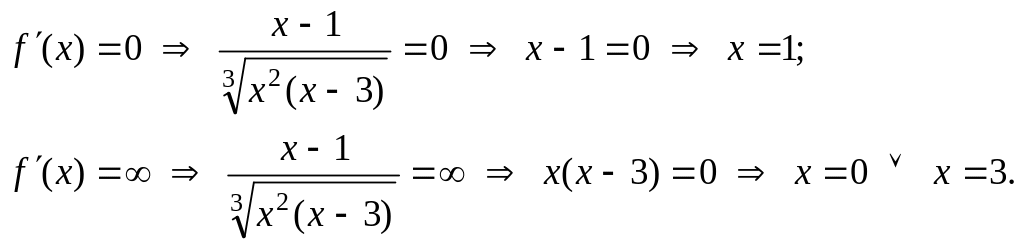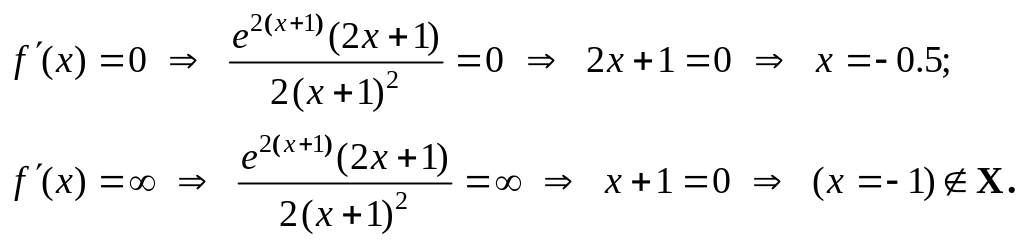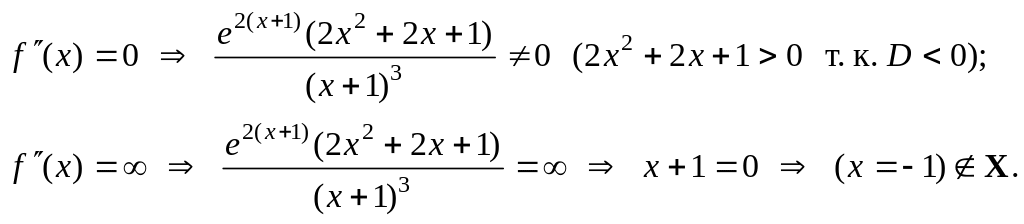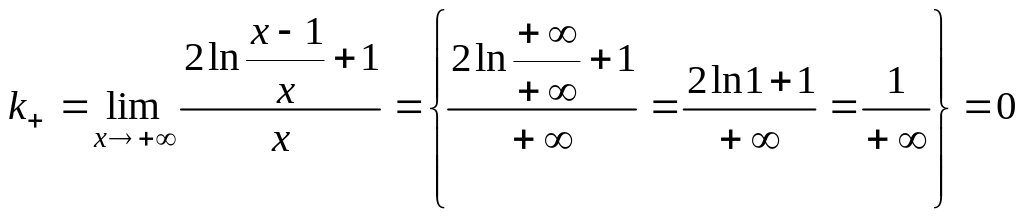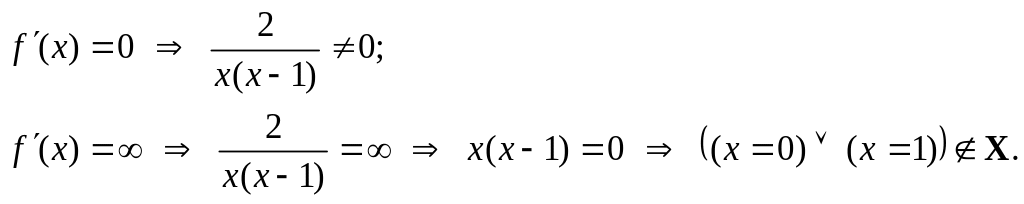Как найти промежутки знакопостоянства функции по графику - Исправление недочетов и поиск решений вместе с Examum.ru

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Остановимся подробнее на свойствах функций.

Нули функции

Определение

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом.
Внимание!

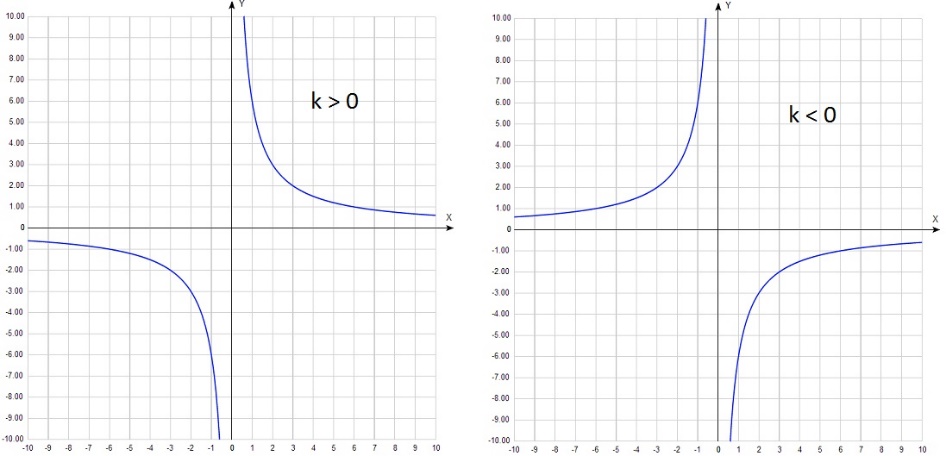
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.

График функции у=k/x выглядит следующим образом:

По данному рисунку видно, что нулей функции не существует.
Как найти нули функции?

Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.

Рассмотрим примеры нахождения нулей функции.

Пример №1. Найти нули функции (если они существуют):

а) у= –11х +22

б) у= (х + 76)(х – 95)

в) у= – 46/х

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11

Получим х=2.

Таким образом, мы нашли нуль функции: х=2

б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.

в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.

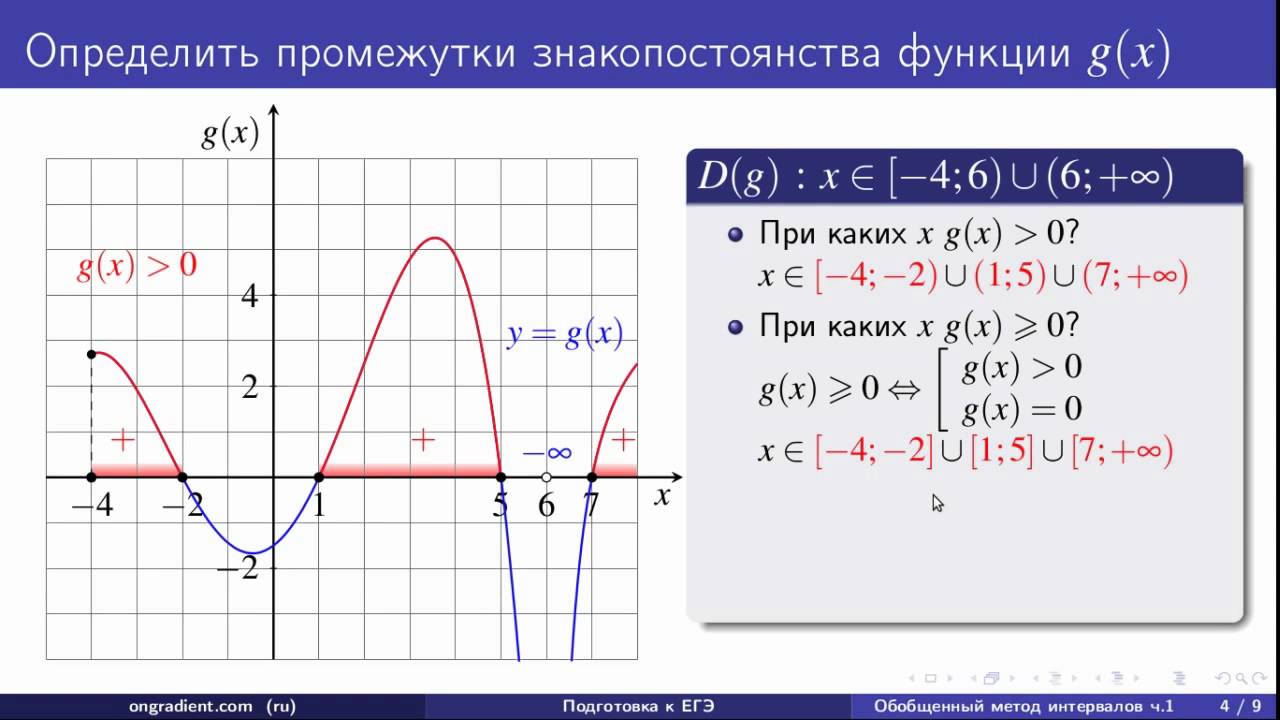
Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Определение

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.

На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.

Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.

Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Определение

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Даниил Романович | Просмотров: 16.1k

Источник

Промежутки знакопостоянства — такие промежутки на области определения, в которых значения функции сохраняют свой знак.

Для нахождения промежутков знакопостоянства функции y=f(x) надо решить неравенства f(x)>0, f(x)<0.

Пример:
Найдем промежутки знакопостоянства функции y=x2+x−2.
Решим неравенство: x2+x−2<0.
Сначала найдем нули функции f(x)=x2+x−2:

x2+x−2=0
D=1−4⋅(−2)=9
x=−1±32
x1=1,x2=−2

Таким образом, получились промежутки значений аргумента, в которых функция сохраняет знак:

(−∞;−2),(−2;1),(1;+∞)

Для того, чтобы определить знак функции на каждом из этих промежутков, найдем значение функции в произвольной точке из каждого промежутка. Точки выбираются из соображений удобства вычислений.
Возьмем значения аргумента: −3∈(−∞;−2), 0∈(−2;1) и 2∈(1;+∞) и найдем для них значения функции.
f(−3)=(−3)2+(−3)−2=9−3−2=4
f(0)=−2
f(2)=4

Значит, в промежутке (−∞;−2) функция принимает положительные значения, в промежутке (−2;1) — отрицательные и в промежутке (1;+∞) — положительные.
Это же можно наблюдать на графике функции:

Источник

Свойства функции

В этой статье мы коротко суммируем сведения, которые касаются такого важного математического понятия, как функция. Мы поговорим о том, что такое числовая функция и какие свойства функции необходимо знать и уметь исследовать.

Что такое числовая функция? Пусть у нас есть два числовых множества: Х и Y, и между этими множествами есть определенная зависимость. То есть каждому элементу х из множества Х по определенному правилу ставится в соответствие единственный элемент y из множества Y.

Важно, что каждому элементу х из множества Х соответствует один и только один элемент y из множества Y.

Правило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией.

Множество Х называется областью определения функции.

Множество Y называется множеством значений значений функции.

Равенство называется уравнением функции. В этом уравнении — независимая переменная, или аргумент функции. — зависимая переменная.

Если мы возьмем все пары и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции — это графической изображение зависимости между множествами Х и Y.

Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.

Основные свойства функций.

1. Область определения функции.

Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции имеет смысл. Другими словами, это область допустимых значений выражения .

Чтобы по графику функции найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.

2. Множество значений функции.

Множество значений функции Е(y)— это множество всех значений, которые может принимать зависимая переменная y.

Чтобы по графику функции найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.

Нули функции — это те значения аргумента х, при которых значение функции (y) равно нулю.

Чтобы найти нули функции , нужно решить уравнение . Корни этого уравнения и будут нулями функции .

Чтобы найти нули функции по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции .

4. Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции — это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть или .

Чтобы найти промежутки знакопостоянства функции , нужно решить неравенства и .

Чтобы найти промежутки знакопостоянства функции по ее графику, нужно

найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ — при этих значениях аргумента ,
найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ — при этих значениях аргумента .

5. Промежутки монотонности функции.

Промежутки монотонности функции — это такие промежутки значений аргумента х, при которых функция возрастает или убывает.

Говорят, что функция возрастает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: .

Другими словами, функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Чтобы по графику функции определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.

Говорят, что функция убывает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: .

Другими словами, функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Чтобы по графику функции определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.

6. Точки максимума и минимума функции.

Точка называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:

Графически это означает что точка с абсциссой x_0 лежит выше других точек из окрестности I графика функции y=f(x).

Точка называется точкой минимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:

Графически это означает что точка с абсциссой лежит ниже других точек из окрестности I графика функции .

Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.

7. Четность (нечетность) функции.

Функция называется четной, если выполняются два условия:

а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.

Другими словами, область определения четной функции симметрична относительно начала координат.

б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .

Функция называется нечетной, если выполняются два условия:

Другими словами, область определения нечетной функции симметрична относительно начала координат.

б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .

Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.

Чтобы определить четность функции, нужно:

а). Найти область определения функции , и определить, является ли она симметричным множеством.

Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция — функция общего вида.

Если область определения функции — симметричное множество, то проверяем п. б)

б). В уравнение функции нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду или .

Если , то функция четная.

Если , то функция нечетная.

Если не удалось привести ни к тому ни к другому, то наша функция — общего вида.

График четной функции симметричен относительно оси ординат ( прямой OY ).

График нечетной функции симметричен относительно начала координат ( точки (0,0) ).

8. Периодичность функции.

Функция называется периодической, если существует такое положительное число Т, что

для любого значения х из области определения функции, х+Т также принадлежит D(x)

В программе средней школы из числа периодических функций изучают только тригонометрические функции.

Предлагаю вам посмотреть ВИДЕОУРОК, в котором я рассказываю, как определить свойства функции по ее графику.

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.

теория по математике 📈 функции

Остановимся подробнее на свойствах функций.

Нули функции

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

График функции у=k/x выглядит следующим образом: По данному рисунку видно, что нулей функции не существует. Как найти нули функции?

Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.

Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):

Находим х, разделив 22 на 11: х=22:11

Таким образом, мы нашли нуль функции: х=2

Пример №2. Найти нули функции у=f(x) по заданному графику.

Промежутки знакопостоянства

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

стационарные и критические точки;
точки экстремума;
нули функции;
точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

Найти область определения функции.
Найти область допустимых значений функции.
Проверить не является ли функция четной или нечетной.
Проверить не является ли функция периодической.
Найти нули функции.
Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
Найти асимптоты графика функции.
Найти производную функции.
Найти критические точки в промежутках возрастания и убывания функции.
На основании проведенного исследования построить график функции.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

источники:

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.

http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij

Источник

Промежутки знакопостоянства

		0		3
	–	0	+	0	+

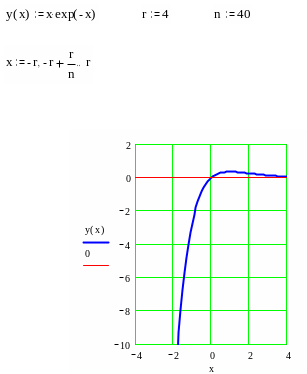
II. Исследование
графика функции по первой производной.

Для нахождения
участков монотонности и экстремальных
точек найдем первую производную функции:

к. т. I.

Область определения
функции разобьем на интервалы

и определим знак

в каждом из них (для удобства вычислений
в каждом интервале выбираем фиксированную
точку). Результаты исследования знака
производной на интервалах между
критическими точками (с учетом

)
с указанием поведения функции на этих
интервалах занесем в таблицу:

	0		1		3
+		+	0	–		+
	0

Так как функция в
точке

определена и непрерывна и при переходе
через нее

меняет знак с плюса на минус, то в этой
точке максимум, причем

.
В точке

функция определена и непрерывна и при
переходе через нее

меняет знак с минуса на плюс, следовательно,
в этой точке минимум, причем

.

III. Исследование
графика функции по второй производной.

Для нахождения
участков выпуклости вверх и вниз найдем
вторую производную функции

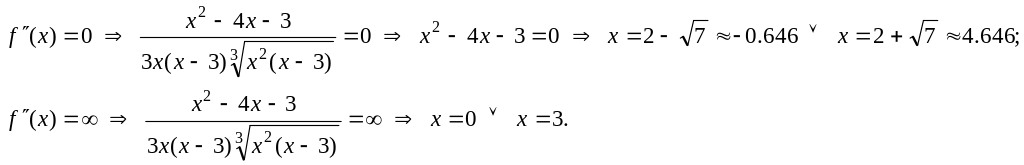
к. т.
II.

Область определения
функции разобьем на интервалы

,

и определим знак

в каждом из них. Результат исследования
знака функции

на указанных интервалах с указанием
выпуклости вверх и вниз запишем в
таблицу:

	–0.646		0		3		4.646
–	0	+		–		–	0	+
			0		0

При переходе через
точки

вторая производная меняет знак,
следовательно, это точки перегиба
функции, причем

Точки перегиба:

.

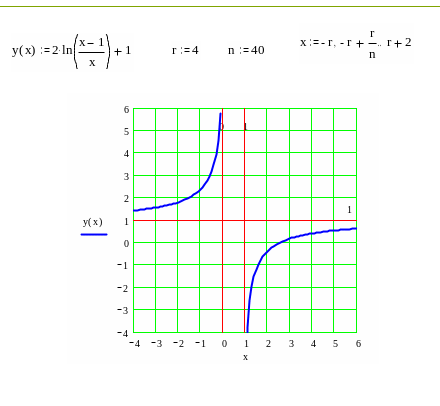
Построение
графика начнем с нанесения асимптот,
точек пересечения с осями координат,
экстремума, перегиба и фрагментов
графика функции вблизи этих точек и
асимптот.

В окончательном
виде график изображен на следующем
рисунке.

▼

Пример
15. Провести полное исследование
функции

и построить ее график.

▲
Исследование
функции будем проводить, придерживаясь
приведенной выше схемы.

I. Элементарное
исследование

Область
определения функции.

.
Исследуем
функцию на симметричность (определить
четность и нечетность функции) и
периодичность.

Функция
общего вида.

. Функция
не периодична.

Выясним
существование асимптот.

Вертикальных
асимптот нет, так как нет точек разрыва.

Найдем наклонные
асимптоты

Слева

.

.
Слева
наклонной асимптоты нет.

Справа

.

Справа
горизонтальная асимптота:

.

Определим
точки пересечения графика функции с
координатными осями, найдем интервалы
знакопостоянства функции.

Точки
пересечения с осью

Промежутки
знакопостоянства

		0
	–	0	+

II.
Исследование графика функции по
первой производной.

Для
нахождения участков монотонности и
экстремальных точек найдем первую
производную функции:

к. т. I.

Область определения
функции разобьем на интервалы

и определим знак

)
с указанием поведения функции на этих
интервалах занесем в таблицу:

	1
+	0	–

Так как функция в
точке

определена и непрерывна и при переходе
через нее

меняет знак с плюса на минус, то в этой
точке максимум, причем

.

III. Исследование
графика функции по второй производной.

Для нахождения
участков выпуклости вверх и вниз найдем
вторую производную функции

к. т. II.

Область определения
функции разобьем на интервалы

и определим знак

в каждом из них. Результат исследования
знака функции

на указанных интервалах с указанием
выпуклости вверх и вниз запишем в
таблицу:

	2
–	0	+

При переходе через
точку

вторая производная меняет знак,
следовательно, это точка перегиба
функции, причем

.
Точка перегиба:

.

Построение графика
начнем с нанесения асимптот, точек
пересечения с осями координат, экстремума,
перегиба и фрагментов графика функции
вблизи этих точек и асимптот.

В окончательном
виде график изображен на следующем
рисунке.

▼

Пример
16. Провести полное исследование
функции

и построить ее график.

▲
Исследование
функции будем проводить, придерживаясь
приведенной выше схемы.

I. Элементарное
исследование

Область определения
функции

.
Точка разрыва:

.
Исследуем
функцию на симметричность (определить
четность и нечетность функции) и
периодичность.

Функция
общего вида.

. Функция
не периодична.

Выясним
существование асимптот. В точке

функция имеет разрыв II рода, ибо,

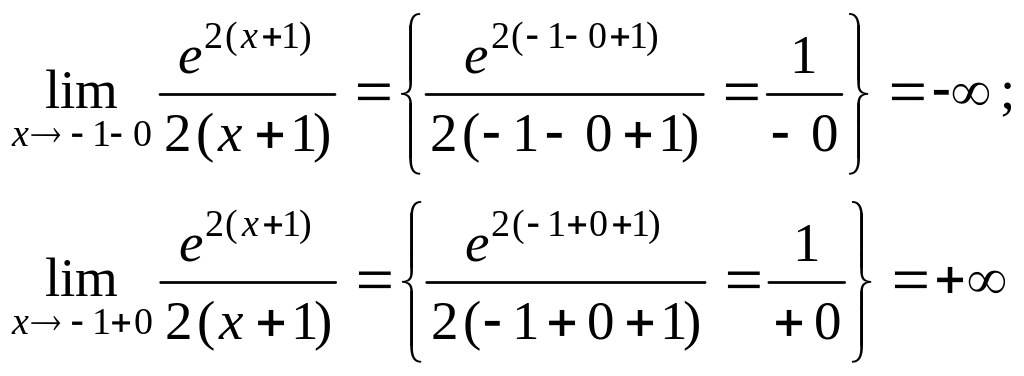
в
остальных точках она непрерывна. Прямая

является вертикальной асимптотой.

Найдем наклонные
асимптоты

Слева

Уравнение
горизонтальной асимптоты слева:

.

Справа

Справа наклонной
асимптоты нет.

Определим
точки пересечения графика функции с
координатными осями, найдем интервалы
знакопостоянства функции.

Точки
пересечения с осью

Точек
пересечения с осью

нет.

Точки пересечения
с осью

:

Точка
пересечения с осью

:

Промежутки
знакопостоянства

		–1
	–		+

II. Исследование
графика функции по первой производной.

Для нахождения
участков монотонности и экстремальных
точек найдем первую производную функции:

к. т. I.

Область определения
функции разобьем на интервалы

и определим знак

)
с указанием поведения функции на этих
интервалах занесем в таблицу:

	–1		–0.5
–		–	0	+

Так как функция в
точке

определена и непрерывна и при переходе
через нее

меняет знак с минуса на плюс, то в этой
точке минимум, причем

.

III. Исследование
графика функции по второй производной.

Для нахождения
участков выпуклости вверх и вниз найдем
вторую производную функции

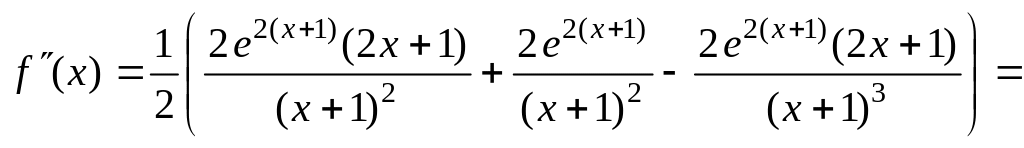
к. т. II нет.

Область определения
функции разобьем на интервалы

и определим знак

в каждом из них. Результат исследования
знака функции

на указанных интервалах с указанием
выпуклости вверх и вниз запишем в
таблицу:

	–1
–		+

Точек перегиба
нет.

В окончательном
виде график изображен на следующем
рисунке.

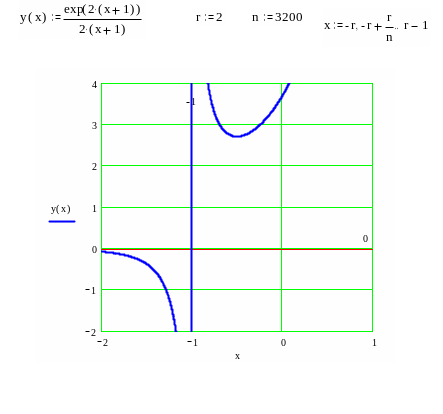
Пример
17. Провести полное исследование
функции

и построить ее график.

▲
Исследование
функции будем проводить, придерживаясь
приведенной выше схемы.

I. Элементарное
исследование

Область
определения функции.
.
Исследуем
функцию на симметричность (определить
четность и нечетность функции) и
периодичность.

Функция
общего вида.

. Функция
не периодична.

Выясним
существование асимптот. Вертикальная
асимптота может существовать лишь на
конечных границах области определения.
Найдем

Значит, прямая

– вертикальная асимптота.

Найдем

Следовательно,
прямая

– вертикальная асимптота.

Найдем
наклонные асимптоты

Слева

Уравнение
горизонтальной асимптоты слева

.

Справа

Уравнение
горизонтальной асимптоты справа

Определим
точки пересечения графика функции с
координатными осями, найдем интервалы
знакопостоянства функции.

Точки
пересечения с осью

Точка
пересечения с осью

Точек пересечения
с осью

нет.

Промежутки
знакопостоянства

		0	1		2.533
	+			–	0	+

II. Исследование
графика функции по первой производной.

Для нахождения
участков монотонности и экстремальных
точек найдем первую производную функции:

к.
т. I нет.

Область определения
функции разобьем на интервалы

и определим знак

)
с указанием поведения функции на этих
интервалах занесем в таблицу:

	0	1
+			+

Экстремумов
нет.

III. Исследование
графика функции по второй производной.

Для нахождения
участков выпуклости вверх и вниз найдем
вторую производную функции

;

К.
т. II нет.

Область определения
функции разобьем на интервалы

и определим знак

в каждом из них. Результат исследования
знака функции

на указанных интервалах с указанием
выпуклости вверх и вниз запишем в
таблицу:

	0	1
+			–

Точек перегиба
нет.

Построение графика
начнем с нанесения асимптот, точек
пересечения с осями координат, экстремума,
перегиба и фрагментов графика функции
вблизи этих точек и асимптот.

В окончательном
виде график изображен на следующем
рисунке.

▼

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Свойства функций.

Итак, мы познакомились с функцией, узнали, что такое область определения и область значений функции. Теперь рассмотрим свойства функций. Их существует много, однако, изучаются они постепенно. В 9 классе мы знакомимся с нулями функции, промежутками возрастания и убывания (монотонность) и промежутками знакопостоянства и чётностью (нечётностью) функции. Рассмотрим их подробно.

Нулями функции называются значения независимой переменной (аргумента), при которых значение функции равно нулю. В графической интерпретации нулями функции являются абсциссы точек пересечения графика с осью абсцисс (осью х).

На графике нули функции: .

Для того, чтобы найти нули функции, заданной аналитически, необходимо решить уравнение: . Корни этого уравнения являются нулями функции.

Например, найти нули функции .

или

Значит, нули функции: .

Промежутками знакопостоянства функции называются промежутки значений аргумента, на которых значения функции либо только положительны, либо только отрицательны. Другими словами, это те промежутки, на которых функция сохраняет свой знак.

Рассматривая график сверху, найдём промежутки знакопостоянства.

функция принимает только положительные значения на тех участках графика, где он находится выше оси Ох, т.е. при ;
функция принимает только отрицательные значения на тех участках графика, где он находится ниже оси Ох, т.е. при .

Для того, чтобы найти промежутки знакопостоянства функции, заданной аналитически, необходимо решить неравенства: и . Решения этих неравенств и будут промежутками знакопостоянства функции.

Например, найти промежутки знакопостоянства функции .

Это неравенство можно решить двумя способами: с помощью систем неравенств и методом интервалов. Метод интервалов будет рассмотрен нами чуть позже, поэтому воспользуемся системами неравенств. Произведение двух множителей положительно, если эти множители имеют одинаковый знак. Значит, получается совокупность двух систем:

или

Значит, при

Теперь находим промежутки, на которых функция принимает отрицательные значения.

Произведение двух множителей отрицательно, если эти множители имеют разные знаки, т.е.

или

Значит, при .

Чётной называется функция, если противоположным значениям аргумента соответствуют одинаковые значения функции, т.е. . График чётной функции симметричен относительно оси ординат (оси Оу).

Нечётной называется функция, если противоположным значениям аргумента соответствуют противоположные значения функции, т.е. . График нечётной функции симметричен относительно начала координат.

На рисунке слева график чётной функции, на рисунке справа – нечётной функции.

Для того, чтобы определить чётность функции, заданной аналитически, необходимо в заданную функцию вместо х подставить –х и произвести упрощение. Если в результате получится функция, равная заданной, то функция чётная; если получится функция, противоположная заданной, то она нечётная; если не получится ни один из предложенных вариантов, то функция не является ни чётной, ни нечётной.

Например, исследовать на чётность функцию .

Находим значение этой функции при противоположном значении х, т.е.

Полученное выражение не совпадает с заданным и не противоположно ему, значит, функция не является ни чётной, ни нечётной. Её график не симметричен относительно оси Оу и не симметричен относительно начала координат.

Приведём ещё один пример: .

После упрощения получили выражение, полностью совпадающее с заданным. Значит, функция является чётной и её график симметричен относительно начала координат.

Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции (или меньшему значению аргумента соответствует меньшее значение функции), т.е. если при , то функция возрастающая.

Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции (или меньшему значению аргумента соответствует большее значение функции), т.е. если при , то функция убывающая.

Для примера рассмотрим графики на рисунках выше.

Синий график: функция возрастает при

функция убывает при

Зелёный график: функция возрастает при

функция убывает при

Промежутки возрастания и убывания функции называются промежутками монотонности функции.

Если функция задана аналитически, то нахождение промежутков монотонности является более сложным процессом и он изучается в 11 классе. Мы ограничимся определением этих промежутков по графикам.

Наибольшим значением функции называется самое большое значение функции по сравнению со всеми остальными.

Наименьшим значением функции называется самое маленькое значение функции по сравнению со всеми остальными.

Строгое определение наибольшего и наименьшего значения функции будет дано в старших классах.

На синем графике наибольшего значения нет, т.к. график бесконечен в положительном направлении оси Оу. А наименьшее значение равно . Записывается это так: .

На зелёном графике нет ни наибольшего, ни наименьшего значения функции.

На рисунках изображены части графиков нечётных функций. Достройте эти графики.

Какая из данных функций является чётной, а какая – нечётной:

Приведите необходимые обоснования.

Докажите, что – чётная функция, а – нечётная, если:

Является ли чётной или нечётной функция , если:

На рисунках изображены части графиков чётных функций. Достройте эти графики.

Постройте график функции , зная, что при её значения могут быть найдены по формуле:

Известно, что функция – чётная и она обращается в нуль при и . Укажите другие значения аргумента, при которых .

Известно, что функция – чётная и она принимает значения, равные нулю, при и . Укажите другие значения аргумента, при которых .

Известно, что уравнение , где – нечётная функция с областью определения , имеет положительные корни и . Найдите неположительные корни уравнения.

Известно, что уравнение , где – нечётная функция с областью определения , имеет положительные корни и . Найдите неположительные корни уравнения.

Линейная функция является нечётной. Найдите значение .

Функция , где – некоторое число, является чётной. Найдите значение .

Известно, что и – нечётные функции. Верно ли утверждение, что нечётной является функция , если:

Известно, что и – нечётные функции. Верно ли утверждение, что чётной является функция , если: Представьте каким-либо способом функцию в виде суммы чётной и нечётной функций, если:
1. Функция , область определения которой – промежуток , задана графиком на рисунке. Укажите промежутки, на которых эта функция возрастает и на которых убывает.
1. Функция , область определения которой – промежуток , задана графиком на рисунке. Укажите промежутки, на которых эта функция возрастает и на которых убывает.
1. Какая из линейных функций и является возрастающей, убывающей и почему?
1. Докажите, что функция является убывающей на промежутке и возрастающей на промежутке .
1. Докажите, что функция является возрастающей на промежутке и убывающей на промежутке .
1. Укажите промежутки возрастания и убывания функций .
1. Определите характер монотонности функций и . Докажите, что функция возрастающая, а функция — убывающая.
1. Известно, что функция является монотонной и что уравнение имеет корень, равный . Имеет ли это уравнение другие корни?
1. Известно, что уравнение , где – монотонная функция, имеет корень, равный . Имеет ли это уравнение другие корни?
1. Известно, что функция возрастает на промежутке . При каких значениях, принадлежащих этому промежутку, верно неравенство:
  
  Известно, что функция убывает на промежутке . При каких значениях, принадлежащих этому промежутку, верно неравенство: Известно, что функции и – убывающие. Является ли убывающей функция , если: Известно, что функции и – возрастающие. Является ли возрастающей функция , если: Известно, что функция определена на множестве и возрастает на промежутке , где . Как изменяется эта функция на промежутке , если:
  1. – функция нечётная?
2. Известно, что функция определена на множестве и убывает на промежутке , где . Как изменяется эта функция на промежутке , если:
  1. – функция нечётная?
3. Найдите наибольшее и наименьшее значения функции:
  1. ;
4. Укажите значение аргумента, при котором функция принимает наименьшее значение. Существует ли наибольшее значение этой функции?
  1. Укажите значение аргумента, при котором функция принимает наибольшее значение. Существует ли наименьшее значение этой функции?
  1. Найдите область определения функции:
  Найдите нули функции и области положительных и отрицательных значений, если:
  
  Изобразите схематически график функции , зная результаты исследования функции:
  
  функция является непрерывной и нечётной;
  
  при
  
  функция возрастает на промежутке .
  
  Изобразите схематически график функции , зная результаты исследования функции:
  
  функция является непрерывной и чётной;
  
  при при
  
  функция возрастает на промежутке .
  
  С помощью графика определите свойства функции:
  
  область определения функции;
  
  область значений функции;
  
  нули функции;
  
  промежутки знакопостоянства;
  
  чётность функции;
  
  монотонность функции (промежутки возрастания и убывания);
  
  наибольшее и наименьшее значение функции.
  
  Определить свойства функций, заданных формулами:
  
  С помощью графика определите свойства функции:
  
  область определения функции;
  
  область значений функции;
  
  нули функции;
  
  промежутки знакопостоянства;
  
  чётность функции;
  
  монотонность функции (промежутки возрастания и убывания);
  
  наибольшее и наименьшее значение функции.
  
  Найдите нули функции (если они существуют):
  
  С помощью графика определите свойства функции:
  
  область определения функции;
  
  область значений функции;
  
  нули функции;
  
  промежутки знакопостоянства;
  
  чётность функции;
  
  монотонность функции (промежутки возрастания и убывания);
  
  наибольшее и наименьшее значение функции.
  
  Постройте график функции и опишите её свойства.
  
  Постройте график функции и опишите её свойства.
  
  Выясните свойства функции
  
  Выясните свойства функции
  
  С помощью графика определите свойства функции:
  
  область определения функции;
  
  область значений функции;
  
  нули функции;
  
  промежутки знакопостоянства;
  
  чётность функции;
  
  монотонность функции (промежутки возрастания и убывания);
  
  наибольшее и наименьшее значение функции.
  
  Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?
  
  Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?
  
  Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?
  
  Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?
  
  12

Источник