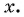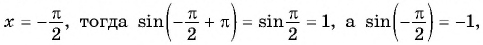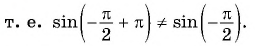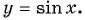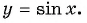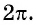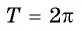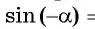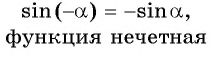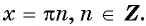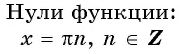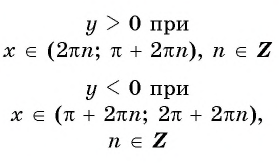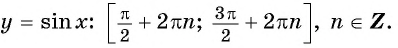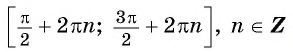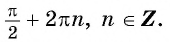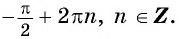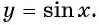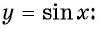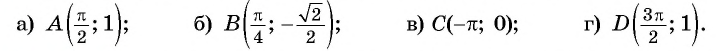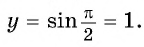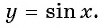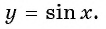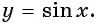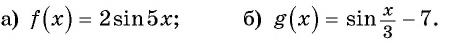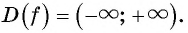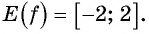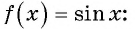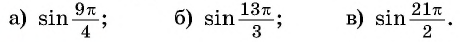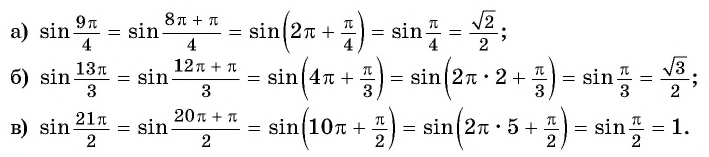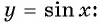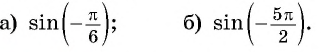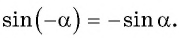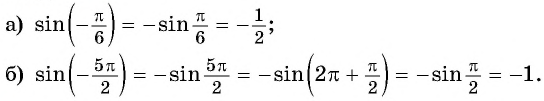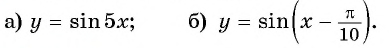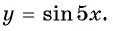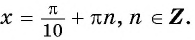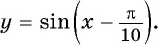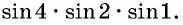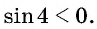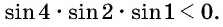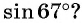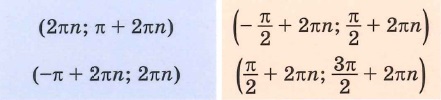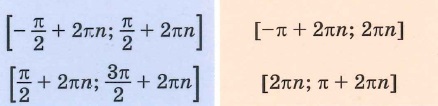Содержание:
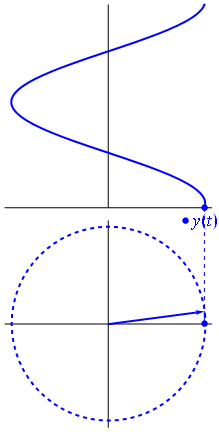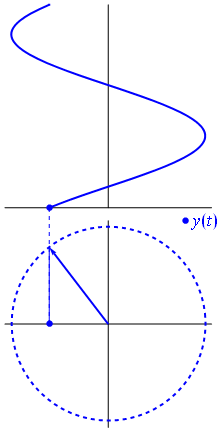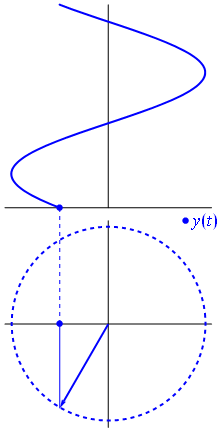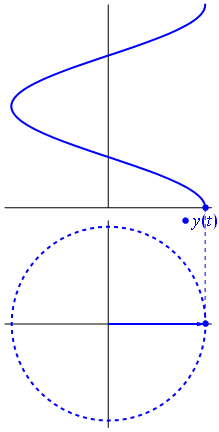
Рассматривая произвольное действительное число
Таким образом, мы установим соответствие между множеством действительных чисел и множеством значений синусов углов. Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Определение функция y=sin x
Определение:
Зависимость, при которой каждому действительному числу 
Рассмотрим свойства функции 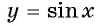
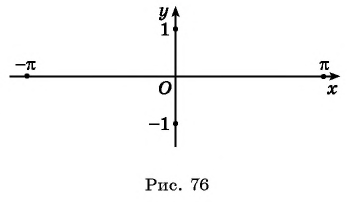
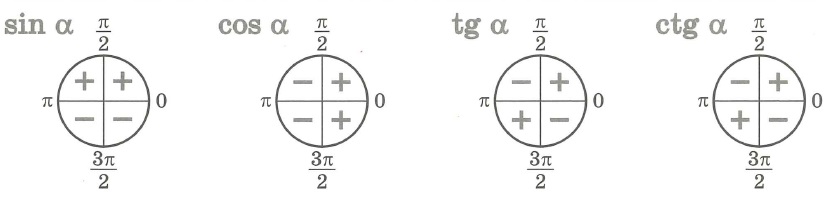
Область определения функции y=sin x
Областью определения функции 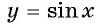
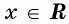
Графически это означает, что для любой абсциссы найдется точка графика функции
Множеством значений функции y=sin x
Множеством значений функции 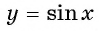
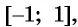
Графически это означает, что график функции 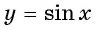
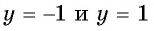
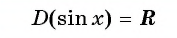
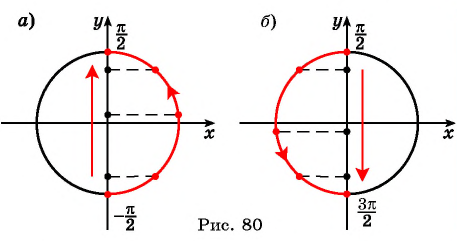
Периодичность функции y=sin x
Периодичность функции 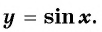
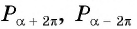
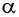
Говорят, что число 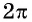
Определение:
Функция 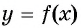
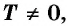
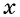
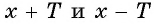
Чтобы определить, является ли функция периодической с периодом 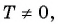
- принадлежат ли области определения функции числа
если
принадлежит области определения функции;
- выполняется ли равенство
Определим, верно ли, что число 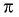
- Числа
принадлежат области определения функции, так как
- Проверим, выполняется ли равенство
для всех
Пусть
Значит, число 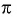
Периодом функции 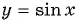
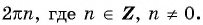
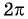
Функция 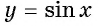
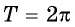
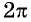
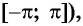
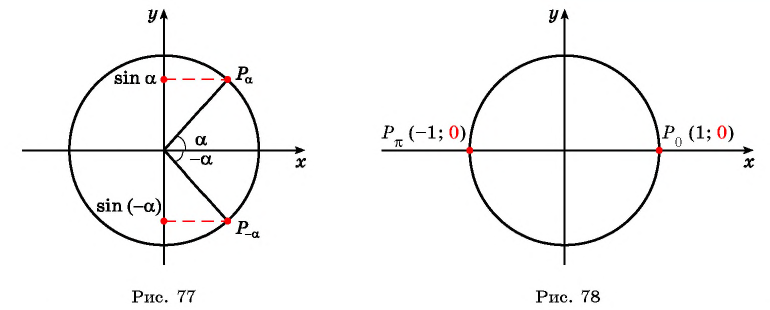
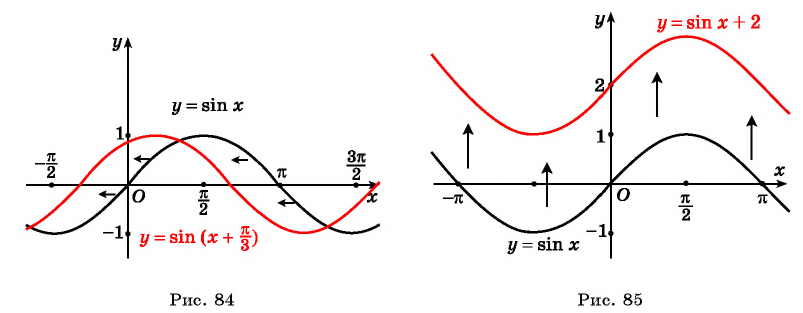
Четность (нечетность) функции y=sin x
Четность (нечетность) функции y=sin x 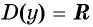
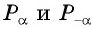
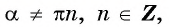
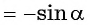
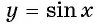
Для построения ее графика достаточно построить его часть для неотрицательных значений аргумента и отобразить эту часть симметрично относительно начала координат.
Нули функции y=sin x
Нули функции. Ординаты точек 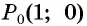
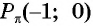
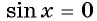
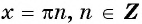
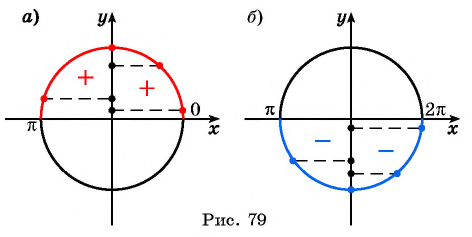
Промежутки знакопостоянства функции y=sin x
На промежутках 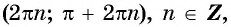
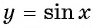
На промежутках 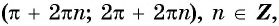
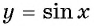
Монотонность функции y=sin x
Монотонность функции. Так как ординаты точек единичной окружности увеличиваются от -1 до 1 при изменении угла от 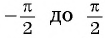
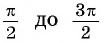
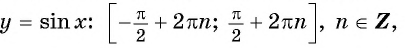
Функции 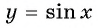
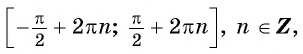
Наибольшее значение функции 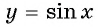
Наименьшее значение функции 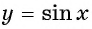
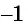
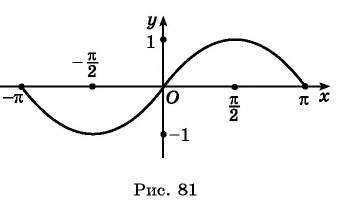
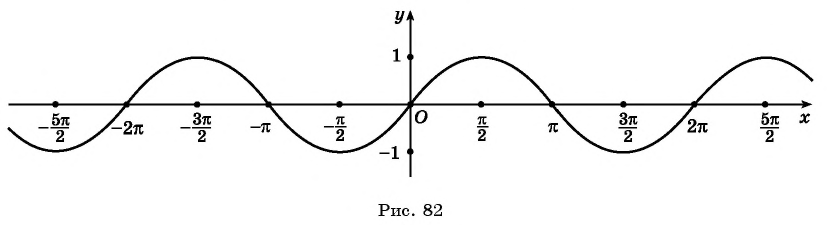
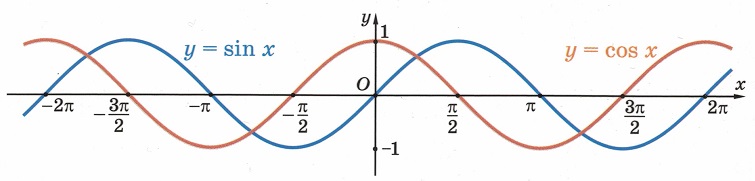
На основании проведенного исследования построим график функции 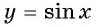
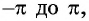
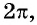
На этом периоде функция
На рисунке 81 изображена часть графика функции 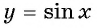
Перенесем эту часть на другие периоды и получим график функции 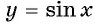
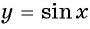
Примеры заданий и их решения
Пример №1
Определите, принадлежит ли графику функции 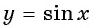
Решение:
а) Подставим в формулу 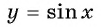
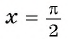
Полученное значение функции равно ординате точки 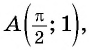
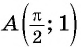
б) При 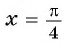
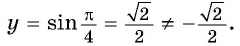
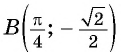
в) При 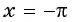
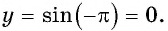
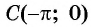
г) При 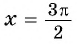
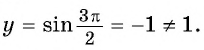
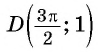
Пример №2
Найдите область определения и множество значений функции:
Решение:
а) Так как область определения функции 
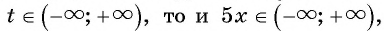
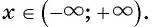
Множеством значений функции 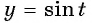
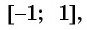
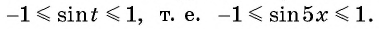
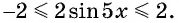
б) 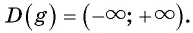
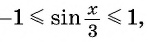
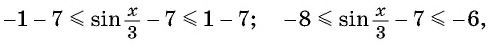
Пример №3
Найдите наибольшее значение функции
Решение:
Так как 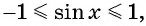
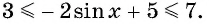
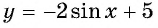
- Заказать решение задач по высшей математике
Пример №4
Найдите значение выражения, используя свойство периодичности функции
Решение:
Так как число 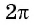
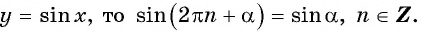
Пример №5
Найдите значение выражения, используя свойство нечетности функции
Решение:
Так как функция 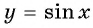
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
a) 
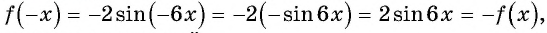
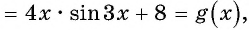
Пример №7
Найдите нули функции:
Решение:
а) Пусть 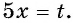
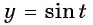
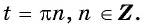
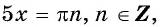
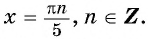
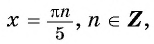
б) Пусть 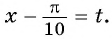
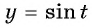
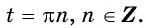
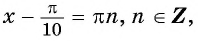
Таким образом, числа 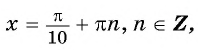
Пример №8
Определите знак произведения
Решение:
Так как 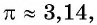
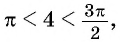
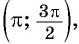
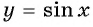
Углы 2 радиана и 1 радиан принадлежат промежутку 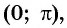
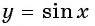
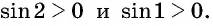
Пример №9
Что больше: 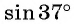
Решение. Так как функция 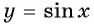
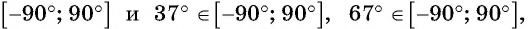
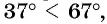
Пример №10
Постройте график функции:
Решение:
а) График функции 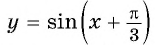
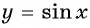
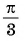
б) График функции 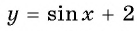
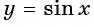
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
Решить тригонометрическое неравенство — это значит, найти множество значений неизвестных, входящих в неравенство, при которых неравенство выполняется.
Тригонометрические неравенства можно решать с помощью графиков функций y = sin x, y = cos x, y = tg x, y= ctg x 
Решение тригонометрических неравенств, сводится, как правило, к решению простейших неравенств вида: sin x>a, sin x

с помощью единичной окружности.
1) На оси ординат (абсцисс) отметить точку a и провести прямую y = a (x = a), перпендикулярную соответствующей оси.
2) Отметить на окружности дугу, состоящую из точек окружности, удовлетворяющих данному неравенству (эти точки расположены по одну сторону от построенной прямой).
3) Записать числовой промежуток, точки которого заполняют отмеченную дугу, и к обеим частям неравенства прибавить период функции ( для y = sin x и y = cos x 
Таким образом, решением неравенства будут все значения на интервале 



Простейшие и сложные тригонометрические неравенства
Неравенства – это соотношения вида a › b, где a и b – есть выражения, содержащие как минимум одну переменную. Неравенства могут быть строгими – ‹, › и нестрогими – ≥, ≤.
Тригонометрические неравенства представляют собой выражения вида: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, в которых F(x) представлено одной или несколькими тригонометрическими функциями.
Простейшие тригонометрические неравенства
Примером простейшего тригонометрического неравенства является: sin x ‹ 1/2. Решать подобные задачи принято графически, для этого разработаны два способа.
Способ 1 – Решение неравенств с помощью построения графика функции
Чтобы найти промежуток, удовлетворяющий условиям неравенство sin x ‹ 1/2, необходимо выполнить следующие действия:
- На координатной оси построить синусоиду y = sin x.
- На той же оси начертить график числового аргумента неравенства, т. е. прямую, проходящую через точку ½ ординаты ОY.
- Отметить точки пересечения двух графиков.
- Заштриховать отрезок являющийся, решением примера.
Когда в выражении присутствуют строгие знаки, точки пересечения не являются решениями. Так как наименьший положительный период синусоиды равен 2π, то запишем ответ следующим образом:
Если знаки выражения нестрогие, то интервал решений необходимо заключить в квадратные скобки – [ ]. Ответ задачи можно также записать в виде очередного неравенства:
Способ 2 – Решение тригонометрических неравенств с помощью единичной окружности
Подобные задачи легко решаются и с помощью тригонометрического круга. Алгоритм поиска ответов очень прост:
- Сначала стоит начертить единичную окружность.
- Затем нужно отметить значение аркфункции аргумента правой части неравенства на дуге круга.
- Нужно провести прямую проходящую через значение аркфункции параллельно оси абсциссы (ОХ).
- После останется только выделить дугу окружности, являющуюся множеством решений тригонометрического неравенства.
- Записать ответ в требуемой форме.
Разберем этапы решения на примере неравенства sin x › 1/2. На круге отмечены точки α и β – значения
Точки дуги, расположенные выше α и β, являются интервалом решения заданного неравенства.
Если нужно решить пример для cos, то дуга ответов будет располагаться симметрично оси OX, а не OY. Рассмотреть разницу между интервалами решений для sin и cos можно на схемах приведенных ниже по тексту.
Графические решения для неравенств тангенса и котангенса будут отличаться и от синуса, и от косинуса. Это обусловлено свойствами функций.
Арктангенс и арккотангенс представляют собой касательные к тригонометрической окружности, а минимальный положительный период для обеих функций равняется π. Чтобы быстро и правильно пользоваться вторым способом, нужно запомнить на какой из оси откладываются значения sin, cos, tg и ctg.
Касательная тангенс проходит параллельно оси OY. Если отложить значение arctg a на единичном круге, то вторая требуемая точка будет расположено в диагональной четверти. Углы

В случае с котангенсом касательная проходит параллельно оси OX, а функция прерывается в точках π и 2π.
Сложные тригонометрические неравенства
Если аргумент функции неравенства представлен не просто переменной, а целым выражением содержащим неизвестную, то речь уже идет о сложном неравенстве. Ход и порядок его решения несколько отличаются от способов описанных выше. Допустим необходимо найти решение следующего неравенства:
Графическое решение предусматривает построение обычной синусоиды y = sin x по произвольно выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек графика:
В результате должна получиться красивая кривая.
Для простоты поиска решения заменим сложный аргумент функции
Пересечение двух графиков позволяет определить область искомых значений, при которых выполняется условие неравенства.
Найденный отрезок является решением для переменной t:
Однако, цель задания найти все возможные варианты неизвестной x:
Решить двойное неравенство достаточно просто, нужно перенести π/3 в крайние части уравнения и произвести требуемые вычисления:
Ответ на задание будет выглядеть как интервал для строгого неравенства:
Подобные задачи потребует опыта и сноровки учащихся в обращении с тригонометрическими функциями. Чем больше тренировочных заданий будет решено в процессе подготовке, тем проще и быстрее школьник найдет ответ на вопрос ЕГЭ теста.
Простейшие тригонометрические неравенства
п.1. Решение неравенств с синусом
Алгоритм решения неравенства (sinxgt a)
Шаг 1. В числовой окружности на оси синусов отметить точку с ординатой (a). Провести горизонталь (y=a), отметить точки её пересечения с окружностью.
Шаг 2. Решить уравнение (sinx=a). Про решение простейших тригонометрических уравнений – см. §19 данного справочника. Полученные базовые решения являются значениями точек пересечения, подписать их.
Шаг 3. Дуга числовой окружности над проведенной горизонталью – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((arcsina+2pi k; pi-arcsin a+2pi k))
 |
$$ sin xgt frac12 $$ 1. Проводим горизонталь (y=frac12), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое). 2. Решаем уравнение (sinx=frac12) begin x=(-1)^kfracpi6+pi k= left[ begin fracpi6+2pi k\ frac<5pi><6>+2pi k end right. end Подписываем точку справа (fracpi6) и точку слева (frac<5pi><6>). 3. При обходе полученной дуги против часовой стрелки получаем интервал: ((fracpi6; frac<5pi><6>)). Добавляем к концам интервала полный период. Ответ: (left(fracpi6;+2pi k; frac<5pi><6>+2pi kright)) |
Алгоритм решения неравенства (sinxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).
Алгоритм решения неравенства (sinxlt a) будет отличаться тем, что в ответе нужно записывать дугу под горизонталью (y=a). При этом не забываем, что дугу нужно обходить в сторону возрастания. Поэтому угол слева пишут отрицательным (отсчитывая период назад).
Наконец, в неравенстве (sinxleq a) всё будет то же, что и в (sinxlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).
 |
$$ sin xleq -frac<sqrt<2>> <2>$$ 1. Проводим горизонталь (y=-frac<sqrt<2>><2>), отмечаем точки пересечения (закрашенные, т.к. неравенство нестрогое). 2. Решаем уравнение (sinx=-frac<sqrt<2>><2>) begin x=(-1)^kleft(-fracpi4right)+pi k= left[ begin -frac<3pi><4>+2pi k\ -frac<pi><4>+2pi k end right. end Подписываем точку справа (-frac<3pi><4>) и точку слева (-frac<pi><4>). 3. При обходе полученной дуги против часовой стрелки получаем отрезок: (left[-frac<3pi><4>;-frac<pi><4>right]). Добавляем к концам отрезка полный период. Ответ: (left[-frac<3pi><4>+2pi k;-frac<pi><4>+2pi kright]) |
п.2. Решение неравенств с косинусом
Алгоритм решения неравенства (cosxgt a)
Шаг 1. В числовой окружности на оси косинусов отметить точку с абсциссой (a). Провести вертикаль (x=a), отметить точки её пересечения с окружностью.
Шаг 2. Решить уравнение (cosx=a). Полученные базовые решения являются значениями точек пересечения, подписать их.
Шаг 3. Дуга числовой окружности справа от проведенной вертикали – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((-arccosa+2pi k; arccosa+2pi k))
 |
$$ cosxgt frac<sqrt<3>> <2>$$ 1. Проводим вертикаль (x=frac<sqrt<3>><2>), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое). 2. Решаем уравнение (cosx=frac<sqrt<3>><2>) begin x=pmfracpi6+2pi k end Подписываем точку снизу (-fracpi6) и точку сверху (frac<pi><6>). 3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi6right)). Добавляем к концам интервала полный период. Ответ: (left(-fracpi6;+2pi k; frac<pi><6>+2pi kright)) |
Алгоритм решения неравенства (cosxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).
Алгоритм решения неравенства (cosxlt a) будет отличаться тем, что в ответе нужно записывать дугу слева от вертикали (x=a). При этом не забываем, что дугу нужно обходить в сторону возрастания, сверху вниз. Значение угла снизу должно быть больше, чем угла сверху.
Наконец, в неравенстве (cosxleq a) всё будет то же, что и в (cosxlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).
п.3. Решение неравенств с тангенсом
Алгоритм решения неравенства (tgxgt a)
Шаг 1. На оси тангенсов (касательной к числовой окружности в точке (1,0)) отметить точку с ординатой (a). Провести луч из начала координат через отмеченную точку, отметить точку её пересечения с окружностью.
Шаг 2. Решить уравнение (tgx=a). Полученное базовое решение является значением точки пересечения.
Шаг 3. Дуга числовой окружности от отмеченной точки до (fracpi2) (в которой (tgxrightarrow +infty)) – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: (left(arctga+pi k; fracpi2+pi kright))
 |
$$ tg xgt -frac<1><sqrt<3>> $$ 1. На оси тангенсов отмечаем точку (-frac<1><sqrt<3>>). Проводим луч из начала координат через эту точку. 2. Решаем уравнение (tgx=-frac<1><sqrt<3>>) begin x=-fracpi6+pi k end Подписываем точку снизу (-fracpi6.) Верхней границей интервала будет (fracpi2), угол, в котором (tgxrightarrow +infty .) 3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi2right)). Добавляем к концам интервала период для тангенса. Строго говоря, на числовой окружности длиной (2pi) получим две дуги для тангенса с периодом (pi). Ответ: (left(-fracpi6;+pi k; frac<pi><2>+pi kright)) |
Алгоритм решения неравенства (tgxlt a) будет отличаться тем, что в ответе нужно записывать дугу от точки (-fracpi2) (в которой (tgxrightarrow -infty)) до найденного арктангенса.
Для нестрогих неравенств будут получаться полуинтервалы, в которых точки (pmfracpi2) ((tgxrightarrow pminfty)) будут ограничены круглой скобкой, а найденные арктангенсы – квадратной.
п.4. Решение неравенств с котангенсом
Решение неравенств с котангенсом аналогично решению с тангенсом. Для решения используется ось котангенсов (касательная к числовой окружности в точке (0;1)).
В неравенствах вида (ctgxgt a) пределу (ctgxrightarrow +infty) соответствует угол 0.
В неравенствах вида (ctgxlt a) пределу (ctgxrightarrow -infty) соответствует угол (pi).
п.5. Примеры
Пример 1. Решите неравенства:
Пример 2*. Решите неравенства:
 |
a) (cosxgt -1) Справа от вертикали (x=-1) расположена вся числовая окружность, кроме точки (pi). |
Ответ: (xne pi+2pi k)
б) (4cos^2frac x2-3leq 0)
(4cdot frac<1+cosx><2>leq 3)
(2+2cosxleq 3)
(cosxleqfrac12)
Ответ: (left[fracpi3+2pi k; frac<5pi><3>+2pi kright])
в) (-sqrt<3>lt tgxleq 5)
(-arctgsqrt<3>+pi klt xleq arctg5+pi k)
(-fracpi3+pi klt xleq arctg5+pi k)
Ответ: (left.left(-frac<pi><3>+pi k; arctg5+pi kright.right])
г) (tgleft(x-fracpi4right)gtsqrt<3>)
(arctgsqrt<3>+pi klt x-fracpi4ltfracpi2+pi k)
(fracpi4+fracpi3+pi klt xltfracpi4+fracpi2+pi k)
(frac<7pi><12>+pi klt xltfrac<3pi><4>+pi k)
Ответ: (left(frac<7pi><12>+pi k; frac<3pi><4>+pi kright))
http://karate-ege.ru/trigonometricheskie-neravenstva/
http://reshator.com/sprav/algebra/10-11-klass/prostejshie-trigonometricheskie-neravenstva/
урок 5. Математика ЕГЭ
Тригонометрические уравнения
Тригонометрия – одна из самых важных тем на ЕГЭ по профильной математике. Она может встретиться в №1 (простейшие уравнения), №4 (преобразование выражений, в том числе тригонометрических), знание свойств тригонометрических функций может пригодится в №9, №11 (производные) и в задании из второй части №12 (тригонометрические уравнения).
Как видите, потенциально хорошие знания по тригонометрии могут принести вам до 6 первичных баллов на ЕГЭ. Конечно, вряд ли тригонометрия будет сразу во всех перечисленных номерах, но без нее написать хорошо профильную математику будет сложно.
Самой сложной темой из тригонометрии являются тригонометрические уравнения. Здесь вам понадобятся все ваши умения по работе с тригонометрической окружностью, знание тригонометрических формул, умение работать с тригонометрическими выражениями и переводить градусы в радианы и наоборот. Тригонометрические уравнения почти всегда попадаются в 12-м номере ЕГЭ, а это уже вторая часть, и за это задание дают целых два первичных балла.
Что такое тригонометрические уравнения?
Итак, если в уравнении переменная (x) (или какое-то выражение от (x)) содержится внутри функций синуса, косинуса, тангенса или котангенса, то такое уравнение называется тригонометрическим. Например:
$$3sin(2x)-2cos(x)^2=0;$$
Но будьте внимательными, если уравнения имеет вид:
$$cos(x)+2x=3;$$
То уравнение уже будет называться смешанным, так как в нем есть и тригонометрическая функция ((cos(x))), и линейная ((2x)). Такое уравнение уже значительно сложнее, и в ЕГЭ они если и встречаются, то очень редко. Здесь смешанные уравнения мы рассматривать не будем.
Но начинать изучение мы будем с простейших тригонометрических уравнений. Это фундамент, на котором строится все остальное. Простейшие уравнения имеют такой вид:
$$sin(f(x))=a;$$
$$cos(f(x))=a;$$
$$tg(f(x))=a;$$
$$ctg(f(x))=a;$$
где (a) — некоторое число, а (f(x)) – некоторое выражение, зависящее от (x);
Примеры простейших тригонометрических уравнений:
$$sin(x)=frac{1}{2};$$
$$cos(3x)=-1;$$
Как решать простейшие тригонометрические уравнения?
Существует два основных метода решения:
- При помощи единичной окружности;
- С использованием готовых формул;
Лично я сторонник решения при помощи единичной окружности. С использованием формул решать, на мой взгляд, не очень удобно, потому что нужно их учить и теряется, как и при любой зубрежке, элемент понимания того, что ты делаешь. Но мы разберем оба способа.
Решение тригонометрического уравнения с синусом на окружности
Здесь необходимо идеальное знание тригонометрической окружности. Если его нет (а без нее в тригонометрии, в любом случае, делать нечего), то рекомендую почитать про нее по ссылке, либо же переходите сразу к методу решения через формулы.
Будем учиться на примере простейшего тригонометрического уравнения:
Пример 1
$$sin(x)=frac{1}{2};$$
Что такое решить уравнение? Значит найти такие значения углов (x), синус от которых будет равен (frac{1}{2}).
Чтобы найти эти самые углы, нарисуем тригонометрическую окружность. (Рис.1)
Рис.1. Тригонометрические уравнения с синусом
На оси синусов (вертикальная ось) отметим значение (frac{1}{2}), обозначим эту точку за (K).
Для того, чтобы понять, какие углы соответствуют этому значению, необходимо провести перпендикуляр (прямая (a)) к оси синусов через точку (K).
Этот перпендикуляр пересечет нашу единичную окружность в двух точках (M) и (N).
Эти точки как раз и будут соответствовать углам, синус от которых будет равен (frac{1}{2}).
На рисунке 1 эти углы отмечены как (angle{MOA}) и (angle{NOA}).
Понятное дело, что мы с вами не можем точно понять по рисунку, что это за углы. Для этого нам понадобится очень точный рисунок на миллиметровке. В нашем случае рисунок показывает нам, что оказывается, есть как минимум два угла (angle{MOA}) и (angle{NOA}), синус от которых будет (frac{1}{2}).
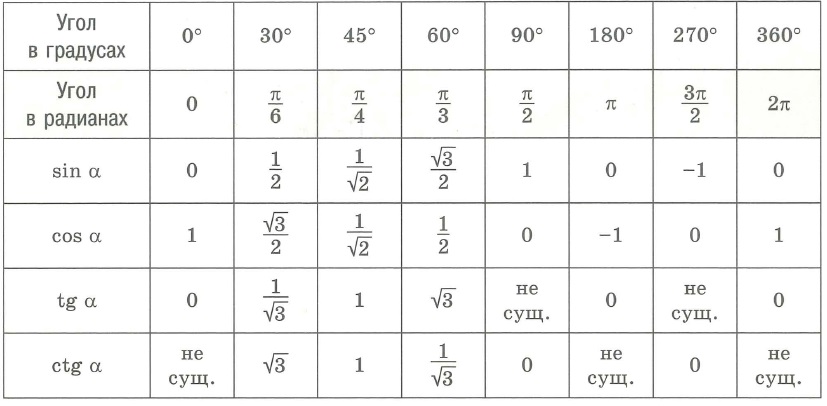
А чтобы найти эти самые углы, мы воспользуемся таблицей значений тригонометрических функций. Видим, что синус равен (frac{1}{2}) от угла в (30^o) или, если в радианах,(frac{pi}{6}).
Рис.2. Таблица значений тригонометрических функций
Но в таблице дан только один угол, синус от которого (frac{1}{2}). И этот угол, если вспомнить, что все положительные углы на единичной окружности отсчитываются от отрезка (OA) против часовой стрелки, судя по всему, соответствует углу (angle{MOA}).
$$x_{1}=frac{pi}{6};$$
А где же взять значение второго угла (angle{NOA})?
И тут нам опять поможет единичная окружность. Посмотрите на рисунок 1: он абсолютно симметричен относительно оси синусов, его можно сложить, как открытку, и правая часть окружности полностью совпадет с левой. Это значит, что углы (angle{MOA}) и (angle{KOC}) равны геометрически:
$$angle{MOA}=angle{KOC}=30^o=frac{pi}{6};$$
Этот интуитивный факт можно строго доказать из равенства треугольников (triangle{MKO}) и (triangle{NKO}).
Итак, из равенства (angle{MOA}=angle{KOC}) можно легко найти угол (angle{NOA}):
$$angle{NOA}=180-angle{KOC}=180-30=150^o;$$
Или в радианах:
$$angle{NOA}=pi-angle{KOC}=pi-frac{pi}{6}=frac{6pi-pi}{6}=frac{5pi}{6};$$
Мы нашли значения обоих углов. Получается, что теперь можем записать значения искомого в уравнении (x):
$$x_{1}=30^o=frac{pi}{6};$$
$$x_{2}=150^o=frac{5pi}{6};$$
Но, к сожалению, ответ пока записывать рано. Потому что есть еще один очень важный момент!
Если вы внимательно изучали предыдущие темы по тригонометрии, то должны знать, что если прибавить к углам (angle{MOA}) и (angle{NOA}) полный оборот ((360^p) или (2pi)), то мы получим новые углы равные соответственно (30^o+360^o=390^o) и (150^o+360^o=510^o), значение синуса которых тоже будет (frac{1}{2})! Так как эти углы тоже соответствуют точкам (M) и (N).
Кроме того, я могу прибавить не один оборот, а хоть миллион оборотов, и опять попаду в те же самые точки (M) и (N), соответствующие синусу (frac{1}{2}). А углы еще бывают отрицательные, и еще можно вычитать полные обороты и опять попадать в эти точки.
Другими словами, у функции синуса есть период, равный ((360^o=2pi)), то есть каждый полный оборот значение синуса будет повторяться.
Для нас это все означает, что существует БЕСКОНЕЧНОЕ количество углов, синус от которых будет (frac{1}{2}) c периодом (360^o=2pi)).
И вот теперь мы можем записать ответ. Он записывается в виде правила, которое описывает это бесконечное количество решений нашего уравнения (правил у нас будет два, каждое соответствует точкам (M) и (N)). И запишу я ответ в радианах, так как в градусах его никто не пишет:
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=frac{5pi}{6}+2pi*n, quad n in Z;$$
Обратите внимание, что к нашим первоначальным корням (x_{1}=30^o=frac{pi}{6}) и (x_{2}=150^o=frac{5pi}{6}) теперь прибавляется слагаемое (2pi*n), где (n) — это некоторое целое число. Подставляя вместо (n) различные целые числа, вы будете получать углы, удовлетворяющие нашему уравнению. Например, при (n=3) получим корни:
$$x_{1}=frac{pi}{6}+2pi*3=frac{pi}{6}+6pi=frac{37pi}{6};$$
$$x_{2}=frac{5pi}{6}+2pi*3=frac{5pi}{6}+6pi=frac{41pi}{6};$$
А при (n=-2) корни:
$$x_{1}=frac{pi}{6}+2pi*(-2)=frac{pi}{6}-4pi=-frac{23pi}{6};$$
$$x_{2}=frac{5pi}{6}+2pi*(-2)=frac{5pi}{6}-4pi=-frac{19pi}{6};$$
И так можно подставлять абсолютно любые (n) и получать корни.
Таким образом, тригонометрические уравнения обычно имеют бесконечное количество решений, которые записываются в виде некоторых правил, как в нашем примере. Запомните это, почему-то немногие это понимают.
Ответ:
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=frac{5pi}{6}+2pi*n, quad n in Z.$$
Пример 2
$$sin(x)=-frac{sqrt{2}}{2};$$
Этот пример так подробно, как предыдущий, разбирать не будем, а только распишем алгоритм решения:
- Рисуем тригонометрическую окружность;
- Отмечаем примерное значение (-frac{sqrt{2}}{2}approx-frac{1,4}{2}=-0,7) на оси синусов в точке (P);
- Проводим перпендикуляр к оси синусов через точку (P);
- Получили две точки пересечения с единичной окружностью (F) и (T);
- Согласно построению, углы (angle{AOF}) и (angle{AOT}) искомые (показаны на рис. 3 синим цветом): синус от них будет равен (-frac{sqrt{2}}{2}). Не забываем отсчитывать углы от отрезка (OA) ПРОТИВ часовой стрелки, здесь углы будут тупыми, как показано на рисунке;
- Выяснили при помощи окружности, что нас устраивает как минимум два значения (x) (угол (angle{AOF}) и (angle{AOT}));
- Внимание! Осталось найти значения этих углов. И вот тут у нас загвоздка, так как значение синуса у нас отрицательное, и его нет в таблице стандартных углов. Как же найти углы?
Но зато в таблице есть значение (frac{sqrt{2}}{2})! (См.Рис. 2)
Проделаем и отметим на окружности все предыдущие шаги, как будто мы решаем уравнение (sin(x)=frac{sqrt{2}}{2}). Теперь все происходит в верхней половине окружности. Обозначим углы, синус от которых (frac{sqrt{2}}{2}) за (angle{MOA}) и (angle{NOA}). Эти углы мы найти можем, так как значение синуса (frac{sqrt{2}}{2}) есть в таблице стандартных углов:
$$angle{MOA}=45^o=frac{pi}{4};$$
Аналогично примеру №1 находим:
$$angle{NOA}=180^o-angle{NOC}=180^o-45^o=135^o=frac{3pi}{4};$$Получилась абсолютно симметричная картина относительно горизонтальной оси (оси косинусов). (См. Рис. 3). Если согнуть рисунок по горизонтальной оси, то верхняя половина единичной окружности точно совпадет с нижней. Это значит, что (angle{MOA}=angle{FOA}) и (angle{TOA}=angle{NOA}) (углы показаны на рис.3. зелёным цветом).
Тогда согласно рис.3 мы можем выразить искомые углы:
$$angle{AOF}=360^o-angle{FOA}=360^o-angle{MOA}=360^o-45^o=315^o=2pi-frac{pi}{4}=frac{7pi}{4};$$
$$angle{AOT}=360^o-angle{TOA} =360^o-angle{NOA}=360^o-135^o=225^o=2pi-frac{3pi}{4}=frac{5pi}{4};$$ - Углы найдены, добавляем к каждому период (2pi*n) и записываем ответ.
Ответ:
$$x_{1}=frac{5pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=frac{7pi}{4}+2pi*n, quad n in Z;$$
Важное замечание!Напоминаю, что углы на тригонометрической окружности можно отсчитывать от отрезка (OA) и ПО часовой стрелке, только тогда они будут со знаком минус. А для нас это прекрасная новость, ведь тогда:
$$angle{FOA}=-angle{MOA}=-45^o=-frac{pi}{4};$$
$$angle{TOA}=-angle{NOA}=-135^o=-frac{3pi}{4};$$
И ответ на пример №2 можно записать в другом виде через углы (angle{FOA}) и (angle{TOA}), отсчитанным против часовой стрелки:
Ответ:
$$x_{1}=-frac{pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{3pi}{4}+2pi*n, quad n in Z;$$
Абсолютно без разницы в каком виде записать ответ в примере №2, по сути, первый и второй вариант ответа это одно и то же. Напоминаю, что ответы в тригонометрии мы записываем в виде правила, которому подчиняются бесконечное количество углов. Правило одно и то же, и задает одни и те же углы, только разная точка отсчета, к которой прибавляется период (2pi*n.) Попробуйте на бумаге поподставлять различные значения (n) и туда, и туда. Убедитесь сами, что корни будут получаться одинаковые.
Я бы использовал второй вариант написания ответа, на мой взгляд, он легче.
Пример 3
$$sin(x)=1;$$
Решим вот такое интересное тригонометрическое уравнение.
- Рисуем единичную окружность;
- На оси синусов отмечаем значение (1);
- Проводим перпендикуляр к оси синусов через (1);
- Наш перпендикуляр пересечет окружность только в одной точке! На Рис.4. эта точка отмечена как (B);
- Раз у нас всего лишь одна точка, значит и угол будет один. Точка (B) соответствует углу (90^o=frac{3pi}{2});
- Записываем ответ, не забывая про период;
Ответ:(x=frac{3pi}{2}+2pi*n, quad n in Z;)
Пример 4
$$sin(x)=5;$$
Это пример-ловушка. Дело в том, что (sin(x)) – это функция ограниченная. Синус не может принимать значения большие (1) и меньшие (-1):
$$sin(x)in[-1;1];$$
Этот факт следует из определения синуса. Его нужно запомнить и быть внимательным.
Арксинус. Обратная тригонометрическая функция синусу
И разберем последнее типовое тригонометрическое уравнение с синусом:
Пример 5
$$sin(x)=frac{1}{3};$$
Алгоритм решения здесь такой же. Не будем четвертый раз повторяться.
Но здесь есть большая проблема. Дело в том, что значение синуса (frac{1}{3}) не табличное, его нет в таблице стандартных углов! Как же тогда искать углы, синус от которых будет (frac{1}{3})?
Чтобы было возможно решать такие тригонометрические уравнения без калькулятора, люди придумали дополнительную функцию, которую назвали арксинус.
(arcsin(frac{1}{3})) – это обозначение такого угла, синус от которого равен (frac{1}{3}).
$$sin(arcsinleft(frac{1}{3}right))=frac{1}{3};$$
В общем случае (arcsin(a)) – это угол, синус от которого равен (a). Где (ain[-1;1]), так как значения синуса принадлежат промежутку ([-1;1].)
$$sin(arcsin(a))=a;$$
Кстати, для арксинуса справедлива очень важная формула:
$$mathbf{arcsin(-a)=-arcsin(a);}$$
Запомните ее, мы еще с ней встретимся.
В общем, арксинус – это просто обозначение угла. Но так как в предыдущих примерах мы выяснили, что практически любому значению синуса соответствует как минимум два угла, то какой из этих углов это арксинус?
Посмотрите выше на рис. 5. Значению (frac{1}{3}) соответствует два угла (angle{MOA}) и (angle{NOA}), какой именно угол из этих двух будет равен (arcsin(frac{1}{3}))?
Для того, чтобы не было такой неопределённости, и чтобы арксинусу (frac{1}{3}) однозначно соответствовал ровно один угол, придумали ограничения, накладываемые на функцию арксинуса:
$$arcsin(a)in[-frac{pi}{2};frac{pi}{2}];$$
То есть арксинусы – это углы, обязательно лежащие в промежутке ([-frac{pi}{2};frac{pi}{2}].). На рисунке промежуток показан фиолетовым цветом.
Тогда в нашем примере:
$$angle{MOA}=arcsin(frac{1}{3});$$
Для того, чтобы найти (angle{NOA}), нужно просто из геометрических соображений из угла (180^o=pi) вычесть угол (angle{NOB}=angle{MOA}=arcsin(frac{1}{3})):
$$angle{NOA}=pi-arcsin(frac{1}{3});$$
Добавляем к получившимся углам период и получаем:
Ответ:
$$angle{MOA}=arcsin(frac{1}{3})+2pi*n, quad n in Z;$$
$$angle{NOA}=pi-arcsin(frac{1}{3})+2pi*n, quad n in Z.$$
Решение тригонометрического уравнения с косинусом на окружности
На самом деле, уравнения с косинусом мало чем отличаются от уравнений с синусом. Рассмотрим алгоритм решения на примере:
Пример 6
$$cos(x)=frac{1}{2};$$
- Рисуем единичную окружность;
- Отмечаем на линии косинусов (горизонтальная линия) значение (frac{1}{2}) в точке (P);
- Проводим перпендикуляр (a) к линии косинусов через точку (P);
- Перпендикуляр (a) пересечет окружность в точках (K) и (L);
- Точки (K) и (L) соответствуют углам (angle{KOA}) и (angle{LOA});
- Косинус от углов (angle{KOA}) и (angle{LOA}) будет равен (frac{1}{2}) по построению;
- Осталось найти значение этих углов. Смотрим в таблицу стандартных значений и находим, что косинус от угла (60^o=frac{pi}{3}) будет как раз равен (frac{1}{2});
- Тогда, держа в голове, что углы отсчитываются ПРОТИВ часовой стрелки от отрезка (OA) делаем вывод, что (angle{KOA}=60^o=frac{pi}{3};)
- Угол (angle{LOA}) находим из соображения симметрии картинки относительно горизонтальной оси косинусов: (angle{LOA}=-angle{KOA}=-60^o=-frac{pi}{3}.) Знак минус появляется потому что (angle{LOA}) мы отсчитываем от отрезка (OA) ПО часовой стрелке.
- Мы нашли углы, косинус от которых будет равен (frac{1}{2}), добавляем период (2pi*n) и записываем ответ;
Ответ:
$$x_{1}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{pi}{3}+2pi*n, quad n in Z;$$
Тригонометрические уравнения с косинусом легче, чем с синусом: находишь один угол, а второй просто записываешь со знаком минус из горизонтальной симметрии.
Пример 7
$$cos(x)=- frac{sqrt{3}}{2};$$
- Рисуем тригонометрическую окружность;
- Отмечаем на линии косинусов примерное значение (-frac{sqrt{3}}{2}approx-frac{1,7}{2}=-0,85) в точке (F);
- Проводим перпендикуляр к линии косинусов через точку (F);
- Обозначим точки пересечения с окружностью за (M) и (N);
- Точки (M) и (N) соответствуют углам (angle{MOA}) и (angle{NOA});
- Осталось найти значение этих углов. Но у нас опять небольшая проблема: в таблице стандартных углов нет значения (-frac{sqrt{3}}{2}). Зато там есть (frac{sqrt{3}}{2}).
Отметим на той же окружности решение уравнения (cos(x)=frac{sqrt{3}}{2}) (см. Рис. 7), оно будет в правой части окружности, а углы (angle{EOA}) и (angle{TOA}) будут решениями. Из таблицы стандартных углов находим, что косинус от угла (30^o=frac{pi}{6}) будет равен (frac{sqrt{3}}{2}). Значит (angle{EOA}=frac{pi}{6}), а (angle{TOA}=-frac{pi}{6}), если его отсчитать по часовой стрелке.
Обратите внимание, что рисунок симметричен относительно вертикальной оси синусов, что нам дает равенство углов (angle{MOC}=angle{EOA}=30^o=frac{pi}{6}). Теперь можем найти (angle{MOA}):
$$angle{MOA}=180^o-angle{MOC}=180^o-30^o=150^o=pi-frac{pi}{6}=frac{5pi}{6};$$
А угол (angle{NOA}) из геометрических соображений равен (angle{MOA}), но отсчитываем мы его ПО часовой стрелке:
$$angle{NOA}=-angle{MOA}=-frac{5pi}{6};$$ - Мы нашли углы, косинус от которых будет равен (-frac{sqrt{3}}{2}), добавляем период (2pi*n) и записываем ответ;
Ответ:
$$x_{1}=frac{5pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{3}+2pi*n, quad n in Z.$$
Пример 8
$$cos(x)=0;$$
- Как обычно, рисуем окружность;
- На оси косинусов отмечаем значение (0), оно лежит прямо в пересечении осей синуса и косинуса;
- Проводим перпендикуляр к оси косинусов через точку (0). Будьте внимательны, этот перпендикуляр полностью совпадет с осью синусов и пересечет окружность в точках (B) и (D;)
- Углы (angle{BOA}) и (angle{DOA}) искомые;
- Точки (B) и (D) соответствуют на окружности углам (90^o=frac{pi}{2}) и (-90^o=-frac{3pi}{2}.)
- Учитывая период, записываем ответ:
Ответ:
$$x_{1}=frac{pi}{2}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{pi}{2}+2pi*n, quad n in Z;$$
Арккосинус. Обратная тригонометрическая функция косинусу
По аналогии с арксинусом существует функция обратная косинусу. Каждый раз, когда вам встречается не табличное значение, придется использовать арккосинус. Познакомимся с ним на примере:
Пример 9
$$cos(x)=frac{1}{5};$$
Как обычно, отметим на оси косинусов (frac{1}{5}) и нарисуем соответствующие этому значению углы (angle{KOA}) и (angle{LOA}).
В таблице значения (frac{1}{5}) нет. И чтобы этот пример можно было решить, люди придумали функцию арккосинуса, при помощи которой обозначают нестандартные углы.
(arccos(frac{1}{5})) – это обозначение угла, косинус от которого будет равен (frac{1}{5}).
$$cos(arccosleft(frac{1}{5}right))=frac{1}{5};$$
В общем виде (arccos(a)) – это угол, косинус от которого будет равен (a), где (ain[-1;1]), ведь значения косинуса лежат в промежутке ([-1;1].)
Так как почти любому значению косинуса соответствует минимум две точки (два угла) на окружности, то для того, чтобы понять, какой именно угол из этих двух будет арккосинусом, на функцию арккосинус накладываются определенные ограничения:
$$arccos(a)in[0;pi];$$
То есть, арккосинус – это углы, лежащие в верхней половине единичной окружности в промежутке ([0;pi].)
Кстати, для арккосинуса справедлива формула:
$$mathbf{arccos(-a)=pi-arccos(a);}$$
Возвращаясь к нашему примеру:
$$angle{KOA}=arccos(frac{1}{5});$$
А для того, чтобы найти второй угол (angle{LOA}), нужно заметить, что:
$$angle{LOA}=-angle{KOA}=-arccos(frac{1}{5});$$
Если считать угол по часовой стрелке.
Не забываем про период и записываем ответ:
Ответ:
$$angle{KOA}=arccos(frac{1}{5})+2pi*n, quad n in Z;$$
$$angle{LOA}=-arccos(frac{1}{5}+2pi*n, quad n in Z;$$
Важно! Значения косинуса, так же, как и синуса, принадлежат промежутку ([-1;1]). Если вы встретите уравнение по типу (cos(x)=3), то оно не будет иметь решений.
Тригонометрическое уравнение с тангенсом на окружности
Тангенс и котангенс на единичной окружности ведут себя несколько иначе, чем синус и косинус. Кто не помнит, как тангенс и котангенс отображаются на окружности и какими свойствами обладают, рекомендую повторить.
Как обычно, будем учиться на примерах:
Пример 10
$$tg(x)=1;$$
- На тригонометрической окружности необходимо нарисовать ось тангенсов. Напоминаю, что она параллельна оси синусов и проходит через точку (A);
- На оси тангенсов отмечаем значение (1), обозначим эту точку за (K);
- Соединим точку (K) с центром окружности и продлим до пересечения с окружностью;
- Получим две точки на окружности (M) и (N);
- Они соответствуют углам (angle{MOA}) и (angle{NOA}), тангенс от которых будет равен (1);
- По таблице стандартных углов находим, что тангенс равен (1) от угла (45^o=frac{pi}{4}), судя по рисунку №10, это будет угол (angle{MOA});
- Угол (angle{NOA}) можно найти по формуле:
$$angle{NOA}=180^o+angle{MOA}=pi+angle{MOA}=pi+frac{pi}{4}=frac{5pi}{4};$$
Это следует из окружности, посмотрите на Рис.10. Наши два угла отличаются ровно на (180^o=pi) градусов. Это важный момент, который дает нам возможность записывать ответ в одну строчку, а не в две, как у синуса и косинуса:
$$x=frac{pi}{4}+pi*n, quad n in Z;$$
Это весь ответ, больше ничего писать не нужно. Обратите внимание на период, здесь он у нас (pi*n), а не (2pi*n), как было у синуса и косинуса. Подставляя различные значения (n), вы будет прибавлять к (frac{pi}{4}):
$$n=1 qquad x_{1}=frac{pi}{4}+pi;$$
Смотрите, прибавив (pi) при (n=1) вы из точки (M) попали в точку (N).
$$n=2 qquad x_{2}=frac{pi}{4}+2pi;$$
При (n=2) мы опять вернулись из точки (N) в точку (M).
$$n=3 qquad x_{1}=frac{pi}{4}+3pi;$$
При (n=3) попадаем из (M) в точку (N).
Другими словами, период (pi*n) означает, что ваши корни лежат на окружности с периодом в половину окружности, а правило (x=frac{pi}{4}+pi*n, quad n in Z;) покрывает обе точки и (M), и (N).
Главный вывод в том, что у простейшего уравнения с тангенсом записывается в ответ только одна точка (любая) и прибавляется период (pi*n). Этот факт можно просто запомнить.
Ответ: (x=frac{pi}{4}+pi*n, quad n in Z.)
Арктангенс. Обратная тригонометрическая функция тангенсу
По аналогии с арксинусом и арккосинусом существует и арктангенс – функция, обратная тангенсу. Она необходима, когда перед вами нестандартные (не табличные) значения тангенса.
В общем виде арктангенс от некоторого числа (a) – это угол, тангенс от которого равен (a):
$$tg(arctg(a))=a; qquad ain(-infty;+infty); $$
$$arctg(a)in(-frac{pi}{2};frac{pi}{2}).$$
Обратите внимание, что значения арктангенса всегда по определению лежат в промежутке ((-frac{pi}{2};frac{pi}{2})): в правой полуокружности.
Кстати, для арктангенса справедлива формула:
$$mathbf{arctg(-a)=-arctg(a)};$$
Пример 11
$$tg(x)=3;$$
- Рисуем единичную окружность;
- Отмечаем на оси тангенсов значение (3), обозначим за точку (K);
- Через точку (K) и центр окружности проводим прямую, которая пересечет окружность в двух точках (M) и (N);
- В таблице стандартных углов тангенс, равный (3), вы не найдете. И тут нам пригодится арктангенс. Арктангенсом мы будем называть угол, тангенс от которого равен 3-м. Поэтому угол (angle{MOA}=arctg(3),) согласно определению арктангенса;
- Угол (angle{NOA}) можно найти по формуле:
$$angle{NOA}=angle{MOA}+180^0=angle{MOA}+pi=arctg(3)+pi;$$ - Но на самом деле, оба угла (angle{MOA}) и (angle{MOA}) для ответа нам не нужны. В ответ мы можем записать любой из них и указать период (pi*n), который покроет оба угла;
Ответ: (x=arctg(3)+pi*n, quad n in Z.)
Тригонометрическое уравнение с котангенсом
Уравнения с котангенсом очень похожи на уравнения с тангенсом с одним исключением: ось котангенсов на единичной окружности параллельна горизонтальной оси косинусов, полностью ее дублирует и проходит через точку (B).
Пример 12
$$ctg(x)=sqrt{3};$$
- Рисуем единичную окружность;
- Проводим через точку (B) ось котангенсов параллельно горизонтальной оси;
- На оси котангенсов отмечаем значение (sqrt{3}approx1,7), обозначим за точку (P);
- Соединяем точку (P) с центром окружности и продляем до пересечения с ней в двух точках: (L) и (F);
- Котангенс от углов (angle{LOA}) и (angle{FOA}) и будет равен (sqrt{3});
- В таблице стандартных углов находим, что (ctg(frac{pi}{6})=sqrt{3};)
- Согласно рисунку (angle{LOA}=frac{pi}{6}), а угол (angle{FOA}=frac{pi}{6}+pi=frac{7pi}{6};)
- Как и с тангенсом, оба угла нам не нужно, достаточно в ответе указать одну точку с периодом (pi*n);
Ответ: (x=frac{pi}{6}+pi*n, quad n in Z.)
В простейших уравнениях с котангенсом в ответе мы указываем любой из двух получившихся углов, при этом не забываем про период (pi*n).
Разберем еще уравнение с отрицательной правой частью:
Пример 13
$$ctg(x)=-1;$$
Отметим на тригонометрической окружности ось котангенсов и на ней значение (-1). Так подробно расписывать решение, как в прошлых примерах, мы не будем, идея уже должна быть давно понятна.
На рисунке искомыми углами будут (angle{MOA}) и (angle{NOA}). Мы не можем воспользоваться таблицей стандартных углов, так как там нет значения котангенса (-1), но зато есть значение (1.)
Решим на этой же самой окружности уравнение (ctg(x)=1). Котангенс от углов (angle{KOA}) и (angle{LOA}) будет равен (1). Из таблицы стандартных углов делаем вывод, что (angle{KOA}=frac{pi}{4}).
Так как получившийся рисунок симметричен относительно вертикальной оси синусов, то из геометрических соображений:
$$angle{KOA}=angle{MOC};$$
Тогда:
$$angle{MOA}=pi-angle{MOC}=pi-angle{KOA}=pi-frac{pi}{4}=frac{3pi}{4};$$
Кроме того, наш рисунок симметричен относительно горизонтальной оси косинусов. Из чего легко сделать вывод:
$$angle{NOA}=-angle{KOA}=-frac{pi}{4};$$
Знак минус возникает из-за того, что мы отсчитываем угол (angle{NOA}) ПО часовой стрелке.
Записываем ответ, указывая любой из углов (angle{MOA}) или (angle{NOA}) с учетом периода (pi*n).
Ответ: (x=-frac{pi}{4}+pi*n, quad n in Z.)
Арккотангенс. Обратная тригонометрическая функция котангенсу
И нам осталось обсудить последнюю тригонометрическую функцию в школьной программе: арккотангенс.
Как и другие обратные функции, арккотангенс от некоторого числа (a) – это угол, котангенс от которого будет равен (a):
$$tg(arcctg(a))=a; qquad ain(-infty;+infty); $$
$$arcctg(a)in(0;pi).$$
Обратите внимание на ограничения, которые по определению накладываются на арккотангенс: его значения принадлежат промежутку ((0;pi)), то есть это углы, лежащие в верхней половине окружности. Эти ограничения необходимы для однозначности функции арккотангенса, так как любому значению котангенса всегда соответствует две точки на окружности, а значит минимум два угла (в верхней и нижней полуокружностях).
Кстати, для арккотангенса справедлива формула:
$$mathbf{arcctg(-a)=pi-arcctg(a);}$$
Арккотангенс используется, когда в уравнении встречаются нестандартные значения:
Пример 14
$$ctg(x)=5;$$
Отметим все на окружности. Искомыми углами будут (angle{MOA}) и (angle{KOA}).
Так как значение (5) нестандартное, то нам придется воспользоваться функцией арккотангенса: (arcctg(5)).
На нашей окружности (angle{MOA}=arcctg(5)) так как именно он лежит в верхней половине окружности.
Второй угол, как и во всех уравнениях с тангенсом и котангенсом искать совсем не обязательно, но для тренировки сделаем это:
$$angle{KOA}=pi+arcctg(5);$$
И записываем в ответ любой из этих углов с периодом (pi*n).
Ответ: (x=arcctg(5)+pi*n, quad n in Z.)
Формулы для решения тригонометрических уравнений
Мы разобрали решения всех основные типы простейших тригонометрических уравнений при помощи единичной окружности. Я бы рекомендовал всегда решать именно при помощи окружности, это очень полезно для понимания.
А сейчас мы запишем формулы, при помощи которых можно решать уравнения без единичной окружности.
Пусть у нас есть простейшие тригонометрические уравнения:
$$sin(x)=a;$$
где (a) некоторое число, удовлетворяющее условию (ain[-1;1]);
Тогда решением этого уравнения будет:
$$x=(-1)^n*arcsin(a)+pi*n, quad n in Z;$$
$$cos(x)=a;$$
где (a) некоторое число, удовлетворяющее условию (ain[-1;1]);
Тогда решением этого уравнения будет:
$$x=pmarccos(a)+2pi*n, quad n in Z;$$
$$tg(x)=a;$$
где (a) некоторое число, удовлетворяющее условию (ain(-infty;+infty));
Тогда решением этого уравнения будет:
$$x=arctg(a)+pi*n, quad n in Z;$$
$$ctg(x)=a;$$
где (a) некоторое число, удовлетворяющее условию (ain(-infty;+infty));
Тогда решением этого уравнения будет:
$$x=arcctg(a)+pi*n, quad n in Z;$$
Можно просто запомнить формулы и решать уравнения с их помощью.
И полезно помнить формулы, которые мы вводили, когда давали определение обратных функций:
$$arcsin(-a)=-arcsin(a);$$
$$arccos(-a)=pi-arccos(a);$$
$$arctg(-a)=-arctg(a);$$
$$arcctg(-a)=pi-arcctg(a).$$
Рассмотрим примеры:
Пример 15
$$sin(x)=frac{1}{2};$$
Сразу выпишем общую формулу ответа:
$$x=(-1)^n*arcsin(a)+pi*n, quad n in Z;$$
где (a=frac{1}{2});
$$x=(-1)^n*arcsin(frac{1}{2})+pi*n, quad n in Z;$$
В таком виде лучше не оставлять. Если вы можете посчитать, чему равен арксинус, то это обязательно нужно сделать.
Арксинус от (frac{1}{2}), согласно определению, это угол, синус от которого равен (frac{1}{2}). По таблице стандартных углов мы видим, что синус равен (frac{1}{2}) от угла (frac{pi}{6}):
$$arcsin(frac{1}{2})=frac{pi}{6};$$
$$x=(-1)^n*frac{pi}{6}+pi*n, quad n in Z;$$
В таком виде уже можно записывать ответ:
Ответ: (x=(-1)^n*frac{pi}{6}+pi*n, quad n in Z.)
Пример 16
$$cos(x)=-frac{sqrt{2}}{2};$$
Общий вид решения:
$$x=pmarccos(a)+2pi*n, quad n in Z;$$
где (a=-frac{sqrt{2}}{2});
$$x=pmarccos(-frac{sqrt{2}}{2})+2pi*n, quad n in Z;$$
Арккосинус от (-frac{sqrt{2}}{2}) это угол, косинус от которого будет равен (-frac{sqrt{2}}{2}). Но в таблице нет значения (-frac{sqrt{2}}{2}), зато есть (frac{sqrt{2}}{2}).
Используя свойство арккосинуса:
$$arccos(-a)=pi-arccos(a);$$
Можно записать:
$$x=pm(pi-arccos(frac{sqrt{2}}{2}))+2pi*n, quad n in Z;$$
Учитывая:
$$arccos(frac{sqrt{2}}{2})=frac{pi}{4};$$
Подставляем:
$$x=pm(pi-frac{pi}{4})+2pi*n, quad n in Z;$$
$$x=pmfrac{3pi}{4}+2pi*n, quad n in Z;$$
Ответ: (x=pmfrac{3pi}{4}+2pi*n, quad n in Z.)
Пример 17
$$tg(x)=-sqrt{3};$$
Общий вид решения:
$$x=arctg(a)+pi*n, quad n in Z;$$
где (a=-sqrt{3});
$$x=arctg(-sqrt{3})+pi*n, quad n in Z;$$
Арктангенс от (-sqrt{3}) это угол, тангенс от которого равен (-sqrt{3}). В таблице опять нет такого значения (-sqrt{3}), но есть положительное (sqrt{3}), арктангенс от которого можно посчитать:
$$arctg(sqrt{3})=frac{pi}{3};$$
Учитывая свойство арктангенса:
$$arctg(-a)=-arctg(a);$$
Подставляем в нашу формулу:
$$x=-arctg(sqrt{3})+pi*n, quad n in Z;$$
$$x=-frac{pi}{3}+pi*n, quad n in Z;$$
Ответ: (x=-frac{pi}{3}+pi*n, quad n in Z.)
Замена переменной в тригонометрических уравнениях
Замена выражения под тригонометрической функцией
Мы научились решать простейшие уравнения. И на этом строится решение всех остальных тригонометрических уравнений. Они все так или иначе сводятся к решению простейших. И один из способов – это введение замены переменной.
Вы должны были с этим регулярно сталкиваться в младших классах при решении, например, биквадратных уравнений. Все дальнейшие рассуждения предполагают, что вы знаете, что такое замена переменной. Итак, разберем пример:
Пример 18
$$sin(2x)=frac{sqrt{3}}{2};$$
Обратите внимание, что теперь у нас под синусом стоит не просто (x), а целое выражение. Давайте избавимся от него, убрав (2x) в замену: пусть (t=2x).
$$sin(t)=frac{sqrt{3}}{2};$$
Теперь наше уравнение превратилось в простейшее тригонометрическое. Решаем его относительно переменной (t) (вы можете решать при помощи единичной окружности или по готовым формулам, как вам удобнее. Я же буду просто выписывать ответ):
$$t_{1}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$t_{2}=frac{2pi}{3}+2pi*n, quad n in Z;$$
На этом решение не заканчивается. Мы нашли значения (t), а нам надо найти (x). Делаем обратную замену, вспоминая, что (t=2x):
$$2x_{1}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$2x_{2}=frac{2pi}{3}+2pi*n, quad n in Z;$$
И просто выражаем из получившихся выражений (x), для этого разделим левую и правую часть равенства на (2):
$$frac{2x_{1}}{2}=frac{frac{pi}{3}+2pi*n}{2}, quad n in Z;$$
$$frac{2x_{2}}{2}=frac{frac{2pi}{3}+2pi*n}{2}, quad n in Z;$$
$$x_{1}=frac{1}{2}*frac{pi}{3}+pi*n, quad n in Z;$$
$$x_{2}=frac{1}{2}*frac{2pi}{3}+pi*n, quad n in Z;$$
Обратите внимание, что период тоже не забываем поделить на (2).
Ответ:
$$x_{1}=frac{pi}{6}+pi*n, quad n in Z;$$
$$x_{2}=frac{pi}{3}+pi*n, quad n in Z.$$
Аналогичным образом можно решать тригонометрические уравнения с более сложным подтригонометрическим выражением:
Пример 19
$$tg(frac{2x+pi}{3})=1;$$
Под тангенсом тут стоит целая дробь, зависящая от (x). Засунем всю эту дробь в замену:
$$t=frac{2x+pi}{3};$$
Уравнение примет вид:
$$tg(t)=1;$$
Решением этого простейшего уравнения будет:
$$t=frac{pi}{4}+pi*n, quad n in Z;$$
Делаем обратную замену, вместо (t) подставляем (frac{2x+pi}{3}):
$$frac{2x+pi}{3}=frac{pi}{4}+pi*n, quad n in Z;$$
И выражаем отсюда (x). Домножим равенство на (3):
$$2x+pi=3*(frac{pi}{4}+pi*n), quad n in Z;$$
$$2x+pi=frac{3pi}{4}+3pi*n, quad n in Z;$$
Перенесем (pi) направо:
$$2x=-pi+frac{3pi}{4}+3pi*n, quad n in Z;$$
Приведем подобные слагаемые:
$$2x=-frac{pi}{4}+3pi*n, quad n in Z;$$
И разделим на (2):
$$x=-frac{pi}{8}+frac{3}{2}*pi*n, quad n in Z;$$
Ответ:
$$x=-frac{pi}{8}+frac{3}{2}*pi*n, quad n in Z;$$
Замена всей тригонометрической функции
Что делать с подтригонометрическим выражением, мы разобрались. Теперь решим пример на замену, при помощи которой тригонометрическое уравнение сводится к квадратному.
Пример 20
$$2*sin^2(x)+sin(x)-1=0;$$
Обращаем внимание на одинаковое выражение (sin(x)). Сделаем замену:
$$t=sin(x);$$
$$2t^2+t-1=0;$$
Получили обыкновенное квадратное уравнение, которое решается через дискриминант:
$$D=1-4*2*(-1)=9;$$
$$t_{1}=frac{-1+3}{4}=frac{1}{2};$$
$$t_{2}=frac{-1-3}{4}=-1;$$
Делаем обратную замену и получаем два простейших тригонометрических уравнения. Первое:
$$sin(x)=frac{1}{2};$$
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=frac{5pi}{6}+2pi*n, quad n in Z;$$
Второе:
$$sin(x)=-1;$$
$$x_{3}=frac{3pi}{2}+2pi*n, quad n in Z;$$
Записываем ответ из трех наборов решений.
Ответ:
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=frac{5pi}{6}+2pi*n, quad n in Z;$$
$$x_{3}=frac{3pi}{2}+2pi*n, quad n in Z;$$
Тригонометрические уравнения в ЕГЭ
В ЕГЭ в большинстве тригонометрических уравнений нужно уметь преобразовать исходное уравнение и сделать замену. Для того, чтобы правильно преобразовывать уравнение, необходимо хорошо знать тригонометрические формулы и помнить главное правило:
Стараться свести уравнение к виду, в котором все тригонометрические функции и выражения, от которых они берутся, одинаковы.
Другими словами, нужно сделать так, чтобы во всем уравнении везде был, например, только синус от (x).
Рассмотрим несложный реальный пример из ЕГЭ.
Пример 21
$$2cos^2(x)+sin(x)+1=0;$$
Смотрите, в уравнении сразу две тригонометрические функции и синус, и косинус. Это плохо. Нужно сделать так, чтобы была только одна из них. Тут нам поможет основное тригонометрическое тождество:
$$sin^2(x)+cos^2(x)=1;$$
$$cos^2(x)=1-sin^2(x);$$
И подставим в исходное уравнение:
$$1-sin^2(x)+sin(x)+1=0;$$
Приведем подобные слагаемые:
$$-sin^2(x)+sin(x)+2=0;$$
Теперь в уравнении везде (sin(x)), можно сделать замену:
$$t=sin(x);$$
Уравнение примет вид:
$$-t^2+t+2=0;$$
Находим корни квадратного уравнения:
$$D=9;$$
$$t_{1}=frac{-1+3}{-2}=-1;$$
$$t_{2}=frac{-1-3}{-2}=2;$$
Обратная замена:
$$sin(x)=-1;$$
$$x=frac{3pi}{2}+2pi*n, quad n in Z;$$
И второе уравнение:
$$sin(x)=2;$$
Оно не имеет решений, так как синус может принимать значения только из промежутка ([-1;1]).
Ответ:
$$x=frac{3pi}{2}+2pi*n, quad n in Z;$$
Пример 22
$$2*sin^2(pi+x)-5*cos(frac{pi}{2}+x)+2=0;$$
Этот пример уже сложнее: во-первых, под тригонометрическими функциями стоят какие-то непонятные, да еще и разные, выражения; во-вторых, в уравнении у нас и синус, и косинус, а должно быть что-то одно.
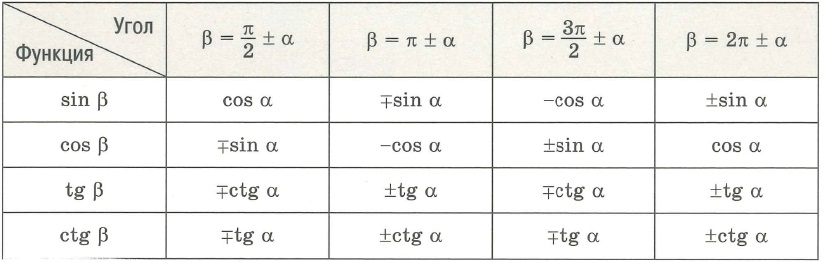
Читатель, который знаком с формулами приведения, обязательно должен был заметить, что под синусом и косинусом стоят не просто какие-то выражения, а это формулы приведения. Выпишем их отдельно и преобразуем:
$$sin(pi+x)=-sin(x);$$
$$cos(frac{pi}{2}+x)=-sin(x);$$
Подставим преобразования в исходное уравнение.
Внимание! Когда мы будем подставлять (-sin(x)) вместо (sin(pi+x)), то знак минус сгорит, так как у нас (sin(pi+x)) под квадратом. Это очень частая ошибка.
$$2*(-sin(x))^2-5*(-sin(x))+2=0;$$
$$2*sin^2(x)+5*sin(x)+2=0;$$
Применив формулы привидения, у нас чудесным образом получилось уравнение, в котором можно сделать замену:
$$t=sin(x);$$
$$2*t^2+5*t+2=0;$$
$$D=9;$$
$$t_{1}=frac{-5+3}{4}=-frac{1}{2};$$
$$t_{2}=frac{-5-3}{4}=-2;$$
Обратная замена:
$$sin(x)=-frac{1}{2};$$
$$x_{1}=-frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{6}+2pi*n, quad n in Z;$$
И второе уравнение:
$$sin(x)=-2;$$
Решений не имеет, так как (sin(x)in[-1;1]) по определению.
Ответ:
$$x_{1}=-frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{6}+2pi*n, quad n in Z;$$
Однородные тригонометрические уравнения
Мы выяснили, что для того, чтобы решить уравнение, необходимо привести все к одинаковым тригонометрическим функциям от одинаковых аргументов. Но иногда сделать это затруднительно. Например, как вы будете решать вот такое уравнение:
Пример 23
$$sin(x)+cos(x)=0;$$
Нет такой удобной формулы, по которой можно превратить синус в косинус или наоборот. Хотя, конечно, можно воспользоваться основным тригонометрическим тождеством и выразить оттуда синус через косинус:
$$sin^2(x)+cos^2(x)=1;$$
$$sin^2(x)=1-cos^2(x);$$
$$sin(x)=pmsqrt{1-cos^2(x)};$$
Подставив это выражение вместо синуса в исходное уравнение, мы получим в уравнении одни косинусы, но уравнение станет иррациональным (то есть с корнем). Его можно решить, но это достаточно сложно. И так никто не делает.
Оптимальным решением здесь будет поделить исходное уравнение на синус или косинус, давайте поделим на косинус:
$$frac{sin(x)+cos(x)}{cos(x)}=frac{0}{cos(x)};$$
$$frac{sin(x)}{cos(x)}+frac{cos(x)}{cos(x)}=0;$$
$$tg(x)+1=0;$$
$$tg(x)=-1;$$
$$x=-frac{pi}{4}+pi*n, quad n in Z;$$
Ответ:
$$x=-frac{pi}{4}+pi*n, quad n in Z;$$
Рассмотрим еще один пример:
Пример 24
$$sin(x)+sqrt{3}*cos(x)=0;$$
Аналогично предыдущему примеру поделим все уравнение на (sin(x)):
$$1+sqrt{3}*frac{cos(x)}{sin(x)}=0;$$
$$1+sqrt{3}*ctg(x)=0;$$
$$sqrt{3}*ctg(x)=-1;$$
$$ctg(x)=-frac{1}{sqrt{3}};$$
$$x=frac{pi}{3}+pi*n, quad n in Z;$$
Ответ:
$$x=frac{pi}{3}+pi*n, quad n in Z;$$
Мы рассмотрели два примера так называемых однородных уравнений первой степени. Рассмотрим пример на однородное уравнение второй степени.
Пример 25
$$3sin^2(x)+sin(x)*cos(x)=2cos^2(x);$$
Здесь тоже будем применять деление, только в этот раз будем делить каждое слагаемое на (cos^2(x)) (можно поделить и на (sin^2(x)), это не имеет значения):
$$3frac{sin^2(x)}{cos^2(x)}+frac{sin(x)*cos(x)}{sin^2(x)}=frac{2cos^2(x)}{cos^2(x)};$$
$$3tg^2(x)+tg(x)=2;$$
Теперь можно сделать замену (t=tg(x)):
$$3t^2+t=2;$$
$$3t^2+t-2=0;$$
$$D=1+24=25;$$
$$t_{1}=frac{-1-5}{6}=-1;$$
$$t_{2}=frac{-1+5}{6}=frac{2}{3};$$
Обратная замена:
Первое уравнение:
$$tg(x)=-1;$$
$$x=-frac{pi}{4}+pi*n, quad n in Z;$$
Второе уравнение:
$$tg(x)=frac{2}{3};$$
$$x=arctg(frac{2}{3})+pi*n, quad n in Z;$$
Ответ:
$$x=-frac{pi}{4}+pi*n, quad n in Z;$$
$$x=arctg(frac{2}{3})+pi*n, quad n in Z;$$
Есть нюанс, на котором школьники часто сыпятся. Освоив метод деления, ученик начинает пытаться решить тригонометрические уравнения только через него и на экзамене, решив вроде все правильно, получает 0 баллов.
Оказывается, что не всякое уравнение можно разделить на выражение зависящее от (x). Посмотрите пример №26, это убережет вас от подобных ошибок на экзамене.
Пример 26
$$sin^2(x)+sin(x)=0;$$
Разделим уравнение на (sin(x)):
$$sin(x)+1=0;$$
$$sin(x)=-1;$$
$$x=frac{3pi}{2}+2pi*n, quad n in Z;$$
И тут, кажется, можно записывать ответ, но это неверное решение уравнения, так решать нельзя. Достаточно легко заметить, что (sin(x)=0) тоже будет являться решением исходного уравнения. Подставьте вместо (sin(x)) ноль и получите верное равенство. А в нашем решении такого ответа нет, значит где-то по дороге мы потеряли корни. А потеряли мы их именно в тот момент, когда сделали деление.
Запомните важное правило! Делить уравнение можно только тогда, когда выражение, на которое вы делите, равное нулю не будет корнем исходного уравнения.
В нашем случае мы делим на (sin(x)), но (sin(x)=0) является решением, поэтому делить нельзя.
Чтобы все-таки решить это уравнение правильно, нужно воспользоваться вынесением общего множителя за скобки.
Вынесение общего множителя в тригонометрических уравнениях
Еще один распространенный на ЕГЭ тип тригонометрических уравнений, в которых необходимо вынести общий множитель.
Пример 27
$$sin(2x)-2sin^2(x)=0;$$
В этом уравнении только одна тригонометрическая функция — (sin(x)). Но под синусами стоят разные выражения. Поэтому избавимся от двойного угла под синусом при помощи формулы синуса двойного угла:
$$sin(2x)=2sin(x)*cos(x);$$
Уравнение примет вид:
$$2sin(x)*cos(x)-2sin^2(x)=0;$$
Замечаем общий множитель (2*sin(x)), вынесем его за скобки:
$$2*sin(x)*(cos(x)-sin(x))=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Уравнение разбивается на два:
Либо:
$$2sin(x)=0;$$
$$sin(x)=0;$$
$$x_{1}=0+2pi*n=2pi*n, quad n in Z;$$
$$x_{2}=pi+2pi*n, quad n in Z;$$
(Кстати, эти два решения можно объединить в одно: (x=0+pi*n=pi*n, quad n in Z;))
Либо второе уравнение:
$$cos(x)-sin(x)=0;$$
Это уравнение решается при помощи деления. Разделим левую и правую часть уравнения на (cos(x)):
$$frac{cos(x)-sin(x)}{cos(x)}=frac{0}{cos(x)};$$
$$1-frac{sin(x)}{cos(x)}=0;$$
$$1-tg(x)=0;$$
$$tg(x)=1;$$
$$x=frac{pi}{4}+pi*n, quad n in Z;$$
Ответ:
$$x_{1}=pi*n, quad n in Z;$$
$$x_{2}=frac{pi}{4}+pi*n, quad n in Z;$$
Пример 28
$$2cos(frac{pi}{2}-x)=tg(x);$$
Сразу замечаем формулу приведения под косинусом:
$$cos(frac{pi}{2}-x)=sin(x);$$
Подставляем в исходное уравнение
$$2sin(x)=tg(x);$$
Распишем тангенс по определению:
$$tg(x)=frac{sin(x)}{cos(x)};$$
$$2sin(x)=frac{sin(x)}{cos(x)};$$
$$2sin(x)-frac{sin(x)}{cos(x)}=0;$$
И здесь тоже будет общий множитель (sin(x)):
$$sin(x)*(2-frac{1}{cos(x)})=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
Первый множитель:
$$sin(x)=0;$$
$$x_{1}=0+pi*n=pi*n, quad n in Z;$$
Второй множитель:
$$2-frac{1}{cos(x)}=0;$$
Приведем к общему знаменателю:
$$frac{2cos(x)}{cos(x)}-frac{1}{cos(x)}=0;$$
$$frac{2cos(x)-1}{cos(x)}=0;$$
Дробь равна нулю, когда числитель равен нулю – избавляемся от знаменателя:
$$2cos(x)-1=0;$$
$$2cos(x)=1;$$
$$cos(x)=frac{1}{2};$$
$$x_{2}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$x_{3}=-frac{pi}{3}+2pi*n, quad n in Z;$$
Ответ:
$$x_{1}=pi*n, quad n in Z;$$
$$x_{2}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$x_{3}=-frac{pi}{3}+2pi*n, quad n in Z;$$
Метод группировки в тригонометрических уравнениях
Рассмотрим еще уравнение, которое было на ЕГЭ 2015 года на метод группировки. Тоже нужно обязательно это знать. Сам метод, если кто не знает, сводится, по сути, к вынесению общего множителя за скобки, только немного сложнее.
Пример 29
$$sin(2x)+sqrt{2}sin(x)=2cos(x)+sqrt{2};$$
Избавляемся от двойного угла:
$$2*sin(x)cos(x)+sqrt{2}sin(x)=2cos(x)+sqrt{2};$$
И перенесем все в левую часть:
$$2*sin(x)cos(x)+sqrt{2}sin(x)-2cos(x)-sqrt{2}=0;$$
У нас 4 слагаемых, сгруппируем их попарно: 1-е со 2-м, а 3-е с 4-м, и вынесем в каждой паре общий множитель:
$$sin(x)(2cos(x)+sqrt{2})-1(2cos(x)+sqrt{2})=0;$$
У 3-го и 4-го слагаемых я вынес за скобки (-1).
Теперь обратите внимание, что в скобках получились идентичные выражения, то есть эти скобки абсолютно одинаковые. Вынесем эту общую скобку за скобку!
$$(2cos(x)+sqrt{2})(sin(x)-1)=0;$$
Вот мы и сгруппировали, теперь приравниваем каждый множитель к нулю:
Первый множитель:
$$2cos(x)+sqrt{2}=0;$$
$$cos(x)=frac{-sqrt{2}}{2};$$
$$x_{1}=frac{3pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{3pi}{4}+2pi*n, quad n in Z;$$
Второй множитель:
$$sin(x)-1=0;$$
$$sin(x)=1;$$
$$x_{3}=frac{pi}{2}+2pi*n, quad n in Z;$$
Ответ:
$$x_{1}=frac{3pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{3pi}{4}+2pi*n, quad n in Z;$$
$$x_{3}=frac{pi}{2}+2pi*n, quad n in Z;$$
ОДЗ в тригонометрических уравнениях
С областью допустимых значений мы сталкиваемся в уравнениях и неравенствах, в которых есть знаменатели, корни и логарифмы.
Тригонометрические уравнения не исключение, в них тоже встречается все вышеперечисленное. И в этом случае мы вынуждены не забывать про ограничения и выписывать ОДЗ перед тем, как решать.
Пример 30
$$frac{2sin^2(x)-sin(x)}{2cos(x)-sqrt{3}}=0;$$
В этом уравнении есть знаменатель, при некоторых значениях (x) он может быть равен (0), а тогда у нас будет деление на 0, что запрещено правилами математики. Поэтому надо исключить такие значения (x). Посмотрим, при каких (x) знаменатель равен (0):
$$2cos(x)-sqrt{3}=0;$$
$$cos(x)=frac{sqrt{3}}{2};$$
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{pi}{6}+2pi*n, quad n in Z;$$
Мы получили значения, которые (x) не может принимать, так как возникает деление на (0). Другими словами, мы нашли ОДЗ.
Теперь решим исходное уравнение:
$$frac{2sin^2(x)-sin(x)}{2cos(x)-sqrt{3}}=0;$$
Дробь равна (0), когда числитель равен (0). Избавляемся от знаменателя и приравниваем числитель к (0):
$$2sin^2(x)-sin(x)=0;$$
Вынесем общий множитель:
$$sin(x)(2sin(x)-1)=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю.
Первый:
$$sin(x)=0;$$
$$x_{1}==pi*n, quad n in Z;$$
Второй множитель:
$$2sin(x)-1=0;$$
$$sin(x)=frac{1}{2};$$
$$x_{2}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{3}=frac{5pi}{6}+2pi*n, quad n in Z;$$
Получилось три набора решений, но не все они подходят. Вспоминаем про ОДЗ и видим, что решение (x_{2}=frac{pi}{6}+2pi*n, quad n in Z;) не удовлетворяет ОДЗ, так как при этих значениях (x) возникает деление на (0). Исключаем его из ответа.
Ответ:
$$x_{1}=pi*n, quad n in Z;$$
$$x_{3}=frac{5pi}{6}+2pi*n, quad n in Z;$$
Пример 31
$$frac{sin(2x)}{cos(frac{pi}{2}+x)}=sqrt{3};$$
Найдем ОДЗ:
$$cos(frac{pi}{2}+x)=0;$$
Сделаем замену, пусть (t=frac{pi}{2}+x):
$$cos(t)=0;$$
$$t=frac{pi}{2}+pi*n, quad n in Z;$$
Обратная замена:
$$frac{pi}{2}+x=frac{pi}{2}+pi*n, quad n in Z;$$
$$x=pi*n, quad n in Z;$$
Это и будет наше ОДЗ, (x) не может принимать значения (pi*n, quad n in Z), так как при этих (x) будет деление на (0).
А теперь приступим непосредственно к решению исходного уравнения:
$$frac{sin(2x)}{cos(frac{pi}{2}+x)}=sqrt{3};$$
Используем формулы приведения, чтобы упростить знаменатель. И формулу двойного угла в числителе:
$$frac{2sin(x)*cos(x)}{-sin(x)}=sqrt{3};$$
$$-2cos(x)=sqrt{3};$$
$$cos(x)=-frac{sqrt{3}}{2};$$
$$x_{1}=frac{5pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{6}+2pi*n, quad n in Z;$$
Смотрим на ОДЗ и видим, что оба набора решения нам подходят, пересечения с ОДЗ не случилось. Записываем ответ:
Ответ:
$$x_{1}=frac{5pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{6}+2pi*n, quad n in Z;$$
Пример 32
$$(tg^2(x)-1)*sqrt{13cos(x)}=0;$$
В этом уравнении есть квадратный корень, а значит подкоренное выражение не может быть меньше нуля, невозможно взять корень из отрицательного числа. ОДЗ будет выглядеть:
$$13cos(x)ge0;$$
$$cos(x)ge0;$$
Получили тригонометрическое неравенство, которое мы решать еще не умеем. Более того, в школах часто совсем не проходят тему тригонометрических неравенств. Поэтому постараемся решить исходя из логики при помощи единичной окружности.
Если посмотреть на рисунок, то видно, что косинус будет положительным от углов, лежащих в правой половине окружности. Закрашенная часть круга удовлетворяет ОДЗ, а не закрашенная – нет. Запомним это и начнем решать исходное уравнение:
$$(tg^2(x)-1)*sqrt{13cos(x)}=0;$$
Из произведения двух множителей получаем два уравнения. Первое:
$$tg^2(x)-1=0;$$
$$tg(x)=pm1;$$
Обратите внимание на (pm), из-за квадрата будет два решения. Будьте осторожны!
$$tg(x)=1;$$
$$x_{1}=frac{pi}{4}+pi*n, quad n in Z;$$
$$tg(x)=-1;$$
$$x_{2}=-frac{pi}{4}+pi*n, quad n in Z;$$
Второе уравнение:
$$sqrt{13cos(x)}=0;$$
$$13cos(x)=0;$$
$$cos(x)=0;$$
$$x_{3}=frac{pi}{2}+pi*n, quad n in Z;$$
Помним, что нам еще как-то надо проверить, подходят ли получившиеся корни под ОДЗ. На старом рисунке отметим наши корни. Все точки, которые попадают в левую часть окружности, не удовлетворяют ОДЗ, а в правой части – удовлетворяют.
Ответ:
$$x_{1}=frac{pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{pi}{4}+2pi*n, quad n in Z;$$
$$x_{3}=frac{pi}{2}+pi*n, quad n in Z;$$
Обратите внимание, что в ответе период стал (2pi*n), а не (pi*n), как у нас получалось при решении. Это связано с тем, что период (pi*n) покрывает на окружности две точки: из левой полуокружности, которая нам не подходит по ОДЗ, и из правой, которая подходит. А раз нам подходит только одна правая точка, то период будет (2pi*n).
Разные типы тригонометрических уравнений
Подведем важные итоги. Существует три основных метода решения тригонометрических уравнений: замена переменной, вынесение общего множителя (группировка), и деление (однородные уравнения).
Во избежание ошибок, я бы всегда стремился решать либо через замену, либо через вынесение общего множителя. А деление использовать, когда у вас не получается решить другими способами. Это убережет от ошибок, описанных в конце главы про однородные уравнения.
Порешаем разные полезные нестандартные уравнения, которые могут встретиться на ЕГЭ.
Пример 32
$$4cos^4(x)-4cos^2(x)+1=0;$$
Уравнение с четвертой степенью, но пугаться не надо. Это биквадратное уравнение, которое мы решим при помощи простой замены:
$$t=cos^2(x);$$
$$4t^2-4t+1=0;$$
Перед вами формула сокращенного умножения – полный квадрат:
$$(2t-1)^2=0;$$
$$t=frac{1}{2};$$
Обратная замена:
$$cos^2(x)=frac{1}{2};$$
Перед нами еще одно квадратное уравнение. Чтобы такое решить, перенесем все в левую часть и разложим по формуле разности квадратов:
$$cos^2(x)-frac{1}{2}=0;$$
$$(cos(x)-sqrt{frac{1}{2}})(cos(x)-sqrt{frac{1}{2}})=0;$$
Произведение равно нулю, когда один из множителей равен нулю. Первый множитель:
$$cos(x)-sqrt{frac{1}{2}}=0;$$
$$cos(x)=sqrt{frac{1}{2}};$$
$$cos(x)=frac{1}{sqrt{2}};$$
$$x_{1,2}=pmfrac{pi}{4}+2pi*n, quad n in Z;$$
Второй множитель:
$$cos(x)+sqrt{frac{1}{2}}=0;$$
$$cos(x)=-sqrt{frac{1}{2}};$$
$$cos(x)=-frac{1}{sqrt{2}};$$
$$x_{3,4}=pmfrac{3pi}{4}+2pi*n, quad n in Z;$$
Ответ:
$$x_{1,2}=pmfrac{pi}{4}+2pi*n, quad n in Z;$$
$$x_{3,4}=pmfrac{3pi}{4}+2pi*n, quad n in Z;$$
Пример 33
$$sqrt{3}sin(2x)+3cos(2x)=0;$$
Обратите внимание, что тут обе тригонометрические функции берутся от (2x). В предыдущих примерах мы всегда избавлялись от (2x) и старались преобразовать так, чтоб аргумент был просто (x).
Но, оказывается, так делать необязательно. Так как тут аргумент везде (2x), то будем решать с ним. Нам, на самом деле, не важно, какой у вас аргумент, главное, чтобы он был одинаковый у всех тригонометрических функций, входящих в уравнение.
Разделим исходное уравнение на (cos(2x)), при этом убедимся, что (cos(2x)=0) не будет являться решением. Так как (sin(2x)) и (cos(2x)) одновременно при одинаковых значениях (x) не могут равняться нулю, то (cos(2x)=0) не является решением уравнения и можно спокойно делить:
$$sqrt{3}tg(2x)+3=0;$$
$$tg(2x)=frac{-3}{sqrt{3}};$$
$$tg(2x)=-sqrt{3};$$
$$2x=-frac{pi}{3}+pi*n, quad n in Z;$$
$$x=-frac{pi}{6}+frac{pi*n}{2}, quad n in Z;$$
Ответ:
$$x=-frac{pi}{6}+frac{pi*n}{2}, quad n in Z;$$
Как пользоваться формулами приведения? Правило лошади, единичная окружность и формулы суммы и разности для нахождения формул приведения.
Как пользоваться тригонометрической окружностью? Синус, косинус, тангнес и котангнес на единичной окружности. Свойства симметрии. Перевод градусов в радианы.
Разбираем тригонометрию с нуля. Синус, косинус, тангенс и котангенс в прямоугольном треугольнике. Таблица стандартных углов и свойства тригонометрических функций.
Как решать показательные неравенства. Общий алгоритм решения. Замена переменной. Однородные степенные неравенства.
Как решать неравенства с логарифмами. Общий алгоритм решения. Замена переменной. Переменное основание в логарифмических неравенствах. Сужение ОДЗ.
Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.
Как решать уравнения со степенями. Разбираем основные методы и способы решения простейших показательных уравнений.
Урок по теме логарифмы и их свойства. Разбираемся, что такое логарифм и какие у него свойства. Научимся считать выражения, содержащие логарифмы. И рассмотри несколько возможных заданий №4 из ЕГЭ по профильной математике.
Цикл уроков про степени и логарифмы и их свойства. Учимся решать показательные и логарифмические уравнения и неравенства. Задания №9 и №15 ЕГЭ по профильной математике.
Индивидуальные занятия с репетитором для учеников 6-11 классов. Для каждого ученика я составляю индивидуальную программу обучения. Стараюсь заинтересовать ребенка предметом, чтобы он с удовольствием занимался математикой и физикой.
Цель урока:
а) закрепить умения решать
простейшие тригонометрические уравнения;
б) научить выбирать корни
тригонометрических уравнений из заданного
промежутка
Ход урока.
1. Актуализация знаний.
а)Проверка домашнего задания: классу
дано опережающее домашнее задание – решить
уравнение и найти способ выбора корней из
данного промежутка.
1)cos x = -0,5, где хI [- ]. Ответ:
.
2) sin x = , где хI [0;2?]. Ответ:
;
.
3)cos 2x = —, где хI [0;
]. Ответ:
Ученики записывают решение на доске
кто-то с помощью графика, кто-то методом подбора.
В это время класс работает устно.
Найдите значение выражения:
а) tg –
sin + cos
+ sin
. Ответ: 1.
б) 2arccos 0 + 3 arccos 1. Ответ: ?
в) arcsin + arcsin
. Ответ:
.
г) 5 arctg (-) – arccos (-
). Ответ:–
.
– Проверим домашнее задание, откройте
свои тетради с домашними работами.
Некоторые из вас нашли решение методом
подбора, а некоторые с помощью графика.
См. приложение 1
Приложение 2
Приложение 3
2. Вывод о способах решения данных
заданий и постановка проблемы, т. е. сообщение
темы и цели урока.
– а) С помощью подбора решать сложно,
если задан большой промежуток.
– б) Графический способ не даёт точных
результатов, требует проверку, и занимает много
времени.
– Поэтому должен быть ещё как минимум
один способ, наиболее универсальный -попробуем
его найти. Итак, чем мы будем заниматься сегодня
на уроке? (Учиться выбирать корни
тригонометрического уравнения на заданном
промежутке.)
– Пример 1. (Ученик выходит к доске)
cos x = -0,5, где хI [- ].
Вопрос: Отчего зависит ответ на данное
задание? (От общего решения уравнения. Запишем
решение в общем виде). Решение записывается на
доске
х = + 2?k, где k
R.
– Запишем это решение в виде
совокупности:

– Как вы считаете, при какой записи
решения удобно выбирать корни на промежутке? (из
второй записи). Но это ведь опять способ подбора.
Что нам необходимо знать, чтобы получить верный
ответ? (Надо знать значения k).
(Составим математическую модель для
нахождения k).
Ответ: .
Вывод: Чтобы выбрать корни
из заданного промежутка при решении
тригонометрического уравнения надо:
- для решения уравнения вида sin x = a, cos x = a
удобнее записать корни уравнения, как две серии
корней. - для решения уравнений вида tg x = a, ctg x = a
записать общую формулу корней. - составить математическую модель для каждого
решения в виде двойного неравенства и найти
целое значение параметра k или n. - подставить эти значения в формулу корней и
вычислить их.
3. Закрепление.
Пример №2 и №3 из домашнего задания
решить, используя полученный алгоритм.
Одновременно у доски работают два ученика, с
последующей проверкой работ.
4. Самостоятельная работа.
Самопроверка с выбором ответа. Выбрать №
правильного ответа, получив закодированное
число (312).
1) sin x = —, x
2) 3 tg x = —, x I [0; 2
]
3) 2 cos ,
х [
]
Приложение. Ответы
к примерам
5. Домашнее задание:
1 уровень: № 295 (а,б), № 317 (а,б)
2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).
6. Итог урока.

Таблицы DPVA.ru — Инженерный Справочник
Адрес этой страницы (вложенность) в справочнике dpva.ru: 
|
|||||||||||||||||||||||||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator

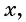
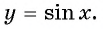
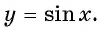
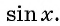
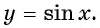
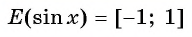
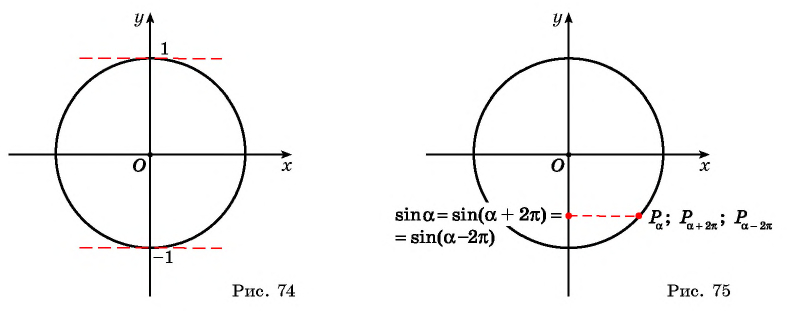
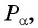
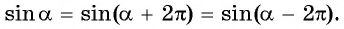
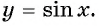
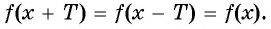
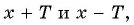 если
если 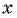 принадлежит области определения функции;
принадлежит области определения функции;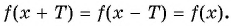
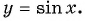
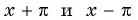 принадлежат области определения функции, так как
принадлежат области определения функции, так как 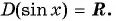
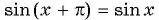 для всех
для всех