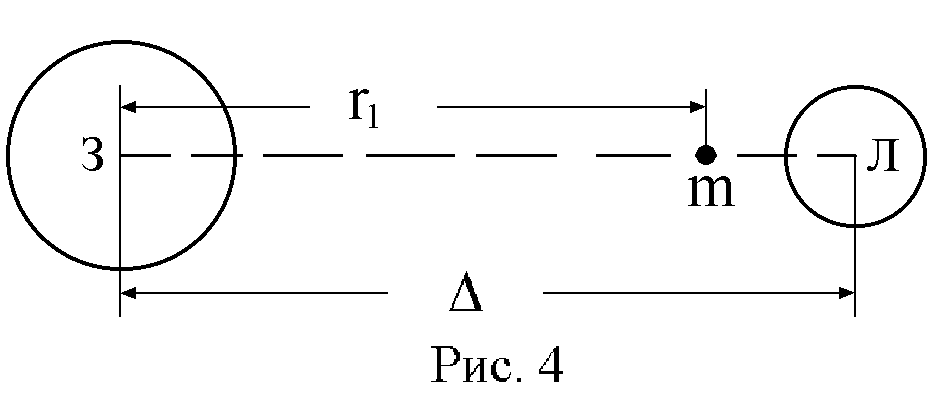поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
|
СБ, 11/20/2010 — 09:37 — mav Случились вместе два Астронома в пиру Урок 2/8 презентация Тема: Развитие представлений о Солнечной системе. Цель: Познакомить учащихся со становлением представлений человечества о строении Солнечной системы, геоцентрической и гелиоцентрической системах. Объяснение петлеобразного движения планет. Задачи: Знать: Оборудование: Таблица “Солнечная система”, к/ф “Планетная система”, “Астрономия и мировоззрение”. ПКЗН. CD- «Red Shift 5.1″(принцип нахождение небесного объекта в заданный момент времени). Демонстрация и комментирование диафильмов «Борьба за становление научного мировоззрения в астрономии» (I и II фрагменты) и «Развитие представлений о Вселенной». Фильм «Астрономия» (ч.1, фр. 2 «Самая древняя наука») Межпредметная связь: Представления о Земле в Древнем мире и Средние века (история, 5-6 кл). Солнечная система, ее состав; планеты, метеоры, метеориты (природоведение, 5 кл). Борьба церкви против передовой науки (история, 6 кл). Ход урока: 1. Повторение материала (8-10мин).
Б) По карточкам:
В) Остальные:
2. Новый материал (20мин) Геоцентрическая система строения мира (от Аристотеля до Птолемея).
Гелиоцентрическая система строения мира (Коперника).
Подтверждение гелиоцентрической системы мира.
III. Закрепление материала (8 мин).
Итог: Домашнее задание: §8; вопросы и задания стр. 40, стр. 52 п.1-5. Рассказ об ученом – астрономе (любом из перечисленных на уроке). Не решившим с/р №4 доделать. Можно дать составить презентацию о каком либо ученом с данного урока, открытиях Г. Галилея, об одной из систем строения мира и т.д. Урок оформили члены кружка «Интернет-технологии» — Прытков Денис (10кл) и Березуцкая Аня (11кл) Изменен 21.10.2009 года
|
Методику решения задач по теме “Движение
планет. Законы Кеплера”
продемонстрируем на решении типовых
задач.
Задача 1.
Определить промежуток времени между
двумя последовательными противостояниями
планеты Плутон, если сидерический период
планеты ТПлут
равен 248,6 лет.
Решение: Дано: ТПлут
= 248,6 лет. Требуется найти SПлут.
Так как Плутон – верхняя планета, то
для решения задачи используем формулу
(2). Принимая T
= 1 год, получим:
SПлут
= ТПлутT/(ТПлут
— T)
= 248,61/(248,6
— 1) = 1,004 г.
Ответ: SПлут
= 1,004 года.
Задача 2.
Определить наименьшую и наибольшую
элонгации планеты Меркурий, если большая
полуось орбиты Меркурия 0,387 а.е.,
эксцентриситет орбиты 0,2066, большая
полуось орбиты Земли 1а.е., эксцентриситет
орбиты Земли 0,0167.
Решение: Дано: аМер
= 0,387 а.е., еМер
= 0,2066, а
= 1 а.е., е
= 0,0167. Найти: ΘМер,max,
Θ Мер,min.
Из рис. 1 видно, что элонгация Меркурия
будет наименьшей тогда, когда в момент
элонгации Меркурий будет в перигелии,
а Земля в афелии. Воспользовавшись
формулами (5), запишем:
qМер
= aМер(1
— eМер);
Q
= а(1
+ е);
Из треугольника ⊙●2:
sin ΘМер,min
= (⊙●2)/(
⊙)
= aМер(1
— eМер)/а(1
+ е)
= 0,387(1
— 0,2066)/1(1
+ 0,0167) = 0,3070/1,0167= 0,3020;
ΘМер,min
= 17,6.
Элонгация Меркурия будет наибольшей
тогда, когда в момент элонгации Меркурий
будет в афелии, а Земля в перигелии.
ΘМер,max
= aМер(1
+ eМер);
q
= а(1
— е);
Из треугольника ⊙●2:
sin ΘМер,max
= aМер(1
+ eМер)/а(1
— е)
= 0,387(1
+ 0,2066)/1(1
— 0,0167) = 0,4670/0,9833 = 0,4749;
ΘМер,max
= 28,3.
Ответ: ΘМер,min
= 17,6,
ΘМер,max
= 28,3.
Задача 3.
Определить наименьшее и наибольшее
расстояния между Землей и Плутоном,
если большая полуось земной орбиты 1
а.е., эксцентриситет земной орбиты
0,0167, большая полуось орбиты Плутона
39,44 а.е., эксцентриситет орбиты Плутона
0,247.
Решение: Дано: а
= 1 а.е., е
= 0,0167, aПлут
= 39,48 а.е., eПлут
= 0,249. Требуется определить ΔПлут,min,
ΔПлут,max.
Из рис. 2 видно, что расстояние между
Землей и Плутоном будет минимальным
тогда, когда Земля будет находиться в
афелии, а Плутон в перигелии и
противостоянии. Учитывая формулы (5),
можем записать:
ΔПлут,min =
qПлут
— Q
= aПлут(1
— eПлут)
— a(1
+ e),
ΔПлут,min =
39,480,751 — 11,0167
= 28,63 а.е.
Расстояние между Землей и Плутоном
будет максимальным тогда, когда Земля
будет находиться в афелии, а Плутон в
афелии и соединении.
ΔПлут,max =
QПлут
+ Q
= aПлут(1
+ eПлут)
+ a(1
+ e),
ΔПлут,max =
39,481,249 + 11,0167
= 50,33 а.е.
Ответ: ΔПлут,min
= 28,63 а.е., ΔПлут,max
= 50,33 а.е.
Задача 4.
Круговая скорость движения Земли по
орбите 29,78 км/с. Найти минимальную и
максимальную скорости движения Земли
по орбите, если эксцентриситет орбиты
Земли 0,0167.
Решение: Дано: vк
= 29,78 км/с, e
= 0,0167. Найти vmin,
vmax.
Воспользуемся
формулами (6):
vmin
= vк[(1
— e)/(1
+ e)]1/2
= 29,780,9834
= 29,29 км/с;
vmax
= vк[(1
+ e)/(1
— e)]1/2
= 29,781,0168
= 30,28 км/с;
Ответ: vmin
= 29,29 км/с, vmax
= 30,28 км/с.
Задача 5.
Максимальное расстояние планеты Меркурий
от Солнца 0,467 а.е. Чему равен сидерический
период планеты, если эксцентриситет
орбиты Меркурия 0,2066.
Решение: Дано: QМерк
= 0,467 а.е., еМерк
= 0,2066. Найти ТМерк.
Для решения
воспользуемся соотношениями (5) и (8):
QМерк
= aМерк(1
+ eМерк);
aМерк
= QМеркк/(1
+ eМерк)
= 0,467/1,2066 =
0,387 а.е ;
ТМерк
= (aМерк)3/2
= 0,24 года.
Ответ: ТМерк
= 0,24 года = 87,9
ср. солн. cуток.
Задача 6.
Расстояние между центрами Земли и Луны
равно 60R.
Отношение масс Земли и Луны равно 81:1. В
какой точке прямой, проведенной между
центрами планет, какое-либо тело m
будет притягиваться Землей и Луной с
одинаковой силой?
Р
ешение:
Дано:
Δ = 60R,
M/MЛун
= 81/1. Найти r1. (см.
рис. 4)
Воспользуемся
для решения формулой (15):
Ускорение,
которое получает тело m от притяжения
Землей:
g1
= GM/r12
,
Ускорение,
которое получает тело m от притяжения
Луной:
g2
= GMЛун/(Δ
— r1)2,
= GMЛун/(60R
— r1)2.
В искомой
точке эти ускорения равны, то есть g1
= g2.
GM/r12
= GMЛун/(60R
— r1)2,
M/MЛун
= r12/(60R
— r1)2,
81 = r12/(60R
— r1)2,
9 = r1/(60R
— r1),
9(60R
— r1)
= r1,
540R
= 10r1,
r1
= 54R.
Ответ: Искомое расстояние равно
54R
от центра Земли.
Задача 7.
Среднее расстояние спутника Марса
Фобоса 9,4103
км. Сидерический период обращения Фобоса
0,3189 суток. Найти массу планеты Марс в
массах Земли. Воспользоваться данными
о системе Земля-Луна.
Решение: Дано: аФоб
= 9,4103
км, ТФоб
= 0,3189 сут., аЛун
= 3,844105
км, ТЛун =
27,3117 сут., М/MЛун
= 81,3. Найти ММарс
в М.
Для решения
воспользуемся третьим законом Кеплера
(13):
а3Фоб/T2Фоб(MМарс
+ MФоб)
= a3Лун/T2Лун(M
+ MЛун).
Так как МЛун
= 0,0123М,
МФоб
<< MМарс,
то
а3Фоб/T2Фоб
MМарс
= a3Лун/T2Лун(M
+ 0,0123М)
=
= a3Лун/1,0123T2ЛунM,
откуда
MМарс
= 1,0123(TЛун/TФоб)2(аФоб
/aЛун)3M
=
= 1,0123(27,3117/0,3189)2(9,4103/3,844105)3M
=0,108M.
Ответ: MМарс
= 0,108M.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
12.02.201513.99 Mб14Давидсон А. Сесиль Родс.pdf
- #
- #
- #
- #
- #
- #
- #
Дано:
Tc = 29,5 года
T⊕ = 1 год
————————
Найти:
S — ?
Решение:
Воспользуемся формулой синодического периода обращения для высоких планет:
1/S = 1/T⊕ — 1/Tc ⇒ 1/S = Tc-T⊕/T⊕×Tc ⇒ S = T⊕×Tc/Tc-T⊕
Теперь мы сможем определить промежуток времени между двумя его противостояниями:
S = 1 год × 29,5 года/29,5 года — 1 год = 29,5 года/28,5 года ≈ 1,0351 а.е.
Ответ: S = 1,0351 а.е.
1.
а) по Птолемею: геоцентрическая система, все небесные тела движутся около неподвижной Земли, которая является центром.
б) по Копернику: Земля — третья планета от Солнца и обращает Солнце за один звёздный год; планеты движутся в пространстве вокруг Солнца — центра.
2.
Планетой называют небесное тело, движущееся вокруг звезды в её гравитационном поле, имеющее форму, близкую к сферической, светящееся отражённым от звезды светом.
Помимо общего суточного движения планеты на фоне звезд описывают сложные петлеобразные пути. При медленном перемещении с запада на восток движение планеты называют прямым, а при перемещения с востока на запад — обратным, или попятным.
Конфигурациями планет называют характерные взаимные расположения планет, Земли и Солнца.
3.
а) нижние планеты: Венера и Меркурий;
б) верхние планеты: Марс, Юпитер, Уран, Нептун, Сатурн.
4.
- Соединение
- верхнее соединение
- наибольшее удаление (восточная элонгация)
- нижнее соединение
- наибольшее удаление (западная элонгация)
- противостояние
- восточная квадратура
- западная квадратура
5.
В какой конфигурации на минимальное расстояние к Земле подходит нижняя планета?
В нижнем соединении.
В какой конфигурации на минимальное расстояние к Земле подходит верхняя планета?
В противостоянии.
6.
7.
8.
Синодический период обращения — промежуток времени между двумя последовательными одноимёнными конфигурациями планеты.
Сидерический (или звездный) период обращения — промежуток времени, в течение которого планета совершает полный оборот вокруг Солнца по орбите относительно звёзд.
9.
а) для нижних планет: $dfrac{1}{S} = dfrac{1}{T} = dfrac{1}{T_З}$
б) для верхних планет: $dfrac{1}{S} = dfrac{1}{T_З} — dfrac{1}{T}$
10.
Вариант 1.
$1$. Каков синодический период Марса, если его звездный период $T- 1,88$ земного года?
$2$. Нижние соединения Меркурия повторяются через $116$ суток. Определите сидерический период Меркурия.
Вариант 2.
$1$. Определите звездный период Венеры, если ее нижние соединения повторяются через $584$ суток.
$2$. Через какой промежуток времени повторяются противостояния Юпитера, если его сидерический период $T= 11,86$ года?
Присоединяйтесь к Telegram-группе @superresheba_11,
делитесь своими решениями и пользуйтесь материалами, которые присылают другие участники группы!



 окончательно кинематически разработана к 150г НЭ александрийским астрономом Клавдием Птолемеем (87-165) в сочинении, состоящем из 13 книг “Великое математическое построение астрономии” (Альмагест). Для объяснения движения планет, применив систему эпициклов и деферентов, сделав их гармоническими: сложное петлеобразное движение представлялось суммой нескольких гармонических движений, выражаемых формулой:
окончательно кинематически разработана к 150г НЭ александрийским астрономом Клавдием Птолемеем (87-165) в сочинении, состоящем из 13 книг “Великое математическое построение астрономии” (Альмагест). Для объяснения движения планет, применив систему эпициклов и деферентов, сделав их гармоническими: сложное петлеобразное движение представлялось суммой нескольких гармонических движений, выражаемых формулой: , где где
, где где 
.jpg)