Как найти пропорциональные отрезки в прямоугольном треугольнике - Исправление недочетов и поиск решений вместе с Examum.ru

Признак подобия прямоугольных треугольников

Признак подобия треугольников с прямым углом является частным случаем первого признака подобия треугольников, который предполагает следующее: при соответствии двух углов одного треугольника двум углам другого такие треугольники являются подобными.

Теорема

Формулировка для треугольников с углами в 90°: подобие прямоугольных треугольников имеет место, когда острый угол одного треугольника является равным острому углу другого.

Рассмотрим наглядно на схеме:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Треугольники

∠C=∠C₁=90°

∠A=∠A₁

∠B=180°−(∠C+∠A)

∠B₁=180°−(∠C₁+∠A₁)

Отсюда следует, что ΔABC∼ΔA₁B₁C₁.

Примечание

Сумма острых углов прямоугольного треугольника равна 90°.

Пропорциональные отрезки в прямоугольном треугольнике — отношение

Определение

Средним пропорциональным двух величин a и b называется число c при условии, что квадрат c равен произведению a и b, то есть c²=ab.

Среднее пропорциональное

На рисунке изображен прямоугольный треугольник с катетами a и b, гипотенузой c и проведенной к ней высоте h. Высота делит гипотенузу на два отрезка: a_c и b_c, именуемые проекциями катетов на гипотенузу.

Теорема 1

Среднее пропорциональное между гипотенузой и проекцией на нее – это каждый катет прямоугольного треугольника, то есть:

(a^2=a_ctimes c )

(b^2=b_ctimes c)

Доказательство

Пусть в ΔABC ∠C=90°, ∠A=α, CH – высота.

Доказательство теоремы

1. Сначала докажем, подобие ΔABC и ΔCBH.

Поскольку CH – высота, то ∠CHB равен 90°.

∠B=90°−α – это общий угол рассматриваемых треугольников ABC и CBH.

∠HCB=90°−∠B=90°−(90°−α)=α.

Доказательство теоремы 2

Следовательно, в ΔABC и ΔCBH:

∠ACB=∠HCB=90°

∠B – общий и равен 90°−α

∠CAB=∠HCB=α

Отсюда следует, что ΔABC∼ΔCBH.

2. Теперь докажем, что ΔABC∼ΔACH.

∠ACB=∠AHC=90°, т.к. СН – высота ΔABC.

∠A – общий и равен α.

∠ACH=90−α, а значит, равен ∠AВC.

Следовательно, ΔABC∼ΔACH.

3. Сделаем на схеме дополнительные обозначения проекций катетов:

Доказательство теоремы 3

4. Применим доказанное подобие ΔABC и ΔCBH и запишем пропорции сторон:

(frac ac=frac{a_c}a)

В переводе с математического языка это означает следующее: отношение противолежащих прямому углу сторон, ровняется отношению сторон, расположенных напротив угла α. Из данного соотношения получается:

((1)a^2=a_ctimes c)

5. Воспользуемся тем, что ΔABC∼ΔACH. Запишем пропорции сторон:

(frac bc=frac{b_c}b)

Это значит, что отношение сторон, противолежащих прямому углу равно отношению сторон, лежащих напротив α. Выведем из пропорции следующее уравнение:

((2)b^2=b_ctimes c)

Полученные равенства (1) и (2) доказывают теорему.

Теорема 2

Средним пропорциональным между проекциями катетов является высота, опущенная на гипотенузу из вершины угла в 90°, то есть при умножении отрезков ac и bc получается величина, равная квадрату высоты:

(h^2=a_ctimes b_c)

Доказательство:

Поскольку ранее мы доказали подобия треугольников ΔABC∼ΔCBH и ΔABC∼ΔACH, то ΔCBH∼ΔACH. Используем этот факт для доказательства второй теоремы. Запишем пропорцию:

(frac h{a_c}=frac{b_c}h)

Она значит, что отношение сторон, противолежащих углу (90°−α), равно соотношению сторон, противолежащих углу α.

Выведем отсюда значение h:

(h^2=a_ctimes b_c)

Теорема доказана.

Следствие

Гипотенуза разделена высотой на отрезки, соотношение которых равно отношению квадратов катетов. В виде формулы это свойство выглядит так:

(frac{a_c}{b_c}=frac{a^2}{b^2})

Альтернативное доказательство теоремы Пифагора

Сформулированные и доказанные теоремы позволяют привести альтернативу традиционному доказательству пифагоровой теоремы:

(left.begin{array}{r}b^2=b_ctimes c\a^2=a_ctimes cend{array}right}Rightarrow a^2+b^2=a_ctimes c+b_ctimes c=cleft(a_c+b_cright)=ctimes c=c^2)

Примеры решения задач на использование пропорциональных отрезков в прямоугольном треугольнике

Задача 1

В ΔABC: ∠С=90°, СН – высота, отрезок АН=9 см, отрезок АН=16 см. Вычислите длину катетов и высоты треугольника ABC.

Задача 1

Решение

Определим длину гипотенузы: AB=9+16=25 см.
Применим доказанные теоремы:

(BC=sqrt{ABtimes BH}=sqrt{25times16}=5times4=20)

(AC=sqrt{ABtimes AH}=sqrt{25times9}=5times3=15)

(CH=sqrt{BHtimes AH}=sqrt{16times9}=4times3=12)

Ответ: сторона ВС=20 см, сторона АС=15 см, высота СН=12 см.

Задача 2

В прямоугольном треугольнике ABC сторона АС равна 8 см, сторона AB равна 10 см. Вычислить длину высоты CD.

Задача 2

Решение

1. Так как треугольники АВС и АСD подобны, можно составить пропорции сторон:

(frac{AB}{AC}=frac{BC}{CD})

2. Найдем длину катета ВС:

(BC=sqrt{AB^2-AC^2}=sqrt{10^2-8^2}=sqrt{100-64}=36=6)

(ВС=6) см

3. Далее подставим полученную величину в соотношение, записанное в первом пункте:

(frac{10}8=frac6{CD})

Теперь выведем отсюда уравнение с неизвестным CD:

(CD=frac{8times6}{10}=frac{48}{10}=4,8)

Ответ: CD=4,8 см.

Источник

Запомнить соотношения, связывающие пропорциональные отрезки в прямоугольном треугольнике, помогает цветовая ассоциация.

Высота прямоугольного треугольника, проведенная к гипотенузе, делит ее на отрезки, которые называются проекциями катетов на гипотенузу.

Свойства прямоугольного треугольника:

1. Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.

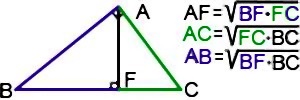
2. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Например, в треугольнике ABC AF — высота, проведенная к гипотенузе BC, BF — проекция катета AB на гипотенузу, FC — проекция катета AC на гипотенузу.

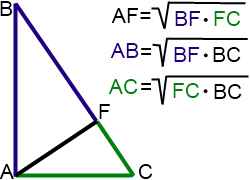
Если выделить каждую пару — катет и его проекция на гипотенузу — одним цветом, запомнить пропорциональные отрезки в прямоугольном треугольнике можно быстро и легко.

Как бы ни был расположен на чертеже прямоугольный треугольник, цветовая ассоциация поможет найти пропорциональные отрезки и правильно составить связывающие их соотношения:

Выделить пропорциональные отрезки цветами можно на черновике. При решении задачи, в которой прямоугольный треугольник — только один из элементов чертежа, достаточно для нахождения связи между пропорциональными отрезками на черновике изобразить отдельный фрагмент с этим треугольником.

Источник

Щебетун Виктор

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Признак подобия прямоугольных треугольников

Введем для начала признак подобия прямоугольных треугольников.

Признак подобия прямоугольных треугольников: два прямоугольных треугольника подобны тогда, когда у них есть по одному равному острому углу (рис. 1).

прямоугольные треугольники»>

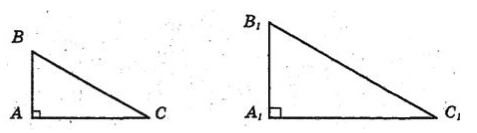
Рисунок 1. Подобные прямоугольные треугольники

Доказательство.

Пусть нам дано, что $angle B=angle B_1$. Так как треугольники прямоугольные, то $angle A=angle A_1={90}^0$. Следовательно, они подобны по первому признаку подобия треугольников.

Теорема доказана.

Теорема о высоте в прямоугольном треугольнике

Теорема 2

Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Доказательство.

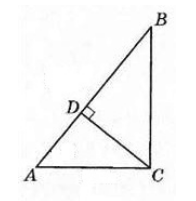
Пусть нам дан прямоугольный треугольник $ABC$ с прямым углом $C$. Проведем высоту $CD$ (рис. 2).

Рисунок 2. Иллюстрация теоремы 2

Докажем, что треугольники $ACD$ и $BCD$ подобны треугольнику $ABC$ и что треугольники $ACD$ и $BCD$ подобны между собой.

Так как $angle ADC={90}^0$, то треугольник $ACD$ прямоугольный. У треугольников $ACD$ и $ABC$ угол $A$ общий, следовательно, по теореме 1, треугольники $ACD$ и $ABC$ подобны.
Так как $angle BDC={90}^0$, то треугольник $BCD$ прямоугольный. У треугольников $BCD$ и $ABC$ угол $B$ общий, следовательно, по теореме 1, треугольники $BCD$ и $ABC$ подобны.
Рассмотрим теперь треугольники $ACD$ и $BCD$

[angle A={90}^0-angle ACD] [angle BCD={90}^0-angle ACD=angle A]

Следовательно, по теореме 1, треугольники $ACD$ и $BCD$ подобны.

«Пропорциональные отрезки в прямоугольном треугольнике» 👇

Теорема доказана.

Среднее пропорциональное

Определение 1

Отрезок $x$ называется средним пропорциональным или средним геометрическим дл отрезков $a$ и $b$, если выполняется следующее равенство

[x=sqrt{ab}]

Теорема 3

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые высота делит гипотенузу данного треугольника.

Доказательство.

В доказательстве теоремы будем пользоваться обозначениями из рисунка 2.

По теореме 2, имеем, что треугольники $ACD$ и $BCD$ подобны, следовательно

Теорема доказана.

Теорема 4

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины угла.

Доказательство.

В доказательстве теоремы будем пользоваться обозначениями из рисунка 2.

По теореме 2, имеем, что треугольники $ACD$ и $ABC$ подобны, следовательно

Теорема доказана.

Примеры задач на использование пропорциональных отрезков в прямоугольном треугольнике

Пример 1

Катеты прямоугольного треугольника $ABC$ с прямым углом $C$ относятся как $2:3$, а гипотенуза равна $39$ см. Найти отрезки, на которые высота $CD$ делит гипотенузу данного треугольника.

Решение.

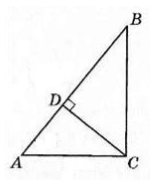
Изобразим условие на рисунке:

Рисунок 3.

По теореме 4, с одной стороны, получим

[AC=sqrt{ABcdot AD}]

А с другой стороны, получим

[BC=sqrt{ABcdot BD}]

Тогда

[frac{AC}{BC}=frac{sqrt{ABcdot AD}}{sqrt{ABcdot BD}}=sqrt{frac{AD}{BD}}=frac{2}{3}]

Следовательно

[frac{AD}{BD}=frac{4}{9}] [AD=frac{4}{9}BD]

Так как $AD+BD=AB=39$, то

[frac{4}{9}BD+BD=39] [13BD=39cdot 9] [BD=27] [ AD=12]

Ответ: $12$ и $27$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Пропорциональные отрезки в прямоугольном треугольнике

Следующие соотношения позволяют найти стороны и углы прямоугольного треугольника по любым двум элементам (сторонам или стороне и углу).

Рис. (1). Прямоугольный треугольник

Теорема Пифагора:c2=a2+b2;a2=c2−b2;b2=c2−a2.

sinα=ac;cosα=bc;tgα=ab;ctgα=ba.

cos2α+sin2α=1;tgα⋅ctgα=1.

Очень важные соотношения можно получить, заметив, что

∠DCB=∠CAD;∠DBC=∠ACD.

Мы получаем три пары подобных треугольников:

ΔACD∼ΔCBD;ΔACD∼ΔABC;ΔCBD∼ΔABC.

Из подобий:

ΔACD∼ΔCBD:ACCB=CDBD=ADCD;ba=hac=bch⇒h2=ac⋅bc.

ΔACD∼ΔABC:ACAB=CDBC=ADAC;bc=ha=bcb⇒b2=c⋅bc.

ΔCBD∼ΔABC:CBAB=BDBC=CDAC;ac=aca=hb⇒a2=c⋅ac.

Из последних соотношений можно получить ещё одно важное соотношение:

ac=hb⇒h=abc.

Это же равенство можно получить, используя две формулы для вычисления площади прямоугольного треугольника:

S=12ab=12hc⇒ab=hc⇒h=abc.

Отметим ещё одно важное свойство медианы прямоугольного треугольника, проведённого к гипотенузе.

Рис. (2). Дополнительные построения

Как видно из рисунка, если мы достроим прямоугольный треугольник до прямоугольника, то окажется, что медиана (CO) — это половина диагонали прямоугольника, а следовательно, и гипотенузы.

mc=c2.

Источники:

Источник

Узнать ещё

Знание — сила. Познавательная информация

Пропорциональные отрезки в прямоугольном треугольнике

Свойства прямоугольного треугольника:

2. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Геометрия. 8 класс

Конспект
Теорема: В прямоугольном треугольнике высота, проведенная из вершины прямоуго угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

∆CAD
Доказательство:
∠А − общий угол, ∠АСВ = ∠ADC = 90°, следовательно, ∆ACD

∆CAD
Отрезок MN называется средним пропорциональным (или средним геометрическим) между отрезками АВ и CD, если выполняется равенство для длин отрезков
MN = √(AB ∙ CD)
Пример:
АВ = 5 см, CD = 125 см, MN = 25 см.
Является ли отрезок MN средним пропорциональным между отрезками AB и CD?
Решение:
Воспользуемся равенством MN = √(AB ∙ CD)
25 = √(5 ∙ 125)
25 = √625 – верно, следовательно, отрезок MN является средним пропорциональным между отрезками AB и CD.
Докажем утверждение: высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Дано: ∆ABC, ∠С = 90°, CD⊥AB

∆CAD, поэтому AD/CD = CD/BD, следовательно, CD 2 = AD ∙ BD, откуда CD = √(AD ∙ BD).
Для прямоугольного треугольника верно еще одно утверждение: катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы.
Таким образом, в прямоугольном треугольнике выполняются равенства:
CD = √(AD ∙ BD)
AC = √(AB ∙ AD) или BC = √(AB ∙ BD)

Прямоугольные треугольники

Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.

3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.

5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$

6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$<1>/<2>$	$<√2>/<2>$	$<√3>/<2>$
$cosα$	$<√3>/<2>$	$<√2>/<2>$	$<1>/<2>$
$tgα$	$<√3>/<3>$	$1$	$√3$
$ctgα$	$√3$	$1$	$<√3>/<3>$

Площадь прямоугольного треугольника равна половине произведения его катетов

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√<91>$. Найдите косинус внешнего угла при вершине $В$.

Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то

Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:

Катет $ВС$ мы можем найти по теореме Пифагора:

Подставим найденное значение в формулу косинуса

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sin⁡A=<4>/<5>, AC=9$. Найдите $АВ$.

Распишем синус угла $А$ по определению:

Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.

Применим теорему Пифагора, чтобы отыскать $«х»$

Так как длина $АВ$ составляет пять частей, то $3∙5=15$

В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

источники:

http://resh.edu.ru/subject/lesson/3035/main/

http://examer.ru/ege_po_matematike/teoriya/pryamougolnie_treugolniki

Источник