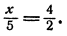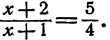Загрузить PDF
Загрузить PDF
Пропорция — это математическое выражение, в котором два или более числа сравниваются друг с другом. В пропорциях могут сравниваться абсолютные величины и количества или части более крупного целого. Пропорции можно записывать и вычислять несколькими различными способами, однако в основе лежит один и тот же общий принцип.
-
1
Узнайте, для чего служат пропорции. Пропорции используются как в научных исследованиях, так и в повседневной жизни для сравнения различных величин и количеств. В простейшем случае сравниваются два числа, но пропорция может включать в себя любое количество величин. При сравнении двух или большего количества величин всегда можно применить пропорцию. Знание того, как величины соотносятся друг с другом, позволяет, к примеру, записать химические формулы или рецепты различных блюд. Пропорции пригодятся вам для самых разных целей.[1]
-
2
Ознакомьтесь с тем, что означает пропорция. Как отмечено выше, пропорции позволяют определить соотношение между двумя и более величинами. Например, если для приготовления печенья необходимо 2 стакана муки и 1 стакан сахара, мы говорим, что между количеством муки и сахара существует пропорция (отношение) 2 к 1.
- С помощью пропорций можно показать, как различные величины относятся друг к другу, даже если они не связаны между собой непосредственно (в отличие от рецепта). Например, если в классе пять девочек и десять мальчиков, отношение количества девочек к числу мальчиков составляет 5 к 10. В этом случае одно число не зависит от другого и не связано с ним непосредственно: пропорция может измениться, если кто-то покинет класс или наоборот, в него придут новые ученики. Пропорция просто позволяет сравнить две величины.
-
3
Обратите внимание на различные способы выражения пропорций. Пропорции можно записать словами или использовать математические символы.[2]
- В обыденной жизни пропорции чаще выражают словами (как приведено выше). Пропорции используются в самым разных областях, и если ваша профессия не связана с математикой или другой наукой, чаще всего вам будет попадаться именно такой способ записи пропорций.
- Пропорции часто записывают посредством двоеточия. При сравнении двух чисел с помощью пропорции их можно записать через двоеточие, например 7:13. Если сравнивается более двух чисел, двоеточие ставится последовательно между каждыми двумя числами, например 10:2:23. В приведенном выше примере для класса мы сравниваем количество девочек и мальчиков, причем 5 девочек : 10 мальчиков. Таким образом, в этом случае пропорцию можно записать в виде 5:10.
- Иногда при записи пропорций используют знак дроби. В нашем примере с классом отношение 5 девочек к 10 мальчикам запишется как 5/10. В этом случае не следует читать знак “делить” и необходимо помнить, что это не дробь, а соотношение двух разных чисел.
Реклама
-
1
Приведите пропорцию к простейшей форме. Пропорции можно упрощать, как и дроби, за счет сокращения входящих в них членов на общий делитель. Чтобы упростить пропорцию, поделите все входящие в нее числа на общие делители. Однако при этом не следует забывать о первоначальных величинах, которые привели к данной пропорции.[3]
- В приведенном выше примере с классом из 5 девочек и 10 мальчиков (5:10) обе стороны пропорции имеют общий делитель 5. Поделив обе величины на 5 (наибольший общий делитель), получаем отношение 1 девочка на 2 мальчика (то есть 1:2). Однако при использовании упрощенной пропорции следует помнить о первоначальных числах: в классе не 3 ученика, а 15. Сокращенная пропорция лишь показывает отношение между количеством девочек и мальчиков. На каждую девочку приходится два мальчика, но это отнюдь не означает, что в классе 1 девочка и 2 мальчика.
- Некоторые пропорции не поддаются упрощениям. Например, отношение 3:56 нельзя сократить, так как входящие в пропорцию величины не имеют общего делителя: 3 является простым числом, а 56 не делится на 3.
-
2
Для “масштабирования” пропорции можно умножать или делить. Пропорциями часто пользуются для того, чтобы увеличить или уменьшить числа в пропорции друг к другу. Умножение или деление всех входящих в пропорцию величин на одно и то же число сохраняет неизменным отношение между ними. Таким образом, пропорции можно умножать или делить на “масштабный” фактор.[4]
- Предположим, пекарю необходимо утроить количество выпекаемого печенья. Если мука и сахар берутся в пропорции 2 к 1 (2:1), для увеличения количества печенья в три раза данную пропорцию следует умножить на 3. В результате получится 6 стаканов муки на 3 стакана сахара (6:3).
- Можно поступать и наоборот. Если пекарю необходимо уменьшить количество печенья в два раза, следует обе части пропорции поделить на 2 (или умножить на 1/2). В результате получится 1 стакан муки на полстакана (1/2, или 0,5 стакана) сахара.
-
3
Научитесь по двум эквивалентным пропорциям находить неизвестную величину. Еще одной распространенной задачей, для решения которой широко используются пропорции, является нахождение неизвестной величины в одной из пропорций, если дана аналогичная ей вторая пропорция. Правило умножения дробей значительно упрощает эту задачу. Запишите каждую пропорцию в виде дроби, затем приравняйте эти дроби друг другу и найдите искомую величину.[5]
- Предположим, у нас есть небольшая группа учеников из 2 мальчиков и 5 девочек. Если мы хотим сохранить соотношение между мальчиками и девочками, сколько мальчиков должно быть в классе, в который входит 20 девочек? Для начала составим обе пропорции, одна из которых содержит неизвестную величину: 2 мальчика : 5 девочек = x мальчиков : 20 девочек. Если мы запишем пропорции в виде дробей, у нас получится 2/5 и x/20. После умножения обеих частей равенства на знаменатели получаем уравнение 5x=40; делим 40 на 5 и в итоге находим x=8.
Реклама
-
1
При операциях с пропорциями избегайте сложения и вычитания. Многие задачи с пропорциями звучат подобно следующей: “Для приготовления блюда требуется 4 картофелины и 5 морковок. Если вы хотите использовать 8 картофелин, сколько морковок вам понадобится?” Многие допускают ошибку и пытаются просто сложить соответствующие величины. Однако для сохранения прежней пропорции следует умножать, а не складывать. Вот ошибочное и правильное решение данной задачи:
- Неправильный метод: “8 — 4 = 4, то есть в рецепте добавилось 4 картофелины. Значит, необходимо взять прежние 5 морковок и прибавить к ним 4, чтобы… что-то не то! С пропорциями действуют по-другому. Попробуем еще раз“.
- Правильный метод: “8/4 = 2, то есть количество картофелин выросло в 2 раза. Это значит, что и число морковок следует умножить на 2. 5 x 2 = 10, то есть в новом рецепте необходимо использовать 10 морковок“.
-
2
Переведите все значения в одинаковые единицы измерения. Иногда проблема возникает из-за того, что величины имеют разные единицы измерения. Прежде чем записывать пропорцию, переведите все величины в одинаковые единицы измерения. Например:
- У дракона есть 500 граммов золота и 10 килограммов серебра. Каково соотношение золота к серебру в драконьих запасах?
- Граммы и килограммы являются различными единицами измерения, поэтому их следует унифицировать. 1 килограмм = 1 000 граммов, то есть 10 килограммов = 10 килограммов x 1 000 граммов/1 килограмм = 10 x 1 000 граммов = 10 000 граммов.
- Итак, дракон имеет 500 граммов золота и 10 000 граммов серебра.
- Отношение массы золота к массе серебра составляет 500 граммов золота/10 000 граммов серебра = 5/100 = 1/20.
-
3
Записывайте в решении задачи единицы измерения. В задачах с пропорциями намного легче найти ошибку в том случае, если записывать после каждой величины ее единицы измерения. Помните о том, что если в числителе и знаменателе стоят одинаковые единицы измерения, они сокращаются. После всех возможных сокращений в ответе должны получиться правильные единицы измерения.
- Например: даны 6 коробок, и в каждых трех коробках находится 9 шариков; сколько всего шариков?
- Неправильный метод: 6 коробок х 3 коробки/9 шариков = … Хм, ничего не сокращается, и в ответе выходит “коробки x коробки / шарики“. Это не имеет смысла.
- Правильный метод: 6 коробок х 9 шариков/3 коробки = 6 коробок х 3 шарика/1 коробка = 6 х 3 шарика/1 = 18 шариков.
Реклама
Об этой статье
Эту страницу просматривали 58 014 раз.
Была ли эта статья полезной?
Proportion in Maths is an equation used to find that the two given ratios are equivalent to each other. Generally, we say that proportion defines that the equality of the two fractions of the ratios. If two sets of given numbers are increasing or decreasing in the same ratio with respect to each other, then the ratios are said to be directly proportional to each other. For example, the time taken by car to cover 200km per hour is equal to the time taken by it to cover the distance of 1200km for 6 hours. Such as 200km/hr = 1200km/6hrs.
Also, See:
- Ratios
- Practice Test on Ratio and Proportion
- Worked out Problems on Ratio and Proportion
Let us take, in proportion, the two ratios are x:y and m:n. The two terms m and n are called means or mean terms and x and y are called extremes or extreme terms.
x : y :: m: n
(frac { x }{ y } ) = (frac { m }{ n } )
Example:
Let us consider the number of persons in a theater. Our first ratio of the number of girls to boys is 5:7 and that of the other is 3:5, then the proportion can be written as:
5 : 7 :: 3 : 5 or 5/7 = 3/5
Here, 5 & 5 are the extremes, while 7 & 3 are the means.
Note: The ratio value does not affect when the same non-zero number is multiplied or divided on each term.
Important Properties of Proportion
The below are the important properties of proportions.
- Addendo – If a : b = c : d, then a + c : b + d
- Subtrahendo – If a : b = c : d, then a – c : b – d
- Componendo – If a : b = c : d, then a + b : b = c+d : d
- Dividendo – If a : b = c : d, then a – b : b = c – d : d
- Invertendo – If a : b = c : d, then b : a = d : c
- Alternendo – If a : b = c : d, then a : c = b: d
- Componendo and dividendo – If a : b = c : d, then a + b : a – b = c + d : c – d
Types of Proportions
The Proportions are classified into two types. They are
- Direct Proportion
- Inverse Proportion
Direct Proportion: The Direct Proportion describes the direct relationship between two quantities. If one of the quantities increases, the other quantity increases and if one of the quantities decreases, the other quantity also decreases.
Example: If the speed of a vehicle increased, then it covers more distance in a fixed amount of time. It is denoted as y ∝ x.
Inverse Proportion: The Inverse Proportion describes the indirect relationship between two quantities. If one quantity increases, the other quantity decreases, and If one quantity decreases the other quantity increases. It is denoted as y ∝ 1/x.
Example: If a vehicle speed increases, then the result in converting a fixed distance in less time.
Important Points on Proportion
Check out the important points that need to remember in the proportion concept.
- Proportion is the comparison between two quantities.
- The proportions are two types. One is direct proportions and inverse proportions.
- Formula of proportion is (frac { x }{ y } ) = (frac { m }{ n } )
- The proportion is an equation.
How to Solve Proportions?
Finding proportion is easy if the ratios are given. Follow the below procedure and find out the process to calculate proportions.
1. Multiply the first term with the last term: x x n
2. Multiply the second term with the third term: y x m
3. If the product of extreme terms is equal to the product of mean terms, then the ratios are proportional: x x n = y x m.
Continued Proportions
If we considered three quantities and the ratio of the first and second quantities is equal to the ratio between the second and the third quantities, then the three quantities are in Continued Proportions.
Example:
Let us take the ratios a:b and c:d
If a: b :: b: c, then we can say that a, b, c quantities are in continued proportion. Also, c is the third proportional of a and b.
b is called the mean proportional between a and C.
If a, b, c are in continued proportion then b² = ac or b = √ac.
Proportion Examples with Answers
Example 1.
Determine if 4, 7, 8, 14 are in proportion?
Solution:
Given numbers are 4, 7, 8, 14.
From the given data, extreme terms are 4 and 13, mean terms are 7 and 6.
Find the Product of extreme terms and mean terms.
Product of extreme terms = 4 × 14 = 56
Product of mean terms = 7 × 8 = 56.
Compare the Product of extreme terms and the Product of mean terms.
The product of means = product of extremes
56 = 56
Therefore, 4, 7, 8, 14 are in proportion.
Example 2.
Check if 3, 6, 12 are in proportion.
Solution:
Given numbers are 3, 6, 12.
From the given data, 3 is the first term, 6 is the middle term, and 12 is the third term.
Find the Product of the first term and third term.
Product of first and third term = 3 × 12 = 36
Square of the middle terms = 6 × 6 = 36 = 3 × 12.
Compare the Product of the first and third term and Square of the middle terms.
The Product of first and third term = Square of the middle terms
56 = 56
Therefore, 3, 6, 12 are in proportion, and 6 is called the mean proportional between 3 and 12.
Example 3.
Find the fourth proportional to 3, 19, 21?
Solution:
Given numbers are 3, 19, 21.
To find the fourth Proportional, let us assume the fourth proportional is x.
Then, 3: 19 :: 21: x
Compare the Product of extreme terms and Product of mean terms.
3x = 19 × 21
3x = 399
x = 399/3
x = 133.
Hence, the fourth proportional to 3, 19, 21 is 133.
Example 4.
Find the third proportional to 4 and 8?
Solution:
Given numbers are 4 and 8.
Let the third proportional to 4 and 8 be x.
Compare the Product of the first and third term and Square of the middle terms.
4x = 8 × 8
4x = 64
x = 64/4
x = 16
Therefore, the third proportional to 4 and 8 is 16.
Example 5.
The ratio of income to expenditure is 3: 4. Find the savings if the expenditure is $24,000.
Solution:
Given that the ratio of income to expenditure is 3: 4.
Therefore, income = $ (3 × 24000)/4 = $18000
Savings = Income – Expenditure = $24,000 – $18000 = $6000
The savings are $6000 if the expenditure is $24,000.
Example 6.
Find the mean proportional between 3 and 27?
Solution:
Given numbers are 3 and 27.
Let the mean proportional between 3 and 27 be x.
Then, x × x = 3 × 27
x² = 81
x = √81
x = 9.
Therefore, the mean proportion between 3 and 27 is 9.
Общие сведения
Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.
Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.
Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.
Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.
Сферы применения
Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.
В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.
Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.
Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.
В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.
Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.
Основные свойства
Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:
- Обращение или обратное пропорциональное соотношение: [x / y = v / z] = [y / x = z / v].
- Перемножение «крест-накрест»: x * z = y * v.
- Перестановка: x / v = y / z и v / x = z / y.
- Увеличение или уменьшение: x + у / y = v + z / z и x — у / y = v — z / z.
- Составление через арифметические операции сложения и вычитания: (x + v) / (y + z) = x / y = v / z и (x — v) / (y — z) = x / y = v / z.
Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).
Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.
Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.
Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.
Методика исследования
Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.
Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.
В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:
- Записать функцию.
- Рассмотреть составные части.
- Если простой тип, перейти к 5 пункту.
- Сложная — разложить на простые элементы, а затем перейти к 5 пункту.
- Определить тип зависимости ее значения от аргумента: линейная или нелинейная. Если получен второй тип, то свойства пропорции применить невозможно.
- Определить тип линейности, построив график.
По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.
К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.
Универсальный алгоритм
Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:
- Записать соотношение пропорции.
- Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.
- Применить свойство умножения «крест-накрест».
- Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.
- Решить уравнение.
Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.
Уравнения с пропорцией
Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:
- Линейные.
- Квадратные.
- Кубические.
- Биквадратные.
Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.
Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:
- Два корня, когда D > 0: р1 = (-b — [D]^(½)) / 2a и р2 = (-b + [D]^(½)) / 2a.
- При D равном 0 (один): р = (-b) / 2a.
- Если D < 0, то решений нет.
Решение уравнений кубического и биквадратного видов сводятся к разложению на множители. В результате этого происходит понижение степени до двойки. Кроме того, эффективным методом нахождения корней считается введение замены переменной.
Пример решения
Решение уравнений в виде пропорции осуществляется по такому же принципу. При этом рекомендуется использовать любые свойства. Необходимо проходить процесс обучения постепенно. Начинать нужно с простых примеров, а затем практиковаться на сложных заданиях. Первый тип был рассмотрен выше на примере sin (p).
Итак, необходимо решить уравнение [(t — 5) / (t — 2)] = [(t — 5) / (t — 1)]. Для начала следует определить тип функций каждого из элементов. Просмотрев список нелинейных выражений, можно сделать вывод о том, что все члены пропорции являются линейными. Далее нужно решить равенства с неизвестными, находящихся в знаменателях: t1 = 2 и t2 = 1. Корни не являются решениями уравнения.
Затем следует воспользоваться третьим пунктом алгоритма: (t — 5)(t — 1) = (t — 2)(t — 5). Если раскрыть скобки, то должно получиться такое равенство: t 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.
Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.
Определение пропорции:
Связь между четырьмя алгебраическими выражениями А, В, С и D, имеющая вид
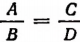
называется пропорцией.
(Равенство 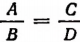
Примеры пропорции:
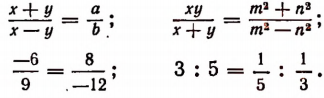
В пропорции 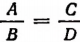
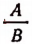
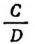
Главное свойство пропорции
Умножив левую и правую части пропорции
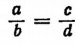
на произведение bd, получим ad = be, т. е. во всякой пропорции произведение крайних членов равно произведению средних.
Составление пропорции по данному равенству двух произведений
Пусть pq = ху. Разделив левую и правую части этого равенства на qx, получим
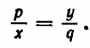
Этот результат можно сформулировать следующим образом.
Если произведение двух чисел равно произведению двух других, то из этих четырех чисел можно составить пропорцию, беря множители одного произведения за крайние, а множители другого произведения за средние члены пропорции. (При этом дополнительно требуется, чтобы оба последующих члена пропорции не оказались равными нулю.)
Перестановка членов пропорции
Пусть ad = be и числа а, b, с, d — все отличны от нуля. Разделив левую и правую части равенства ad = bc первый раз на bd, второй на ab, третий на ас и четвертый на cd, получим соответственно четыре пропорции:
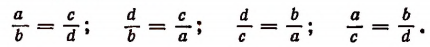
Поменяв местами отношения в этих равенствах, получим еще четыре пропорции:
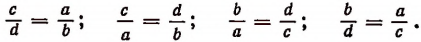
Этот результат показывает, что в пропорции можно менять местами средние и крайние члены и ставить оба крайних члена на места средних, а оба средних на места крайних.
Производные пропорции
1. Прибавив к левой и правой частям пропорции 
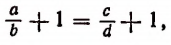
или
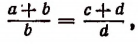
т. е. во всякой пропорции сумма членов первого отношения так относится к своему последующему, как сумма членов второго отношения — к своему последующему.
2. Вычтя из левой и правой частей пропорции 
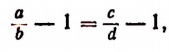
или
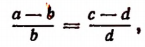
т. е. во всякой пропорции разность членов первого отношения так относится к своему последующему, как разность членов второго отношения — к своему последующему.
3. Разделив левую часть равенства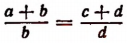
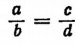
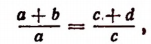
т. е. во всякой пропорции сумма членов первого отношения так относится к своему предыдущему, как сумма членов второго отношения — к своему предыдущему.
4. Разделив левую часть равенства 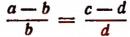

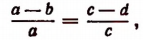
т. е. во всякой пропорции разность членов первого отношения так относится к своему предыдущему, как разность членов второго отношения —к своему предыдущему.
5. Разделив левую часть равенства 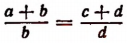
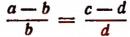
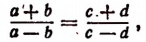
т. е. во всякой пропорции сумма членов первого отношения так относится к их разности, как сумма членов второго отношения — к их разности.
Из пропорции 

Например, умножив обе части пропорции 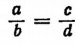
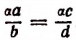
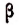
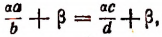
или
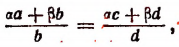
т. е. получим новую производную пропорцию.
Определение неизвестного члена пропорции
Пусть в пропорции 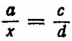
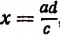
Примеры:
1. Найти неизвестное число х из пропорции 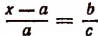
Составим производную пропорцию по правилу: сумма членов первого отношения так относится к своему последующему члену, как сумма членов второго отношения к своему последующему:
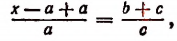
т. е.
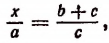
откуда
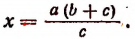
2. Найти неизвестное х из пропорции 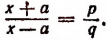
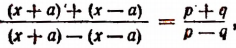
или
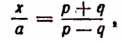
отсюда
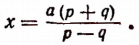
Ряд равных отношений
Иногда бывает удобно вместо различных букв употреблять для обозначения чисел одну и ту же букву, снабженную дополнительными значками — индексами. Например 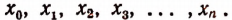
Основное свойство ряда равных отношений
Пусть имеется ряд равных отношений:
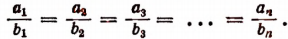
Обозначим общее значение всех этих отношений буквой k. Тогда
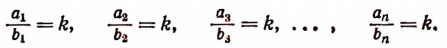
Отсюда
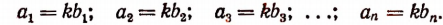
Складывая левые и правые части этих равенств, получим:
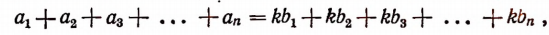
или
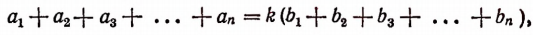
или
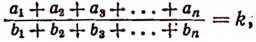
т.е.
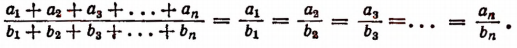
Итак, доказано следующее:
если несколько отношений равны друг другу, то отношение суммы их предыдущих членов к сумме последующих равно каждому из этих отношений.
Пример:
Пусть длины 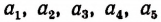
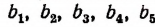
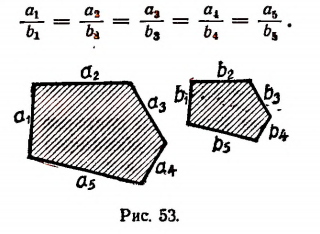
По свойству ряда равных отношений получим:
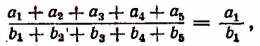
или
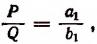
где Р и Q периметры многоугольников.
Прямая пропорциональность
Сначала рассмотрим несколько примеров.
Пример:
Пусть буква х обозначает в годах возраст сына, а буква у — возраст отца и пусть в данный момент сыну один год, а отцу 25 лет.
Составим таблицу значений х и соответствующих им значений буквы у. В третьей строке этой таблицы выпишем значения отношения 
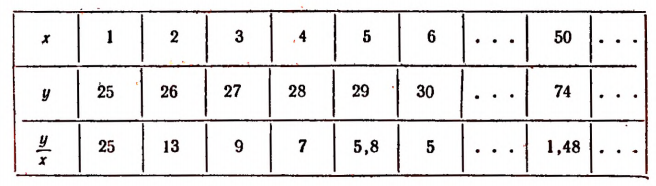
В этом примере отношение 
Пример:
Пусть буква х обозначает в сантиметрах длину стороны квадрата, а буква у — площадь квадрата в квадратных сантиметрах.
Составим таблицу, подобную предыдущей.
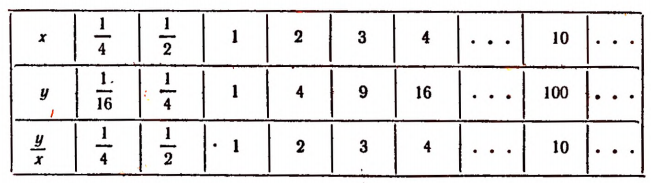
Отношение 
Пример:
Пусть буква х обозначает в кубических сантиметрах объем ртути при температуре 0°, а буква у — вес этой ртути в граммах. Известно, что 1 куб. см ртути при температуре 0° весит 13,6 г.
Опять составим таблицу значений х, у и 

Этот третий пример существенно отличается от двух предыдущих. Здесь отношение 
Определение:
Две величины у и х называются прямо пропорциональными (или просто пропорциональными), если при всех их возможных изменениях отношение 
Значит, вес ртути и объем ртути при постоянной температура являются величинами пропорциональными.
Возраст отца и возраст сына не пропорциональны.
Также не пропорциональны сторона квадрата и его площадь.
Пусть изменяющиеся величины у и х пропорциональны. Тогда отношение 
Обозначая это постоянное число буквой k, получим:
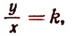
или
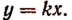
Следовательно, если величины у и х пропорциональны и отношение 
Число k называется коэффициентом пропорциональности (величины у по отношению к величине х).
Теперь докажем обратное положение. Пусть
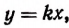
где k — постоянное число.
Отсюда следует, что при х = 0 и у = 0 и что 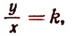
Из того что 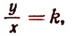
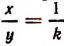
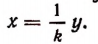
Если коэффициентом пропорциональности величины у по отношению к величине х служит постоянное число k, то коэффициентом пропорциональности величины х по отношению к величине у будет служить число 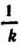
Приведем еще один пример пропорциональных величин. Путь s, пройденный при равномерном движении, пропорционален. времени t, т. е.
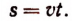
Здесь постоянное число v есть коэффициент пропорциональности величины s по отношению к величине t (v есть скорость равномерного движения).
Сделаем еще два замечания.
Замечание:
Если имеется два ряда чисел:

и

и если
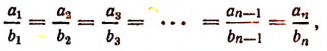
то числа одного из этих рядов называются пропорциональными числам другого ряда.
Замечание:
Если имеются только два постоянных числа а и b, то бессмысленно говорить о них, что они пропорциональны или не пропорциональны.
В этом случае можно интересоваться либо характером этих чисел, либо их разностью, либо их отношением и т. д.
В заключение решим две простые задачи на пропорциональные величины.
Задача:
На карте в масштабе 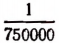
Решение:
Длина на карте прямо пропорциональна масштабу. Поэтому.

Задача:
С помощью непосредственного измерения установили, что при повышении температуры рельса на 24°С его длина увеличивается на 1,5 мм. Требуется вычислениями определить изменение длины рельса при понижении его температуры на 40°С. (Считать изменение длины рельса величиной, прямо пропорциональной изменению температуры.)
Решение:
Обозначив искомое изменение (в мм) буквой х, получим:
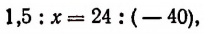
откуда
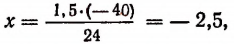
т. е. при понижении температуры рельса на 40°С его длина сократится на 2,5 мм.
Обратная пропорциональность
Сначала приведем примеры.
1. Рассмотрим изменяющийся прямоугольный параллелепипед с квадратным основанием, имеющий неизменный объем, равный 3600 куб. см (рис. 54).
Пусть буква х обозначает в сантиметрах изменяющуюся сторону основания, а буква у — изменяющуюся высоту параллелепипеда.
Рассматривая таблицу:
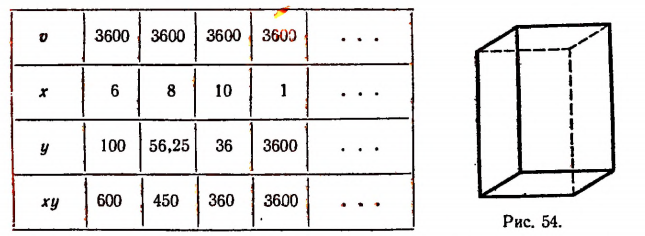
легко видеть, что произведение ху не остается неизменным при постоянстве объема.
2. Рассмотрим изменяющийся прямоугольник, имеющий неизменную площадь, равную 100 кв. см.
Пусть буква х обозначает одно изменяющееся измерение (например, длину прямоугольника), а буква у — другое изменяющееся измерение (ширину). Пусть х и у выражены в сантиметрах.
Так как произведение измерений прямоугольника равно его площади, то величины х и у при всех своих возможных изменениях будут давать в своем произведении число 100, т. е. произведение изменяющихся величин х и у будет оставаться неизменным.
Существенное отличие второго примера от первого заключается в том, что в нем произведение ху остается неизменным, в то время как в первом оно изменяется.
Определение:
Две величины х и у называются обратно пропорциональными, если при всех их возможных изменениях произведение ху остается равным одному и тому же числу.
Обозначая это число буквой k, получим
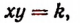
или
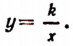
Следовательно, если величины х и у обратно пропорциональны, то величина у выражается через величину х по формуле следующего вида:
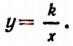
Число k называется коэффициентом обратной пропорциональности.
Длина прямоугольника и ширина прямоугольника при заранее заданной площади прямоугольника являются величинами обратно пропорциональными. Коэффициентом обратной пропорциональности служит как раз эта площадь.
Сторона основания прямоугольного параллелепипеда с квадратным основанием и высота параллелепипеда при заранее заданном объеме не являются величинами обратно пропорциональными.
Задача:
Зал освещается m лампами по а свечей каждая. Сколькими лампами в b свечей можно получить ту же освещенность зала?
Число ламп и число свечей каждой лампы при данной освещенности зала являются величинами обратно пропорциональными. Поэтому, обозначая число ламп в b свечей буквой x, получим

откуда
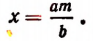
Пропорциональное деление
Задача:
Число А разделить на n слагаемых прямо пропорционально числам
Обозначим искомые слагаемые буквами 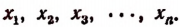
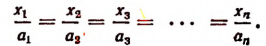
Пользуясь свойством ряда равных отношений, получим
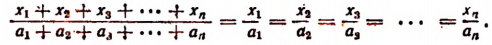
Но
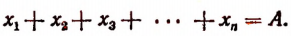
Поэтому
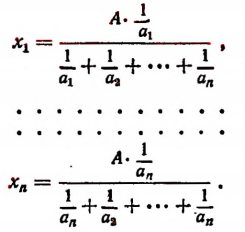
Задача:
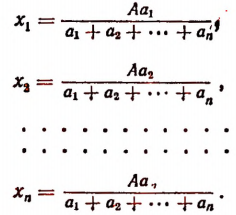
Число А разделить на n слагаемых обратно пропорционально числам
Обозначим искомые слагаемые буквами 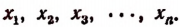
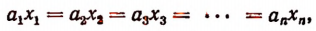
или
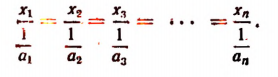
По свойству ряда равных отношений получим
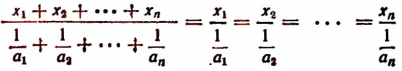
Но

Поэтому
Пропорции и пропорциональная зависимость
- Отношением числа а к числу b называется частное
, а называется предыдущим, b — последующим членом отношения.
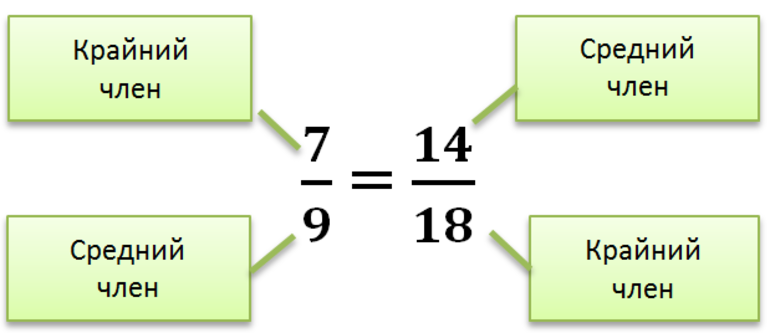
- Пропорцией называется равенство, каждая часть которого является отношением двух чисел. В пропорции
члены а и d называются крайними, а b и с средними.
При изложении свойств пропорции будем считать, что ни один из членов пропорции не равен нулю.
Пример:
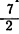
Пример:
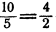
Главное свойство пропорции
Теорема:
Во всякой пропорции произведение крайних
членов равно произведению средних.
Доказательство:
Дана пропорция

Умножим обе части равенства (1) на bd, получим
Теорема доказана.
Теорема:
Если произведение двух чисел
равно произведению двух других чисел, то из этих четырех чисел можно составить пропорцию^ крайними членами которой являются сомножители одного из двух произведений, а средними—сомножители другого.
При этом предполагается, что ни один из сомножителей не равен нулю.
Доказательство:
Пусть
a, b, с, d все отличны от нуля. Разделим обе части равенства на bd, получим
Теорема доказана.
Пример:
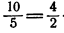
Пример:
8 • 9 = 3 • 24 — равенство двух произведений.
Разделим обе части этого равенства на 9 • 24, получим пропорцию
Определение неизвестного члена пропорции
Теорема:
Средний член пропорции равен произведению крайних, деленному на другой средний. Крайний член пропорции равен произведению средних, деленному на другой крайний.
Пусть

Покажем, что

На основании теоремы 1 имеем

Разделим обе части равенства (4) на с, получим равенство (2). Разделим обе части равенства (4) на d, получим равенство (3). Теорема доказана.
Пример:
Найти х, если
Решение:
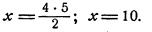
Пример:
Найти х, если 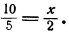
Решение:
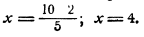
Перестановка членов пропорции
Теорема:
Во всякой пропорции можно переставить
средние члени, переставить крайние члени, переставить и средние члени и крайние, средние поставить на место крайних, а крайние на место средних.
Иными словами, если

то

(переставлены средние члены),

(в (1) переставлены крайние члены),

(в (1) переставлены и средние и крайние члены),

(средние поставлены на место крайних, крайние — на место средних).
Доказательство:
В пропорций (1)

Разделим обе части равенства (6) на cd, получим равенство (2). Точно так же, разделив обе части равенства (6) на аb, а затем на ас, получим равенства (3) и (4). Равенство (5) получается из равенства (4) посредством перестановки отношений. Теорема доказана.
Следствие:
Переставим отношения в равенствах (I), (2), (3), получим еще три пропорции
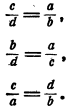
Таким образом, всякую пропорцию посредством перестановки ее членов можно представить в восьми различных видах.
Производные пропорции
Теорема:
1) Во всякой пропорции сумма членов первого отношения так относится к последующему члену этого отношения, как сумма членов второго отношения относится к своему последующему.
2) Во всякой пропорции разность членов первого отношения так относится к последующему члену этого отношения, как разность членов второго отношения относится к своему последующему.
Иными словами, если

то

Доказательство:
Прибавим к каждой части равенства (1)
по 1, получим равенство (2). Вычтем из каждой части равенства (1) по 1, получим равенство (3). Теорема доказана.
Теорема:
1) Во всякой пропорции сумма членов первого отношения так относится к предыдущему члену этого отношения, как сумма членов второго отношения относится к своему предыдущему.
2) Во всякой пропорции разность членов первого отношения так относится к предыдущему члену этого отношения, как разность членов второго отношения относится к своему предыдущему.
Иными словами, если
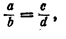
то

Доказательство:
Разделим равенство (2) почленно на
равенство (1), т. е., левую часть равенства (2) разделим на левую часть равенства (1), а правую часть равенства (2) на правую часть равенства (1). Получим равенство (4). Разделив равенство (3) почленно на равенство (1), получим равенство 5). Теорема доказана.
Теорема:
Во всякой пропорции сумма членов первого
отношения так относится к их разности, как сумма членов второго отношения относится к их разности, если только эти разности отличны от нуля.
Иными словами, если
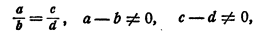
то

Доказательство:
Разделив почленно равенство (4) на
равенство (5), получим равенство (6).
Ряд равных отношений
Теорема:
Если даны несколько равных отношений* то
сумма всех предыдущих членов отношений относится к сумме всех последующих как любой из предыдущих к своему последующему.
Доказательство:
Пусть имеется несколько равных отношений
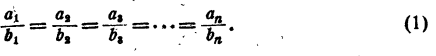
Обозначим результат деления 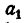
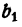
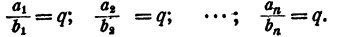
Отсюда
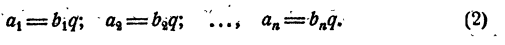
Сложив почленно все равенства (2), имеем
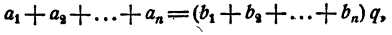
откуда
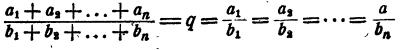
Теорема доказана.
Задача:
Дано, что
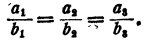
Доказать, что при любых 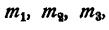
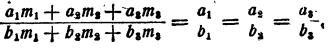
Решение:
Умножим каждый, член первого отношения на 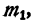
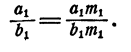
Точно так же
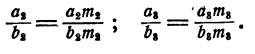
Значит,
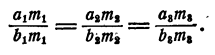
На основании теоремы 8 имеем
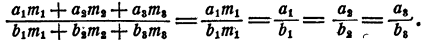
Задача:
Решить уравнение
Решение:
Пользуясь теоремой 7 § 5, имеем
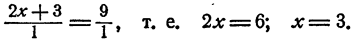
Пропорциональная зависимость
Мы много раз составляли уравнения, выражающие зависимость между величинами, и могли наблюдать, что. зависимости эти бывают весьма разнообразны.
При решении многих задач мы встречаемся с двумя величинами, зависимость между которыми такова, что при изменении этих величин их отношение остается неизменным. Такие величины называются прямо пропорциональными, а зависимость между ними — пропорциональной зависимостью.
Для примера приведем несколько задач, в которых мы встретимся с величинами, находящимися в пропорциональной зависимости.
Задача:
Скорость течения реки 3 км в час. Плот за t часов прошел вниз по реке S км. Составить уравнение, выражающее зависимость между S и t.
Ответ. S = 3t.
Задача:
С каждого гектара собрано 30 ц ржи и, таким образом, с k га собрано А ц. Составить уравнение, выражающее зависимость между А и k.
Ответ. А = 30k
Задача:
Основание прямоугольника 2 см, высота h см, площадь Q 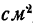
Ответ. Q = 2h.
Задача:
1 м материи стоит 20 руб. За m м этой материи
уплатили N pyб. Составить уравнение, выражающее зависимость между N и m.
Ответ. N=20m.
Мы рассмотрели четыре задачи, которые по своему содержанию относятся к различным областям практической деятельности. Нетрудно убедиться, что в каждой из этих задач мы действительно имеем дело с прямо пропорциональными величинами.
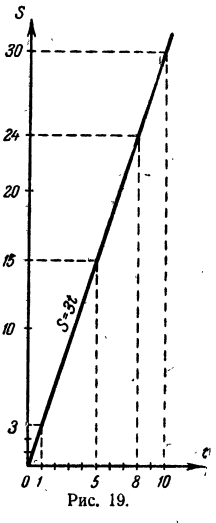
Так, в первой задаче отношение расстояния (в kм), пройденного плотом, к времени (в часах), в течение которого плот находился в пути, всегда одно и то же и равно 3. Поэтому расстояние, которое проходит плот вниз по реке, пропорционально времени, в течение которого плот находится в пути, при условии, что скорость течения реки повсюду одна и та же.
Точно так же во второй задаче количество ржи, собранной с нескольких гектаров, пропорционально количеству ржи, собранной с одного гектара, при условии, что с каждого гектара собрано по одному и тому же количеству ржи и т. д.
Заметим, что уравнения, к которым мы пришли в рассмотренных задачах, имеют один и тот же вид. В этих уравнениях одна, из величин равна произведению некоторого числового множителя на другую величину. Этот множитель называется коэффициентом пропорциональности. В первой задаче коэффициент
пропорциональности равен 3, во второй задаче он равен 30, в третьей задаче он равен 2, в четвертой задаче он равен 20.
Таким образом, пропорциональная зависимость между величинами всегда выражается уравнением y = kx, где k — коэффициент пропорциональности. Известно, что зависимость между двумя величинами может быть наглядно представлена таблицей, а затем и графиком.
Для примера представим таблицей зависимость, выражаемую уравнением S = 3/ (первая задача):
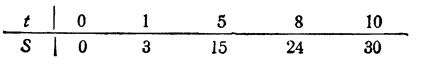
Построим график зависимости S = 3t (рис. 19). Обратим внимание на следующие обстоятельства:
- Отношение чисел, находящихся в одном столбце таблицы, повсюду одно и то же и равно коэффициенту пропорциональности:
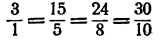
и т. д. (для первого столбца это отношение не имеет смысла; так как на нуль делить нельзя).
2, График представляет собой луч, выходящий из начала координат (при t= 0, S = 0). (Доказательство этого утверждения здесь провести нельзя, так как для этого требуются некоторые сведения из геометрии.)
То же самое можно наблюдать и при графическом представлении любой другой пропорциональной зависимости между двумя величинами.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Математика
6 класс
Урок № 5
Пропорции
Перечень рассматриваемых вопросов:
- Понятие пропорции.
- Основное свойство пропорции.
- Как правильно составить пропорцию.
- Как найти неизвестный член пропорции.
Тезаурус
Равенство двух отношений называют пропорцией.
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.
Рассмотрим 3 способа нахождения неизвестного члена пропорции.
1 способ.
2 способ.
Способ 3.
Задача.
Решение:
Ответ:
1) можно;
2) можно;
3) нельзя;
4) нельзя.
Разбор решения заданий тренировочного модуля
№1. Тип задания: сортировка элементов по категориям.
№2. Тип задания: Подстановка элементов в пропуски в тексте.
Найдите неизвестный член пропорции.
Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.
Ответ: 3.










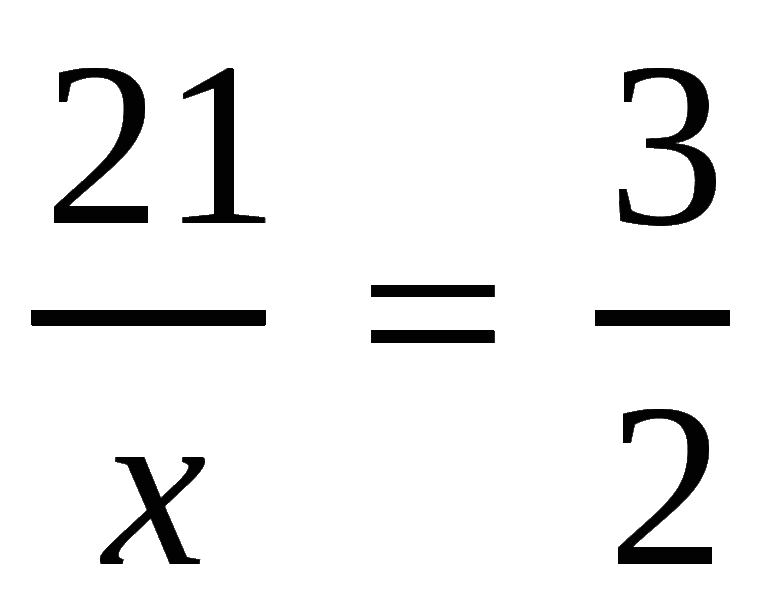



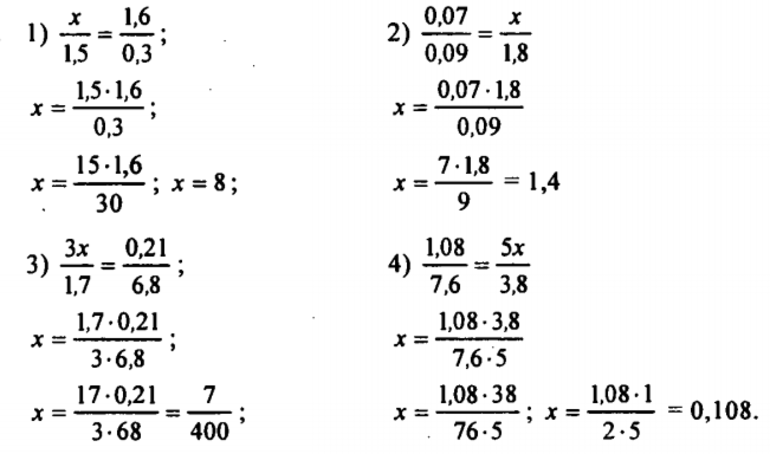


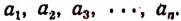
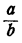 , а называется предыдущим, b — последующим членом отношения.
, а называется предыдущим, b — последующим членом отношения.