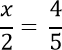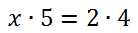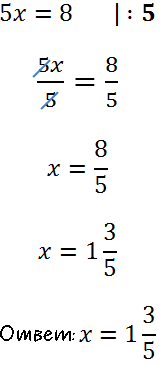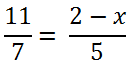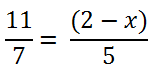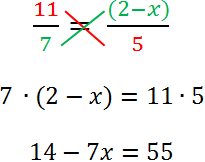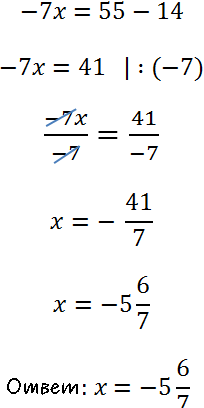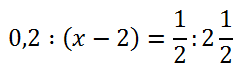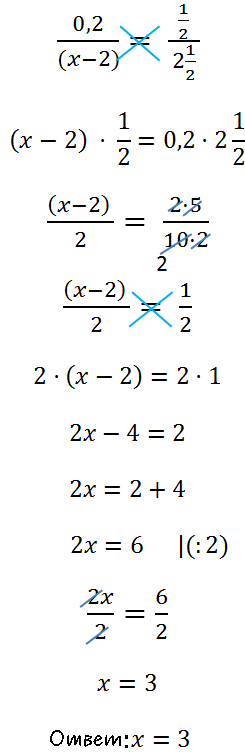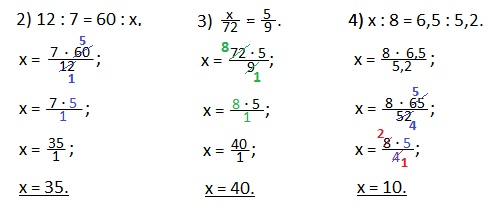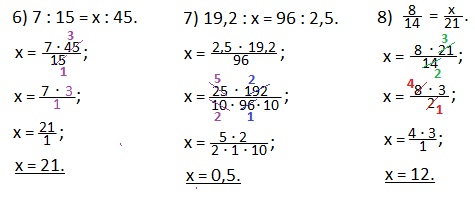Пропорции
- Члены пропорции: крайние и средние
- Главное свойство пропорции
- Нахождение неизвестного члена пропорции
Равенство двух отношений называется пропорцией.
Пример.
10 : 5 = 6 : 3
или
Пропорцию
a : b = c : d
или
можно прочитать так: отношение a к b равно отношению c к d
, или a относится к b, как c относится к d
.
Члены пропорции: крайние и средние
Члены отношений, составляющих пропорцию, называются членами пропорции. Числа a и d называют крайними членами пропорции, а числа b и c — средними членами пропорции:
Эти названия условны, так как достаточно написать пропорцию в обратном порядке (переставить отношения местами):
c : d = a : b
или
и крайние члены станут средними, а средние — крайними.
Главное свойство пропорции
Произведение крайних членов пропорции равно произведению средних.
Пример. Рассмотрим пропорцию
Если воспользоваться вторым свойством равенства и умножить обе её части на произведение bd (для приведения обеих частей равенства от дробного вида к целому), то получим:
Сокращаем дроби и получаем:
ad = cb.
Из главного свойства пропорции следует:
- Крайний член равен произведению средних, разделённому на другой крайний. То есть для пропорции
:
- Средний член равен произведению крайних, разделённому на другой средний. То есть для пропорции :
:
Нахождение неизвестного члена пропорции
Свойства пропорции позволяют найти любой из членов пропорции, если он неизвестен. Рассмотрим пропорцию:
x : 8 = 6 : 3.
Тут неизвестен крайний член. Так как крайний член равен произведению средних, разделённому на другой крайний, то
x = (8 · 6) : 3 = 16.
В случае, когда необходимо определить один неизвестный член пропорции, говорят, что надо решить пропорцию.
Рассмотрим пропорции, в которых надо найти крайний член.
Любой крайний член пропорции равен произведению средних членов, делённому на другой крайний член пропорции.
Решение.
а) Применив основное свойство пропорции и сократив, получим:
t8=1016;t⋅16=8⋅10;t=81⋅10162=1⋅10521=51=5;t=5¯¯.
б) Применим основное свойство пропорции и сократим на (2), тогда получим:
23=8x;2⋅x=3⋅8;x=3⋅8421=3⋅41=12;x=12.¯¯
Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию.
Например, рассмотрим такое уравнение.
Для решения уравнения с пропорцией используют правило пропорции или,
как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке
«Пропорции».
В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Правило пропорции или правило креста
Запомните!
Произведение крайних членов пропорции равно произведению средних.
По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции,
то произведения членов пропорции, которые лежат на концах креста, равны .
Вернемся к нашему уравнению. Решим его, использую правило пропорции.
Нарисуем поверх пропорции крест.
Теперь по правилу пропорции (правило креста) запишем пропорцию
в виде равенства произведений крайних и средних членов пропорции.
Вспомним правило деления и
решим уравнение до конца.
В ответе не забудем выделить целую часть у дроби.
Рассмотрим другой пример уравнения с пропорцией.
Такое уравнение также решается с помощью правила пропорции.
Важно!
Если в члене пропорции присутствуют знаки «+» или «−»,
обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда
будете использовать правило пропорции.
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции
для дальнейшего решения.
Теперь раскроем скобки с помощью
правила раскрытия
скобок.
Из урока «Решение линейных уравнений» используем
правило переноса и
правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать
правило знаков.
Иногда уравнения с пропорцией могут быть представлены следующим образом:
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение,
в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.
Другие примеры решения уравнений с пропорцией
-
=
18 · x = 6 · 3x
18x = 18x
18x − 18x = 0
0 = 0
Ответ: x — любое число
-
=
3x · 6,8 = 0,21 · 1,7
20,4 x=
·
20
x =
=204x · 1000 = 21 · 17 · 10 |:(204 · 1000)
x =
x =
x =
x =
x =
Ответ: x =
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
Пропорции
Пропорции — это сильный инсрумент, который бывает полезен вплоть до 11 класса. Преимущество пропорций в том, что алгоритм нахождения неизвестного члена пропорции хорошо запоминается.
Пропорция
Пропорция — это равенство двух отношений. Пример пропорции:
4/12 = 9/27. 4 и 27 называются крайние члены пропорции, а 12 и 9 — называются средние члены пропорции.
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов. То есть, пропорцию
4/12 = 9/27
мы можем записать по-другому:
4 × 27 = 12 × 9.
Как найти средний член пропорции?
Средний член пропорции равен произведению крайних членов делённому на другой средний член. То есть, пропорцию
4/? = 9/27
мы можем записать по-другому — вот так:
? = 4 × 27/9
или пропорцию
4/12 = ?/27
мы можем записать по-другому — вот так:
? = 4 × 27/12
Как найти крайний член пропорции?
Крайний член пропорции равен произведению средних членов, делённому на другой крайний член. То есть, пропорцию
?/12 = 9/27
мы можем записать по-другому — вот так:
? = 12 × 9/27
или пропорцию
4/12 = 9/?
мы можем записать по-другому — вот так:
? = 12 × 9/4
На чтение 3 мин. Просмотров 17.4k.
Равенство двух отношений называют пропорцией.
Тема: «Отношение» рассмотрена на предыдущем занятии («6.1. Отношение»).
a:b=c:d. Это пропорция. Читают: а так относится к b, как c относится к d. Числа a и d называют крайними членами пропорции, а числа b и c – средними членами пропорции.
Пример пропорции: 12 : 3 = 16 : 4. Это равенство двух отношений: 12:3=4 и 16:4=4. Читают: двенадцать так относится к трем, как шестнадцать относится к четырем. Здесь 12 и 4 -крайние члены пропорции, а 3 и 16 — средние члены пропорции.
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов.
Для пропорции a:b=c:d или a/b=c/d основное свойство записывается так: a·d=b·c.
Для нашей пропорции 12 : 3 = 16 : 4 основное свойство запишется так: 12·4=3·16. Получается верное равенство: 48=48.
Чтобы найти неизвестный крайний член пропорции, нужно произведение средних членов пропорции разделить на известный крайний член.
Примеры. Найти неизвестный крайний член пропорции.
1) х : 20 = 2 : 5. У нас х и 5 — крайние члены пропорции, а 20 и 2 — средние.
Решение.
х = (20·2):5 — нужно перемножить средние члены (20 и 2) и результат разделить на известный крайний член (число 5);
х = 40 : 5 — произведение средних членов (40) разделим на известный крайний член (5);
х = 8. Получили искомый крайний член пропорции.
Удобнее записывать нахождение неизвестного члена пропорции с помощью обыкновенной дроби. Вот как тогда запишется рассмотренный нами пример:
Искомый крайний член пропорции (х) будет равен произведению средних членов (20 и 2), деленному на известный крайний член (5).
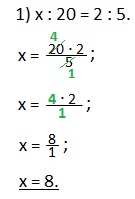
Сокращаем дробь на 5 (делим на 5 и числитель и знаменатель дроби). Находим значение х.
Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»
Еще такие примеры на нахождение неизвестного крайнего члена пропорции.
Чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов пропорции разделить на известный средний член.
Примеры. Найти неизвестный средний член пропорции.
5) 9 : х = 3 : 14. Число 3 — известный средний член данной пропорции, числа 9 и 14 — крайние члены пропорции.
Решение.
х = (9·14):3 — перемножим крайние члены пропорции и результат разделим на известный средний член пропорции;
х= 136:3;
х=42.
Решение этого примера можно записать иначе:
Искомый средний член пропорции (х) будет равен произведению крайних членов (9 и 14), деленному на известный средний член (3).
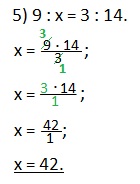
Сокращаем дробь на 3 (делим на 3 и числитель и знаменатель дроби). Находим значение х.
Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»
Еще такие примеры на нахождение неизвестного среднего члена пропорции.
