Персональные компьютеры, ноутбуки, смартфоны и другие гаджеты обмениваются информацией, используя кабельные, оптоволоконные и другие каналы связи.
Передача информации в общем виде выглядит следующим образом.
Рис. (1). Передача информации
Скорость передачи информации — это скорость, с которой передаются данные через канал связи, показывающая, какое количество бит информации передаётся за единицу времени.
Базовой единицей измерения скорости передачи информации является бит в секунду и обозначается бит/с.
Пропускная способность канала — одна из важных характеристик каналов передачи информации, которая показывает, какова максимальная скорость передачи информации по каналу связи в единицу времени.
С другой стороны, пропускная способность канала — это количество информации, передаваемое в единицу времени.
, где (V) — пропускная способность канала; (I) — объём переданной информации; (t) — время передачи информации.
Основные единицы измерения пропускной способности канала: бит/с; Кбит/с; Мбит/с.
Дополнительные единицы измерения: байт/с; Кбайт/с; Мбайт/с.
| (1) байт/с | (8) бит/с |
| (1) Кбит/с | (1024) бит/с |
| (1) Мбит/с | (1024) Кбит/с |
| (1) Гбит/с | (1024) Мбит/с |
При решении задач используется формула
I=V
·t
, где (V) — пропускная способность канала; (I) — объём переданной информации; (t) — время передачи информации.
Если скорость передачи информации задана в бит/с, а размер файла — в мегабайтах, то следует привести все единицы в один формат и только после этого делать вычисления.
Источники:
Рис. 1. Передача информации. © ЯКласс.
From Wikipedia, the free encyclopedia
Channel capacity, in electrical engineering, computer science, and information theory, is the tight upper bound on the rate at which information can be reliably transmitted over a communication channel.
Following the terms of the noisy-channel coding theorem, the channel capacity of a given channel is the highest information rate (in units of information per unit time) that can be achieved with arbitrarily small error probability. [1][2]
Information theory, developed by Claude E. Shannon in 1948, defines the notion of channel capacity and provides a mathematical model by which it may be computed. The key result states that the capacity of the channel, as defined above, is given by the maximum of the mutual information between the input and output of the channel, where the maximization is with respect to the input distribution. [3]
The notion of channel capacity has been central to the development of modern wireline and wireless communication systems, with the advent of novel error correction coding mechanisms that have resulted in achieving performance very close to the limits promised by channel capacity.
Formal definition[edit]
The basic mathematical model for a communication system is the following:
where:
Let 






which, in turn, induces a mutual information 
where the supremum is taken over all possible choices of 
Additivity of channel capacity[edit]
Channel capacity is additive over independent channels.[4] It means that using two independent channels in a combined manner provides the same theoretical capacity as using them independently.
More formally, let 





We define the product channel 

This theorem states:
Proof
We first show that 
Let 







By definition 
Since 






For now we only need to find a distribution 







ie. 
Now let us show that 
Let 









By definition of mutual information, we have

Let us rewrite the last term of entropy.

By definition of the product channel, 
For a given pair 

![{displaystyle {begin{aligned}H(Y_{1},Y_{2}|X_{1},X_{2}=x_{1},x_{2})&=sum _{(y_{1},y_{2})in {mathcal {Y}}_{1}times {mathcal {Y}}_{2}}mathbb {P} (Y_{1},Y_{2}=y_{1},y_{2}|X_{1},X_{2}=x_{1},x_{2})log(mathbb {P} (Y_{1},Y_{2}=y_{1},y_{2}|X_{1},X_{2}=x_{1},x_{2}))\&=sum _{(y_{1},y_{2})in {mathcal {Y}}_{1}times {mathcal {Y}}_{2}}mathbb {P} (Y_{1},Y_{2}=y_{1},y_{2}|X_{1},X_{2}=x_{1},x_{2})[log(mathbb {P} (Y_{1}=y_{1}|X_{1}=x_{1}))+log(mathbb {P} (Y_{2}=y_{2}|X_{2}=x_{2}))]\&=H(Y_{1}|X_{1}=x_{1})+H(Y_{2}|X_{2}=x_{2})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/733594496825a6d2bf9543f0df96fe19033e9c58)
By summing this equality over all 

We can now give an upper bound over mutual information:

This relation is preserved at the supremum. Therefore
Combining the two inequalities we proved, we obtain the result of the theorem:
Shannon capacity of a graph[edit]
If G is an undirected graph, it can be used to define a communications channel in which the symbols are the graph vertices, and two codewords may be confused with each other if their symbols in each position are equal or adjacent. The computational complexity of finding the Shannon capacity of such a channel remains open, but it can be upper bounded by another important graph invariant, the Lovász number.[5]
Noisy-channel coding theorem[edit]
The noisy-channel coding theorem states that for any error probability ε > 0 and for any transmission rate R less than the channel capacity C, there is an encoding and decoding scheme transmitting data at rate R whose error probability is less than ε, for a sufficiently large block length. Also, for any rate greater than the channel capacity, the probability of error at the receiver goes to 0.5 as the block length goes to infinity.
Example application[edit]
An application of the channel capacity concept to an additive white Gaussian noise (AWGN) channel with B Hz bandwidth and signal-to-noise ratio S/N is the Shannon–Hartley theorem:
C is measured in bits per second if the logarithm is taken in base 2, or nats per second if the natural logarithm is used, assuming B is in hertz; the signal and noise powers S and N are expressed in a linear power unit (like watts or volts2). Since S/N figures are often cited in dB, a conversion may be needed. For example, a signal-to-noise ratio of 30 dB corresponds to a linear power ratio of 
Channel capacity in wireless communications[edit]
This section[6] focuses on the single-antenna, point-to-point scenario. For channel capacity in systems with multiple antennas, see the article on MIMO.
Bandlimited AWGN channel[edit]
AWGN channel capacity with the power-limited regime and bandwidth-limited regime indicated. Here, 
If the average received power is 


[bits/s],
where 
When the SNR is large (SNR ≫ 0 dB), the capacity 
When the SNR is small (SNR ≪ 0 dB), the capacity 
The bandwidth-limited regime and power-limited regime are illustrated in the figure.
Frequency-selective AWGN channel[edit]
The capacity of the frequency-selective channel is given by so-called water filling power allocation,
where 



Slow-fading channel[edit]
In a slow-fading channel, where the coherence time is greater than the latency requirement, there is no definite capacity as the maximum rate of reliable communications supported by the channel, 


,
in which case the system is said to be in outage. With a non-zero probability that the channel is in deep fade, the capacity of the slow-fading channel in strict sense is zero. However, it is possible to determine the largest value of 



Fast-fading channel[edit]
In a fast-fading channel, where the latency requirement is greater than the coherence time and the codeword length spans many coherence periods, one can average over many independent channel fades by coding over a large number of coherence time intervals. Thus, it is possible to achieve a reliable rate of communication of 
Feedback Capacity[edit]
Feedback capacity is the greatest rate at which information can be reliably transmitted, per unit time, over a point-to-point communication channel in which the receiver feeds back the channel outputs to the transmitter. Information-theoretic analysis of communication systems that incorporate feedback is more complicated and challenging than without feedback. Possibly, this was the reason C.E. Shannon chose feedback as the subject of the first Shannon Lecture, delivered at the 1973 IEEE International Symposium on Information Theory in Ashkelon, Israel.
The feedback capacity is characterized by the maximum of the directed information between the channel inputs and the channel outputs, where the maximization is with respect to the causal conditioning of the input given the output. The directed information was coined by James Massey[8] in 1990, who showed that its an upper bound on feedback capacity. For memoryless channels, Shannon showed[9] that feedback does not increase the capacity, and the feedback capacity coincides with the channel capacity characterized by the mutual information between the input and the output. The feedback capacity is known as a closed-form expression only for several examples such as: the Trapdoor channel,[10] Ising channel,[11][12] the binary erasure channel with a no-consecutive-ones input constraint, NOST channels.
The basic mathematical model for a communication system is the following:
Communication with feedback
Here is the formal definition of each element (where the only difference with respect to the nonfeedback capacity is the encoder definition):
That is, for each time 



![{displaystyle {mathcal {W}}=[1,2,dots ,2^{nR}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8165bbe91b46c99cc81c985199b5716f42fecb48)





The feedback capacity is denoted by 
Main results on feedback capacity[edit]
Let 





![{displaystyle I(X^{N}rightarrow Y^{N})=mathbf {E} left[log {frac {P(Y^{N}||X^{N})}{P(Y^{N})}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a80fd8f7886755bdf075cf0837f6649b3f1c526a)
The feedback capacity is given by
,
where the supremum is taken over all possible choices of 
Gaussian feedback capacity[edit]
When the Gaussian noise is colored, the channel has memory. Consider for instance the simple case on an autoregressive model noise process 

Solution techniques[edit]
The feedback capacity is difficult to solve in the general case. There are some techniques that are related to control theory and Markov decision processes if the channel is discrete.
See also[edit]
- Bandwidth (computing)
- Bandwidth (signal processing)
- Bit rate
- Code rate
- Error exponent
- Nyquist rate
- Negentropy
- Redundancy
- Sender, Data compression, Receiver
- Shannon–Hartley theorem
- Spectral efficiency
- Throughput
Advanced Communication Topics[edit]
- MIMO
- Cooperative diversity
External links[edit]
- «Transmission rate of a channel», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- AWGN Channel Capacity with various constraints on the channel input (interactive demonstration)
References[edit]
- ^ Saleem Bhatti. «Channel capacity». Lecture notes for M.Sc. Data Communication Networks and Distributed Systems D51 — Basic Communications and Networks. Archived from the original on 2007-08-21.
- ^ Jim Lesurf. «Signals look like noise!». Information and Measurement, 2nd ed.
- ^ Thomas M. Cover, Joy A. Thomas (2006). Elements of Information Theory. John Wiley & Sons, New York. ISBN 9781118585771.
- ^ Cover, Thomas M.; Thomas, Joy A. (2006). «Chapter 7: Channel Capacity». Elements of Information Theory (Second ed.). Wiley-Interscience. pp. 206–207. ISBN 978-0-471-24195-9.
- ^ Lovász, László (1979), «On the Shannon Capacity of a Graph», IEEE Transactions on Information Theory, IT-25 (1): 1–7, doi:10.1109/tit.1979.1055985.
- ^ David Tse, Pramod Viswanath (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK, ISBN 9780521845274
- ^ The Handbook of Electrical Engineering. Research & Education Association. 1996. p. D-149. ISBN 9780878919819.
- ^ Massey, James (Nov 1990). «Causality, Feedback and Directed Information» (PDF). Proc. 1990 Int. Symp. On Information Theory and Its Applications (ISITA-90), Waikiki, HI.: 303–305.
- ^ Shannon, C. (September 1956). «The zero error capacity of a noisy channel». IEEE Transactions on Information Theory. 2 (3): 8–19. doi:10.1109/TIT.1956.1056798.
- ^ Permuter, Haim; Cuff, Paul; Van Roy, Benjamin; Weissman, Tsachy (July 2008). «Capacity of the trapdoor channel with feedback» (PDF). IEEE Trans. Inf. Theory. 54 (7): 3150–3165. arXiv:cs/0610047. doi:10.1109/TIT.2008.924681. S2CID 1265.
- ^ Elishco, Ohad; Permuter, Haim (September 2014). «Capacity and Coding for the Ising Channel With Feedback». IEEE Transactions on Information Theory. 60 (9): 5138–5149. doi:10.1109/TIT.2014.2331951.
- ^ Aharoni, Ziv; Sabag, Oron; Permuter, Haim H. (September 2022). «Feedback Capacity of Ising Channels With Large Alphabet via Reinforcement Learning». IEEE Transactions on Information Theory. 68 (9): 5637–5656. doi:10.1109/TIT.2022.3168729.
- ^ Permuter, Haim Henry; Weissman, Tsachy; Goldsmith, Andrea J. (February 2009). «Finite State Channels With Time-Invariant Deterministic Feedback». IEEE Transactions on Information Theory. 55 (2): 644–662. arXiv:cs/0608070. doi:10.1109/TIT.2008.2009849. S2CID 13178.
департамент
образования вологодской области
бюджетное
профессиональное образовательное учреждение Вологодской области
«Череповецкий многопрофильный колледж»
УРОК ПО ИНОФОРМАТИКЕ НА
ТЕМУ
«СКОРОСТЬ ПЕРЕДАЧИ
ИНФОРМАЦИИ.
ПРОПУСКНАЯ СПОСОБНОСТЬ»
Череповец
2021 г.
Организация-разработчик: бюджетное профессиональное
образовательное учреждение Вологодской области «Череповецкий многопрофильный
колледж»
Разработчик:
Меледичева Т.С — преподаватель первой квалификационной
категории.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Краткая аннотация: Разработка представляет собой урок, который проводится для обучающихся
1-ых курсов СПО и нацеленный на углубленное изучение темы «Организация
глобальных сетей». Материал включает в себя вводную лекцию, примеры и
контрольные задания.
Тип занятия: комбинированный.
Цели:
Образовательная: усвоить
понятия пропускной способности, скорости передачи данных и канала связи,
отработать знания и умения по переводу чисел из более крупных единиц в мелкие и
наоборот.
Воспитательная:
воспитывать стремление к самостоятельному решению задач и способности к
самостоятельному применению знаний и умений для решения задач, формирование
культуры поведения и привитие интереса к теме занятия через осознание
значимости полученных знаний в жизни.
Развивающая: развитие
логического мышления через умение устанавливать логические
взаимосвязи, аналитических способностей через умение сравнивать,
внимательности и самостоятельности через самоконтроль, самоорганизацию и
взаимоконтроль.
Развивать ключевые
компетенции, в том числе:
· учебно-познавательную как
способность к самостоятельной познавательной деятельности, владение знаниями и
умениями организации, планирования, рефлексии и самооценки
учебно-познавательной деятельности;
· компетенцию
личностного самосовершенствования как
стремление к интеллектуальному саморазвитию и владению навыками эмоциональной
саморегуляции;
· профессиональную
компетенцию как способность использовать знания
и профессиональные умения на практике.
Оборудование:
компьютер, интерактивная доска, проектор.
Время: 90 мин.
СКОРОСТЬ ПЕРЕДАЧИ ИНФОРМАЦИИ И ПРОПУСКНАЯ
СПОСОБНОСТЬ
КАНАЛА
СВЯЗИ
Теория:
Обмен
информацией производится по каналам передачи информации.
Каналы
передачи информации могут использовать различные физические принципы. Так, при
непосредственном общении людей информация передаётся с помощью звуковых волн, а
при разговоре по телефону — с помощью электрических сигналов, которые
распространяются по линиям связи.
Канал связи —
технические средства, позволяющие осуществлять передачу данных на расстоянии.
Компьютеры
могут обмениваться информацией с использованием каналов связи различной
физической природы: кабельных, оптоволоконных, радиоканалов и др.
Скорость передачи информации (скорость
информационного потока) — количество
информации, передаваемое за единицу времени.
Общая
схема передачи информации включает в себя отправителя информации, канал
передачи информации и получателя информации.
Основной
характеристикой каналов передачи информации является их пропускная
способность.
Пропускная способность канала —
максимальная скорость передачи информации по каналу связи в единицу времени.
Пропускная
способность канала равна количеству информации, которое может передаваться по
нему в единицу времени.
Объем
переданной информации V вычисляется по формуле:
V=qt
где q —
пропускная способность канала (в битах в секунду или подобных единицах),
а t— время передачи.
Обычно
пропускная способность измеряется в битах в секунду (бит/с) и кратных
единицах Кбит/с и Мбит/с.
Однако
иногда в качестве единицы используется байт в секунду (байт/с) и кратные ему
единицы Кбайт/с иМбайт/с.
Соотношения
между единицами пропускной способности канала передачи информации такие же, как
между единицами измерения количества информации:
1 байт/с = 23 бит/с = 8 бит/с;
1 Кбайт/с = 210 байт/с = 1024 байт/с;
1 Мбайт/с = 210 Кбайт
/с = 1024 Кбайт/с;
1 Гбайт/с = 210 Мбайт/с = 1024 Мбайт/с.
Рис. 1. Перевод единиц измерения
информации
ПРИМЕРЫ
П
р и м е р 1. Скорость передачи данных через ADSL-соединение равна
1 024 000 бит/c. Передача файла через данное соединение заняла 5
секунд. Определите размер файла в Кбайт.
|
Дано: |
Решение: |
|
q t V— |
V Переведем Ответ: 625 |
П
р и м е р 2.Какое количество байтов будет передаваться за 1 секунду по
каналу передачи информации с пропускной способностью 100 Мбит/с?
|
Дано: |
Решение: |
|
q t V |
V Переведем V Для Ответ: 12,5 |
П
р и м е р 3. Скорость передачи данных составляет 56 000 бит/c. Необходимо
передать файл размером 280 000 байт. Определите время передачи файла в
секундах.
|
Дано: |
Решение: |
|
q V t |
Ответ: 40 |
П р и м е р 4.Максимальная
скорость передачи данных по модемному протоколу V.92 составляет
56 000 бит/c. Какое максимальное количество байт можно передать за 5
секунд по этому протоколу?
|
Дано: |
Решение: |
|
q t V |
Ответ: 35 |
П р и м е р 5: Сколько секунд потребуется модему,
передающему информацию со скоростью 14 400 бит/с, чтобы передать
цветное растровое изображение размером 800×600 пикселей, при условии, что
в палитре 256 цветов. Результат представьте целым числом.
|
Дано: |
Решение: |
|
q 800×600 пикселей Палитра t |
1) Используем формулу N = 2i, где N — 256 = 2i то есть вес одного пикселя i = 8 бит. 2) Всего пикселей K = x * y = 800 · 600 Найдем объем растрового изображения по формуле: V = K * i, где V — объем, K — количество пикселей, i — вес V = 800 * 600 * 8 =3 840 000 3) Теперь воспользуемся формулой V = q Ответ: 267 c |
П
р и м е р 6:Сколько секунд потребуется модему, передающему сообщения со
скоростью 28800бит/с, чтобы передать 100 страниц текста
в 30 строк по 60 символов каждая, при условии, что каждый символ
кодируется 1 байтом?
Р
е ш е н и е. Вычислим объем файла в битах
V=100⋅30⋅60⋅8 бит =1440000 бит
весит
файл из 100 страниц текста в 30 строк по 60 символов каждая, при
условии, что каждый символ кодируется 1 байтом
Скорость
передачи сообщения q=28800бит/с.
О
т в е т: 50 секунд
П
р и м е р 7: Данные объемом 100 Мбайт передаются из
пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 220 бит
в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему
скорость передачи данных 222 бит в секунду. Задержка в пункте Б
(время между окончанием приема данных из пункта А и началом передачи в пункт В)
составляет 24 секунды. Сколько времени (в секундах) прошло с момента начала
передачи данных из пункта А до их полного получения в пункте В?
В
ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.
Построим
диаграмму Ганта, которая показывает все этапы передачи данных из пункта А в
пункт В (рис. .2).
Рис.
2. Пояснение к примеру 7
|
Дано: |
Решение: |
|
Дано: V = 100 Мбайт Найти |
переводим 100 вычисляем вычисляем общее
Ответ: |
САМОСТОЯТЕЛЬНАЯ
РАБОТА
1
вариант
1.
Передача данных через
ADSL-соединение происходит со скоростью 1024000 бит/c и заняла 5 секунд.
Определите размер файла в килобайтах.
2.
Передача файла размером 100 Мбайт через
ADSL-соединение осуществляется со скоростью 1 000 000 бит/с.
Определите время передачи файла в минутах.
3.
Передача данных через
ADSL-соединение происходит со скоростью 128000 бит/с. Передача текстового файла
заняла 1 минуту через это соединение. Сколько символов содержал переданный
текст, если известно, что он был представлен в 16-битной кодировке Unicode.
4.
Передача данных через ADSL-соединение
происходит со скоростью 2 621 440 бит/с. Через данное
соединение передают файл размером 10 Мбайт. Определите время передачи файла в
секундах.
5.
Осуществляется передача файла
размером 8 Мбайт через ADSL-соединение
со скоростью 128 000 бит/с. Определите время передачи файла в секундах.
6.
Передача данных через ADSL-соединение
происходит со скоростью 3 000 000 бит/с. Определите наибольший
размер файла, который может быть передан через данное соединение за
9 секунд.
7.
Скорость передачи данных через ADSL-соединение
равна 128 000 бит/с. Определите наибольший размер файла, который может
быть передан через данное соединение за 7 минут.
8.
Передача файла размером
1 Гбайт через ADSL-соединение происходит со
скоростью 5 242 880 бит/с. Определите время
передачи файла в минутах.
9.
Сколько секунд потребуется модему, передающему
информацию со скоростью 102 400 бит/с, чтобы передать цветное
растровое изображение размером 1024×800 пикселей, при условии, что в
палитре 65 536 цветов (216). Результат представьте целым
числом.
10. Передача модемом текстового файла со скоростью 7680
бит/сзаняла 1,5 мин. Сколько страниц содержал переданный текст, если известно,
что он был представлен в 16-битной кодировке Unicode, а на одной странице – 400
символов.
11. Данные
объемом 60 Мбайт передаются из пункта А в пункт Б по каналу связи,
обеспечивающему скорость передачи данных 220 бит в секунду, а
затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи
данных 223 бит в секунду. От начала передачи данных из пункта А
до их полного получения в пункте В прошло 10 минут. Сколько времени в секундах
составила задержка в пункте Б, т.е. время между окончанием приема данных из
пункта А и началом передачи данных в пункт В?
САМОСТОЯТЕЛЬНАЯ
РАБОТА
2
вариант
1.
Передача данных через ADSL-соединение
происходит со скоростью 256 000 бит/c и заняла 16 секунд.
Определите размер файла в Кбайт.
2.
Передача данных через
ADSL-соединение происходит со скоростью 256000 бит/c. Передача файла через это
соединение заняла 2 минуты. Определите размер файла в килобайтах.
3.
Передача данных через модемное
соединение происходит со скоростью 51 200 бит/с. Передача Word-файла через
это соединение заняла 10 с. Сколько символов содержал переданный текст, если
известно, что он был представлен в 16-битной кодировке Unicode.
4.
Необходимо передать файл размером 210 000
байт со скоростью передачи 56 000 бит/c. Какого будет время передачи файла в
секундах.
5.
Осуществляется передача файла 3,5
Мбайт через ADSL-соединение со скоростью 256 000 бит/с. Определите
время передачи файла в секундах.
6.
Передача данных через ADSL-соединение
происходит со скоростью 1 000 000 бит/с. Определите наибольший
размер файла, который может быть передан через данное соединение за 11 секунд.
7.
Передача данных через ADSL-соединение
происходит со скоростью 256 000 бит/с. Какой наибольший размер файла
в килобайтах может быть передан через данное соединение за 10 минут.
8.
Передача файла размером
100Мбайт через ADSL-соединение происходит со
скоростью 1 000 000 бит/с. Определите время
передачи файла в минутах.
9.
Сколько секунд потребуется модему, передающему
информацию со скоростью 33 600 бит/с, чтобы передать цветное
растровое изображение размером 640×480 пикселей, при условии, что в
палитре 16 777 216 цветов (224). Результат
представьте целым числом.
10. Сколько
секунд потребуется модему, передающему сообщения со скоростью 28 800 бит/с,
чтобы передать 100 страниц текста в 30 строк по 60 символов каждая, при
условии, что каждый символ кодируется 1 байтом?
11. Данные
объемом 80 Мбайт передаются из пункта А в пункт Б по каналу связи,
обеспечивающему скорость передачи данных 222 бит в секунду, а
затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи
данных 223 бит в секунду. От начала передачи данных из пункта А
до их полного получения в пункте В прошло 10 минут. Сколько времени в минутах
составила задержка в пункте Б, т.е. время между окончанием приема данных из
пункта А и началом передачи данных в пункт В?
Эталоны
ответов к самостоятельной работе:
|
1 вариант |
2 вариант |
|
|
1 |
Ответ: 625 |
Ответ: 500 |
|
2 |
Ответ: 14 |
Ответ: 3750 |
|
3 |
Ответ: 480 |
Ответ: 32000 |
|
4 |
Ответ: |
Ответ: 30 |
|
5 |
Ответ: 524,3 |
Ответ: 114,7 |
|
6 |
Ответ: 3295,898 |
Ответ: 1342,77 |
|
7 |
Ответ: |
Ответ: 18750 |
|
8 |
Ответ: 27,31 |
Ответ: 13,98(14) |
|
9 |
Ответ: |
Ответ: 219 |
|
10 |
Ответ:108 |
Ответ: 50 |
|
11 |
Ответ:360 |
Ответ: 60 |
Критерии
оценивания
За
правильный ответ на задания 1-2 выставляется положительная оценка – 0,5 баллов,
3 – 8 – 1 балла, 9-10 – 1,5 балла, 11 – 2 балла.
Максимальное
число баллов – 12.
Критерии оценки
задания 9-10:
•
1,5 балла ставится, если правильно выбран способ решения,
верно выполнен алгоритм решения, решение записано последовательно, аккуратно и
верно
•
0,5 балла
ставится, если допущена одна несущественная ошибка.
•
0 баллов- если
допущены существенные ошибки.
Общее количество баллов
суммируется
Критерии оценки
задания 11:
•
2 балла ставится, если правильно выбран способ решения,
верно выполнен алгоритм решения, решение записано последовательно, аккуратно и
верно
•
1 балла ставится,
если допущена одна ошибка.
•
0 баллов- если
допущены существенные ошибки.
Общее количество баллов
суммируется
Таблица переводов баллов в отметку:
|
Количество баллов |
Отметка |
|
10,5-12 |
отметка «5» |
|
8,5-10 |
отметка |
|
6-8 |
отметка «3» |
|
менее 6 |
отметка |
|
если |
отметка |
Пропускная
способность дискретных каналов связи
Пропускной
способностью канала связи называется
максимально возможная скорость передачи
по этому каналу, которая обеспечивается
при источнике с максимальной энтропией.
Еще раз подчеркнем,
пропускная способность – характеристика
канала связи. Для дискретного канала
она зависит от технической скорости
передачи, которая ограничивается полосой
пропускания канала, и от потерь информации.
Последние зависят от помех, действующих
в канале, способов обработки сигналов
в передатчике и приемнике, а также и от
технической скорости передачи. Рассмотрим
с точки зрения пропускной способности
дискретный канал связи без помех и
дискретный канал связи с помехами.
Пропускная
способность дискретного канала без
помех
Докажем, что для
дискретного канала пропускная
способность зависит
от технической скорости передачи.
Известно,
что среднее количество информации,
переносимое одним символом, равно
энтропии символа на входе канала
[бит/символ].
Скорость
передачи информации I`
будет зависеть от количества информации,
приходящейся на один символ
или
энтропии символа H(X)
на входе канала и скорости передачи
элементарных символов сигнала
(электрических
кодовых сигналов)
.
Т.е.:
[бит./с].
(2.6)
Из
выражения (2.6) следует, что пропускная
способность канала связи это действительно
наибольшая теоретически достижимая
для данного канала скорость передачи
информации. От свойства сигнала пропускная
способность не зависит.
Пропускная
способность
представляет
собой максимальное количество информации,
которое можно передать по каналу при
данных условиях за единицу времени.
Математически это записывается в
следующей форме:
(2.7)
где
С
– пропускная способность,
–
количество информации передаваемое в
единицу времени с помощью входных
сигналов X
и выходных Y.
Запись
означает, что отыскание максимума
выражения (2.7) ведется по всем возможным
источникам сообщений.
Считая,
скорость передачи
заданной и раскрывая значение I`(…)
получим, что максимальная скорость
передачи информации будет обеспечена
при максимальном значении энтропии
сигнала.
Известно,
что максимальное значение энтропии
обеспечивается при равномерном
распределении вероятностей и статисческой
независимости символов алфавита сигнала.
Таким образом:
, (2.8)
— количество
букв в алфавите.
Из
формулы видно, что пропускная способность
измеряется в единицах измерения
количества информации за единицу
времени.
Рассмотрим
методику определения пропускной
способности канала связи без помех на
следующем примере.
В
информационном канале без помех для
передачи сообщений используется алфавит
с четырьмя различными символами
=4,
а код каждого сообщения содержит
=2
бита. Длительности всех разрядов,
соответствующих битам одинаковы и равны
одной миллисекунде: tс=
1 мс.
Определить
пропускную способность канала передачи.
Решение.
Для
расчета пропускной способности
дискретного канала без помех используется
выражение (2.12).
.
Скорость
передачи одного символа
,
где
–
средняя длительность передачи символа.
Так
как код каждого символа содержит 2 бита,
то длительность всех сигналов будет
постоянна и равна
[мс].
.
И,
следовательно
.
Пропускная
способность дискретного канала с
помехами
При определении
пропускной способности канала
предполагается, что задано свойства
канала (структура и уровень сигнала и
помех, вид модуляции, методы кодирования
и декодирования и др.). Эти свойства
определяют статистические связи между
принимаемыми сигналами, которые в свою
очередь выражаются условными вероятностями
вида р(хiyi)
и р(уiхi)
(рис.2.2). При заданных таким образом
свойствах канала максимальную скорость
передачи информации можно обеспечить
выбором оптимального ансамбля сигналов.
При этом накладываются ограничения в
отношении уровня сигнала, его структуры,
спектра, объёма алфавита и др. Выбор
оптимального ансамбля сигналов означает
выбор оптимального распределения
вероятностей р(хi).
В
соответствии с этим пропускная способность
дискретного канала с помехами определяется
как максимальная скорость передачи
информации, которая может быть достигнута
при заданных свойствах канала и наложенных
ограничениях:
.
(2.9)
В
соотношении (2.9) максимум берётся по
всем допустимым распределениям
вероятности р(хi).
Здесь
–
максимальное число сообщений, которое
может быть передано по каналу за единицу
времени. Величина Vmax
зависит от электрических характеристик
канала и вида модуляции. При передаче
с большой скоростью, т.е. короткими
импульсами, через канал с ограниченной
полосой, недостаточно для неискаженного
воспроизведения этих импульсов возникает
взаимное перекрытия ряда соседних
сигналов, снижающее достоверность
приёма. Предельная удельная скорость
передачи дискретных сигналов, при
которой может быть достигнут безыскаженный
прием, составляет 2 бода на 1 Герц полосы
канала.
Для
двоичного канала Vmax
представляет собой максимально возможную
скорость манипуляции Вmax.
Напомним, что в отсутствие помех Н(XY)=0.
Пропускная способность двоичного канала
равна скорости манипуляции Вmax.
В
дальнейшем будем рассматривать только
такие каналы, которые называют каналами
без памяти. Дискретный
канал называется
каналом без
памяти,
если вероятность перехода любого
входного символа в любой выходной не
зависит от того, какие символы передавались
до этого и как они были приняты.
Если
алфавит входных (X)
и выходных (Y)
сигналов состоит из двух символов, то
канал называется двоичным. Диаграмма
переходных вероятностей такого канала
представлена на рис. 2.4.
Алфавит
входных сигналов имеет два символа х0
и
х1
.
Выбранный случайным образом источником
сообщений, один из этих символов подаётся
на вход дискретного канала. На приёме
регистрируется у0
и
y1
. Выходной алфавит тоже имеет два символа.
Символ у0
может быть зарегистрирован при передаче
сигнала х0
. Вероятность такого события – р(y0x0).
Символ у0
может быть зарегистрирован при передаче
сигнала х1
. Вероятность такого события – р(y0x1).
Символ y1
может быть зарегистрирован при передачи
сигналов х0
и
х1
с вероятностями р(y1x0)
и р(y1
x1)
соответственно. Правильному приёму
соответствуют события с вероятностями
появления р(y1x1)
и р(y0x0).
Ошибочный прием символа происходит при
появлении событий с вероятностями
р(y1x0)
и р(y0x1).
Стрелки на рисунке 2.5 показывают, что
возможные события заключаются в переходе
символа х1
в
y1
и х0
в
y0
(это соответствует безошибочному
приему), а также в переходе х1
в y0
и х0
в
y1
(это соответствует ошибочному приему).
Такие переходы характеризуются
соответствующими вероятностями р(y1x1),
р(y0x0),
р(y1x0),
р(y0x1),
а сами вероятности называют переходными.
Переходные вероятности характеризуют
вероятности воспроизведения на выходе
канала переданных символов.
Канал
без памяти называют симметричным, если
соответствующие переходные вероятности
одинаковы, а именно одинаковы вероятности
правильного приёма, а также одинаковы
вероятности любых ошибок. То есть:
Канал с произвольным
объёмом алфавита называется симметричным,
если
(2.11)
В
(2.11)
– объём алфавита сигналов.
Дискретный
канал считается полностью определенным,
если известна скорость передачи отдельных
элементов дискретных сигналов и
определены (переходные) вероятности
.
Переходные
вероятности
и распределение вероятностей р(хi)
позволяют определить апостериорную
неопределённость
не устраняемую полностью при приеме,
так как в канале с помехами возможно
искажение передаваемых сигналов.
Напомним, что
определяется выражением
(2.12)
В выражении 2.12
условная энтропия входного символа
при принятом символе
;
р(хiyj
)
– условная вероятность передачи хi,
если принят yj.
Границы условной энтропии
определяются неравенством
(2.13)
При
чем
при отсутствии помех в канале. Это
означает, что остаточной (апостериорной)
неопределённости нет. Помеха не искажает
передаваемые сигналы. Сообщение на
приеме восстанавливаются полностью и
из них извлекается вся информация.
при
обрыве канала. При обрыве канала
информация по каналу не передается и
неопределенность на приёме не уменьшается.
Таким
образом, при неполной достоверности
сообщений, среднее количество информации
равно разности безусловной энтропии
Н(X)
и условной энтропии
характеризующей остаточную неопределённость
сообщений. И в результате передачи по
каналу одного элемента сообщения X
неопределенность на выходе уменьшиться
в среднем на величину
(2.14)
В
выражении 2.14 условная вероятность
определяется распределением вероятностей
и переходными вероятностями
(2.15)
где q
= 1-р
– вероятность ошибочного приема символа,
р
– вероятность правильного приёма
символа, N
– алфавит сигналов.
Подставляя
(2.15) в выражение (2.9) для пропускной
способности получаем
(2.16)
Максимальное
значение энтропия принимает при равно
вероятных символах сообщения. Т.к. Н(Y)
= log
N,
где N
– алфавит выходных сигналов, то для
пропускной способности можем окончательно
записать
[бит/сек].
(2.17)
Пропускная
способность канала в расчете на один
символ
определяется путем деления С
на количество элементов сообщения,
передаваемых в единицу времени, т.е. на
скорость передачи
.
Пропускная
способность канала в расчете на один
символ
составляет
[бит/символ].
(2.18)
Из
выражения 2.18 следует, что при
и
пропускная
способность симметричного канала равна
нулю. Действительно, представляя значения
q
и p
выражение 2.18 получаем
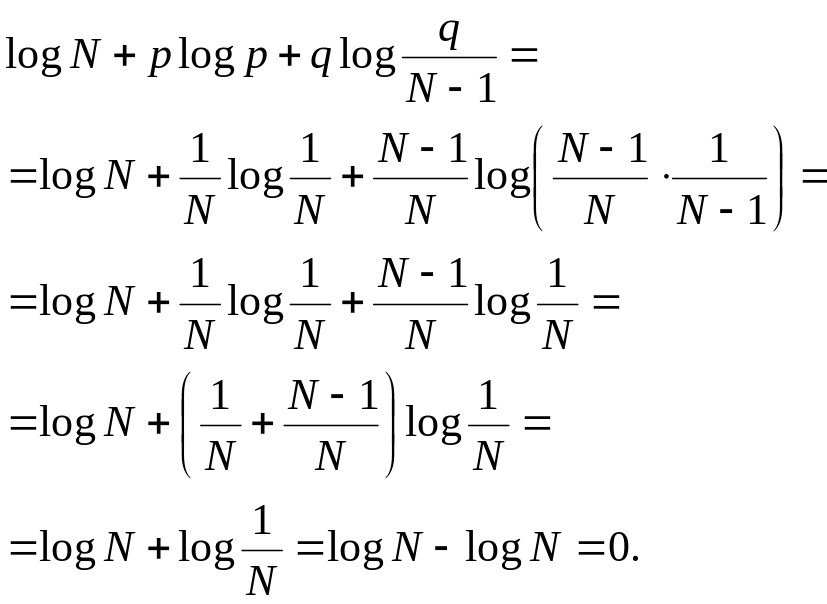
Этот
случай соответствует обрыву канала.
Физически, это означает, что по каналу
идет передача информации, на выходе
канала её получить невозможно, т.к. при
любом переданном символе xi
все принимаемые символы уj
равновероятные, т.е. р(уj|xi)
= 1/N.
Максимальной пропускная способность
становится при отсутствии помех. В этом
случае вероятность ошибки q
становится равной 0: q
= 0, а вероятность безошибочного приёма
р=
1. Подставляя эти значения в (2.18) получаем
[бит/сек].
В
частном случае двоичного симметричного
канала без памяти, т.е. при N=
2 получаем:
Cс
=
1 + p
log p
+ (1-p)
log (1-p).
Беря
различные значения р,
можем определить пропускную способность
для такого канала.
Проанализируем
пропускную способность симметричного
канала без памяти при N
= 2:
C
=
1 + p
log p
+ (1-p)
log (1-p)
где
— вероятность правильного приема,
— вероятность
ошибки.
C
Из графика (рис.2.2)
видно, что пропускная способность
максимальна, если вероятность ошибки
q равна 0. При
увеличении вероятности q
от 0 до 0,5 пропускная способность С
уменьшается до нуля. В точке q=0,5
пропускная способность равна нулю. Этот
случай соответствует обрыву канала.
При дальнейшем возрастании вероятности
ошибок q пропускная
способность С начинает увеличиваться
и достигает максимума при q=1.
это означает, что все переданные «1» под
воздействием помех переходят в «0», а
все «0» переходят в «1». Поэтому, изменением
полярности на приеме можно полностью
исключить ошибки.
Пропускная
способность непрерывных
каналов связи
Определение
пропускной способности непрерывного
канала с
белым шумом
Непрерывный
канал связи, как и дискретный,
характеризуется количеством передаваемой
информации и пропускной способностью
– максимально возможной скоростью
передачи информации.
Рассмотрим
непрерывный канал с дискретным временем,
т.е. канал, по которому со скоростью
передаются отсчеты дискретного по
времени и непрерывного по интенсивности
сигнала.
В
соответствии со схемой (рис.2.1)
,
где
–
дифференциальная энтропия суммы
на выходе непрерывного канала;
– условная
дифференциальная энтропия суммы
при известном входном сигнале
.
Если
помехи в канале связи являются аддитивными,
т.е.
,
то можно показать, что
,
где
–
дифференциальная энтропия помехи. Тогда
среднее количество информации, переносимое
одним отсчетом, равно
,
а
скорость передачи информации
.
В
частном случае, если средние мощности
сигнала и шума на выходе канала ограничены
(в определенной полосе частот), а
распределение плотности вероятностей
и
являются нормальными (гауссовскими),
то
,
,
где
Рс
и Рп
– средние мощности полезного сигнала
и помехи
на выходе канала;
Рс+Рп
–
средняя мощность (дисперсия) суммы
(при независимости
и n(t)).
Тогда
пропускная
способность непрерывного канала с
дискретным временем рассчитывается по
формуле:

(2.20)
где
Рс
/Рп
– отношение
сигнал/помеха
на выходе канала связи.
В
полностью непрерывном канале с широкой
полосой пропускания
минимальная скорость передачи отсчетов
определяется в соответствии с теоремой
Котельникова
,
так
что
(2.21)
Это выражение
называется формулой Шеннона, которая
справедлива лишь по отношению к гауссовым
каналам, т.е. к каналам с белым гауссовским
шумом.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5.2.2 Пропускная способность канала и количество принятой информации
Определение 5.14 Пропускная способность канала связи — наибольшая теоретически достижимая скорость передачи информации при условии, что погрешность не превосходит заданной величины.
Определение 5.15 Скорость передачи информации — среднее количество информации, передаваемое в единицу времени. Определим выражения для расчета скорости передачи информации и пропускной способности дискретного канала связи.
При передаче каждого символа в среднем по каналу связи проходит количество информации, определяемое по формуле:
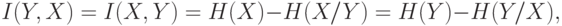 |
( 5.3) |
где 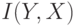




При передаче сообщения 


 |
( 5.4) |
![H(Y_T)-H(Y_T/X_T) = n[H(X)-H(X/Y)],](https://intuit.ru/sites/default/files/tex_cache/04975fe6fd40329c368c84020b818b37.png) |
( 5.5) |
где 



Для символов равной длительности 
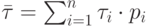
При этом скорость передачи информации
![C=bar{I}(X_T,Y_T)=lim_{Trightarrow infty} frac{(X_T,Y_T)}{T} text{ [бит/с]}.](https://intuit.ru/sites/default/files/tex_cache/cf3c5e54a774f391e1c47def09a32617.png) |
( 5.6) |
Скорость передачи информации зависит от статистических свойств источника, метода кодирования и свойств канала.
Пропускная способность дискретного канала связи
 |
( 5.7) |
Пример 5.4 [2] Источник вырабатывает 3 сообщения с вероятностями: 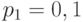

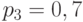


Решение. Энтропия источника равна
Для передачи 3 сообщений равномерным кодом необходимо два разряда, при этом длительность кодовой комбинации равна 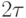
Средняя скорость передачи сигнала
Скорость передачи информации
Пример 5.5 По каналу связи передаются сообщения, вероятности которых соответственно равны:
Канальная матрица, определяющая потери информации в канале связи имеет вид:
Определить:
- Энтропию источника информации —
.
- Безусловную энтропию приемника информации —
.
- Общую условную энтропию —
.
- Скорость передачи информации, если время передачи одного символа первичного алфавита
мс.
- Определить потери информации в канале связи при передаче
символов алфавита.
- Среднее количество принятой информации.
- Пропускную способность канала связи.
Решение:
- Энтропия источника сообщений равна
- Вероятности появления символов на входе приемника
Проверка:
Энтропия приемника информации равна
- Общая условная энтропия равна
- Скорость передачи информации равна:
- Потери информации в канале связи при передаче 500 символов алфавита равны:
- Среднее количество принятой информации равно:
- Пропускная способность канала связи
Список литературы
- Харин Ю.С., Берник В.И., Матвеев Г.В. Математические основы криптологии — Минск: БГУ, 1999. — 319 с.
- Блинцов С.В. Сборник примеров и задач по теории информации. Николаев: НУК им. адмирала Макарова, 2004..
- Рябко Б.А., Филонов А.Н. Криптографические методы защиты информации: Учебное пособие для ВУЗов. Новосиб.: СибГУТИ, 2008. — 229 с.


![Channel model {displaystyle {xrightarrow[{text{Message}}]{W}}{begin{array}{|c|}hline {text{Encoder}}\f_{n}\hline end{array}}{xrightarrow[{mathrm {Encoded atop sequence} }]{X^{n}}}{begin{array}{|c|}hline {text{Channel}}\p(y|x)\hline end{array}}{xrightarrow[{mathrm {Received atop sequence} }]{Y^{n}}}{begin{array}{|c|}hline {text{Decoder}}\g_{n}\hline end{array}}{xrightarrow[{mathrm {Estimated atop message} }]{hat {W}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39d63076666d80bf3b6140eadf87155187e371a2)















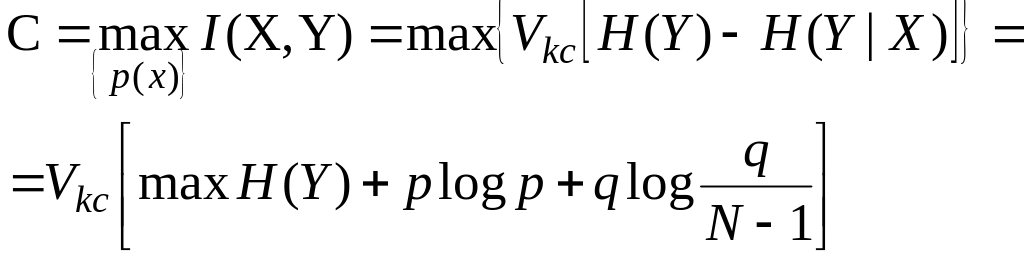

![H=-sum_{i=1}^{m} p_i log_2 p_i = - left( 0,1 log_2 0,1 + 0,2 log_2 0,2+ 0,7 log_2 0,7right)=1,16 text{ [бит/с].}](https://intuit.ru/sites/default/files/tex_cache/2a0002e1b850da8a288fdf2663e4377b.png)
![V =1/2tau = 500 text{ [1/c]}.](https://intuit.ru/sites/default/files/tex_cache/45efa89b1f23b0d9ab15c04a22c641ba.png)
![C = vH = 500cdot1,16 = 580 text{ [бит/с]}.](https://intuit.ru/sites/default/files/tex_cache/b90a9eb20bbfeb5e50b2a2bd57815436.png)
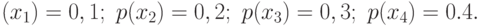
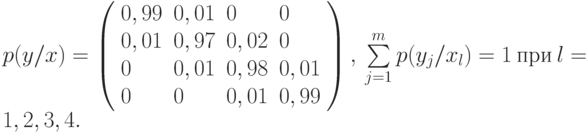
 .
.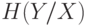 .
. мс.
мс.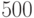 символов алфавита.
символов алфавита.![begin{equation}
H(X)=-sumlimits_{i=1}^{m} p(x_i) log_2 p(x_i) = \
- ( 0,1 log_2 0,1+0,2 log_2 0,2+0,3 log_2 0,3+0,4 log_2 0,4)= \
0,3322+0,4644+0,5211+0,5288=1,8465 text{ [бит/симв.]}
end{equation}](https://intuit.ru/sites/default/files/tex_cache/a60a2049b105aa2c437671171a4e7e03.png)

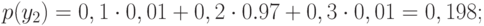

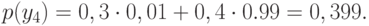
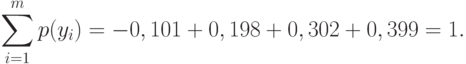
![begin{equation}
H(Y)=-sumlimits_{i=1}^m p(y_i) log_2 p(y_i)=\
-(0,101 log_2 0,101 + 0,198 log_2 0,198 + 0,302 log_2 0,302 + 0,399 log_2 0,399 =\
0,334+0,4626+0,5216+0,5290=1,85 text{ [бит/симв].}
end{equation}](https://intuit.ru/sites/default/files/tex_cache/b544af09eac6d119c1930ae31d4b6bd4.png)
![H(Y/X)=-sum_{i=1}^m sum_{j=1}^m p(x_i) p(y_j/x_i) log_2 p(y_j/x_i)=\
-left(
0,1(0,99 log_2 0,99 + 0,01 log_2 0,01)+right.\
0,2(0,01 log_2 0,01 + 0,97 log_2 0,97+ 0,02 log_2 0,02)+\
0,3(0,01 log_2 0,01 + 0,98 log_2 0,98+ 0,01 log_2 0,01)+\
left. 0,4(0,01 log_2 0,01 + 0,99 log_2 0,99)
right)= \
0,008+0,044+0,048+0,032=0,133 text{ [бит/симв].}](https://intuit.ru/sites/default/files/tex_cache/74843564106f76f8f95ac25a4fc705f9.png)
![C=Vleft(H(Y)-H(Y/X)right)=Vleft(H(X)-H(X/Y)right)=\
(1,85-0,132)/0,0001=17,18 text{ [Кбит/с].}](https://intuit.ru/sites/default/files/tex_cache/98641d4a43f3ccd0f86d43f819c88915.png)
![Delta I=kH(Y/X) = 500cdot 0,132=66 text{ [бит.]}](https://intuit.ru/sites/default/files/tex_cache/0c2e5146bd4e76f604cbf210969eab36.png)
![I=kleft(H(Y)-H(Y/X)right)=kleft(H(X)-H(X/Y)right)=\
500cdot(1,85-0,132)=859 text{ [бит].}](https://intuit.ru/sites/default/files/tex_cache/86eb34cc9b542188889a88d7a4979274.png)
![C_n=Vleft( log_2 m - H(Y/X) right)=(2-0,132)/0,0001=18,68 text{ [Кбит/с].}](https://intuit.ru/sites/default/files/tex_cache/3a4f73a36fc44d940041310882541e24.png)