Простые числа Мерсенна и тест Люка-Лемера
Время на прочтение
7 мин
Количество просмотров 23K
Перевод поста Джона Макги (John McGee) «Mersenne Primes and the Lucas–Lehmer Test».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Полине Сологуб за помощь в переводе и подготовке публикации
.
Содержание
— Введение.
— Теорема множителей Эйлера и Мерсенна
— Люка и Лемер
—
От до
— Совершенные числа
— 21-е, 22-е и 23-е числа Мерсенна
— 24-е, 25-е и 26-е числа Мерсенна.
— 27-е и 28-е числа Мерсенна
— 29-е число Мерсенна
— 30-е и 31-е числа Мерсенна
— Великий интернет-поиск чисел Мерсенна
— Факторизация чисел Мерсенна
Введение
Простое число Мерсенна — простое число вида
(значение степени р также должно быть простым). Эти простые числа получили свое название от имени французского математика и религиозного ученого Мерсенна, который и составил данный список простых чисел этой формы в первой половине семнадцатого века. Первые четыре из них были известны уже давно:
,
,
и
.
Мерсенн утверждал, что значение
будет простым для простых чисел
, принадлежащих множеству
. Во всем ли он был прав, можно проверить с помощью функции Wolfram Language — PrimeQ, в которой используются современные методы тестирования чисел на простоту, для которых не требуется поиска конкретного множителя, чтобы доказать, что число составное.
Вполне возможно, что его утверждение о том, что
— простое число, просто опечатка, и на самом деле он имел в виду
. Несложно понять, что проверка на простоту была при жизни Мерсенна делом затруднительным, поскольку проверка делением была одним из немногих доступных инструментов. Например, для
наименьшим множителем оказывается 15-значное число, так что даже с современными методами факторизации его не так-то легко найти. В функции FactorInteger используются наиболее совершенные методы, которые позволяют применять метод факторизации в отношении больших целых чисел.
Теорема множителей Эйлера и Мерсенна
Первые важные достижения в области проверки на простоту принадлежат великому математику Леонарду Эйлеру, который незадолго до 1772 года уточнил, что
является простым. Он сделал это, продемонстрировав, что любой простой делитель
должен быть равен 1 или 62 (mod 248).
Такой относительно короткий список даже во времена Эйлера мог быть проверен с помощью пробного деления (вручную). Ему принадлежит применение теоремы Мерсенна, в которой говорится, что если
является делителем
, то
,
и
для некоторого целого положительного числа
. Эти факты значительно ограничивают количество возможных делителей
. С помощью функций, представленных ниже, демонстрируется использование этой теоремы с целью предоставления списка возможных делителей
, меньших, чем
.
Мы используем эти функции, чтобы быстро найти делитель
. Обратите внимание, что
является делителем
тогда и только тогда, когда
. Это дает возможность использовать функцию PowerMod, что обеспечивает эффективное возведение в степень по модулю.
Ниже приводится число Мерсенна с 161649 знаками:.
Люка и Лемер
Следующим важным шагом стало открытие Эдуардом Люка метода для проверки простоты чисел данной формы. Он использовал свой метод в 1876 году для проверки, является ли
(самое большое число Мерсенна «докомпьютерной» эпохи) простым. В начале двадцатого века, когда основы двоичной арифметики и алгебры стали широко известны, Дерек Генри Лемер усовершенствовал метод Люка. Полученный в результате тест простоты чисел Люка-Лемера обеспечивал эффективную проверку, если число данной формы являлось простым. Проверка проводилась с помощью сравнения по модулю:
Это означает, что
идентично числу, представленному его
битами низшего порядка, плюс — числами, представленными остальными битами. Это соотношение может применяться рекурсивно до тех пор, пока
.
Рассмотрим следующий пример. Здесь мы покажем, что 
. Обратите внимание, что


Функция ниже задает этот метод для вычисления
с использованием только битовых операций (без деления). Обратите внимание на то, что
имеет двоичную форму
, при этом нет ни одного 0, и поэтому она также служит в качестве маски для
битов низшего порядка числа
.
Следующая функция реализует тест простоты Люка-Лемера (LLT). Определим последовательность
,
. Тогда
является простым тогда и только тогда, когда
.
Опыт показывает, что основное время выполнения этих функций тратится на целочисленную арифметику.
Чтобы проверить, является ли
простым, лучше сначала проверять простоту на небольших простых делителях и выполнять другие проверки простоты. Сначала мы используем теорему делителей простых чисел Мерсенна, закодированную в checkMPDivisors, а затем функцию PrimeQ. Если это не сработает, применим тест Люка-Лемера.
Здесь мы представляем расширенную версию функции PrimeQ, которая применяет тест Люка-Лемера для больших чисел вида
.
От  до
до 
Первым простым числом Мерсенна, обнаруженным на компьютере с помощью теста Люка-Лемера, стало
, найденное Рафаэлем Робинсоном 30 января 1952 года на базе лампового компьютера SWAC (Standards Western Automatic Computer). Ниже вы видите блок памяти этого компьютера, содержащий 256 слов по 37 бит каждое.
20-е простое число Мерсенна было обнаружено Александром Гурвицем в ноябре 1961 года в результате проведения 50-минутного теста Люка-Лемера на IBM 7090. Ниже мы воспроизводим эти результаты (на это потребовалось около 151 секунд машинного времени на современном одноядерном ноутбуке).
Одной из особенностей Wolfram Language, делающей его пригодным для такого рода работы, является его быстрая целочисленная арифметика. Поиск простых чисел Мерсенна стал настоящим вызовом на рассвете эпохи компьютеризированного поиска. Исследователи адаптировали методы быстрого преобразования Фурье для преобразования задачи умножения двух больших целых чисел в простое поэлементное произведение трансформированных цифр. Быстрое умножение целых чисел необходимо для шага возведения в квадрат в тесте Люка-Лемера. В Wolfram Language используются новейшие алгоритмы, оптимизированые для работы с точными целыми числами с миллиардами символов. Например, убедимся, что последнее из них, —
, — на самом деле простое число Мерсенна, и продемонстрируем все его цифры.
Совершенные числа
Существует интересная связь между простыми числами Мерсенна и совершенными числами. Совершенное число — это число, равное сумме всех своих делителей (отличных от самого числа). Евклид предполагал, а Эйлер доказал, что все четные совершенные числа, имеют вид
. Функция Wolfram Language PerfectNumberQ проверяет, является ли число совершенным. Продемонстрируем это свойство на
.
21-е, 22-е и 23-е числа Мерсенна
Перейдем к переоткрытию 21-го, 22-го и 23-го чисел Мерсенна (будем обозначать их далее в форме вида
):
,
,
. Все они были обнаружены Дональдом Гиллисом, который запускал LLT на ILLIAC II всю весну 1963 года (см. здесь). Для проверки всех чисел вида
для простых чисел в промежутке
нам понадобилось около 6 минут.
24-е, 25-е и 26-е числа Мерсенна
Далее мы расширяем поиск, чтобы найти
,
,
. Последнее из них было обнаружено в феврале 1979 г. Лэндоном Куртом Ноллом и Лорой Никель. Они искали в диапазоне от
до
на суперкомпьютере CDC Cyber 174 (почитать об этом можно здесь). Наши расчеты становятся более долгими, так что мы начинаем использовать параллельную обработку. Поскольку тесты независимы, для ускорения работы мы можем использовать ParallelMap. Проверка диапазона
занимает приблизительно три с половиной минуты (используются 4 ядра).
Обратите внимание на то, что специализированный тест Люка-Лемера значительно быстрее, чем более общая функция PrimeQ (для данных чисел Мерсенна).
27-е и 28-е числа Мерсенна
Далее мы проверили диапазон
, чтобы найти число
. Оно было обнаружено в апреле 1979 года Гарри Нельсоном и его командой (они использовали суперкомпьютер Cray-1). Наш поиск завершился за 15 минут.
Следующее число Мерсенна,
. Оно был открыто в сентябре 1982 года Дэвидом Словински — также на Cray-1. Этот суперкомпьютер весил около 5 тонн и потреблял около 115 киловатт электроэнергии, а его вычислительная производительность достигала 160 мегафлопс. Он поставлялся с 1 миллионом 64-разрядных слов памяти (8 мегабайт), а стоил около 16000000$ в сегодняшних ценах. Ниже показана деталь его системы охлаждения. Для сравнения: Raspberry Pi весит несколько унций, работает на 4 Вт, обеспечивает около 410 мегафлопс и снабжен 1Гб оперативной памяти, и это все — за 40$. А еще он поставляется сразу с системой Mathematica.
Число
содержит 25962 цифры. Это значение мы нашли за 1 час и 14 минут (на моем ноутбуке, а не на Raspberry Pi), проводя испытания в диапазоне
.
29-е число Мерсенна
Поскольку теперь нам требуется более серьезное компьютерное время, мы также производим отметку времени для каждого прогона. Теперь мы проверяем диапазон
. Через 1 час и 44 минут компьютер показал:
. Это число впервые было обнаружено 29 января 1988 года Уокер Колкуиттом и Люком Уэлшем (суперкомпьютер NEC DX-2; статью можно найти здесь).
30-е и 31-е числа Мерсенна
Следующие два простых числа Мерсенна:
и
, — были на самом деле обнаружены еще до 29-го (той же командой, которая обнаружила и 28-е). Они использовали Cray X-MP, чтобы найти 30-е число Мерсенна в сентябре 1983 года и 31-е — в сентябре 1985 года. Проверим
с помощью функции поиска в диапазоне
. Для проверки каждого
в этом диапазоне понадобилось 4 часа и 8 минут.
Великий интернет-поиск чисел Мерсенна
С открытием 34-го простого числа Мерсенна —
— в сентябре 1996 года закончилась эпоха суперкомпьютеров для поиска простых чисел Мерсенна. Следующие 15 были найдены добровольцами Великого интернет-поиска простых чисел Мерсенна (GIMPS), в рамках которого проводится вариант теста Люка-Лемера (в качестве фонового процесса) на персональных компьютерах. Этот масштабный проект распределенных вычислений в настоящее время достигает уровня производительности, эквивалентного приблизительно 300 терафлопс в секунду, причем задействуется время простоя более чем 1,3 миллиона компьютеров.
Проверим 34-е число Мерсенна с помощью теста Люка-Лемера. На этом этапе мы достигли предела возможностей личного компьютера. На тестирование тысячи чисел Мерсенна в этом диапазоне потребуется много дней. Интересно отметить, что тест Люка-Лемера часто используется в качестве стресс-теста надежности компьютерного оборудования и программного обеспечения, так как даже одна арифметическая ошибка среди миллиардов вычислений, необходимых для тестирования одного большого простого числа, повлечет за собой неправильный вывод, что будет означать потерю числа Мерсенна или ложный ответ. Тот факт, что мы проверили каждое
для простых чисел в промежутке между 2 и 139901, убедительно доказывает надежность арифметики больших чисел и бинарных операций в системе Mathematica и языке Wolfram Language.
Факторизация чисел Мерсенна
Как мы уже видели, количество возможных множителей в разложении чисел вида
согласно теореме множителей Мерсенна ограниченно. Это позволило провести эффективный компьютеризированный поиск делителей больших чисел этой формы. На момент написания этой статьи все числа Мерсенна (до
) были полностью разложены на множители (иллюстрации можно найти здесь). Проект GIMPS также привел к открытию крупных множителей многих чисел Мерсенна в качестве побочного продукта проверки простоты чисел. Новую статью, которая представляет собой современный подход к решению этой проблемы (наряду с 17 новыми факторизациями), можно найти здесь. Наибольшее факторизованное число составило
; его наименьший из найденных делителей имеет 76 десятичных цифр. Его наименьший делитель равен 23. Общее время, необходимое для того, чтобы получить этот результат составляет 7500 лет (речь о компьютерном времени).
Мы можем быстро найти несколько первых множителей
с помощью функции FactorInteger.
Все простые числа Мерсенна, обнаруженные на сегодняшний день, каталогизированы в Wolfram Language (до 44-го). Доступ к этой информации обеспечивается функциями MersennePrimeExponent и MersennePrimeExponentQ.
Если вас заинтересовала эта тема, вы можете найти более подробную информацию на следующих веб-сайтах:
- GIMPS
- Страницы простых чисел
- Простые числа
Красивые аномалии встречаются в каждом предмете, но если есть одна область красоты, с которой согласится большинство математиков, то это простое число.
Эти числа занимают уникальный пьедестал в математике, особенно в области теории чисел. Великие умы потратили бесчисленные часы для расследования этой проблемы, в том числе такие великие умы, как Пол Эрдос, Г.Х. Харди и Сриниваса Рамануджан, и это лишь некоторые из них. Теперь, прежде чем мы углубимся в различные алгоритмы, чтобы найти простые числа, давайте сначала установим предварительное понимание простых чисел.
Что такое простые числа?
Самое техническое определение простых чисел состоит в том, что это натуральное число больше 1 и может быть получено только путем умножения 1 и самого себя. Если бы понимание натуральных чисел было более интуитивным, то можно было бы сказать, что это числа, которые мы используем для подсчета.
Чтобы понять это более точно, давайте выберем два числа — 5 и 6. Теперь 5 — это число, которое можно получить только умножением на 1 и 5 (само число). Однако, когда мы берем число 6, то замечаем, что его можно получить другим способом, кроме умножения 1 и 6 (само число). Его также можно получить умножением чисел 2 и 3, что означает, что это не простое число. Число, которое не является простым, известно как составное число.
Метод Марена Мерсенна
Метод простого числа Мерсенна — это специальный метод нахождения определенного вида простого числа, известный как простые числа Мерсенна. Название для этого метода происходит от французского монаха Марин Мерсенн, который первым определил его. Простые числа Мерсенна — это те, которые сводимы к виду 2n-1, где n-простое число. Первые несколько чисел в этом методе являются 2, 3, 5, 7, 13, 17, 19, 31, 61, и 89. Долгое время метод простых чисел Мерсенна представлял собой тяжёлую работу, так как при переходе к более высоким простым числам он был очень трудоемким.
Однако, с появлением компьютеров, они теперь могли выполнять эти вычислительные вычисления, которые раньше делались людьми самым кропотливым и трудоемким образом. Мы определенно достигли более высоких простых чисел Мерсенна и простых чисел на общем уровне. Поиск простых чисел так же активен, как и другие численные поиски, выполняемые компьютерами. Другой числовой поиск, аналогичный движению простых чисел, заключается в добавлении десятичных разрядов к некоторым иррациональным числам, таким как пи (отношение длины окружности к диаметру). Однако непрерывный поиск следующего по величине простого числа существенно сложнее, чем поиск следующей цифры числа Пи.
Даже самые большие компьютеры (суперкомпьютеры) тратят значительное количество времени, чтобы проверить, является ли новое число (которое обычно ошеломляюще огромным) само по себе простым числом, и требуется еще больше времени, чтобы проверить, является ли число основным числом Мерсенна. По этой причине числа Мерсенна представляют большой интерес в области кибербезопасности и криптографии, особенно в отношении шифрования.
В августе 2008 года системный администратор UCLA Эдсон Смит нашел наиболее значимое простое число, известное на тот момент. Смит установил программное обеспечение для Great Internet Mersenne Prime Search (Gimps), проекта распределенных вычислений на добровольной основе. Это число было простым числом Мерсенна длиной 12 978 189 цифр. Чтобы дать представление о том, насколько он велик, на его написание уйдет почти два с половиной месяца, а в случае печати он растянется на 50 км!
Метод простых чисел Ферма
Число Ферма, как и число Мерсенна, представляет собой особый вид простого числа. Название происходит от математика 17-го века и юриста Пьера де Ферма. Число Ферма похоже на число Мерсенна… с одной маленькой поправкой. Давайте возьмем число Ферма Fm, где мы можем определить Fm как 2m +1. Здесь m снова равно 2, возведенному в степень n или 2n.
Фермат был твердо убежден в том, что все числа вышеуказанной формы — это простые числа. В дальнейшем он сказал, что он будет производить простые числа для всех целочисленных значений m. Что делает эти числа уникальными и красивыми, но очень хитрыми, так это то, что простые числа становятся чрезвычайно большими очень быстро, даже в пределах первых четырех итераций. Чтобы доказать это, возьмем n в качестве следующих значений, n=0, 1, 2, 3 и 4.
Когда n = 0, m = 20 = 1; поэтому F0 = 2 1 + 1 = 2 + 1 = 3, что является простым. Когда n = 1, m = 21 = 2; поэтому F1 = 22 + 1 = 4 + 1 = 5, что является простым. Когда n = 2, m = 22 = 4; следовательно, F2 = 24 + 1 = 16 + 1 = 17, что является простым. Когда n = 3, m = 23 = 8; следовательно, F3 = 28 + 1 = 256 + 1 = 257, что является простым. Когда n = 4, m = 24 = 16; следовательно, F4 = 216 + 1 = 65536 + 1 = 65537, что является простым числом. Теперь, как вы можете заметить, к тому времени, когда мы достигнем F5, значение достигает 4 294 967 297.
На сегодняшний день мы достигли только F11, даже со всеми лучшими компьютерами и параллельными вычислениями и большой точностью. В конце концов, однако, мы можем сказать, что поиск простых чисел всегда будет идти до бесконечности и дальше!
| Named after | Marin Mersenne |
|---|---|
| No. of known terms | 51 |
| Conjectured no. of terms | Infinite |
| Subsequence of | Mersenne numbers |
| First terms | 3, 7, 31, 127, 8191 |
| Largest known term | 282,589,933 − 1 (December 7, 2018) |
| OEIS index |
|
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form Mn = 2n − 1 for some integer n. They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century. If n is a composite number then so is 2n − 1. Therefore, an equivalent definition of the Mersenne primes is that they are the prime numbers of the form Mp = 2p − 1 for some prime p.
The exponents n which give Mersenne primes are 2, 3, 5, 7, 13, 17, 19, 31, … (sequence A000043 in the OEIS) and the resulting Mersenne primes are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, … (sequence A000668 in the OEIS).
Numbers of the form Mn = 2n − 1 without the primality requirement may be called Mersenne numbers. Sometimes, however, Mersenne numbers are defined to have the additional requirement that n be prime.
The smallest composite Mersenne number with prime exponent n is 211 − 1 = 2047 = 23 × 89.
Mersenne primes were studied in antiquity because of their close connection to perfect numbers: the Euclid–Euler theorem asserts a one-to-one correspondence between even perfect numbers and Mersenne primes. Many of the largest known primes are Mersenne primes because Mersenne numbers are easier to check for primality.
As of October 2022, 51 Mersenne primes are known. The largest known prime number, 282,589,933 − 1, is a Mersenne prime.[1] Since 1997, all newly found Mersenne primes have been discovered by the Great Internet Mersenne Prime Search, a distributed computing project. In December 2020, a major milestone in the project was passed after all exponents below 100 million were checked at least once.[2]
About Mersenne primes[edit]
Unsolved problem in mathematics:
Are there infinitely many Mersenne primes?
Many fundamental questions about Mersenne primes remain unresolved. It is not even known whether the set of Mersenne primes is finite or infinite. The Lenstra–Pomerance–Wagstaff conjecture asserts that there are infinitely many Mersenne primes and predicts their order of growth. It is also not known whether infinitely many Mersenne numbers with prime exponents are composite, although this would follow from widely believed conjectures about prime numbers, for example, the infinitude of Sophie Germain primes congruent to 3 (mod 4). For these primes p, 2p + 1 (which is also prime) will divide Mp, for example, 23 | M11, 47 | M23, 167 | M83, 263 | M131, 359 | M179, 383 | M191, 479 | M239, and 503 | M251 (sequence A002515 in the OEIS). Since for these primes p, 2p + 1 is congruent to 7 mod 8, so 2 is a quadratic residue mod 2p + 1, and the multiplicative order of 2 mod 2p + 1 must divide 



The first four Mersenne primes are M2 = 3, M3 = 7, M5 = 31 and M7 = 127 and because the first Mersenne prime starts at M2, all Mersenne primes are congruent to 3 (mod 4). Other than M0 = 0 and M1 = 1, all other Mersenne numbers are also congruent to 3 (mod 4). Consequently, in the prime factorization of a Mersenne number ( ≥ M2 ) there must be at least one prime factor congruent to 3 (mod 4).
A basic theorem about Mersenne numbers states that if Mp is prime, then the exponent p must also be prime. This follows from the identity
This rules out primality for Mersenne numbers with a composite exponent, such as M4 = 24 − 1 = 15 = 3 × 5 = (22 − 1) × (1 + 22).
Though the above examples might suggest that Mp is prime for all primes p, this is not the case, and the smallest counterexample is the Mersenne number
- M11 = 211 − 1 = 2047 = 23 × 89.
The evidence at hand suggests that a randomly selected Mersenne number is much more likely to be prime than an arbitrary randomly selected odd integer of similar size.[3] Nonetheless, prime values of Mp appear to grow increasingly sparse as p increases. For example, eight of the first 11 primes p give rise to a Mersenne prime Mp (the correct terms on Mersenne’s original list), while Mp is prime for only 43 of the first two million prime numbers (up to 32,452,843).
The current lack of any simple test to determine whether a given Mersenne number is prime makes the search for Mersenne primes a difficult task, since Mersenne numbers grow very rapidly. The Lucas–Lehmer primality test (LLT) is an efficient primality test that greatly aids this task, making it much easier to test the primality of Mersenne numbers than that of most other numbers of the same size. The search for the largest known prime has somewhat of a cult following.[citation needed] Consequently, a large amount of computer power has been expended searching for new Mersenne primes, much of which is now done using distributed computing.
Arithmetic modulo a Mersenne number is particularly efficient on a binary computer, making them popular choices when a prime modulus is desired, such as the Park–Miller random number generator. To find a primitive polynomial of Mersenne number order requires knowing the factorization of that number, so Mersenne primes allow one to find primitive polynomials of very high order. Such primitive trinomials are used in pseudorandom number generators with very large periods such as the Mersenne twister, generalized shift register and Lagged Fibonacci generators.
Perfect numbers[edit]
Mersenne primes Mp are closely connected to perfect numbers. In the 4th century BC, Euclid proved that if 2p − 1 is prime, then 2p − 1(2p − 1) is a perfect number. In the 18th century, Leonhard Euler proved that, conversely, all even perfect numbers have this form.[4] This is known as the Euclid–Euler theorem. It is unknown whether there are any odd perfect numbers.
History[edit]
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 |
|---|---|---|---|---|---|---|---|
| 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 |
| 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 |
| 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 |
| 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 |
| 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 |
| 269 | 271 | 277 | 281 | 283 | 293 | 307 | 311 |
| The first 64 prime exponents with those corresponding to Mersenne primes shaded in cyan and in bold, and those thought to do so by Mersenne in red and bold |
Mersenne primes take their name from the 17th-century French scholar Marin Mersenne, who compiled what was supposed to be a list of Mersenne primes with exponents up to 257. The exponents listed by Mersenne in 1644 were as follows:
-
- 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257.
His list replicated the known primes of his time with exponents up to 19. His next entry, 31, was correct, but the list then became largely incorrect, as Mersenne mistakenly included M67 and M257 (which are composite) and omitted M61, M89, and M107 (which are prime). Mersenne gave little indication of how he came up with his list.[5]
Édouard Lucas proved in 1876 that M127 is indeed prime, as Mersenne claimed. This was the largest known prime number for 75 years until 1951, when Ferrier found a larger prime, 
Searching for Mersenne primes[edit]
Fast algorithms for finding Mersenne primes are available, and as of June 2019, the eight largest known prime numbers are Mersenne primes.
The first four Mersenne primes M2 = 3, M3 = 7, M5 = 31 and M7 = 127 were known in antiquity. The fifth, M13 = 8191, was discovered anonymously before 1461; the next two (M17 and M19) were found by Pietro Cataldi in 1588. After nearly two centuries, M31 was verified to be prime by Leonhard Euler in 1772. The next (in historical, not numerical order) was M127, found by Édouard Lucas in 1876, then M61 by Ivan Mikheevich Pervushin in 1883. Two more (M89 and M107) were found early in the 20th century, by R. E. Powers in 1911 and 1914, respectively.
The most efficient method presently known for testing the primality of Mersenne numbers is the Lucas–Lehmer primality test. Specifically, it can be shown that for prime p > 2, Mp = 2p − 1 is prime if and only if Mp divides Sp − 2, where S0 = 4 and Sk = (Sk − 1)2 − 2 for k > 0.
During the era of manual calculation, all the exponents up to and including 257 were tested with the Lucas–Lehmer test and found to be composite. A notable contribution was made by retired Yale physics professor Horace Scudder Uhler, who did the calculations for exponents 157, 167, 193, 199, 227, and 229.[10] Unfortunately for those investigators, the interval they were testing contains the largest known relative gap between Mersenne primes: the next Mersenne prime exponent, 521, would turn out to be more than four times as large as the previous record of 127.
Graph of number of digits in largest known Mersenne prime by year – electronic era. The vertical scale is logarithmic in the number of digits, thus being a 
The search for Mersenne primes was revolutionized by the introduction of the electronic digital computer. Alan Turing searched for them on the Manchester Mark 1 in 1949,[11] but the first successful identification of a Mersenne prime, M521, by this means was achieved at 10:00 pm on January 30, 1952, using the U.S. National Bureau of Standards Western Automatic Computer (SWAC) at the Institute for Numerical Analysis at the University of California, Los Angeles, under the direction of D. H. Lehmer, with a computer search program written and run by Prof. R. M. Robinson. It was the first Mersenne prime to be identified in thirty-eight years; the next one, M607, was found by the computer a little less than two hours later. Three more — M1279, M2203, and M2281 — were found by the same program in the next several months. M4,423 was the first prime discovered with more than 1000 digits, M44,497 was the first with more than 10,000, and M6,972,593 was the first with more than a million. In general, the number of digits in the decimal representation of Mn equals ⌊n × log102⌋ + 1, where ⌊x⌋ denotes the floor function (or equivalently ⌊log10Mn⌋ + 1).
In September 2008, mathematicians at UCLA participating in the Great Internet Mersenne Prime Search (GIMPS) won part of a $100,000 prize from the Electronic Frontier Foundation for their discovery of a very nearly 13-million-digit Mersenne prime. The prize, finally confirmed in October 2009, is for the first known prime with at least 10 million digits. The prime was found on a Dell OptiPlex 745 on August 23, 2008. This was the eighth Mersenne prime discovered at UCLA.[12]
On April 12, 2009, a GIMPS server log reported that a 47th Mersenne prime had possibly been found. The find was first noticed on June 4, 2009, and verified a week later. The prime is 242,643,801 − 1. Although it is chronologically the 47th Mersenne prime to be discovered, it is smaller than the largest known at the time, which was the 45th to be discovered.
On January 25, 2013, Curtis Cooper, a mathematician at the University of Central Missouri, discovered a 48th Mersenne prime, 257,885,161 − 1 (a number with 17,425,170 digits), as a result of a search executed by a GIMPS server network.[13]
On January 19, 2016, Cooper published his discovery of a 49th Mersenne prime, 274,207,281 − 1 (a number with 22,338,618 digits), as a result of a search executed by a GIMPS server network.[14][15][16] This was the fourth Mersenne prime discovered by Cooper and his team in the past ten years.
On September 2, 2016, the Great Internet Mersenne Prime Search finished verifying all tests below M37,156,667, thus officially confirming its position as the 45th Mersenne prime.[17]
On January 3, 2018, it was announced that Jonathan Pace, a 51-year-old electrical engineer living in Germantown, Tennessee, had found a 50th Mersenne prime, 277,232,917 − 1 (a number with 23,249,425 digits), as a result of a search executed by a GIMPS server network.[18] The discovery was made by a computer in the offices of a church in the same town.[19][20]
On December 21, 2018, it was announced that The Great Internet Mersenne Prime Search (GIMPS) discovered the largest known prime number, 282,589,933 − 1, having 24,862,048 digits. A computer volunteered by Patrick Laroche from Ocala, Florida made the find on December 7, 2018.[21]
In late 2020, GIMPS began using a new technique to rule out potential Mersenne primes called the Probable prime (PRP) test, based on development from Robert Gerbicz in 2017, and a simple way to verify tests developed by Krzysztof Pietrzak in 2018. Due to the low error rate and ease of proof, this nearly halved the computing time to rule out potential primes over the Lucas-Lehmer test (as two users would no longer have to perform the same test to confirm the other’s result), although exponents passing the PRP test still require one to confirm their primality.[22]
Theorems about Mersenne numbers[edit]
- If a and p are natural numbers such that ap − 1 is prime, then a = 2 or p = 1.
- Proof: a ≡ 1 (mod a − 1). Then ap ≡ 1 (mod a − 1), so ap − 1 ≡ 0 (mod a − 1). Thus a − 1 | ap − 1. However, ap − 1 is prime, so a − 1 = ap − 1 or a − 1 = ±1. In the former case, a = ap, hence a = 0, 1 (which is a contradiction, as neither −1 nor 0 is prime) or p = 1. In the latter case, a = 2 or a = 0. If a = 0, however, 0p − 1 = 0 − 1 = −1 which is not prime. Therefore, a = 2.
- If 2p − 1 is prime, then p is prime.
- Proof: Suppose that p is composite, hence can be written p = ab with a and b > 1. Then 2p − 1 = 2ab − 1 = (2a)b − 1 = (2a − 1)((2a)b−1 + (2a)b−2 + … + 2a + 1) so 2p − 1 is composite. By contraposition, if 2p − 1 is prime then p is prime.
- If p is an odd prime, then every prime q that divides 2p − 1 must be 1 plus a multiple of 2p. This holds even when 2p − 1 is prime.
- For example, 25 − 1 = 31 is prime, and 31 = 1 + 3 × (2 × 5). A composite example is 211 − 1 = 23 × 89, where 23 = 1 + (2 × 11) and 89 = 1 + 4 × (2 × 11).
- Proof: By Fermat’s little theorem, q is a factor of 2q−1 − 1. Since q is a factor of 2p − 1, for all positive integers c, q is also a factor of 2pc − 1. Since p is prime and q is not a factor of 21 − 1, p is also the smallest positive integer x such that q is a factor of 2x − 1. As a result, for all positive integers x, q is a factor of 2x − 1 if and only if p is a factor of x. Therefore, since q is a factor of 2q−1 − 1, p is a factor of q − 1 so q ≡ 1 (mod p). Furthermore, since q is a factor of 2p − 1, which is odd, q is odd. Therefore, q ≡ 1 (mod 2p).
- This fact leads to a proof of Euclid’s theorem, which asserts the infinitude of primes, distinct from the proof written by Euclid: for every odd prime p, all primes dividing 2p − 1 are larger than p; thus there are always larger primes than any particular prime.
- It follows from this fact that for every prime p > 2, there is at least one prime of the form 2kp+1 less than or equal to Mp, for some integer k.
- If p is an odd prime, then every prime q that divides 2p − 1 is congruent to ±1 (mod
.
- Proof: 2p+1 ≡ 2 (mod q), so 21/2(p+1) is a square root of 2 mod q. By quadratic reciprocity, every prime modulus in which the number 2 has a square root is congruent to ±1 (mod
.
- Proof: 2p+1 ≡ 2 (mod q), so 21/2(p+1) is a square root of 2 mod q. By quadratic reciprocity, every prime modulus in which the number 2 has a square root is congruent to ±1 (mod
- A Mersenne prime cannot be a Wieferich prime.
- Proof: We show if p = 2m − 1 is a Mersenne prime, then the congruence 2p−1 ≡ 1 (mod p2) does not hold. By Fermat’s little theorem, m | p − 1. Therefore, one can write p − 1 = mλ. If the given congruence is satisfied, then p2 | 2mλ − 1, therefore 0 ≡ 2mλ − 1/2m − 1 = 1 + 2m + 22m + … + 2(λ − 1)m ≡ −λ mod (2m − 1). Hence 2m − 1 | λ, and therefore λ ≥ 2m − 1. This leads to p − 1 ≥ m(2m − 1), which is impossible since m ≥ 2.
- If m and n are natural numbers then m and n are coprime if and only if 2m − 1 and 2n − 1 are coprime. Consequently, a prime number divides at most one prime-exponent Mersenne number.[23] That is, the set of pernicious Mersenne numbers is pairwise coprime.
- If p and 2p + 1 are both prime (meaning that p is a Sophie Germain prime), and p is congruent to 3 (mod 4), then 2p + 1 divides 2p − 1.[24]
- Example: 11 and 23 are both prime, and 11 = 2 × 4 + 3, so 23 divides 211 − 1.
- Proof: Let q be 2p + 1. By Fermat’s little theorem, 22p ≡ 1 (mod q), so either 2p ≡ 1 (mod q) or 2p ≡ −1 (mod q). Supposing latter true, then 2p+1 = (21/2(p + 1))2 ≡ −2 (mod q), so −2 would be a quadratic residue mod q. However, since p is congruent to 3 (mod 4), q is congruent to 7 (mod
and therefore 2 is a quadratic residue mod q. Also since q is congruent to 3 (mod 4), −1 is a quadratic nonresidue mod q, so −2 is the product of a residue and a nonresidue and hence it is a nonresidue, which is a contradiction. Hence, the former congruence must be true and 2p + 1 divides Mp.
- All composite divisors of prime-exponent Mersenne numbers are strong pseudoprimes to the base 2.
- With the exception of 1, a Mersenne number cannot be a perfect power. That is, and in accordance with Mihăilescu’s theorem, the equation 2m − 1 = nk has no solutions where m, n, and k are integers with m > 1 and k > 1.
List of known Mersenne primes[edit]
As of 2023, the 51 known Mersenne primes are 2p − 1 for the following p:
- 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, 43112609, 57885161, 74207281, 77232917, 82589933. (sequence A000043 in the OEIS)
Factorization of composite Mersenne numbers[edit]
Since they are prime numbers, Mersenne primes are divisible only by 1 and themselves. However, not all Mersenne numbers are Mersenne primes. Mersenne numbers are very good test cases for the special number field sieve algorithm, so often the largest number factorized with this algorithm has been a Mersenne number. As of June 2019, 21,193 − 1 is the record-holder,[25] having been factored with a variant of the special number field sieve that allows the factorization of several numbers at once. See integer factorization records for links to more information. The special number field sieve can factorize numbers with more than one large factor. If a number has only one very large factor then other algorithms can factorize larger numbers by first finding small factors and then running a primality test on the cofactor. As of September 2022, the largest completely factored number (with probable prime factors allowed) is 212,720,787 − 1 = 1,119,429,257 × 175,573,124,547,437,977 × 8,480,999,878,421,106,991 × q, where q is a 3,829,294-digit probable prime. It was discovered by a GIMPS participant with nickname «Funky Waddle».[26][27] As of September 2022, the Mersenne number M1277 is the smallest composite Mersenne number with no known factors; it has no prime factors below 268,[28] and is very unlikely to have any factors below 1065 (~2216).[29]
The table below shows factorizations for the first 20 composite Mersenne numbers (sequence A244453 in the OEIS).
| p | Mp | Factorization of Mp |
|---|---|---|
| 11 | 2047 | 23 × 89 |
| 23 | 8388607 | 47 × 178,481 |
| 29 | 536870911 | 233 × 1,103 × 2,089 |
| 37 | 137438953471 | 223 × 616,318,177 |
| 41 | 2199023255551 | 13,367 × 164,511,353 |
| 43 | 8796093022207 | 431 × 9,719 × 2,099,863 |
| 47 | 140737488355327 | 2,351 × 4,513 × 13,264,529 |
| 53 | 9007199254740991 | 6,361 × 69,431 × 20,394,401 |
| 59 | 576460752303423487 | 179,951 × 3,203,431,780,337 (13 digits) |
| 67 | 147573952589676412927 | 193,707,721 × 761,838,257,287 (12 digits) |
| 71 | 2361183241434822606847 | 228,479 × 48,544,121 × 212,885,833 |
| 73 | 9444732965739290427391 | 439 × 2,298,041 × 9,361,973,132,609 (13 digits) |
| 79 | 604462909807314587353087 | 2,687 × 202,029,703 × 1,113,491,139,767 (13 digits) |
| 83 | 967140655691…033397649407 | 167 × 57,912,614,113,275,649,087,721 (23 digits) |
| 97 | 158456325028…187087900671 | 11,447 × 13,842,607,235,828,485,645,766,393 (26 digits) |
| 101 | 253530120045…993406410751 | 7,432,339,208,719 (13 digits) × 341,117,531,003,194,129 (18 digits) |
| 103 | 101412048018…973625643007 | 2,550,183,799 × 3,976,656,429,941,438,590,393 (22 digits) |
| 109 | 649037107316…312041152511 | 745,988,807 × 870,035,986,098,720,987,332,873 (24 digits) |
| 113 | 103845937170…992658440191 | 3,391 × 23,279 × 65,993 × 1,868,569 × 1,066,818,132,868,207 (16 digits) |
| 131 | 272225893536…454145691647 | 263 × 10,350,794,431,055,162,386,718,619,237,468,234,569 (38 digits) |
The number of factors for the first 500 Mersenne numbers can be found at (sequence A046800 in the OEIS).
Mersenne numbers in nature and elsewhere[edit]
In the mathematical problem Tower of Hanoi, solving a puzzle with an n-disc tower requires Mn steps, assuming no mistakes are made.[30] The number of rice grains on the whole chessboard in the wheat and chessboard problem is M64.[31]
The asteroid with minor planet number 8191 is named 8191 Mersenne after Marin Mersenne, because 8191 is a Mersenne prime (3 Juno, 7 Iris, 31 Euphrosyne and 127 Johanna having been discovered and named during the 19th century).[32]
In geometry, an integer right triangle that is primitive and has its even leg a power of 2 ( ≥ 4 ) generates a unique right triangle such that its inradius is always a Mersenne number. For example, if the even leg is 2n + 1 then because it is primitive it constrains the odd leg to be 4n − 1, the hypotenuse to be 4n + 1 and its inradius to be 2n − 1.[33]
Mersenne–Fermat primes[edit]
A Mersenne–Fermat number is defined as 2pr − 1/2pr − 1 − 1, with p prime, r natural number, and can be written as MF(p, r). When r = 1, it is a Mersenne number. When p = 2, it is a Fermat number. The only known Mersenne–Fermat primes with r > 1 are
- MF(2, 2), MF(2, 3), MF(2, 4), MF(2, 5), MF(3, 2), MF(3, 3), MF(7, 2), and MF(59, 2).[34]
In fact, MF(p, r) = Φpr(2), where Φ is the cyclotomic polynomial.
Generalizations[edit]
The simplest generalized Mersenne primes are prime numbers of the form f(2n), where f(x) is a low-degree polynomial with small integer coefficients.[35] An example is 264 − 232 + 1, in this case, n = 32, and f(x) = x2 − x + 1; another example is 2192 − 264 − 1, in this case, n = 64, and f(x) = x3 − x − 1.
It is also natural to try to generalize primes of the form 2n − 1 to primes of the form bn − 1 (for b ≠ 2 and n > 1). However (see also theorems above), bn − 1 is always divisible by b − 1, so unless the latter is a unit, the former is not a prime. This can be remedied by allowing b to be an algebraic integer instead of an integer:
Complex numbers[edit]
In the ring of integers (on real numbers), if b − 1 is a unit, then b is either 2 or 0. But 2n − 1 are the usual Mersenne primes, and the formula 0n − 1 does not lead to anything interesting (since it is always −1 for all n > 0). Thus, we can regard a ring of «integers» on complex numbers instead of real numbers, like Gaussian integers and Eisenstein integers.
Gaussian Mersenne primes[edit]
If we regard the ring of Gaussian integers, we get the case b = 1 + i and b = 1 − i, and can ask (WLOG) for which n the number (1 + i)n − 1 is a Gaussian prime which will then be called a Gaussian Mersenne prime.[36]
(1 + i)n − 1 is a Gaussian prime for the following n:
- 2, 3, 5, 7, 11, 19, 29, 47, 73, 79, 113, 151, 157, 163, 167, 239, 241, 283, 353, 367, 379, 457, 997, 1367, 3041, 10141, 14699, 27529, 49207, 77291, 85237, 106693, 160423, 203789, 364289, 991961, 1203793, 1667321, 3704053, 4792057, … (sequence A057429 in the OEIS)
Like the sequence of exponents for usual Mersenne primes, this sequence contains only (rational) prime numbers.
As for all Gaussian primes, the norms (that is, squares of absolute values) of these numbers are rational primes:
- 5, 13, 41, 113, 2113, 525313, 536903681, 140737471578113, … (sequence A182300 in the OEIS).
Eisenstein Mersenne primes[edit]
One may encounter cases where such a Mersenne prime is also an Eisenstein prime, being of the form b = 1 + ω and b = 1 − ω. In these cases, such numbers are called Eisenstein Mersenne primes.
(1 + ω)n − 1 is an Eisenstein prime for the following n:
- 2, 5, 7, 11, 17, 19, 79, 163, 193, 239, 317, 353, 659, 709, 1049, 1103, 1759, 2029, 5153, 7541, 9049, 10453, 23743, 255361, 534827, 2237561, … (sequence A066408 in the OEIS)
The norms (that is, squares of absolute values) of these Eisenstein primes are rational primes:
- 7, 271, 2269, 176419, 129159847, 1162320517, … (sequence A066413 in the OEIS)
Divide an integer[edit]
Repunit primes[edit]
The other way to deal with the fact that bn − 1 is always divisible by b − 1, it is to simply take out this factor and ask which values of n make
be prime. (The integer b can be either positive or negative.) If, for example, we take b = 10, we get n values of:
- 2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343, … (sequence A004023 in the OEIS),
corresponding to primes 11, 1111111111111111111, 11111111111111111111111, … (sequence A004022 in the OEIS).
These primes are called repunit primes. Another example is when we take b = −12, we get n values of:
- 2, 5, 11, 109, 193, 1483, 11353, 21419, 21911, 24071, 106859, 139739, … (sequence A057178 in the OEIS),
corresponding to primes −11, 19141, 57154490053, ….
It is a conjecture that for every integer b which is not a perfect power, there are infinitely many values of n such that bn − 1/b − 1 is prime. (When b is a perfect power, it can be shown that there is at most one n value such that bn − 1/b − 1 is prime)
Least n such that bn − 1/b − 1 is prime are (starting with b = 2, 0 if no such n exists)
- 2, 3, 2, 3, 2, 5, 3, 0, 2, 17, 2, 5, 3, 3, 2, 3, 2, 19, 3, 3, 2, 5, 3, 0, 7, 3, 2, 5, 2, 7, 0, 3, 13, 313, 2, 13, 3, 349, 2, 3, 2, 5, 5, 19, 2, 127, 19, 0, 3, 4229, 2, 11, 3, 17, 7, 3, 2, 3, 2, 7, 3, 5, 0, 19, 2, 19, 5, 3, 2, 3, 2, … (sequence A084740 in the OEIS)
For negative bases b, they are (starting with b = −2, 0 if no such n exists)
- 3, 2, 2, 5, 2, 3, 2, 3, 5, 5, 2, 3, 2, 3, 3, 7, 2, 17, 2, 3, 3, 11, 2, 3, 11, 0, 3, 7, 2, 109, 2, 5, 3, 11, 31, 5, 2, 3, 53, 17, 2, 5, 2, 103, 7, 5, 2, 7, 1153, 3, 7, 21943, 2, 3, 37, 53, 3, 17, 2, 7, 2, 3, 0, 19, 7, 3, 2, 11, 3, 5, 2, … (sequence A084742 in the OEIS) (notice this OEIS sequence does not allow n = 2)
Least base b such that bprime(n) − 1/b − 1 is prime are
- 2, 2, 2, 2, 5, 2, 2, 2, 10, 6, 2, 61, 14, 15, 5, 24, 19, 2, 46, 3, 11, 22, 41, 2, 12, 22, 3, 2, 12, 86, 2, 7, 13, 11, 5, 29, 56, 30, 44, 60, 304, 5, 74, 118, 33, 156, 46, 183, 72, 606, 602, 223, 115, 37, 52, 104, 41, 6, 338, 217, … (sequence A066180 in the OEIS)
For negative bases b, they are
- 3, 2, 2, 2, 2, 2, 2, 2, 2, 7, 2, 16, 61, 2, 6, 10, 6, 2, 5, 46, 18, 2, 49, 16, 70, 2, 5, 6, 12, 92, 2, 48, 89, 30, 16, 147, 19, 19, 2, 16, 11, 289, 2, 12, 52, 2, 66, 9, 22, 5, 489, 69, 137, 16, 36, 96, 76, 117, 26, 3, … (sequence A103795 in the OEIS)
Other generalized Mersenne primes[edit]
Another generalized Mersenne number is
with a, b any coprime integers, a > 1 and −a < b < a. (Since an − bn is always divisible by a − b, the division is necessary for there to be any chance of finding prime numbers.)[a] We can ask which n makes this number prime. It can be shown that such n must be primes themselves or equal to 4, and n can be 4 if and only if a + b = 1 and a2 + b2 is prime.[b] It is a conjecture that for any pair (a, b) such that a and b are not both perfect rth powers for any r and −4ab is not a perfect fourth power, there are infinitely many values of n such that an − bn/a − b is prime.[c] However, this has not been proved for any single value of (a, b).
| a | b | numbers n such that an − bn/a − b is prime (some large terms are only probable primes, these n are checked up to 100000 for |b| ≤ 5 or |b| = a − 1, 20000 for 5 < |b| < a − 1) |
OEIS sequence |
|---|---|---|---|
| 2 | 1 | 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, 43112609, 57885161, …, 74207281, …, 77232917, …, 82589933, … | A000043 |
| 2 | −1 | 3, 4*, 5, 7, 11, 13, 17, 19, 23, 31, 43, 61, 79, 101, 127, 167, 191, 199, 313, 347, 701, 1709, 2617, 3539, 5807, 10501, 10691, 11279, 12391, 14479, 42737, 83339, 95369, 117239, 127031, 138937, 141079, 267017, 269987, 374321, 986191, 4031399, …, 13347311, 13372531, … | A000978 |
| 3 | 2 | 2, 3, 5, 17, 29, 31, 53, 59, 101, 277, 647, 1061, 2381, 2833, 3613, 3853, 3929, 5297, 7417, 90217, 122219, 173191, 256199, 336353, 485977, 591827, 1059503, … | A057468 |
| 3 | 1 | 3, 7, 13, 71, 103, 541, 1091, 1367, 1627, 4177, 9011, 9551, 36913, 43063, 49681, 57917, 483611, 877843, … | A028491 |
| 3 | −1 | 2*, 3, 5, 7, 13, 23, 43, 281, 359, 487, 577, 1579, 1663, 1741, 3191, 9209, 11257, 12743, 13093, 17027, 26633, 104243, 134227, 152287, 700897, 1205459, … | A007658 |
| 3 | −2 | 3, 4*, 7, 11, 83, 149, 223, 599, 647, 1373, 8423, 149497, 388897, … | A057469 |
| 4 | 3 | 2, 3, 7, 17, 59, 283, 311, 383, 499, 521, 541, 599, 1193, 1993, 2671, 7547, 24019, 46301, 48121, 68597, 91283, 131497, 148663, 184463, 341233, … | A059801 |
| 4 | 1 | 2 (no others) | |
| 4 | −1 | 2*, 3 (no others) | |
| 4 | −3 | 3, 5, 19, 37, 173, 211, 227, 619, 977, 1237, 2437, 5741, 13463, 23929, 81223, 121271, … | A128066 |
| 5 | 4 | 3, 43, 59, 191, 223, 349, 563, 709, 743, 1663, 5471, 17707, 19609, 35449, 36697, 45259, 91493, 246497, 265007, 289937, … | A059802 |
| 5 | 3 | 13, 19, 23, 31, 47, 127, 223, 281, 2083, 5281, 7411, 7433, 19051, 27239, 35863, 70327, … | A121877 |
| 5 | 2 | 2, 5, 7, 13, 19, 37, 59, 67, 79, 307, 331, 599, 1301, 12263, 12589, 18443, 20149, 27983, … | A082182 |
| 5 | 1 | 3, 7, 11, 13, 47, 127, 149, 181, 619, 929, 3407, 10949, 13241, 13873, 16519, 201359, 396413, 1888279, … | A004061 |
| 5 | −1 | 5, 67, 101, 103, 229, 347, 4013, 23297, 30133, 177337, 193939, 266863, 277183, 335429, … | A057171 |
| 5 | −2 | 2*, 3, 17, 19, 47, 101, 1709, 2539, 5591, 6037, 8011, 19373, 26489, 27427, … | A082387 |
| 5 | −3 | 2*, 3, 5, 7, 17, 19, 109, 509, 661, 709, 1231, 12889, 13043, 26723, 43963, 44789, … | A122853 |
| 5 | −4 | 4*, 5, 7, 19, 29, 61, 137, 883, 1381, 1823, 5227, 25561, 29537, 300893, … | A128335 |
| 6 | 5 | 2, 5, 11, 13, 23, 61, 83, 421, 1039, 1511, 31237, 60413, 113177, 135647, 258413, … | A062572 |
| 6 | 1 | 2, 3, 7, 29, 71, 127, 271, 509, 1049, 6389, 6883, 10613, 19889, 79987, 608099, … | A004062 |
| 6 | −1 | 2*, 3, 11, 31, 43, 47, 59, 107, 811, 2819, 4817, 9601, 33581, 38447, 41341, 131891, 196337, … | A057172 |
| 6 | −5 | 3, 4*, 5, 17, 397, 409, 643, 1783, 2617, 4583, 8783, … | A128336 |
| 7 | 6 | 2, 3, 7, 29, 41, 67, 1327, 1399, 2027, 69371, 86689, 355039, … | A062573 |
| 7 | 5 | 3, 5, 7, 113, 397, 577, 7573, 14561, 58543, … | A128344 |
| 7 | 4 | 2, 5, 11, 61, 619, 2879, 2957, 24371, 69247, … | A213073 |
| 7 | 3 | 3, 7, 19, 109, 131, 607, 863, 2917, 5923, 12421, … | A128024 |
| 7 | 2 | 3, 7, 19, 79, 431, 1373, 1801, 2897, 46997, … | A215487 |
| 7 | 1 | 5, 13, 131, 149, 1699, 14221, 35201, 126037, 371669, 1264699, … | A004063 |
| 7 | −1 | 3, 17, 23, 29, 47, 61, 1619, 18251, 106187, 201653, … | A057173 |
| 7 | −2 | 2*, 5, 23, 73, 101, 401, 419, 457, 811, 1163, 1511, 8011, … | A125955 |
| 7 | −3 | 3, 13, 31, 313, 3709, 7933, 14797, 30689, 38333, … | A128067 |
| 7 | −4 | 2*, 3, 5, 19, 41, 47, 8231, 33931, 43781, 50833, 53719, 67211, … | A218373 |
| 7 | −5 | 2*, 11, 31, 173, 271, 547, 1823, 2111, 5519, 7793, 22963, 41077, 49739, … | A128337 |
| 7 | −6 | 3, 53, 83, 487, 743, … | A187805 |
| 8 | 7 | 7, 11, 17, 29, 31, 79, 113, 131, 139, 4357, 44029, 76213, 83663, 173687, 336419, 615997, … | A062574 |
| 8 | 5 | 2, 19, 1021, 5077, 34031, 46099, 65707, … | A128345 |
| 8 | 3 | 2, 3, 7, 19, 31, 67, 89, 9227, 43891, … | A128025 |
| 8 | 1 | 3 (no others) | |
| 8 | −1 | 2* (no others) | |
| 8 | −3 | 2*, 5, 163, 191, 229, 271, 733, 21059, 25237, … | A128068 |
| 8 | −5 | 2*, 7, 19, 167, 173, 223, 281, 21647, … | A128338 |
| 8 | −7 | 4*, 7, 13, 31, 43, 269, 353, 383, 619, 829, 877, 4957, 5711, 8317, 21739, 24029, 38299, … | A181141 |
| 9 | 8 | 2, 7, 29, 31, 67, 149, 401, 2531, 19913, 30773, 53857, 170099, … | A059803 |
| 9 | 7 | 3, 5, 7, 4703, 30113, … | A273010 |
| 9 | 5 | 3, 11, 17, 173, 839, 971, 40867, 45821, … | A128346 |
| 9 | 4 | 2 (no others) | |
| 9 | 2 | 2, 3, 5, 13, 29, 37, 1021, 1399, 2137, 4493, 5521, … | A173718 |
| 9 | 1 | (none) | |
| 9 | −1 | 3, 59, 223, 547, 773, 1009, 1823, 3803, 49223, 193247, 703393, … | A057175 |
| 9 | −2 | 2*, 3, 7, 127, 283, 883, 1523, 4001, … | A125956 |
| 9 | −4 | 2*, 3, 5, 7, 11, 17, 19, 41, 53, 109, 167, 2207, 3623, 5059, 5471, 7949, 21211, 32993, 60251, … | A211409 |
| 9 | −5 | 3, 5, 13, 17, 43, 127, 229, 277, 6043, 11131, 11821, … | A128339 |
| 9 | −7 | 2*, 3, 107, 197, 2843, 3571, 4451, …, 31517, … | A301369 |
| 9 | −8 | 3, 7, 13, 19, 307, 619, 2089, 7297, 75571, 76103, 98897, … | A187819 |
| 10 | 9 | 2, 3, 7, 11, 19, 29, 401, 709, 2531, 15787, 66949, 282493, … | A062576 |
| 10 | 7 | 2, 31, 103, 617, 10253, 10691, … | A273403 |
| 10 | 3 | 2, 3, 5, 37, 599, 38393, 51431, … | A128026 |
| 10 | 1 | 2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343, … | A004023 |
| 10 | −1 | 5, 7, 19, 31, 53, 67, 293, 641, 2137, 3011, 268207, … | A001562 |
| 10 | −3 | 2*, 3, 19, 31, 101, 139, 167, 1097, 43151, 60703, 90499, … | A128069 |
| 10 | −7 | 2*, 3, 5, 11, 19, 1259, 1399, 2539, 2843, 5857, 10589, … | |
| 10 | −9 | 4*, 7, 67, 73, 1091, 1483, 10937, … | A217095 |
| 11 | 10 | 3, 5, 19, 311, 317, 1129, 4253, 7699, 18199, 35153, 206081, … | A062577 |
| 11 | 9 | 5, 31, 271, 929, 2789, 4153, … | A273601 |
| 11 | 8 | 2, 7, 11, 17, 37, 521, 877, 2423, … | A273600 |
| 11 | 7 | 5, 19, 67, 107, 593, 757, 1801, 2243, 2383, 6043, 10181, 11383, 15629, … | A273599 |
| 11 | 6 | 2, 3, 11, 163, 191, 269, 1381, 1493, … | A273598 |
| 11 | 5 | 5, 41, 149, 229, 263, 739, 3457, 20269, 98221, … | A128347 |
| 11 | 4 | 3, 5, 11, 17, 71, 89, 827, 22307, 45893, 63521, … | A216181 |
| 11 | 3 | 3, 5, 19, 31, 367, 389, 431, 2179, 10667, 13103, 90397, … | A128027 |
| 11 | 2 | 2, 5, 11, 13, 331, 599, 18839, 23747, 24371, 29339, 32141, 67421, … | A210506 |
| 11 | 1 | 17, 19, 73, 139, 907, 1907, 2029, 4801, 5153, 10867, 20161, 293831, … | A005808 |
| 11 | −1 | 5, 7, 179, 229, 439, 557, 6113, 223999, 327001, … | A057177 |
| 11 | −2 | 3, 5, 17, 67, 83, 101, 1373, 6101, 12119, 61781, … | A125957 |
| 11 | −3 | 3, 103, 271, 523, 23087, 69833, … | A128070 |
| 11 | −4 | 2*, 7, 53, 67, 71, 443, 26497, … | A224501 |
| 11 | −5 | 7, 11, 181, 421, 2297, 2797, 4129, 4139, 7151, 29033, … | A128340 |
| 11 | −6 | 2*, 5, 7, 107, 383, 17359, 21929, 26393, … | |
| 11 | −7 | 7, 1163, 4007, 10159, … | |
| 11 | −8 | 2*, 3, 13, 31, 59, 131, 223, 227, 1523, … | |
| 11 | −9 | 2*, 3, 17, 41, 43, 59, 83, … | |
| 11 | −10 | 53, 421, 647, 1601, 35527, … | A185239 |
| 12 | 11 | 2, 3, 7, 89, 101, 293, 4463, 70067, … | A062578 |
| 12 | 7 | 2, 3, 7, 13, 47, 89, 139, 523, 1051, … | A273814 |
| 12 | 5 | 2, 3, 31, 41, 53, 101, 421, 1259, 4721, 45259, … | A128348 |
| 12 | 1 | 2, 3, 5, 19, 97, 109, 317, 353, 701, 9739, 14951, 37573, 46889, 769543, … | A004064 |
| 12 | −1 | 2*, 5, 11, 109, 193, 1483, 11353, 21419, 21911, 24071, 106859, 139739, … | A057178 |
| 12 | −5 | 2*, 3, 5, 13, 347, 977, 1091, 4861, 4967, 34679, … | A128341 |
| 12 | −7 | 2*, 3, 7, 67, 79, 167, 953, 1493, 3389, 4871, … | |
| 12 | −11 | 47, 401, 509, 8609, … | A213216 |
*Note: if b < 0 and n is even, then the numbers n are not included in the corresponding OEIS sequence.
When a = b + 1, it is (b + 1)n − bn, a difference of two consecutive perfect nth powers, and if an − bn is prime, then a must be b + 1, because it is divisible by a − b.
Least n such that (b + 1)n − bn is prime are
- 2, 2, 2, 3, 2, 2, 7, 2, 2, 3, 2, 17, 3, 2, 2, 5, 3, 2, 5, 2, 2, 229, 2, 3, 3, 2, 3, 3, 2, 2, 5, 3, 2, 3, 2, 2, 3, 3, 2, 7, 2, 3, 37, 2, 3, 5, 58543, 2, 3, 2, 2, 3, 2, 2, 3, 2, 5, 3, 4663, 54517, 17, 3, 2, 5, 2, 3, 3, 2, 2, 47, 61, 19, … (sequence A058013 in the OEIS)
Least b such that (b + 1)prime(n) − bprime(n) is prime are
- 1, 1, 1, 1, 5, 1, 1, 1, 5, 2, 1, 39, 6, 4, 12, 2, 2, 1, 6, 17, 46, 7, 5, 1, 25, 2, 41, 1, 12, 7, 1, 7, 327, 7, 8, 44, 26, 12, 75, 14, 51, 110, 4, 14, 49, 286, 15, 4, 39, 22, 109, 367, 22, 67, 27, 95, 80, 149, 2, 142, 3, 11, … (sequence A222119 in the OEIS)
See also[edit]
- Repunit
- Fermat prime
- Power of two
- Erdős–Borwein constant
- Mersenne conjectures
- Mersenne twister
- Double Mersenne number
- Prime95 / MPrime
- Great Internet Mersenne Prime Search (GIMPS)
- Largest known prime number
- Wieferich prime
- Wagstaff prime
- Cullen prime
- Woodall prime
- Proth prime
- Solinas prime
- Gillies’ conjecture
- Williams number
Notes[edit]
- ^ This number is the same as the Lucas number Un(a + b, ab), since a and b are the roots of the quadratic equation x2 − (a + b)x + ab = 0.
- ^ Since a4 − b4/a − b = (a + b)(a2 + b2). Thus, in this case the pair (a, b) must be (x + 1, −x) and x2 + (x + 1)2 must be prime. That is, x must be in OEIS: A027861.
- ^ When a and b are both perfect rth powers for some r > 1 or when −4ab is a perfect fourth power, it can be shown that there are at most two values of n with this property: in these cases, an − bn/a − b can be factored algebraically.[citation needed]
References[edit]
- ^ «GIMPS Project Discovers Largest Known Prime Number: 282,589,933-1″. Mersenne Research, Inc. 21 December 2018. Retrieved 21 December 2018.
- ^ «GIMPS Milestones Report». Mersenne.org. Mersenne Research, Inc. Retrieved 5 December 2020.
- ^ Caldwell, Chris. «Heuristics: Deriving the Wagstaff Mersenne Conjecture».
- ^ Chris K. Caldwell, Mersenne Primes: History, Theorems and Lists
- ^ The Prime Pages, Mersenne’s conjecture.
- ^ Hardy, G. H.; Wright, E. M. (1959). An Introduction to the Theory of Numbers (4th ed.). Oxford University Press.
- ^ Cole, F. N. (1 December 1903). «On the factoring of large numbers». Bulletin of the American Mathematical Society. 10 (3): 134–138. doi:10.1090/S0002-9904-1903-01079-9.
- ^ Bell, E.T. and Mathematical Association of America (1951). Mathematics, queen and servant of science. McGraw-Hill New York. p. 228.
- ^ «h2g2: Mersenne Numbers». BBC News. Archived from the original on December 5, 2014.
- ^ Horace S. Uhler (1952). «A Brief History of the Investigations on Mersenne Numbers and the Latest Immense Primes». Scripta Mathematica. 18: 122–131.
- ^ Brian Napper, The Mathematics Department and the Mark 1.
- ^ Maugh II, Thomas H. (2008-09-27). «UCLA mathematicians discover a 13-million-digit prime number». Los Angeles Times. Retrieved 2011-05-21.
- ^ Tia Ghose. «Largest Prime Number Discovered». Scientific American. Retrieved 2013-02-07.
- ^ Cooper, Curtis (7 January 2016). «Mersenne Prime Number discovery – 274207281 − 1 is Prime!». Mersenne Research, Inc. Retrieved 22 January 2016.
- ^ Brook, Robert (January 19, 2016). «Prime number with 22 million digits is the biggest ever found». New Scientist. Retrieved 19 January 2016.
- ^ Chang, Kenneth (21 January 2016). «New Biggest Prime Number = 2 to the 74 Mil … Uh, It’s Big». The New York Times. Retrieved 22 January 2016.
- ^ «Milestones». Archived from the original on 2016-09-03.
- ^ «Mersenne Prime Discovery — 2^77232917-1 is Prime!». www.mersenne.org. Retrieved 2018-01-03.
- ^ «Largest-known prime number found on church computer». christianchronicle.org. January 12, 2018.
- ^ «Found: A Special, Mind-Bogglingly Large Prime Number». January 5, 2018.
- ^ «GIMPS Discovers Largest Known Prime Number: 2^82,589,933-1». Retrieved 2019-01-01.
- ^ «GIMPS — The Math — PrimeNet». www.mersenne.org. Retrieved 29 June 2021.
- ^ Will Edgington’s Mersenne Page Archived 2014-10-14 at the Wayback Machine
- ^ Caldwell, Chris K. «Proof of a result of Euler and Lagrange on Mersenne Divisors». Prime Pages.
- ^ Kleinjung, Thorsten; Bos, Joppe W.; Lenstra, Arjen K. (2014). «Mersenne Factorization Factory». Advances in Cryptology – ASIACRYPT 2014. Lecture Notes in Computer Science. Vol. 8874. pp. 358–377. doi:10.1007/978-3-662-45611-8_19. ISBN 978-3-662-45607-1.
- ^ Henri Lifchitz and Renaud Lifchitz. «PRP Top Records». Retrieved 2022-09-05.
- ^ «M12720787 Mersenne number exponent details». www.mersenne.ca. Retrieved 5 September 2022.
- ^ «Exponent Status for M1277». Retrieved 2021-07-21.
- ^ «M1277 Mersenne number exponent details». www.mersenne.ca. Retrieved 24 June 2022.
- ^ Petković, Miodrag (2009). Famous Puzzles of Great Mathematicians. AMS Bookstore. p. 197. ISBN 978-0-8218-4814-2.
- ^ Weisstein, Eric W. «Wheat and Chessboard Problem». Mathworld. Wolfram. Retrieved 2023-02-11.
- ^ Alan Chamberlin. «JPL Small-Body Database Browser». Ssd.jpl.nasa.gov. Retrieved 2011-05-21.
- ^ «OEIS A016131». The On-Line Encyclopedia of Integer Sequences.
- ^ «A research of Mersenne and Fermat primes». Archived from the original on 2012-05-29.
- ^ Solinas, Jerome A. (1 January 2011). «Generalized Mersenne Prime». In Tilborg, Henk C. A. van; Jajodia, Sushil (eds.). Encyclopedia of Cryptography and Security. Springer US. pp. 509–510. doi:10.1007/978-1-4419-5906-5_32. ISBN 978-1-4419-5905-8.
- ^ Chris Caldwell: The Prime Glossary: Gaussian Mersenne (part of the Prime Pages)
- ^ Zalnezhad, Ali; Zalnezhad, Hossein; Shabani, Ghasem; Zalnezhad, Mehdi (March 2015). «Relationships and Algorithm in order to Achieve the Largest Primes». arXiv:1503.07688 [math.NT].
- ^ (x, 1) and (x, −1) for x = 2 to 50
- ^ (x, 1) for x = 2 to 160
- ^ (x, −1) for x = 2 to 160
- ^ (x + 1, x) for x = 1 to 160
- ^ (x + 1, −x) for x = 1 to 40
- ^ (x + 2, x) for odd x = 1 to 107
- ^ (x, −1) for x = 2 to 200
- ^ PRP records, search for
, that is, (a, b)
- ^ PRP records, search for
, that is, (a, −b)
External links[edit]
- «Mersenne number», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- GIMPS home page
- GIMPS Milestones Report – status page gives various statistics on search progress, typically updated every week, including progress towards proving the ordering of the largest known Mersenne primes
- GIMPS, known factors of Mersenne numbers
- Mq = (8x)2 − (3qy)2 Property of Mersenne numbers with prime exponent that are composite (PDF)
- Mq = x2 + d·y2 math thesis (PS)
- Grime, James. «31 and Mersenne Primes». Numberphile. Brady Haran. Archived from the original on 2013-05-31. Retrieved 2013-04-06.
- Mersenne prime bibliography with hyperlinks to original publications
- report about Mersenne primes – detection in detail (in German)
- GIMPS wiki
- Will Edgington’s Mersenne Page – contains factors for small Mersenne numbers
- Known factors of Mersenne numbers
- Decimal digits and English names of Mersenne primes
- Prime curios: 2305843009213693951
- http://www.leyland.vispa.com/numth/factorization/cunningham/2-.txt Archived 2014-11-05 at the Wayback Machine
- http://www.leyland.vispa.com/numth/factorization/cunningham/2+.txt Archived 2013-05-02 at the Wayback Machine
- OEIS sequence A250197 (Numbers n such that the left Aurifeuillian primitive part of 2^n+1 is prime) – Factorization of Mersenne numbers Mn (n up to 1280)
- Factorization of completely factored Mersenne numbers
- The Cunningham project, factorization of bn ± 1, b = 2, 3, 5, 6, 7, 10, 11, 12
- http://www.leyland.vispa.com/numth/factorization/cunningham/main.htm Archived 2016-03-04 at the Wayback Machine
- http://www.leyland.vispa.com/numth/factorization/anbn/main.htm Archived 2016-02-02 at the Wayback Machine
MathWorld links[edit]
- Weisstein, Eric W. «Mersenne number». MathWorld.
- Weisstein, Eric W. «Mersenne prime». MathWorld.
Числа Мерсенна в природе и в других местах
В математической задаче Ханойская башня для решения головоломки с башней из n дисков требуется M n шаги, если не допустить ошибок. The number of rice grains on the whole chessboard in the wheat and chessboard problem is M64.
The asteroid with minor planet number 8191 is named 8191 Mersenne after Marin Mersenne, because 8191 is a Mersenne prime (3 Juno, 7 Iris, 31 Euphrosyne and 127 Johanna having been discovered and named during the 19th century).
In geometry, an integer right triangle that is primitive and has its even leg a power of 2 ( ≥ 4) generates a unique right triangle such that its inradius is always a Mersenne number. For example, if the even leg is 2 then because it is primitive it constrains the odd leg to be 4 − 1, the hypotenuse to be 4 + 1 and its inradius to be 2 − 1.
The Mersenne numbers were studied with respect to the total number of accepting paths of non-deterministic polynomial time Turing machines in 2018 and intriguing inclusions were discovered.
Mersenne–Fermat primes
A Mersenne–Fermat numberis defined as 2 − 1/2 − 1, with p prime, r natural number, and can be written as MF(p, r). Когда r = 1, это число Мерсенна. When p = 2, it is a Fermat number. The only known Mersenne–Fermat primes with r>1 are
- MF(2, 2), MF( 2, 3), MF (2, 4), MF (2, 5), MF (3, 2), MF (3, 3), MF (7, 2) и MF (59, 2).
Фактически, MF (p, r) = Φ p (2), где Φ — циклотомический многочлен.
Обобщения
Простейшие обобщенные простые числа Мерсенна — это простые числа вида f (2), где f (x) — многочлен низкой степени с малыми целыми коэффициентами. Пример: 2-2 + 1, в данном случае n = 32, а f (x) = x — x + 1; другой пример — 2-2-1, в данном случае n = 64, и f (x) = x — x — 1.
Также естественно попытаться обобщить простые числа вида 2-1 на простые числа вида b — 1 (при b ≠ 2 и n>1). Однако (см. Также теоремы выше), b — 1 всегда делится на b — 1, поэтому, если последнее не является единицей, первое не является простым. Это можно исправить, разрешив b быть алгебраическим целым числом вместо целого:
Комплексные числа
В кольце целых чисел (на вещественных числах ), если b — 1 — это единица, то b — это либо 2, либо 0. Но 2 — 1 — обычные простые числа Мерсенна, и формула 0 — 1 не приводит ни к чему интересному (поскольку он всегда равен -1 для всех n>0). Таким образом, мы можем рассматривать кольцо «целых чисел» на комплексных числах вместо действительных чисел, например, гауссовских целых и целых чисел Эйзенштейна.
гауссовских Простые числа Мерсенна
Если мы рассмотрим кольцо целых гауссовских чисел, мы получим случай b = 1 + i и b = 1 — i, и можем спросить (WLOG ), для которого n число (1 + i) — 1 является гауссовым простым, которое затем будет называться гауссовым простым числом Мерсенна .
(1 + i) — 1 является гауссовым простым числом для следующие n:
- 2, 3, 5, 7, 11, 19, 29, 47, 73, 79, 113, 151, 157, 163, 167, 239, 241, 283, 353, 367, 379, 457, 997, 1367, 3041, 10141, 14699, 27529, 49207, 77291, 85237, 106693, 160423, 203789, 364289, 991961, 1203793, 1667321, 3704053, 4792057,… (последовательность A057429 в OEIS )
Подобно последовательности показателей для обычных простых чисел Мерсенна, эта последовательность содержит только (рациональные) простые числа.
Что касается всех простых чисел Гаусса, нормы (что есть квадраты абсолютных значений) эти числа являются рациональными простыми числами:
- 5, 13, 41, 113, 2113, 525313, 536903681, 140737471578113,… (последовательность A182300 в OEIS ).
простых числах Эйзенштейна Мерсенна
Мы также можем рассматривать кольцо целых чисел Эйзенштейна, мы получаем случай b = 1 + ω и b = 1 — ω, и можем спросить, для какого n число (1 + ω) — 1 — простое число Эйзенштейна, которое затем будет называться простым числом Эйзенштейна-Мерсенна .
(1 + ω) — 1 — простое число Эйзенштейна для следующего n:
- 2, 5, 7, 11, 17, 19, 79, 163, 193, 239, 317, 353, 659, 709, 1049, 1103, 1759, 2029, 5153, 7541, 9049, 10453, 23743, 255361, 534827, 2237561,… (последовательность A066408 в OEIS )
Нормы (то есть квадраты абсолютных значений) этих простых чисел Эйзенштейна являются рациональными простыми числами:
- 7, 271, 2269, 176419, 129159847, 1162320517,… (последовательность A066413 в OEIS )
Разделите целое число
Перегруппируйте простые числа
Другой способ справиться с тем фактом, что b — 1 всегда делится по b — 1, нужно просто вычесть этот коэффициент и спросить, какие значения n составляют
- bn — 1 b — 1 { displaystyle { frac {b ^ {n} -1} {b-1}}}
быть первоклассным. (Целое число b может быть положительным или отрицательным.) Если, например, мы возьмем b = 10, мы получим n значений:
- 2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343,… (последовательность A004023 в OEIS ),. соответствующий простым числам 11, 11111111111111111, 11111111111111111111111,… (последовательность A004022 в OEIS ).
Эти простые числа называются простыми числами повторного объединения. Другой пример: когда мы берем b = −12, мы получаем n значений:
- 2, 5, 11, 109, 193, 1483, 11353, 21419, 21911, 24071, 106859, 139739,… (последовательность A057178 в OEIS ),., соответствующий простым числам -11, 19141, 57154490053,….
Это предположение, что для любого целого числа b, которое не является совершенной степенью, существует бесконечно много значений n таких, что b — 1 / b — 1 является простым числом (когда b — совершенная степень, это можно показать, что существует не более одного значения n, такого что b — 1 / b — 1 простое число)
Наименьшее число n таких, что b — 1 / b — 1 простое число (начиная с b = 2, 0, если такого n не существует)
- 2, 3, 2, 3, 2, 5, 3, 0, 2, 17, 2, 5, 3, 3, 2, 3, 2, 19, 3, 3, 2, 5, 3, 0, 7, 3, 2, 5, 2, 7, 0, 3, 13, 313, 2, 13, 3, 349, 2, 3, 2, 5, 5, 19, 2, 127, 19, 0, 3, 4229, 2, 11, 3, 17, 7, 3, 2, 3, 2, 7, 3, 5, 0, 19, 2, 19, 5, 3, 2, 3, 2,… (последовательность A084740 в OEIS )
Для отрицательных оснований b они равны (начиная с b = −2, 0, если такого n не существует)
- 3, 2, 2, 5, 2, 3, 2, 3, 5, 5, 2, 3, 2, 3, 3, 7, 2, 17, 2, 3, 3, 11, 2, 3, 11, 0, 3, 7, 2, 109, 2, 5, 3, 11, 31, 5, 2, 3, 53, 17, 2, 5, 2, 103, 7, 5, 2, 7, 1153, 3, 7, 21943, 2, 3, 37, 53, 3, 17, 2, 7, 2, 3, 0, 19, 7, 3, 2, 11, 3, 5, 2,… (последовательность A084742 в OEIS ) (обратите внимание, что эта последовательность OEIS не допускает n = 2)
Наименьшее основание b, такое что b — 1 / b — 1 является простым, равно
- 2, 2, 2, 2, 5, 2, 2, 2, 10, 6, 2, 61, 14, 15, 5, 24, 19, 2, 46, 3, 11, 22, 41, 2, 12, 22, 3, 2, 12, 86, 2, 7, 13, 11, 5, 29, 56, 30, 44, 60, 304, 5, 74, 118, 33, 156, 46, 183, 72, 606, 602, 223, 115, 37, 52, 104, 41, 6, 338, 217,… (след. значение A066180 в OEIS )
Для отрицательных оснований b они равны
- 3, 2, 2, 2, 2, 2, 2, 2, 2, 7, 2, 16, 61, 2, 6, 10, 6, 2, 5, 46, 18, 2, 49, 16, 70, 2, 5, 6, 12, 92, 2, 48, 89, 30, 16, 147, 19, 19, 2, 16, 11, 289, 2, 12, 52, 2, 66, 9, 22, 5, 489, 69, 137, 16, 36, 96, 76, 117, 26, 3,… (последовательность A103795 в OEIS )
Другие обобщенные простые числа Мерсенна
Другое обобщенное число Мерсенна
- an — bna — b { displaystyle { frac {a ^ {n} -b ^ {n}} {ab}}}
с a, b любыми взаимно простыми целыми числами, a>1 и -a < b < a. (Since a − b is always divisible by a − b, the division is necessary for there to be any chance of finding prime numbers. In fact, this number is the same as the числом Люка Un(a + b, ab), поскольку a и b являются корнями квадратного уравнения x — (a + b) x + ab = 0, и это число равно 1, когда n = 1) Мы можем спросить, какое n делает это число простым. Можно показать, что такие n сами должны быть простыми числами или равными 4, а n может быть 4 тогда и только тогда, когда a + b = 1 и a + b простое число. (Поскольку a — b / a — b = (a + b) (a + b). Таким образом, в этом случае пара (a, b) должна быть (x + 1, −x) и x + (x + 1) должно быть простым. То есть x должен быть в OEIS : A027861.) Это гипотеза, что для любой пары (a, b) такой, что для любого натурального числа r>1, a и b не являются одновременно совершенными r-ми степенями, и −4ab не являются совершенными четвертой степенью. существует бесконечно много значений n таких, что a — b / a — b простое число. (Когда a и b обе являются совершенной r-й степенью для r>1 или когда −4ab является совершенной четвертой степенью, можно показать, что существует не более двух значений n с этим свойством, так как если это так, то a — b / a — b можно факторизовать алгебраически) Однако это не было доказано ни для одного значения (a, b).
| a | b | числа n, такие что a — b / a — b является простым. (некоторые большие члены представляют собой только вероятные простые числа, эти n проверяются до 100000 для | b | ≤ 5 или | b | = a — 1, 20000 для 5 < |b| < a − 1) | OEIS последовательность |
|---|---|---|---|
| 2 | 1 | 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, 43112609,…, 57885161,…, 74207281,…, 77232917,…, 82589933,… | A000043 |
| 2 | -1 | 3, 4, 5, 7, 11, 13, 17, 19, 23, 31, 43, 61, 79, 101, 127, 167, 191, 199, 313, 347, 701, 1709, 2617, 3539, 5807, 10501, 10691, 11279, 12391, 14479, 42737, 83339, 95369, 117239, 127031, 138937, 141079, 267017, 269987, 374321, 986191, 4031399,…, 13347311, 13372531,… | A000978 |
| 3 | 2 | 2, 3, 5, 17, 29, 31, 53, 59, 101, 277, 647, 1061, 2381, 2833, 36 13, 3853, 3929, 5297, 7417, 90217, 122219, 173191, 256199, 336353, 485977, 591827, 1059503,… | A057468 |
| 3 | 1 | 3, 7, 13, 71, 103, 541, 1091, 1367, 1627, 4177, 9011, 9551, 36913, 43063, 49681, 57917, 483611, 877843,… | A028491 |
| 3 | -1 | 2, 3, 5, 7, 13, 23, 43, 281, 359, 487, 577, 1579, 1663, 1741, 3191, 9209, 11257, 12743, 13093, 17027, 26633, 104243, 134227, 152287, 700897, 1205459,… | A007658 |
| 3 | −2 | 3, 4, 7, 11, 83, 149, 223, 599, 647, 1373, 8423, 149497, 388897,… | A057469 |
| 4 | 3 | 2, 3, 7, 17, 59, 283, 311, 383, 499, 521, 541, 599, 1193, 1993, 2671, 7547, 24019, 46301, 48121, 68597, 91283, 131497, 148663, 184463, 341233,… | A059801 |
| 4 | 1 | 2 (других нет) | |
| 4 | −1 | 2, 3 (нет других) | |
| 4 | −3 | 3, 5, 19, 37, 173, 211, 227, 619, 977, 1237, 2437, 5741, 13463, 23929, 81223, 121271,… | A128066 |
| 5 | 4 | 3, 43, 59, 191, 223, 349, 563, 709, 743, 1663, 5471, 17707, 19609, 35449, 36697, 45259, 91493, 246497, 265007, 289937,… | A059802 |
| 5 | 3 | 1 3, 19, 23, 31, 47, 127, 223, 281, 2083, 5281, 7411, 7433, 19051, 27239, 35863, 70327,… | A121877 |
| 5 | 2 | 2, 5, 7, 13, 19, 37, 59, 67, 79, 307, 331, 599, 1301, 12263, 12589, 18443, 20149, 27983,… | A082182 |
| 5 | 1 | 3, 7, 11, 13, 47, 127, 149, 181, 619, 929, 3407, 10949, 13241, 13873, 16519, 201359, 396413, 1888279,… | A004061 |
| 5 | −1 | 5, 67, 101, 103, 229, 347, 4013, 23297, 30133, 177337, 193939, 266863, 277183, 335429,… | A057171 |
| 5 | −2 | 2, 3, 17, 19, 47, 101, 1709, 2539, 5591, 6037, 8011, 19373, 26489, 27427,… | A082387 |
| 5 | −3 | 2, 3, 5, 7, 17, 19, 109, 509, 661, 709, 1231, 12889, 13043, 26723, 43963, 44789,… | A122853 |
| 5 | −4 | 4, 5, 7, 19, 29, 61, 137, 883, 1381, 1823, 5227, 25561, 29537, 300893,… | A128335 |
| 6 | 5 | 2, 5, 11, 13, 23, 61, 83, 421, 1039, 1511, 31237, 60413, 113177, 135647, 258413,… | A062572 |
| 6 | 1 | 2, 3, 7, 29, 71, 127, 271, 509, 1049, 6389, 6883, 10613, 19889, 79987, 608099,… | A004062 |
| 6 | -1 | 2, 3, 11, 31, 43, 47, 59, 107, 811, 2819, 4817, 9601, 33581, 38447, 41341, 131891, 196337,… | A057172 |
| 6 | −5 | 3, 4, 5, 17, 397, 409, 643, 1783, 2617, 4583, 8783,… | A128336 |
| 7 | 6 | 2, 3, 7, 29, 41, 67, 1327, 1399, 2027, 69371, 86689, 355039,… | A062573 |
| 7 | 5 | 3, 5, 7, 113, 397, 577, 7573, 14561, 58543,… | A128344 |
| 7 | 4 | 2, 5, 11, 61, 619, 2879, 2957, 24371, 69247,… | A213073 |
| 7 | 3 | 3, 7, 19, 109, 131, 607, 863, 2917, 5923, 12421,… | A128024 |
| 7 | 2 | 3, 7, 19, 79, 431, 1373, 1801, 2897, 46997,… | A215487 |
| 7 | 1 | 5, 13, 131, 149, 1699, 14221, 35201, 126037, 371669, 1264699,… | A004063 |
| 7 | −1 | 3, 17, 23, 29, 47, 61, 1619, 18251, 106187, 201653,… | A057173 |
| 7 | −2 | 2, 5, 23, 73, 101, 401, 419, 457, 811, 1163, 1511, 8011,… | A125955 |
| 7 | −3 | 3, 13, 31, 313, 3709, 7933, 14797, 30689, 38333,… | A128067 |
| 7 | −4 | 2, 3, 5, 19, 41, 47, 8231, 33931, 43781, 50833, 53719, 67211,… | A218373 |
| 7 | −5 | 2, 11, 31, 173, 271, 547, 1823, 2111, 5519, 7793, 22963, 41077, 49739,… | A128337 |
| 7 | −6 | 3, 53, 83, 487, 743,… | A187805 |
| 8 | 7 | 7, 11, 17, 29, 31, 79, 113, 131, 139, 4357, 44029, 76213, 83663, 173687, 336419, 615997,… | A062574 |
| 8 | 5 | 2, 19, 1021, 5077, 34031, 46099, 65707,… | A128345 |
| 8 | 3 | 2, 3, 7, 19, 31, 67, 89, 9227, 43891,… | A128025 |
| 8 | 1 | 3 (других нет) | |
| 8 | −1 | 2 (других нет) | |
| 8 | −3 | 2, 5, 163, 191, 229, 271, 733, 21059, 25237,… | A128068 |
| 8 | −5 | 2, 7, 19, 167, 173, 223, 281, 21647,… | A128338 |
| 8 | −7 | 4, 7, 13, 31, 43, 269, 353, 383, 619, 829, 877, 4957, 5711, 8317, 21739, 24029, 38299,… | A181141 |
| 9 | 8 | 2, 7, 29, 31, 67, 149, 401, 2531, 19913, 30773, 53857, 170099,… | A059803 |
| 9 | 7 | 3, 5, 7, 4703, 30113,… | A273010 |
| 9 | 5 | 3, 11, 17, 173, 839, 971, 40867, 45821,… | A128346 |
| 9 | 4 | 2 (других нет) | |
| 9 | 2 | 2, 3, 5, 13, 29, 37, 1021, 1399, 2137, 4493, 5521,… | A173718 |
| 9 | 1 | (нет) | |
| 9 | −1 | 3, 59, 223, 547, 773, 1009, 1823, 3803, 49223, 193247, 703393,… | A057175 |
| 9 | −2 | 2, 3, 7, 127, 283, 883, 1523, 4001,… | A125956 |
| 9 | −4 | 2, 3, 5, 7, 11, 17, 19, 41, 53, 109, 167, 2207, 3623, 5059, 5471, 7949, 21211, 32993, 60251,… | A211409 |
| 9 | −5 | 3, 5, 13, 17, 43, 127, 229, 277, 6043, 11131, 11821,… | A128339 |
| 9 | −7 | 2, 3, 107, 197, 2843, 3571, 4451,…, 31517,… | A301369 |
| 9 | −8 | 3, 7, 13, 19, 307, 619, 2089, 7297, 75571, 76103, 98897,… | A187819 |
| 10 | 9 | 2, 3, 7, 11, 19, 29, 401, 709, 2531, 15787, 66949, 282493,… | A062576 |
| 10 | 7 | 2, 31, 103, 617, 10253, 10691,… | A273403 |
| 10 | 3 | 2, 3, 5, 37, 599, 38393, 51431,… | A128026 |
| 10 | 1 | 2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343,… | A004023 |
| 10 | −1 | 5, 7, 19, 31, 53, 67, 293, 641, 2137, 3011, 268207,… | A001562 |
| 10 | −3 | 2, 3, 19, 31, 101, 139, 167, 1097, 43151, 60703, 90499,… | A128069 |
| 10 | −7 | 2, 3, 5, 11, 19, 1259, 1399, 2539, 2843, 5857, 10589,… | |
| 10 | −9 | 4, 7, 67, 73, 1091, 1483, 10937,… | A217095 |
| 11 | 10 | 3, 5, 19, 311, 317, 1129, 4253, 7699, 18199, 35153, 206081,… | A062577 |
| 11 | 9 | 5, 31, 271, 929, 2789, 4153,… | A273601 |
| 11 | 8 | 2, 7, 11, 17, 37, 521, 877, 2423,… | A273600 |
| 11 | 7 | 5, 19, 67, 107, 593, 757, 1801, 2243, 2383, 6043, 10181, 11383, 15629,… | A273599 |
| 11 | 6 | 2, 3, 11, 163, 191, 269, 1381, 1493,… | A273598 |
| 11 | 5 | 5, 41, 149, 229, 263, 739, 3457, 20269, 98221,… | A128347 |
| 11 | 4 | 3, 5, 11, 17, 71, 89, 827, 22307, 45893, 63521,… | A216181 |
| 11 | 3 | 3, 5, 19, 31, 367, 389, 431, 2179, 10667, 13103, 90397,… | A128027 |
| 11 | 2 | 2, 5, 11, 13, 331, 599, 18839, 23747, 24371, 29339, 32141, 67421,… | A210506 |
| 11 | 1 | 17, 19, 73, 139, 907, 1907, 2029, 4801, 5153, 10867, 20161, 293831,… | A005808 |
| 11 | −1 | 5, 7, 179, 229, 439, 557, 6113, 223999, 327001,… | A057177 |
| 11 | −2 | 3, 5, 17, 67, 83, 101, 1373, 6101, 12119, 61781,… | A125957 |
| 11 | −3 | 3, 103, 271, 523, 23087, 69833,… | A128070 |
| 11 | −4 | 2, 7, 53, 67, 71, 443, 26497,… | A224501 |
| 11 | −5 | 7, 11, 181, 421, 2297, 2797, 4129, 4139, 7151, 29033,… | A128340 |
| 11 | −6 | 2, 5, 7, 107, 383, 17359, 21929, 26393,… | |
| 11 | −7 | 7, 1163, 4007, 10159,… | |
| 11 | −8 | 2, 3, 13, 31, 59, 131, 223, 227, 1523,… | |
| 11 | −9 | 2, 3, 17, 41, 43, 59, 83,… | |
| 11 | −10 | 53, 421, 647, 1601, 35527,… | A185239 |
| 12 | 11 | 2, 3, 7, 89, 101, 293, 4463, 70067,… | A062578 |
| 12 | 7 | 2, 3, 7, 13, 47, 89, 139, 523, 1051,… | A273814 |
| 12 | 5 | 2, 3, 31, 41, 53, 101, 4 21, 1259, 4721, 45259,… | A128348 |
| 12 | 1 | 2, 3, 5, 19, 97, 109, 317, 353, 701, 9739, 14951, 37573, 46889, 769543,… | A004064 |
| 12 | −1 | 2, 5, 11, 109, 193, 1483, 11353, 21419, 21911, 24071, 106859, 139739,… | A057178 |
| 12 | −5 | 2, 3, 5, 13, 347, 977, 1091, 4861, 4967, 34679,… | A128341 |
| 12 | −7 | 2, 3, 7, 67, 79, 167, 953, 1493, 3389, 4871,… | |
| 12 | −11 | 47, 401, 509, 8609,… | A213216 |
Примечание: если b < 0 and n is even, then the numbers n are not included in the corresponding OEIS sequence.
Гипотеза, связанная с обобщенными простыми числами Мерсенна: (гипотеза предсказывает, где следующее обобщенное простое число Мерсенна, если гипотеза верна, то существует бесконечно много простых чисел для всех таких (a, b) пар)
Для любых целых чисел a и b, удовлетворяющих условиям:
- a>1, -a < b < a.
- a и b являются взаимно простыми. (таким образом, b не может быть 0)
- Для любого натурального числа r>1, a и b не являются одновременно совершенной r-й степенью. (поскольку, когда a и b оба являются совершенными степенями r-й степени, можно показать, что существует не более двух значений n, таких что a — b / a — b является простым числом, и эти значения n сами являются r или корнем of r, или 2)
- −4ab не является точной четвертой степенью (если это так, то число имеет аврифейлевское разложение ).
имеет простые числа вида
- R p ( a, b) = ap — bpa — b { displaystyle R_ {p} (a, b) = { frac {a ^ {p} -b ^ {p}} {ab}}}
для простого p, простые числа будут распределены рядом с линией наилучшего соответствия
- Y = G ⋅ log a (log a (R (a, b) (n))) + C { displaystyle Y = G cdot log _ {a} ( log _ {a} (R _ {(a, b)} (n))) + C}
где
- lim n → ∞ G = 1 e γ = 0,561459483566… { displaystyle lim _ {n rightarrow infty} G = { frac {1} {e ^ { gamma}}} = 0,561459483566 ldots}
и их около
- (log e (N) + м ⋅ журнал е (2) ⋅ журнал е (журнал е (N)) + 1 N — δ) ⋅ е γ журнал е (а) { Displaystyle ( журнал _ {е} (N) + м cdot log _ {e} (2) cdot log _ {e} left ( log _ {e} (N)) + { frac {1} { sqrt { N}}} — delta right) cdot { frac {e ^ { gamma}} { log _ {e} (a)}}}
простые числа этой формы меньше N.
- e — основание натурального логарифма.
- γ — постоянная Эйлера – Маскерони.
- log a — логарифм в основании a.
- R(a, b) (n) — это n-е простое число в форме a — b / a — b для простого p.
- C — константа соответствия данных, которая изменяется в зависимости от a и b.
- δ — константа соответствия данных, которая изменяется в зависимости от a и b.
- m — наибольшее натуральное число, такое что a и −b являются точными 2-ю степенями.
Мы также имеют следующие три свойства:
- Количество простых чисел формы a — b / a — b (с простым p), меньших или равных n, составляет примерно e log a (log a (n)).
- Ожидаемое количество простых чисел формы a — b / a — b с простым p между n и an составляет около e.
- вероятность того, что число в форме a — b / a — b является простым (для простого p), составляет около e / p log e (a).
Если эта гипотеза верна, то n для всех таких пар (a, b), пусть q будет n-м простым числом формы a — b / a — b, график log a (log a (q)) по сравнению с n почти линейно. (См.)
Когда a = b + 1, это (b + 1) — b, разность двух последовательных совершенных n-х степеней, и если a — b простое число, тогда a должно быть b + 1, потому что он делится на a — b.
Наименьшее n таких, что (b + 1) — b простое число, равны
- 2, 2, 2, 3, 2, 2, 7, 2, 2, 3, 2, 17, 3, 2, 2, 5, 3, 2, 5, 2, 2, 229, 2, 3, 3, 2, 3, 3, 2, 2, 5, 3, 2, 3, 2, 2, 3, 3, 2, 7, 2, 3, 37, 2, 3, 5, 58543, 2, 3, 2, 2, 3, 2, 2, 3, 2, 5, 3, 4663, 54517, 17, 3, 2, 5, 2, 3, 3, 2, 2, 47, 61, 19,… (последовательность A058013 в OEIS )
Наименьшее b такое, что (b + 1) — b равно простые числа
- 1, 1, 1, 1, 5, 1, 1, 1, 5, 2, 1, 39, 6, 4, 12, 2, 2, 1, 6, 17, 46, 7, 5, 1, 25, 2, 41, 1, 12, 7, 1, 7, 327, 7, 8, 44, 26, 12, 75, 14, 51, 110, 4, 14, 49, 286, 15, 4, 39, 22, 109, 367, 22, 67, 27, 95, 80, 149, 2, 142, 3, 11,… (последовательность A222119 в OEIS )
См. Также
- Repunit
- Простое число Ферма
- Степень двойки
- Константа Эрдеша – Борвейна
- Гипотезы Мерсенна
- Твистер Мерсенна
- Двойное число Мерсенна
- Prime95 / MPrime
- Great Internet Mersenne Prime Search (GIMPS)
- Наибольшее известное простое число
- Титаническое простое число
- Гигантское простое число
- Мегапростое число
- Виферих pri me
- простое число Вагстаффа
- простое число Каллена
- простое число Вудалла
- простое число прот
- простое число Солинаса
- гипотеза Гиллиса
- число Вильямса
Литература
Внешние ссылки
- , Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Домашняя страница GIMPS
- Статус GIMPS — страница статуса предоставляет различные статистические данные о ходе поиска, обычно обновляемые каждую неделю, включая прогресс в доказательстве упорядочения самых больших известных простых чисел Мерсенна
- GIMPS, известных факторов чисел Мерсенна
- Mq= (8x) — (3qy) Свойство составных чисел Мерсенна с простым показателем (PDF)
- Mq= x + d · y математическая диссертация (PS)
- Грайм, Джеймс. «Число 31 и Мерсенна». Numberphile. Брэди Харан. Архивировано 31 мая 2013 года из оригинального. Проверено 6 апреля 2013 г.
- Основная библиография Мерсенна с гиперссылками на оригинальные публикации
- отчет о простых числах Мерсенна — подробное обнаружение (на немецком языке)
- GIMPS wiki
- Мерсенн Уилла Эджингтона Страница — содержит множители для малых чисел Мерсенна
- Известные множители чисел Мерсенна
- Десятичные цифры и английские названия простых чисел Мерсенна
- Простые редкости: 2305843009213693951
- Факторизация чисел Мерсенна M n, с нечетным n, n до 1199
- Факторизация чисел Мерсенна M 2n, 2n до 2398 (n до 1199) или 2n в форме от 8k + 4 до 4796 ( n имеет вид от 4k + 2 до 2398)
- OEIS последовательность A250197 (числа n такие, что левая примитивная часть Аурифейля 2 ^ n + 1 является простой) — Факторизация Мерсенна числа M n (n до 1280)
- Факторизация полностью факторизованных чисел Мерсенна
- Проект Каннингема, факторизация b ± 1, b = 2, 3, 5, 6, 7, 10, 11, 12
- Факторизация b ± 1, 2 ≤ b ≤ 12
- Fa cторирование a ± b с взаимно простыми a, b, 2 ≤ b < a ≤ 12
MathWorld ссылки
- Weisstein, Eric W. «Число Мерсенна». MathWorld.
- Вайсштейн, Эрик У. «Простое число Мерсенна». MathWorld.
- Найден 47-й Мерсенн Прайм
Контакты: mail@wikibrief.org
Последняя правка сделана 2021-05-25 04:33:17
Содержание доступно по лицензии CC BY-SA 3.0 (если не указано иное).
Простое число Мерсе́нна (англ. Mersenne prime) — простое число вида 
Числа Мерсенна названы в честь французского математика Марена Мерсенна, который исследовал их в 17 веке.
Содержание
- 1 Определения
- 2 Свойства
- 3 Поиск простых чисел Мерсенна
- 4 Вариации и обобщения
- 5 Открытые проблемы
- 6 Применение
- 7 Примечания
- 8 Ссылки
Определения[править | править вики-текст]
Числа Мерсе́нна (англ. Mersenne numbers) — числа вида 
- 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 8191, 16 383, 32 767, 65 535, 131 071, … (последовательность A000225 в OEIS)
Иногда числами Мерсенна называют числа 
- 3, 7, 31, 127, 2047, 8191, 131 071, 524 287, 8 388 607, 536 870 911, 2 147 483 647, 137 438 953 471, … (последовательность A001348 в OEIS)
Простые числа Мерсе́нна (англ. Mersenne primes) — числа Мерсенна, являющиеся простыми. Для всех простых чисел вида 
- 3, 7, 31, 127, 8 191, 131 071, 524 287, 2 147 483 647, 2 305 843 009 213 693 951, 618 970 019 642 690 137 449 562 111, 162 259 276 829 213 363 391 578 010 288 127, 170 141 183 460 469 231 731 687 303 715 884 105 727, … (последовательность A000668 в OEIS)
Индексы p простых чисел Мерсенна образуют последовательность
- 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11 213, 19 937, 21 701, 23 209, 44 497, 86 243, 110 503, 132 049, 216 091, 756 839, 859 433, 1 257 787, 1 398 269, 2 976 221, 3 021 377, 6 972 593, 13 466 917, 20 996 011, 24 036 583, 25 964 951, 30 402 457, 32 582 657, 37 156 667, 42 643 801, 43 112 609, 57 885 161, … (последовательность A000043 в OEIS)
Свойства[править | править вики-текст]
Поиск простых чисел Мерсенна[править | править вики-текст]
Числа Мерсенна получили известность в связи с эффективным тестом простоты Люка — Лемера, благодаря которому простые числа Мерсенна давно удерживают лидерство как самые больши́е известные простые числа[1].
На сентябрь 2013 года самым больши́м известным простым числом является число Мерсенна 

Всего известно 48 простых чисел Мерсенна. При этом до начала 2014 года порядковые номера были с уверенностью установлены только у первых 42 чисел[2]; 23 февраля 2014 года после произведенных перепроверок было установлено, что 43-е найденное число Мерсенна 
За нахождение 45-го простого числа Мерсенна
Вариации и обобщения[править | править вики-текст]
- Двойные числа Мерсенна определяются как
. На сегодняшний день известны только четыре простых числа такого вида (при n = 2,3,5,7).
Открытые проблемы[править | править вики-текст]
- Бесконечность количества простых чисел Мерсенна и их асимптотика.
- Простота числа
.
Применение[править | править вики-текст]
На практике простые числа Мерсенна применяются для построения генераторов псевдо-случайных чисел с большими периодами[5], таких, как вихрь Мерсенна.
Примечания[править | править вики-текст]
- ↑ The Largest Known Primes (англ.)
- ↑ Mersenne Primes: History, Theorems and Lists (англ.)
- ↑ Great Internet Mersenne Prime Search (англ.)
- ↑ EFF Cooperative Computing Awards (англ.)
- ↑ R. P. Brent, P. Zimmermann Random number generators with period divisible by a Mersenne prime // Lecture Notes in Computer Science. — 2003. — Т. 2667. — С. 1-10.
Ссылки[править | править вики-текст]
- Weisstein, Eric W. Mersenne Prime (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Mersenne Number (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Double Mersenne Numbers (англ.) на сайте Wolfram MathWorld.
- Андрей Коняев Проще некуда. Найдено простое число длиной в пять романов «Война и мир» // lenta.ru. — 12 февраля 2013.




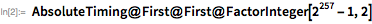

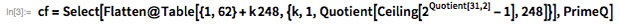

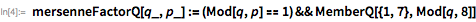
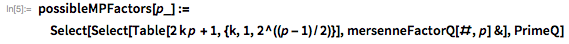


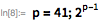
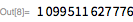


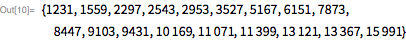

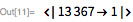
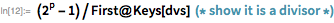
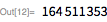


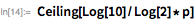


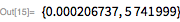
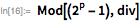




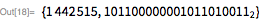
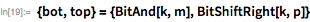



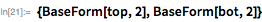
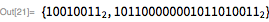

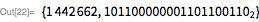















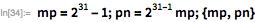

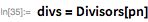


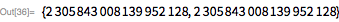




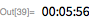
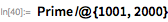
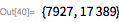

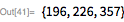
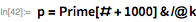






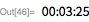
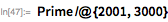
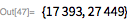


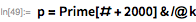
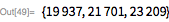

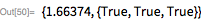
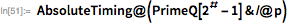



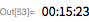
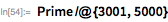


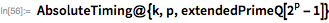
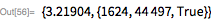





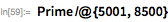





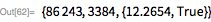
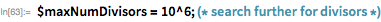






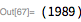




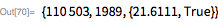










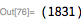

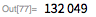

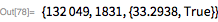



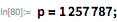




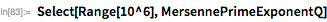



















 . На сегодняшний день известны только четыре простых числа такого вида (при n = 2,3,5,7).
. На сегодняшний день известны только четыре простых числа такого вида (при n = 2,3,5,7). .
.