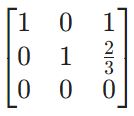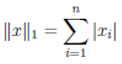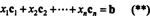Все курсы > Линейная алгебра > Занятие 6 (часть 1)
Сегодня мы еще раз рассмотрим полученные ранее знания о векторных пространствах, линейных преобразованиях, системе линейных уравнений и определителе матрицы в контексте новых понятий ранга и четырех фундаментальных подпространств матрицы, а именно пространства столбцов, пространства строк, ядра и коядра матрицы.
Продолжим работать в том же ноутбуке⧉
Ранг матрицы
При нулевом определителе в трехмерном пространстве матрица может «схлопнуть» пространство до плоскости, линии или точки (во всех трех случаях определитель равен нулю).
Ранее мы сказали, что для того чтобы в системе уравнений, например, трехмерная матрица $A$ при нулевом определителе все же имела решение, вектор $mathbf b$, на который матрица $A$ переводит вектор $mathbf x$, должен лежать на плоскости или линии, в которые «схлопывается» трехмерное пространство.
Размерность пространства после трансформации принято описывать рангом матрицы (rank).
Если преобразование трехмерной матрицы «сворачивает» размерность до линии, то ранг такого преобразования равен единице, до плоскости — двум и т.д. В случае матрицы $2 times 2$ самый высокий ранг матрицы — два. Это значит, что при преобразовании размерность сохранилась (и соответственно определитель не равен нулю).
Пространство столбцов
Пространством столбцов (column space, а также образом, image) называют множество всех возможных линейных комбинаций вектор-столбцов.
С точки зрения линейных преобразований, пространством столбцов называют векторы, которые определяют пространство после трансформации.
В случае линейно зависимых векторов таких векторов будет меньше, чем в исходной матрице. Приведем пример линейно зависимых векторов и рассчитаем ранг матрицы.
|
M = np.array([[1, 0, 1], [2, 3, 4], [—1, —3, —3]]) np.linalg.matrix_rank(M) |
Приведем матрицу к упрощенному ступенчатому виду (reduced row-echelon form) с помощью Питона. Для этого воспользуемся методом .rref() библиотеки sympy.
|
from sympy import * M = Matrix([[1, 0, 1], [2, 3, 4], [—1, —3, —3]]) M_rref = M.rref() M_rref[0] |
Как мы видим, с одной стороны, пространство сократилось до двух измерений (поэтому ранг матрицы равен двум), с другой, двумерное пространство можно описать первыми двумя столбцами (их еще называют разрещающими, ведущими или базисными, pivot columns), где все элементы кроме одного равны нулю.
Разрешающие столбцы и образуют пространство столбцов. Найдем пространство столбцов с помощью Питона.
|
# вторым элементом метод .rref() выводит # индексы разрешающих столбцов (pivot columns), # используем их для нахождения пространства столбцов M.col(M.rref()[1]) |
|
# то же самое можно найти с помощью # метода .columnspace() M_columnspace = M.columnspace() M_columnspace[0] |
Откуда такое название? Столбцы матрицы говорят куда «приземлятся» координаты базисных векторов. В этом смысле, оболочка вектор-столбцов то же самое, что и пространство столбцов.
В матрице $2 times 2$ первый столбец показывает, где окажется вектор $mathbf i$, второй — вектор $mathbf j$. И оболочка этих столбцов определит пространство столбцов. Если, например, в матрице $2 times 2$ столбцы линейно независимы и преобразование не приводит к снижению размерности, то пространство столбцов задается этими двумя векторами.
Замечу, что столбцы, не являющиеся разрешающими, называются свободными (free).
Ядро матрицы
Если преобразование уменьшает размерность (например, преобразовывает плоскость в линию), то несколько векторов оказываются в начале координат (становятся нулевыми векторами). Видео ниже прекрасно иллюстрирует эту трансформацию.
Множество таких «исчезающих» векторов называется ядром матрицы или ее нуль-пространством (null space, kernel).
Видео про обратные матрицы, ранг и ядро⧉.
Система уравнений
$Ax = b$
Рассмотрим пространство столбцов и ядро с точки зрения системы линейных уравнений. В первую очередь представим пространство столбцов, как решение системы $ A mathbf x = mathbf b $, т.е. линейную комбинацию вектор-столбцов $A$, умноженных на компоненты $mathbf x$.
$$ x_1 begin{bmatrix} vdots \ mathbf a_1 \ vdots end{bmatrix} + x_2 begin{bmatrix} vdots \ mathbf a_2 \ vdots end{bmatrix} + x_3 begin{bmatrix} vdots \ mathbf a_3 \ vdots end{bmatrix} = begin{bmatrix} vdots \ mathbf b \ vdots end{bmatrix} $$
Всегда ли $A mathbf x = mathbf b$ будет иметь решение? Нет. Возьмем некоторую матрицу $A$ и соответствующие ей векторы $mathbf x$ и $mathbf b$.
$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} b_1 \ b_2 \ b_3 \ b_4 end{bmatrix} $$
В такой системе будет много векторов $mathbf b$, которые не будут являться линейной комбинацией трех столбцов матрицы A.
В каком случае такое решение все-таки будет существовать? Если $mathbf b$ будет являться линейной комбинацией векторов $A$, т.е. будет находиться в пространстве столбцов $A$, $mathbf b in col(A) $.
Например, если $mathbf b$ будет равен одному из столбцов $A$.
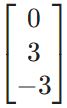
$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} 1 \ 2 \ 3 \ 4 end{bmatrix} $$
Тогда решением может быть
$$ mathbf x = begin{bmatrix} 1 \ 0 \ 0 end{bmatrix} $$
Что интересно, все возможные решения $mathbf x$ именно такой системы $A mathbf x = mathbf b$, где $mathbf b in col(A) $ сами по себе не образуют векторное пространство (хотя бы потому что нулевой вектор не включен в эти решения).
Дополнительно замечу, что так как в матрице $A$ только два линейно независимых вектора (третий вектор является суммой первых двух), то в данном случае мы имеем двумерное подпространство $R^4$.
$Ax = 0$
В системе линейных уравнений $A mathbf x = mathbf b$, если $mathbf b$ — нулевой вектор, т.е. $A mathbf x = mathbf 0$, то ядро дает все возможные решения этой системы (все возможные $mathbf x$). Можно также сказать, что ядро $mathbf x $ представляет собой комбинацию вектор-столбцов $A$, обращающихся в ноль.
$$ x_1 begin{bmatrix} vdots \ mathbf a_1 \ vdots end{bmatrix} + x_2 begin{bmatrix} vdots \ mathbf a_2 \ vdots end{bmatrix} + x_3 begin{bmatrix} vdots \ mathbf a_3 \ vdots end{bmatrix} = begin{bmatrix} vdots \ mathbf 0 \ vdots end{bmatrix} $$
В примере выше обратите внимание, что $col(A) in R^4$, в то время как $null(A) in R^3$. Решением же этой системы при нулевом векторе $mathbf b$, $A mathbf x = mathbf 0$ будет
$$ null(A) = k begin{bmatrix} 1 \ 1 \ -1 end{bmatrix} $$
где $k in mathbb{R} $. Другими словами, $null(A)$ представляет собой линию в $R^3$.
Убедимся, что для матрицы $M$ выше мы правильно нашли ядро (а также решение $M mathbf x = 0$).
|
M = np.array([[1, 0, 1], [2, 3, 4], [—1, —3, —3]]) Null = np.array([—1, —2/3, 1]) M @ Null |
Общее и частное решение
Приведем общее решение (complete solution) следующей системы, состоящее из частного решения (particular solution) системы $A mathbf x = mathbf b$ и ядра, то есть решения $A mathbf x = mathbf 0$.
$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} 1 \ 2 \ 3 \ 4 end{bmatrix} $$
$$ mathbf x = begin{bmatrix} 1 \ 0 \ 0 end{bmatrix} + k begin{bmatrix} 1 \ 1 \ -1 end{bmatrix} $$
Независимость векторов, базис и размерность
В свете новых знаний еще раз рассмотрим линейную независимость векторов и базис векторного пространства. Возьмем некоторую матрицу $A$.
Независимые вектор-столбцы
Можно сказать, что вектор-столбцы, образующие матрицу $A$ независимы, если ядро матрицы состоит только из нулевого вектора, $null(A) = { mathbf 0 }$ (решением $A mathbf x = mathbf 0$ будет только нулевой вектор $mathbf x$). Одновременно все столбцы такой матрицы являются разрешающими, и матрица имеет полный ранг, равный количеству столбцов $n$, $rank(A) = n$.
Если матрица $А$ квадратная и ее столбцы линейно независимы, то можно сказать, что
- Вектор-столбцы матрицы образуют базис $R^n$
- Такая матрица будет обратима (!)
Приведем примеры обратимых матриц, столбцы которых формируют базис.
$$ begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end{bmatrix}, begin{bmatrix} 1 & 2 & 3 \ 1 & 2 & 1 \ 2 & 5 & 8 end{bmatrix} $$
|
A = np.array([[1, 2, 3], [1, 2, 1], [2, 5, 8]]) np.linalg.matrix_rank(A) |
|
array([[ 5.5, -0.5, -2. ], [-3. , 1. , 1. ], [ 0.5, -0.5, 0. ]]) |
Зависимые вектор-столбцы
Если же столбцы зависимы, то ядро матрицы содержит также ненулевые векторы и решением $A mathbf x = mathbf 0$ будет или будут некоторые ненулевые векторы $mathbf x$. Столбцы матрицы будут как разрешающими, так и свободными. Ранг матрицы будет равен количеству разрещающих столбцов.
Базис пространства будет определяться именно линейно независимыми векторами, входящими в пространство столбцов. Размерностью (dimension) векторного пространства будет как раз количество векторов базиса.
Например, возьмем следующую матрицу $A$.
$$ A = begin{bmatrix} 1 & 2 & 3 & 1 \ 1 & 1 & 2 & 1 \ 1 & 2 & 3 & 1 end{bmatrix} $$
В данном случае у матрицы два линейно независимых столбца. В частности, это
$$ col(A) = left{ begin{bmatrix} 1 \ 1 \ 1 end{bmatrix}, begin{bmatrix} 2 \ 1 \ 2 end{bmatrix} right} $$
Как следствие,
$$ dim(col(A)) = rank(A) = dim(basis) = text{# of pivots} = 2 $$
Одновременно, нулевое пространство задано векторами
$$ null(A) = left{ begin{bmatrix} -1 \ -1 \ 1 \ 0 end{bmatrix}, begin{bmatrix} -1 \ 0 \ 0 \ 1 end{bmatrix} right} $$
Как следствие,
$$ dim(null(A)) = text{# of free columns} = 2 $$
Код на Питоне для нахождения пространства столбцов и ядра приведен в ноутбуке к занятию⧉.
В качестве дополнения, замечу, что размерность векторного пространства характеризуется следом (trace) единичной матрицы этого пространства или суммой элементов главной диагонали. Например, размерность $R^3$ можно охарактеризовать через
$$ dim(col(A)) = tr left( begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end{bmatrix} right) = 3 $$
Пространство строк и коядро
Пространством строк (row space) называют множество всех возможных линейных комбинаций вектор-строк.
Если матрицу транспонировать, то можно сказать, что
$$ row(A) = col(A^T) $$
Коядром или левым нуль-пространством (left null-space, cokernel) матрицы $A$ будет ядро матрицы $A^T$.
$$ leftnull(A) = null(A^T) $$
Продемонстрируем, почему это пространством называется именно левым нуль-пространством. По определению ядра, как решения $A mathbf x = mathbf 0$, можно сказать, что коядро будет решением $A^T mathbf y = mathbf 0$.
$$ A^T mathbf y = mathbf 0 $$
$$ mathbf y^T(A^T)^T = mathbf 0^T $$
$$ mathbf y^T A = mathbf 0^T $$
Схематично это можно представить следующим образом.

Можно также сказать, что коядро $ mathbf y $ в системе $ A^T mathbf y = mathbf 0 $ дает все возможные комбинации столбцов $A^T$, обращающиеся в нулевой вектор (что то же самое, что линейные комбинации строк $mathbf x^T A = 0$). Приведем пример. Найдем коядро матрицы $A$.
|
A = Matrix([[1, 2, 3, 1], [1, 1, 2, 1], [1, 2, 3, 1]]) A.T.nullspace()[0] |
Другими словами, нам нужно взять $-1R_1 + 0R_2 + 1R_3$, чтобы получить нулевой вектор. Проверим полученный результат.
|
A = np.array([[1, 2, 3, 1], [1, 1, 2, 1], [1, 2, 3, 1]]) Leftnull = np.array([—1, 0, 1]) Leftnull.T @ A |
Фундаментальные подпространства матрицы
Обобщим изложенную выше информацию. Возьмем матрицу $A$ размерностью $m times n$. Тогда
- $ null(A) in R^n$ (так как должно быть решением $A mathbf x = mathbf 0$)
- $ col(A) in R^m $ (количество строк $A$)
- $ row(A) = col(A^T) in R^n $ (количество столбцов $A$)
- $ leftnull(A) = null(A^T) in R^m $ (так как должно быть решением $A^T mathbf y = mathbf 0$)
Тогда схематично эти подпространства можно представить следующим образом.
Несколько пояснений и дополнений:
- $r$ означает ранг (rank) матрицы
- $r+(n-r) = n$, т.е. столбцы матрицы $A$
- $r+(m-r) = m$, т.е. строки матрицы $A$ или столбцы $A^T$
Про пересечение подпространств. Может ли вектор $mathbf v = begin{bmatrix} 1 \ 2 end{bmatrix}$ быть одновременно в нуль-пространстве и являться частью пространства строк A (или в целом строкой в A)? Нет.
$$ begin{bmatrix} 1 & 2 \ dots & dots end{bmatrix} begin{bmatrix} 1 \ 2 end{bmatrix} not= begin{bmatrix} 0 \ 0 end{bmatrix} $$
Пересечением пространства строк и нуль-пространства будет только нулевой вектор.
$$ row(A) cap null(A) = { mathbf 0 } $$
Ортогональность подпространств матрицы
Более того, ядро ортогонально пространству строк $row(A) perp null(A)$, так как их скалярное произведение равно нулю. Это следует из определения ядра $A mathbf x = mathbf 0$ (произведение $mathbf x$ на каждую вектор-строку $mathbf a_m$ равно нулю).
$$ begin{bmatrix} dots & mathbf a_1 & dots \ dots & mathbf a_2 & dots \ dots & dots & dots \ dots & mathbf a_m & dots end{bmatrix} begin{bmatrix} vdots \ mathbf x \ vdots end{bmatrix} = begin{bmatrix} 0 \ 0 \ 0 \ 0 end{bmatrix} $$
Более того, так как $null(A)$ содержит все векторы, ортогональные $row(A)$, то ядро можно считать ортогональным дополнением пространства строк в $R^n$: $null(A) = row(A)^{perp} $.
То же самое справедливо для пространства столбцов и коядра.
$$ col(A) perp leftnull(A) perp null(A^T) text{ в } R^m $$
$$ leftnull(A), null(A^T) = col(A)^{perp} $$
Количество решений системы уравнений
Систематизируем наши знания о подпространствах матрицы с точки зрения возможного количества решений системы уравнений.
Система не имеет решений
В случае если система не имеет решений, существует некоторый вектор $mathbf b $, при котором $A mathbf x = mathbf b $ не будет иметь решения.
$$ exists mathbf b implies A mathbf x not= mathbf b $$
С точки зрения матрицы $underset{m times n}{A}$, можно говорить о том, что некоторые строки линейно зависимы и после преобразования методом Гаусса обратятся в нули. Как следствие, ранг матрицы меньше количества строк, $r < m$.
Система имеет единственное решение
Если мы знаем, что система имеет единственное решение, то это означает, что нуль-пространство матрицы $A$ содержит только нулевой вектор, $null(A) = { mathbf 0 }$ и все столбцы линейно независимы, $ r = n $.
Система имеет множество решений
В этом случае решение состоит из частного решения и решения системы $A mathbf x not= mathbf 0 $. Другими словами, это означает, что нуль-пространство содержит не только нулевой вектор, а значит столбцы матрицы линейно зависимы и $ r < n $.
Теперь приведем пример, иллюстрирующий применение матрицы для моделирования физического процесса, а также посмотрим как подпространства такой матрицы одновременно характеризуют свойства этого процесса.


В линейной алгебре пространство столбцов (также называемое диапазоном или изображение ) матрицы A — диапазон (набор всех возможных линейных комбинаций ) его векторов-столбцов. Пространство столбцов матрицы — это изображение или диапазон соответствующего преобразования матрицы.
. Пусть F { displaystyle mathbb {F}}



Строковое пространство определяется аналогично.
В этой статье рассматриваются матрицы действительных чисел. Пространства строк и столбцов являются подпространствами вещественных пространств Rи R соответственно.
Содержание
- 1 Обзор
- 1.1 Пример
- 2 Пространство столбцов
- 2.1 Определение
- 2.2 Основа
- 2.3 Размерность
- 2.4 Отношение к левому пустому пространству
- 2.5 Для матриц над кольцом
- 3 Строка
- 3.1 Определение
- 3.2 Основа
- 3.3 Измерение
- 3.4 Отношение к пустому пространству
- 3.5 Отношение к coimage
- 4 См. Также
- 5 Примечания
- 6 Ссылки
- 6.1 Учебники
- 7 Внешние ссылки
Обзор
Пусть A — матрица размером m на n. Тогда
- rank (A) = dim (rowsp (A)) = dim (colsp (A)),
- rank (A) = количество pivots в любой эшелонированной форме A,
- rank (A) = максимальное количество линейно независимых строк или столбцов A.
Если рассматривать матрицу как линейное преобразование из R до R, тогда пространство столбцов матрицы равно изображению этого линейного преобразования.
Пространство столбцов матрицы A — это набор всех линейных комбинаций столбцов в A. Если A = [a1,…., an], то colsp (A) = диапазон {a1,…., an}.
Концепция пространства строк обобщается для матриц более C, поля комплексных чисел или любого поля .
Интуитивно, учитывая матрицу A, действие матрицы A на вектор x вернет линейную комбинацию столбцов A, взвешенных по координатам x в качестве коэффициентов. Другой способ взглянуть на это состоит в том, что он (1) сначала проецирует x в пространство строк A, (2) выполняет обратимое преобразование и (3) помещает результирующий вектор y в пространстве столбцов A. Таким образом, результат y = A x должен находиться в пространстве столбцов A. См. разложение по сингулярным значениям для получения дополнительных сведений. по этой второй интерпретации.
Пример
Дана матрица J:
- J = [2 4 1 3 2 — 1-2 1 0 5 1 6 2 2 2 3 6 2 5 1] { displaystyle J = { begin {bmatrix} 2 4 1 3 2 \ — 1 -2 1 0 5 \ 1 6 2 2 2 \ 3 6 2 5 1 end {bmatrix}}}
строки r1= (2,4,1, 3,2), r2= (−1, −2,1,0,5), r3= (1,6,2,2,2), r4= (3,6,2, 5,1). Следовательно, пространство строк J является подпространством R, покрытым на {r1, r2, r3, r4}. Поскольку эти четыре вектора-строки являются линейно независимыми, пространство строк является 4-мерным. Более того, в этом случае можно увидеть, что все они ортогональны вектору n = (6, −1,4, −4,0), поэтому можно вывести что пространство строк состоит из всех векторов в R, которые ортогональны n.
Пространство столбцов
Определение
Пусть K будет полем из скаляры. Пусть A — матрица размера m × n с векторами-столбцами v1, v2,…, vn. линейной комбинацией этих векторов является любой вектор вида
- c 1 v 1 + c 2 v 2 + ⋯ + cnvn, { displaystyle c_ {1} mathbf {v} _ {1 } + c_ {2} mathbf {v} _ {2} + cdots + c_ {n} mathbf {v} _ {n},}
где c 1, c 2,…, c n — скаляры. Набор всех возможных линейных комбинаций v1,…, vnназывается пространством столбцов A. То есть пространство столбцов A является диапазоном векторов v1,…, vn.
Любая линейная комбинация векторов-столбцов матрицы A может быть записана как произведение A и вектора-столбца:
- A [c 1 ⋮ cn] = [ a 11 ⋯ a 1 n ⋮ ⋱ ⋮ am 1 ⋯ amn] [c 1 ⋮ cn] = [c 1 a 11 + ⋯ + cna 1 n ⋮ ⋮ ⋮ c 1 am 1 + ⋯ + cnamn] = c 1 [a 11 ⋮ am 1] + ⋯ + cn [a 1 n ⋮ amn] = c 1 v 1 + ⋯ + cnvn { displaystyle { begin {array} {rcl} A { begin {bmatrix} c_ {1} \ vdots \ c_ {n} end {bmatrix}} = { begin {bmatrix} a_ {11} cdots a_ {1n} \ vdots ddots vdots \ a_ {m1} cdots a_ {mn} end {bmatrix}} { begin {bmatrix} c_ {1} \ vdots \ c_ {n} end {bmatrix}} = { begin {bmatrix} c_ {1} a_ {11} + cdots + c_ {n} a_ {1n} \ vdots vdots vdots \ c_ {1} a_ {m1} + cdots + c_ {n} a_ {mn } end {bmatrix}} = c_ {1} { begin {bmatrix} a_ {11} \ vdots \ a_ {m1} end {bmatrix}} + cdots + c_ {n} { begin { bmatrix} a_ {1n} \ vdots \ a_ {mn} end {bm atrix}} \ = c_ {1} mathbf {v} _ {1} + cdots + c_ {n} mathbf {v} _ {n} end {array}}}
Следовательно, пространство столбцов A состоит из всех возможных произведений A x для x∈ C. Это то же самое, что и изображение (или диапазон ) соответствующего матричного преобразования.
- Пример
- Если A = [1 0 0 1 2 0] { displaystyle A = { begin {bmatrix} 1 0 \ 0 1 \ 2 0 end {bmatrix}}}
, тогда векторы-столбцы v1= (1, 0, 2) и v2= (0, 1, 0).
- Линейная комбинация v1и v2- это любой вектор формы
- c 1 [1 0 2] + c 2 [0 1 0] = [c 1 c 2 2 c 1] { displaystyle c_ {1} { begin {bmatrix} 1 \ 0 \ 2 end {bmatrix}} + c_ {2} { begin {bmatrix} 0 \ 1 \ 0 end {bmatrix}} = { begin {bmatrix} c_ {1} \ c_ {2} \ 2c_ {1} end {bmatrix}} ,}
- c 1 [1 0 2] + c 2 [0 1 0] = [c 1 c 2 2 c 1] { displaystyle c_ {1} { begin {bmatrix} 1 \ 0 \ 2 end {bmatrix}} + c_ {2} { begin {bmatrix} 0 \ 1 \ 0 end {bmatrix}} = { begin {bmatrix} c_ {1} \ c_ {2} \ 2c_ {1} end {bmatrix}} ,}
- Набор всех таких векторов является пространством столбцов A. В этом случае пространство столбцов — это в точности набор векторов (x, y, z) ∈ R, удовлетворяющих уравнению z = 2x ( используя декартовы координаты, этот набор представляет собой плоскость через начало координат в трехмерном пространстве ).
Basis
Столбцы A охватывают пространство столбцов, но они не могут образовывать базис, если векторы-столбцы не t линейно независимый. К счастью, операции с элементарной строкой не влияют на отношения зависимости между векторами столбцов. Это позволяет использовать сокращение строки, чтобы найти базис для пространства столбцов.
Например, рассмотрим матрицу
- A = [1 3 1 4 2 7 3 9 1 5 3 1 1 2 0 8]. { displaystyle A = { begin {bmatrix} 1 3 1 4 \ 2 7 3 9 \ 1 5 3 1 \ 1 2 0 8 end {bmatrix}} { text {.}}}
Столбцы этой матрицы охватывают пространство столбцов, но они могут не быть линейно независимыми, и в этом случае некоторое их подмножество будет составлять основу. Чтобы найти этот базис, мы уменьшаем A до сокращенной формы эшелона строк :
- [1 3 1 4 2 7 3 9 1 5 3 1 1 2 0 8] ∼ [1 3 1 4 0 1 1 1 0 2 2 — 3 0 — 1 — 1 4] ∼ [1 0 — 2 1 0 1 1 1 0 0 0 — 5 0 0 0 5] ∼ [1 0 — 2 0 0 1 1 0 0 0 0 1 0 0 0 0]. { displaystyle { begin {bmatrix} 1 3 1 4 \ 2 7 3 9 \ 1 5 3 1 \ 1 2 0 8 end {bmatrix}} sim { begin {bmatrix} 1 3 1 4 \ 0 1 1 1 1 \ 0 2 2 -3 \ 4 end {bmatrix}} sim { begin {bmatrix} 1 0 -2 1 \ 0 1 1 1 \ 0 0 0 -5 \ 0 0 0 5 end {bmatrix}} sim { begin {bmatrix} 1 0 -2 0 \ 0 1 1 0 \ 0 0 0 1 \ 0 0 0 0 end {bmatrix}} { text {.}}}
На этом этапе ясно, что первый, второй и четвертый столбцы линейно независимы, а третий столбец представляет собой линейную комбинацию первые два. (В частности, v3= –2 v1+ v2.) Следовательно, первый, второй и четвертый столбцы исходной матрицы являются основой для пространства столбцов:
- [1 2 1 1], [3 7 5 2], [4 9 1 8]. { Displaystyle { begin {bmatrix} 1 \ 2 \ 1 \ 1 end {bmatrix}}, ; ; { begin {bmatrix} 3 \ 7 \ 5 \ 2 end {bmatrix }}, ; ; { begin {bmatrix} 4 \ 9 \ 1 \ 8 end {bmatrix}} { text {.}}}
Обратите внимание, что независимые столбцы уменьшенного эшелона строк форма — это именно столбцы с поворотными точками. Это позволяет определить, какие столбцы являются линейно независимыми, сводя их только к форме эшелона.
. Вышеупомянутый алгоритм может быть использован в общем для поиска отношений зависимости между любым набором векторов и выбора основы из любого охватывающий набор. Также поиск основы для пространства столбцов A эквивалентен поиску основы для пространства строк матрицы A транспонирования
Найти основу в практических условиях (например, для большие матрицы) обычно используется разложение по сингулярным числам.
Размер
Размер пространства столбцов называется рангом матрицы. Ранг равен количеству точек поворота в сокращенной форме эшелона строк и является максимальным количеством линейно независимых столбцов, которые могут быть выбраны из матрицы. Например, матрица 4 × 4 в приведенном выше примере имеет третий ранг.
Поскольку пространство столбцов является изображением соответствующего матричного преобразования, ранг матрицы такой же, как размер изображения. Например, преобразование R→ R, описанное вышеприведенной матрицей, отображает все R в некоторое трехмерное подпространство.
. Нулевое значение матрицы — это размерность пустое пространство и равно количеству столбцов в сокращенной форме эшелона строк, не имеющих точек поворота. Ранг и нулевое значение матрицы A с n столбцами связаны уравнением:
- rank (A) + nullity (A) = n. { displaystyle { text {rank}} (A) + { text {nullity}} (A) = n. ,}
Это известно как теорема ранга – недействительности.
Связь с левое пустое пространство
Левое пустое пространство в A — это набор всех векторов x таких, что x A = 0 . Это то же самое, что и пустое пространство в транспонировании из A. Произведение матрицы A и вектора x может быть записано в терминах скалярное произведение векторов:
- AT x = [v 1 ⋅ xv 2 ⋅ x ⋮ vn ⋅ x], { displaystyle A ^ { mathsf {T}} mathbf {x} = { begin {bmatrix} mathbf {v} _ {1} cdot mathbf {x} \ mathbf {v} _ {2} cdot mathbf {x} \ vdots \ mathbf {v} _ {n} cdot mathbf {x} end {bmatrix}},}
, поскольку векторы-строки из A являются транспонированными векторами-столбцами vkиз A. Таким образом, A x= 0if и только если x ортогонально (перпендикулярно) каждому из векторов-столбцов A.
Отсюда следует, что левое пустое пространство (нулевое пространство A) равно ортогональное дополнение к пространству столбцов матрицы A.
Для матрицы A пространство столбцов, пространство строк, пустое пространство и левое пустое пространство иногда называют четырьмя фундаментальными подпространствами.
Для матриц по кольцу
Аналогично пространство столбцов (иногда обозначаемое как пространство правого столбца) может быть определено для матриц по кольцу K как
- ∑ k = 1 nvkck { displaystyle sum limits _ {k = 1} ^ {n} mathbf {v} _ {k} c_ {k}}
для любого c 1,…, c n, с заменой векторного m-пространства на «правый свободный модуль », который изменяет порядок скалярного умножения вектора vkв скаляр c k таким образом, чтобы он был записан в векторном скаляре необычного порядка.
Строка
Определение
Пусть K будет полем из скаляров. Пусть A — матрица размера m × n с векторами-строками r1, r2,…, rm. линейная комбинация этих векторов — это любой вектор вида
- c 1 r 1 + c 2 r 2 + ⋯ + cmrm, { displaystyle c_ {1} mathbf {r} _ {1 } + c_ {2} mathbf {r} _ {2} + cdots + c_ {m} mathbf {r} _ {m},}
где c 1, c 2,…, c m — скаляры. Набор всех возможных линейных комбинаций r1,…, rmназывается пространством строк A. То есть пространство строк A является диапазоном векторов r1,…, rm.
Например, если
- A = [1 0 2 0 1 0], { displaystyle A = { begin {bmatrix} 1 0 2 \ 0 1 0 end { bmatrix}},}
тогда векторы-строки будут r1= (1, 0, 2) и r2= (0, 1, 0). Линейная комбинация r1и r2- это любой вектор вида
- c 1 (1, 0, 2) + c 2 (0, 1, 0) = (c 1, c 2, 2 c 1). { displaystyle c_ {1} (1,0,2) + c_ {2} (0,1,0) = (c_ {1}, c_ {2}, 2c_ {1}). ,}
Множество всех таких векторов — это пространство строк матрицы A. В этом случае пространство строк — это в точности набор векторов (x, y, z) ∈ K, удовлетворяющих уравнению z = 2x (с использованием декартовых координат, этот набор представляет собой плоскость , проходящую через начало координат в трехмерном пространстве ).
Для матрицы, представляющей однородную систему линейных уравнений, пространство строк состоит из всех линейных уравнений, которые следуют из уравнений системы.
Пространство столбца A равно пространству строки A.
Основа
На пространство строки не влияют операции с элементарной строкой. Это позволяет использовать сокращение строки, чтобы найти базис для пространства строки.
Например, рассмотрим матрицу
- A = [1 3 2 2 7 4 1 5 2]. { displaystyle A = { begin {bmatrix} 1 3 2 \ 2 7 4 \ 1 5 2 end {bmatrix}}.}
Строки этой матрицы охватывают пространство строк, но не могут быть линейно независимыми, и в этом случае ряды не будут основой. Чтобы найти основу, мы сокращаем A до эшелон строки, форма :
r1, r2, r3представляет строки.
- [1 3 2 2 7 4 1 5 2] ∼ ⏟ r 2 — 2 r 1 [1 3 2 0 1 0 1 5 2] ∼ ⏟ r 3 — r 1 [1 3 2 0 1 0 0 2 0 ] ∼ r 3 — 2 r 2 [1 3 2 0 1 0 0 0 0] ∼ r 1 — 3 r 2 [1 0 2 0 1 0 0 0 0]. { displaystyle { begin {bmatrix} 1 3 2 \ 2 7 4 \ 1 5 2 end {bmatrix}} underbrace { sim} _ {r_ {2} -2r_ {1}} { begin {bmatrix} 1 3 2 \ 0 1 0 \ 1 5 2 end {bmatrix}} underbrace { sim} _ {r_ {3} -r_ {1}} { begin {bmatrix} 1 3 2 \ 0 1 0 \ 0 2 0 end {bmatrix}} underbrace { sim} _ {r_ {3} -2r_ {2}} { begin {bmatrix} 1 3 2 \ 0 1 0 \ 0 0 0 end {bmatrix}} underbrace { sim} _ {r_ {1} -3r_ {2} } { begin {bmatrix} 1 0 2 \ 0 1 0 \ 0 0 0 end {bmatrix}}.}
Когда матрица находится в эшелонированной форме, ненулевые строки являются основой для пространства строк. В этом случае базис — {(1, 3, 2), (2, 7, 4)}. Другой возможный базис {(1, 0, 2), (0, 1, 0)} возникает в результате дальнейшего сокращения.
Этот алгоритм может использоваться в общем случае для поиска основы для диапазона набора векторов. Если матрица дополнительно упрощается до сокращенного эшелона строк формы, то результирующий базис однозначно определяется пространством строк.
Иногда удобно вместо этого найти основу для пространства строк среди строк исходной матрицы (например, этот результат полезен для элементарного доказательства того, что детерминантный ранг матрицы равен ее рангу). Поскольку операции со строками могут влиять на отношения линейной зависимости векторов-строк, такой базис вместо этого находят косвенно, используя тот факт, что пространство столбцов A равно пространству строк A. Используя приведенный выше пример матрицы A, найдите A и уменьшите его в виде эшелона строки:
- AT = [1 2 1 3 7 5 2 4 2] ∼ [1 2 1 0 1 2 0 0 0]. { displaystyle A ^ {T} = { begin {bmatrix} 1 2 1 \ 3 7 5 \ 2 4 2 end {bmatrix}} sim { begin {bmatrix} 1 2 1 \ 0 1 2 \ 0 0 0 end {bmatrix}}. }
Сводные точки указывают, что первые два столбца A образуют основу пространства столбцов A. Следовательно, первые две строки A (до любых сокращений строк) также образуют основу пространства строк A.
Размер
Размер пространства строк называется рангом матрицы. Это то же самое, что и максимальное количество линейно независимых строк, которые могут быть выбраны из матрицы, или, что то же самое, количество точек поворота. Например, матрица 3 × 3 в приведенном выше примере имеет ранг 2.
Ранг матрицы также равен размерности пространства столбцов. Размерность пустого пространства называется нулевой матрицы и связана с рангом следующим уравнением:
- ранг (A) + нулевое значение (A) = n, { displaystyle operatorname {rank} (A) + operatorname {nullity} (A) = n,}
, где n — количество столбцов в матрице A. Вышеприведенное уравнение известно как теорема ранга – недействительности.
Отношение к пустому пространству
пустое пространство матрицы A — это набор всех векторов x, для которых A x= 0. Произведение матрицы A и вектора x может быть записано в терминах скалярного произведения векторов:
- A x = [r 1 ⋅ xr 2 ⋅ x ⋮ rm ⋅ Икс], { Displaystyle A mathbf {x} = { begin {bmatrix} mathbf {r} _ {1} cdot mathbf {x} \ mathbf {r} _ {2} cdot mathbf {x} \ vdots \ mathbf {r} _ {m} cdot mathbf {x} end {bmatrix}},}
где r1,…, rm- векторы-строки A. Таким образом, A x= 0тогда и только тогда, когда x является ортогональным (перпендикулярно) каждому из векторов-строк A.
Отсюда следует что пустое пространство A является ортогональным дополнением к пространству строки. Например, если пространство строки представляет собой плоскость, проходящую через начало координат в трех измерениях, то пустое пространство будет перпендикулярной линией, проходящей через начало координат. Это обеспечивает доказательство теоремы ранга и недействительности (см. размерность выше).
Пространство строки и пустое пространство — это два из четырех основных подпространств, связанных с матрицей A (два других — это пространство столбцов и слева пустым пробел ).
Связь с совместным изображением
Если V и W являются векторными пространствами, то ядро линейного преобразования T: V → W — это множество векторов v ∈ V, для которых T (v ) = 0 . Ядро линейного преобразования аналогично пустому пространству матрицы.
Если V является внутренним пространством продукта, то ортогональное дополнение к ядру можно рассматривать как обобщение пространства строк. Это иногда называют сообразом T. Преобразование T взаимно однозначно по своему соизображению, а коимаж изоморфно отображает на изображение T.
Когда V не является внутренним пространством продукта, совместное изображение T может быть определено как факторное пространство V / ker (T).
См. Также
- Евклидово подпространство
Примечания
Ссылки
Учебники
- Антон, Ховард (1987), Элементарная линейная алгебра (5-е изд.), Нью-Йорк: Wiley, ISBN 0-471-84819-0
- Axler, Sheldon Jay (1997), Linear Algebra Done Right (2-е изд.), Springer -Verlag, ISBN 0-387-98259-0
- Банерджи, Судипто; Рой, Аниндья (6 июня 2014 г.), Линейная алгебра и матричный анализ для статистики (1-е изд.), CRC Press, ISBN 978-1-42-009538-8
- Борегар, Raymond A.; Фрали, Джон Б. (1973), Первый курс линейной алгебры: с дополнительным введением в группы, кольца и поля, Бостон: Houghton Mifflin Company, ISBN 0-395-14017-X
- Lay, David C. (22 августа 2005 г.), Linear Algebra and Its Applications (3-е изд.), Addison Wesley, ISBN 978-0-321-28713-7
- Леон, Стивен Дж. (2006), Линейная алгебра с приложениями (7-е изд.), Пирсон Прентис Холл
- Мейер, Карл Д. (15 февраля 2001 г.), Матричный анализ и прикладная линейная алгебра, Общество промышленной и прикладной математики (SIAM), ISBN 978-0-89871-454-8 , заархивировано с исходный 1 марта 2001 г.
- Пул, Дэвид (2006), Linear Algebra: A Modern Introduction (2 ed.), Brooks / Cole, ISBN 0-534 -99845-3
- Стрэнг, Гилберт (19 июля 2005 г.), Линейная алгебра и ее приложения (4-е изд.), Брукс Коул, ISBN 978-0-03-010567-8
Внешние ссылки
- Вайсштейн, Эрик У. «Пространство строк» . MathWorld.
- Вайсштейн, Эрик У. «Пространство столбца». MathWorld.
- Гилберт Стрэнг, Лекция по линейной алгебре Массачусетского технологического института по четырем фундаментальным подпространствам в Google Video, из MIT OpenCourseWare
- Видеоурок Академии Хана
- Лекция по пространство столбцов и пустое пространство Гилберта Стрэнга из MIT
- Пространство строк и пространство столбцов
Линейная алгебра для исследователей данных
Время на прочтение
5 мин
Количество просмотров 14K

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».
Ирвинг Капланский
Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.
В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.
Произведения векторов
Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy
называется следующее вещественное число:
Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество
.
Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть
След
Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:
След обладает следующими свойствами:
-
Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.
-
Для любых матриц A,B ∈ ℝⁿˣⁿ: tr(A + B) = trA + trB.
-
Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.
-
Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.
-
Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).
Нормы
Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:
Заметим, что ‖x‖₂²=xᵀx.
Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:
-
Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).
-
f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).
-
Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).
-
Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)
Другими примерами норм являются норма l₁
и норма l∞
Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как
Нормы также могут быть определены для матриц, например норма Фробениуса:
Линейная независимость и ранг
Множество векторов {x₁, x₂, …, xₙ} ⊂ ℝₘ называют линейно независимым, если никакой из этих векторов не может быть представлен в виде линейной комбинации других векторов этого множества. Если же такое представление какого-либо из векторов множества возможно, эти векторы называют линейно зависимыми. То есть, если выполняется равенство
для некоторых скалярных значений α₁,…, αₙ-₁ ∈ ℝ, то мы говорим, что векторы x₁, …, xₙ линейно зависимы; в противном случае они линейно независимы. Например, векторы
линейно зависимы, так как x₃ = −2xₙ + x₂.
Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.
Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).
-
Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).
-
Для любых матриц A,B ∈ ℝᵐˣⁿ: rank(A + B) ≤ rank(A) + rank(B).
Ортогональные матрицы
Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м
атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.
Непосредственно из определений ортогональности и нормированности следует, что
Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n < m), но ее столбцы являются ортонормированными, то UᵀU = I, но UUᵀ ≠ I. Поэтому, говоря об ортогональных матрицах, мы будем по умолчанию подразумевать квадратные матрицы.
Еще одно удобное свойство ортогональных матриц состоит в том, что умножение вектора на ортогональную матрицу не меняет его евклидову норму, то есть
для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.
Область значений и нуль-пространство матрицы
Линейной оболочкой множества векторов {x₁, x₂, …, xₙ} является множество всех векторов, которые могут быть представлены в виде линейной комбинации векторов {x₁, …, xₙ}, то есть
Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,
Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть
Квадратичные формы и положительно полуопределенные матрицы
Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:
Заметим, что
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как
(или просто A > 0), а множество всех положительно определенных матриц часто обозначают
.
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как
(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают
.
-
Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной
-
, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx < 0.
-
Далее, симметричная матрица A ∈ 𝕊ⁿ называется отрицательно полуопределенной (
), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.
-
Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что
и
.
Собственные значения и собственные векторы
Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство
На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).
Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.
-
ЗАПИСАТЬСЯ НА ДЕМОУРОК
The row vectors of a matrix. The row space of this matrix is the vector space spanned by the row vectors.
The column vectors of a matrix. The column space of this matrix is the vector space spanned by the column vectors.
In linear algebra, the column space (also called the range or image) of a matrix A is the span (set of all possible linear combinations) of its column vectors. The column space of a matrix is the image or range of the corresponding matrix transformation.
Let 



The row space is defined similarly.
The row space and the column space of a matrix A are sometimes denoted as C(AT) and C(A) respectively.[2]
This article considers matrices of real numbers. The row and column spaces are subspaces of the real spaces 

Overview[edit]
Let A be an m-by-n matrix. Then
- rank(A) = dim(rowsp(A)) = dim(colsp(A)),[4]
- rank(A) = number of pivots in any echelon form of A,
- rank(A) = the maximum number of linearly independent rows or columns of A.[5]
If one considers the matrix as a linear transformation from 

The column space of a matrix A is the set of all linear combinations of the columns in A. If A = [a1 ⋯ an], then colsp(A) = span({a1, …, an}).
The concept of row space generalizes to matrices over 
Intuitively, given a matrix A, the action of the matrix A on a vector x will return a linear combination of the columns of A weighted by the coordinates of x as coefficients. Another way to look at this is that it will (1) first project x into the row space of A, (2) perform an invertible transformation, and (3) place the resulting vector y in the column space of A. Thus the result y = Ax must reside in the column space of A. See singular value decomposition for more details on this second interpretation.[clarification needed]
Example[edit]
Given a matrix J:
the rows are




Consequently, the row space of J is the subspace of 
Since these four row vectors are linearly independent, the row space is 4-dimensional. Moreover, in this case it can be seen that they are all orthogonal to the vector n = [6, −1, 4, −4, 0], so it can be deduced that the row space consists of all vectors in 
Column space[edit]
Definition[edit]
Let K be a field of scalars. Let A be an m × n matrix, with column vectors v1, v2, …, vn. A linear combination of these vectors is any vector of the form
where c1, c2, …, cn are scalars. The set of all possible linear combinations of v1, …, vn is called the column space of A. That is, the column space of A is the span of the vectors v1, …, vn.
Any linear combination of the column vectors of a matrix A can be written as the product of A with a column vector:
Therefore, the column space of A consists of all possible products Ax, for x ∈ Kn. This is the same as the image (or range) of the corresponding matrix transformation.
Example[edit]
If 
A linear combination of v1 and v2 is any vector of the form
The set of all such vectors is the column space of A. In this case, the column space is precisely the set of vectors (x, y, z) ∈ R3 satisfying the equation z = 2x (using Cartesian coordinates, this set is a plane through the origin in three-dimensional space).
Basis[edit]
The columns of A span the column space, but they may not form a basis if the column vectors are not linearly independent. Fortunately, elementary row operations do not affect the dependence relations between the column vectors. This makes it possible to use row reduction to find a basis for the column space.
For example, consider the matrix
The columns of this matrix span the column space, but they may not be linearly independent, in which case some subset of them will form a basis. To find this basis, we reduce A to reduced row echelon form:
[6]
At this point, it is clear that the first, second, and fourth columns are linearly independent, while the third column is a linear combination of the first two. (Specifically, v3 = −2v1 + v2.) Therefore, the first, second, and fourth columns of the original matrix are a basis for the column space:
Note that the independent columns of the reduced row echelon form are precisely the columns with pivots. This makes it possible to determine which columns are linearly independent by reducing only to echelon form.
The above algorithm can be used in general to find the dependence relations between any set of vectors, and to pick out a basis from any spanning set. Also finding a basis for the column space of A is equivalent to finding a basis for the row space of the transpose matrix AT.
To find the basis in a practical setting (e.g., for large matrices), the singular-value decomposition is typically used.
Dimension[edit]
The dimension of the column space is called the rank of the matrix. The rank is equal to the number of pivots in the reduced row echelon form, and is the maximum number of linearly independent columns that can be chosen from the matrix. For example, the 4 × 4 matrix in the example above has rank three.
Because the column space is the image of the corresponding matrix transformation, the rank of a matrix is the same as the dimension of the image. For example, the transformation 

The nullity of a matrix is the dimension of the null space, and is equal to the number of columns in the reduced row echelon form that do not have pivots.[7] The rank and nullity of a matrix A with n columns are related by the equation:
This is known as the rank–nullity theorem.
Relation to the left null space[edit]
The left null space of A is the set of all vectors x such that xTA = 0T. It is the same as the null space of the transpose of A. The product of the matrix AT and the vector x can be written in terms of the dot product of vectors:
because row vectors of AT are transposes of column vectors vk of A. Thus ATx = 0 if and only if x is orthogonal (perpendicular) to each of the column vectors of A.
It follows that the left null space (the null space of AT) is the orthogonal complement to the column space of A.
For a matrix A, the column space, row space, null space, and left null space are sometimes referred to as the four fundamental subspaces.
For matrices over a ring[edit]
Similarly the column space (sometimes disambiguated as right column space) can be defined for matrices over a ring K as
for any c1, …, cn, with replacement of the vector m-space with «right free module», which changes the order of scalar multiplication of the vector vk to the scalar ck such that it is written in an unusual order vector–scalar.[8]
Row space[edit]
Definition[edit]
Let K be a field of scalars. Let A be an m × n matrix, with row vectors r1, r2, …, rm. A linear combination of these vectors is any vector of the form
where c1, c2, …, cm are scalars. The set of all possible linear combinations of r1, …, rm is called the row space of A. That is, the row space of A is the span of the vectors r1, …, rm.
For example, if
then the row vectors are r1 = [1, 0, 2] and r2 = [0, 1, 0]. A linear combination of r1 and r2 is any vector of the form
The set of all such vectors is the row space of A. In this case, the row space is precisely the set of vectors (x, y, z) ∈ K3 satisfying the equation z = 2x (using Cartesian coordinates, this set is a plane through the origin in three-dimensional space).
For a matrix that represents a homogeneous system of linear equations, the row space consists of all linear equations that follow from those in the system.
The column space of A is equal to the row space of AT.
Basis[edit]
The row space is not affected by elementary row operations. This makes it possible to use row reduction to find a basis for the row space.
For example, consider the matrix
The rows of this matrix span the row space, but they may not be linearly independent, in which case the rows will not be a basis. To find a basis, we reduce A to row echelon form:
r1, r2, r3 represents the rows.
Once the matrix is in echelon form, the nonzero rows are a basis for the row space. In this case, the basis is { [1, 3, 2], [2, 7, 4] }. Another possible basis { [1, 0, 2], [0, 1, 0] } comes from a further reduction.[9]
This algorithm can be used in general to find a basis for the span of a set of vectors. If the matrix is further simplified to reduced row echelon form, then the resulting basis is uniquely determined by the row space.
It is sometimes convenient to find a basis for the row space from among the rows of the original matrix instead (for example, this result is useful in giving an elementary proof that the determinantal rank of a matrix is equal to its rank). Since row operations can affect linear dependence relations of the row vectors, such a basis is instead found indirectly using the fact that the column space of AT is equal to the row space of A. Using the example matrix A above, find AT and reduce it to row echelon form:
The pivots indicate that the first two columns of AT form a basis of the column space of AT. Therefore, the first two rows of A (before any row reductions) also form a basis of the row space of A.
Dimension[edit]
The dimension of the row space is called the rank of the matrix. This is the same as the maximum number of linearly independent rows that can be chosen from the matrix, or equivalently the number of pivots. For example, the 3 × 3 matrix in the example above has rank two.[9]
The rank of a matrix is also equal to the dimension of the column space. The dimension of the null space is called the nullity of the matrix, and is related to the rank by the following equation:
where n is the number of columns of the matrix A. The equation above is known as the rank–nullity theorem.
Relation to the null space[edit]
The null space of matrix A is the set of all vectors x for which Ax = 0. The product of the matrix A and the vector x can be written in terms of the dot product of vectors:
where r1, …, rm are the row vectors of A. Thus Ax = 0 if and only if x is orthogonal (perpendicular) to each of the row vectors of A.
It follows that the null space of A is the orthogonal complement to the row space. For example, if the row space is a plane through the origin in three dimensions, then the null space will be the perpendicular line through the origin. This provides a proof of the rank–nullity theorem (see dimension above).
The row space and null space are two of the four fundamental subspaces associated with a matrix A (the other two being the column space and left null space).
Relation to coimage[edit]
If V and W are vector spaces, then the kernel of a linear transformation T: V → W is the set of vectors v ∈ V for which T(v) = 0. The kernel of a linear transformation is analogous to the null space of a matrix.
If V is an inner product space, then the orthogonal complement to the kernel can be thought of as a generalization of the row space. This is sometimes called the coimage of T. The transformation T is one-to-one on its coimage, and the coimage maps isomorphically onto the image of T.
When V is not an inner product space, the coimage of T can be defined as the quotient space V / ker(T).
See also[edit]
- Euclidean subspace
References & Notes[edit]
- ^ Linear algebra, as discussed in this article, is a very well established mathematical discipline for which there are many sources. Almost all of the material in this article can be found in Lay 2005, Meyer 2001, and Strang 2005.
- ^ Strang, Gilbert (2016). Introduction to linear algebra (Fifth ed.). Wellesley, MA: Wellesley-Cambridge Press. pp. 128, 168. ISBN 978-0-9802327-7-6. OCLC 956503593.
- ^ Anton (1987, p. 179)
- ^ Anton (1987, p. 183)
- ^ Beauregard & Fraleigh (1973, p. 254)
- ^ This computation uses the Gauss–Jordan row-reduction algorithm. Each of the shown steps involves multiple elementary row operations.
- ^ Columns without pivots represent free variables in the associated homogeneous system of linear equations.
- ^ Important only if K is not commutative. Actually, this form is merely a product Ac of the matrix A to the column vector c from Kn where the order of factors is preserved, unlike the formula above.
- ^ a b The example is valid over the real numbers, the rational numbers, and other number fields. It is not necessarily correct over fields and rings with non-zero characteristic.
Further reading[edit]
- Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley, ISBN 0-471-84819-0
- Axler, Sheldon Jay (1997), Linear Algebra Done Right (2nd ed.), Springer-Verlag, ISBN 0-387-98259-0
- Banerjee, Sudipto; Roy, Anindya (June 6, 2014), Linear Algebra and Matrix Analysis for Statistics (1st ed.), CRC Press, ISBN 978-1-42-009538-8
- Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Company, ISBN 0-395-14017-X
- Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7
- Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall
- Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8, archived from the original on March 1, 2001
- Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3
- Strang, Gilbert (July 19, 2005), Linear Algebra and Its Applications (4th ed.), Brooks Cole, ISBN 978-0-03-010567-8
External links[edit]
- Weisstein, Eric W. «Row Space». MathWorld.
- Weisstein, Eric W. «Column Space». MathWorld.
- Gilbert Strang, MIT Linear Algebra Lecture on the Four Fundamental Subspaces at Google Video, from MIT OpenCourseWare
- Khan Academy video tutorial
- Lecture on column space and nullspace by Gilbert Strang of MIT
- Row Space and Column Space
Линейная алгебра — это широкая тема математики с приложениями в различных реальных ситуациях, особенно в машинном обучении. Матрицы и векторы являются фундаментальными строительными блоками линейной алгебры, и они используются во множестве процедур и инструментов. В этой статье будет обсуждаться столбцовое пространство матрицы. Мы также рассмотрим несколько необходимых терминов для понимания пространства столбца матрицы.
Что такое размах вектора?
Промежуток просто означает, что для данного набора векторов, если любая линейная комбинация применяется к этому набору векторов и остается в этом векторном пространстве, она охватывает это векторное пространство. Это означает, что если вы умножите любой скаляр на определенный вектор, он останется в пределах этого измерения, независимо от того, работаете ли вы с первым, вторым, третьим или n-м измерением. Говорят, что он «протягивается» повсюду в этом измерении. Когда вы умножаете набор векторов на скаляр, это просто указывает, что набор векторов, который вы работа с которым может охватывать (или размещаться где-либо внутри) полное измерение (или векторное пространство), с которым вы работаете с.
Что такое линейная комбинация?
Предположим, у вас есть набор математических объектов {x1….Иксн} которые поддерживают скалярное умножение и сложение (например, элементы кольца или векторного пространства), то y = a1Икс1+а2Икс2+… анИксн (где ai — некоторые скалярные значения). Наиболее популярной иллюстрацией является использование трехмерных векторов в евклидовом пространстве. Вектор, который находится в той же плоскости через начало координат, что и исходные два вектора, помещенные в начало координат, является линейной комбинацией любых двух таких векторов.
Что такое пространство строк и столбцов?
Предположим, что A — mxn-матрица над полем F. Тогда в строках n-компонентные векторы, и их m. Точно так же каждый m-компонентный вектор представлен n столбцами. Подпространство Fн образованное векторами-строками, является пространством строк A, а его элементы являются линейными комбинациями векторов-строк. Это пространство имеет размерность, и столбцы обуславливают такие отношения между строками и наоборот. Точно так же пространство столбцов матрицы является подпространством Fм формируется векторами-столбцами матрицы. Хотя это пространство отличается от пространства строк в целом, оно имеет те же размеры, что и пространство строк. так как любая линейная связь между столбцами также налагает такие отношения между строками и наоборот наоборот
Подробнее о пространстве столбцов
Span является более фундаментальной концепцией. Проще говоря, диапазон столбцов данного вектора — это то, что мы называем пространством столбцов. Вы можете взять все возможные линейные комбинации векторов, если у вас есть их набор. Результирующее векторное пространство известно как диапазон исходной коллекции. Пространство столбцов представляет собой набор всех возможных линейных комбинаций векторов-столбцов матрицы. Другими словами, если вектор b в Rм может быть выражена как линейная комбинация столбцов A, она находится в пространстве столбцов A. То есть b ∈ CS(A) именно тогда, когда существуют скаляры x1, Икс2, …, Иксн такой, что
Как произведение A на вектор-столбец, любая линейная комбинация векторов-столбцов матрицы A может быть записана:
Таким образом, пространство столбцов матрицы A состоит из всех возможных произведений A*x для x ∈ Cн. Приведенный выше результат также является изображение соответствующих матричное преобразование.
Мы обычно обозначаем пространство строк и столбцов матрицы (скажем, A) через C(AT) и C(A) соответственно.
Вывод
В этой статье были рассмотрены различные темы, связанные с пространством столбцов матрицы. Промежуток вектора — это пространство, которое остается неизменным после применения линейной комбинации к набору векторов. После умножения набора векторов и скаляров суммирование называется линейной комбинацией. Совокупность всех мыслимых линейных комбинаций векторов-столбцов матрицы является пространством столбцов матрицы.