Download Article
Download Article
Often times, you are required to construct some angles without using a protractor. This article teaches you how to draw a 90 degrees angle using a compass and a ruler.
-
1
Mark the vertex of your angle anywhere on the paper. Let us name this point as M.
-
2
Draw a ray MN, extending in any direction and of any length. This will be one of the arms of our angle.[1]
Advertisement
-
3
Place tip of the compass on point M and draw a circle cutting the ray MN at some point (say P).[2]
-
4
Keep the width of the compass the same. Then place its tip on P and draw an arc cutting the circle at some point (say Q).
-
5
Keep the width of the compass the same. Place its tip on Q and draw another arc cutting the circle at another point (say R).[3]
-
6
Keep the tip of the compass still on Q. Draw another arc somewhere outside the circle. For carrying out this step, you can set the width of the compass to any measure.[4]
-
7
Keep the same width of the compass (as set in the previous step). Now place its tip on R and draw another arc which cuts the arc drawn in the previous step at some point (say S).
-
8
Connect the points M and S with a straight line. Extend it to form a ray ML.[5]
- The measure of the angle LMN is 90O.
Advertisement
-
1
Draw a straight line. On a piece of paper, draw a line segment of any convenient length. Make it horizontal for the sake of simplicity, but it could be at any angle. Label the line segment AB.[6]
-
2
Pick any point on AB. Mark it, and label it O. O can be anywhere on the line segment, including at either end point (A or B). For convenience, let’s put O somewhere near the middle of AB. The line segment could now be referred to as AOB.
-
3
Grab a compass. Open the compass to a radius a little shorter than either AO or OB. Now place the compass point at O. Strike short arcs through AB on either side of O. The two arcs should have the same radius. Label those two points of intersection C and D. Now the line segment could be referred to as ACODB.[7]
-
4
Strike two more arcs. Place the compass point at C, and strike an arc to one side of the line segment. Then place the compass point at D, and strike a second arc of the same radius and on the same side of the line segment. Make sure those two arcs intersect. Call that point of intersection E.[8]
-
5
Draw the 90° angle. Draw a straight line from E to O. Line segment EO forms a 90° angle with line segment AB. It actually forms two 90° angles at O. If you were to extend EO beyond AB, you would form four 90° angles at O.[9]
- Note that you can draw a 90° angle at either end of line segment AB if you want to (in other words at point A or point B). Simply extend AB beyond A or beyond B, and then follow the above steps. Point A (or point B) would serve as point O in the above instructions.
- This is essentially the same method featured in How to Construct a Perpendicular Line to a Given Line Through Point on the Line, Method 2.
Advertisement
Add New Question
-
Question
How do I draw a right angle triangle?
First construct a 90° angle as shown above. Extend each leg of the angle any convenient length. Draw a line from the end of one leg to the end of the other. You have a right triangle.
-
Question
How do I construct a 15 degree angle?
First, make a 60 degree angle by constructing an equilateral triangle. Use angle bisection construction to make a 30 degree angle. Bisect the 30 degree angle again to make a 15 degree angle.
-
Question
Can I draw a 133-degree angle?
There is no way to construct such an angle using a compass and a ruler. That’s why they invented the protractor.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Things You’ll Need
- Paper
- Pen or pencil
- Ruler or another straightedge
- Compass
References
About This Article
Thanks to all authors for creating a page that has been read 112,731 times.
Reader Success Stories
-
Payal Sharma
Sep 27, 2016
«A really detailed and elaborate answer! Keep it going! Better than my maths teacher!»
Did this article help you?
|
Легко:
в месте пересечения последней линии и основания треугольника получаем идеальный прямой угол. система выбрала этот ответ лучшим Galina7v7 7 лет назад Я тоже не знаю.что такое-идеальная линейка.но есть идейка.Проведем прямую.на ней откладываем 2 равных отрезка.из центра отрезка произвольно проводим прямую.и на ней отложим такие же равные отрезки как и до этого .и каждую из точек соединим с концами 1-го отрезка.получили прямоугольник т.к. диагонали равны.и в точке пересечения делятся пополам. и угла полученные = 90 град-в. …Вижу «оригинальность «понятия идеальной линейки-ею мерять нельзя..а что ею можно делать?мух бить?Или тупо приложить к бумаге и провести прямой угол по контуру-она же «идеальная линейка»и угол ее прямой и идеальный» bezdelnik 7 лет назад Построить теоретически точно прямой угол с помощью идеальной линейки без делений можно так. На листе бумаги по линейке проводим произвольную прямую, затем складываем лист на две части так, чтобы части прямой совпали. Тогда в пересечении прочерченной прямой с линией складки получим 4-ре прямых угла. Знаете ответ? |
Как начертить прямой угол
Начертить прямой угол кажется простым, если под рукой есть технические приспособления. А если нет? Или вам необходимо построить прямой угол на большой площади, например, участке земли. И сколько существует способов построить прямой угол?

Вам понадобится
- — линейка;
- — чертежный треугольник;
- — карандаш;
- — циркуль;
- — веревка;
- — груз.
Инструкция
Способ первый – с помощью линейки, карандаша и транспортира. Начертите с помощью линейки прямую. Отметьте на ней точку. Совместите точку с серединой транспортира. Найдите на шкале транспортира отметку 90о и обозначьте ее точкой. Проведите линию через две точки. Две прямые линии пересекаются друг с другом под прямым углом.
Способ второй – с помощью линейки-треугольника и карандаша. Один угол у треугольника прямой. Приложите его одной стороной к линии, от которой необходимо построить прямой угол. По перпендикулярной стороне треугольника от линии начертите отрезок. Угол между отрезком и линией будет прямым. Или просто обведите прямой угол треугольника карандашом на бумаге.
Способ третий – с помощью прямоугольного предмета. Так же, как и чертежный треугольник, вы можете использовать любой предмет, углы которого прямые. Например, книгу, папку, коробку.
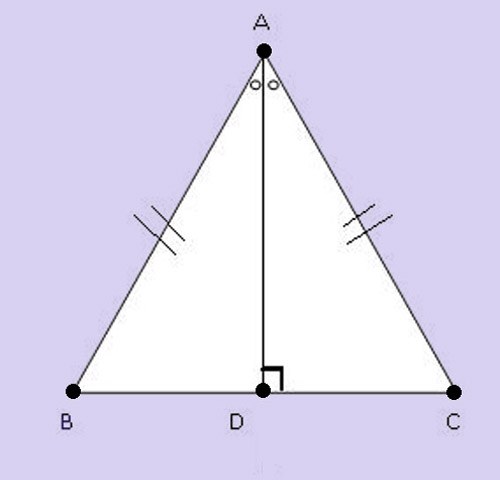
Способ четвертый – с помощью линейки и карандаша. Из точки А отложите два отрезка АВ и АС одной длины под острым углом друг к другу. Соедините их концы – у вас получится равнобедренный треугольник. Найдите середину его основания D и соедините с вершиной A. Отрезок АD является медианой, биссектрисой, высотой, т.е. перпендикулярен основанию ВС.
Способ пятый – с помощью линейки, карандаша и циркуля. В геометрии вписанный угол, опирающийся на диаметр – прямой. Начертите циркулем окружность. Проведите диаметр через ее центр. Отметьте произвольную точку на окружности и соедините ее с концами диаметра отрезками. Угол, образованный отрезками – прямой.

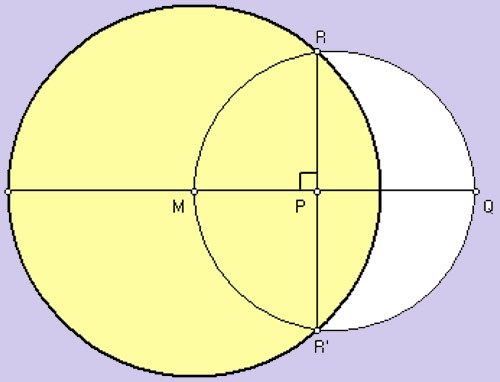
Способ шестой — другой вариант построения прямого угла с помощью циркуля и линейки. Начертите две произвольных окружности так, чтобы они пересекались друг с другом в двух точках. Соедините эти точки отрезком RR’. Затем проведите через центры окружностей прямую. Отрезок и прямая пересекаются под углом 90о.
Способ седьмой – если вам надо построить перпендикуляр на вертикальной поверхности, например стене, воспользуйтесь отвесом. К одному концу веревки привяжите груз. Теперь, если вы держите за другой конец, веревка будет натянута под углом 90о к горизонтали. Приблизив отвес к стене, начертите вдоль веревки прямую линию. Угол между линией и полом будет прямым, если пол у вас горизонтален.
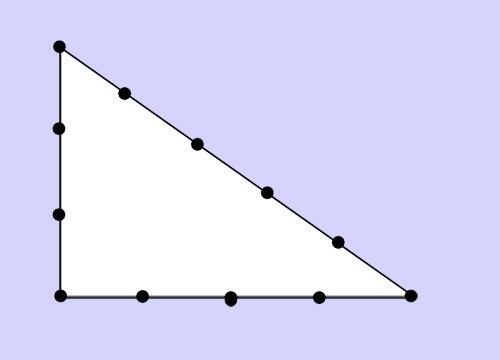
Способ восьмой – с помощью веревки с завязанными через 12 равных промежутков узелками и теоремы Пифагора. Этот способ использовали древние египтяне. Если натянуть эту веревку так, чтобы она образовала треугольник со сторонами в 3, 4 и 5 промежутков, угол напротив длинной стороны будет прямым. По теореме Пифагора: 3^2+4^2 = 5^2. Значит, треугольник – прямоугольный.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
муниципальное
общеобразовательное учреждение
«Средняя школа с углубленным изучением
отдельных
предметов
№
57 Кировского района Волгограда»
10
способов
построения
прямого угла
Подготовили
ученицы 5 «А» класса
Рябцева
Вероника, Парамонова Арина
Учитель
Фомина Е.М.
1. Построение
прямого угла с использованием транспортира

Часто
снег идет зимой
И
приносит радость,
Угол
помните прямой 90 градусов!
1
2. Построение
прямого угла с использованием угольника

Кому
не приятна за труд похвала
Разгонит,
которая тучи.
Развернутый
угол дели пополам
Прямые
углы ты получишь.
2
3. Построение
прямого угла с использованием подручных предметов
Если под рукой нет ни одного специального
чертежного инструмента, то Вам помогут разнообразные предметы прямоугольной
формы, которые можно
обвести: книги, листы бумаги,
упаковки из-под чего-нибудь и любые другие.
Посмотрите
вокруг,
прямые
углы повсюду нас окружают!
3
4.Построение
прямого угла с использованием египетского треугольника
Завяжите на веревке 2
узелка. Это первый отрезок. Согните веревку и отложите равный первому отрезок,
завяжите узелок, получили 3 узелка и 2 равных отрезка. Продолжите до
получения 12 равных отрезков
узелками. Если натянуть эту веревку так, чтобы она образовала треугольник со сторонами в 3, 4 и 5
промежутков, то угол напротив
самой длинной стороны будет прямым!
А почему египетский
треугольник?
Так свойство этого треугольника заметили еще древние египтяне!
4
5. Построение
прямого угла с использованием клочка бумаги или ткани
Вы
догадались, что никакого фокуса здесь нет. Сгибая клочок первый раз, мы
получили развернутый угол. Согнув второй раз, разделили развернутый угол
пополам, а это и есть прямой угол! 5
6. Построение
прямого угла с использованием грузика
Груз, подвешенный на нити, за
счет силы тяжести всегда перпендикулярен поверхности земли (поверхность
земли, подразумевается без уклонов, впадин).
6
7. Построение
прямого угла с использованием понятия «кратчайшее расстояние»
Оказывается, кратчайший путь от
точки до прямой, проходит под прямым углом к заданной прямой!
Потренируйтесь, строить
от руки прямые углы. Измерьте полученные углы, оцените свой глазомер.
7
8. Построение
прямого угла с использованием свойства диагоналей ромба
Почему так
происходит?
Разрежьте ромбик
по диагоналям на 4 части, сложите из них 2 «прямоугольника». Сомневаетесь,
что эти фигуры действительно прямоугольники.
А что
известно про прямоугольник, кроме того, что все углы прямые. У прямоугольника
длины диагоналей равны! Измерьте диагонали … равны?!
8
9. Построение
прямого угла с использованием окружности
Данный
способ подразумевает наличие окружности, но не обязательно построенной с
помощью циркуля. Достаточно веревки!

Затем
проводим диаметр. Отмечаем на окружности любую точку. Соединяем концы
диаметра с точкой окружности. Полученный треугольник прямоугольный! А значит,
прямой угол построен.
9
10. Построение
прямого угла с использованием циркуля и линейки
10
Наверное,
кто то скажет, что одни способы построения прямого угла более точные, чем
другие. Не торопитесь с выводами!
Построение
прямого угла с использованием транспортира, на первый взгляд, обеспечивает
точное построение прямого угла. Однако, любой прибор имеет погрешность
измерения равное одному делению шкалы, и транспортир не исключение.
Отклонение в 1 ̊, кажется, несущественным. А известна ли нам погрешность
других способов? Возможно, их погрешность также не превышает 1 ̊.
Неоспоримое
преимущество некоторых способов построения прямого угла в минимуме необходимых
приспособлений. Ведь, в природе редко встречается прямой угол. Окажись, вдали
от цивилизации Вы, в случае необходимости, достаточно точно построите прямые
углы.
11



















