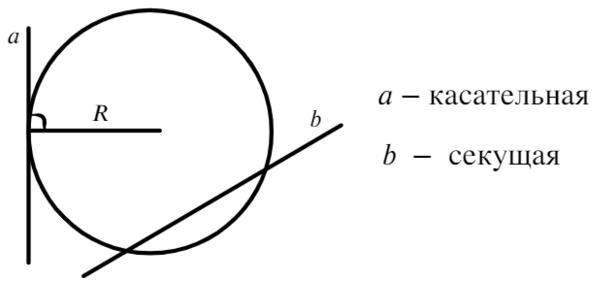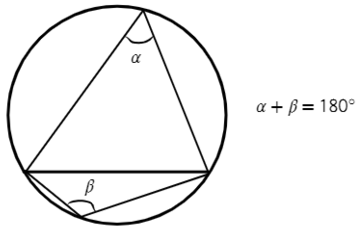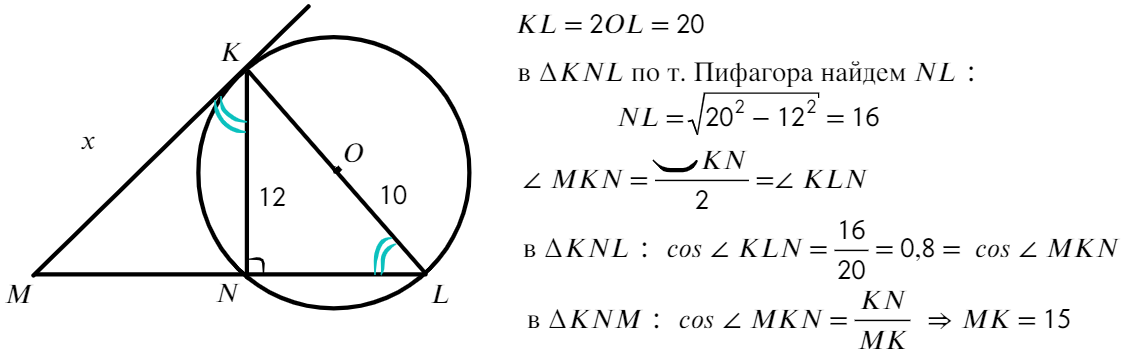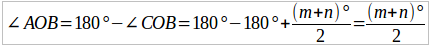Как найти прямой угол в окружности

Прямой угол

Чему равен прямой угол? Как изобразить прямой угол? Как найти прямые углы на рисунке?

Прямой угол — это угол, градусная мера которого равна 90º.

I. Проще всего изобразить прямой угол по клеточкам.

1) Точку — вершину прямого угла — ставим на пересечении клеточек.

2) Из вершины проводим лучи — стороны угла: один — горизонтально, другой — вертикально.

3) Ставим знак прямого угла — маленький квадрат при вершине: □

то есть угол ABC — прямой.

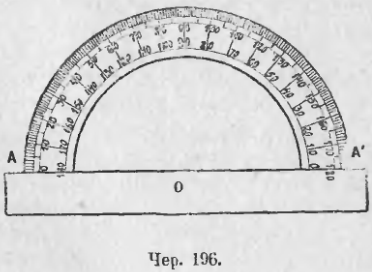
II. Другой способ построения прямого угла — при помощи транспортира:

1) Отмечаем точку — вершину угла.

2) От вершины проводим луч — сторону угла.

3) Совмещаем вершину угла с отметкой в центре транспортира (у разных моделей положение отметки может быть различным) так, чтобы отметка 0º располагалась на стороне угла.

4) На отметке 90 градусов ставим точку.

5) От вершины через эту точку проводим второй луч — другую сторону угла:

III. Ещё один способ построения прямого угла — с помощью угольника.

1) Отмечаем точку — вершину угла.

1) От вершины угла проводим луч — первую сторону угла.

2) Прикладываем угольник прямым углом к вершине угла так, чтобы одна сторона угольника проходила через первую сторону угла.

3) Вдоль другой стороны угольника проводим другой луч — вторую сторону угла.

Чтобы по рисунку найти прямой угол, также можно использовать угольник.

Если приложить угольник к вершине угла вдоль одной из сторон, то в остром угле вторую сторону угольник частично закроет (так как градусная мера острого угла меньше 90º), в тупом — вторая сторона окажется за угольником (поскольку тупой угол больше 90º), и только в прямом угле другая сторона угольника пройдёт ровно вдоль второй стороны:

Треугольник, один из углов которого — прямой, называется прямоугольным.

Как начертить угол на окружности

Математика

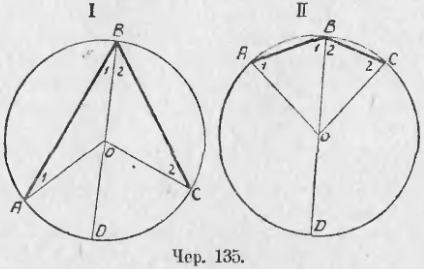
132. Мы уже знакомы с центральными углами. Построим теперь угол, вершина которого лежит на окружности и сторонами служат хорды. Такой угол называется вписанным в круг. Пусть построен ∠ABC (чер. 135, I или II), вписанный в круг O. Он опирается на дугу AC. Построим еще центральный ∠AOC, опирающийся на ту же дугу. Тогда между ∠ABC и ∠AOC существует простая зависимость. Для ее выяснения построим диаметр DB — мы будем сначала рассматривать случай, когда этот диаметр идет внутри ∠ABC, – получим два равнобедренных треугольника — ∆AOB и ∆BOC, у которых углы при основании равны: на чертеже равные углы обозначены одним и тем же нумером, – ∠A = ∠ABO = ∠1 и ∠C = ∠CBO = ∠2.

Тогда ∠AOD является внешним для ∆AOB, и он равен сумме внутренних с ним несмежных, т. е.

Также ∠DOC есть внешний для ∆BOC и, следовательно,

Отсюда сложением находим:

∠AOC = ∠AOD + ∠DOC = 2∠1 + 2∠2 = 2(∠1 + ∠2) = 2∠B, где под обозначением ∠B понимаем ∠ABC.

∠AOC = 2∠ABC
или ∠ABC = ½ ∠AOC = ∠AOC / 2.

Если одна из сторон вписанного угла проходила бы чрез центр, то дело упрощалось бы и еще скорее получилась бы та же зависимость. Например, для вписанного угла ABD:

∠AOD = 2∠1 = 2∠ABD или ∠ABD = ½ ∠AOD = ∠AOD / 2.

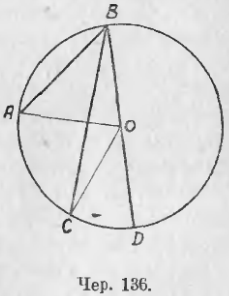
Рассмотрим теперь случай, когда диаметр BD проходит вне угла ABC (чер. 136). Тогда, согласно предыдущему, имеем:

∠ABD = ½ ∠AOD,
∠CBD = ½ ∠COD,

так как одна сторона углов ABD и CBD служит диаметром.

∠ABC = ∠ABD – ∠CBD = ½ ∠AOD – ½ ∠COD =
= ½ (∠AOD – ∠COD) = (∠AOD – ∠COD) / 2.

Но разность ∠AOD – ∠COD равна ∠AOC, следовательно, ∠ABC = ∠AOC / 2.

Итак, найденная зависимость справедлива для всех возможных случаев. Поэтому имеем:

Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

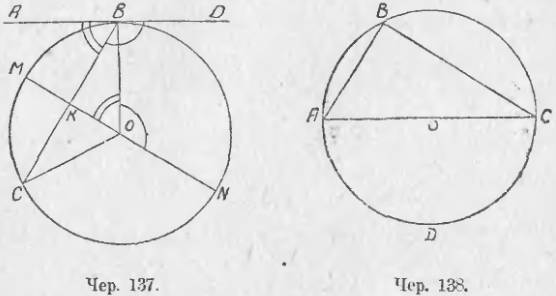
133. Если хорду AB (чер. 136) вращать по направлению от BC вокруг точки B, то вписанный угол ABC станет увеличиваться, но все время будет сохраняться найденная выше зависимость между вписанным и центральным углом. Наконец, прямая AB может сделаться касательною к кругу (чер. 137) и тогда получим ∠ABC, составленный хордою и касательною; если касательную продолжить, то получим другой такой же ∠DBC. Уже из того процесса вращения, которым мы перешли от вписанного угла к этому новому углу, видно, что угол, составленных хордою и касательною, являясь предельным случаем вписанного угла, должен подчиниться той же зависимости, которая была найдена в предыдущем п. для вписанного угла. Но возможно то же самое увидать иначе. Рассмотрим, например, ∠CBD (чер. 137). Построим диаметр MN ⊥ BC и соединим точку касания B с O; тогда BO ⊥ AD. Так как ∆KBO прямоугольный, то ∠KBO + ∠KOB = d, но ∠ABO = d или ∠ABK + ∠KBO = d. Отсюда заключаем, что ∠KOB = ∠ABK, так как каждый из этих углов дополняет один и тот же ∠KBO до прямого.

Но ∠CBD = выпрямленному углу – ∠ABK и ∠BON = выпрямленному углу – ∠KOB. Следовательно, ∠CBD = ∠BON = ∠COB / 2, где под именем ∠COB надо понимать угол, больший выпрямленного и который опирается на дугу CNB, то и ∠CMB равен половине того же центрального угла COB. Отсюда заключаем, что ∠CBD = ∠CMB. Также (еще проще) можно получить, что ∠ABC = ∠CNB (углы CMB и CNB на чертеже не даны). Этот результат можно выразить в следующей форме:

Угол, составленный хордой и касательной, равен вписанному углу, опирающемуся на дугу, заключенную внутри первого угла.

134. Построим в круге O (чер. 138) диаметр AC и какой-либо вписанный ∠ABC, опирающийся на полуокружность ADC или, как часто говорят, опирающийся на диаметр AC.

Тогда ∠ABC = ½ ∠AOC, но ∠AOC выпрямленный; следовательно, ∠ABC = d, т. е.:

Вписанный угол, опирающийся на диаметр, – прямой.

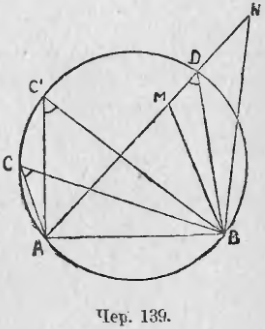
135. Построим в круге какую-либо хорду AB (чер. 139) и ряд вписанных углов, опирающихся на ◡AB: ∠C, ∠C1 и т. д.

Тогда каждый из этих углов равен половине центрального угла, опирающегося на дугу AB, и следовательно ∠C = ∠C1 = …

Этот результат можно истолковать в следующей форме. Пусть в точке C помещен наш глаз, тогда лучи зрения, идущие из глаза к концам отрезка AB, составляют ∠ACB, – говорят, что из точки C отрезок AB виден под углом ACB. Переместим наш глаз в точку C1; тогда отрезок AB будет виден под углом AC1B, который равен прежнему. Вообще, в какую бы точку дуги ACDB мы ни поместили наш глаз, отрезок AB будет виден все под таким же углом.

Поместим теперь наш глаз в какую-либо точку M, находящуюся внутри круга; тогда из этой точки отрезок AB будет виден под углом AMB, который уже неравен прежнему; продолжив AM до пересечения с окружностью в точке D и соединив D с B, получим ∆MBD, для которого ∠AMB есть внешний, и, следовательно, ∠AMB > ∠ADB или ∠AMB > ∠C (ибо ∠ADB = ∠C).

Поместим теперь наш глаз в какую-либо точку N вне круга. Чтобы упростить чертеж, возьмем точку N на продолжении прямой AD; тогда из точки N отрезок AB виден под углом ANB. Рассматривая ∆BDN, найдем ∠ADB > ∠N (ибо ∠ADB внешний для ∆BDN) или ∠N Геометрическим местом точек, из которых какой-либо отрезок виден под одним и тем же углом, есть дуга круга, проходящего чрез концы этого отрезка.

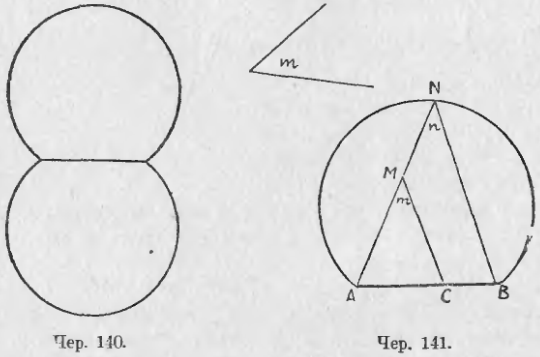
Если бы мы захотели рассмотреть точки и по другую сторону прямой AB, то нашли бы и с другой ее стороны такую же дугу, так что полное геометрическое место указанных точек состоит из двух дуг (см. чер. 140).

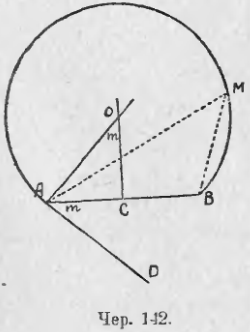
136. Построить геометрическое место точек, из которых данный отрезок виден под данным углом.

Пусть дан отрезок AB и угол m (чер. 141). Построим геометрическое место точек, из которых AB виден под углом m. Постараемся сначала найти одну точку этого места. Чрез точку A построим произвольный луч AN и на нем выберем произвольную точку M, при которой построим ∠AMC = ∠m. Тогда замечаем, что из нашей точки M виден под углом m не весь отрезок AB, а лишь его часть AC. Но теперь не трудно на луче AM найти такую точку, из которой весь отрезок AB виден под углом m, для чего следует построить чрез точку B прямую BN || CM, – точка N пересечения луча AN и BN и явится искомою точкою. Чтобы получить искомое геометрическое место, остается построить круг чрез точки A, N и B, что мы умеем делать (п. 113).

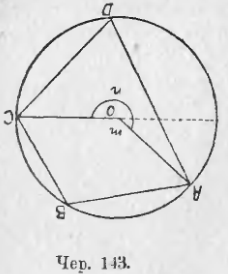
Вот другой способ построения того же геометрического места. При точке A (чер. 142) отрезка AB построим ∠BAD = m, затем построим чрез середину отрезка AB перпендикуляр CO к этому отрезку AO ⊥ AD; точка пересечения O этих двух перпендикуляров служит центром искомого круга; так как O лежит на CO, то круг, описанный радиусом OA, принимая O за центр, пройдет и чрез точку B; ∠AOC = ∠BAD = ∠m, ибо ∠AOC И ∠BAD каждый в отдельности дополняет ∠OAB до прямого, но ∠AOC есть половина центрального угла AOB; поэтому всякий вписанный ∠AMB должен равняться ∠AOC и, следовательно, = ∠m.

137. Упражнения. 1. Найти точки, из которых два данных отрезка видны под прямыми углами.
2. Найти точки, из которых два данных отрезка видны каждый под данным углом.
3. Построить треугольник по основанию, противолежащему углу и по высоте.
Треугольников, имеющих данное основание и данный противолежащий угол, можно построить бесчисленное множество: их вершины расположены на том же геометрическом месте точек, из которых данное основание видно под данным углом. Остается среди этих вершин выбрать те, которые удалены от основания на расстояние, равное данной высоте, для чего строим прямую, параллельную основанию и отстоящую от него на расстояние, равное данной высоте.
4. Построить треугольник по основанию, медиане и углу при вершине.

138. В круг O (чер. 143) впишем какой-либо четырехугольник (выпуклый), для чего возьмем 4 точки A, B, C и D круга и соединим их по порядку прямыми. Рассмотрим полученные вписанные углы. Построив радиусы OA и OC и называя 2 полученных центральных угла m и n, а именно ∠AOC, опирающийся на дугу ABC, обозначим m (он меньше выпрямленного) и ∠AOC, опирающийся на дугу ADC, обозначим n (он больше выпрямленного), найдем:

Сложением отсюда получим:

но углы m и n в сумме составляют два выпрямленных угла (что легко увидеть, продолжив, напр. сторону OC) или 4 прямых угла; поэтому (m + n) / 2 = выпрямленному углу = 2d и, следовательно, ∠D + ∠B = 2d.

То же можно получить и для суммы углов A и C. Поэтому имеем:

Во всяком вписанном в круг выпуклом четырехугольнике сумма противоположных углов равна 2d.

Найденное свойство является необходимым признаком вписанного в круг четырехугольника, т. е., если 4-угольник вписан в круг, то необходимо, чтобы сумма двух противоположных углов = 2d. Посмотрим, достаточен ли этот признак для того, чтобы четырехугольник мог быть вписанным, или, другими словами, чтобы около него можно было бы описать круг (ведь, вообще говоря, через 4 произвольно взятых точки нельзя построить окружность, так как она определяется вполне тремя точками и может, следовательно, не пройти чрез четвертую точку).

Пусть имеем 4-угольник ABCD такой, что ∠B + ∠D = 2d (чер. 144). Прежде всего заметим, что тогда непременно сумма двух других углов, т. е. ∠A + ∠C, тоже равна 2d: в самом деле, мы имели (п. 81), что сумма всех четырех углов четырехугольника = 4d; так как ∠B + ∠D = 2d, то, следовательно, ∠A + ∠C = 2d.

Построим чрез три точки A, B и C круг, что делать умеем; возникает вопрос: пройдет ли он чрез точку D или нет? Допустим сначала, что точка D окажется вне круга и последний пересечет сторону AD в точке E. Соединив C и E, получим 4-угольник ABCE, вписанный в этот круг, и тогда имеем:

Сравнивая это равенство с данным, что ∠B + ∠D = 2d, придем к заключению, что ∠E = ∠D (суммы равны и одно слагаемое одинаковое, следовательно, и другие слагаемые равны), но этого быть не может, так как ∠E (точнее ∠AEC) есть внешний для ∆ECD, а ∠D внутренний.

Допустим, что точка D окажется внутри круга и последний пересечет продолжение стороны AD в точке F. Тогда ∠B + ∠F = 2d, так как 4-угольник ABCF вписанный. Сравнивая с данным равенством ∠B + ∠D = 2d, получим, что ∠D = ∠F, чего быть не может, так как ∠D есть внешний, а ∠F внутренний угол для ∆DCF.

Остается, следовательно, принять, что круг пройдет чрез точку D и что, следовательно, около данного четырехугольника можно описать круг. Итак:

Если в выпуклом четырехугольнике сумма противоположных углов равна 2d, то около него можно описать круг.

Четырехугольник, около которого можно описать круг, называют часто вписываемым.

Прямое и обратное заключение этого п. можно выразить в иной форме:

Для того, чтобы выпуклый четырехугольник был вписываемым, необходимо и достаточно, чтобы сумма его двух противоположных углов равнялась 2d .

Упражнения. 1. В каком случае около параллелограмма можно описать круг?
2. В каком случае можно описать круг около трапеции?

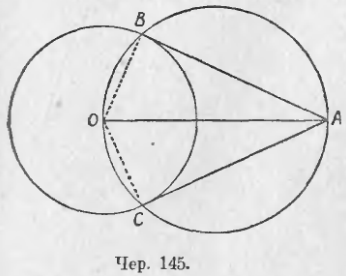
139. Задача. Построить касательную к данному кругу чрез точку, данную вне круга.
Пусть дан круг O и точка A вне его (чер. 145). Требуется чрез A построить касательную к кругу.

Соединив центр круга O с данною точкою A, примем отрезок OA за диаметр нового круга. Построив этот второй круг (его центр есть середина отрезка OA), найдем его точки пересечения B и C с первым. Тогда прямые AB и AC служат касательными из точки A к кругу O.

В самом деле, соединив B с O, получим ∠OBA, вписанный во второй круг и опирающийся на его диаметр OA; такой угол прямой (п. 134), следовательно, AB ⊥ OB, а этого достаточно для того, чтобы прямая AB была касательной к кругу (п. 118). Также выясним, что AC есть касательная к кругу O.

OA есть линия центров наших кругов, поэтому она является осью симметрии всей фигуры: перегибая фигуру по оси OA, найдем, что B совместится с C и AB с AC, т. е. AB = AC. Итак, имеем:

Чрез точку, взятую вне круга, можно построить две касательных к этому кругу, и отрезки их от данной точки до точек касания равны между собою.

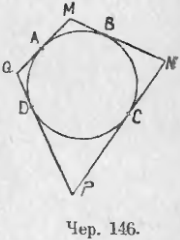
140. Построим треугольник, описанный около круга; для этого возьмем 4 точки A, B, C и D данного круга (чер. 146) и построим чрез эти точки касательные к кругу, точки пересечения M, N, P и Q последовательных касательных служат вершинами этого четырехугольника.

Выбор 4 точек A, B, C и D несколько ограничен: две соседних точки не должны лежать на одном диаметре круга; напр., если бы точки B и C были концами одного диаметра, то касательные в них были бы параллельны и вершины N нельзя было бы найти.

Применяя к полученному описанному 4-угольнику MNPQ свойство касательных предыдущего п., найдем:

MA = MB = a; NB = NC = b; PC = PD = C; QD = QA = d,

где мы ввели обозначения a, b, c и d для четырех пар отрезков, равных между собой.

Мы можем скомбинировать 8 полученных отрезков в две группы, по 4 в каждой, равных попарно отрезков. Такая комбинация напрашивается сама собою. Возьмем сумму двух противоположных сторон четырехугольника:

MN + PQ = MB + BN + PD + DQ = a + b + c + d.

Также для двух других сторон найдем:

QM + PN = QA + AM + NC + CP = d + a + b + c.

т. е. сумма двух противоположных сторон описанного четырехугольника равна сумме двух других сторон.

Найденное свойство является необходимым признаком описанного 4-угольника, т. е., если 4-угольник описан около круга, то необходимо должно иметь место найденное свойство.

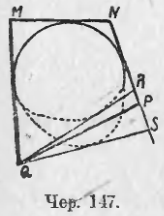
Посмотрим, является ли это свойство достаточным признаком для того, чтобы при его наличности этот четырехугольник мог бы быть рассматриваем, как описанный около круга, т. е. достаточно ли этого свойства для того, чтобы в четырехугольник можно было вписать круг (вписать круг в 4-угольник значит построить такой круг, который касался бы всех четырех его сторон).

Пусть имеем 4-угольник MNPQ (чер. 147), у которого

Построим круг, касающийся прямых MQ, MN и NP, чтобы его центр лежал внутри полосы QMNP (п. 125 задача 4). Возникает вопрос, коснется ли этот круг стороны QP?

Допустим, что круг не коснется стороны QP и расположится внутри 4-угольника QMNP. Тогда, построив чрез Q вторую касательную QR к кругу, которая пересечет сторону NP в точке R, получим описанный 4-угольник QMNR, для которого имеем:

Вычитая это равенство по частям из данного, найдем:

QP – QR = NP – NR или QP – QR = RP.

Но это равенство противоречит свойству треугольника RPQ (п. 91), согласно которому должны иметь

Допустим затем, что круг пересекает сторону QP. Тогда касательная к этому кругу чрез точку Q займет положение QS и пересечет сторону NP в точке S. Из описанного 4-угольника QMNS имеем:

Вычитая отсюда данное равенство MN + QP = MQ + NP по частям, получим:

QS – QP = NS – NP или QS – QP = PS,

что опять-таки невозможно, так как из треугольника SQP имеем:

Поэтому остается принять, что построенный нами круг касается и стороны QP, т. е. в наш 4-угольник удалось вписать круг. Итак:
Если сумма двух противоположных сторон выпуклого четырехугольника равна сумме двух других его противоположных сторон, то в такой четырехугольник можно вписать круг.

Четырехугольник, в который можно вписать круг, называют описываемым. Прямое и обратное заключение этого пункта можно выразить в такой форме:

Для того, чтобы четырехугольник был описываемым, необходимо и достаточно, чтобы сумма одной пары его противоположных сторон равнялась сумме другой пары.

Упражнения. 1. Найти необходимый и достаточный признак того, чтобы параллелограмм был описываемым.

2. Пусть около данной трапеции можно описать круг и в нее можно вписать круг. Показать, что каждая из непараллельных сторон этой трапеции равна ее средней линии.

141. Упражнения на всю главу.

1. Свойство углов вписанного в круг 4-угольника, найденное в п. 138, можно выяснить иным способом. Построим диагональ BD (чер. 143) четырехугольника и касательную MN к кругу в точке B. Тогда ∠ADC = ∠MBA + ∠NBC (на осн. п. 133). Отсюда можно увидать, что ∠B + ∠D = выпрямленному углу (на чер. 143 BD и MN не даны).
2. Геометрическим местом середин хорд, проходящих чрез данную точку внутри данного круга, служит другой круг, диаметр которого есть прямолинейный отрезок между центром данного круга и данною точкою.
3. Отрезки прямых, проходящих чрез точку пересечения двух кругов, ограниченные двумя другими точками пересечения с этими кругами, видны из другой точки пересечения кругов под одним и тем же углом.
   Следует построить 2 таких отрезка и углы, под которыми они видны из другой точки; тогда можно заметить, что каждый из углов слагается из двух других углов: одно слагаемое общее и другие слагаемые равны между собою.
4. Найти точку, из которой стороны треугольника видны под равными углами.
   (Надо суметь построить угол = 1(1/3)d.)
5. Около треугольника описан круг; из какой-либо точки этого круга опущены перпендикуляры на его стороны. Основания всех трех перпендикуляров расположены на одной прямой (прямая Симсона).
   Надо найти четырехугольник, около которых можно описать круги, и рассмотреть полученные вписанные углы.
6. Биссекторы внутренних углов какого-либо четырехугольника образуют, пересекаясь, вписываемый 4-угольник.

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Числовая и единичная окружность

В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.

Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.

Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:

Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.

Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.

Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:

В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.

Выглядит единичная окружность так:

Откладывание углов на единичной окружности

Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:

Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.

Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:

Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:

Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:

В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.

Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:

Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:

Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:

Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.

Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:

С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:

Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:

Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:

Например, верны следующие равенства:

15° + 3•360° = 15° + 1080° = 1095°

100° + 10•360° = 100° + 3600° = 3700°

1000° = 1000° – 2•360° = 1000° – 720° = 280°

Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5

Сопряжения

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

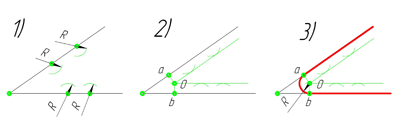
Сопряжение углов (Сопряжение пересекающихся прямых)

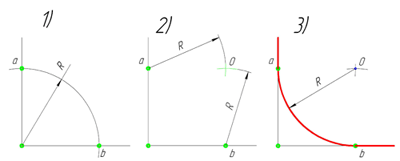
Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

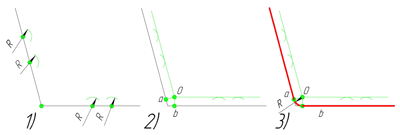
Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

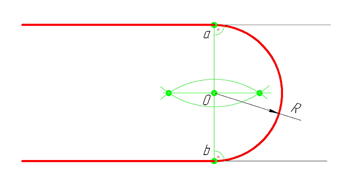
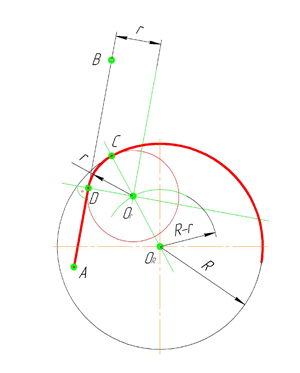
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности O R радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой О r .

Из центра сопряжения, точки О r , опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности О R и центр сопряжения О r линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности O R радиусом R-r. Точка О r , полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности О R прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки О r , центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

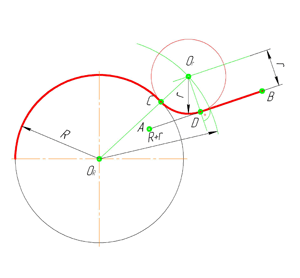
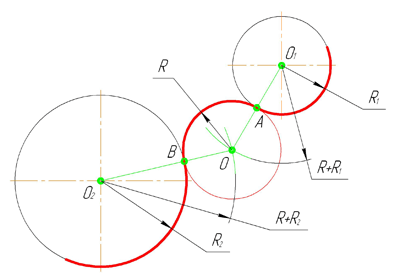
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

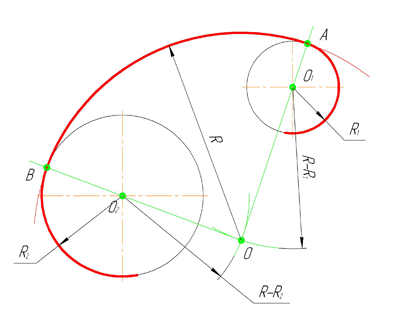
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Математика

132. Мы уже знакомы с центральными углами. Построим теперь угол, вершина которого лежит на окружности и сторонами служат хорды. Такой угол называется вписанным в круг. Пусть построен ∠ABC (чер. 135, I или II), вписанный в круг O. Он опирается на дугу AC. Построим еще центральный ∠AOC, опирающийся на ту же дугу. Тогда между ∠ABC и ∠AOC существует простая зависимость. Для ее выяснения построим диаметр DB — мы будем сначала рассматривать случай, когда этот диаметр идет внутри ∠ABC, – получим два равнобедренных треугольника — ∆AOB и ∆BOC, у которых углы при основании равны: на чертеже равные углы обозначены одним и тем же нумером, – ∠A = ∠ABO = ∠1 и ∠C = ∠CBO = ∠2.

Тогда ∠AOD является внешним для ∆AOB, и он равен сумме внутренних с ним несмежных, т. е.

Также ∠DOC есть внешний для ∆BOC и, следовательно,

Отсюда сложением находим:

∠AOC = ∠AOD + ∠DOC = 2∠1 + 2∠2 = 2(∠1 + ∠2) = 2∠B, где под обозначением ∠B понимаем ∠ABC.

∠AOC = 2∠ABC
или ∠ABC = ½ ∠AOC = ∠AOC / 2.

Если одна из сторон вписанного угла проходила бы чрез центр, то дело упрощалось бы и еще скорее получилась бы та же зависимость. Например, для вписанного угла ABD:

∠AOD = 2∠1 = 2∠ABD или ∠ABD = ½ ∠AOD = ∠AOD / 2.

Рассмотрим теперь случай, когда диаметр BD проходит вне угла ABC (чер. 136). Тогда, согласно предыдущему, имеем:

∠ABD = ½ ∠AOD,
∠CBD = ½ ∠COD,

так как одна сторона углов ABD и CBD служит диаметром.

∠ABC = ∠ABD – ∠CBD = ½ ∠AOD – ½ ∠COD =
= ½ (∠AOD – ∠COD) = (∠AOD – ∠COD) / 2.

Но разность ∠AOD – ∠COD равна ∠AOC, следовательно, ∠ABC = ∠AOC / 2.

Итак, найденная зависимость справедлива для всех возможных случаев. Поэтому имеем:

Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

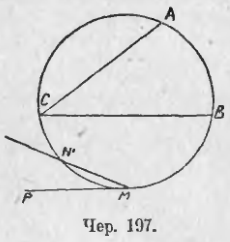
133. Если хорду AB (чер. 136) вращать по направлению от BC вокруг точки B, то вписанный угол ABC станет увеличиваться, но все время будет сохраняться найденная выше зависимость между вписанным и центральным углом. Наконец, прямая AB может сделаться касательною к кругу (чер. 137) и тогда получим ∠ABC, составленный хордою и касательною; если касательную продолжить, то получим другой такой же ∠DBC. Уже из того процесса вращения, которым мы перешли от вписанного угла к этому новому углу, видно, что угол, составленных хордою и касательною, являясь предельным случаем вписанного угла, должен подчиниться той же зависимости, которая была найдена в предыдущем п. для вписанного угла. Но возможно то же самое увидать иначе. Рассмотрим, например, ∠CBD (чер. 137). Построим диаметр MN ⊥ BC и соединим точку касания B с O; тогда BO ⊥ AD. Так как ∆KBO прямоугольный, то ∠KBO + ∠KOB = d, но ∠ABO = d или ∠ABK + ∠KBO = d. Отсюда заключаем, что ∠KOB = ∠ABK, так как каждый из этих углов дополняет один и тот же ∠KBO до прямого.

Но ∠CBD = выпрямленному углу – ∠ABK и ∠BON = выпрямленному углу – ∠KOB. Следовательно, ∠CBD = ∠BON = ∠COB / 2, где под именем ∠COB надо понимать угол, больший выпрямленного и который опирается на дугу CNB, то и ∠CMB равен половине того же центрального угла COB. Отсюда заключаем, что ∠CBD = ∠CMB. Также (еще проще) можно получить, что ∠ABC = ∠CNB (углы CMB и CNB на чертеже не даны). Этот результат можно выразить в следующей форме:

Угол, составленный хордой и касательной, равен вписанному углу, опирающемуся на дугу, заключенную внутри первого угла.

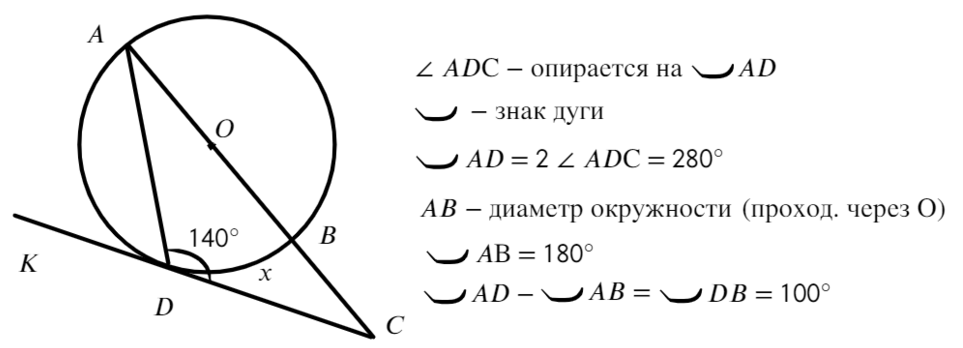
134. Построим в круге O (чер. 138) диаметр AC и какой-либо вписанный ∠ABC, опирающийся на полуокружность ADC или, как часто говорят, опирающийся на диаметр AC.

Тогда ∠ABC = ½ ∠AOC, но ∠AOC выпрямленный; следовательно, ∠ABC = d, т. е.:

Вписанный угол, опирающийся на диаметр, – прямой.

135. Построим в круге какую-либо хорду AB (чер. 139) и ряд вписанных углов, опирающихся на ◡AB: ∠C, ∠C1 и т. д.

Тогда каждый из этих углов равен половине центрального угла, опирающегося на дугу AB, и следовательно ∠C = ∠C1 = …

Этот результат можно истолковать в следующей форме. Пусть в точке C помещен наш глаз, тогда лучи зрения, идущие из глаза к концам отрезка AB, составляют ∠ACB, – говорят, что из точки C отрезок AB виден под углом ACB. Переместим наш глаз в точку C1; тогда отрезок AB будет виден под углом AC1B, который равен прежнему. Вообще, в какую бы точку дуги ACDB мы ни поместили наш глаз, отрезок AB будет виден все под таким же углом.

Поместим теперь наш глаз в какую-либо точку M, находящуюся внутри круга; тогда из этой точки отрезок AB будет виден под углом AMB, который уже неравен прежнему; продолжив AM до пересечения с окружностью в точке D и соединив D с B, получим ∆MBD, для которого ∠AMB есть внешний, и, следовательно, ∠AMB > ∠ADB или ∠AMB > ∠C (ибо ∠ADB = ∠C).

Поместим теперь наш глаз в какую-либо точку N вне круга. Чтобы упростить чертеж, возьмем точку N на продолжении прямой AD; тогда из точки N отрезок AB виден под углом ANB. Рассматривая ∆BDN, найдем ∠ADB > ∠N (ибо ∠ADB внешний для ∆BDN) или ∠N Геометрическим местом точек, из которых какой-либо отрезок виден под одним и тем же углом, есть дуга круга, проходящего чрез концы этого отрезка.

Если бы мы захотели рассмотреть точки и по другую сторону прямой AB, то нашли бы и с другой ее стороны такую же дугу, так что полное геометрическое место указанных точек состоит из двух дуг (см. чер. 140).

136. Построить геометрическое место точек, из которых данный отрезок виден под данным углом.

Пусть дан отрезок AB и угол m (чер. 141). Построим геометрическое место точек, из которых AB виден под углом m. Постараемся сначала найти одну точку этого места. Чрез точку A построим произвольный луч AN и на нем выберем произвольную точку M, при которой построим ∠AMC = ∠m. Тогда замечаем, что из нашей точки M виден под углом m не весь отрезок AB, а лишь его часть AC. Но теперь не трудно на луче AM найти такую точку, из которой весь отрезок AB виден под углом m, для чего следует построить чрез точку B прямую BN || CM, – точка N пересечения луча AN и BN и явится искомою точкою. Чтобы получить искомое геометрическое место, остается построить круг чрез точки A, N и B, что мы умеем делать (п. 113).

Вот другой способ построения того же геометрического места. При точке A (чер. 142) отрезка AB построим ∠BAD = m, затем построим чрез середину отрезка AB перпендикуляр CO к этому отрезку AO ⊥ AD; точка пересечения O этих двух перпендикуляров служит центром искомого круга; так как O лежит на CO, то круг, описанный радиусом OA, принимая O за центр, пройдет и чрез точку B; ∠AOC = ∠BAD = ∠m, ибо ∠AOC И ∠BAD каждый в отдельности дополняет ∠OAB до прямого, но ∠AOC есть половина центрального угла AOB; поэтому всякий вписанный ∠AMB должен равняться ∠AOC и, следовательно, = ∠m.

137. Упражнения. 1. Найти точки, из которых два данных отрезка видны под прямыми углами.
2. Найти точки, из которых два данных отрезка видны каждый под данным углом.
3. Построить треугольник по основанию, противолежащему углу и по высоте.
Треугольников, имеющих данное основание и данный противолежащий угол, можно построить бесчисленное множество: их вершины расположены на том же геометрическом месте точек, из которых данное основание видно под данным углом. Остается среди этих вершин выбрать те, которые удалены от основания на расстояние, равное данной высоте, для чего строим прямую, параллельную основанию и отстоящую от него на расстояние, равное данной высоте.
4. Построить треугольник по основанию, медиане и углу при вершине.

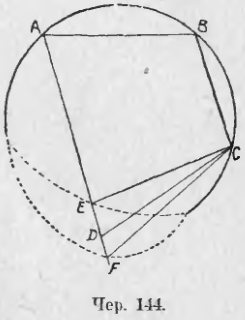
138. В круг O (чер. 143) впишем какой-либо четырехугольник (выпуклый), для чего возьмем 4 точки A, B, C и D круга и соединим их по порядку прямыми. Рассмотрим полученные вписанные углы. Построив радиусы OA и OC и называя 2 полученных центральных угла m и n, а именно ∠AOC, опирающийся на дугу ABC, обозначим m (он меньше выпрямленного) и ∠AOC, опирающийся на дугу ADC, обозначим n (он больше выпрямленного), найдем:

Сложением отсюда получим:

но углы m и n в сумме составляют два выпрямленных угла (что легко увидеть, продолжив, напр. сторону OC) или 4 прямых угла; поэтому (m + n) / 2 = выпрямленному углу = 2d и, следовательно, ∠D + ∠B = 2d.

То же можно получить и для суммы углов A и C. Поэтому имеем:

Во всяком вписанном в круг выпуклом четырехугольнике сумма противоположных углов равна 2d.

Найденное свойство является необходимым признаком вписанного в круг четырехугольника, т. е., если 4-угольник вписан в круг, то необходимо, чтобы сумма двух противоположных углов = 2d. Посмотрим, достаточен ли этот признак для того, чтобы четырехугольник мог быть вписанным, или, другими словами, чтобы около него можно было бы описать круг (ведь, вообще говоря, через 4 произвольно взятых точки нельзя построить окружность, так как она определяется вполне тремя точками и может, следовательно, не пройти чрез четвертую точку).

Пусть имеем 4-угольник ABCD такой, что ∠B + ∠D = 2d (чер. 144). Прежде всего заметим, что тогда непременно сумма двух других углов, т. е. ∠A + ∠C, тоже равна 2d: в самом деле, мы имели (п. 81), что сумма всех четырех углов четырехугольника = 4d; так как ∠B + ∠D = 2d, то, следовательно, ∠A + ∠C = 2d.

Построим чрез три точки A, B и C круг, что делать умеем; возникает вопрос: пройдет ли он чрез точку D или нет? Допустим сначала, что точка D окажется вне круга и последний пересечет сторону AD в точке E. Соединив C и E, получим 4-угольник ABCE, вписанный в этот круг, и тогда имеем:

Сравнивая это равенство с данным, что ∠B + ∠D = 2d, придем к заключению, что ∠E = ∠D (суммы равны и одно слагаемое одинаковое, следовательно, и другие слагаемые равны), но этого быть не может, так как ∠E (точнее ∠AEC) есть внешний для ∆ECD, а ∠D внутренний.

Допустим, что точка D окажется внутри круга и последний пересечет продолжение стороны AD в точке F. Тогда ∠B + ∠F = 2d, так как 4-угольник ABCF вписанный. Сравнивая с данным равенством ∠B + ∠D = 2d, получим, что ∠D = ∠F, чего быть не может, так как ∠D есть внешний, а ∠F внутренний угол для ∆DCF.

Остается, следовательно, принять, что круг пройдет чрез точку D и что, следовательно, около данного четырехугольника можно описать круг. Итак:

Если в выпуклом четырехугольнике сумма противоположных углов равна 2d, то около него можно описать круг.

Четырехугольник, около которого можно описать круг, называют часто вписываемым.

Прямое и обратное заключение этого п. можно выразить в иной форме:

Для того, чтобы выпуклый четырехугольник был вписываемым, необходимо и достаточно, чтобы сумма его двух противоположных углов равнялась 2d .

Упражнения. 1. В каком случае около параллелограмма можно описать круг?
2. В каком случае можно описать круг около трапеции?

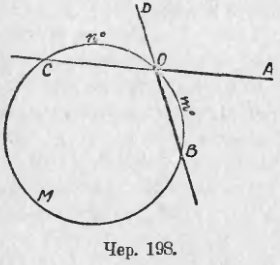
139. Задача. Построить касательную к данному кругу чрез точку, данную вне круга.
Пусть дан круг O и точка A вне его (чер. 145). Требуется чрез A построить касательную к кругу.

Соединив центр круга O с данною точкою A, примем отрезок OA за диаметр нового круга. Построив этот второй круг (его центр есть середина отрезка OA), найдем его точки пересечения B и C с первым. Тогда прямые AB и AC служат касательными из точки A к кругу O.

В самом деле, соединив B с O, получим ∠OBA, вписанный во второй круг и опирающийся на его диаметр OA; такой угол прямой (п. 134), следовательно, AB ⊥ OB, а этого достаточно для того, чтобы прямая AB была касательной к кругу (п. 118). Также выясним, что AC есть касательная к кругу O.

OA есть линия центров наших кругов, поэтому она является осью симметрии всей фигуры: перегибая фигуру по оси OA, найдем, что B совместится с C и AB с AC, т. е. AB = AC. Итак, имеем:

Чрез точку, взятую вне круга, можно построить две касательных к этому кругу, и отрезки их от данной точки до точек касания равны между собою.

140. Построим треугольник, описанный около круга; для этого возьмем 4 точки A, B, C и D данного круга (чер. 146) и построим чрез эти точки касательные к кругу, точки пересечения M, N, P и Q последовательных касательных служат вершинами этого четырехугольника.

Выбор 4 точек A, B, C и D несколько ограничен: две соседних точки не должны лежать на одном диаметре круга; напр., если бы точки B и C были концами одного диаметра, то касательные в них были бы параллельны и вершины N нельзя было бы найти.

Применяя к полученному описанному 4-угольнику MNPQ свойство касательных предыдущего п., найдем:

MA = MB = a; NB = NC = b; PC = PD = C; QD = QA = d,

где мы ввели обозначения a, b, c и d для четырех пар отрезков, равных между собой.

Мы можем скомбинировать 8 полученных отрезков в две группы, по 4 в каждой, равных попарно отрезков. Такая комбинация напрашивается сама собою. Возьмем сумму двух противоположных сторон четырехугольника:

MN + PQ = MB + BN + PD + DQ = a + b + c + d.

Также для двух других сторон найдем:

QM + PN = QA + AM + NC + CP = d + a + b + c.

т. е. сумма двух противоположных сторон описанного четырехугольника равна сумме двух других сторон.

Найденное свойство является необходимым признаком описанного 4-угольника, т. е., если 4-угольник описан около круга, то необходимо должно иметь место найденное свойство.

Посмотрим, является ли это свойство достаточным признаком для того, чтобы при его наличности этот четырехугольник мог бы быть рассматриваем, как описанный около круга, т. е. достаточно ли этого свойства для того, чтобы в четырехугольник можно было вписать круг (вписать круг в 4-угольник значит построить такой круг, который касался бы всех четырех его сторон).

Пусть имеем 4-угольник MNPQ (чер. 147), у которого

Построим круг, касающийся прямых MQ, MN и NP, чтобы его центр лежал внутри полосы QMNP (п. 125 задача 4). Возникает вопрос, коснется ли этот круг стороны QP?

Допустим, что круг не коснется стороны QP и расположится внутри 4-угольника QMNP. Тогда, построив чрез Q вторую касательную QR к кругу, которая пересечет сторону NP в точке R, получим описанный 4-угольник QMNR, для которого имеем:

Вычитая это равенство по частям из данного, найдем:

QP – QR = NP – NR или QP – QR = RP.

Но это равенство противоречит свойству треугольника RPQ (п. 91), согласно которому должны иметь

Допустим затем, что круг пересекает сторону QP. Тогда касательная к этому кругу чрез точку Q займет положение QS и пересечет сторону NP в точке S. Из описанного 4-угольника QMNS имеем:

Вычитая отсюда данное равенство MN + QP = MQ + NP по частям, получим:

QS – QP = NS – NP или QS – QP = PS,

что опять-таки невозможно, так как из треугольника SQP имеем:

Поэтому остается принять, что построенный нами круг касается и стороны QP, т. е. в наш 4-угольник удалось вписать круг. Итак:
Если сумма двух противоположных сторон выпуклого четырехугольника равна сумме двух других его противоположных сторон, то в такой четырехугольник можно вписать круг.

Четырехугольник, в который можно вписать круг, называют описываемым. Прямое и обратное заключение этого пункта можно выразить в такой форме:

Для того, чтобы четырехугольник был описываемым, необходимо и достаточно, чтобы сумма одной пары его противоположных сторон равнялась сумме другой пары.

Упражнения. 1. Найти необходимый и достаточный признак того, чтобы параллелограмм был описываемым.

2. Пусть около данной трапеции можно описать круг и в нее можно вписать круг. Показать, что каждая из непараллельных сторон этой трапеции равна ее средней линии.

141. Упражнения на всю главу.

1. Свойство углов вписанного в круг 4-угольника, найденное в п. 138, можно выяснить иным способом. Построим диагональ BD (чер. 143) четырехугольника и касательную MN к кругу в точке B. Тогда ∠ADC = ∠MBA + ∠NBC (на осн. п. 133). Отсюда можно увидать, что ∠B + ∠D = выпрямленному углу (на чер. 143 BD и MN не даны).
2. Геометрическим местом середин хорд, проходящих чрез данную точку внутри данного круга, служит другой круг, диаметр которого есть прямолинейный отрезок между центром данного круга и данною точкою.
3. Отрезки прямых, проходящих чрез точку пересечения двух кругов, ограниченные двумя другими точками пересечения с этими кругами, видны из другой точки пересечения кругов под одним и тем же углом.
   Следует построить 2 таких отрезка и углы, под которыми они видны из другой точки; тогда можно заметить, что каждый из углов слагается из двух других углов: одно слагаемое общее и другие слагаемые равны между собою.
4. Найти точку, из которой стороны треугольника видны под равными углами.
   (Надо суметь построить угол = 1(1/3)d.)
5. Около треугольника описан круг; из какой-либо точки этого круга опущены перпендикуляры на его стороны. Основания всех трех перпендикуляров расположены на одной прямой (прямая Симсона).
   Надо найти четырехугольник, около которых можно описать круги, и рассмотреть полученные вписанные углы.
6. Биссекторы внутренних углов какого-либо четырехугольника образуют, пересекаясь, вписываемый 4-угольник.

План урока:

Центральный угол и градусная мера дуги

Вписанный угол

Углы между хордами и секущими

Теорема о произведении отрезков хорд

Задачи на квадратной решетке

Центральный угол и градусная мера дуги

Любые две точки на окружности разбивают ее на две дуги. Чтобы отличать эти дуги, на каждой из них ставят точку, которую и указывают в обозначении дуги:

Здесь красным цветом показана⋃АСВ, а синим – ⋃ADB. Однако иногда для простоты указывают только концы дуги, то есть используют обозначение ⋃AВ. Это делается тогда, когда ясно, о какой дуге окружности идет речь. Обычно всегда подразумевается та дуга, которая меньше.

Можно заметить, что дуги отличаются по размеру, поэтому возникает потребность их измерения. Для этого используют такое понятие, как градусная мера дуги.

Для ее определения необходимо соединить концы дуги с центром окруж-ти. В результате получаются радиусы, которые пересекаются в центре окружности. Угол между ними именуется центральным углом окруж-ти.

Для каждой дуги можно построить единственный центральный угол, поэтому логично измерять дугу с помощью такого угла. Правда, обратное неверно. На рисунке видно, что центральному углу ∠АОВ соответствует сразу две дуги: ⋃АСВ и ⋃АDB:

Поэтому условно считают, градусная мера той из двух дуг, которая меньше, как раз и равна центральному углу:

Дуги, также как отрезки или углы, можно складывать или вычитать. Например, пусть есть две дуги, ⋃AВ и ⋃ВС, чьи градусные меры составляют 40° и 30°.

Как найти ⋃АС? Ей соответствует центральный угол ∠АОС, который в свою очередь равен сумме ∠АОВ и ∠ВОС:

Диаметр делит окруж-ть на две равные друг другу дуги, которые называются полуокружностями. При этом диаметр окружности можно рассматривать как угол между двумя радиусами, равный 180°. Получается, что градусная мера полуокружности составляет 180°:

Вместе две полуокружности образуют полную окруж-ть. Получается, что градусная мера всей окруж-ти составляет 180° + 180° = 360°.

Этот факт известен и из жизни – когда кто-то делает полный оборот вокруг своей оси, говорят, что он повернулся на 360°. Теперь мы можем вернуться к случаю, когда две точки делят окруж-ть на две неравные друг другу дуги. Градусная мера меньшей из них будет равна величине соответствующего центрального угла (обозначим его как α). В сумме две дуги должны дать 360°. Значит, градусная мера большей дуги будет составлять 360° – α:

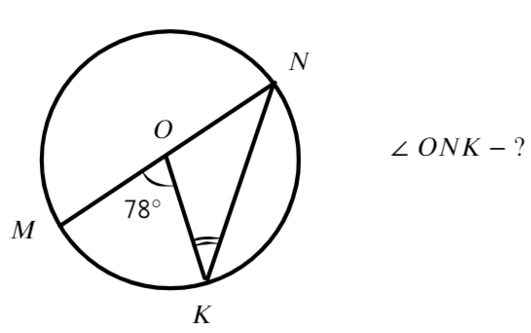
Задание. Точки А, В, С и D лежат на одной окруж-ти. Известно, что ⋃АСВ составляет 107°. Какова величина ⋃ADB?

Решение. Вместе дуги ⋃АСВ и ⋃АDВ образуют полную окруж-ть, поэтому их сумма равна 360°. Это позволяет составить уравнение и найти из него ⋃АDB:

Задание. Найдите величину ∠АОС на рисунке, если известны ⋃AВ и ⋃ВС:

Решение. Сначала найдем ⋃АС, учтя, что все три дуги, показанные на рисунке, в сумме составляют 360°:

Для доказательства построим две одинаковые хорды AВ и СD в окруж-ти и соединим их концы с центром:

В результате получились ∆АОВ и ∆ОСD. У них равны все три стороны, значит, сами эти треугольники равны. Тогда 

∠COD = ∠AOB

Но эти углы – центральные для дуг ⋃AВ и ⋃CD. Получается, что у этих дуг одинаковы их градусные меры, поэтому они также равны, ч. т. д.

Примечание. Всякая хорда окружности разбивает ее на две дуги – большую и меньшую. В данном правиле говорится именно равенстве меньших дуг.

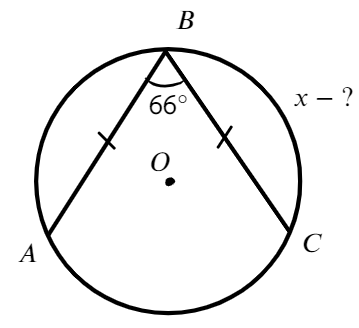
Задание. На окруж-ти отмечены точки А, В и С так, что хорды AВ, ВС и АС равны. Найдите угол между радиусами окружности АО и ВО.

Решение.

Дуги ⋃AВ, ⋃ВС и ⋃АС стянуты равными хордами AВ, ВС и АС. Значит, они одинаковы. Но в сумме эти три дуги образуют окруж-ть величиной в 360°. Значит, каждая из этих дуг втрое меньше:

⋃AВ = ⋃BC = ⋃AC = 360°:3 = 120°

∠АОВ – центральный для ⋃AВ, значит, он равен ее градусной мере, то есть он составляет 120°.

Ответ: 120°.

Вписанный угол

В окруж-ти можно построить ещё один угол, который именуют вписанным углом. Его отличие от центрального заключается в том, что его вершина лежит на окруж-ти, а не в ее центре. Сторонами же вписанного угла являются хорды окруж-ти.

Здесь дуга ⋃ВС находится внутри угла, а ее концы лежат на его сторонах. В таких случаях говорят, что ∠ВАС опирается на дугу ВС. Оказывается, что между величиной вписанного угла и дугой, на которую он опирается, есть взаимосвязь.

Обозначим вписанный угол ∠СAВ буквой α. Так как радиусы АО и ОС одинаковы, то ∆АОС – равнобедренный, и тогда углы при его основании будут одинаковы:

∠OCA = ∠OAC = α

∠СОВ – внешний для ∆АОС. Напомним, что такой угол равен сумме тех 2 углов треуг-ка, которые с ним не смежны. В частности, в данном случае можно записать

∠СОВ = ∠OCA = ∠OAC = α + α = 2α

Но этот же угол – центральный, и его величина равна ⋃ВС:

⋃BC = 2α

Получается, что дуга вдвое больше вписанного угла.

Далее рассмотрим случай, когда диаметр, проведенный из вершины вписанного угла, делит его на две части:

В этом случае вписанный угол ∠СAВ можно представить как сумму углов ∠САD (обозначен как α)и ∠ВАD (обозначен как β). Мы уже доказали, что дуги, на которые опираются эти углы, вдвое больше самих углов:

Осталось рассмотреть третий случай, при котором обе стороны вписанного угла ∠ВАС лежат по одну сторону от диаметра:

Если здесь обозначить ∠САD как α, а ∠ВАD как β, то интересующий нас ∠СAВ можно представить как их разность:

Итак, во всех трех возможных случаях вписанный угол оказывается вдвое меньше дуги, на которую он опирается.

Задание. Найдите ∠ВАС на рисунке:

Задание. Найдите вписанный ∠AВС, сели прилегающие к нему дуги ⋃AВ и ⋃ВС равны 100° и 128°.

Решение. В сумме дуги ⋃АС, ⋃ВС и ⋃AВ образуют окруж-ть, поэтому их сумма составляет 360°. Тогда можно найти ⋃АС:

Задание. Найдите дугу ⋃SM на рисунке:

Решение. Сначала найдем дугу ⋃MN, она вдвое больше соответствующего ей вписанного угла:

⋃NM = 2*∠NSM = 2*35° = 70°

Заметим, что ⋃SN– это полуокружность, то есть она составляет 180°. При этом ⋃SM и ⋃MN вместе как раз образуют эту полуокружность, то есть их сумма также составляет 180°. Значит, ⋃МS можно найти, вычтя из полуокружности ⋃MN:

⋃MS = ⋃SN — ⋃MN = 180° — 70° = 110°

Ответ: 110°.

Заметим, что для одной дуги можно построить несколько вписанных углов. Каждый из них будет равен половине дуги, то есть все эти углы окажутся одинаковыми.

Задание. Найдите ∠АСD на рисунке:

Решение. Так как ∠ACD и ∠ABD опираются на одну дугу ⋃AD, то они должны быть одинаковыми:

∠ACD = ∠ABD = 63°

Ответ: 63°.

Задание. Докажите, что две дуги, находящиеся между двумя параллельными секущими окруж-ти, равны друг другу.

Решение.

Нам надо доказать, что ⋃AВ и ⋃CD равны, если АС||BD. Проведем секущую ВС:

∠СВD и ∠АСВ равны, ведь они накрест лежащие. Получается, что ⋃AВ и ⋃CD являются основаниями равных вписанных углов. Отсюда вытекает, что эти дуги должны быть равными.

Напомним, что диаметр разбивает окруж-ть на две дуги по 180°. Отсюда можно сделать вывод – любой угол, опирающийся на полуокружность, должен составлять 180°:2 = 90°:

Задание. Диаметр окруж-ти AВ равен 17. Хорда ВС имеет длину 8. Какова длина хорды АС?

Решение.

Так как ∠АСВ опирается на диаметр AВ, то он прямой. Значит, и ∆АСВ – прямоугольный, причем диаметр AВ в нем – гипотенуза. Неизвестный катет можно найти по теореме Пифагора:

Задание. Окруж-ть разбита на две дуги, ⋃AВС и ⋃СDA. Известно, что ∠AВС = 72°. Найдите ∠ADC.

Решение.

Зная ∠AВС, мы легко найдем дугу ⋃ADC, она вдвое больше опирающегося на нее вписанного угла:

Углы между хордами и секущими

До этого мы рассматривали простые углы в окруж-ти, вершины которых лежали либо на самой окруж-ти, либо в ее центре. Однако иногда хорды и секущие пересекаются в другой точке, либо внутри, либо вне окруж-ти. Рассмотрим подобные задачи.

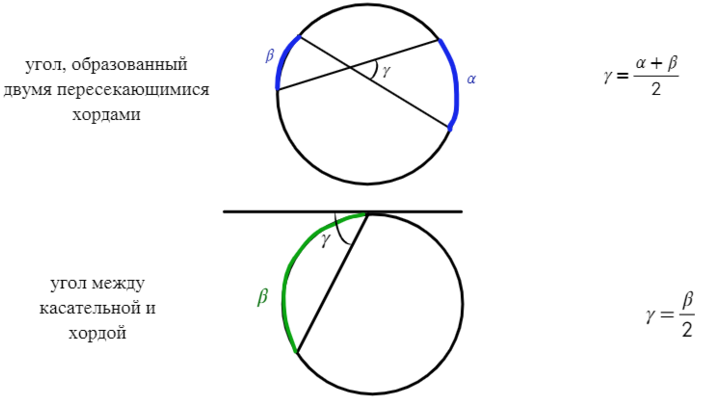
Более прост случай, когда необходимо найти угол между двумя пересекающимися хордами. Пусть хорды при пересечении образовали дуги ⋃AВ и ⋃СD величиной α и β. Каков угол между ними?

Проведем ещё одну хорду АD. В результате получим вписанные ∠САD и ∠ADB, которые будут равны половинам от соответствующих дуг, то есть α/2 и β/2. Интересующий нас ∠СPD оказывается внешним для ∆APD, и потому равен сумме двух углов в ∆APD (тех, которые с ним не смежны), то есть он составляет величину α/2 + β/2:

Величину α/2 + β/2 можно записать и иначе, вынеся множитель 1/2 за скобки:

α/2 + β/2 = (α + β)/2

Эту величину можно назвать полусуммой дуг, на которые опирается интересующий нас угол.

Задание. Найдите ∠МКВ на рисунке:

Решение. Интересующий нас угол опирается на хорды величиной 38° и 42°. Значит, он равен половине от их суммы:

∠MKB = (42° + 38°)/2 = 80°/2 = 40°

Ответ: 40°.

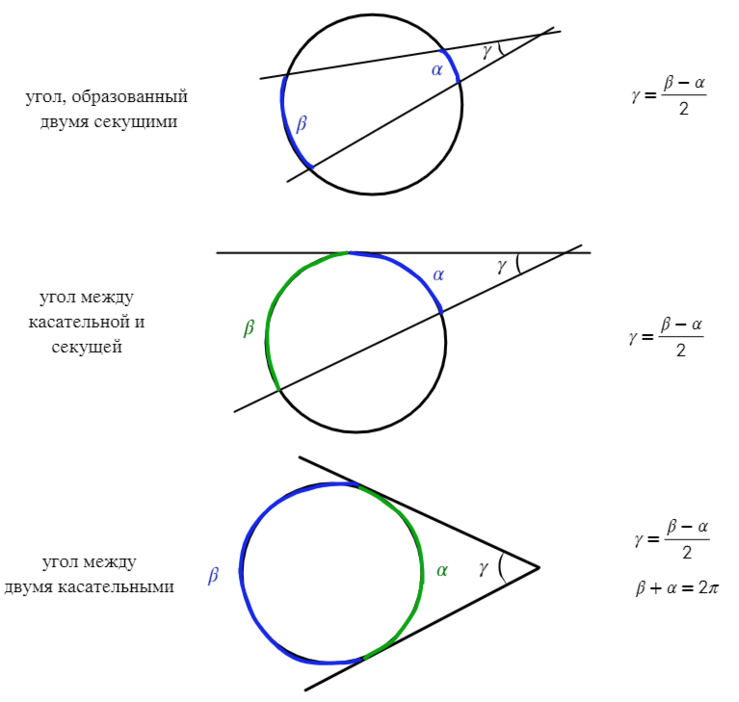
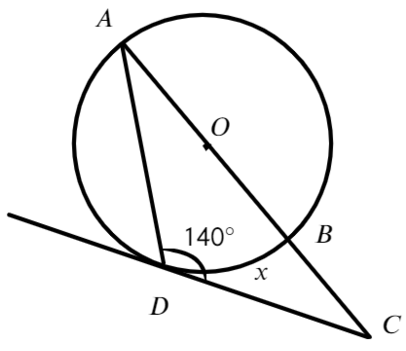
В более сложном случае необходимо найти угол между секущими, которые пересекаются вне окруж-ти. При этом известны дуги, образованные этими секущими:

Снова проведем хорду АD, чтобы у нас получились два вписанных угла, ∠ADB и ∠СAD, которые соответственно будут иметь величину β/2 и α/2:

Теперь уже ∠САD оказывается внешним для ∆ADK, а потому он является суммой двух других углов:

В итоге получили, что угол между секущими составляет половину от разности дуг, которые они отсекают от окруж-ти.

Задание. Найдите на рисунке величину∠К, если ⋃AВ и ⋃СD соответственно равны 42° и 130°:

Решение. В этой задаче просто используем доказанную теорему об углах между секущими. Искомый угол составляет половину от разности дуг, заключенных между секущими:

∠K = (130° — 42°):2 = 88°/2 = 44°

Ответ: 44°.

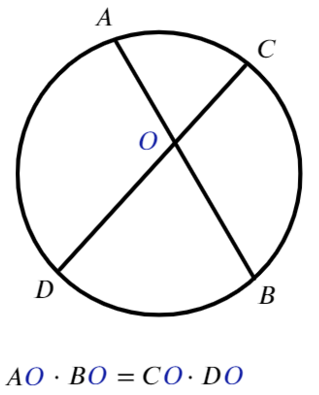
Теорема о произведении отрезков хорд

Можно заметить, что при пересечении двух хорд образуется пара подобных треугольников. Пусть хорды ADи ВС пересекаются в точке K. Добавим хорды AВ и СD и получим ∆AВК и ∆КСD:

На дугу ⋃BD опираются вписанные углы∠А и ∠С, значит, они одинаковы. Также на одну дугу АС опираются ∠D и∠В, поэтому и они одинаково. Равенство двух углов уже означает, что треугольники подобны по первому признаку подобия (дополнительно можно заметить, что ∠АКВ и ∠СКD равны как вертикальные углы).

Из подобия ∆AВК и ∆СКD вытекает пропорция между их сторонами:

Перемножив члены пропорции крест накрест, получим соотношение:

AK*KD = CK*BK

В результате нам удалось доказать следующее утверждение:

Задание. Хорды AВ и CD пересекаются в точке М. Известны, что АМ = 9, МВ = 3, МС = 2. Какова длина отрезка МD?

Решение.

Хорда AВ разбивается на отрезки АМ и МВ, а хорда CD – на отрезки СМ и МD. Произведения этих отрезков одинаковы:

AM*MB = CM*MD

Подставим в это равенство известные величины

Рассмотрим ещё одну геометрическую конструкцию. Пусть из некоторой точки А к окруж-ти проведена как касательная к окружности АК, так и секущая, пересекающая окруж-ть в точках В и С:

Какие здесь есть взаимосвязи между углами и длинами отрезков? Для начала проведем хорды ВК и СК, а также радиусы ОК и ОВ. Обозначим буквой α угол ∠ВСК. Он вписанный, поэтому дуга, на которую он опирается (это ⋃ВК), вдвое больше и равна 2α. Тогда и центральный угол ∠ВОК также составляет 2α:

Теперь исследуем ∆ВОК. Он равнобедренный (ВО и ОК – одинаковые радиусы), поэтому углы при его основании совпадают:

Итак, углы при основании ∆ОВК, в частности ∠ОКВ, равны 90° – α. Заметим, что ∠ОКА – прямой, так как образован радиусом ОК и касательной АК, при этом он состоит из двух углов, ∠АКВ и ∠ВКО. Это позволяет найти ∠АКВ:

В результате мы получили важный промежуточный результат – угол между касательной и хордой, проведенной из точки касания, вдвое меньше образующейся при этом дуги.

Вернемся к картинке с секущей. Изначально как α мы обозначили ∠ВСК, но в результате получили, что и ∠АКВ = α.

Рассмотрим ∆AВК и ∆САК. У них есть общий∠А, а также одинаковые ∠AКВ и ∠ВСК, которые отмечены буквой α. Значит, ∆AВК и ∆САК подобны, поэтому мы имеем право записать пропорцию между его сторонами:

Здесь отрезок АС можно назвать секущей, а AВ – ее внешней частью. Тогда выведенное отношение можно сформулировать так:

Решение. Сначала находим длину всей секущей, пользуясь доказанной теоремой:

Решение. Проведем из точки А ещё и касательную АК к окруж-ти:

Величину квадрата касательной АК можно найти, используя секущую АС. Сначала вычислим длину АС:

Ответ: 3,8.

Задачи на квадратной решетке

Рассмотрим несколько несложных задач, часто встречающихся на экзаменах.

Задание. Найдите ∠AВС на рисунке:

Решение. Здесь следует заметить, что расстояние между А и С составляет 8 клеток, при этом в окруж-ть как раз можно вписать квадрат со стороной 8.

Такой квадрат разобьет окруж-ть на 4 дуги, причем так как эти дуги опираются на хорды одинаковой длины, то они и сами равны. Вся окруж-ть составляет 360°, значит, каждая из этих дуг составляет 360°:4 = 90°. ∠AВС – вписанный, то есть он составляет половину дуги, на которую он опирается, а это⋃АС, равная 90°. Тогда

∠ABC = 90°:2 = 45°

Ответ: 45°.

Задание. Найдите ∠AВС, используя рисунок:

Решение. Используя рассуждения из предыдущей задачи, легко определить, что∠А составляет 45°.При этом ∆AВС – равнобедренный, и ВС – его основание. Это следует хотя бы из того факта, что высота АН делит сторону ВН пополам.

Углы∠В и ∠С одинаковы, так как лежат при основании равнобедренного треуг-ка. Найдем их, используя тот факт, что все 3 угла в ∆AВС составляют в сумме 180°:

Задание. Вычислите ∠AВС:

Решение. Снова в окруж-ть можно вписать квадрат со стороной 8 клеток. Из этого следует что ⋃АВС составляет 90° (показана фиолетовым цветом):

Но ∠АВС опирается на синюю дугу. Так как вместе фиолетовая и синяя дуга составляют окружность, равную 360°, то синяя дуга должна быть равна 360° – 90° = 270°. ∠АВС как вписанный будет вдвое меньше, то есть он равен 270°:2 = 135°.

Ответ: 135°.

Задание. Чему равен ∠AВС на рисунке?

Решение.

Если вписать в окруж-ть квадрат то он разобьет окруж-ти на дуги по 90°. В свою очередь точка А является серединой такой дуги, то есть она разбивает ее на две дуги по 45°.

∠AВС как вписанный будет вдвое меньше, то есть он равен 22,5°.

Что такое центральный и вписанный угол в окружности

Центром окружности называют точку, которая равноудалена от всех других точек окружности.

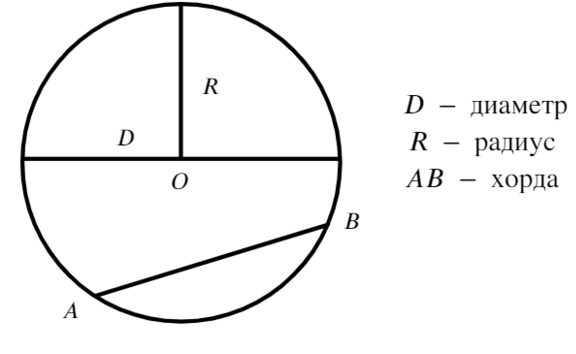
Радиус — является отрезком, который соединяет центр и точку на окружности.

Круг может обладать множеством радиусов, в соответствии с количеством точек, расположенных на рассматриваемой окружности. При этом все радиусы будут обладать одинаковой длиной. В некоторых случаях за радиус принимают длину отрезка, соединяющего центр с точкой окружности, а не сам отрезок.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Когда отрезок соединяет пару точек, расположенных на окружности, его называют хордой.

Существует устоявшееся выражение: «хорда стягивает дугу». К примеру, хорда displaystyle AB стягивает дугу displaystyle AB.

В том случае, когда хорда пересекает центр, она является диаметром.

Как правило, под диаметром подразумевают длину отрезка, который соединяет пару точек окружности и проходит через ее центр. Радиус составляет ½ диаметра.

В окружности можно отметить не только хорды, но и секущие. С примером можно ознакомиться на рисунке:

Центральный угол представляет собой угол, который расположен между двумя радиусами окружности.

Стороны, которые принадлежат центральному углу, выходят из центра окружности. В связи с этим, данный угол называют центральным.

Вписанный угол является углом между парой хорд, пересекающихся в точке на окружности.

В данном случае вписанный угол (displaystyle ABC) опирается на дугу (или на хорду) (displaystyle AC). При этом не каждый угол, который расположен внутри окружности, является вписанным, а лишь тот, у которого вершина расположены на самой окружности.

В качестве единиц измерения дуг и углов используют градусы и радианы.

Градусной мерой или величиной дуги является величина, выраженная в градусах, соответствующего центрального угла.

На рисунке изображена пара дуг (displaystyle AB) и два центральных угла. Большей дуге соответствует больший угол, несмотря на то, что он превышает ( displaystyle 180{}^circ), а меньшей дуге соответствует меньший угол.

Радианы представляют собой способ измерения угла в радиусах, то есть угол, равный (displaystyle 1) радиан является таким центральным углом, длина дуги которого равна радиусу окружности.

Выражать отношение длины окружности к радиусу не корректно в таких числах, как (displaystyle 1,text{ }2,text{ }3,frac{7}{5},frac{2}{239}). Не допустимо говорить, что половина окружности в (displaystyle 2,5) раза или в (displaystyle sqrt{17}) раз больше радиуса. В таком случае целесообразно использовать букву (displaystyle pi).

( pi) является числом, которое выражает отношение длины полуокружности к радиусу.

Таким образом, развернутый угол составляет ( pi) радиан, так как половина окружности в (pi) раз больше радиуса. Принято, что (displaystyle pi approx 3,14).

Исходя из того, что развернутый угол равен (pi) радиан, можно выразить любые углы в радианах.

(displaystyle 30{}^circ displaystyle frac{pi }{6})

(displaystyle 45{}^circ displaystyle frac{pi }{4})

(displaystyle 90{}^circ displaystyle frac{pi }{2})

(displaystyle 180{}^circ displaystyle pi)

(displaystyle 270{}^circ displaystyle frac{3pi }{2})

(displaystyle 360{}^circ displaystyle 2pi)

Свойства центральных и вписанных углов

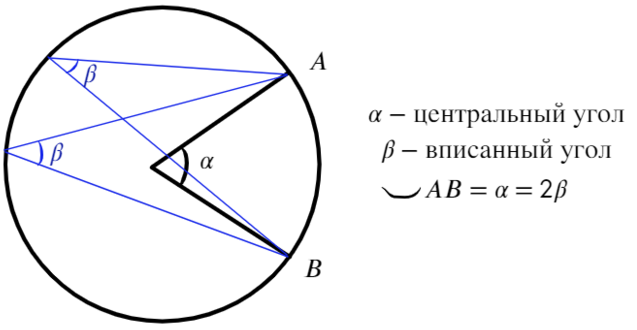
При решении задач по геометрии часто используют свойства центрального и вписанного углов. Например, вписанный угол в два раза меньше центрального угла в том случае, когда оба этих угла опираются на одну и ту же дугу.

Угол AOC и угол ABC, который вписан в круг, опираются на дугу AC. При этом центральный угол соответствует дуге AC, а угол ABC равен половине угла AOC.

Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается.

На примере, угол АОВ равен дуге АВ.

В том случае, когда в круг вписаны углы, опирающиеся на одну и ту же дугу, то такие углы будут равны.

На примере, угол ADC равен углу ABC и равен углу AEC, так как эти углы вписаны в окружность и опираются на одну и ту же дугу.

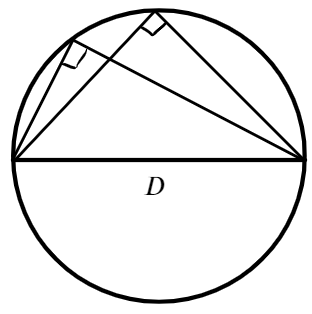
Если в окружность вписан угол, который опирается на ее диаметр, то такой угол является прямым.

К примеру, угол ACB опирается на диаметр и на дугу AB. При этом с помощью диаметра окружность делится на пару равных частей. Таким образом, дуга AB равна 180 градусов, а угол СAB составляет половину этой дуги, то есть равен 90 градусов.

Описанный угол является углом, который образован двумя касательными к окружности.

К примеру, угол CAB, который образован двумя касательными к окружности, является описанным. В этом случае AO представляет собой биссектрису угла CAB. Таким образом, центр окружности расположен на биссектрисе описанного угла.

Градусная мера вписанного угла составляет половину градусной меры дуги, на которую он опирается, и равна половине градусной меры центрального угла, опирающегося на эту же дугу.

Хорда является отрезком, который соединяет пару точек круга. Когда две хорды в окружности имеют точку пересечения, произведения отрезков одной равно произведению отрезков другой.

Например, AB * AC = AE * AD

Таким образом, сторонами вписанного в окружность угла являются хорды. Если вписанные углы опираются на одну и ту же хорду, они равны при условии, что их вершины находятся по одну сторону от хорды.

К примеру, угол BAC равен углу CAB, так как данные углы расположены на хорде BC.

В том случае, когда пара вписанных углов опираются на одну и ту же хорду, их градусная мера в сумме составляет 180 градусов при условии, что их вершины находятся по разные стороны от хорды.

Например, сумма углов BAC и BDC составляет 180 градусов.

Доказательство теоремы

Существует определенная закономерность, которая связывает вписанный и центральный угол. Величина вписанного угла в два раза меньше величины соответствующего центрального угла.

Соответствующим центральным углом называют такой, у которого концы совпадают с концами вписанного угла, а вершина — с центром окружности. Также соответствующий центральный угол «смотрит» на ту же хорду ((displaystyle AC)), что и вписанный угол. Предположим, что какая-то из хорд пересекает центр окружности.

Геометрическая фигура (displaystyle Delta AOB) является равнобедренным треугольником, так как (displaystyle AO и displaystyle OB) представляют собой радиусы. Таким образом:

(displaystyle angle A=angle B) (обозначили их ( displaystyle alpha)).

(displaystyle angle AOC) является внешним углом для (displaystyle Delta AOB). Согласно свойству, внешний угол соответствует сумме двух внутренних углов, которые не являются с ним смежными:

(displaystyle angle AOC=angle A+angle B)

В результате:

(displaystyle angle AOCtext{ }=text{ }2alpha)

С другой стороны, (displaystyle angle AOC) является центральным углом для вписанного ( angle ABC.)

В данном случае получилось доказать, что центральный угол в два раза больше, чем вписанный. Однако, не всегда хорда (displaystyle BC) пересекает центр окружности. Можно рассмотреть вторая вариант построения углов, когда центр окружности расположен внутри (displaystyle angle ABC).

Если провести диаметр окружности, то ситуация станет подобна первому случаю. В связи с этим, можно записать:

(displaystyle angle ~AOK=2~angle ~ABK)

(displaystyle angle ~COK=2~angle CBK)

С другой стороны:

(displaystyle angle ~ABC=angle ~ABK+~angle ~CBK)

(displaystyle angle ~AOC=angle ~AOK+~angle ~COK)

Таким образом:

(displaystyle angle ~AOC=2~angle ~ABC)

На чертеже:

(displaystyle angle ~ABC=~{{alpha }_{1}}+{{alpha }_{2}})

(displaystyle angle ~AOC=2{{alpha }_{1}}+2{{alpha }_{2}})

Во втором случае теорема также доказана.

Можно смоделировать еще один вариант построения окружности и углов, при котором центр вне угла (displaystyle ABC).

Порядок действий будет аналогичный. Необходимо построить диаметр, который пересекает точку (displaystyle text{B}). В данном случае вместо суммы используется разность:

(displaystyle angle ~ABC=~{{alpha }_{1}}-{{alpha }_{2}})

(displaystyle angle ~AOC=2{{alpha }_{1}}-2{{alpha }_{2}})

(displaystyle angle ~AOC=2~angle ~ABC)

В результате теорема справедлива и в третьем варианте. Из утверждения можно сделать два важных вывода.

На рисунке изображена дуга (displaystyle AC). Существует множество вписанных углов, которые на нее опираются. Данные углы могут отличаться, но, в любом случае, имеют одинаковый соответствующий центральный угол (displaystyle angle ~AOC). Можно сделать вывод, что все эти вписанные углы равны между собой.

Центральным для вписанного угла (displaystyle angle ABC) является угол (displaystyle angle ~AOC), который составляет (displaystyle 180{}^circ). Таким образом, (displaystyle angle ~ABC) и все вписанные углы, опирающиеся на (displaystyle AC) равны (displaystyle 90{}^circ.)

Примеры решения задач

Решение:

Окружность составляет (displaystyle 360{}^circ). Для того чтобы найти дугу АВ, требуется:

(displaystyle 360{}^circ — AC — CB = 360 — 200 — 80 = 80)

Согласно теореме о вписанном угле, его величина равна половине дуги, на которую он опирается. Таким образом:

(АCB = ½ AB = displaystyle 40{}^circ)

Ответ: угол АСВ равен (displaystyle 40{}^circ)

Решение:

На рисунке видно, что в окружности расположен центральный угол и дуга AC, которая равна (displaystyle 140{}^circ). Исходя из теоремы о вписанном и центральном углах, вписанный угол составляет половину центрального. Можно записать формулу:

(ABC = ½ AC = 140/2 = displaystyle 70{}^circ)

Ответ: угол ABC равен (displaystyle 70{}^circ).

Известно, что окружность равна (displaystyle 360{}^circ). Таким образом:

(СB = ⅕ от 360 = displaystyle 72{}^circ)

Согласно теореме о вписанном угле, он составляет половину дуги, на которую опирается:

(CAB = ½) от (CB = 72/36 = displaystyle 36{}^circ)

Ответ: угол САВ равен (displaystyle 36{}^circ)

Свойство касательных.

Свойства касательных и секущих.

Свойства хорд.

Углы окружности.

Площадь, сектор, длина окружности.

Задачи на окружности.

---

По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!

Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.

В окружности может быть проведено 3 типа отрезка:

Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).

Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).

Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).

А также две прямые снаружи от окружности:

Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.

Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.

Теперь чуть-чуть об углах и дугах:

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.

Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.

Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.

Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.

А вот такой угол НЕвписанный, такой угол «никто и звать никак».

Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:

Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.

Запишем основные свойства углов в окружности:

Нашел что-то общее?

Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.

Если угол находится внутри окружности, то находим его через полусумму дуг.

Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.

Отношение отрезков:

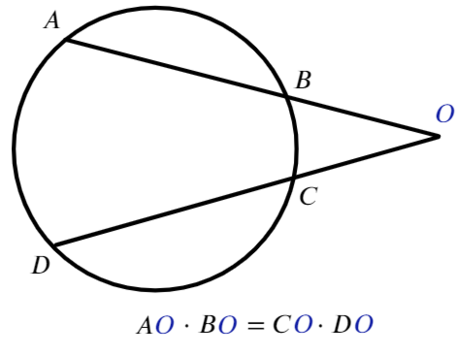
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:

Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:

Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).

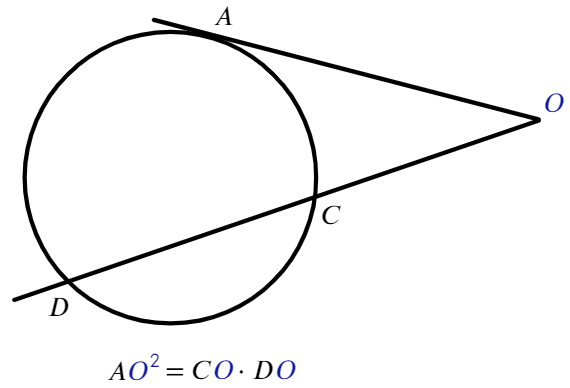
Если из точки, лежащей вне окружности, проведены касательная и секущая:

Аналогично в каждом отрезке присутствует точка, вне окружности (О).

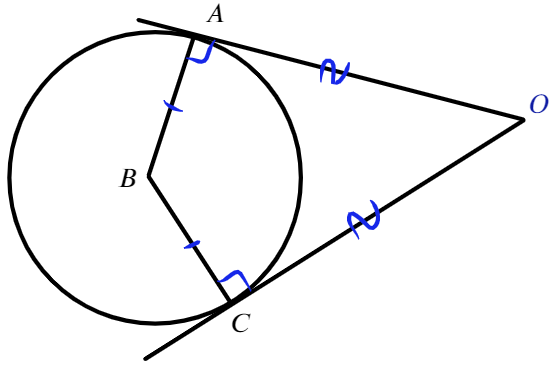
Если теперь провести две касательные из точки O, то получим такие равные отрезки:

Касательные равны, как, сообственно, и радиусы!

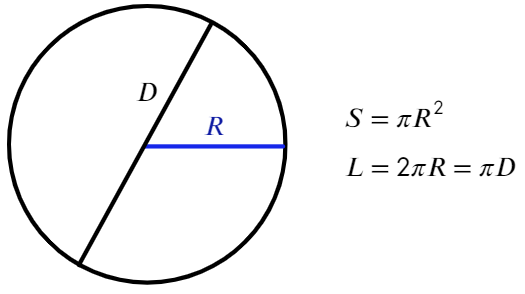
Площадь и длина окружности находятся по формуле:

По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD

Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!

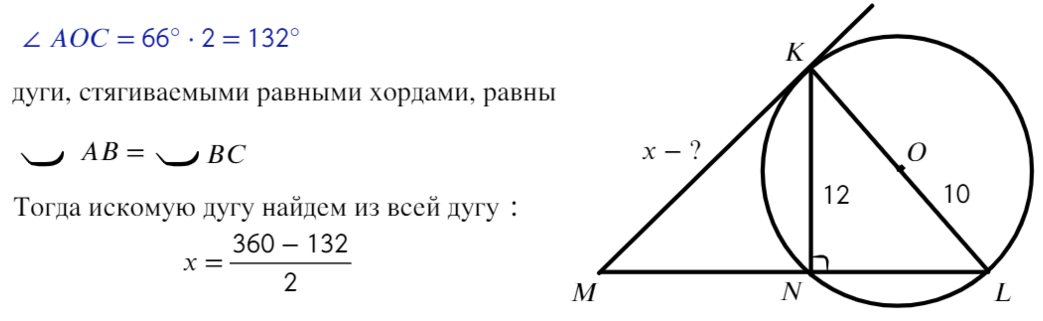
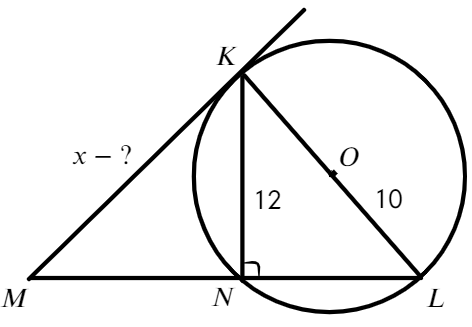
Задача №1. Дано на рисунке:

Достаточно вспомнить свойства центральных и вписанных углов.

Ответ: 39°

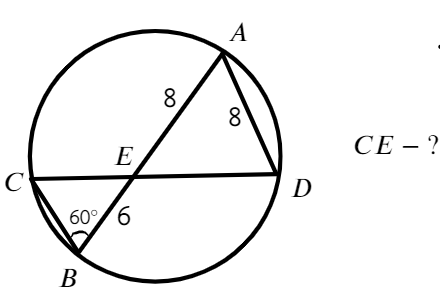
Задача №2. Дано на рисунке:

Найти нужно меньшую дугу BD

Ответ: 100°Задача №3. Дано на рисунке:

Найти меньшую дугу ВС

Ответ: 114°

Задача №4. Дано на рисунке:

Найти отрезок МК

Ответ: МК = 15.

Задача №5. Дано на рисунке:

Попробуй найти подобные треугольники

Ответ: 6

Задача №5. Дано на рисунке:

Без свойства секущей и касательной здесь будет тяжело

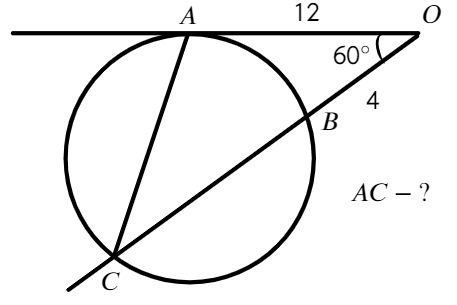
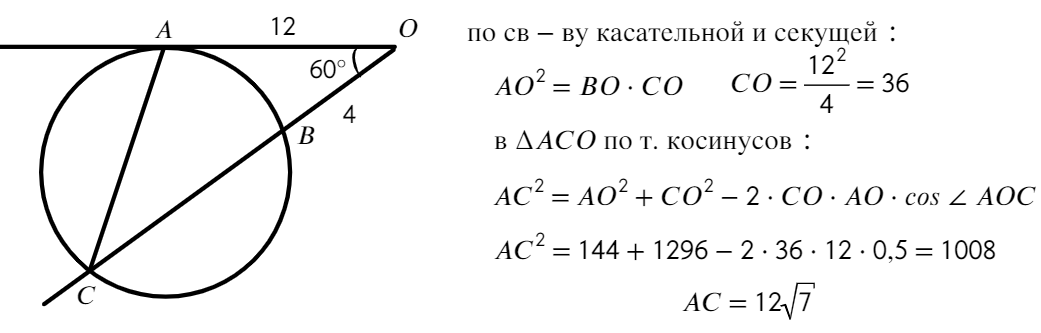
Ответ: 12√7.

Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.

Попробуй эти задачи с подсказками.

О треугольниках
О четырехуголникахp.s. Не бойся ошибаться и задавать вопросы!

Если нашел опечатку, или что-то непонятно − напиши.

Измерение углов и дуг круга

186. В самом начале курса геометрии было установлено, что значит равные углы, что значит один угол больше другого и что значит найти сумму двух углов, причем, чтобы не делать каких-либо ограничений, надо принять во внимание п. 19, где угол рассматривается, как результат поворота луча около точки (в плоскости). Благодаря этому, углы составляют систему величин, а каждый отдельный угол является определенным ее значением.

Так как здесь налицо те же основные положения, как и при рассмотрении отрезков, то все, что мы нашли для отрезков, справедливо и для углов: также можно измерять углы, принимая один из них за единицу, или находить отношение двух углов.

Чтобы измерять отрезки, нужно было только одно умение (пп. 165 и 172): откладывать на большем отрезке меньший. Так же точно, чтобы выполнять измерение углов, мы должны уметь откладывать меньший угол на большем, – а это мы умеем делать, умеем отличать больший угол от меньшего и умеем строить угол, равный данному.

Что же касается приближенного измерения углов (подобного изложенному в п. 181 для отрезков), то мы можем средствами геометрии лишь выполнять эти измерения с точностью до ½, ¼, 1/8, 1/16 и т. д., так как умеем угол делить только на 2, 4, 8, 16 и т. д. Равных частей. Существуют механические способы деления угла на сколько угодно равных частей.

За единицу при измерении углов принимают прямой угол; в предыдущем курсе мы часто встречались с углами, измеренными прямым углом. Например, если в равнобедренном треугольнике один угол прямой, то каждый из остальных = ½ прямого (½ d); каждый из углов равностороннего треугольника = 2/3 d; сумма внутренних углов n-угольника = 2d (n – 2) и т. д.

Но эта единица оказывается очень велика и на практике берут другую единицу, которая = 1/90 части прямого угла (1/90 d) и которая называется угловым градусом, при письме обозначают эту единицу знаком (°) и, следовательно,

угол равностороннего треугольника = 2/3 d = 60°,
сумма углов треугольника = 2d = 180° и т. д.

Затем вводят еще единицы: угловой градус делят на 60 равных частей, и такую часть называют угловою минутою, – ее знак (‘); угловую минуту делят еще на 60 равных частей и такую часть называют угловой секундою, – ее знак (»).

Например, имеем ¼ d = 22°30′; 1/16 d = 5°37’30».

Деление прямого угла на 90 равных частей, а углового градуса на 60 равных частей и т. д. Нельзя выполнять геометрически (циркулем и линейкою), а возможно лишь выполнять механическими способами.

187. Упражнения. 1. Часы показывают 25 минут второго. Вычислить в градусах угол между стрелками часов.

2. Вычислить в градусах (минутах и секундах) внутренний угол правильного 8-угольника, 12-угольника, 20-угольника (его еще мы не умеем строить), 14-угольника (его геометрическими способами невозможно построить).

3. Даны 2 угла; найти отношение этих углов, полагая, что при отыскании общей меры этих углов дойдем до остатка, о котором можно, хоть приближенно, принять, что он укладывается в предыдущем целое число раз (наложение одного угла на другой надо выполнять при помощи циркуля).

188. В п. 21 мы научились различать равные дуги одного круга (или равных кругов) и неравные дуги (знаем, что значит одна дуга больше другой), составили понятие о сумме двух дуг. Надо лишь иметь в виду, что сумма нескольких дуг может оказаться больше всего круга: прикладывая к одной дуге другую, к полученной сумме третью и т. д., можем обойти весь круг и зайти за ту точку, где начинается первая дуга. На основании этих сведений мы также, как и для отрезков, можем утверждать, что дуги одного круга можно выражать числами, принимая за единицу любую дугу. Для выполнения измерения дуг необходимо лишь одно умение, – умение откладывать равные дуги, а это можно выполнять при помощи циркуля, которым можно откладывать равные хорды: равным хордам соответствуют равные дуги (п. 119).

Обычно за единицу при измерении дуг принимают 1/360 часть всей окружности; разделить окружность на 360 частей геометрическими способами мы не можем, можем достигнуть этого механическими приемами (п. 148). Эта единица называется дуговым градусом; дуговой градус делят еще на 60 равных частей и эту часть называют дуговою минутою; разделив последнюю на 60 равных частей, получим дуговую секунду. Знаки для их обозначения употребляются такие же (°, ‘ и ») как и для угловых градуса, минуты и секунды. Недоразумения здесь быть не может, так как всегда видно, об измерении угла или дуги идет речь. Например,

∠AOB = 56° 8′ 24» и ◡MN = 17° 42′ 5»

(в первом случае угловые единицы, во втором — дуговые).

189. В том случае, когда две дуги одного круга или два угла несоизмеримы, отношение этих дуг или отношение этих углов признается нами равным какому-то иррациональному числу. Однако, мы не можем утверждать, что эти числа таковы же, как и те, которым равны отношения каких-либо двух отрезков: чтобы это утверждать, надо было бы убедиться, что для любой пары углов (или дуг одного круга) можно было бы построить два таких отрезка, чтобы можно было признать отношение двух углов (или дуг круга) равным отношению двух построенных отрезков, т. е. чтобы быть убежденным, что всякое рациональное число, большее одного из этих отношений, больше и другого, и всякое рациональное число, меньшее одного из этих отношений, меньше и другого. Геометрического решения указанного вопроса (построить требуемые два отрезка) вообще не возможно, но общая теория иррациональных чисел позволяет утверждать, что отношение двух несоизмеримых значений одной и той же системы величин (напр., углов) дает иррациональное число, которое можно рассматривать, как отношение двух несоизмеримых отрезков.

190. В частном случае мы можем легко усмотреть, что отношение двух углов равно отношению двух определенных дуг.

Построим круг O (чер. 194) и два центральных угла ∠AOB и ∠COD, которые опираются соответственно на дуги AB и CD. Рассмотрим два отношения ∠AOB/∠COD и ◡AB/◡CD. Найдем самое большое число со знаменателем n, чтобы оно было меньше первого отношения. Для этого разделим ∠COD на n равных частей (выполнить на самом деле такое построение мы можем лишь тогда, когда число n есть степень числа 2, т. е. 4, 8, 16, 32 …, если же число n какое-либо иное число, то все дальнейшее должно основываться на допущении, что существует угол, хотя мы его построить и не умеем, составляющий 1/n часть данного ∠COD) и станем такие углы укладывать на угле AOB, – допустим, что их уложится m с остатком KOB (∠KOB < 1/n ∠COD); тогда мы найдем число m/n, самое большое со знаменателем n, которое меньше ∠AOB/∠COD (здесь же получим самое малое число со знаменателем n, которое больше ∠AOB/∠COB, – оно есть (m+1)/n).

Мы знаем (п. 23), что равным центральным углам соответствуют равные дуги и обратно, что большему центральному углу соответствует большая дуга и обратно. Поэтому делением ∠COD на n равных частей мы и дугу CD разделим на n равных частей; затем, когда откладывали n-ые части ∠COD на ∠AOB, мы в то же самое время откладывали n-ые части ◡CD на ◡AB: их на ◡AB уложилось тоже m, и остаток KB меньше 1/n части ◡CD. Поэтому дробь m/n должна быть также меньше отношения ◡AB/◡CD (а число (m+1)/n должно быть больше ◡AB/◡CD).

Отсюда мы приходим к заключению, что нельзя найти такое число, чтобы оно было больше одного из рассматриваемых отношений и меньше другого; поэтому

∠AOB/∠COD = ◡AB/◡CD,

т. е. отношение двух центральных углов равно отношению соответствующих им дуг.

191. Обращаясь к практическому измерению углов угловыми градусами, а дуг — дуговыми градусами, мы прежде всего обратим внимание на то, что центральному углу в 1° соответствует дуга в 1°.

Это ясно из следующего: построим для круга O (чер. 195) два перпендикулярных диаметра CC’ ⊥ BB’; тогда окружность разделится на 4 равные части и каждой из них соответствует прямой центральный угол. Но в четвертой части окружности 360/4 = 90 дуговых градусов; следов., прямому углу, в котором 90 угловых градусов, соответствует дуга, в которой 90 дуговых градусов.

Если мы дугу B’C’ (четверть окружности) разделим на 90 равных частей и точки деления соединим с центром O, то в силу первого положения (равным дугам соответствуют равные центральные углы) и прямой ∠C’OB’ разделится на 90 равных частей. Следовательно, наше положение оправдывается.

Если, напр., ◡B’M = 1°, то ∠B’OM = 1°.

Пусть теперь имеем какой-либо центральный ∠AOB, которому соответствует дуга AB. Отложим от точки A по дуге AB дуговые градусы и концы откладываемых дуг соединим с центром; тогда увидим, что в центральном угле AOB уместится столько угловых градусов, сколько дуговых уместится на дуге AB. Если при отложении дугового градуса на ◡AB получим остаток, меньший дугового градуса, то соответственный центральный угол должен быть меньше углового градуса. Если в этом остатке укладывается определенная часть дугового градуса несколько раз без остатка, то, в силу первого положения, в угловом остатке уложится столько же раз такая же часть углового градуса.

Напр., если в дуговом остатке дуговая минута уложится несколько раз с остатком, то в угловом остатке уложится столько же угловых минут с остатком. В этих остатках (угловом и дуговом) угловая секунда и дуговая секунда или их одинаковые части также должны укладываться по одинаковому числу раз.

Отсюда заключаем:
В центральном угле столько угловых градусов, минут, секунд и их частей (вообще угловых единиц), сколько дуговых градусов, минут, секунд и их таких же частей (вообще соответствующих дуговых единиц) в соответствующей этому углу дуге.

То же выражают короче: центральные углы измеряются соответствующими им дугами.

Если, напр., нашли, что ◡AB = 66° 12′ 48», то и ∠AOB = 66° 12′ 48» (в первом случае дуговые градусы, минуты и секунды, а во втором — угловые).

192. На практике для измерения углов градусами употребляется инструмент, основанный на предыдущем свойстве и называемый транспортиром. Вот его устройство.

Берется металлический полукруг (чер. 196), разделенный на градусы (в хороших транспортирах делают деления чрез ½ градуса или даже чрез 1/3 градуса). На линейке, связанной в одно целое с полукругом, отмечается центр последнего O. Для измерения какого-либо угла располагают транспортир так, чтобы точка O транспортира совместилась с вершиною угла и прямая OA (или OA’) транспортира совместилась с одною из сторон угла. Тогда надо заметить, в каком месте разделенной дуги транспортира эта последняя пересекается с другою стороною угла, – найденное деление и дает выражение угла в градусах. Также транспортиром можно пользоваться для того, чтобы чертить углы данного числа градусов.

193. В пп. 132 и 133 было найдено, что вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и угол, составленный хордою и касательною, равен вписанному углу, опирающемуся на дугу, заключенную внутри первого угла.

Теперь, пользуясь предыдущим п., мы можем установить, что вписанный угол и угол, составленный хордою и касательною, измеряется половиною дуги, заключенной внутри этих углов. Например, если ◡AB (чер. 197) = 80° 21′ 18», то ∠ACB = 40° 10′ 39» и если ◡MN’ = 41° 10′, то ∠N’MP = 20° 35′.

194. Рассмотрим еще AOB (чер. 198), вершина которого расположена на окружности, а стороны как-либо пересекают окружность. Продолжив сторону OA в направлении OC, получим вписанный ∠COB, который опирается на ◡CMB. Пусть в ◡OB заключено m° и в дуге OC — n°; тогда ◡CMB = 360° – (m + n), а 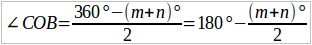. Тот же угол ∠AOB, который нам нужен, дополняет ∠COB до выпрямленного, т. е.

Поэтому, построив еще луч OD, продолжение луча OB, и замечая, что ◡OB = m° лежит внутри ∠AOB, а ◡OC = n° лежит между продолжениями сторон этого угла, мы имеем:

Угол, вершина которого расположена на окружности, а стороны пересекают окружность, измеряется половиною суммы дуг, заключенных между сторонами угла и их продолжениями.

195. Упражнения.

1. 1. Угол, вершина которого расположена внутри круга, измеряется полусуммою дуг, заключенных между сторонами этого угла и их продолжениями.
   (Можно построить треугольник, для которого данный угол явится внешним, а внутренние, с ним не смежные, сумме которых он равен, явятся вписанными в этот круг углами).
2. 2. Угол, вершина которого лежит вне круга, а стороны или пересекают круг, или касаются его, измеряется полуразностью дуг, заключенных между его сторонами.
3. 3. Окружность разделена на 4 части, относящиеся как 2 : 3 : 5 : 6, и точки деления соединены по порядку прямыми. Вычислить углы полученного вписанного 4-угольника.
4. 4. Окружность разделена на 3 части, относящиеся как 8 : 9 : 10, и в точках деления построены касательные. Вычислить углы полученного описанного треугольника.