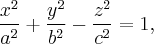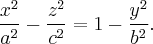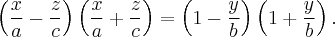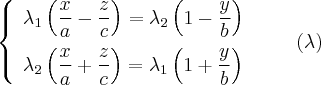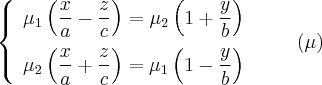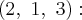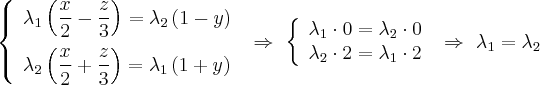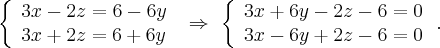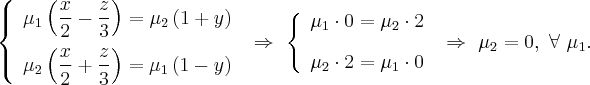255
АГ: Глава 6
При
рассмотрении конических и цилиндрических
поверхностей легко заметить, что эти
поверхности образованы движением
прямой линии.
Движение применялось простейшее:
вращение вокруг неподвижной оси.
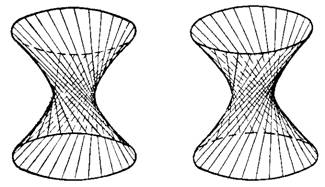
Рисунки
поверхностей однополостного гиперболоида
и гиперболического параболоида не
подсказывают, что эти поверхности могут
быть построены за счёт какого-то, пусть
даже сложного, движения прямолинейных
образующих:
ведь это значило бы, что какие-то прямые
целиком лежат на этих поверхностях!
Не будем
делать выводов, применяя только
впечатления от восприятия формы
геометрических фигур. Применим логически
оправданные действия. Если допустить,
что прямая линия принадлежит какой-то
поверхности, необходимо, выполнить
действия:
▫ взять
произвольную точку
,
принадлежащую исследуемой поверхности;
▫ взять
прямую линию, проходящую через точку
,
и определяемую общими уравнениями;
▫ доказать, что
за счёт выбора значений общих параметров
прямой можно добиться того, что прямая
линия целиком принадлежит поверхности.
Пусть
уравнение прямой задано параметрическими
уравнениями
:
Из этих уравнений следует: точка
принадлежит прямой линии, направление
прямой определяет вектор
=
.
У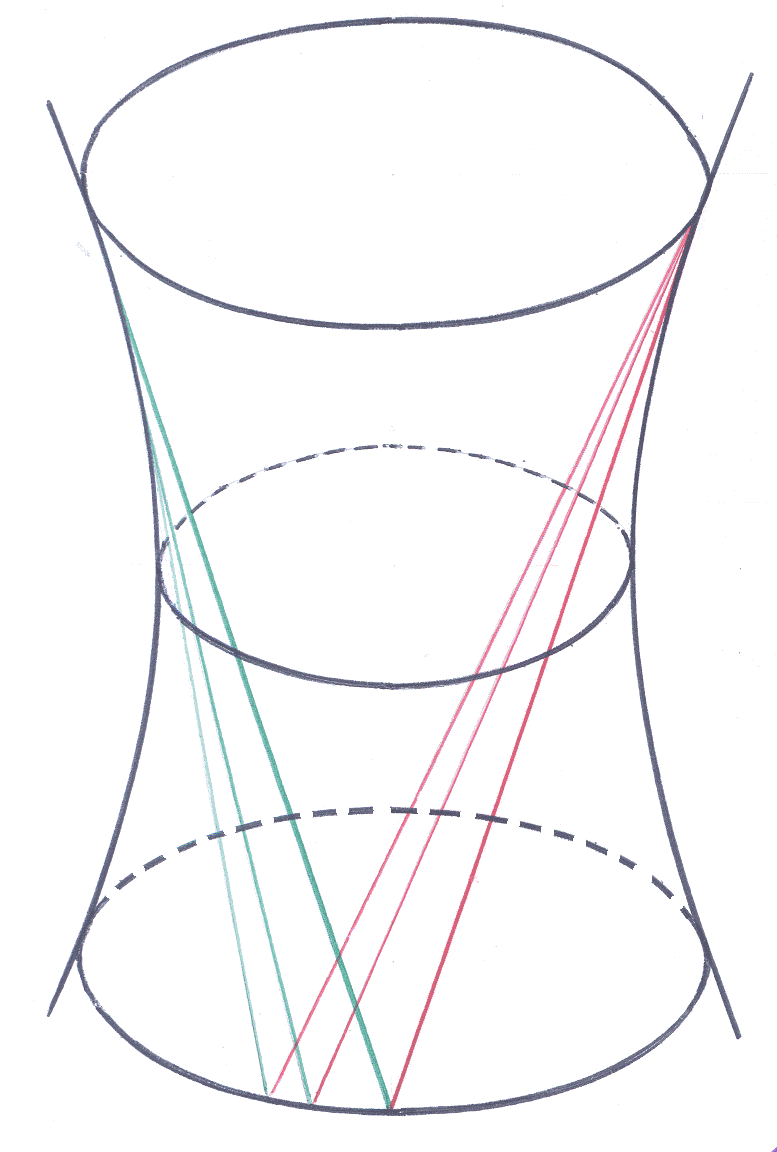
что любые преобразования прямоугольных
координат не изменяют геометрические
фигуры, расположенные в пространстве,
станем использовать такую систему
координат, в которой рассматриваемая
фигура определяется простейшим
алгебраическим выражением: каноническим
уравнением.
Однополостный
гиперболоид.
Его каноническое уравнение:
.
Для упрощения записи используемых
алгебраических выражений запишем
уравнение поверхности в виде:
.
Пусть
точка
принадлежит поверхности однополостного
гиперболоида. Так как прямая должна
принадлежать его поверхности, то точка
также должна принадлежит рассматриваемой
поверхности. Подставим значения
переменных:
из параметрических уравнений прямой в
каноническое уравнение поверхности.
Получим уравнение 2-го порядка относительно
переменной
:
,
(1)
где
коэффициенты могут быть записаны в виде
выражений:
=
;
=
;
=
.
Если
прямая линия
принадлежит рассматриваемой поверхности,
то уравнению (1) удовлетворяют любые
значения
.
Возьмём три различных значения переменной
:
.
Для этих значений получим систему
уравнений:

этой системы:
=

Так как
система трёх линейных однородных
уравнений относительно неизвестных
,
,
имеет определитель, не равный нулю, то
её единственным решением является
нулевое решение:
=0,
=0,
=0.
Верно
и обратное. Если коэффициенты уравнения
(1)
=0,
=0,
=0,
то оно удовлетворяется любыми значениями
.
В нашем случае это значит, что прямая
линия
принадлежит поверхности:
.
Применим
полученный результат к однополостному
гиперболоиду. Учтём сразу, что на его
поверхности значения
,
,
не могут быть равны нулю одновременно.
Пусть
0.
Из
условия
=0
следует:
.
Тогда можем записать:
=
=0. (2)
Координаты
вектора
=
не могут быть равны нулю одновременно.
Из условия
=0
мы получили бы одновременно:
=0.
Последнее невозможно, так как
0.
Пусть
0.
Применяя несложные алгебраические
преобразования, равенство (2) можем
записать в виде выражения: 
Решая
квадратное уравнение (3) относительно
отношения
,
запишем решение в виде:
=

Так как
=
=0,
то
и выражение (4) ещё более упростится: =
(5)
Из
выражения (5) следует: для существования
действительных решений уравнения (3)
необходимо и достаточно, чтобы выполнялось
условие:
<
0. Возможны следующие комбинации
знаков в уравнении (1):
|
A |
B |
C |
|
|
I |
– |
– |
– |
|
II |
+ |
+ |
– |
В случае
I
уравнение (1) определяет мнимый эллипсоид
– прямолинейных образующих не имеет.
В случае II
уравнение (1) определяет однополостный
гиперболоид – прямолинейные образующие
имеет.
Так как
для однополостного гиперболоида
0,
то для каждой точки
имеем две прямолинейные образующие (на
рисунке показаны разным цветом).
Учитывая,
что для однополостного гиперболоида
имеем:
=
,
=
,
=–
,
получаем выражения:
=


Учитывая
выражение (6), и используя выражение
,
получим полную характеристику необходимого
для точки
вектора
:
=
. (7)
Если в
выражении (6) выбирать всё время знак
,
будем получать прямолинейные образующие
поверхности одного семейства. Знаку
будет соответствовать второе семейство
образующих той же поверхности.
Важно
то, что
.
Это значит, что
0,
то есть никакая прямолинейная образующая
не параллельна плоскости координат
.
Из этого следует, что все образующие
однополостного гиперболоида пересекают
горловой
эллипс:
По поводу
прямолинейных образующих однополостного
гиперболоида
полезно знать две теоремы (из рисунка
вполне можно видеть намёк-подтверждение!).
|
Теорема: (6.1) |
Две |
►Пусть
имеем две прямолинейные образующие
и
,
принадлежащие различным семействам.
Пусть
пересекает горловой эллипс в точке
,
а
– в точке
.
Если
точки
и
совпадают, то утверждение очевидно.
Пусть теперь точки
и
различны. Учтём, что для горлового
эллипса
=0
и
.
В этом случае имеем:
=
и
=–
или
=
. (8)
и
одновременно: =
. (9)
Обозначим
векторы
=
,
=
и
.
Условием принадлежности образующих
и
одной плоскости является:
=0.
Из
выражений (8) и (9) видно, что векторы
и
только в случае, когда
и
проходят через диаметрально противоположные
точки горлового эллипса:
=
,
=
,
=
=0.
Теорема
доказана! ◄
Замечание:
если
детали доказательства теоремы применить
к тому же рисунку, то нетрудно признаться
себе, что интуиция –
только помощница при доказательстве
теорем, но не само доказательство!
теоремы (из рисунка
вполне можно видеть намёк-подтверждение!).
|
Теорема: (6.2) |
Любые |
►Пусть
имеем две прямолинейные образующие
и
,
которые принадлежат одному семейству
и пересекают горловой эллипс в точке
и в точке
,
соответственно. Точки
и
различны, иначе образующие совпадали
бы!
В этом случае
имеем:
=
и
=
. (10)
Вычисления
показывают, что на этот раз:
0.
Из этого следует, что
и
– скрещивающиеся прямолинейные
образующие однополостного гиперболоида.
Теорема
доказана! ◄
Используя
результаты теорем, можно попробовать
найти прямолинейные образующие
однополостного гиперболоида, выполняя
формальные алгебраические действия с
исходным выражением
:
→
. (11)
Используя (11),
запишем уравнения прямых линий:


Нетрудно
заметить, учитывая (11), что при любых
значениях чисел:
и
прямые
и
лежат на поверхности однополосного
гиперболоида: для этого достаточно
перемножить первое и второе уравнения
для системы
,
аналогично для системы
.
Формальное
использование уравнений (12) полезно
тем, что эти уравнения могут быть легко
записаны. Конечно, способ, опирающийся
на выражения (11) и (12), не
отменяет
важность доказанных теорем!
Интересно:
Однополостные гиперболоиды используют
при сооружении прочных, лёгких и простых
в изготовлении башен. Такую конструкцию
предложил русский инженер Шухов В.Г.
(1853-1939). В соответствии с его идеей
построена Останкинская телебашня в
Москве (каждый может ею полюбоваться!).
☺☺
Пример 6–16:
Для однополостного гиперболоида:
найти прямолинейные образующие,
проходящие через точку
(3,2,1).
Решение:
1). Запишем
исходное выражение в виде:
,
откуда уравнения прямолинейных образующих
можно записать в виде:

2).
Подставляя в полученные уравнения
координаты заданной точки
(3,2,1),
получаем: из уравнений системы
:
,
причём
–
произвольное число, а для системы
:
–
произвольное число и =0.
Используя полученные значения пар
и ,
запишем уравнения образующих:
и
Ответ: уравнения
образующих:
и
Замечание:
Используя полученные уравнения, без
особого труда можно получить параметрические
уравнения образующих (ведь именно с их
помощью была решена рассмотренная
задача).
☻
Г
параболоид.
Его каноническое уравнение:
.
Для упрощения записи используемых
алгебраических выражений запишем
уравнение поверхности в виде:
.
Пусть
точка
принадлежит поверхности однополостного
гиперболоида. Так как прямая должна
принадлежать его поверхности, то точка
также должна принадлежит рассматриваемой
поверхности. Подставим значения
переменных:
из параметрических уравнений прямой в
каноническое уравнение поверхности.
Получим уравнение 2-го порядка относительно
переменной
:
,
(1)
где
коэффициенты могут быть записаны в виде
выражений:
=
;
=
;
=
.
Если
прямая линия
принадлежит рассматриваемой поверхности,
то уравнению (1) удовлетворяют любые
значения
.
Возьмём три различных значения переменной
:
.
Для этих значений получим систему
уравнений:

этой системы:
=

Так как
система трёх линейных однородных
уравнений относительно неизвестных
,
,
имеет определитель, не равный нулю, то
её единственным решением является
нулевое решение:
=0,
=0,
=0.
Верно
и обратное. Если коэффициенты уравнения
(1)
=0,
=0,
=0,
то оно удовлетворяется любыми значениями
.
В нашем случае это значит, что прямая
линия
принадлежит поверхности:
.
Используя
условия:
=0,
=0,
=0,
как и в случае однополостного гиперболоида,
получаем: =
и =

Так как
имеет действительные значения только
в случае, если числа
и
имеют разные знаки, то есть:
,
то это имеет место только в случае
гиперболического параболоида.
Из формул
(3) видно, что через каждую точку поверхности
проходит две прямолинейные образующие,
принадлежащие к различным семействам.
Так как
постоянная величина, то в каждой точке
поверхности одна из прямолинейных
образующих параллельна плоскости
,
а другая плоскости
,
причём
>0,
<
0. Это значит, что образующие одного
семейства параллельны одной плоскости,
а образующие другого параллельны другой
плоскости.
Как и в
случае однополостного гиперболоида,
можно показать, что две прямолинейные
образующие одного семейства не принадлежат
одной плоскости, а две прямолинейные
образующие различных семейств
пересекаются. Нетрудно также получить
прямолинейные образующие, непосредственно
используя уравнение поверхности:
. (4)
Используя (4),
запишем уравнения прямых линий:


Прямолинейные
образующие
и
принадлежат поверхности гиперболического
параболоида.
☺☺
Пример 6–17:
Убедившись, что точка
(1,3,–1)
лежит на гиперболическом параболоиде:
,
составить уравнения его прямолинейных
образующих, проходящих через точку
.
Решение:
1). Запишем
уравнение гиперболического параболоида
в виде:
.
2). Запишем
уравнения прямолинейных образующих
для заданной поверхности:
и
3).
Проверка того, что точка
принадлежит поверхности, делается
устно!
Подставляя в полученные уравнения
координаты заданной точки
(1,3,–1),
получаем:
▫ для
образующей
соотношение;
▫ для
образующей
соотношение.
4).
Используя
полученные значения пар
и ,
запишем уравнения образующих:
:
и
:
5). Найдём
канонические уравнения образующей
:
▫ из
системы выделяем произвольную точку,
принадлежащую
:
(0,–1,1);
▫ используя
нормали:
=(2,
–1,
–1),
=(2,0,
1) плоскостей, вычисляем направляющий
вектор образующей:
=
×
=(1,4,–2).
▫ записываем
каноническое уравнение образующей:
.
6). Найдём
канонические уравнения образующей
:
▫ из
системы выделяем произвольную точку,
принадлежащую
:
(0,–9,
–3);
▫ используя
нормали:
=(2,
0,–1),
=(6,–1,
3) плоскостей, вычисляем направляющий
вектор образующей:
=
×
=(1,
12, 2).
▫ записываем
каноническое уравнение образующей:
.
Ответ: уравнения
образующих
:
и
:
.
Замечание:
Используя полученные уравнения, без
особого труда можно получить параметрические
уравнения образующих (ведь именно с их
помощью была решена рассмотренная
задача).
☻
Исследование
свойств поверхностей 2-го порядка полезно
не только потому, что эти поверхности
всегда привлекали изяществом своих
форм. Эти поверхности великолепны ещё
и своими механическими свойствами: их
прочность изумительна!
В
давнюю пасхальную шутку на Руси:
предлагают известному своей силой Ване
попытаться раздавить куриное яйцо (чаще
это пасхальное яйцо!). Силач, сцепив
пальцы рук, начинает сжимать его между
ладоней. Доверчивым силачам (и высокого
мнения о своей силе!) кажется, что работа
займёт несколько секунд!..
На самом деле,
редко кому удаётся подтвердить свою
безграничную силу! Обычно успех бывает
только в случае, если яйцо имеет дефекты.
Или силач хитрил: усилия прикладывались
несимметрично!
Вспомним
ещё изящную форму фюзеляжа самолёта,
корпус подводной лодки! У них внутри
спрятаны цилиндрические шпангоуты:
лёгкие, но очень прочные!
Соседние файлы в папке ЛА и АГ пособие
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Прямолинейные образующие на поверхности однополостного гиперболоида
Уравнение однополостного гиперболоида имеет вид:
Разложим на множители:
Рассмотрим следующую систему линейных уравнений:
Каждое линейное уравнение задает в пространстве плоскость. Данные плоскости не параллельны, следовательно эта система из двух линейных уравнений задает прямую. Покажем, что эта прямая лежит на Однополостный гиперболоид. Действительно, если точка принадлежит этой прямой, то она удовлетворяет каждое из линейных уравнений системы, следовательно удовлетворяет произведения этих уравнений, то есть уравнению однополостного гиперболоида.
Это утверждение справедливо для любых 
Уравнение второй семьи :
Теорема. Однополостный гиперболоид несет на себе две семьи прямолинейных образующих, имеющих следующие свойства:
· через любую точку проходит ровно одна прямая с каждой семьи ;
· любые две образующие из разных семей лежат в одной плоскости;
· любые две образующие с одной семьи является скрещивающимися;
· любые три образующие с одной семьи не параллельны одной плоскости.
Доказательство можно посмотреть в методичке.
Пример. Найти прямолинейные образующие поверхности 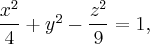
Запишем уравнение первой семьи прямолинейных образующих 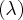
Можем взять любые числа, удовлетворяющие этому равенства, например: 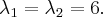
Уравнение второй семьи
Возьмем, 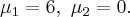
121. Однополостные гиперболоиды и его прямолинейные образующие
Определение 1. Поверхность, которая в некоторой прямоугольной системе координат имеет уравнение

Называется Однополостным гиперболоидом, A > 0, B > 0, C > 0. Числа A, B, C называются Полуосями однополостным гиперболоидом.
Исследуем поверхность однополостного гиперболоида по уравнению (10). Так как все переменные входят в уравнение (10) в четной степени, то вместе с точкой (X, Y, Z) однополостному гиперболоиду принадлежат все восемь точек (±X, ±Y, ±Z) (с произвольными комбинациями знаков). Таким образом, однополостной гиперболоид симметричен относительно, всех трех координатных плоскостей и начала координат. Он пересекает координатные оси OX, OY соответственно в точках (±A, 0, 0), (0, ±B, 0), которые называются Вершинами Однополостного гиперболоида.
Уравнение прямолинейных образующих однополостного гиперболоида через точку
Глава 46. Поверхности второго порядка
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
(1).
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (2)
. (3)
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (4)
, (5)
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.
Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .
Таким образом, мы получаем искомые выражения:
, , (6)
, , (7)
Предположим, что M(x; y; z ) — произвольная точка сферы
.
Заменим здесь x, y, z их выражениями (7); получим
,
.
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам
, , ;
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.
Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.
имеет две системы прямолинейных образующих, которые определяются уравнениями:
, ;
, ,
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид
также имеет две системы прямолинейных образующих, которые определяются уравнениями
, ;
, .
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).
http://matica.org.ua/metodichki-i-knigi-po-matematike/algebra-i-geometriia-tolstikov-a-v/121-odnopolostnye-giperboloidy-i-ego-priamolineinye-obrazuiushchie
http://a-geometry.narod.ru/problems/problems_46.htm

Прямолинейные образующие поверхностей второго порядка. Основные формулы
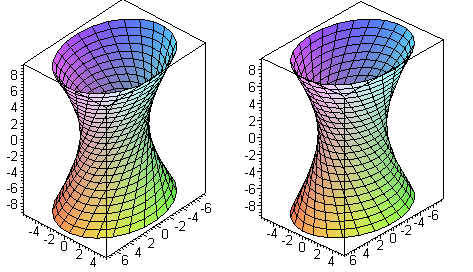
Рис.1 Рис.2
Прямолинейной образующей поверхности называется прямая линия, целиком лежащая на данной поверхности. Например, прямолинейные образующие конической и цилиндрической поверхности.
Однополостный гиперболоид (рис.1,2)
имеет два семейства прямолинейных образующих:
и
где k и l — произвольные параметры, не зависящие от х, у и z.
Каждая из систем (1) и (2) при определенных значениях k и l определяет прямую линию.
При произвольных k и l каждая система дает семейство прямых линий.
Рис.3
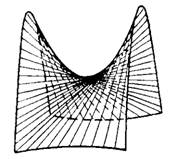
Гиперболический параболоид (рис.3)
имеет также два семейства прямолинейных образующих:
и
где k и l — произвольные параметры.
-
Поверхности вращения.
Начать изучение
-
Эллипсоид.
Начать изучение
-
Конус второго порядка.
Начать изучение
-
Однополостный гиперболоид.
Начать изучение
-
Двуполостный гиперболоид.
Начать изучение
-
Эллиптический параболоид.
Начать изучение
-
Гиперболический параболоид.
Начать изучение
Поверхности вращения.
Определение.
Поверхность (S) называется поверхностью вращения с осью (d), если она составлена из окружностей, которые имеют центры на прямой (d) и лежат в плоскостях, перпендикулярных данной прямой.
Рассмотрим линию (L), которая лежит в плоскости (P), проходящей через ось вращения (d) (рис. 43), и будем вращать ее вокруг этой оси. Каждая точка линии опишет окружность, а вся линия — поверхность вращения.
Выберем начало декартовой прямоугольной системы координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}) на оси (d), вектор (boldsymbol{e}_{3}) направим вдоль (d), а вектор (boldsymbol{e}_{1}) поместим в плоскости (P). Таким образом, (O, boldsymbol{e}_{1}, boldsymbol{e}_{3}) — декартова система координат в плоскости (P). Пусть линия (L) имеет в этой системе координат уравнение (f(x, y)=0).
Рассмотрим точку (M(x, y, z)). Через нее проходит окружность, которая имеет центр на оси (d) и лежит в плоскости, перпендикулярной этой оси. Радиус окружности равен расстоянию от (M) до оси, то есть (sqrt{x^{2}+y^{2}}). Точка (M) лежит на поверхности вращения тогда и только тогда, когда на указанной окружности имеется точка Мь принадлежащая вращаемой линии (L).
Точка (M_{1}(x_{1}, y_{1}, z_{1})) лежит в плоскости (P), и потому (y_{1}=0). Кроме того, (z_{1}=z) и (|x|=sqrt{x^{2}+y^{2}}), так как (M_{1}) лежит на той же окружности, что и (M). Координаты точки (M_{1}) удовлетворяют уравнению линии (L): (f(x_{1}, z_{1})=0). Подставляя в это уравнение (x_{1}) и (z_{1}), мы получаем условие на координаты точки (M), необходимое и достаточное для того, чтобы (M) лежала на поверхности вращения (S): равенство
$$
fleft(pm sqrt{x^{2}+y^{2}}, zright)=0label{ref1}
$$
должно быть выполнено хотя бы при одном из двух знаков перед корнем. Это условие, которое можно записать также в виде
$$
fleft(sqrt{x^{2}+y^{2}}, zright)fleft(-sqrt{x^{2}+y^{2}}, zright)=0,label{ref2}
$$
и является уравнением поверхности вращения линии (L) вокруг оси (d).
Эллипсоид.
Рассмотрим поверхности, которые получаются при вращении эллипса вокруг его осей симметрии. Направив вектор (boldsymbol{e}_{3}) сначала вдоль малой оси эллипса, а затем вдоль большой оси, мы получим уравнения эллипса в следующих видах:
$$
frac{x^{2}}{a^{2}}+frac{z^{2}}{c^{2}}=1, frac{z^{2}}{a^{2}}+frac{x^{2}}{c^{2}}=1.nonumber
$$
(Здесь через (c) обозначена малая полуось эллипса.) В силу формулы eqref{ref1} уравнениями соответствующих поверхностей вращения будут
$$
frac{x^{2}+y^{2}}{a^{2}}+frac{z^{2}}{c^{2}}=1, frac{z^{2}}{a^{2}}+frac{x^{2}+y^{2}}{c^{2}}=1 (a > c).label{ref3}
$$
Поверхности с такими уравнениями называются соответственно сжатым и вытянутым эллипсоидами вращения (рис. 10.2).
Каждую точку (M(x, y, z)) на сжатом эллипсоиде вращения сдвинем к плоскости (y=0) так, чтобы расстояние от точки до этой плоскости уменьшилось в постоянном для всех точек отношении (lambda < 1). После сдвига точка попадет в положение (M'(x’, y’, z’)), где (x’=x), (y’=y), (z’=z).
Таким образом, точки эллипсоида вращения переходят в точки поверхности с уравнением
$$
frac{x’^{2}}{a^{2}}+frac{y’^{2}}{b^{2}}+frac{z’^{2}}{c^{2}}=1,label{ref4}
$$
где (b=lambda a). Поверхность, которая в некоторой декартовой системе координат имеет уравнение eqref{ref4}, называется эллипсоидом (рис. 10.3). Если случайно окажется, что (b=c), мы получим снова эллипсоид вращения, но уже вытянутый.
Эллипсоид так же, как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения eqref{ref4} видно, что начало канонической системы координат — центр симметрии эллипсоида, а координатные плоскости — его плоскости симметрии.
Эллипсоид можно получить из сферы (x^{2}+y^{2}+z^{2}=a^{2}) сжатиями к плоскостям (y=0) и (z=0) в отношениях (lambda=b/a) и (mu=c/a).
В этой статье нам часто придется прибегать к сжатию, и мы не будем его каждый раз описывать столь подробно.
Конус второго порядка.
Рассмотрим на плоскости (P) пару пересекающихся прямых, задаваемую в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{3}) уравнением (a^{2}x^{2}-c^{2}z^{2}=0). Поверхность, получаемая вращением этой линии вокруг оси аппликат, имеет уравнение
$$
a^{2}(x^{2}+y^{2})-c^{2}z^{2}=0label{ref5}
$$
и носит название прямого кругового конуса (рис. 10.4). Сжатие к плоскости (y=0) переводит прямой круговой конус в поверхность с уравнением
$$
a^{2}x^{2}+b^{2}y^{2}-c^{2}z^{2}=0label{ref6}
$$
называемую конусом второго порядка.
Обратите внимание на то, что левая часть уравнения eqref{ref6} — однородная функция, и поверхность является конусом в смысле определения, введенного ранее.
Однополостный гиперболоид.
Однополостный гиперболоид вращения — это поверхность вращения гиперболы
$$
frac{x^{2}}{a^{2}}-frac{z^{2}}{c^{2}}=1nonumber
$$
вокруг той оси, которая ее не пересекает. По формуле eqref{ref1} мы получаем уравнение этой поверхности (рис. 10.5)
$$
frac{x^{2}+y^{2}}{a^{2}}-frac{z^{2}}{c^{2}}=1.label{ref7}
$$
В результате сжатия однополостного гиперболоида вращения к плоскости (y=0) мы получаем однополостный гиперболоид с уравнением
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}-frac{z^{2}}{c^{2}}=1.label{ref8}
$$
Интересное свойство однополостного гиперболоида — наличие у него прямолинейных образующих. Так называются прямые линии, всеми своими точками лежащие на поверхности. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие, уравнения которых можно получить следующим образом.
Уравнение eqref{ref8} можно переписать в виде
$$
left(frac{x}{a}+frac{z}{c}right)left(frac{x}{a}-frac{z}{c}right)=left(1+frac{y}{b}right)left(1-frac{y}{b}right).nonumber
$$
Рассмотрим прямую линию с уравнениями
$$
begin{array}{cc}
& displaystylemuleft(frac{x}{a}+frac{z}{c}right)=lambdaleft(1+frac{y}{b}right),\
& \
& displaystylelambdaleft(frac{x}{a}-frac{z}{c}right)=muleft(1-frac{y}{b}right),
end{array}label{ref9}
$$
где (lambda) и (mu) — некоторые числа ((lambda^{2}+mu^{2} neq 0)). Координаты каждой точки прямой удовлетворяют обоим уравнениям, а следовательно, и уравнению eqref{ref8}, которое получается их почленным перемножением. Поэтому каковы бы ни были (lambda) и (mu), прямая с уравнениями eqref{ref9} лежит на однополостном гиперболоиде. Таким образом, система eqref{ref9} определяет семейство прямолинейных образующих.
Второе семейство прямолинейных образующих определяется системой
$$
begin{array}{cc}
& mu’left(frac{x}{a}+frac{z}{c}right)=lambda’left(1-frac{y}{b}right),\
& \
& lambda’left(frac{x}{a}-frac{z}{c}right)=mu’left(1+frac{y}{b}right),
end{array}label{ref10}
$$
Покажем на примере, как найти образующие, проходящие через данную точку поверхности. Рассмотрим поверхность (x^{2}+y^{2}-z^{2}=0) и точку (M_{0}(1, 1, 1)) на ней. Подставляя координаты (M_{0}) в уравнения eqref{ref9}, мы получаем условия на (lambda) и (mu): (2lambda=2mu) и (0 cdot lambda=0 cdot mu). Первое из них определяет (lambda) и (mu) с точностью до общего множителя, но только с такой точностью они и нужны. Подставляя эти значения в eqref{ref9}, получаем уравнения прямолинейной образующей
$$
x+z=1+y, x-z=1-y.nonumber
$$
Она проходит через (M_{0}), так как (lambda) и (mu) так и выбирались, чтобы координаты (M_{0}) удовлетворяли этой системе. Аналогично, подставляя координаты (M_{0}) в (10), находим условия на (lambda’) и (mu’): (2mu’=0) и (2mu’=0). Коэффициент (lambda’) можно взять любым ненулевым, и мы приходим к уравнению второй образующей: (x=z), (y=1).
Если вместе с гиперболой мы будем вращать ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. При сжатии гиперболоида вращения его асимптотический конус сжимается в асимптотический конус общего однополостного гиперболоида.
Двуполостный гиперболоид.
Двуполостный гиперболоид вращения — это поверхность, получаемая вращением гиперболы
$$
frac{z^{2}}{c^{2}}-frac{x^{2}}{a^{2}}=1nonumber
$$
вокруг той оси, которая ее пересекает. По формуле eqref{ref1} мы получаем уравнение двуполостного гиперболоида вращения
$$
frac{z^{2}}{c^{2}}-frac{x^{2}+y^{2}}{a^{2}}=1.label{ref11}
$$
В результате сжатия этой поверхности к плоскости у=0 получается поверхность с уравнением
$$
frac{z^{2}}{c^{2}}-frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref12}
$$
Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение вида eqref{ref12}, называется двуполостным гиперболоидом (рис. 10.6). Двум ветвям гиперболы здесь соответствуют две не связанные между собой части (“полости”) поверхности, в то время как при построении однополостного гиперболоида вращения каждая ветвь гиперболы описывала всю поверхность.
Асимптотический конус двуполостного гиперболоида определяется так же, как и для однополостного.
Эллиптический параболоид.
Вращая параболу (x^{2}=2pz) вокруг ее оси симметрии, мы получаем поверхность с уравнением
$$
x^{2}+y^{2}=2pz.label{ref13}
$$
Она называется параболоидом вращения. Сжатие к плоскости (y=0) переводит параболоид вращения в поверхность, уравнение которой приводится к виду
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=2z.label{ref14}
$$
Поверхность, которая имеет такое уравнение в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом (рис. 10.7).
Гиперболический параболоид.
По аналогии с уравнением eqref{ref14} мы можем написать уравнение
$$
frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=2z.label{ref15}
$$
Поверхность, которая имеет уравнение вида eqref{ref15} в некоторой декартовой прямоугольной системе координат, называется гиперболическим параболоидом.
Исследуем форму этой поверхности. Для этого рассмотрим ее сечение плоскостью (x=alpha) при произвольном (alpha). В этой плоскости выберем декартову прямоугольную систему координат (O’, boldsymbol{e}_{2}, boldsymbol{e}_{3}) с началом в точке (O'(alpha, 0, 0)). Относительно этой системы координат линия пересечения имеет уравнение
$$
-frac{y^{2}}{b^{2}}=2left(z-frac{alpha^{2}}{2a^{2}}right).label{ref16}
$$
Эта линия — парабола, в чем легко убедиться, перенеся начало координат в точку (O″) с координатами ((0, alpha^{2}/(2a^{2}))). (Координаты этой точки относительно исходной системы координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}) в пространстве равны ((alpha, 0, alpha^{2}/(2a^{2}))).)
Точка (O″), очевидно, является вершиной параболы, ось параболы параллельна вектору (boldsymbol{e}_{3}), а знак минус в левой части равенства eqref{ref16} означает, что ветви параболы направлены в сторону, противоположную направлению (boldsymbol{e}_{3}). Заметим, что после переноса начала координат в точку (O″) величина а не входит в уравнение параболы, и, следовательно, сечения гиперболического параболоида плоскостями (x=alpha) при всех (alpha) представляют собой равные параболы.
Будем теперь менять величину (alpha) и проследим за перемещением вершины параболы (O″) в зависимости от (alpha). Из приведенных выше координат точки (O″) следует, что эта точка перемещается по линии с уравнениями
$$
z=frac{x^{2}}{2a^{2}}, y=0nonumber
$$
в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}). Эта линия — парабола в плоскости (y=0). Вершина параболы находится в начале координат, ось симметрии совпадает с осью аппликат, а ветви параболы направлены в ту же сторону, что и вектор (boldsymbol{e}_{3}).
Теперь мы можем построить гиперболический параболоид следующим образом: зададим две параболы и будем перемещать одну из них так, чтобы ее вершина скользила по другой, оси парабол были параллельны, параболы лежали во взаимно перпендикулярных плоскостях и ветви их были направлены в противоположные стороны.
При таком перемещении подвижная парабола описывает гиперболический параболоид (рис. 10.8).
Сечения гиперболического параболоида плоскостями с уравнениями (z=alpha) при всевозможных (alpha) — гиперболы. Эти сечения нарисованы на рис. 10.9.
Гиперболический параболоид, как и однополостный гиперболоид, имеет два семейства прямолинейных образующих (рис. 10.10). Уравнения одного семейства —
$$
lambdaleft(frac{x}{a}-frac{y}{b}right)=mu, muleft(frac{x}{a}+frac{y}{b}right)=2lambda z,nonumber
$$
а другого —
$$
lambda’left(frac{x}{a}+frac{y}{b}right)=mu’, mu’left(frac{x}{a}-frac{y}{b}right)=2lambda’ z,nonumber
$$
Выводятся эти уравнения так же, как и уравнения прямолинейных образующих однополостного гиперболоида.