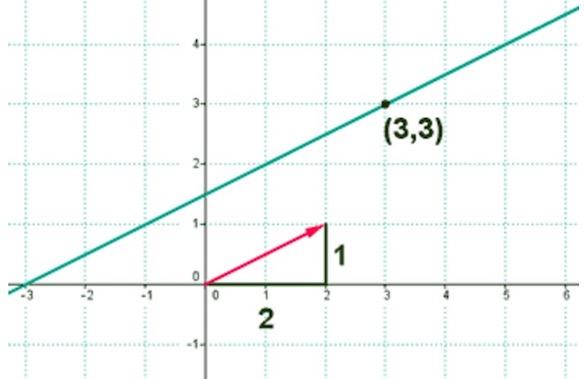
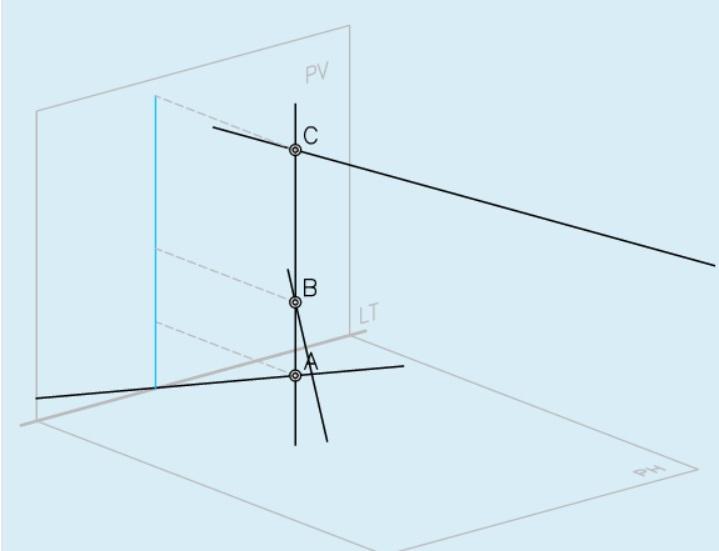
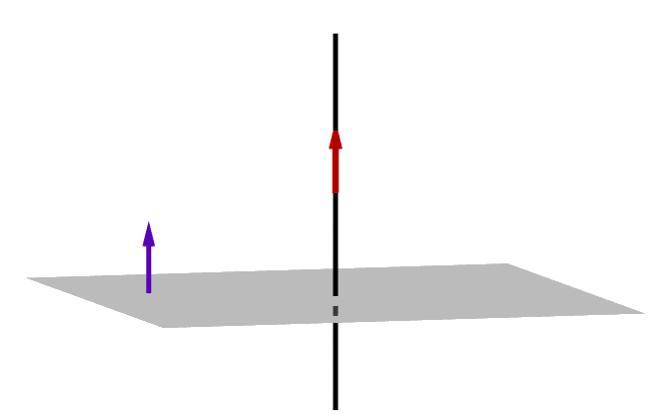
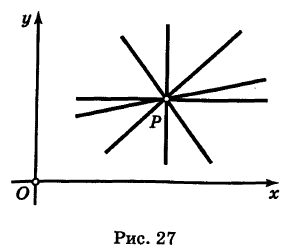
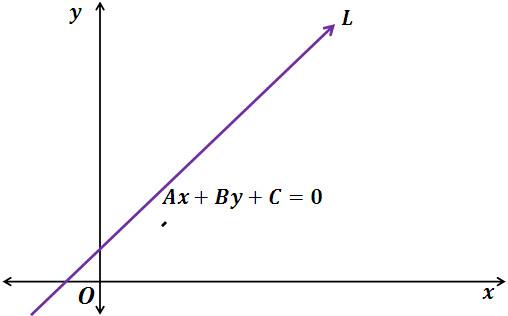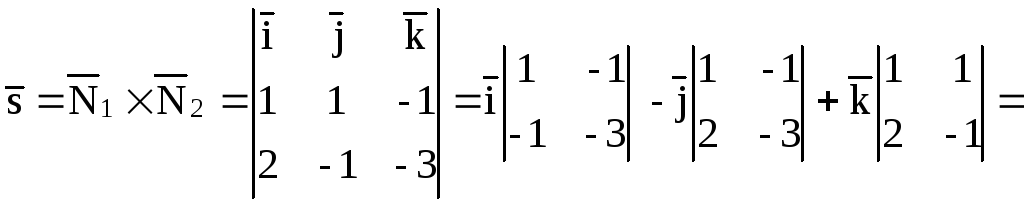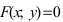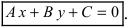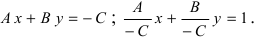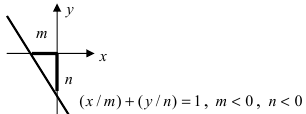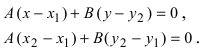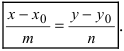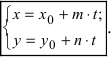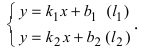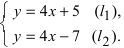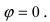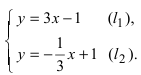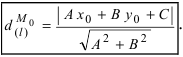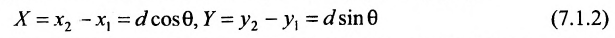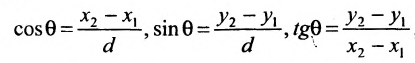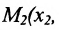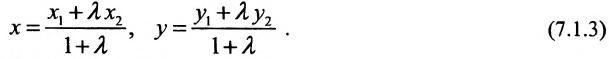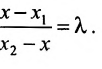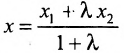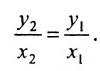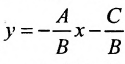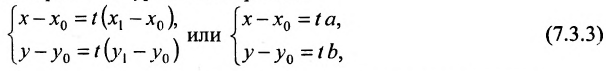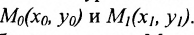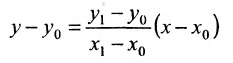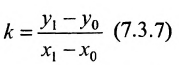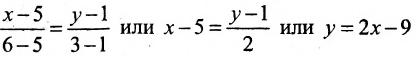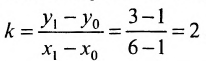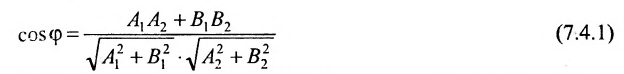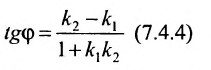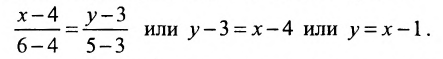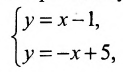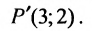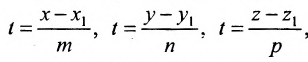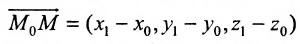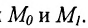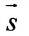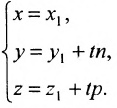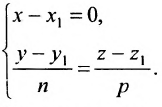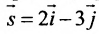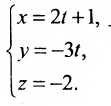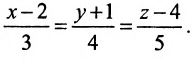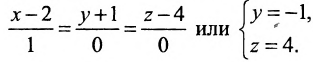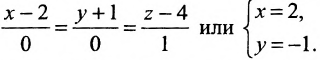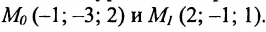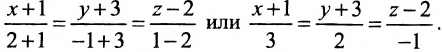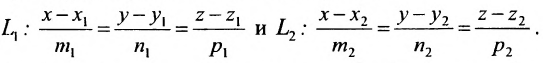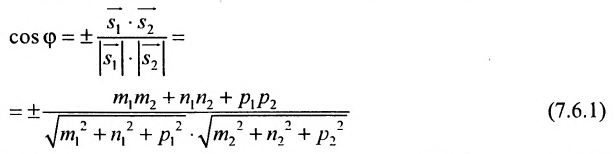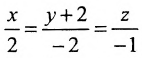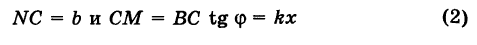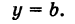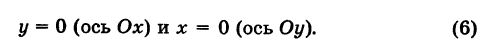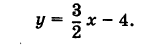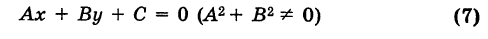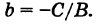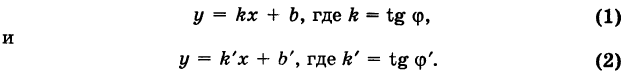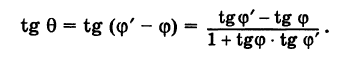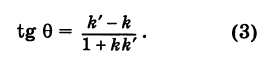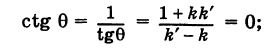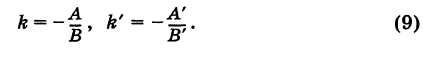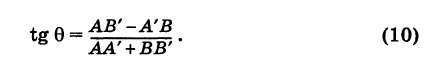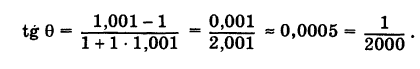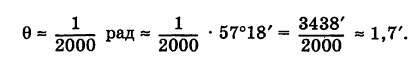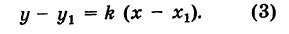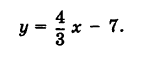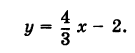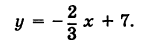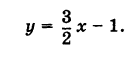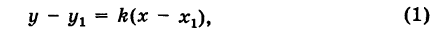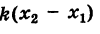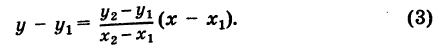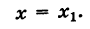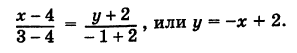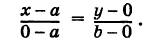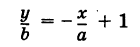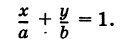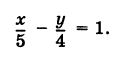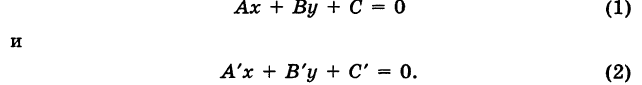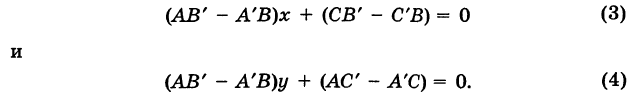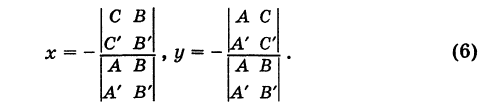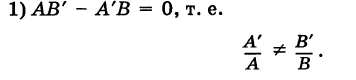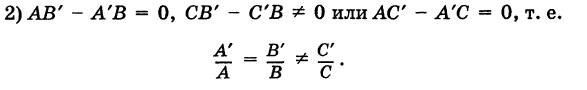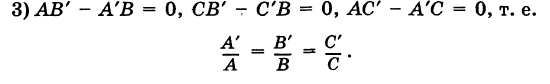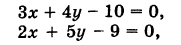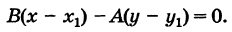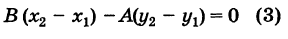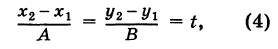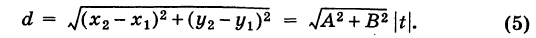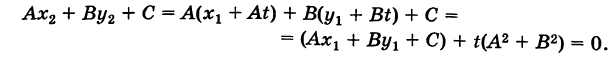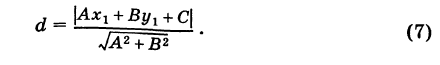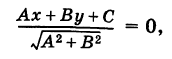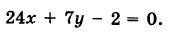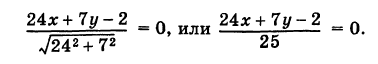Направляющий вектор прямой, координаты направляющего вектора прямой
С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.
В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.
Что такое направляющий вектор прямой
Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.
Сформулируем, что такое направляющий вектор.
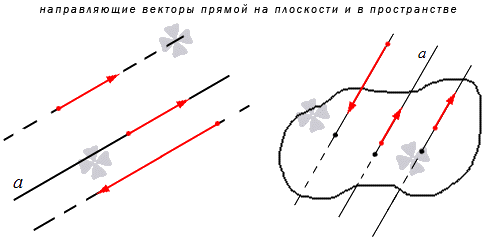
Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.
Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a → является направляющий вектором прямой a , то другой направляющий вектор мы можем обозначить как t · a → при любом значении t , соответствующем действительному числу.
Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a 1 являются параллельными, то вектор a → будет направляющим и для a , и для a 1 .
Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a , то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.
Приведем пример направляющего вектора: в прямоугольной системе координат для осей O x , O y и O z направляющими будут координатные векторы i → , j → и k → .
Как вычислить координаты направляющего вектора по уравнениям прямой
Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой O x y , а потом с системой O x y z , расположенной в трехмерном пространстве.
1. Прямую линию в O x y можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.
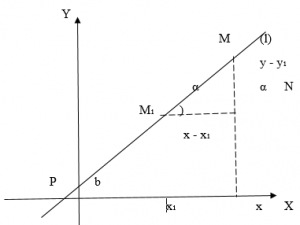
Допустим, у нас есть канонический случай уравнения, которое имеет вид x — x 1 a x = y — y 1 a y . С его помощью на плоскости задана прямая с направляющим вектором a → = ( a x , a y ) .
Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.
Приведем пример задачи.
В прямоугольной системе координат задана прямая, которую можно описать уравнением x — 1 4 = y + 1 2 — 3 . Вычислите координаты одного из направляющих векторов прямой.
Решение
Из уравнения мы можем сразу взять координаты направляющего вектора. Берем числа в знаменателях и записываем: 4 , — 3 . Это и будет нужный нам ответ.
Ответ: 4 , — 3 .
Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.
У нас есть прямая, которую можно описать с помощью системы параметрических уравнений x = — 1 y = 7 — 5 · λ , при этом λ ∈ R . Найдите координаты направляющих векторов.
Решение
Для начала перепишем данные параметрические уравнения в виде x = — 1 + 0 · λ y = 7 — 5 · λ . Посмотрим на коэффициенты. Они сообщат нам нужные координаты направляющего вектора – a → = ( 0 , 5 ) . Учитывая, что все направляющие векторы одной прямой будут коллинеарны, мы можем задать их в виде t · a → или 0 , — 5 · t , где t может быть любым действительным числом. О том, как проводить действия с векторами в координатах, мы писали в отдельной статье.
Ответ: 0 , — 5 · t , t ∈ R , t ≠ 0
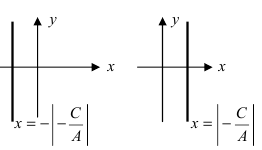
Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида A x + B y + C = 0 . Если A = 0 , то исходное уравнение можно переписать как B y + C = 0 . Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i → = 1 , 0 .
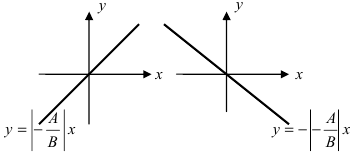
А если B = 0 , то уравнение прямой мы можем записать как A x + C = 0 . Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j → = 0 , 1 также будет направляющим. Рассмотрим конкретную задачу.
У нас есть прямая, заданная при помощи общего уравнения x — 2 = 0 . Найдите координаты любого направляющего вектора.
Решение
В прямоугольной системе координат исходное уравнение будет соответствовать прямой, параллельной оси ординат. Значит, мы можем взять координатный вектор j → = ( 0 , 1 ) . Он будет для нее направляющим.
Ответ: ( 0 , 1 )
А как быть в случае, если ни один коэффициент в A x + B y + C = 0 не будет равен 0? Тогда мы можем использовать несколько разных способов.
1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.
2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.
3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n → = A , B .
Самым простым является первый подход. Проиллюстрируем его на примере задачи.
Есть прямая на плоскости, заданная уравнением 3 x + 2 y — 10 = 0 . Запишите координаты любого направляющего вектора.
Решение
Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3 x, в правую с противоположным знаком. У нас получится:
3 x + 2 y — 10 = 0 ⇔ 3 x = — 2 y + 10
Получившееся равенство преобразовываем и получаем:
3 x = — 2 y + 10 ⇔ 3 x = — 2 ( y — 5 ) ⇔ x — 2 = y — 5 3
Отсюда мы уже можем вывести координаты нужного нам направляющего вектора: -2 , 3
К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках x a + y b = 1 и уравнение прямой с угловым коэффициентом y = k · x + b , так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.
Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.
Вектор a → = ( a x , a y , a z ) является направляющим для прямой, выраженной с помощью:
1) канонического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z
2) параметрического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z
Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.
Рассмотрим конкретную задачу.
Прямая в пространстве задана уравнением вида x — 1 4 = y + 1 2 0 = z — 3 . Укажите, какие координаты будет иметь направляющий вектор данной прямой.
Решение
В каноническом уравнении необходимые числа видны сразу в знаменателях. Получается, что ответом будет вектор с координатами 4 , 0 , — 3 . Координаты всех направляющих векторов данной прямой можно записать в виде 4 · t , 0 , — 3 · t при условии, что t является действительным числом.
Ответ: 4 · t , 0 , — 3 · t , t ∈ R , t ≠ 0
Вычислите координаты любого направляющего вектора для прямой, которая задана в пространстве с помощью параметрического уравнения x = 2 y = 1 + 2 · λ z = — 4 — λ .
Решение
Перепишем данные уравнения в виде x = 2 + 0 · λ y = 1 + 2 · λ z = — 4 — 1 · λ .
Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.
Разберем еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 ?
Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.
Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.
Направляющий вектор прямой, образованной пересечением двух плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , будет перпендикулярен нормальным векторам n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) . То есть в качестве направляющего вектора мы может взять произведение векторов n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
n 1 → × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2 — это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.
Решим задачу, в которой применяется этот подход.
Запишите координаты направляющего вектора прямой, выраженной с помощью уравнения x + 2 y + 3 z — 1 = 0 2 x + 4 y — 4 z + 5 = 0 .
Решение
Возьмем произведение двух нормальных векторов плоскостей x + 2 y + 3 z — 1 = 0 и 2 x + 4 y — 4 z + 5 = 0 . У них следующие координаты: 1 , 2 , 3 и 2 , 4 , — 4 .
У нас получится:
n 1 → × n 2 → = i → j → k → 1 2 3 2 4 — 4 = i → · 2 · ( — 4 ) + j → · 3 · 2 + k → · 1 · 4 — — k → · 2 · 2 — i → · 3 · 4 — j → · 1 · ( — 4 ) = — 20 · i → + 10 · j → + 0 · k →
Выходит, что вектор n 1 → × n 2 → = — 20 · i → + 10 · j → + 0 · k → ⇔ n 1 → × n 2 → = — 20 , 10 , 0 – это и есть нужный нам направляющий вектор прямой.
Ответ: — 20 , 10 , 0
В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.
Направляющий вектор прямой: определение и примеры
Важным геометрическим объектом, который изучают в плоском пространстве, является прямая. В трехмерном же пространстве, помимо прямой, появляется еще плоскость. Оба объекта удобно задавать с помощью направляющих векторов. Что это такое, как применяют эти вектора для определения уравнений прямой и плоскости? Эти и другие вопросы освещаются в статье.
Прямая и способы ее задавания
Каждый школьник хорошо представляет, о каком геометрическом объекте идет речь. С точки зрения математики, прямая представляет собой набор точек, которые в случае их попарного произвольного соединения между собой приводят к получению совокупности параллельных векторов. Это определение прямой используют для написания уравнения для нее как в двумерном, так и в трехмерном пространстве.

Для описания рассматриваемого одномерного объекта пользуются разными видами уравнений, которые перечислены в списке ниже:
- общего вида;
- параметрическое;
- векторное;
- каноническое или симметричное;
- в отрезках.
Каждый из названных видов имеет некоторые преимущества по отношению к другим. Например, уравнением в отрезках удобно пользоваться при изучении поведения прямой относительно осей координат, уравнение общего вида удобно при нахождении направления, перпендикулярного заданной прямой, а также при вычислении угла ее пересечения с осью x (для плоского случая).

Поскольку тема данной статьи связана с направляющим вектором прямой, то далее будем рассматривать только уравнение, где этот вектор является принципиальным и содержится явно, то есть векторное выражение.
Задание прямой через вектор
Предположим, что у нас имеется некоторый вектор v¯ с известными координатами (a; b; c). Поскольку координат три, то вектор задан в пространстве. Как изобразить его в прямоугольной системе координат? Делается это очень просто: на каждой из трех осей откладывается отрезок, длина которого равна соответствующей координате вектора. Точка пересечения трех перпендикуляров, восстановленных к плоскостям xy, yz и xz, будет концом вектора. Началом же его является точка (0; 0; 0).
Тем не менее приведенное положение вектора не является единственным. Аналогичным образом можно нарисовать v¯, располагая его начало в произвольной точке пространства. Эти рассуждения говорят о том, что задать конкретную прямую с помощью вектора нельзя. Он задает семейство из бесконечного числа параллельных прямых.
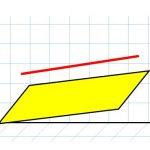
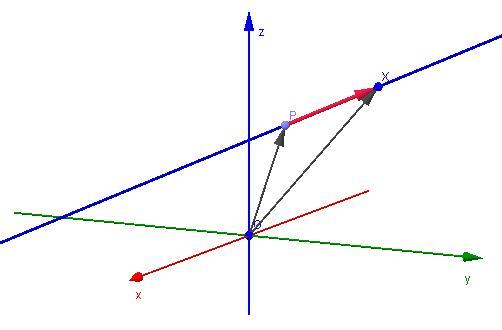
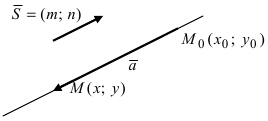
Теперь зафиксируем некоторую точку P(x0; y0; z0) пространства. И зададим условие: через P должна проходить прямая. В этом случае вектор v¯ тоже должен содержать эту точку. Последний факт означает, что можно задать одну единственную прямую, используя P и v¯. Она запишется в виде следующего уравнения:
Здесь Q — любая точка, принадлежащая прямой. Эту точку можно получить, подобрав соответствующий параметр λ. Записанное уравнение называется векторным, а v¯ получил название направляющего вектора прямой. Располагая его так, чтобы он проходил через P, и изменяя его длину с помощью параметра λ, мы получаем каждую точку Q прямой.
В координатной форме уравнение запишется так:
(x; y; z) = (x0; y0; z0) + λ × (a; b; c)
И в явном (параметрическом) виде можно записать:
Если в приведенных выражениях исключить третью координату, то мы получим векторные уравнения прямой на плоскости.
Для каких задач полезно знать направляющий вектор ?
Как правило, это задачи на определение параллельности и перпендикулярности прямых. Также определяющий направление прямой вектор используется при вычислении дистанции между прямыми и точкой и прямой, для описания поведения прямой относительно плоскости.
Две прямые будут параллельными, если таковыми являются их направляющие вектора. Соответственно, перпендикулярность прямых доказывается с помощью перпендикулярности их векторов. В этих типах задач достаточно рассчитать скалярное произведение рассматриваемых векторов, чтобы получить ответ.
В случае задач на вычисление расстояний между прямыми и точками направляющий вектор входит явно в соответствующую формулу. Запишем ее:
Здесь P1P2¯ — построенный на точках P1 и P2 направленный отрезок. Точка P2 является произвольной, лежащей на прямой с вектором v¯, точка же P1 является той, до которой следует определить расстояние. Она может быть как самостоятельной, так и принадлежать другой прямой или плоскости.
Отметим, что рассчитывать расстояние между прямыми имеет смысл только тогда, когда они являются параллельными или скрещивающимися. Если же они пересекаются, то d равно нулю.
Приведенная формула для d справедлива и для расчета дистанции между плоскостью и параллельной ей прямой, только в этом случае P1 должна принадлежать плоскости.
Решим несколько задач, чтобы нагляднее показать, как пользоваться рассматриваемым вектором.
Задача на составление векторного уравнения
Известно, что прямая описывается следующим равенством:
Следует написать соответствующее выражение в векторной форме.
Это типичное уравнение прямой, известное каждому школьнику, записано в общем виде. Покажем, как его переписать в векторной форме.
Выражение можно представить в виде:
Видно, что если его раскрыть, то получится исходное равенство. Теперь разделим его правую часть на два вектора так, чтобы только один из них содержал иксы, имеем:
(x; y) = (x; 3 × x) + (0; -4)
Остается вынести x за скобки, обозначить его греческим символом и поменять вектора правой части местами:
(x; y) = (0; -4) + λ × (1; 3)
Мы получили векторную форму записи исходного выражения. Координаты направляющего вектора прямой равны (1; 3).
Задача на определение взаимного расположения прямых
В пространстве заданы две прямые:
(x; y; z) = (1; 0; -2) + λ × (-1; 3; 1);
(x; y; z) = (3; 2; 2) + γ × (1; 2; 0)
Они являются параллельными, скрещивающимися или пересекающимися?
Ненулевые вектора (-1; 3; 1) и (1; 2; 0) будут направляющими для этих прямых. Выразим в параметрической форме эти уравнения и подставим координаты первого во второе. Получаем:
x = 3 + γ = 1 — λ => γ = -2 — λ;
y = 2 + 2 × γ = 3 × λ => γ = 3 / 2 × λ — 1;
z = 2 = -2 + λ => λ = 4
Подставляем найденный параметр λ в два уравнения выше, получаем:
γ = 3 / 2 × λ — 1 = 5
Параметр γ не может одновременно принимать два разных значения. Это означает, что прямые не имеют ни одной общей точки, то есть являются скрещивающимися. Параллельными они не являются, так как ненулевые векторы не параллельны друг другу (для их параллельности должно существовать число, которое бы путем умножения на один вектор приводило к координатам второго).
Математическое описание плоскости
Для задания плоскости в пространстве приведем уравнение общего вида:
A × x + B × y + C × z + D = 0
Здесь латинские большие буквы представляют собой конкретные числа. Первые три из них определяют координаты нормального вектора плоскости. Если его обозначить n¯, тогда:
Этот вектор является перпендикулярным плоскости, поэтому его называют направляющим. Его знание, а также известные координаты какой-либо точки, принадлежащей плоскости, однозначно задают последнюю.
Если точка P(x1; y1; z1) плоскости принадлежит, тогда свободный член D рассчитывается следующим образом:
D = -1 × (A × x1 + B × y1 + C × z1)
Решим пару задач с использованием общего уравнения для плоскости.
Задача на нахождение нормального вектора плоскости
Плоскость задана в следующем виде:
(y — 3) / 2 + (x + 1) / 3 — z / 4 = 1
Как найти направляющий вектор для нее?
Из приведенной выше теории следует, что координаты нормального вектора n¯ являются коэффициентами, стоящими перед переменными. В связи с этим для нахождения n¯ следует записать уравнение в общем виде. Имеем:
1 / 3 × x + 1 / 2 × y — 1 / 4 × z — 13 / 6 = 0
Тогда нормальный вектор плоскости равен:
Задача на составление уравнения плоскости
Даны координаты трех точек:
Как будет выглядеть уравнение плоскости, содержащей все эти точки.
Через три точки, которые одной прямой не принадлежат, можно провести только одну плоскость. Чтобы найти ее уравнение, сначала вычислим направляющий вектор плоскости n¯. Для этого поступим следующим образом: найдем произвольные два вектора, принадлежащие плоскости, и вычислим их векторное произведение. Оно даст вектор, который этой плоскости будет перпендикулярен, то есть n¯. Имеем:
M1M2¯ = (1; -1; 5); M1M3¯ = (-1; -2; -2);
n¯ = [M1M2¯ × M1M3¯] = (12; -3; -3)
Возьмем точку M1 для составления выражения плоскости. Получаем:
D = -1 × (12 × 1 + (-3) × 0 + (-3) × 0) = -12;
12 × x — 3 × y — 3 × z — 12 = 0 =>
4 × x — y — z — 4 = 0
Мы получили выражение общего типа для плоскости в пространстве, определив сначала направляющий вектор для нее.
Свойство векторного произведения следует запомнить при решении задач с плоскостями, поскольку оно позволяет простым способом определять координаты нормального вектора.
Уравнения прямой в пространстве векторное, общее, канонические, параметрические (Таблица)
Способ задания прямой в пространстве
Вид уравнения прямой
Векторное уравнение прямой, проходящей через точку М параллельно заданному вектору s .
s — направляющий вектор прямой
где t — скалярный множитель (параметр)
Канонические уравнения прямой, проходящей через точку M0(x0,y0,z0) и параллельно вектору s =
Параметрические уравнения прямой, проходящей через точку (x0,y0,z0) параллельно вектору s =
Прямая как линия пересечения двух непараллельных плоскостей (общие уравнения прямой)
http://1ku.ru/obrazovanie/41097-napravljajushhij-vektor-prjamoj-opredelenie-i-primery/
http://infotables.ru/matematika/57-analiticheskaya-geometriya-v-prostranstve/573-uravneniya-pryamoj-v-prostranstve
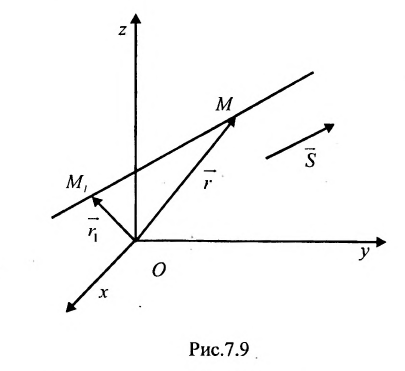
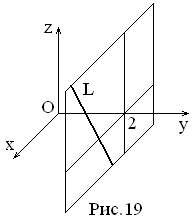
3.1. Канонические
уравнения прямой.
Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку

вектор, параллельный данной прямой.
Векторназываетсянаправляющим
вектором прямой.
Возьмем на прямой точку и рассмотрим вектор
Векторы
коллинеарны, следовательно, их
соответствующие координаты пропорциональны:
(3.3.1)
Эти уравнения
называются каноническими
уравнениями прямой.
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору
Решение:
Вектор
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:
Это канонические
уравнения прямой.
Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.
3.2.
Параметрические
уравнения прямой.
Пусть прямая
задана каноническими уравнениями
Обозначим тогда
Величина t
называется параметром и может принимать
любые значения:
.
Выразим x,
y
и z
через t
:
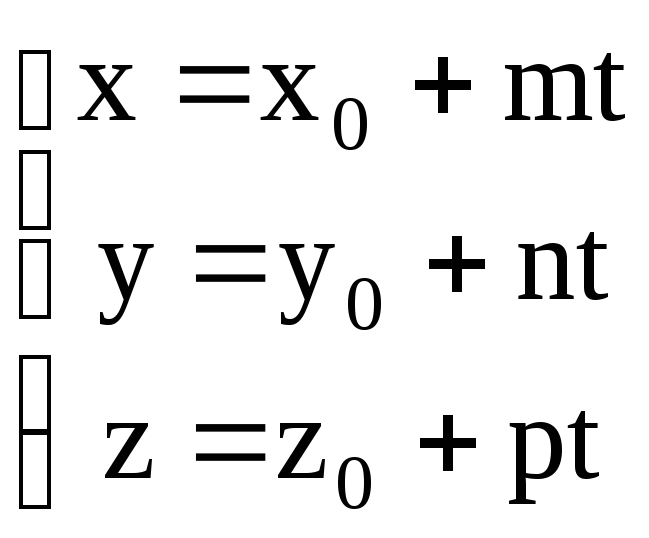
Полученные уравнения
называются параметрическими
уравнениями прямой.
Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору
Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:
Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):
Итак,

прямой.
Ответ:
Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
гдеA
(2, 1, –1), B
(–1, 3, 2).
Решение:
Вектор является направляющим
вектором искомой прямой.
Найдем вектор .
= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:

параметрические уравнения прямой.
3.3. Уравнения
прямой, проходящей через две заданные
точки.
Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
Вектор
можно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
наход
по формулам (3.1.1):).
(3.3.1)
Пример 1.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
Применяем
формулу (3.3.1)
Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим

уравнения прямой.
Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
По формулам
(3.3.1) получим:
Это канонические
уравнения.
Переходим к
параметрическим уравнениям:

уравнения.
Полученная прямая
параллельна оси oz
(см. рис.21).
3.4. Прямая как
линия пересечения двух плоскостей.
Пусть в
пространстве даны две плоскости
и
Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:
Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
лежащую на прямой, и направляющий вектор
Координаты точки
получим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
можно взять векторное произведение
векторовто есть
Пример 1.
Составить
канонические уравнения прямой
Решение: Пусть
z
= 0. Решим систему
Сложив эти уравнения,
получим: 3x
+ 6 = 0
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
y
= 1.
Итак, точка
лежит на искомой прямой.
Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
и найдем их векторное произведение:
Уравнения прямой
находим по формулам (3.1.1):
Ответ: .
Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).
Пример 2.
Составить канонические и параметрические
уравнения прямой
Решение:
Пусть y
= 0. Тогда система примет вид:
Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
z
= –1. Итак, нашли точку
Для нахождения
второй точки положим x
= 0. Будем иметь:
То есть
Далее применяем
формулы (3.3.1):
Получили канонические
уравнения прямой.
Составим
параметрические уравнения прямой:
Ответ:
; 
3.5. Взаимное
расположение двух прямых в пространстве.
Пусть прямые
заданы уравнениями:
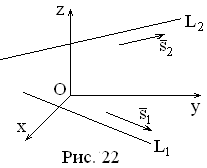
;
:
.
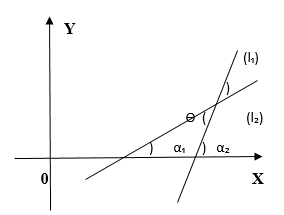
Под углом между
этими прямыми понимают угол между их
направляющими векторами
(см. рис.22). Этот угол
находим по формуле из векторной алгебры:
или
(3.5.1)
Если прямые перпендикулярны
(),то
Следовательно,
(3.5.2)
Это условие
перпендикулярности двух прямых в
пространстве.
Если прямые
параллельны (),то их направляющие
векторы коллинеарны (),
то есть
(3.5.3)
Это условие
параллельности двух прямых в пространстве.
Пример 1. Найти
угол между прямыми:
а).
и
б). и
Решение:
а). Запишем направляющий вектор прямой
Найдем направляющий вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему
Затем найдем их векторное произведение:
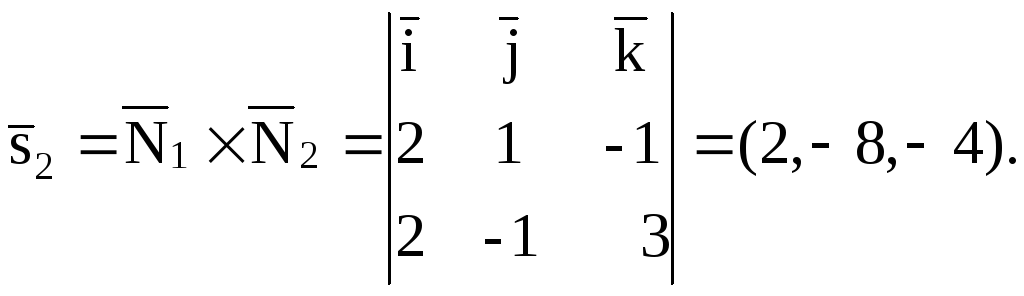
пункта 3.4).
По формуле (3.5.1)
получим:
Следовательно,
б). Запишем
направляющие векторы данных прямых:
Векторы
коллинеарны, так как их соответствующие
координаты пропорциональны:
Значит прямые
параллельны (
),
то есть
Ответ: а).
б).
Пример 2. Доказать
перпендикулярность прямых:
и
Решение:
Запишем направляющий вектор первой
прямой
Найдем направляющий
вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему:
Вычислим их векторное произведение:

Применим условие
перпендикулярности прямых (3.5.2):
Условие выполнено;
следовательно, прямые перпендикулярны
().
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #
План урока:
Разложение векторов
Координаты векторов
Сложение и вычитание векторов
Признак коллинеарности векторов
Разложение векторов
Заметим, что если два вектора a и b коллинеарны, то обязательно найдется такое число k, для которого будет справедливо равенство:
Длина а составляет 6 клеток, а длина b – 9 клеток, при этом они сонаправлены. Получается, что b длиннее a в 9/6 = 1,5 раза, а потому можно записать:
Мы смогли выразить b через а. Иначе можно сказать, что мы разложили вектор b по вектору a. Можно и наоборот, выразить b через a:
Теперь посмотрим на вектора с и d. Их длины составляют 4 и 8 клеток, то есть отличаются в 2 раза, при этом они противоположно направлены. Поэтому эти вектора можно выразить так:
Обратите внимание, что выразить, например, а через с не удастся. Действительно, предположим, что есть такое число k, что
Тогда, по определению операции умножения вектора на число, вектора а и c должны быть коллинеарными, но они таковыми не являются.
Вектор можно раскладывать не на один, а на два вектора, которые ему не коллинеарны. Покажем это на примере:
Здесь вектора р, а и b не коллинеарны, при этом р выражен через а и b:
В данном случае говорят, что р разложен на вектора а и b, а числа 2 и 4 именуют коэффициентами разложения.
Верно следующее утверждение:
Продемонстрируем, как можно осуществить такое разложение. Пусть заданы вектора с, а и b, и требуется разложить c на а и b:
На первом шаге просто отложим все три вектора от одной точки. Далее построим прямые, проходящие через вектора а и b:
Далее через конец вектора с проведем прямые, параллельные построенным на предыдущем шаге прямым. В результате у нас получится некоторый параллелограмм АВСD:
Заметим, что вектор с оказался диагональю в этом параллелограмме. Тогда, согласно правилу параллелограмма, можно записать:
Ясно, что вектора АВ и b коллинеарны, так как лежат на одной и той же прямой. Тогда найдется такое число k, для которого будет верно отношение:
Конкретно в данном случае видно по рисунку, что АВ вдвое длиннее вектора b, поэтому
Аналогично коллинеарными являются вектора а и АD, поэтому существует число m, при котором справедливо равенство:
Понятно, что числа k и m определяются единственным образом. В общем случае они могут быть не только целыми, но и дробными (в том числе иррациональными) и даже отрицательными числами. Проще говоря, они могут быть любыми действительными числами.
Задание. Найдите коэффициенты разложения вектора d на вектора e и f:
Решение. Отложим все три вектора от одной точки. Далее проведем прямые, на которых лежат вектора e и f:
Теперь через конец d проводим ещё две прямые, параллельные двум уже построенным прямым, и в результате получаем параллелограмм:
Вектор d можно представить в виде суммы:
Особняком стоит случай, когда раскладываемый вектор коллинеарен одному из тех векторов, на которые он раскладывается. В этом случае один из коэффициентов разложения оказывается равным нулю. Например, пусть с надо разложить на а и b:
Строить параллелограмм в данном случае не нужно. Так как а и с коллинеарны, то найдется некоторое число k, при котором будет выполняться равенство:
Координаты векторов
Из курса алгебры нам известна прямоугольная система координат. В ней есть оси Ох и Оу, а каждая отмеченная на плоскости точка имеет свои координаты:
Естественно, что на координатной плоскости можно отметить и вектора. Построим два вектора, которые начинаются в начале координат, имеют длину, равную единице, и направление которых совпадает с направлениями осей координат. Тот вектор, который лежит на оси Ох, обозначают буквой i, а тот, который лежит на оси Оу, обозначают как j.
Эти вектора называют единичными векторами, или ортами (ещё используется термин координатный вектор). Они не коллинеарны друг другу, а это означает, что любой вектор на плоскости можно разложить на единичные вектора. Коэффициенты такого разложения как раз и являются координатами вектора.
Посмотрим на примере, как находить координаты вектора. Пусть задан вектор а:
Нам надо разложить а по векторам i и j. Для этого их следует отложить от одной точки. Удобно перенести вектор а к началу координат:
Теперь надо через конец а провести прямые, параллельные векторам iи j. В результате получится прямоугольник АВСD:
Можно записать равенство:
Значит, и координаты данного вектора – это числа 3 и 2. Записывается это так:
Обратите внимание, что порядок чисел в скобках принципиально важен. Первое число – это коэффициент разложения, стоящий перед вектором i. Эту координату можно называть координатой х (по аналогии с координатами точек). Второе число – это коэффициент при векторе j, оно является координатой у. Также заметим очевидный факт, что координаты равных векторов одинаковы.
В приведенном выше примере легко заметить, что после того, как мы перенесли вектор в начало координат, координаты его конца (он обозначен точкой С) совпали с координатами самого вектора. Действительно, точка С имеет координаты (3; 2).
Это правильно несколько упрощает определение координат вектора. Достаточно просто отложить вектор от точки начала координат, после чего посмотреть на координаты его конечной точки. Отметим, что вектор, чье начало совпадает с началом координат, имеет особое название – радиус-вектор.
Задание. Определите координаты векторов a, b, c и d, отмеченных на рисунке:
Решение. Во всех случаях будем просто переносить вектора к началу координат, получая радиус вектора. Далее будем просто смотреть, каковы координаты конца радиус-вектора. Начнем с а:
После переноса а его конец оказался в точке А(4; 3), поэтому и координаты всего вектора можно записать так:
После переноса вершина радиус-вектора попала в точку B (1; – 3), поэтому вектор имеет координаты {1; – 3}.
Выполним построение и для с:
Конец вектора попал в точку С (3,5; 0), а потому и координаты вектора составляют {3,5; 0}.
Осталось рассмотреть d:
Здесь координаты вектора будут равны {– 2,5; – 2,5}, так как такие же координаты имеет точка D.
Ответ: а{4;3}; b{1; – 3}; с{3,5; 0}; d{– 2,5; – 2,5}.
Рассмотрим решение обратной задачи, в которой необходимо построить вектор по заранее заданным координатам.
Задание. Даны координаты вектора:
Постройте по три вектора, имеющие заданные координаты.
Решение. Проще всего построить радиус-вектор, вершина которого будет иметь те же координаты, что и требуемый вектор:
Чтобы построить ещё два вектора с такими же координатами, надо просто отложить уже построенный вектор от любых других точек:
Аналогично поступаем и во второй задаче – сначала откладываем радиус-вектор с заданными координатами, а потом добавляем ещё два равных ему вектора, отложенных от других точек:
Отдельно отметим нулевой вектор. Очевидно, что все его координаты равны нулю, так как для него можно записать такое разложение на орты:
Также можно сказать, что если отложить нулевой вектор от начала координат, то его конец также будет находиться в начале координат (так как у нулевого вектора начало и конец совпадают), то есть в точке с координатами (0; 0).
Сложение и вычитание векторов
Пусть у нас есть векторы a{x1; у1} и b{x2; у2}. Можно ли, зная только их координаты, определить их сумму и разность? Оказывается, можно. Действительно, по определению координат векторов (напомним, они являются коэффициентами разложения вектора на орты) можно записать:
Эта запись означает, что с имеет координаты {х1 + х2; у1 + у2}. В результате мы можем сформулировать правило сложения векторов:
Проиллюстрируем правило на примере. Пусть надо сложить вектора а {2; 3} и b {4; 5}. Понятно, что в результате получится новый вектор, который мы обозначим как с {х; у}. Чтобы найти его первую координату, надо сложить первые координаты векторов a и b:
x = 2 + 4 = 6
Для нахождения второй координаты складываем соответственно вторые координаты векторов:
y = 3 + 5 = 8
В итоге получился вектор с {6; 8}.
Задание. Сложите вектора, имеющие координаты:
Решение. Сначала просто складываем первые числа в скобках (и получаем координату х), а потом – вторые (и получаем координату у):
Теперь попытаемся понять, как вычислять разность двух векторов. Пусть есть вектора с заранее заданными координатами a{x1; у1} и b{x2; у2}. Снова запишем их разложение на единичные вектора:
Теперь мы можем сформулировать правило вычитания векторов:
Например, пусть надо вычесть из вектора а{5; 3} вектор b{2;1}. Искомая разность будет представлять собой вектор, чья координата х будет равна разности первых координат векторов а и b:
x = 5 — 2 = 3
Аналогично вычисляем и координату у:
y = 3 — 1 = 2
В итоге получили вектор с координатами {3; 2}.
Задание. Вычтите из вектора а вектор b, если известны их координаты:
Решение. Во всех случаях мы сначала из первой координаты вектора а вычитаем первую координату b, в результате чего получаем координату х искомого вектора. Далее повторяем процесс со второй координатой (то есть с у):
Далее рассмотрим такую операцию, как умножение вектора на число. Снова запишем, что вектор а с координатами х1и у1 можно разложить на орты следующим образом:
Это означает, что при умножении вектора на число надо просто умножить на это число каждую его координату.
Например, есть вектор а{3; 7}, который надо умножить на 5. Умножим на 5 по отдельности каждую координату:
x = 5*3 = 15
y = 5*7 = 35
В результате получился вектор {15; 35}.
Задание. Умножьте вектор а на число k, если известно, что:
Решение. Надо всего лишь умножить каждую координату а на число k, и таким образом получить новые координаты:
Признак коллинеарности векторов
Напомним, что если два вектора (обозначим их как a и b) коллинеарны, то обязательно существует такое число k, что
Из равенства (1) и рассмотренного нами правила умножения вектора на число вытекают два соотношения между этими координатами:
x1 = k * x2
y1 = k * y2
Если числа х2 и у2 не равны нулю, то можно выразить из каждого уравнения число k, после чего выражения можно будет приравнять:
Получили соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратную сторону – если координаты векторов удовлетворяют выведенному отношению, то можно смело утверждать, что вектора – коллинеарны.
Примечание. Формулировка «тогда и только тогда» означает, что правило действует в обе стороны – из пропорциональности координат следует коллинеарность векторов, а из коллинеарности векторов следует пропорциональность координат.
Покажем, как пользоваться этим признаком коллинеарности векторов. Пусть вектор а имеет координаты {8; 5}, а у вектора b они равны {24; 15}. Нам надо определить, коллинеарны ли они. Для этого поделим друг на друга их координаты х:
24:8 = 3
Получили число 3. Далее поделим и координаты у:
15:5 = 3
Снова получили тройку. То, что в обоих случаях получилось одно и тоже число, указывает на то, что вектора коллинеарны. Более того, можно даже записать, что вектор b втрое больше a:
В данном примере мы делили координаты второго вектора b на координаты первого вектора a. Но можно было поступить и наоборот, делить координаты а на координаты b:
Естественно, снова получилось одинаковое число.
Особняком стоит случай, когда одна из координат вектора равна нулю. Например, пусть вектор имеет координаты {0; у1}, причем у1≠ 0. Любой коллинеарный ему вектор можно получить, умножив вектор на какое-то число k. В этом случае его координаты {x2; у2} составят:
Получается, что и у коллинеарного вектора координата х обязательно будет равняться нулю. В свою очередь координаты у2 и у1 могут быть любыми, ведь мы всегда можем найти такое число k, для которого будет выполняться условие
y2 = ky1
Например, есть вектор {0; 5}. Можно сказать, что ему будет коллинеарен любой вектор, у которого первая координата также равна нулю, в частности,
Но любой вектор, у которого координата х НЕ равна нулю, НЕ будет коллинеарен вектору {0; 5}. В частности, ему не будут коллинеарны вектора:
Аналогичная логика действует и тогда, когда нулю равна не координата х, а координата у.
Если же у вектора обе координаты равны нулю, то он является нулевым вектором, то есть точкой. Напомним, что такой вектор считается коллинеарным любому другому вектору.
Задание. Определите, являются ли коллинеарными два вектора, если их координаты равны:
Решение. В первых пяти случаях все координаты – ненулевые, а поэтому надо просто проверить их пропорциональность. Для этого надо делить координаты друг на друга:
Числа различны, поэтому вектора НЕ коллинеарны.
В следующих примерах как минимум одна из координат равна нулю, поэтому делить координаты уже не нужно.
е) {0; 5} и {0; 12}
У обоих векторов координаты х нулевые, этого достаточно, чтобы утверждать, что они коллинеарны.
ж) {0; 3} и {2; 6}
У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.
з) {9; 0} и {4; 0}
У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.
и) {0; 3} и {12; 0}
Здесь у первого вектора нулю равна координата х, а у второго она ненулевая, поэтому вектора не коллинеарны.
к) {0; 0} и {5; 8}
Здесь имеет место особый случай, ведь первый вектор – нулевой, то есть представляющий собой точку. Считается, что он коллинеарен любому вектору, поэтому в данном примере вектора коллинеарны.
Ответ: а) да; б) нет; в) да; г) да; д) нет; е) да; ж) нет; з) да; и) нет; к) да.
Пока что мы рассматривали задачи, в которых фигурируют только вектора. Однако в будущем мы научимся с помощью метода координат решать и другие задачи, в которых рассматриваются отрезки, треугольники, окружности и прочие геометрические фигуры.
Любая прямая на плоскости может быть задана уравнением первого порядка Ax + By + C = 0. Здесь A и B постоянные и не равны нулю одновременно. Такое уравнение первого порядка всегда называют общим уравнением прямой.
Уравнение прямой проходящей через точку и нормальный вектор
Рассмотрим уравнение прямой проходящей через точку и нормальный вектор. Пусть в системе координат задана точка
и ненулевой вектор
(рис. 1).
Рис. 1
Докажем, что линейное уравнение
+
(1)
это уравнение прямой , то есть координаты каждой точки
прямой
удовлетворяют уравнение (1), но координаты точки, что не лежит на
, уравнения (1) не удовлетворяют.
Для доказательства, обратим внимание, что скалярное произведение векторов и
=
в координатной форме совпадает с левой частью уравнения (1).
x
=
.
(2)
Дальше используем очевидное свойство прямой : векторы
и
перпендикулярны тогда, и только тогда, когда точка
лежит на
. А при условии перпендикулярности обоих векторов их скалярное произведение (2) превращается в
для всех точек
, что лежат на
, и только для них. Значит, (1) – уравнение прямой
.
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Общее уравнение прямой
Превратим уравнение (1)
+
+
–
=
.
Обозначив =
, получим
.
(3)
– общее уравнение прямой.
Таким образом, прямой линии отвечает линейное уравнение вида (3). Наоборот, за данным уравнением вида (3), где хотя бы один из коэффициентов
и
не равен нулю, можно построить прямую.
Действительно, пусть пара чисел удовлетворяют уравнение (3), то есть
.
Отнимая последнее от (3), получим соотношение , которое определяет прямую за вектором
и точкой
.
Исследование общего уравнения прямой
Полезно знать особенности размещения прямой в отдельных случаях, когда одно либо два из чисел
равны нулю.
1. Общее уравнение выглядит так:
. Ему удовлетворяет точка
, значит, прямая проходит через начало координат. Его можно записать:
= –
x
(см. рис. 2).
Рис. 2
Считаем, что:
–>
.
Если положить , тогда
, получается ещё одна точка
(см. рис. 2).
2. , тогда уравнение выглядит так
, где
= –
. Нормальный вектор
лежит на оси
, прямая
. Таким образом, прямая
перпендикулярна
в точке
, либо же параллельна оси
(см. рис. 3). В частности, если и
, тогда
и уравнение
– это уравнение оси ординат.
Рис. 3
3. Аналогично, при уравнение записывается
, где
. Вектор
принадлежит оси
. Прямая
в точке
(рис. 4)
.
Рис. 4
Если же , тогда
уравнение оси
.
Исследование можно сформулировать в такой форме: прямая параллельна той координатной оси, смена которой в общем уравнении прямой отсутствует.
Например:
1. прямая , слагаемое с
отсутствует, поэтому
.
2. прямая .
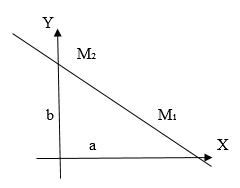
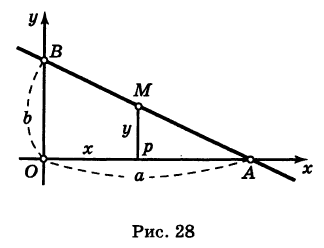
Уравнение прямой в отрезках
Построим прямую по общему уравнению при условии, что
– не равны нулю. Для этого достаточно найти две точки, что лежат на этой прямой. Такие точки иногда удобнее находить на координатных осях.
Положим , тогда
= –
.
При , тогда
= –
.
Обозначим – =
, –
=
. Найдены точки
и
. Отложим на осях
и
и через них проведём прямую (см. рис. 5).
Рис. 5
От общего можно перейти к уравнению, в которое будут входить числа и
:
И тогда получается:
Либо, согласно обозначению, получим уравнение,
+
=
(4)
Которое называется уравнением прямой в отрезках. Числа и
с точностью к знаку равняются отрезкам, которые отсекаются прямой на координатных осях.
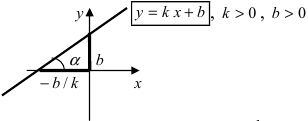
Уравнение прямой с угловым коэффициентом
Чтобы узнать, что такое уравнение прямой с угловым коэффициентом, рассмотрим уравнение (1):
+
= –
x
Обозначив – =
, получим
=
(5)
уравнение прямой, которая проходит через точку в заданном направлении. Геометрическое содержание коэффициента
понятно из рис. 6.
В
=
=
, где
– наименьший угол, на который нужно повернуть положительное направление оси
вокруг общей точки
до совмещения её с прямой
. Очевидно, что если угол
– острый, тогда
; если же
– тупой угол, тогда
.
Раскроем скобки в (5) и упростим его:
=
(6)
где . Соотношение (6) – уравнение прямой с угловым коэффициентом. При
,
– отрезок, который отсекает прямую на оси
(см. рис. 6).
Рис. 6
= –
x
+ –
=
где обозначено = –
,
= –
. Если же
, тогда из исследования общего уравнения уже известно, что такая прямая перпендикулярна оси
.
Каноническое уравнение прямой
Рассмотрим каноническое уравнение прямой при помощи примера.
Пусть в системе координат задана точка
и ненулевой вектор
(рис. 7).
Рис. 7
Необходимо составить уравнение прямой, что проходит через точку параллельно вектору
, который называется направляющим вектором. Произвольная точка
принадлежит этой прямой
тогда и только тогда, когда
. Так как вектор
– задан, а вектор
, тогда согласно условию параллельности, координаты этих векторов пропорциональны, то есть:
=
.
(7)
Соотношение (7) называется уравнением прямой, которая проходит через заданную точку в заданном направлении или каноническом уравнением прямой.
Обратим внимание, что к уравнению вида (7) можно перейти, например, от уравнения пучка прямых (4)
=
,
или от уравнения прямой через точку и нормальный вектор (1):
=
Выше предполагалось, что направляющий вектор – ненулевой, но может так случиться, что одна из его координат, например,
. Тогда выражение (7) формально запишется:
=
,
который, вообще не имеет смысла. Однако, принимают и получают уравнение прямой перпендикулярной оси
. Действительно, из уравнения видно, что прямая определена точкой
и направляющим вектором
, перпендикулярным оси
. Если в этом уравнении освободиться от знаменателя, тогда получим:
.
, либо
– уравнение прямой, перпендикулярной оси
. Аналогично было бы получено
для вектора
.
Параметрическое уравнение прямой
Чтобы понять, что такое параметрическое уравнение прямой, необходимо вернуться к уравнению (7) и приравнять каждую дробь (7) до параметра . Так как хотя бы один из знаменателей в (7) не равен нулю, а соответствующий числитель может приобретать произвольные значения, тогда область смены параметра
– вся числовая ось.
Получим:
=
,
=
или
(8)
Уравнение (8) называется параметрическим уравнением прямой.
Примеры задач на прямую линию
Конечно же, сложно что-либо решить исключительно по определениям, ведь нужно решить самостоятельно хотя бы несколько примеров или задач, которые помогут закрепить пройденный материал. Поэтому, давайте разберём основные задачи на прямую линию, так как похожие задачи часто попадаются на экзаменах и зачётах.
Каноническое и параметрическое уравнение
Задача
Точка движется равномерно со скоростью
по направлению вектора
от начальной точки
. Найти координаты точки
через
от начала движения.
Решение
Сначала нужно найти единичный вектор . Его координаты – это направляющие косинусы:
=
=
;
=
=
Тогда вектор скорости:
=
x
=
x
=
.
Каноническое уравнение прямой теперь запишется:
=
=
,
=
– параметрическое уравнение. После этого нужно воспользоваться параметрическим уравнением прямой при
.
Ответ
.
Угол между двумя прямыми
В равнобедренном прямоугольном треугольнике известна вершина прямого угла
и уравнение гипотенузы
. Составить уравнение катетов.
Решение:
Уравнение прямой, которая проходит через точку находим по формуле пучка прямых
, где угловой коэффициент
для прямой
и
=
для прямой
.
При условии ,
, поэтому
и
находим по формуле :
=
(9)
Учитывая рисунок, где видно, что между прямыми и
– два угла: один острый
, а второй – тупой
. Согласно формуле (9)
– это тот угол между прямыми
и
, на который нужно повернуть прямую
против часовой стрелки относительно их точки пересечения до совмещения её с прямой
.
Итак, формулу вспомнили, с углами разобрались и теперь можно вернуться к нашему примеру. Значит, учитывая формулу (9) находим сначала и уравнения катета
.
Так как поворот прямой на угол
против часовой стрелки относительно точки
приводит к совмещению с прямой
, тогда в формуле (9)
, а
. Из уравнения
:
, поэтому
=
Далее следует:
=
=
=
=
.
По формуле пучка уравнения прямой запишется:
=
.
Аналогично находим , а
,
=
Далее:
=
=
.
Уравнение прямой :
=
.
Ответ: ,
.
Содержание:
Общее уравнение прямой:
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами х и у по этой плоскости порождает линию.
Определение: Любое соотношение
Определение: Порядок линии определяется по высшему показателю степени переменных х и у или по сумме показателей степени в произведении этих величин.
Пример:
а) 2х + Зу-5 = 0 — линия первого порядка; точка A(l; 1) удовлетворяет этому соотношению, а точка, например, В(1; 0) — ему не удовлетворяет;
б)
в) 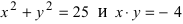
Рассмотрим другое определение линии:
Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению F(x; у)=0, называется линией, а само уравнение F(x; у) = 0 — уравнением линии.
Определение: Общим уравнением прямой называется уравнение первого порядка вида
Рассмотрим частные случаи этого уравнения:
а) С = 0; 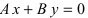
Рис. 20. Прямая, проходящая через начало координат.
б) 5 = 0; Ах+С=0 — прямая проходит параллельно оси ординат Оу (Рис. 21):
Рис. 21. Прямая, проходящая параллельно оси ординат Оу.
в) А = 0; Ву+С=0 — прямая проходит параллельно оси абсцисс Ох (Рис. 22):
Рис. 22. Прямая, проходящая параллельно оси абсцисс Ох.
Виды уравнений прямой
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 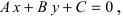
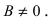
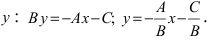
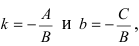
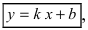
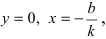
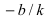
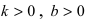
Рис. 23. Отрезки, отсекаемые прямой на координатных осях.
Из рисунка видно, что 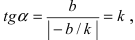
2. Уравнение прямой в отрезках.
Пусть в общем уравнении прямой параметр 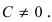
Обозначим через 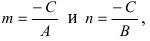
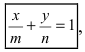
Рис. 24. Отрезки, отсекаемые прямой на координатных осях.
При у=о, х=m, т.е. прямая отсекает на оси абсцисс отрезок m. Следовательно, прямая проходит через 2 точки:
3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой Ах + Ву + С = 0, которая проходит через две известные точки 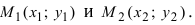
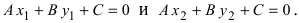
Пусть 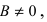
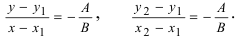
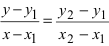
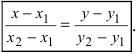
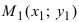
4. Уравнение прямой, проходящей через заданную точку 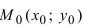
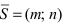
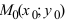
Определение: Вектор 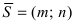
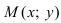
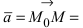
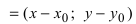
Рис. 25. Прямая, проходящая через данную точку параллельно направляющему вектору.
В силу того, что вектора 
Определение: Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру t, то получим параметрическое уравнение прямой
Основные задачи о прямой на плоскости
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 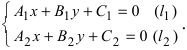
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
Требуется найти угол между этими прямыми (Рис. 26):
Рис. 26. Угол между двумя прямыми.
Из рисунка видно, что 
Наименьший угол между пересекающимися прямыми определим формулой 
Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
Пример:
Определить угол между прямыми
Решение:
В силу того, что 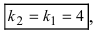
Пример:
Выяснить взаимное расположение прямых
Решение:
Так как угловые коэффициенты 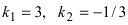
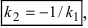
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки 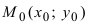
Если прямая 
Прямая линия на плоскости и в пространстве. Системы координат на плоскости
Рассмотрим произвольную прямую. Выберем на этой прямой начальную точку, обозначаемую буквой О, определим положительное направление, выберем некоторый отрезок в качестве линейной единицы, благодаря чему прямая станет осью. После этого условимся называть координатой любой точки М на этой оси величину отрезка 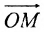
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке, т.е. указано, какая из них считается первой, а какая — второй. Точка пересечения осей называется началом координат и обозначается через О, а сами оси — координатными осями, причем первую из них называют также осью абсцисс и обозначают через Ох, а вторую — осью ординат, обозначаемую Оу.
Пусть М- произвольная точка плоскости. Спроектируем точку M на координатные оси, т.е., проведем через М перпендикуляры к осям Ох и Оу; основания этих перпендикуляров обозначим соответственно 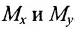
Координатами точки М в заданной системе называются числа 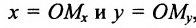
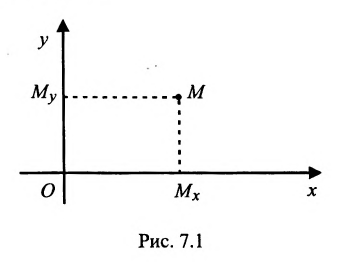
Если задана декартова прямоугольная система координат, то каждая точка М плоскости в этой системе имеет одну вполне определенную пару координат х, у — М(х, у). И обратно, для любых х и у на плоскости найдется одна вполне определенная точка с абсциссой х и ординатой у.
На рис. 7.2 положение точки Р полностью определяется ее координатами (2;3).
Две координатные оси разделяют всю плоскость на четыре части, называемыми координатными плоскостями, определяемыми соответственно:
Декартова прямоугольная система координат является наиболее употребительной. Однако, в отдельных случаях могут оказаться более удобными или косоугольная декартова или полярная системы координат.
Косоугольная система координат от прямоугольной декартовой системы координат отличается только произвольным углом между осями координат.
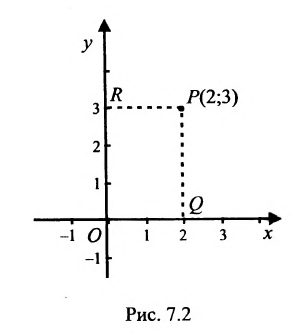
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча OA, называемого полярной осью, масштаба для измерения длин и направления- вращения в плоскости, считаемого положительным (рис. 7.3).
Каждая точка М в полярной системе координат задается парой координат 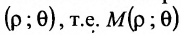
Декартова прямоугольная система координат связана с полярной системой формулами:
Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками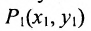
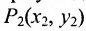
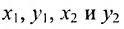
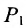
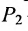
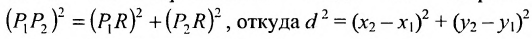
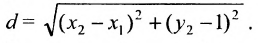
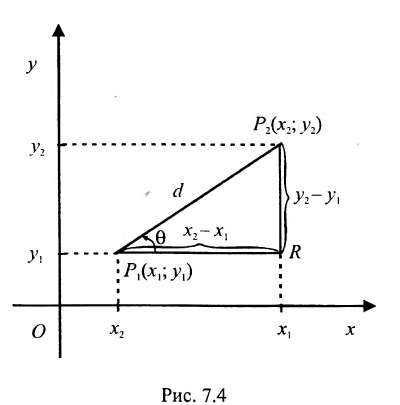
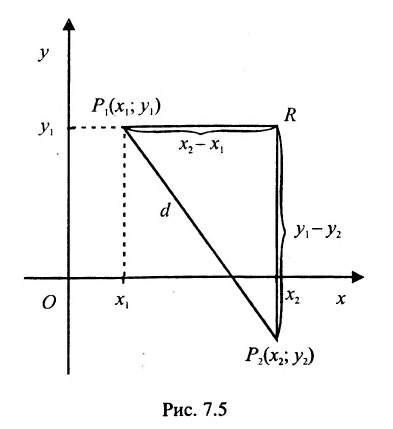
Это и есть формула для вычисления расстояния между двумя точками.
Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки 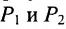
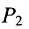
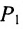
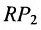
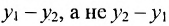
Расстояние между точками, вычисляемое по формуле (7.1.1), от этого не изменится, так как 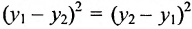
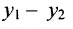
Если обозначить через 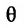
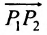
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из формул (7.1.2) получаем формулы:
позволяющие определить полярный угол отрезка по координатам его конца и начала. Кроме того, если u — произвольная ось, а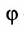
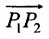
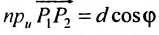
Пусть на плоскости даны две произвольные точки, из которых одна считается первой, другая — второй. Обозначим их в заданном порядке через 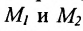
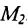
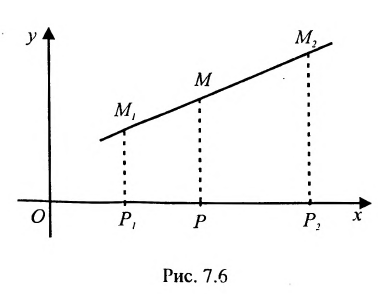
Определение 7.1.1. Число 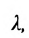
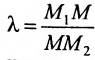
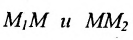
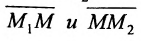
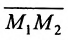
Число 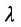
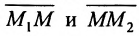
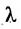
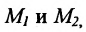
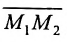
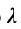
Задача о делении отрезка в данном отношении формулируется следующим образом:
Считая известными координаты двух точек 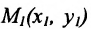
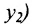
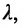
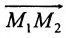
Решение задачи определяется следующей теоремой.
Теорема 7.1.1. Если точка М(х, у) делит направленный отрезок 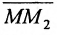
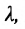
Доказательство:
Спроектируем точки 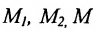
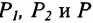
Подставив в (7.1.4) величины отрезков 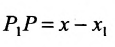
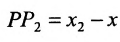
Разрешая это уравнение относительно х, находим:
Вторая формула (7.1.3) получается аналогично.
Если 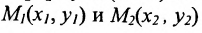
середина отрезка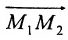
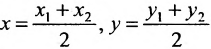
получаются из (7.1.3) при 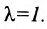
Основная теорема о прямой линии на плоскости
Предположим, что в данной плоскости задана прямоугольная система координат и некоторая прямая l.
Всякий ненулевой вектор, коллинеарный данной прямой, называется её направляющим вектором. Всякие два направляющих вектора 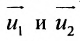
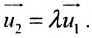
Для всех направляющих векторов 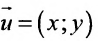
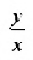
Действительно, если 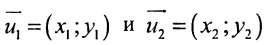
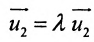
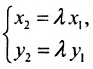
Угловой коэффициент прямой можно определить и по-другому: как тангенс угла, образованного положительным направлением оси абсцисс и заданной прямой.
Справедлива следующая теорема.
Теорема 7.3,1. Всякая прямая на плоскости определяется уравнением первой степени с двумя переменными х и у; и обратно, всякое уравнение первой степени с двумя переменными х и у определяет некоторую прямую на плоскости.
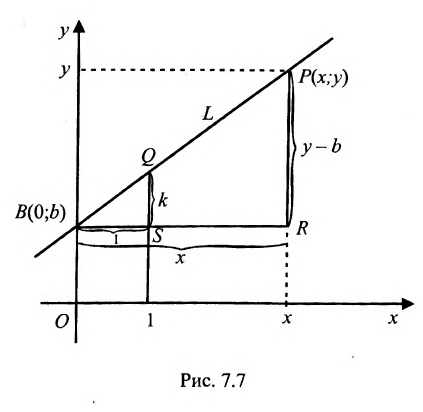
Доказательство: Пусть В = (О,b}- точка пересечения прямой L с осью у, а Р = (х,у) — любая другая точка на этой прямой. Проведем через точку В прямую, параллельную оси х, а через точку Р — прямую, параллельную оси у; проведем также прямую х = 1. Пусть k -угловой коэффициент прямой L (см. рис. 7.7). Случай к =0 не исключается.
Так как треугольники BSQ и BRP подобны, то 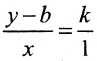
Следовательно, если точка Р принадлежит прямой L, то ее координаты удовлетворяют уравнению (7.2.1). Обратно, нетрудно показать, что если х и у связаны уравнением (7.2.1), то точка Р принадлежит прямой L, проходящей через точку (0;b) и имеющей угловой коэффициент k.
Таким образом, уравнение любой прямой можно записать в виде:
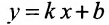
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени ио х и у можно привести к виду (7.2.2) либо (7.2.3).
Докажем обратное утверждение. Предположим, что задано произвольное уравнение первой степени:
Ах+Ву+С=0. (7.2.4)
Если 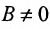
т.е. в виде (7.2.2). При В = 0 уравнение (7.2.3) сводится к уравнению
А х = —С,
или 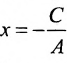
Таким образом, любая прямая описывается уравнением первой степени с неизвестными х и у, и обратно, каждое уравнение первой степени с неизвестными х и v определяет некоторую прямую.
Уравнение (7.2.4) называется общим уравнением прямой. Так
как 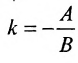
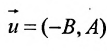
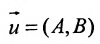
1. 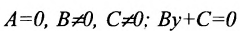
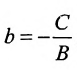
2. 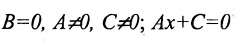
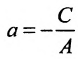
3. 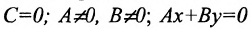
4. А=0; С=0; Ву-0 или у = 0 — это уравнение оси абсцисс Ох.
5. В=0;С=0; Ах=0 или х = 0 — это уравнение оси ординат Оу.
Различные виды уравнений прямой на плоскости
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направляющим вектором; отрезками, отсекаемыми прямой на осях координат и др. Однако, обязательно, должна быть точка, лежащая на этой прямой.
Пусть в уравнении (7.2.4) ни один из коэффициентов А, В, С не равен нулю. Перенесем свободные члены вправо и разделим на (-С). Получим уравнение прямой в отрезках:
где 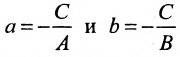
Рассмотрим прямую l на плоскости и выберем на этой прямой какие-нибудь точки 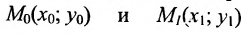
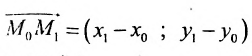
Геометрическое место концов всевозможных векторов вида 
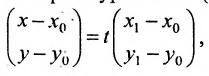
где 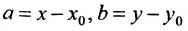
Система (7.3.3) равносильна уравнению
называемым каноническим уравнением прямой на плоскости. Из системы (7.3.3) можно получить уравнение
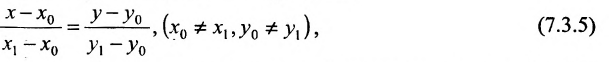
Если абсциссы точек 
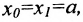
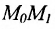
Если ординаты точек 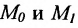
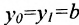
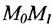
или
где
угловой коэффициент прямой.
Уравнение (7.3.6) называется уравнением прямой, проходящей через точку 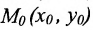
Пример:
Составить уравнение прямой, проходящей через две точки
Решение:
I способ. Воспользуемся уравнением (7.3.5). Подставив известные координаты точек 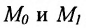
II способ. Зная координаты точек 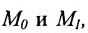
Тогда, воспользовавшись уравнением (7.3.6), найдём искомое уравнение прямой: 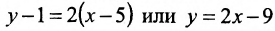
Заметим, что составленное уравнение можно записать как уравнение прямой в отрезках, разделив все члены уравнения
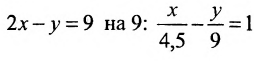
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые общими уравнениями 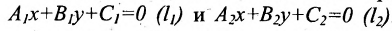
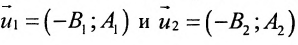
Если прямые параллельны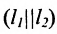
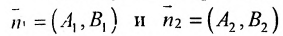
И обратно, если координаты при неизвестных х и у пропорциональны, то прямые параллельны. Следовательно, можно сформулировать следующую теорему:
Теорема 7.4.1. Две прямые
Например, прямые 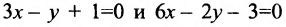
т. к.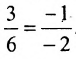
Если прямые перпендикулярны 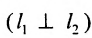
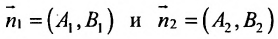
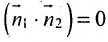
Справедливо и обратное утверждение: если скалярное произведение нормальных векторов равно нулю, то прямые /, и /2 перпендикулярны.
Теорема 7.4.2. Две прямые 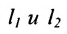
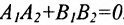
Например, прямые 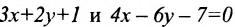
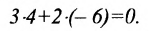
Если прямые заданы уравнениями вида 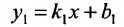
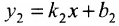
Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы выполнялось равенство
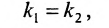
а для их перпендикулярности необходимо и достаточно, чтобы
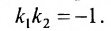
Пример:
Найти проекцию точки Р (2, 3) на прямую, проходящую через точки А (4, 3) и В (6, 5).
Решение:
Проекция точки Р на прямую АВ — это точка пересечения перпендикуляра, проведенного к этой прямой из точки Р.
Вначале составим уравнение прямой АВ. Воспользовавшись уравнением (7.3.5), последовательно получаем:
Для того, чтобы составить уравнение перпендикуляра, проведенного из точки Р на прямую АВ, воспользуемся уравнением (7.3.6). Угловой коэффициент k определим из условия перпендикулярности двух прямых, т. е. из формулы (7.4.6). Поскольку 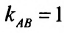
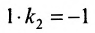
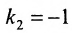
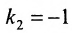
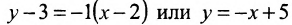
Решая систему уравнений, составленную из уравнений прямой АВ и перпендикуляра
найдём координаты проекции точки Р на прямую АВ: х=3 у=2, т.е.
Пример:
Издержки на производство шести автомобилей составляют 1000 млн. ден. ед., а на производство двадцати автомобилей- 15000 млн. ден. ед. Определить издержки на производство 22 автомобилей при условии, что функция К(х) издержек производства линейна, т.е. имеет вид у = ах + b .
Решение:
Обозначим через х количество автомобилей, а через y- издержки производства. Тогда из условия задачи следует, что заданы координаты двух точек- А(6; 1000) и В(20; 15000), принадлежащих линейной функции у = ах +b. Воспользовавшись уравнением (7.3.6 ), найдём искомое уравнение:
Подставив в найденную функцию х = 22, определим издержки на производство 22 автомобилей:
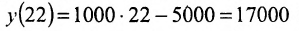
Пример:
Фирма продаёт свои изделия по 10 ден. ед. за единицу. Затраты на изготовление одного изделия составляют 6 ден. ед. Непроизводственные расходы фирмы равны 300 ден. ед. в год. Определить годовой выпуск продукции, необходимой для того, чтобы фирма работала с прибылью.
Решение:
Обозначим через х объём произведенной продукции. Тогда доход фирмы равен D = 10x. Затраты на производство определяются уравнением: 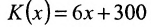
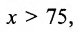
Прямая линия в пространстве
Системы координат в пространстве
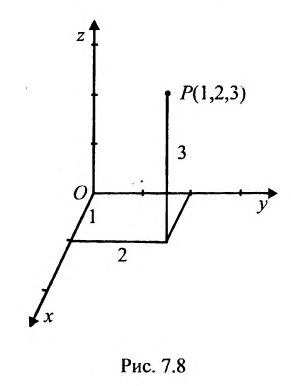
В трехмерном пространстве система координат определяется тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось единицей измерения длин, можно задать тремя упорядоченными числами (называемыми координатами) положение точки в пространстве. Например, точка Р задается упорядоченной тройкой чисел Р( 1,2,3).
Пусть задано пространство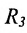
Положение прямой в пространстве вполне определяется заданием какой-либо сё фиксированной точки 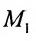
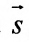
Вектор 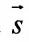
Итак, пусть прямая L проходит через точку 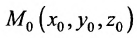
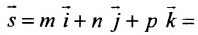
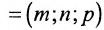
Рассмотрим произвольную точку M(x,y,z) на этой прямой. Из рисунка видно, что вектор 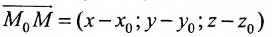
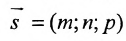
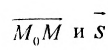
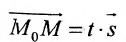
Уравнение 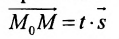
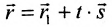
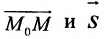
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты х, у и z и точка М перемещается по прямой.
Разрешив уравнения (7.5.2) относительно t
и приравняв найденные значенияt получим канонические уравнения прямой:
Если прямая L в пространстве задается двумя своими точками 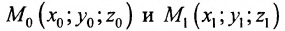
можно взять в качестве направляющего вектора и тогда уравнения (7.5.3) преобразуются в уравнения
где 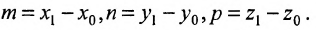
Пример:
Составить параметрические уравнения прямой, проходящей через точку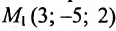
Решение:
В качестве направляющего вектора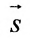
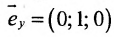
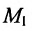
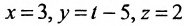
Пример:
Записать уравнения прямой 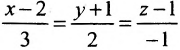
Обозначим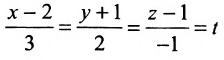
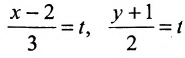
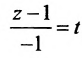
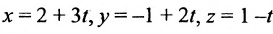
Замечание. Пусть прямая перпендикулярна одной из координатных осей, например, оси Ох. Тогда направляющий вектор
прямой перпендикулярный оси Ох, имеет координаты (о; n; р) и параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае формально можно записывать канонические уравнения прямой в виде 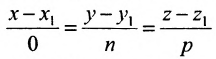
Аналогично, канонические уравнения
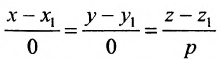
Пример:
Составить канонические и параметрические уравнения прямой, проходящей через точку 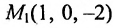
Решение:
Подставив координаты точки 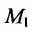
.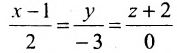
Пример:
Составить канонические уравнения прямой, проходящей через точку М(2, -1,4) параллельно
а) прямой 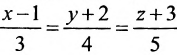
б) оси Ох;
в) оси Оу;
г) оси Oz.
Решение:
а) Поскольку направляющий вектор заданной прямой
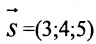
подставив координаты точки М(2; -1; 4) и вектора 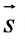
б) Поскольку единичный вектор оси О х: 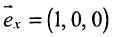
(7.5.3) координаты точки М(2; -1; 4 ) и вектора 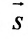
в) В качестве направляющего вектора 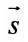
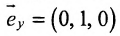
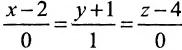
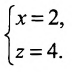
г) Единичный вектор оси Oz : 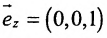
Пример:
Составить уравнение прямой, проходящей через две заданные точки
Решение:
Подставив координаты точек 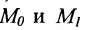
(7.5.4), получим:
Взаимное расположение двух прямых в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. Пусть в пространстве заданы две прямые:
Очевидно, что за угол 
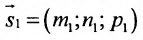
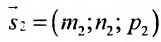
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов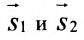
Две прямые параллельны тогда и только тогда, когда пропорциональны соответствующие координаты направляющих векторов:
т.е. 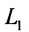
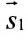
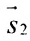
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих координат направляющих векторов равна нулю:
Пример:
Найти угол между прямыми 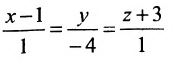
Решение:
Воспользуемся формулой (7.6.1), в которую подставим координаты направляющих векторов 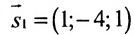
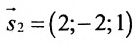
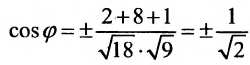
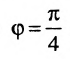
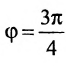
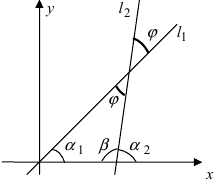
Вычисление уравнения прямой
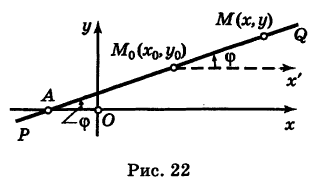
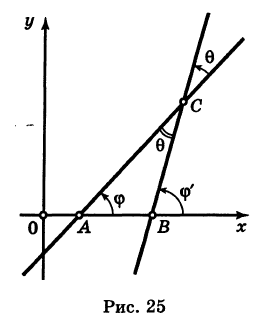
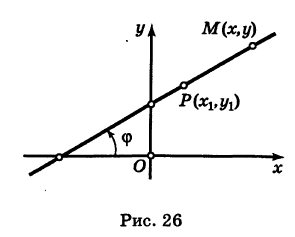
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол 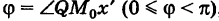
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала 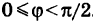
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
при х > 0.
Таким образом,
при х > 0.
Нетрудно проверить, что формула (3) остается справедливой также и при х < 0.
Мы доказали, что координаты любой точки М (х, у) прямой PQ удовлетворяют уравнению (3). Легко убедиться в обратном: если координаты какой-нибудь точки Ml 
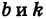
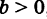
При k = 0 получаем уравнение прямой, параллельной оси Ох:
2) Если 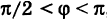
3) Если 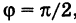
где а — абсцисса следа этой прямой на оси Ох (т. е. ее точки пересечения с осью Ох).
Замечание. Как частные случаи получаем уравнения осей координат:
Прямую легко построить по ее уравнению.
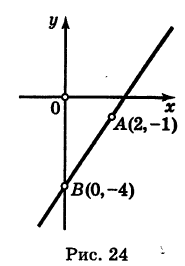
Пример:
Построить прямую, заданную уравнением
Решение:
Известно, что две точки вполне определяют положение прямой. Поэтому достаточно найти две точки, через которые проходит наша прямая. В данном уравнении b = -4. Следовательно, прямая проходит через точку В (0, -4). С другой стороны, координаты х и у любой точки, лежащей на нашей прямой, связаны заданным уравнением. Поэтому, задав абсциссу некоторой точки, лежащей на прямой, мы из уравнения прямой найдем ее ординату. Положим, например, х = 2; из уравнения прямой получим у = -1. Таким образом, наша прямая проходит через точки А (2, -1) и В (0, -4). Построив эти точки по их координатам и проведя через них прямую (рис. 24), мы получим искомую прямую.
Из предыдущего видно, что для произвольной прямой на плоскости можно составить ее уравнение; обратно, зная уравнение некоторой прямой, можно построить эту прямую. Таким образом, уравнение прямой полностью характеризует положение ее на плоскости.
Из формул (3) и (5) видно, что уравнение прямой есть уравнение первой степени относительно текущих координат х и у. Справедливо и обратное утверждение.
Теорема: Всякое невырожденное уравнение первой степени
представляет собой уравнение некоторой прямой линии на плоскости Оху (общее уравнение прямой линии).
Доказательство: 1) Пусть сначала В ^ 0. Тогда уравнение (7) можно представить в виде

2) Пусть теперь В = 0; тогда А 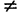
х = -С/А.
Уравнение (9) представляет собой уравнение прямой, параллельной оси Оу и отсекающей на оси Ох отрезок a = -С/А.
Так как все возможные случаи исчерпаны, то теорема доказана.
- Заказать решение задач по высшей математике
Угол между двумя прямыми
Рассмотрим две прямые (не параллельные оси Оу)у заданные их уравнениями с угловыми коэффициентами (рис. 25):
Требуется определить угол 9 между ними. Точнее, под углом 0 мы будем понимать наименьший угол, отсчитываемый против хода часовой стрелки, на который вторая прямая повернута относительно первой (0 < 0 < я). Этот угол 9 (рис. 25) равен углу АСВ треугольника ABC. Далее, из элементарной геометрии известно, что внешний угол треугольника равен сумме внутренних, с ним не смежных. Поэтому ф’ = ф + 0, или
0 = ф’ — ф;
отсюда на основании известной формулы тригонометрии получаем
Заменяя tg ф и tg ф’ соответственно на к и k окончательно будем иметь
Формула (3) дает выражение тангенса угла между двумя прямыми через угловые коэффициенты этих прямых.
Выведем теперь условия параллельности и перпендикулярности двух прямых.
Если прямые (1) и (2) параллельны, то ф’ = ф и, следовательно,
k’ = к. (4)
Обратно, если выполнено условие (4), то, учитывая, что ф’ и ф заключаются в пределах от 0 до я, получаем
Ф’ — ф, (5)
и, следовательно, рассматриваемые прямые или параллельны, или сливаются (параллельность в широком смысле).
Правило 1. Прямые на плоскости параллельны (в широком смысле) тогда и только тогдау когда их угловые коэффициенты равны между собой.
Если прямые перпендикулярны, то 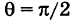
отсюда 1 + kk’ = 0 и
k’ = -l/k.
Справедливо также и обратное утверждение.
Правило 2. Две прямые на плоскости перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку.
Пусть теперь уравнения прямых заданы в общем виде:
Ах + By + С = 0 (7)
и
А’х + В’у + С’ = 0. (8)
Отсюда, предполагая, что 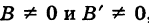
Следовательно, угловые коэффициенты этих прямых есть
Из формулы (3), производя несложные выкладки, находим тангенс угла между этими прямыми:
Отсюда получаем:
1) условие параллельности прямых (0 = 0)
2) условие перпендикулярности прямых
Отметим, в частности, что прямые
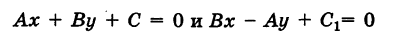
Для прямых, параллельных осям Ох и Оу, условно полагают 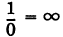
Пример:
Определить угол между прямыми у = х и у = 1,001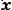
Решение:
По формуле (3) получаем
Так как для малых углов 0 справедливо приближенное равенство 
Уравнение прямой, проходящей через данную точку в данном направлении
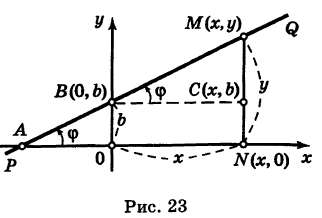
Пусть прямая РМ образует угол ф с положительным направлением оси Ох (рис. 26) и проходит через заданную точку Р 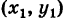
В этом случае, как мы видели, уравнение прямой имеет вид
у = kx + b, (1)
где k = tg ф — угловой коэффициент прямой, а Ь — длина отрезка, отсекаемого нашей прямой на оси Оу. Так как точка Р 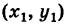
ух = kxt+ b. (2)
Вычитая из равенства (1) равенство (2), получим
Это и есть уравнение искомой прямой.
Если прямая, проходящая через точку Р 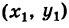
Если k — заданное число, то уравнение (3) представляет вполне определенную прямую. Если же k — переменный параметр, то это уравнение определит пучок прямых у проходящих через точку Р 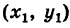
Пример:
Написать уравнение прямой, проходящей через точку Р (3, 2) и параллельной прямой:
Решение:
Так как искомая прямая параллельна данной прямой, то ее угловой коэффициент k = 4/3. Следовательно, на основании формулы (3) уравнение этой прямой имеет вид 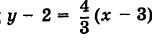
Пример:
Написать уравнение прямой, проходящей через точку Р (4, 5) и перпендикулярной к прямой:
Решение:
Так как искомая прямая перпендикулярна прямой с угловым коэффициентом k = -2/3, то ее угловой коэффициент k’ = -l/k = 3/2. Следовательно, на основании формулы (3) уравнение этой прямой таково:
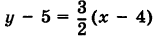
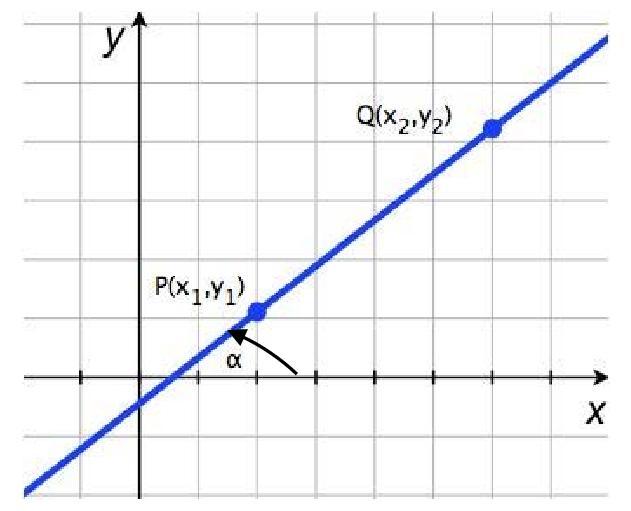
Уравнение прямой, проходящей через две данные точки
Известно, что через две не совпадающие между собой точки можно провести прямую, и притом только одну. Отыщем уравнение прямой, проходящей через точки 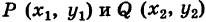
Предположим сначала, что 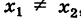
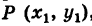
где k — неизвестный нам угловой коэффициент этой прямой. Однако так как наша прямая проходит также через точку Q 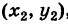
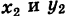
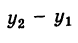
и, следовательно, при 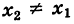
Подставляя выражение (2) для углового коэффициента k в уравнение (1), получим уравнение прямой PQ:
Это уравнение при 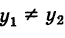
Если 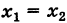
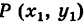
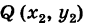
Пример:
Написать уравнение прямой, проходящей через точки Р(4, -2) и Q(3, -1).
Решение:
На основании уравнения (3) имеем
Уравнение прямой в «отрезках»
Выведем теперь уравнение прямой, положение которой на плоскости задано ненулевыми отрезками, отсекаемыми ею на осях координат. Предположим, например, что прямая АВ отсекает на оси Ох отрезок OA = а, а на оси Оу — отрезок О В = b (рис. 28), причем ясно, что тем самым положение прямой вполне определено.
Для вывода уравнения прямой АВ заметим, что эта прямая проходит через точки А (а, 0) и Б 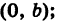
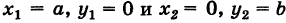
Отсюда
и окончательно
Это и есть так называемое уравнение прямой в «отрезках». Здесь х и у, как обычно, — координаты произвольной точки М (х, у), лежащей на прямой АВ (рис. 28).
Пример:
Написать уравнение прямой АВ, отсекающей на оси Ох отрезок OA = 5, а на оси Оу отрезок ОВ = -4.
Полагая в уравнении (1) а = 5 и b = -4, получим 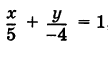
Примечание. Уравнение прямой, проходящей через начало координат или параллельной одной из осей координат, не может быть записано как уравнение прямой в «отрезках».
Точка пересечения двух прямых
Пусть имеем две прямые
Точка пересечения этих прямых лежит как на первой прямой, так и на второй. Поэтому координаты точки пересечения должны удовлетворять как уравнению первой, так и уравнению второй прямой. Следовательно, для того чтобы найти координаты точки пересечения двух данных прямых, достаточно решить совместно систему уравнений этих прямых.
Последовательно исключая из уравнений (1) и (2) неизвестные у и х, будем иметь
Отсюда если 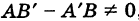
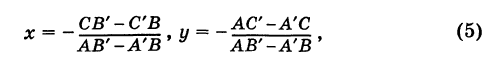
Для прямых (1) и (2) возможны следующие три случая.
На основании прямые не параллельны. Координаты их единственной точки пересечения определяются из формул (6).
Прямые параллельны и точки пересечения нет. Аналитически это видно из того, что по меньшей мере одно из уравнений (3) или (4) противоречиво и, значит, система (1) и (2) несовместна.
Прямые (1) и (2) сливаются, и, таким образом, существует бесчисленное множество точек пересечения. В этом случае левые части уравнений (1) и (2) отличаются только на постоянный множитель и, следовательно, система этих уравнений допускает бесконечно много решений.
Пример:
Решая совместно систему уравнений прямых
получаем х = 2 и у = 1. Следовательно, эти прямые пересекаются в точке N(2,1).
Расстояние от точки до прямой
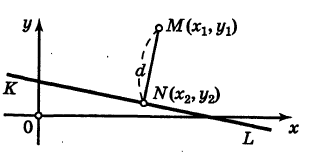
Рассмотрим прямую KL, заданную общим уравнением
и некоторую точку М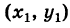
Уравнение перпендикуляра MN можно записать в виде
Отсюда для основания перпендикуляра N(x2, у2) будем иметь
и, следовательно,
где t — коэффициент пропорциональности. Поэтому
С другой стороны, учитывая, что точка N(*2, i/2) лежит на прямой KL, причем из (4) имеем 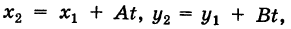
Следовательно,
Таким образом, в силу формулы (5) имеем
В частности, полагая 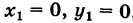
Замечание. Разделив обе части уравнения прямой (1) на 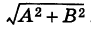
свободный член которого 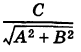
начала координат до прямой. Такое уравнение прямой будем называть нормированным.
Из формулы (7) получаем правило:
чтобы определить расстояние от точки до прямой, нужно в левую часть нормированного уравнения этой прямой подставить координаты данной точки и взять модуль полученного результата.
Пример:
Определить расстояние от точки М (-2, 7) до прямой
Решение:
Нормируя уравнение этой прямой, будем иметь
Отсюда искомое расстояние есть
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление