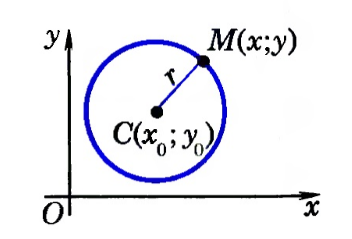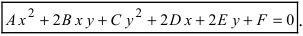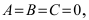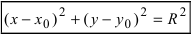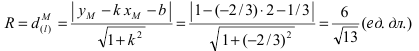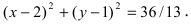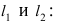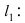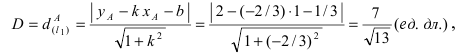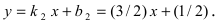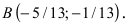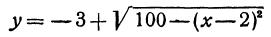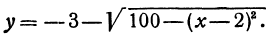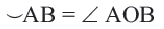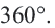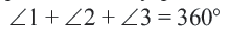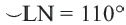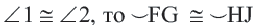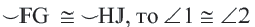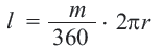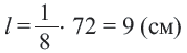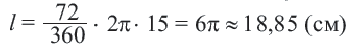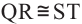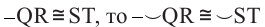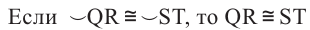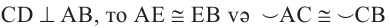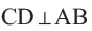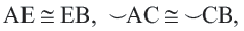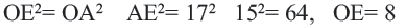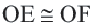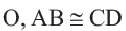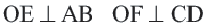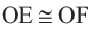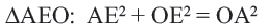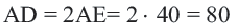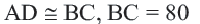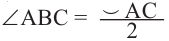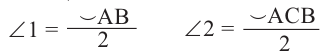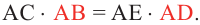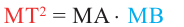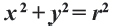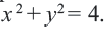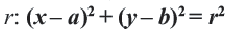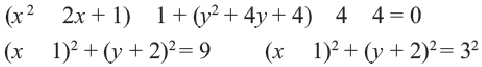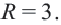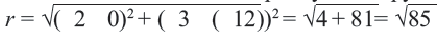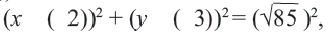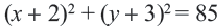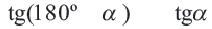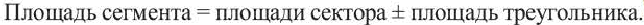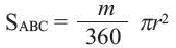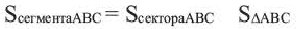Уравнение окружности и прямой — как между собой связаны
Определение
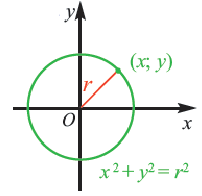
Окружностью называют замкнутую плоскую кривую, состоящую из всех точек на плоскости, которые равноудалены от заданной точки, лежащей в аналогичной плоскости, что и кривая. Данная точка является центром окружности.
Записать уравнение окружности можно, используя известные свойства геометрической фигуры:
- Любые точки окружности равноудалены от ее центра. Расстояние является радиусом.
- Зная координаты точек, можно записать формулу для определения расстояния между ними: (|AB|=sqrt{(x_{A}−x_{B})^{2}+(y_{A}−y_{B})^{2}}). Таким образом, квадрат расстояния равен (AB^{2}=(x_{A}−x_{B})^{2}+(y_{A}−y_{B})).
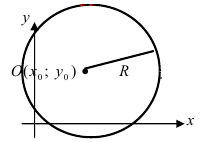
Уравнение для описания окружности, которая имеет радиус R, а ее центр совпадает с точкой (O(x_0;y_0)), имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
((x-x_0)^2+(y-y_0)^2 = R^2)
В том случае, когда центр окружности лежит в точке начала координат, уравнение окружности приобретает упрощенную форму:
(x^2+y^2=R^2)
Предположим, что существует уравнение некой окружности:
((x-1)^2+(y+2)^2=4)
Центром данной геометрической фигуры является точка C(1;-2). Радиус окружности равен R=2.
Определение
Прямая представляет собой линию, которая не имеет начала и не имеет конца, и при этом не искривляется.
Каждую прямую на плоскости можно представить в виде уравнения прямой первой степени. Формула имеет следующий вид:
Ax + By + C = 0
В данном случае А и В не могут одновременно принимать нулевые значения.
С учетом углового коэффициента общее уравнение прямой при значении b, не равном нулю, записывают следующим образом:
y = kx + b
Здесь k является угловым коэффициентом, который можно посчитать, как тангенс угла между рассматриваемой прямой и положительным направлением оси ОХ.
Рассмотрим случай, когда прямая пересекает оси ОХ и ОУ в точках, имеющих следующие координаты:
((a; 0) и (0; b))
Найти рассматриваемую прямую можно с помощью уравнения прямой в отрезках:
(frac{x}{a}+frac{y}{b}=1)
Предположим, что прямая пересекает пару точек (A(x_1;y_1)) и (B(x_2; y_2),) удовлетворяющих данным условиям:
(x_1 ≠ x_2 и y_1 ≠ y_2)
В таком случае уравнение прямой рассчитывают по формуле:
(frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1})
Например, существует некая прямая в прямоугольной системе координат. Данная прямая пересекает пару точек:
(M_1(1;1)) и (M_2(4;2))
Уравнение прямой, проходящей через две обозначенные точки, имеет вид:
(frac{x-1}{4-1}=frac{y-1}{2-1} Leftrightarrow frac{x-1}3=frac{y-1}1)
Преобразуем полученное уравнение:
(frac{x-1}3=frac{y-1}1 Leftrightarrow 1cdot (x-1)=3cdot(y-1) Leftrightarrow x-3y+2=0)
Как составить уравнение прямой, проходящей через центр окружности
Применяя записанные ранее уравнения для прямой и окружности, можно найти уравнение прямой, которая проходит через центр окружности:
(x^2+y^2-6x-8y+16=0)
(x^2+y^2+10x+4y+13=0)
В первую очередь следует рассчитать радиусы и определить координаты центров окружностей:
(x^2 + y^2 — 6x — 8y + 16 = 0)
((x^2 — 6x + 9) + (y^2 — 8y + 16) = 9)
((x — 3)^2 + (y — 4)^2 = 3^2)
(r1 = 3)
(O_1(3;4))
(x^2 + y^2 + 10x + 4y + 13 = 0)
((x^2 + 10x + 25) + (y^2 + 4y + 4) = 16)
((x + 5)^2 + (y + 2)^2 = 4^2)
(r2 = 4)
(O_2(-5;-2))
Уравнение прямой, проходящей через точки (O_1(3;4)) и (O_2(-5;-2)), можно записать следующим образом:
(frac{(x — 3)}{(3 + 5)}=frac{(y — 4)}{(4 + 2)})
(frac{(x — 3)}{8}=frac{(y — 4)}{6})
(3(x — 3) = 4(y — 4))
(3x — 9 = 4y — 16)
(4y = 3x + 7)
(y = frac{3x}{4}+frac{7}{4})
В результате уравнение прямой принимает такой вид:
(y = frac{3x}{4}+frac{7}{4})
Решение задач по теме, примеры
Задача 1
Требуется определить, где находится центр окружности, и чему равен ее радиус. Уравнение окружности:
(x^{2}+(y-3)^{2}=49)
Необходимо представить график окружности в осях абсцисс и ординат.
Решение
Каноническое уравнение окружности имеет вид:
((x-h)^{2}+(y-k)^{2}=r^{2})
В данном случае, центр соответствует О:(h, k), а радиус окружности равен r.
По условиям задачи: (x^{2}+(y-3)^{2}=49)
Таким образом:
(O:(0, 3)qquad r=7)
График:
Ответ: центр совпадает с точкой, имеющей координаты ((0, 3)qquad r=7)
Задача 2
Нужно определить, в какой точке расположен центр окружности, и чему равен ее радиус. Уравнение окружности:
((x+2)^{2}+y^{2}=36)
Решение
В первую очередь следует записать каноническое уравнение окружности:
((x-h)^{2}+(y-k)^{2}=r^{2})
В данном случае, центр окружности совпадает с точкой, имеющей координаты (h, k), а ее радиус равен r.
Согласно условиям задачи:
((x+2)^{2}+y^{2}=36)
Таким образом:
(O:(-2, 0)qquad r=6)
График:
Ответ: центр окружности совпадает с точкой (-2, 0), а ее радиус равен 6.
Задача 3
Требуется преобразовать уравнение в сумму квадратов для расчета радиуса и определения центра окружности:
(2x^{2}+2y^{2}+4x+16y+1=0)
Решение
(2x^{2}+2y^{2}+4x+16y+1=0Longrightarrow x^{2}+y^{2}+2x+8y+frac{1}{2}=0)
В таком случае:
(left(x+1right)^{2}+left( y+4right)^{2}-1-16+frac{1}{2}=0Longrightarrow left(x+1right) ^{2}+left(y+4right) ^{2}=frac{33}{2})
В результате расчетов получим:
центр находится в (-1,-4)
радиус равен (sqrt{frac{33}{2}})
Ответ: (O (-1,-4) и r=sqrt{frac{33}{2}})
Задача 4
Центр окружности совпадает с точкой (4,-5). Необходимо записать уравнение данной окружности, учитывая, что она проходит через точку с координатами (7,-3).
Решение
Каноническое уравнение окружности:
((x-h)^{2}+(y-k)^{2}=r^{2})
Центр находится в точке:
(4,-5)
Радиус соответствует r.
Таким образом:
((x-4)^{2}+(y+5)^{2}=r^{2}Longrightarrow r=sqrt{(x-4)^{2}+(y+5)^{2}})
Учитывая, что окружность проходит через точку (7,-3), запишем:
(r=sqrt{left(3right)^{2}+left(2right)^{2}}=sqrt{13})
Ответ: уравнение окружности имеет вид ((x-4)^{2}+(y+5)^{2}=13)
Задача 5
Необходимо записать уравнение окружности, центр которой соответствует точке O(2,-1), касающейся прямой r:y=x+2. Требуется начертить график.
Решение
Зная, что радиус r является расстоянием, на которое удалены точка O:(h, k) и прямая y-x-2=0, запишем:
(O:(2,-1))
(r=d(O,L)=frac{leftvert -2-1-2rightvert }{sqrt{1^{2}+left( -1right) ^{2}}}=frac{5}{sqrt{2}})
Получим уравнение окружности:
((x-h)^{2}+(y-k)^{2}=r^{2}Longrightarrow (x-2)^{2}+(y+1)^{2}=frac{25}{2})
График:
Ответ: ((x-2)^{2}+(y+1)^{2}=frac{9}{5})
Задача 6
Требуется записать уравнение, описывающее прямую с угловым коэффициентом (k= frac{3}{2}). Искомая прямая пересекает точку А (3;2).
Решение
В первую очередь следует записать стандартную формулу:
(y-y_{0}=k(x-x_{0}))
Применительно к условиям задачи, получим:
(y-(-2)= frac{3}{2} (x-3))
(y+2= frac{3}{2}х-frac{9}{2})
(y= frac{3}{2}х-frac{13}{2})
Ответ: (y= frac{3}{2}х-frac{13}{2})
Решение задач по темам «Уравнение окружности» и «Уравнение прямой»
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На прошлых уроках мы вывели уравнение окружности и решили некоторые задачи на уравнение окружности, вывели уравнение прямой и решили соответствующие задачи. На этом уроке мы продолжим решение задач на уравнение окружности и уравнение прямой.
Планиметрия (прямая и окружность)
Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
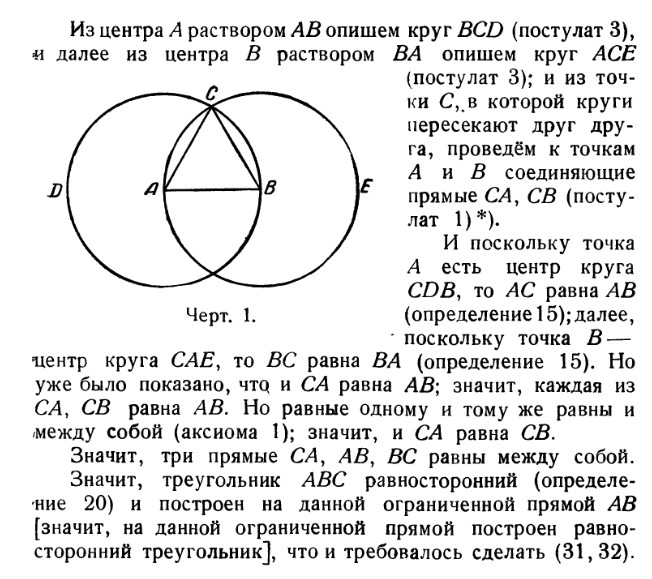
На данной ограниченной прямой построить равносторонний треугольник
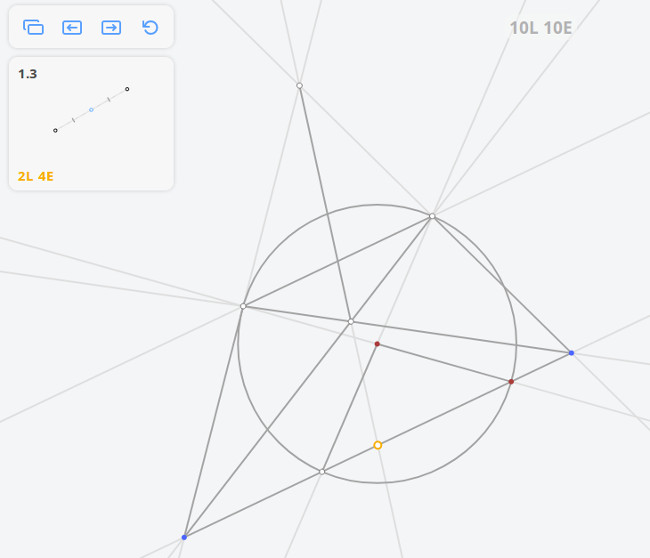
1.3 Середина отрезка
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
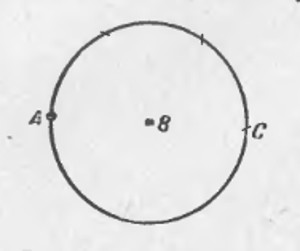
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
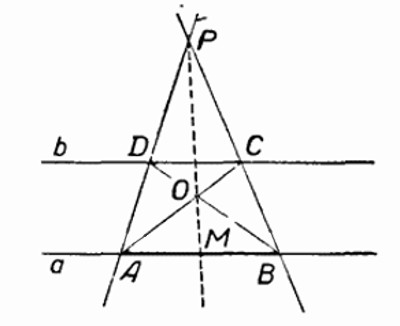
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:
1.4 Окружность, вписанная в квадрат
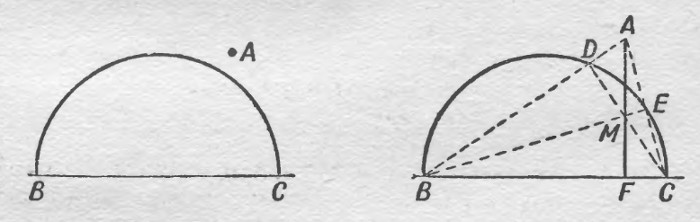
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
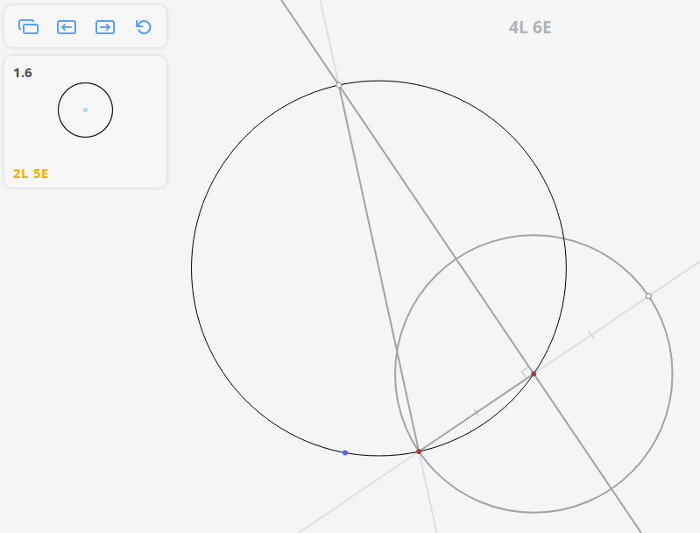
1.6 Найти центр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.
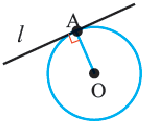
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
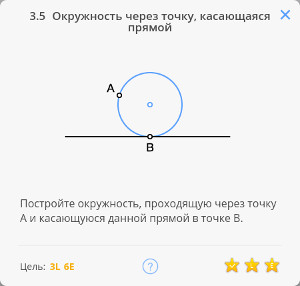
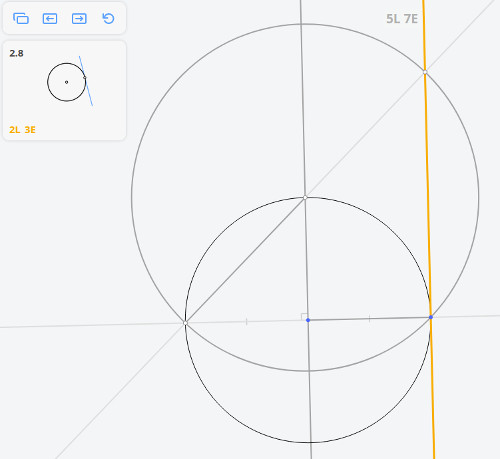
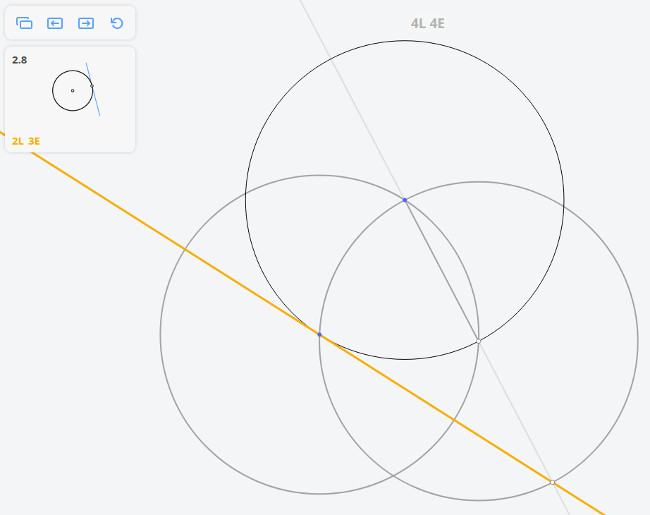
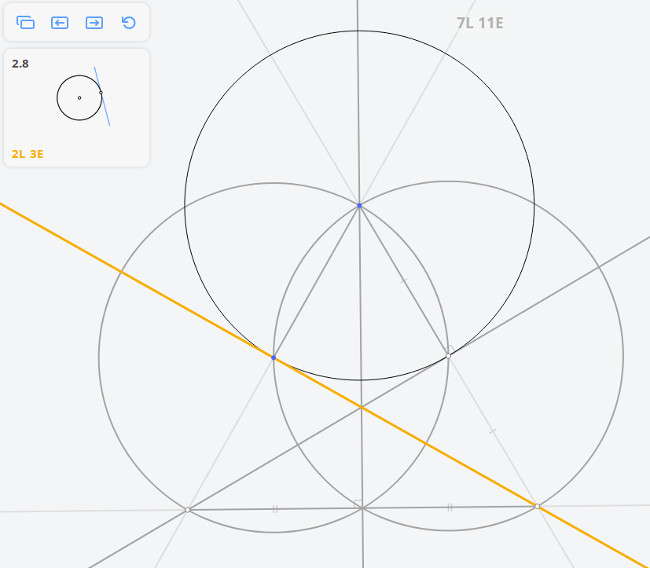
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
1.7 Квадрат, вписанный в окружность
Задача Наполеона
Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом
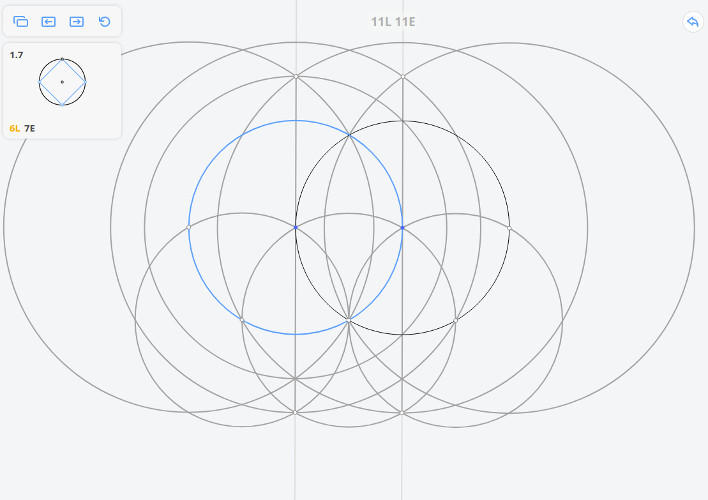
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО
Уравнение окружности и прямой
Вы будете перенаправлены на Автор24
Уравнение линии на плоскости
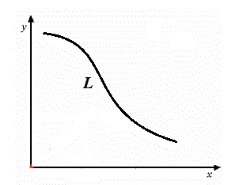
Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).
Рисунок 1. Произвольная линия в системе координат
Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$
Уравнение окружности
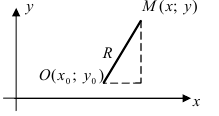
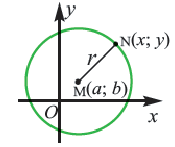
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).
Рисунок 2. Окружность в декартовой системе координат
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
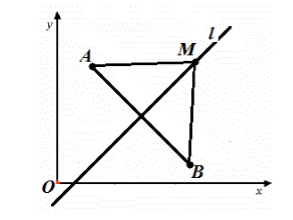
Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $left$ и $$ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ — серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=$, принадлежащую прямой $l$ (рис. 3).
Готовые работы на аналогичную тему
Рисунок 3. Прямая в декартовой системе координат
Так как прямая $l$ — серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.
Найдем длины данных сторон по формуле расстояния между точками:
Обозначим через $a=2left(x_1-x_2right), b=2left(y_1-y_2right), c=^2+^2-^2-^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:
Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=$, тогда
Если прямая $l$ параллельна оси $Ox$, то она имеет вид
Если прямая $l$ параллельна оси $Oy$, то она имеет вид
Пример задачи на нахождение уравнений линий в декартовой системе координат
Найти уравнение окружности с центром в точке $(2, 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2, 4)$, получим
Найдем радиус окружности как расстояние от точки $(2, 4)$ до точки $(0,0)$
Получаем, уравнение окружности имеет вид:
Найдем теперь уравнение окружности, используя частный случай 1. Получим
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 05 04 2022
http://habr.com/ru/post/478410/
http://spravochnick.ru/matematika/metod_koordinat/uravnenie_okruzhnosti_i_pryamoy/
Решение задач по темам «Уравнение окружности» и «Уравнение прямой»
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На прошлых уроках мы вывели уравнение окружности и решили некоторые задачи на уравнение окружности, вывели уравнение прямой и решили соответствующие задачи. На этом уроке мы продолжим решение задач на уравнение окружности и уравнение прямой.
помогите составить уравнение прямой, проходящей через центр окружности
x2 + y2 + 4x − 2y − 20 = 0 параллельно прямой x − 2y + 3 = 0.
Сделать чертеж.
Ход решения
1) определяем координаты центра окружности, для чего приводим уравнение окружности x2 + y2 + 4x − 2y − 20 = 0 к каноническому виду.
2) определяем угловой коэффициент «к» прямой x − 2y + 3 = 0
3) составляем уравнение прямой проходящей через точку (центр окружности) и имеющую угловой коэффициент «к»
Геометрия
План урока:
Уравнение линии в координатах
Если какое-то уравнение содержит две переменные – х и у, то какие-то пары значений этих чисел будут являться его решением, а какие-то нет. Однако каждой такой паре чисел можно сопоставить точку на координатной плоскости. Все вместе такие точки могут образовать линию, которую можно обозначить буквой L. В таком случае исходное уравнение называют уравнением линии L.
Мы уже рассматривали некоторые уравнения линий на плоскости, когда изучали графики функций. Если некоторую функцию у = у(х) рассматривать как уравнение, то тогда график функции у(х) будет той самой линией, которая задается уравнением. Например, парабола может быть задана уравнением у = х 2 .
Однако уравнение линии не обязательно выглядит как функция. Наиболее простой задачей является определение факта, принадлежит ли та или иная точка той линии, которая задана уравнением.
Задание. Какие из точек А (2;1), В (3; 2), С (– 2; 5) и D(0; 0) принадлежат линии, заданной уравнением:
Решение. Надо просто подставить координаты точек в уравнение и посмотреть, превратится ли оно при этом в верное равенство. Сначала подставляем точку А (2; 1):
Получилось верное равенство, значит, А принадлежит заданной линии. Теперь подставляем координаты В (3; 2):
Равенство неверное, следовательно, В на заданной линии не лежит. Проверяем третью точку С (– 2; 5):
Получили, что и С не является частью линии. Проверяем последнюю точку D (0; 0):
Справедливость равенства означает, что D принадлежит линии.
Использование координат и уравнений линии порождает две обратные друг другу задачи:
1) по заранее заданному уравнению определить геометрический вид линии;
2) для заданной геометрической фигуры, построенной на координатной плоскости, найти уравнение линии.
Геометрия занимается в первую очередь решением второй задачи. Первая же задача рассматривается по большей части в курсе алгебры при изучении графиков функций.
Уравнение окружности
Попытаемся составить уравнение окружности, про которую нам известен ее радиус (обозначим его буквой r) и координаты центра окруж-ти(х0; у0). Пусть некоторая точка М с координатами (х; у) лежит на окруж-ти. Тогда, по определению окруж-ти, расстояние между С и М равно радиусу r:
Но расстояние между точками М и С может быть вычислено по формуле
Если же точка М НЕ лежит на окруж-ти, то длина отрезка МС не будет равна r, и потому координаты М не будут удовлетворять уравнению (1). Получается, что (1) как раз и является уравнением окруж-ти.
Задание. Составьте уравнение окружности, имеющей радиус 5, если ее центр находится в точке (6; 7), и проверьте, лежат на ней точки H(2; 10)и Р(3; 8).
Решение. Сначала запишем уравнение окруж-ти в общем виде
Это и есть уравнение окруж-ти. При желании можно раскрыть скобки в правой части, но делать это необязательно. Теперь будем подставлять в полученное уравнение координаты точек Н и Р:
Проверка показала, что Н находится на окруж-ти, а Р – нет.
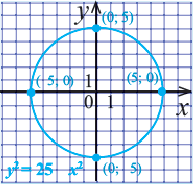
Задание. Начертите окружность, заданную уравнением
Именно эти значения и являются параметрами окруж-ти, которые нужны нам для ее построения. Ее центр находится в точке (х0; у0), то есть в (1; – 2), радиус равен r, то есть 2. В итоге выглядеть она будет так:
Особый случай представляет окруж-ть, центр которой находится в начале координат, то есть в точке (0; 0). В этом случае параметры x0 и y0 окруж-ти равны нулю, и уравнение
Например, окруж-ть с радиусом 4, если ее центр совпадает с началом координат, описывается уравнением:
Если при подстановке координат точки в уравнение получилось неверное равенство, то возможны два случая: либо точка находится внутри окруж-ти, либо она находится вне нее. Заметим, что в уравнении окруж-ти
левая часть представляет собой квадрат расстояния между точкой (х; у) и центром окруж-ти (х0; у0). Если оно больше квадрата радиуса, то точка находится вне окруж-ти, а если меньше – то внутри нее.
Задание. Определите для точек M(3; 4), N(2; 3), F(4; 4), лежат ли они на окруж-ти
внутри нее или за пределами окруж-ти.
Решение.Снова подставляем координаты точек в уравнение окруж-ти:
Это ошибочное равенство, ведь в реальности левая часть больше:
Это значит, что F(4; 4) лежит вне окруж-ти. Убедиться в правильности сделанных выводов можно, построив заданную окруж-ть и отметив точки M, N и F:
Рассмотрим несколько более сложных задач по данной теме.
Задание.Запишите уравнение окружности с центром С(– 4; 2), и окруж-ть проходит через точку А(0; 5).
Решение. В данном случае радиус окруж-ти явно не указан, и его надо найти. Подставим в уравнение окруж-ти известные нам данные:
Задание. Даны точки К (– 2; 6) и М (2; 0). Запишите уравнение окруж-ти, в которой КМ будет являться диаметром.
Решение. Для составления уравнения нужно знать радиус окруж-ти и координаты ее центра. Обозначим центр буквой С. Ясно, что центр окруж-ти делит любой ее диаметр пополам, на два одинаковых радиуса, то есть является серединой диаметра. То есть С – середина КМ, а потому для поиска координат С используем формулы:
Итак, координаты центра теперь известны, это (0; 3). Чтобы найти радиус, поступим также, как и в предыдущей задаче – подставим координаты точек С и, например, К, в уравнение окруж-ти
Обратите внимание, что нам необязательно вычислять радиус, ведь для уравнении окруж-ти нужна его величина, возведенная в квадрат, и мы ее нашли. Теперь можем записать уравнение окончательно
Задание. Дано уравнение окружности
(x — 2) 2 + (y — 4) 2 = 9
Найдите точки этой окруж-ти, абсцисса которых равна 2.
Решение. Напомним, что абсцисса – это координат х точки. Она нам уже известна, х = 2. Остается только найти ординату, то есть координату у. Для этого подставим известное нам значение абсциссы в уравнение и решим его:
Обратите внимание, что у квадратного уравнения нашлось сразу 2 корня, они соответствуют двум точкам, (2; 1) и (2; 7).
Ответ: (2; 1) и (2; 7).
Задание. Составьте уравнение окружности, проходящей через точки D(3; 8), L(6; 7) и K(7; 0).
Решение. Эта задача сложнее предыдущих и потребует громоздких вычислений. Нам надо найти радиус окруж-ти r и ее центр (х0; у0). Запишем для точки D(3; 
Далее раскроем скобки в левой части, используя формулу квадрата разности (это необходимо для упрощения дальнейших расчетов):
В итоге нам удалось составить три уравнения, которые содержат три переменные: r, х0 и у0.Вместе они образуют систему уравнений, которую можно попробовать решить:
Далее можно, например, вычесть из (2) уравнение (3):
Нам удалось найти одно из интересующих нас чисел, у0. С помощью (5) легко найдем и х0:
x0 = 7y0 — 18 = 7*3 — 18 = 21 — 18 = 3
Итак, центр окруж-ти находится в точке (3; 3). Осталось найти радиус окруж-ти. Для этого подставим в уравнение окруж-ти вычисленные нами координаты центра, а также координаты одной из точек из условия, например, K(7; 0):
Радиус окруж-ти равен 5. Теперь мы можем окончательно записать уравнение окруж-ти
Чтобы убедиться в правильности найденного решения, можно подставить в полученное уравнение координаты трех точек из условия и посмотреть, обращают ли они его в верное равенство. Вместо этого мы для наглядности просто построим в координатной плоскости получившуюся окруж-ть и отметим на ней точки из условия:
Ответ: (х – 3) 2 + (у – 3) 2 = 25
Уравнение прямой
Пусть на координатной плоскости построена произвольная прямая m. Для составления его уравнения отметим две точки А(х1; у1) и В(х2; у2) так, чтобы прямая m оказалась серединным перпендикуляром для отрезка АВ:
Тогда, согласно свойству серединного перпендикуляра,про любую точку М(х; у), лежащую на m, можно сказать, что она равноудалена от А и В, и наоборот, любая точка, НЕ лежащая на m, НЕ равноудалена от А и В. Это означает, что для точки M, если она лежит на m, должно выполняться равенство:
Квадратные корни равны, если одинаковы их подкоренные выражения, поэтому
Заметим, что так как точки А и В – различные, то хотя бы одна из разностей (2х2 – 2х1) и (2у2 – 2у1) будет не равна нулю, поэтому в (2) хотя бы один их коэффициентов а и b точно ненулевой. Это означает, что уравнение (2) является уравнением первой степени. Заметим, что (2) называют общим уравнением прямой, так как оно описывает любую прямую на плоскости. При более глубоком изучении геометрии вы познакомитесь с множеством других видов уравнений прямой (нормальным, каноническим, тангенциальным, параметрическим и т. п.).
В последнем примере коэффициент с равен нулю, поэтому его просто не записали.
Заметим важный аспект – одна и та же прямая может описываться различными уравнениями вида (2). Например, пусть уравнение прямой выглядит так:
Это уравнение равносильно предыдущему, хотя у них и различны коэффициенты а, b и c. Это значит, что однозначно определить эти коэффициенты при решении задач в большинстве случаев невозможно. Поэтому удобней рассмотреть два отдельных случая.
1) Если коэффициент b в уравнении прямой (2) не равен нулю, то его можно привести к виду:
Из курса алгебры мы помним, что ее графиком как раз является прямая. В большинстве случаев уравнение прямой удобно записывать именно в таком виде. Напомним, что число k называется угловым коэффициентом прямой.Поэтому (3) так и называют – уравнением прямой с угловым коэффициентом. В качестве примера подобных уравнений можно привести:
Каждое из них описывает вертикальную прямую, параллельную оси Оу.
Задание. Прямая задана уравнением
Постройте ее на координатной плоскости
Решение. Для построения прямой надо всего лишь найти две различные точки, лежащие на ней, и соединить их. Мы будем брать произвольные значения координаты х, подставлять их в уравнение и находить соответствующее им значение координаты у. Подставим х = 1:
Получили другую точку (– 1; – 1). Осталось отметить эти две точки на и соединить их:
Задание. Составьте уравнение прямой, проходящей через точки D(1; 10) и Е(– 1; – 4).
Решение. Задачу можно решить разными способами.
Способ 1 – универсальный и более сложный.
В общем виде уравнение прямой выглядит так:
Нам надо найти коэффициенты а, b и c. Для этого просто подставляем координаты известных точек в уравнение. Начнем с координат D:
Нам удалось выразить коэффициента двумя различными выражениями (1) и (2). Так как в них одинаковы левые части, то можно приравнять и правые части:
Мы можем взять любое значение коэффициента с (кроме нуля), и при этом получатся различные, но равносильные друг другу уравнения. Удобно взять с = 3, тогда в уравнении исчезнут дроби:
Это и есть ответ задания.
Далее рассмотрим более простой способ, который, однако, может потребовать анализа различных вариантов.
Уравнение прямой может иметь либо вид
если прямая является графиком линейной функции, либо вид
если прямая параллельна оси Оу. Во втором случае у всех точек прямой абсцисса должна быть одинакова, однако у точек D(1; 10) и Е(– 1; – 4) она различна, поэтому ее точно можно описать уравнением
Надо найти коэффициенты k и d. Подставим в уравнение координаты D(1; 10):
Итак, уравнение можно записать так:
Задание. Запишите уравнение прямой, если ей принадлежат точки:
Подставим сюда уже известное нам значение d:
В (1) и (2) мы выразили d с помощью разных выражений, которые теперь можно приравнять:
То, что коэффициент k оказался нулевым, означает, что прямая параллельна оси Ох.
в) Попытаемся сделать те же действия, что и в двух предыдущих примерах, подставляя точки в уравнение у = kx + d:
На этот раз мы не смогли найти коэффициент k, а вместо этого получили ошибочное равенство. То есть уравнение просто не имеет решений. Что же это значит? Из этого факта следует, что в этом примере уравнение прямой НЕ может иметь вид
Значит, оно имеет другой вид:
Действительно, у обеих точек (2; 7) и (2; 
Ответ а) у = 1,5х + 3; б) у = 8; в) х = 2.
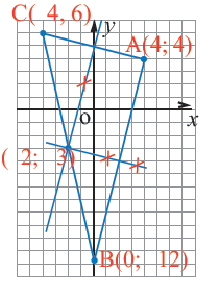
Задание. Найдите площадь треугольника MON, изображенного на рисунке, если известно, что M и N лежат на прямой, задаваемой уравнением:
Решение. ∆MON – прямоугольный, и для вычисления его площади нужно найти длины OM и ON. По рисунку видно, что М лежит на оси Ох, то есть у неё ордината нулевая:
Зная это, легко найдем и абсциссу М, ведь координаты М при их подстановке в уравнение прямой должны давать верное равенство:
Далее рассмотрим точку N. Она уже лежит на Оу, а потому у нее нулевой оказывается абсцисса:
Напомним, что площадь прямоугольного треугольника может быть вычислена по формуле:
Задачи на пересечение двух фигур
Метод координат помогает находить точки, в которых пересекаются те или иные геометрические фигуры. В большинстве случаев надо просто составить систему из уравнений, задающих эти фигуры, и найти их общее решение. В курсе алгебры мы уже рассматривали как решение простых, в основном линейных систем, так и решение более сложных, нелинейных систем. Рассмотрим несколько задач на эту тему.
Задание. Две прямые заданы уравнениями:
Определите, в какой точке они пересекаются.
Решение. Если точка пересечения прямых существует, то ее координаты являются решением каждого из двух уравнений. Таким, образом, нам надо просто решить систему:
Мы нашли единственное решение системы – это пара чисел (3; – 2). Эта же пара определяет координаты искомой нами точки.
Задание. Найдите точки пересечения окруж-ти и прямой, если они задаются уравнениями
Решаем квадратное уравнение, используя дискриминант:
Мы нашли два различных значения у. Это значит, что прямая пересекается с окруж-тью в двух различных точках, а найденные нами числа – их ординаты. Отметим, что возможны случаи, когда корень только один (и тогда у окруж-ти с прямой одна общая точка, то есть они касаются), и когда корней вовсе нет (тогда окруж-ть и прямая не пересекаются). В нашем же примере осталось найти абсциссы точек. Для этого используем уравнение (3):
Получили в итоге пары точек (3; 
Ответ: (3; 
Задание. Две окруж-ти заданы уравнениями:
Для ее решения сначала раскроем скобки в обоих уравнениях и приведем подобные слагаемые:
Нам удалось выразить у через х. Теперь снова запишем одно из исходных уравнений окруж-ти, но заменим в нем у с помощью только что найденного выражения:
Мы нашли абсциссы точек пересечения окруж-тей, теперь можно вернуться к (1), чтобы найти и ординаты:
Получили точки (5; 2) и (4; 3).
В конце решим одну задачу чуть более высокого уровня сложности.
Задание. К окруж-ти радиусом 5, чей центр совпадает с началом координат, построена касательная в точке (3; 4). Составьте уравнение этой касательной.
Решение. Сначала составим уравнение окруж-ти. Так как ее центр находится в начале координат, а радиус имеет длину 5, то оно примет вид:
Нам надо найти коэффициенты k и d, а для этого надо составить какие-нибудь уравнения с этими переменными. Нам известно, что касательная проходит через точку (3; 4), а потому эти координаты можно подставить в (2):
Обратите внимание, что мы получили квадратное уравнение относительно переменной х. Если бы нам были известны k и d, то мы смогли бы его решить, и тогда мы определили бы точки пересечения прямой и окруж-ти. В этой задаче k и d нам неизвестны, но мы знаем, что окруж-ть и прямая касаются, то есть имеют ровно одну общую точку. Но тогда и квадратное уравнение (4) должно иметь только одно решение! Это означает, что его дискриминант равен нулю. Сначала выпишем коэффициенты квадратного уравнения, используемые при вычислении дискриминанта:
Теперь у нас есть два уравнения, (3) и (5), которые содержат только переменные k и d. Осталось лишь совместно решить их. Для этого подставим (3) в (5):
В рамках урока мы выяснили, как выглядят уравнения окруж-ти и прямой, а также научились решать несколько типовых заданий, в которых эти уравнения необходимо использовать. Хотя формулы, используемые при этом, могут показаться слишком сложными, главное – просто набить руку в их применении, решая как можно больше задач.
источники:
http://sprashivalka.com/tqa/q/14347758
http://100urokov.ru/predmety/urok-3-linii-na-ploskosti

ryfi510
- Новичок
- Сообщений: 7
-

Помогите найти прямую, проходящую через центр окружности …
« : 27 Октября 2010, 01:17:38 »
Задача:
Найти прямую, проходящую через центр окружности x^2+y^2-6x+4y=0 перпендикулярно прямой, соединяющей фокус параболы x^2-4y=0 и левый фокус гиперболы x^2/64-y^2/36=1.
Помогите найти прямую, график нарисовала, координаты окружности высчитала Q(3;-2), r=3.6055, дальше уже голову сломала что делать не знаю((((((((
ЗАРАНЕЕ БОЛЬШОЕ СПАСИБО!!!!!
« Последнее редактирование: 29 Октября 2010, 14:20:32 от Asix »
Содержание:
Окружность:
Определение: Кривой второго порядка называется линия, описываемая уравнением
Замечание: Если коэффициенты
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки 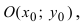
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора 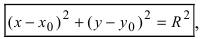
Рис. 28. Окружность.
Если 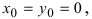
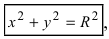
Пример:
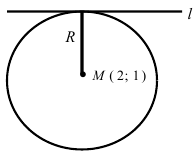
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 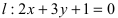
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
В уравнении окружности 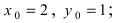
Пример:
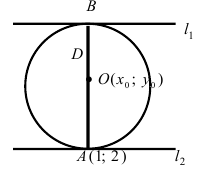
Составить уравнение окружности, касающейся двух параллельных прямых 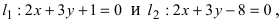
Решение:
Прежде всего определим, на какой из прямых 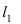
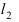
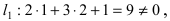
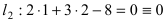
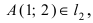
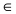
а радиус окружности 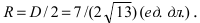
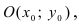
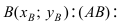
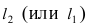
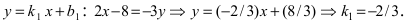
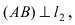
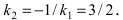
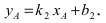
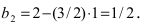
Найдем координаты точки B, которая является пересечением прямых 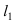
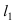
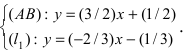
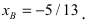
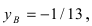
Для вычисления координат точки О применим формулы деления отрезка пополам (О): 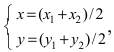
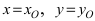
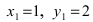
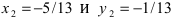
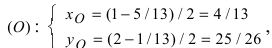
Таким образом, уравнение искомой окружности имеет вид:
Окружность в высшей математике
Рассмотрим уравнение
которое получается из уравнения (I), если положить 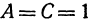
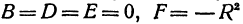
Если в формулу, выражающую расстояние между двумя точками, подставить 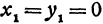
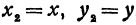
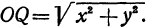
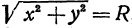
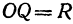
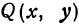
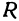

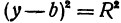

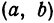
Пример:
Найдем уравнение окружности с центром в точке 
Решение:
Полагая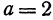
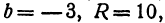
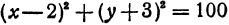
Разрешим это уравнение относительно 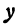
и
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
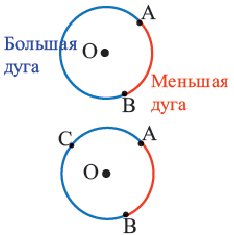
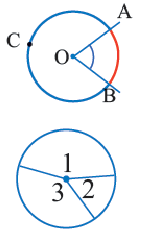
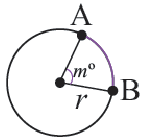
Центральный угол. Градусная мера дуги
Дуга окружности. Если отметить на окружности точки 

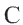
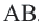
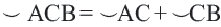


Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла:
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна
Дуги окружности и их величины
Пример: 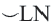
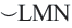
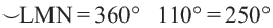
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
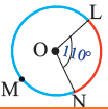
Если
Если
Длина дуги
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
Длина дуги в 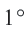
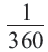
Длина дуги, соответствующей центральному углу с градусной мерой 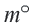
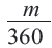
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
Пример №1
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу 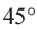
Решение:
Так как центральный угол 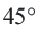
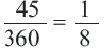
Пример №2
Найдите длину дуги, соответствующей центральному углу 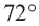
Решение: подставляя значения 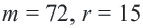
Окружность и хорда
Теорема о конгруэнтных хордах
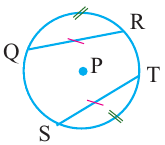
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если 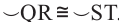
2)Если
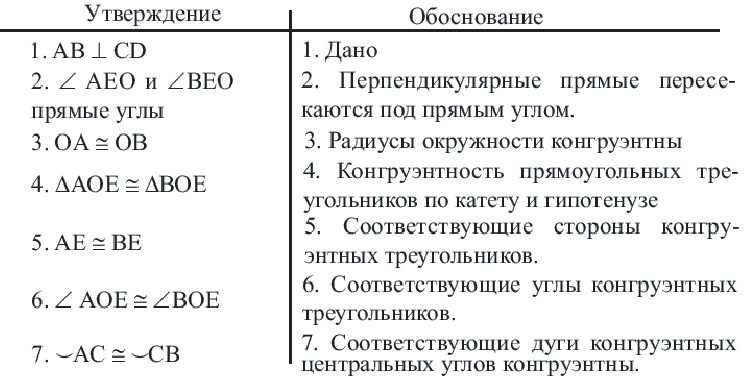
Доказательство теоремы 1:
Теорема о серединном перпендикуляре хорд
Теорема 2.
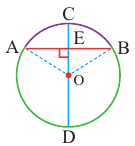
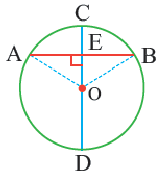
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если
Доказательство теоремы 2.
Дано: 
Докажите:
Начертите радиусы 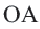
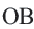
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
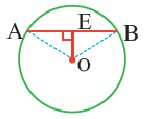
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если 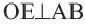
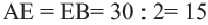
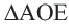
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
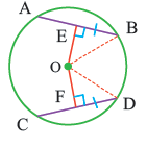
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
Если 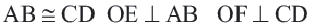
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
Доказательство теоремы 3
Дано: Окружность с центром
Докажите:
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. 

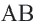
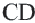

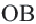
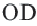
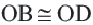
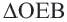
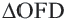


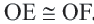
Задача. Хорды 

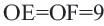
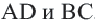
Решение: Так как хорды 

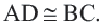
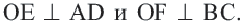
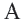
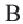
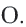
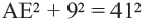
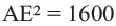
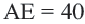
Так как
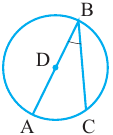
Угол, вписанный в окружность
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
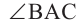
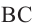
Угол, вписанный в окружность:
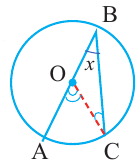
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается.
Доказательство (текстовое): 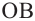
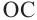
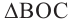
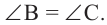
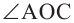
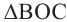
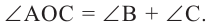
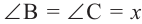
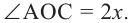
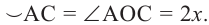
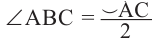
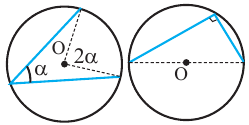
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
Конгруэнтные углы, вписанные в окружность
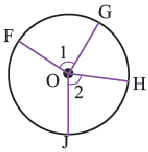
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. 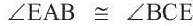
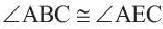
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если 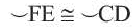
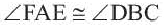
Касательная к окружности
Касательная. Признак касательной
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Прямая 
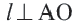
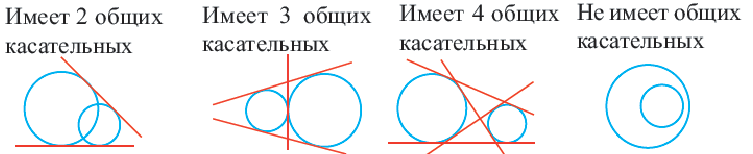
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.
Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
Доказательство теоремы 1. Если прямая 

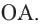
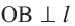

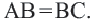
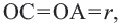
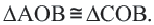
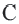

Свойства касательных, проведенных к окружности из одной точки
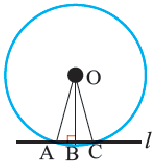
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
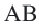
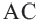
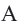
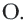
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
Углы между двумя секущими
Вершина угла находится внутри окружности
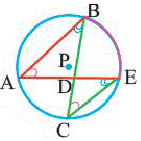
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному.
Углы между касательной и секущей
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
Углы, образованные касательной и секущей
Вершина угла находится вне окружности
Теорема 1.
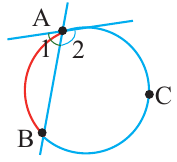
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
Отрезки секущих и касательных
Длина отрезков, секущих окружность
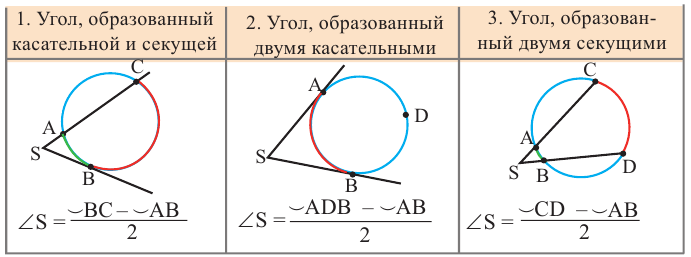
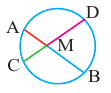
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
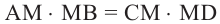
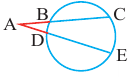
Теорема 2. Если из точки 

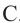
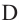
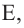
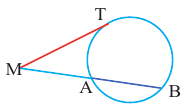
Теорема 3. Если из точки 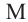


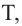
Уравнение окружности
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом 
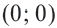
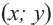

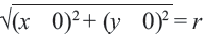
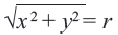
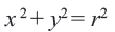
Уравнение окружности с центром в начале координат и радиусом 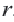
Например, уравнение окружности с центром в начале координат 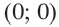
По формуле расстояния между центром окружности 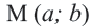
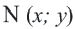
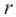
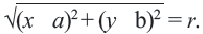
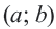
Например, уравнение окружности с центром в точке 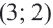
Пример №3
Постройте на координатной плоскости окружность, заданную уравнением
Решение: Напишем уравнение в виде 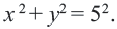
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 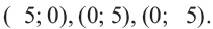
Пример №4
Точка 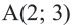
Решение: Записав координаты точки 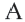
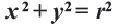
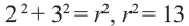
Пример №5
Найдем центр и радиус окружности, заданной уравнением
Решение:
Центр окружности точка 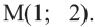
Пример №6
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 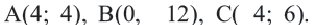
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 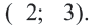
Уравнение окружности:
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
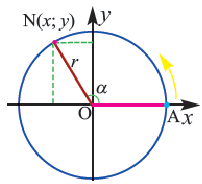
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка 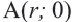
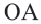
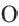
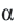
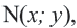
Для координат точки 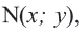

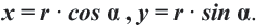

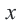
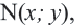
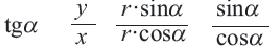
Синусы смежных углов равны, а косинусы взаимно противоположны.
Из этих формул при 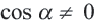
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
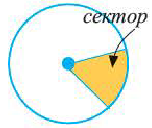
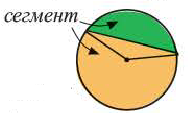
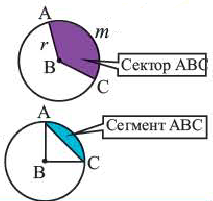
Сектор и сегмент
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
Например, часть круга, соответствующая центральному углу 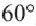
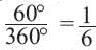
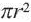

Площадь сектора
Площадь сектора:
Площадь сегмента:
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь
- Эллипс
- Гипербола
- Парабола
- Многогранник
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники