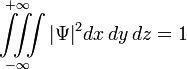Уравнение
Шрёдингера названо в честь австрийского
физика Эрвина Шрёдингера (E. Schrödinger). Это
основной теоретический инструмент
квантовой механики. В квантовой механике
уравнение Шрёдингера играет такую же
роль, как уравнение движения (второй
закон Ньютона) в механике классической.
Уравнение Шрёдингера записывается для
так называемой y —
функции (пси — функции). В общем случае
пси — функция – это функция координат
и времени: y = y (x,y,z,t).
Если микрочастица находится в стационарном
состоянии, то пси — функция не зависит
от времени: y= y (x,y,z).
В
простейшем случае одномерного движения
микрочастицы (например, только по оси x)
уравнение Шрёдингера имеет вид:
|
|
(21) |
где y (x) –
пси — функция, зависящая только от одной
координаты x; m – масса
частицы; —
постоянная Планка (=h/2π ); E –
полная энергия частицы, U –
потенциальная энергия. В классической
физике величина (E
–U) равнялась
бы кинетической энергии частицы. В
квантовой механике вследствие соотношения
неопределенностей понятие
кинетической энергии лишено смысла.
Заметим, что потенциальная энергия U –
это характеристика внешнего
силового поля,
в котором движется частица. Это величина
вполне определенная. Она также является
функцией координат, в данном
случае U=U(x,y,z).
В
трехмерном случае, когда y = y (x,y,z), вместо
первого слагаемого 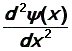
уравнении Шрёдингера следует записать
сумму трех частных производных от
пси-функции по трем координатам.

чего применяется уравнение Шрёдингера?
Как уже отмечалось, это основное уравнение
квантовой механики. Если его записать
и решить (что вообще не простая задача)
для конкретной микрочастицы, то мы
получим значение пси-функции в любой
точке пространства, в котором движется
частица. Что это дает? Квадрат модуля
пси-функции характеризуетвероятность обнаружения
частицы в той или иной области пространства.
Возьмем некоторую точку в пространстве
с координатами x,y,z (рис.6).
Какова вероятность обнаружить частицу
в этой точке? Ответ: эта вероятность
равна нулю! (точка не имеет размеров,
попасть в точку частица просто физически
не может). Значит, вопрос поставлен
некорректно. Поставим его иначе: какова
вероятность обнаружить частицу в малой
области пространства объемом dV
= dx dy dz с
центром в выбранной точке? Ответ:
|
|
(22) |
где dP –
элементарная вероятность обнаружить
частицу в элементарном объеме dV.
Уравнение (22) справедливо для действительной
пси-функции (она может быть и комплексной,
в этом случае в уравнение (22) надо
подставлять квадрат модуля пси-функции).
Если область пространства имеет конечный
объем V,
то вероятность P обнаружить
частицу в этом объеме находится
интегрированием выражения (22) по объему V:
|
|
(23) |
Напомним,
что вероятностное
описание движения микрочастиц –
основная идея квантовой механики. Таким
образом, с помощью уравнения Шрёдингера
решается основная задача квантовой
механики: описание движения исследуемого
объекта, в данном случае квантово-механической
частицы.
Отметим
еще ряд важных обстоятельств. Как видно
из формулы (21), уравнение Шрёдингера
является дифференциальным уравнением
второго порядка. Следовательно, в
процессе его решения появятся две
произвольные постоянные. Как их найти?
Для этого используют так называемые граничные
условия:
из конкретного содержания физической
задачи должно быть известно значение
пси-функции на границах области движения
микрочастицы. Кроме того, используется
так называемое условие
нормировки,
которому должна удовлетворять пси-функция:
|
|
(24) |
Смысл
этого условия прост: вероятность
обнаружить частицу хоть где-нибудь
внутри области ее движения есть
достоверное событие, вероятность
которого равна единице.
Именно
граничные условия наполняют решение
уравнения Шрёдингера физическим смыслом.
Без этих условий решение уравнения есть
чисто математическая задача, лишенная
физического смысла. В следующем разделе
на конкретном примере рассмотрено
применение граничных условий и условия
нормировки при решении уравнения
Шрёдингера.
Пси-функция
Волнова́я
фу́нкция (функция
состояния, пси-функция, амплитуда
вероятности)
— комплекснозначная
функция,
используемая вквантовой
механике для вероятностного
описания состоянияквантовомеханической
системы.
В широком смысле — то же самое, что
и вектор
состояния.
Вариант
названия «амплитуда вероятности» связан
со статистической
интерпретацией волновой
функции: плотность вероятности нахождения
частицы в данной точке пространства в
данный момент времени равна квадрату
абсолютного значения волновой функции
этого состояния.
Физический
смысл квадрата модуля волновой функции
Волновая
функция зависит
от координат (или обобщённых координат)
системы и, в общем случае, от времени, и
формируется таким образом,
чтобы квадрат её модуля представлял
собой плотность вероятности (для
дискретных спектров — просто вероятность)
обнаружить систему в положении,
описываемом координатами в
момент времени :
.
Тогда
в заданном квантовом состоянии системы,
описываемом волновой функцией ,
можно рассчитать вероятность того,
что частица будет обнаружена в любой
области пространства конечного
объема :
.
Набор
координат, которые выступают в
роли аргументов
функции,
представляет собой полный
набор физических величин,
которые можно измерить в системе. В
квантовой механике возможно выбрать
несколько полных наборов величин,
поэтому волновая функция одного и того
же состояния может быть записана от
разных аргументов. Выбранный для записи
волновой функции полный набор величин
определяетпредставление
волновой функции.
Так,
возможны координатное представление, импульсное представление,
в квантовой
теории поля используется вторичное
квантование и представление
чисел заполнения или
представление
Фока и
др.
Если
волновая функция, например, электрона
в атоме, задана в координатном
представлении, то квадрат модуля волновой
функции представляет собой плотность
вероятности обнаружить электрон в той
или иной точке пространства. Если эта
же волновая функция задана в импульсном
представлении, то квадрат её модуля
представляет собой плотность вероятности
обнаружить тот или иной импульс.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Комплексная функция, используемая в квантовой механике для описания состояния квантовомеханической системы.
Волновая функция связана с плотностью вероятности нахождения частицы в некоторой области пространства в некоторый момент времени следующим образом: вероятность нахождения частицы в некоторой точке пропорциональна квадрату модуля волновой функции в ней.
Волновая функция является функцией от всех степеней свободы этой частицы, которым, в свою очередь, соответствует некоторый набор коммутирующих квантовых переменных.
В отличие от классического описания, в котором частицы рассматриваются как материальные точки, имеющие определенную координату, а их движение полностью описывается траекторией и скоростью, волна, когда ее описывает волновая функция, не локализована в одной точке, а в общем виде занимает все бесконечное пространство (хотя большая ее часть, как правило, сосредоточена в некоторой области). Таким образом, при таком описании понятие траектории не имеет смысла, а движение описывается в терминах потока энергии и импульса.
С волновой природой частиц связаны такие явления, как дифракция и интерференция массивных частиц, квантование уровней энергии гармонического осциллятора, принцип неопределенности и другие.
Описание квантовой системы с помощью функции, которая бы описывала ее волновые свойства предложил Эрвин Шредингер.
Свойства волновой функции
Поскольку волновая функция является комплексной, ее можно выразить в виде
ψ=R(x,y,z,t)eiα(x,y,z,t)ψ = R (x, y, z, t) ei α (x, y, z, t)
В таком случае R является модулем функции, аа eiei αα (x,y,z,t)(x, y, z, t) называют фазовым множителем.
Из этой записи видно, что при умножении волновой функции на некоторое число eiei ββ, значения амплитуд вероятности, что ей отвечают, не изменятся. Такое умножение называется глобальным фазовым поворотом, или глобальным калибровочным преобразованием, а симметрия относительно такого преобразования (она относится к группе симметрии U (1)) является одним из видов калибровочной инвариантности.
Из физических соображений, на ψψ-функцию накладываются следующие ограничения: она должна быть однозначной, непрерывной и квадратично-интегрированной (последнее условие означает существование интеграла от квадрата функции).
Также, поскольку частица не может бесследно исчезнуть, вероятность нахождения ее в бесконечно большом пространстве будет равна единице, то есть является достоверной:
∫∞∣ψ(r,t)∣2dV=1{{intlimits_{infty }{left| psi (r,t) right|}}^{2}}dV=1
Это условие называется условием нормирования волновой функции. Она выполняется в практически во всех реальных случаях, однако в некоторых важных теоретических моделях, таких как модель частицы, движущейся при отсутствии внешних полей, ψ-функция не приходит в бесконечности, а потому нормирование не представляется возможным. Такие состояния называют делокализованными.
Обычно при выводе волновой функции из некоторых теоретических соображений, ψψ-функция оказывается ненормированной, и этот интеграл оказывается равным некоторому числу n. В таком случае, для нормирования достаточно разделить ψψ-функцию на n.
Уравнение Шредингера
Основным уравнением квантовой механики, которое используется для нахождения волновой функции в конкретных условиях является уравнение Шредингера:
iℏdψ(r,t)dt=−ℏ22mΔψ(r,t)+U(x,y,z,t)ψ,ihbar frac{dpsi (r,t)}{dt}=-frac{{{hbar }^{2}}}{2m}Delta psi (r,t)+U(x,y,z,t)psi,
где UU — потенциальная энергия, а ΔΔ — лапласиан.
Для нахождения ψψ-функции, уравнение сначала решают в общем виде для заданного U, а затем, подставляя граничные условия, получают частное решение.
Поскольку уравнение Шредингера является линейным и однородным дифференциальным уравнением, оно обладает важным свойством: если оно имеет несколько решений, φ1φ1, φ2φ2, φ3φ3 и т.д., то любая линейная комбинация этих решений также будет решением.
Это свойство называется принципом суперпозиции. Его физическая интерпретация заключается в том, что частица имеет некую вероятность нахождения в любом из возможных для нее состояний.
Практически важным вариантом уравнения Шредингера является случай стационарного поля, то есть такого, когда U не зависит от времени. В таком поле волновая функция тоже является стационарной. Кроме того, в этом случае полная механическая энергия частицы остается постоянной.
Уравнение Шредингера является нерелятивистским и не учитывает спин частиц.
Для таких случаев используются уравнения Клейна-Гордона и уравнение Паули для частиц со спином.
Тест по теме «Волновая функция»
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В соответствии с корпускулярно — волновым дуализмом в квантовой физике состояние частицы описывается при помощи волновой функции ($psi (overrightarrow{r},t)$- пси-функция).
Определение 1
Волновая функция — это функция, которая используется в квантовой механике. Она описывает состояние системы, которая имеет размеры в пространстве. Она является вектором состояния.
Данная функция является комплексной и формально имеет волновые свойства. Движение любой частицы микромира определено вероятностными законами. Распределение вероятности выявляется при проведении большого числа наблюдений (измерений) или большого количества частиц. Полученное распределение аналогично распределению интенсивности волны. То есть в местах с максимальной интенсивностью отмечено максимальное количество частиц.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Набор аргументов волновой функции определяет ее представление. Так, возможно координатное представление: $psi(overrightarrow{r},t)$, импульсное представление: $psi'(overrightarrow{p},t)$ и т.д.
В квантовой физике целью ставится не точность предсказания события, а оценка вероятности того или иного события. Зная величину вероятности, находят средние значения физических величин. Волновая функция позволяет находить подобные вероятности.
Так вероятность присутствия микрочастицы в объеме dV в момент времени t может быть определена как:
где $psi^*$- комплексно сопряженная функция к функции $psi.$ Плотность вероятности (вероятность в единице объёма) равна:
Вероятность является величиной, которую можно наблюдать в эксперименте. В это же время волновая функция не доступна для наблюдения, так как она является комплексной (в классической физике параметры, которые характеризуют состояние частицы, доступны для наблюдения).
Условие нормировки $psi$- функции
Волновая функция определена с точностью до произвольного постоянного множителя. Данный факт не оказывает влияния на состояние частицы, которую $psi$- функция описывает. Однако волновую функцию выбирают таким образом, что она удовлетворяет условию нормировки:
«Волновая функция» 👇
где интеграл берут по всему пространству или по области, в которой волновая функция не равна нулю. Условие нормировки (2) значит то, что во всей области, где $psine 0$ частица достоверно присутствует. Волновую функцию, которая подчинятся условию нормировки, называют нормированной. Если ${left|psiright|}^2=0$, то данное условие означает, что частицы в исследуемой области наверняка нет.
Нормировка вида (2) возможна при дискретном спектре собственных значений.
Условие нормировки может оказаться не осуществимым. Так, если $psi$ — функция является плоской волной де-Бройля и вероятность нахождения частицы является одинаковой для всех точек пространства. Данные случаи рассматривают как идеальную модель, в которой частица присутствует в большой, но имеющей ограничения области пространства.
Принцип суперпозиции волновой функции
Данный принцип является одним их основных постулатов квантовой теории. Его смысл в следующем: если для некоторой системы возможны состояния, описываемые волновыми функциями $psi_1 {rm и} $ $psi_2$, то для этой системы существует состояние:
где $C_{1 }и C_2$ — постоянные коэффициенты. Принцип суперпозиции подтверждается эмпирически.
Можно говорить о сложении любого количества квантовых состояний:
где ${left|C_nright|}^2$ — вероятность того, что система обнаруживается в состоянии, которое описывается волновой функцией $psi_n.$ Для волновых функций, подчиненных условию нормировки (2) выполняется условие:
Стационарные состояния
В квантовой теории особую роль имеют стационарные состояния (состояния в которых все наблюдаемые физические параметры не изменяются во времени). (Сама волновая функция принципиально не наблюдаема). В стационарном состоянии $psi$- функция имеет вид:
где $omega =frac{E}{hbar }$, $psileft(overrightarrow{r}right)$ не зависит от времени, $E$- энергия частицы. При виде (3) волновой функции плотность вероятности ($P$) является постоянной времени:
Из физических свойств стационарных состояний следуют математические требования к волновой функции $psileft(overrightarrow{r}right)to (psi(x,y,z))$.
Математические требования к волновой функции для стационарных состояний
$psileft(overrightarrow{r}right)$- функция должна быть во всех точках:
- непрерывна,
- однозначна,
- конечна.
Если потенциальная энергия имеет поверхность разрыва, то на подобных поверхностях функция $psileft(overrightarrow{r}right)$ и ее первая производная должны оставаться непрерывными. В области пространства, где потенциальная энергия становится бесконечной, $psileft(overrightarrow{r}right)$ должна быть равна нулю. Непрерывность функции $psileft(overrightarrow{r}right)$ требует, чтобы на любой границе этой области $psileft(overrightarrow{r}right)=0$. Условие непрерывности накладывается на частные производные от волновой функции ($frac{partial psi}{partial x}, frac{partial psi}{partial y},frac{partial psi}{partial z}$).
Пример 1
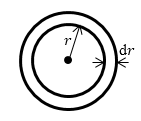
Задание: Для некоторой частицы задана волновая функция вида: $psi=frac{A}{r}e^{-{r}/{a}}$, где $r$ — расстояние от частицы до центра силы (рис.1), $a=const$. Примените условие нормировки, найдите нормировочный коэффициент A.
Рисунок 1.
Решение:
Запишем условие нормировки для нашего случая в виде:
[int{{left|psiright|}^2dV=int{psipsi^*dV=1left(1.1right),}}]
где $dV=4pi r^2dr$ (см.рис.1 Из условий понятно, что задача обладает сферической симметрией). Из условий задачи имеем:
[psi=frac{A}{r}e^{-{r}/{a}}to psi^*=frac{A}{r}e^{-{r}/{a}}left(1.2right).]
Подставим $dV$ и волновые функции (1.2) в условие нормировки:
[intlimits^{infty }_0{frac{A^2}{r^2}e^{-{2r}/{a}}4pi r^2dr=1left(1.3right).}]
Проведем интегрирование в левой части:
[intlimits^{infty }_0{frac{A^2}{r^2}e^{-{2r}/{a}}4pi r^2dr=2pi A^2a=1left(1.4right).}]
Из формулы (1.4) выразим искомый коэффициент:
[A=sqrt{frac{1}{2pi a}}.]
Ответ: $A=sqrt{frac{1}{2pi a}}.$
Пример 2
Задание: Каково наиболее вероятное расстояние ($r_B$) электрона от ядра, если волновая функция, которая описывает основное состояние электрона в атоме водорода может быть определена как: $psi=Ae^{-{r}/{a}}$, где $r$- расстояние от электрона до ядра, $a$ — первый Боровский радиус?
Решение:
Используем формулу, которая определяет вероятность присутствия микрочастицы в объеме $dV$ в момент времени $t$:
[dP={left|psiright|}^2dV=psipsi^*dVleft(2.1right),]
где $dV=4pi r^2dr. $Следователно, имеем:
[dP=4pi r^2A^2e^{-{2r}/{a}}drleft(2.2right).]
В таком случае, $p=frac{dP}{dr}$ запишем как:
[p=4pi r^2A^2e^{-{2r}/{a}}left(2.3right).]
Для определения наиболее вероятного расстояния производную $frac{dp}{dr}$ приравняетм к нулю:
[{left.frac{dp}{dr}right|}_{r=r_B}=8pi rA^2e^{-{2r}/{a}}+4pi r^2A^2e^{-{2r}/{a}}left(-frac{2}{a}right)=8pi rA^2e^{-{2r}/{a}}left(1-frac{r}{a}right)=0(2.4)]
Так как решение $8pi rA^2e^{-{2r_B}/{a}}=0 {rm при} r_Bto infty $, нам не подходит, то отсается:
[1-frac{r_B}{a}=0to r_B=a.]
Ответ: $r_B=a.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
| Квантовая механика |

Принцип неопределённости |
| Введение Математические основы |
|
Основа Классическая механика · Постоянная Планка · Интерференция · Бра и кет · Гамильтониан · Старая квантовая теория |
|
Фундаментальные понятия Квантовое состояние · Квантовая наблюдаемая · Волновая функция · Квантовая суперпозиция · Квантовая запутанность · Смешанное состояние · Измерение · Неопределённость · Принцип Паули · Дуализм · Декогеренция · Теорема Эренфеста · Туннельный эффект |
|
Эксперименты Опыт Дэвиссона — Джермера · Опыт Поппера · Опыт Штерна — Герлаха · Опыт Юнга · Эксперимент квантового ластика · Проверка неравенств Белла · Фотоэффект · Эффект Комптона |
|
Формулировки Представление Шрёдингера · Представление Гейзенберга · Представление взаимодействия · Представление фазового пространства · Матричная квантовая механика · Интегралы по траекториям · Диаграммы Фейнмана |
|
Уравнения Уравнение Шрёдингера · Уравнение Паули · Уравнение Клейна — Гордона · Уравнение Дирака · Уравнение Швингера — Томонаги · Уравнение фон Неймана · Уравнение Блоха · Уравнение Линдблада · Уравнение Гейзенберга |
|
Интерпретации Копенгагенская · Теория скрытых параметров · Многомировая · Теория де Бройля — Бома |
|
Развитие теории Квантовая теория поля · Квантовая электродинамика · Теория Глэшоу — Вайнберга — Салама · Квантовая хромодинамика · Стандартная модель · Квантовая гравитация |
|
Сложные темы Квантовая теория поля · Квантовая гравитация · Теория всего |
|
Известные учёные Планк · Эйнштейн · Шрёдингер · Гейзенберг · Йордан · Бор · Паули · Дирак · Фок · Борн · де Бройль · Ландау · Фейнман · Бом · Эверетт |
| См. также: Портал:Физика |
|
п • о • р |
Волнова́я фу́нкция, или пси-фу́нкция 

где 

Согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.
Содержание
- 1 Физический смысл
- 2 Нормированность волновой функции
- 3 Принцип суперпозиции квантовых состояний
- 4 Условия регулярности волновой функции
- 5 Волновая функция в различных представлениях
- 6 Матричная и векторная формулировки
- 7 Описание смешанных квантовых состояний
- 8 См. также
- 9 Литература
- 10 Ссылки
Физический смысл
В координатном представлении волновая функция 





Тогда в заданном квантовом состоянии системы, описываемом волновой функцией 




Следует также отметить, что возможно измерение и разницы фаз волновой функции, например, в опыте Ааронова — Бома.
Нормированность волновой функции
Волновая функция 
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо в пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении.
Принцип суперпозиции квантовых состояний
Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями 

при любых комплексных 

Очевидно, что можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния системы, которое описывается волновой функцией 
В таком состоянии квадрат модуля коэффициента 

Поэтому для нормированных волновых функций 
Условия регулярности волновой функции
Вероятностный смысл волновой функции накладывает определенные ограничения, или условия, на волновые функции в задачах квантовой механики. Эти стандартные условия часто называют условиями регулярности волновой функции.
- Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких, что интеграл
станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией, т.е принадлежала гильбертовому пространству
. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.
- Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.
- Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции
,
,
. Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.
Волновая функция в различных представлениях
Набор координат, которые выступают в роли аргументов функции, представляет собой полную систему коммутирующих наблюдаемых. В квантовой механике возможно выбрать несколько полных наборов наблюдаемых, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор величин определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и др.
Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.
Матричная и векторная формулировки
Волновая функция одного и того же состояния в различных представлениях — будет соответствовать выражению одного и того же вектора в разных системах координат. Остальные операции с волновыми функциями так же будут иметь аналоги на языке векторов.
В волновой механике используется представление, где аргументами пси-функции является полная система непрерывных коммутирующих наблюдаемых, а в матричной используется представление, где аргументами пси-функции является полная система дискретных коммутирующих наблюдаемых. Поэтому функциональная (волновая) и матричная формулировки очевидно математически эквивалентны.
Описание смешанных квантовых состояний
Волновая функция представляет собой метод описания чистого состояния квантовомеханической системы. Смешанные квантовые состояния (в квантовой статистике) следует описывать при помощи матрицы плотности.
См. также
- Собственное состояние
- Оператор (физика)
- Уравнение Шрёдингера
- Принцип неопределённости Гейзенберга
- Блоховская волна
- Редукция волновой функции
- Функция Вигнера
Литература
- Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др. — М.: Сов. Энциклопедия, 1984. — 944 с.
Ссылки
- Квантовая механика — статья из Большой советской энциклопедии.
- Физический энциклопедический словарь: Квантовая механика»
| Квантовая механика | ||||||||||||||||
|
|
||||||||||||||||
| Принцип неопределённости | ||||||||||||||||
| Введение …
Математическая формулировка …
|
||||||||||||||||
Волнова́я фу́нкция (функция состояния, пси-функция, амплитуда вероятности) — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния квантовомеханической системы, имеющей протяжённость в пространстве. В широком смысле — то же самое, что и вектор состояния.
Вариант названия «амплитуда вероятности» связан с копенгагенской интерпретацией квантовой механики: плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния.
Содержание
- 1 Физический смысл квадрата модуля волновой функции
- 2 Принцип суперпозиции квантовых состояний
- 3 Условия регулярности волновой функции
- 4 Свойство нормировки волновой функции
- 5 Матричная и векторная формулировки
- 6 Философский смысл волновой функции
- 7 См. также
- 8 Литература
- 9 Ссылки
Физический смысл квадрата модуля волновой функции
Волновая функция 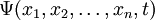
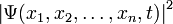
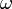
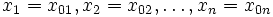
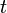
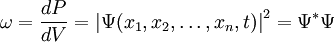
Тогда в заданном квантовом состоянии системы, описываемом волновой функцией 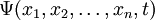
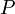
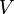
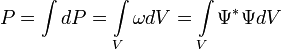
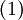
Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор величин определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и др.
Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.
Принцип суперпозиции квантовых состояний
Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями 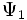
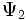
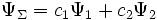
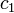
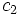
Очевидно, что можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния системы, которое описывается волновой функцией 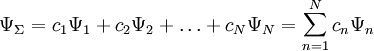
В таком состоянии квадрат модуля коэффициента 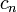
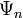
Поэтому для нормированных волновых функций 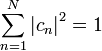
Условия регулярности волновой функции
Вероятностный смысл волновой функции накладывает определенные ограничения, или условия, на волновые функции в задачах квантовой механики. Эти стандартные условия часто называют условиями регулярности волновой функции.
- Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких, что интеграл
станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.
- Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.
- Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции
,
,
. Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.
Свойство нормировки волновой функции
Отметим свойство нормировки волновой функции 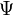
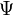
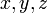
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией во всем пространстве равна единице.
Матричная и векторная формулировки
Одна и та же волновая функция в различных представлениях — будет соответствовать выражению одного и того же вектора в разных системах координат. Остальные операции с волновыми функциями так же будут иметь аналоги на языке векторов.
Функциональная (волновая), матричная и векторная формулировки математически эквивалентны.
Философский смысл волновой функции
Волновая функция представляет собой метод описания чистого состояния квантовомеханической системы. Смешанные квантовые состояния (в квантовой статистике) следует описывать оператором типа матрицы плотности. То есть, некая обобщённая функция от двух аргументов должна описать корреляцию нахождения частицы в двух точках.
Следует понимать, что проблема, которую решает квантовая механика, — это проблема самой сути научного метода познания мира. Если представить себе бильярдный стол, закрытый непроницаемой крышкой, и единственным способом исследования вопроса, есть ли на нём бильярдные шары, предположить закатывание в стол других шаров, то мы и получаем ту самую проблему, для решения которой привлечён метод квантовой механики. Пока вброшенный шар проходит сквозь стол без изменения траектории, предсказуемо, мы можем сделать вывод о том, что на траектории шара других шаров нет. Если в результате взаимодействия шаров на столе мы получаем выкатившиеся несколько шаров с различными конечными импульсами и точками, в которых шары покинули стол, то мы можем лишь предполагать о том, каким образом происходило взаимодействие в системе. Если же лузы в бильярдном столе ограничивают возможность шаров покидать стол (энергетический барьер), то система запутывается ещё больше. Подобный пример с бильярдом очень наглядно демонстрирует те трудности, с которыми сталкиваются исследователи, разрабатывая инструменты квантовой механики.
См. также
- Собственное состояние
- Оператор (физика)
- Уравнение Шрёдингера
- Принцип неопределённости Гейзенберга
- Блоховская волна
- Редукция волновой функции
- Функция Вигнера
Литература
- Физический энциклопедический словарь./Гл. ред. А.М.Прохоров. Ред. кол. Д.М.Алексеев, А.М.Бонч-Бруевич, А.С.Боровик-Романов и др. — М.: Сов. Энциклопедия, 1984. — 944 с.
Ссылки
- Большая Советская Энциклопедия: Квантовая механика, Яндекс.Словари
- Физический энциклопедический словарь: Квантовая механика»
Wikimedia Foundation.
2010.









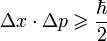
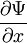 ,
, 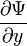 ,
, 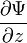 . Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.
. Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.