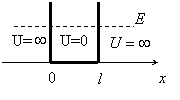Как найти пси по графику

Уравнение
Шрёдингера названо в честь австрийского
физика Эрвина Шрёдингера (E. Schrödinger). Это
основной теоретический инструмент
квантовой механики. В квантовой механике
уравнение Шрёдингера играет такую же
роль, как уравнение движения (второй
закон Ньютона) в механике классической.
Уравнение Шрёдингера записывается для
так называемой y —
функции (пси — функции). В общем случае
пси — функция – это функция координат
и времени: y = y (x,y,z,t).
Если микрочастица находится в стационарном
состоянии, то пси — функция не зависит
от времени: y= y (x,y,z).

В
простейшем случае одномерного движения
микрочастицы (например, только по оси x)
уравнение Шрёдингера имеет вид:

(21)

где y (x) –
пси — функция, зависящая только от одной
координаты x; m – масса
частицы; —
постоянная Планка (=h/2π ); E –
полная энергия частицы, U –
потенциальная энергия. В классической
физике величина (E
–U) равнялась
бы кинетической энергии частицы. В
квантовой механике вследствие соотношения
неопределенностей понятие
кинетической энергии лишено смысла.
Заметим, что потенциальная энергия U –
это характеристика внешнего
силового поля,
в котором движется частица. Это величина
вполне определенная. Она также является
функцией координат, в данном
случае U=U(x,y,z).

В
трехмерном случае, когда y = y (x,y,z), вместо
первого слагаемого 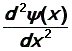в
уравнении Шрёдингера следует записать
сумму трех частных производных от
пси-функции по трем координатам.

Для
чего применяется уравнение Шрёдингера?
Как уже отмечалось, это основное уравнение
квантовой механики. Если его записать
и решить (что вообще не простая задача)
для конкретной микрочастицы, то мы
получим значение пси-функции в любой
точке пространства, в котором движется
частица. Что это дает? Квадрат модуля
пси-функции характеризуетвероятность обнаружения
частицы в той или иной области пространства.
Возьмем некоторую точку в пространстве
с координатами x,y,z (рис.6).
Какова вероятность обнаружить частицу
в этой точке? Ответ: эта вероятность
равна нулю! (точка не имеет размеров,
попасть в точку частица просто физически
не может). Значит, вопрос поставлен
некорректно. Поставим его иначе: какова
вероятность обнаружить частицу в малой
области пространства объемом dV
= dx dy dz с
центром в выбранной точке? Ответ:

(22)

где dP –
элементарная вероятность обнаружить
частицу в элементарном объеме dV.
Уравнение (22) справедливо для действительной
пси-функции (она может быть и комплексной,
в этом случае в уравнение (22) надо
подставлять квадрат модуля пси-функции).
Если область пространства имеет конечный
объем V,
то вероятность P обнаружить
частицу в этом объеме находится
интегрированием выражения (22) по объему V:

(23)

Напомним,
что вероятностное
описание движения микрочастиц –
основная идея квантовой механики. Таким
образом, с помощью уравнения Шрёдингера
решается основная задача квантовой
механики: описание движения исследуемого
объекта, в данном случае квантово-механической
частицы.

Отметим
еще ряд важных обстоятельств. Как видно
из формулы (21), уравнение Шрёдингера
является дифференциальным уравнением
второго порядка. Следовательно, в
процессе его решения появятся две
произвольные постоянные. Как их найти?
Для этого используют так называемые граничные
условия:
из конкретного содержания физической
задачи должно быть известно значение
пси-функции на границах области движения
микрочастицы. Кроме того, используется
так называемое условие
нормировки,
которому должна удовлетворять пси-функция:

(24)

Смысл
этого условия прост: вероятность
обнаружить частицу хоть где-нибудь
внутри области ее движения есть
достоверное событие, вероятность
которого равна единице.

Именно
граничные условия наполняют решение
уравнения Шрёдингера физическим смыслом.
Без этих условий решение уравнения есть
чисто математическая задача, лишенная
физического смысла. В следующем разделе
на конкретном примере рассмотрено
применение граничных условий и условия
нормировки при решении уравнения
Шрёдингера.

Пси-функция

Волнова́я
фу́нкция (функция
состояния, пси-функция, амплитуда
вероятности)
— комплекснозначная
функция,
используемая вквантовой
механике для вероятностного
описания состоянияквантовомеханической
системы.
В широком смысле — то же самое, что
и вектор
состояния.

Вариант
названия «амплитуда вероятности» связан
со статистической
интерпретацией волновой
функции: плотность вероятности нахождения
частицы в данной точке пространства в
данный момент времени равна квадрату
абсолютного значения волновой функции
этого состояния.

Физический
смысл квадрата модуля волновой функции 

Волновая
функция зависит
от координат (или обобщённых координат)
системы и, в общем случае, от времени, и
формируется таким образом,
чтобы квадрат её модуля представлял
собой плотность вероятности (для
дискретных спектров — просто вероятность)
обнаружить систему в положении,
описываемом координатами в
момент времени :

.

Тогда
в заданном квантовом состоянии системы,
описываемом волновой функцией ,
можно рассчитать вероятность того,
что частица будет обнаружена в любой
области пространства конечного
объема :      .

Набор
координат, которые выступают в
роли аргументов
функции,
представляет собой полный
набор физических величин,
которые можно измерить в системе. В
квантовой механике возможно выбрать
несколько полных наборов величин,
поэтому волновая функция одного и того
же состояния может быть записана от
разных аргументов. Выбранный для записи
волновой функции полный набор величин
определяетпредставление
волновой функции.
Так,
возможны координатное представление, импульсное представление,
в квантовой
теории поля используется вторичное
квантование и представление
чисел заполнения или
представление
Фока и
др.

Если
волновая функция, например, электрона
в атоме, задана в координатном
представлении, то квадрат модуля волновой
функции представляет собой плотность
вероятности обнаружить электрон в той
или иной точке пространства. Если эта
же волновая функция задана в импульсном
представлении, то квадрат её модуля
представляет собой плотность вероятности
обнаружить тот или иной импульс.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Печатать эту главу

В настоящей статье приведены значения функций Γ(x)Gamma(x), ψ(x)=(d/dx) Ln Γ(x)psi(x) =(d /d x) ,mathrm{Ln},Gamma(x), Π(x)=Γ(x+1)mathbf{Pi}(x) =Gamma(x +1) и Ψ(x)=ψ(x+1)Psi(x) =psi(x+1) для целых и полуцелых значений их аргументов, а также значения функций ψ(x)psi(x) и Ψ(x)Psi(x) для любых рациональных значений их аргументов.

В формулах используются постоянная Эйлера-Маскерони cEc_{scriptscriptstyle E} и функция Похгамера

Fm(z)≡∏k=0m−1(z+k)  .mathcal{F}_m (z)equiv prod_{k=0}^{m-1}(z+k) ;.

Значения функций Γ(x) и Π(x) для целых и полуцелых значений аргумента

Π(0)=Π(1)=1  ,Γ(1)=Γ(2)=1  ,mathbf{Pi}(0) =mathbf{Pi}(1) =1 ;,
qquad Gamma(1) =Gamma(2) =1 ;,

Π(m)=Γ(m+1)=m!=∏k=1mk=1⋅2⋅3⋅…⋅m(m=1,2,3,…)  ,mathbf{Pi}(m) =Gamma(m+1) =m! =prod_{k=1}^{m} k
= 1cdot 2cdot 3cdot…cdot m qquad (m=1,2,3,…) ;,

Π(−1/2)=Γ(1/2)=π  ,mathbf{Pi}(-1/2) =Gamma(1/2) =sqrt{pi} ;,

Π(m−1/2)=Γ(m+1/2)=Fm(1/2)⋅π=π⋅(2 m)!m! 4m  ,mathbf{Pi}(m -1/2) =Gamma(m +1/2) =mathcal{F}_m (1/2)cdot sqrt{pi}
=sqrt{pi}cdot frac{(2 ,m)!}{m! ,4^m} ;,

Π(−m−1/2)=Γ(−m+1/2)=(−1)m⋅πFm(1/2)=(−1)m π⋅m! 4m(2m)!  .mathbf{Pi}(-m -1/2) =Gamma(-m +1/2) =(-1)^m cdot frac{ sqrt{pi} }{ mathcal{F}_m (1/2) }
=(-1)^m ,sqrt{pi}cdot frac{m! ,4^m}{(2 m)!} ;.

<<<<

Выражение для Π(−1/2)mathbf{Pi}(-1/2) можно получить с помощью формулы умножения Гаусса–Лежандра для функции Π(z)mathbf{Pi}(z) (см. п. 4 статьи «Функциональные уравнения для гамма-функции и пси-функции»), если в этой формуле положить m=2m=2 и z=0z=0.

>>>>

Произведения четных и нечетных чисел

2−m⋅(2 m)!/m!=∏k=1m(2 k−1)=1⋅3⋅5⋅…⋅(2 m−1)  ,2^{-m}cdot (2 ,m)!/m!
=prod_{k=1}^{m} (2 ,k -1) =1cdot 3cdot 5cdot…cdot(2 ,m -1) ;,

2m⋅m!=∏k=1m(2 k)=2⋅4⋅6⋅…⋅2 m  .2^mcdot m!
=prod_{k=1}^{m} (2 ,k) =2cdot 4cdot 6cdot…cdot 2 ,m ;.

Значения функций ψ(x) и Ψ(x) для целых и полуцелых значений аргумента

Ψ(0)=ψ(1)=−cE  ,Psi(0) =psi(1) =-c_{scriptscriptstyle E} ;,

Ψ(m)=ψ(m+1)=−cE+∑k=1mk−1(m=1,2,3,…);Psi(m) =psi(m+1) =-c_{scriptscriptstyle E} +sum_{k=1}^{m} k^{-1} qquad (m=1,2,3,…);

Ψ(−1/2±m)=ψ(1/2±m)=−cE−2 ln⁡2+2 ∑k=1m(2 k−1)−1  .Psi(-1/2 pm m) =psi(1/2 pm m)
=-c_{scriptscriptstyle E} -2 ,ln 2 +2 ,sum_{k=1}^{m} (2 ,k -1)^{-1} ;.

<<<<

Выражение для Ψ(−1/2)Psi(-1/2) можно получить с помощью формулы умножения для функции Ψ(z)Psi(z) (см. п. 4 статьи «Функциональные уравнения для гамма-функции и пси-функции»), если в этой формуле положить m=2m=2 и z=0z=0.

>>>>

Значения функций ψ(x) и Ψ(x) для дробных значений аргумента

Ψ(−m/n)=ψ(−m/n+1)=−cE−ln⁡(2n)+2π4 tan⁡(2πm/(2n))Psi(-m/n) =psi(-m/n +1) = -c_{scriptscriptstyle E} -ln(2 n) +frac{2pi}{ 4 ,tanbigl(2pi m/(2 n)bigr) }

+2 ∑k=1(n−1)/2cos⁡(2πkm/n)⋅ln⁡(sin⁡(2πk/(2n)))  ,+2 ,sum_{k=1}^{(n-1)/2}
cos(2pi km/n)cdot lnBigl(sinbigl(2pi k/(2 n)bigr)Bigr) ;,

Ψ(m/n−1)=ψ(m/n)=−cE−ln⁡(2n)−2π4 tan⁡(2πm/(2n))Psi(m/n -1) =psi(m/n) = -c_{scriptscriptstyle E} -ln(2 n) -frac{2pi}{ 4 ,tanbigl(2pi m/(2 n)bigr)}

+2 ∑k=1(n−1)/2cos⁡(2πkm/n)⋅ln⁡(sin⁡(2πk/(2n)))  .+2 ,sum_{k=1}^{(n-1)/2}
cos(2pi k m/n)cdot lnBigl(sinbigl(2pi k/(2 n)bigr)Bigr) ;.

В частности,

Ψ(−1/2)=ψ(1/2)=−cE−2 ln⁡2  ,Psi(-1/2) =psi(1/2) = -c_{scriptscriptstyle E} -2 ,ln 2 ;,

Ψ(−1/3)=ψ(2/3)=−cE−(3/2)⋅ln⁡3+2π/(43)  ,Psi(-1/3) =psi(2/3) = -c_{scriptscriptstyle E} -(3/2)cdot ln 3 +2pi /bigl(4sqrt{3}bigr) ;,

Ψ(−2/3)=ψ(1/3)=−cE−(3/2)⋅ln⁡3−2π/(43)  ,Psi(-2/3) =psi(1/3) = -c_{scriptscriptstyle E} -(3/2)cdot ln 3 -2pi /bigl(4sqrt{3}bigr) ;,

Ψ(−1/4)=ψ(3/4)=−cE−3 ln⁡2+2π/4  ,Psi(-1/4) =psi(3/4) = -c_{scriptscriptstyle E} -3 ,ln 2 +2pi/4 ;,

Ψ(−3/4)=ψ(1/4)=−cE−3 ln⁡2−2π/4  .Psi(-3/4) =psi(1/4) = -c_{scriptscriptstyle E} -3 ,ln 2 -2pi/4 ;.

<<<<

Вывод второй из приведенных здесь формул см. в приложении A.1.

>>>>

Приложение. Вывод формул и доказательства теорем

Значения функции Ψ(x)Psi(x) для дробных значений аргумента

Здесь будет выведена формула, приведенная в п. 4.

Для функции Ψ(z)Psi(z) используем интегральное представление п. 2-a) статьи «Интегральные представления гамма-функции и связанных с ней функций».

Положив z=m/n−1z=m/n-1, где 0<m<n0<m<n, и сделав подстановку t=snt=s^n, получим

cE+Ψ(m/n−1)=∫011−tm/n−11−t dt=∫01F(s) ds  ,c_{scriptscriptstyle E} +Psi(m/n-1)
=int_0^1 frac{ 1 -t^{m/n-1} }{1-t} ,d t
=int_0^1 F(s) ,d s ;,

где

F(s)=n sm−1−sn−1sn−1  .F(s) =n ,frac{ s^{m-1} -s^{n-1} }{s^n -1} ;.

Учитывая, что

sn−1=(s−1) ∏k=1n−1(s−ei 2πk/n)  ,s^n -1 =(s-1) ,prod_{k=1}^{n-1} bigl(s -e^{i ,2pi k/n}bigr) ;,

мы можем представить функцию F(s)F(s) в виде суммы элементарных дробей

F(s)=∑k=1n−1ei 2πk m/n−1s−ei 2πk/n  .F(s) =sum_{k=1}^{n-1} frac{ e^{i ,2pi k ,m/n} -1 }{ s -e^{i ,2pi k/n} } ;.

В результате получаем

cE+Ψ(m/n−1)=∑k=1n−1(ei 2πk m/n−1)⋅ln⁡(1−e−i 2πk/n)  .c_{scriptscriptstyle E} +Psi(m/n-1)
=sum_{k=1}^{n-1} bigl(e^{i ,2pi k ,m/n} -1bigr)
cdot lnbigl(1 -e^{-i ,2pi k/n}bigr) ;.

Для того чтобы преобразовать выражение в правой части последнего равенства, мы используем несколько вспомогательных соотношений:

a)

∑k=1n−1ln⁡(s−e−i 2πk/n)=ln⁡∏k=1n−1(s−e−i 2πk/n)=ln⁡sn−1s−1=ln⁡(1+s+…+sn−1)  ,sum_{k=1}^{n-1} lnbigl(s -e^{-i ,2pi k/n}bigr)
=ln prod_{k=1}^{n-1} bigl(s -e^{-i ,2pi k/n}bigr)
=ln frac{s^n -1}{s-1} =ln(1 +s +…+s^{n-1}) ;,

откуда следует

∑k=1n−1ln⁡(1−e−i 2πk/n)=ln⁡n  .sum_{k=1}^{n-1} lnbigl(1 -e^{-i ,2pi k/n}bigr) =ln n ;.

b)

∑k=1n−1ei kξ=ei nξ/2 sin⁡((n−1) ξ/2)sin⁡(ξ/2)  ,sum_{k=1}^{n-1} e^{i ,kxi}
=e^{i ,n xi/2} ,frac{ sinbigl((n-1) ,xi/2bigr) }{sin(xi/2)} ;,

откуда следует

∑k=1n−1ei 2πk m/n=−1  .sum_{k=1}^{n-1} e^{i ,2pi k ,m/n} =-1 ;.

c)

∑k=1n−1k ei kξ=14 (sin⁡(ξ/2))2⋅(n ei (n−1) ξ−(n−1) ei nξ−1)  ,sum_{k=1}^{n-1} k ,e^{i ,kxi} =frac{1}{ 4 ,bigl(sin(xi/2)bigr)^2 }
cdot Bigl(n ,e^{i ,(n-1) ,xi} -(n-1) ,e^{i ,n xi} -1Bigr) ;,

откуда следует

∑k=1n−1k ei 2πk m/n=−i n e−i 2πm/(2n)2 sin⁡(2πm/(2n))=−i n2 tan⁡(2πm/(2n))−n2  .sum_{k=1}^{n-1} k ,e^{i ,2pi k ,m/n}
=frac{ -i ,n ,e^{-i ,2pi m/(2n)} }{ 2 ,sinbigl(2pi m/(2n)bigr) }
=frac{-i ,n}{ 2 ,tanbigl(2pi m/(2n)bigr) } -frac{n}{2} ;.

В результате получаем

cE+Ψ(m/n−1)=−ln⁡n+∑k=1n−1ei 2πk m/n⋅ln⁡(1−e−i 2πk/n)c_{scriptscriptstyle E} +Psi(m/n-1) =-ln n
+sum_{k=1}^{n-1} e^{i ,2pi k ,m/n}cdot lnbigl(1 -e^{-i ,2pi k/n}bigr)

=−ln⁡n+∑k=1n−1ei 2πk m/n⋅(ln⁡2+i 2π4−i π kn)+∑k=1n−1ei 2πk m/n⋅ln⁡sin⁡(π k/n)=-ln n
+sum_{k=1}^{n-1} e^{i ,2pi k ,m/n}cdot Bigl(ln 2 +i ,frac{2pi}{4}
-i ,frac{pi ,k}{n}Bigr)
+sum_{k=1}^{n-1} e^{i ,2pi k ,m/n}cdot ln sin(pi ,k/n)

=−ln⁡(2 n)−2π4 tan⁡(π m/n)+∑k=1n−1ei 2πk m/n⋅ln⁡sin⁡(π k/n)  .=-ln(2 ,n) -frac{2pi}{ 4 ,tan(pi ,m/n) }
+sum_{k=1}^{n-1} e^{i ,2pi k ,m/n}cdot ln sin(pi ,k/n) ;.

Последнюю сумму можно преобразовать с помощью соотношения

∑k=1n−1zk=∑k=1(n−1)/2(zk+zn−k)  ;sum_{k=1}^{n-1} z_k =sum_{k=1}^{(n-1)/2} (z_k +z_{n-k}) ;;

в итоге, получаем необходимый результат.

Литература

1. Под ред. М. Абрамовица, И. Стиган. Справочник по специальным функциям с формулами, графиками, математическими таблицами. – Москва, «Наука», 1979, 830 с. Перевод с английского: Edited by M. Abramowitz and I.A. Stegun. Handbook of Mathematical Functions with formulas, graphs and mathematical tables. – National bureau of standards. Applied mathematics series – 55, 1964.

2. Г.Бейтмен, А.Эрдейи. Высшие трансцендентные функции, т. 1. СБМ.
   Высшие трансцендентные функции, т. 1. Гипергеометрическая функция. Функции Лежандра. – Москва, «Наука», 1973; 297с.
   Перевод с английского: H. Bateman, A. Erdelyi. Higher Transcendental Functions, Volume 1. MC Graw-Hill Book Company, Inc., New York — Toronto — London, 1953.

3. http://www.wolfram.com – Internet-page of the firm WolframResearch.

4. А.Ф. Никифоров, В.Б. Уваров. Специальные функции математической физики. – Москва, «Наука», 1984, 344 с.

5. А.П. Прудников, Ю.А. Брычков, О.И. Маричев. Интегралы и ряды. Элементарные функции. – Москва, «Наука», 1981, 800 с.

6. А.П. Прудников, Ю.А. Брычков, О.И. Маричев. Интегралы и ряды. Специальные функции. – Москва, «Наука», 1983, 752 с.

7. А.П. Прудников, Ю.А. Брычков, О.И. Маричев. Интегралы и ряды. Дополнительные главы. – Москва, «Наука», 1986, 800 с.

8. Е. Янке, Ф. Эмде, Ф. Леш. Специальные функции. – Москва, «Наука», 1968, 344 с.
   Перевод с немецкого: E. Janke, F. Emde, F. Lösch. Tafeln Höherer Funktionen. B.G. Teubner–Verlagsgesellschaft–Stuttgart, 1960, 344 p.

УРАВНЕНИЕ ШРЁДИНГЕРА 1

Гипотеза де Бройля Каждой частице можно поставить в соответствие волну вероятности Длина этой волны определяется соотношением

Смысл пси-функции Интенсивность волны пропорциональна квадрату амплитуды. Поэтому мы говорим только о квадрате модуля амплитуды волновой функции который имеет вероятности. смысл плотности

Смысл пси-функции ИТАК: Величина есть плотность вероятности, а величина — вероятность обнаружить частицу в объеме

Свойства пси-функции • Пси функция непрерывная. • Пси функция гладкая (то есть её производная тоже непрерывная). • Пси-функция нормирована, то есть интеграл квадрата её модуля по всему объёму равен единице

Размерность пси-функции Вероятность – безразмерная величина. Поэтому в трехмерном случае откуда получаем

Размерность пси-функции Соответственно в двухмерном случае и в одномерном

ПРИМЕР Задана пси-функция Ψ(x, y, z) частицы. Вероятность того, что частица будет обнаружена в объёме V, определяется выражением … Варианты ответов: 1) 4) 2) 3) 5) Даже не зная определения и смысла пси-функции, видим, что единственная безразмерная величина – в пятом ответе. Но определение лучше знать !

Волновое уравнение – уравнение Шрёдингера Поскольку пси-функция является волной, то она должна удовлетворять волновому уравнению: С другой стороны, волновой процесс предполагает, что в точке с координатами происходит колебательный процесс.

Волновое уравнение – уравнение Шрёдингера В свою очередь, это означает, что процесс в точке удовлетворяет дифференциальному уравнению колебаний где

Волновое уравнение – уравнение Шрёдингера Таким образом, можно сделать подстановку, и из уравнений получить

Волновое уравнение – уравнение Шрёдингера Или, выражая частоту через длину волны

Волновое уравнение – уравнение Шрёдингера Упростим, и учтем, что длина волны функции вероятности равна дебройлевской длине волны

Волновое уравнение – уравнение Шрёдингера Упростим, и учтем, что длина волны функции вероятности равна дебройлевской длине волны где — импульс частицы.

Волновое уравнение – уравнение Шрёдингера Выразим импульс частицы через её энергию. Если частица движется в поле с потенциальной энергией обладая при этом полной энергией то её кинетическую энергию можно записать так:

Волновое уравнение – уравнение Шрёдингера Таким образом Мы получили стационарное, то есть независящее от времени уравнение Шрёдингера. Его надо выучить.

Волновое уравнение – уравнение Шрёдингера Используя оператор Лапласа, уравнение можно переписать в виде или Эти уравнения тоже лучше выучить.

Волновое уравнение – уравнение Шрёдингера Нестационарное, то есть зависящее от времени уравнение Шрёдингера имеет вид где — мнимая единица.

Решение уравнения Шрёдингера Рассмотрим одномерный случай для частицы, находящейся в потенциальной яме шириной l с бесконечно высокими стенками. За пределы ямы частица попасть не может, поэтому вероятность обнаружения частицы вне ямы равна нулю.

Решение уравнения Шрёдингера В силу непрерывности пси-функции её значения на границах ямы также равны нулю Внутри ямы, где потенциальная энергия равна нулю, выполняется условие

Решение уравнения Шрёдингера Обозначив Получим знакомое нам уравнение где двумя штрихами обозначена вторая производная по координате

Решение уравнения Шрёдингера Его решение запишем в виде Используя граничные условия получаем:

Решение уравнения Шрёдингера Из первого следует, что Из второго —

Решение уравнения Шрёдингера Объединяя уравнения и Получаем:

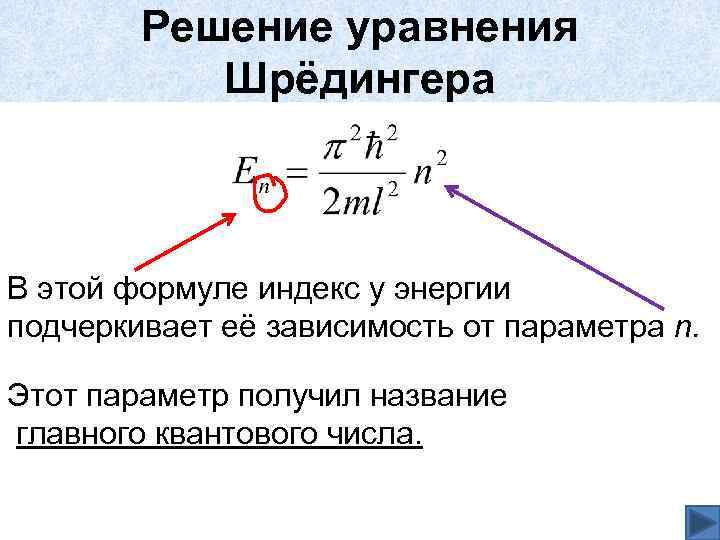
Решение уравнения Шрёдингера В этой формуле индекс у энергии подчеркивает её зависимость от параметра n. Этот параметр получил название главного квантового числа.

Решение уравнения Шрёдингера Теперь решение уравнения Шредингера для частицы в одномерной потенциальной яме с бесконечно высокими стенками имеет вид

Решение уравнения Шрёдингера Амплитуду а найдём из условия нормировки: Интегрирование даёт

Решение уравнения Шрёдингера Итак, окончательно имеем: Далее будут приведены графики пси-функций и соответствующих им плотностей вероятности для нескольких главных квантовых чисел.

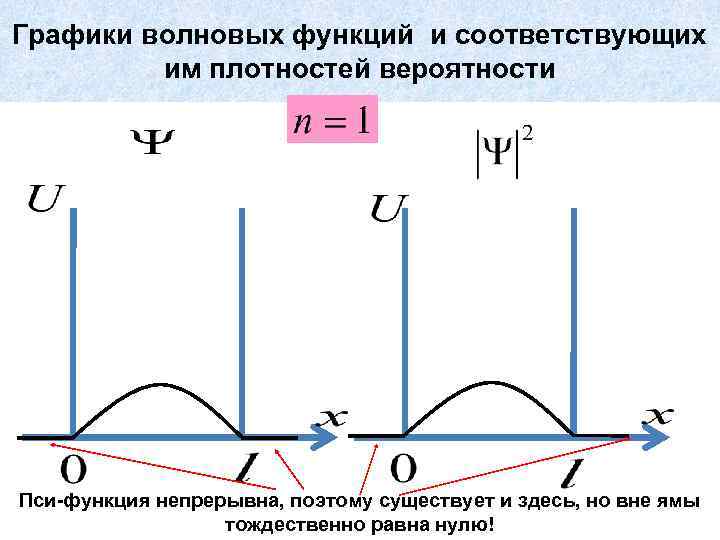
Графики волновых функций и соответствующих им плотностей вероятности Пси-функция непрерывна, поэтому существует и здесь, но вне ямы тождественно равна нулю!

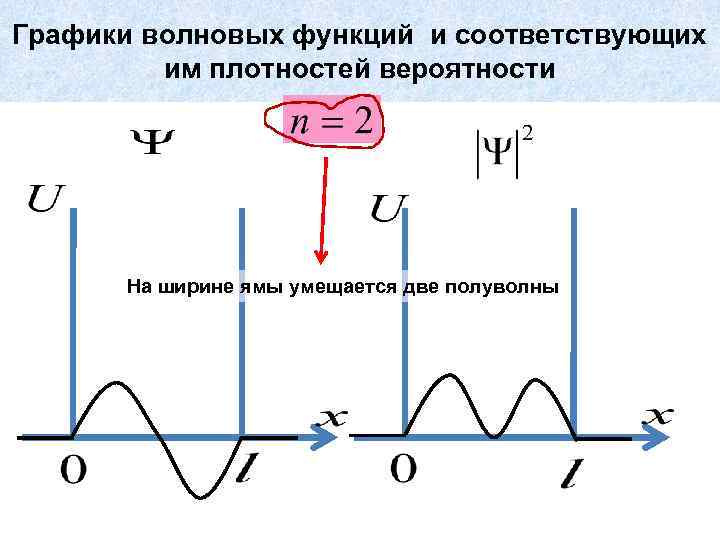
Графики волновых функций и соответствующих им плотностей вероятности На ширине ямы умещается две полуволны

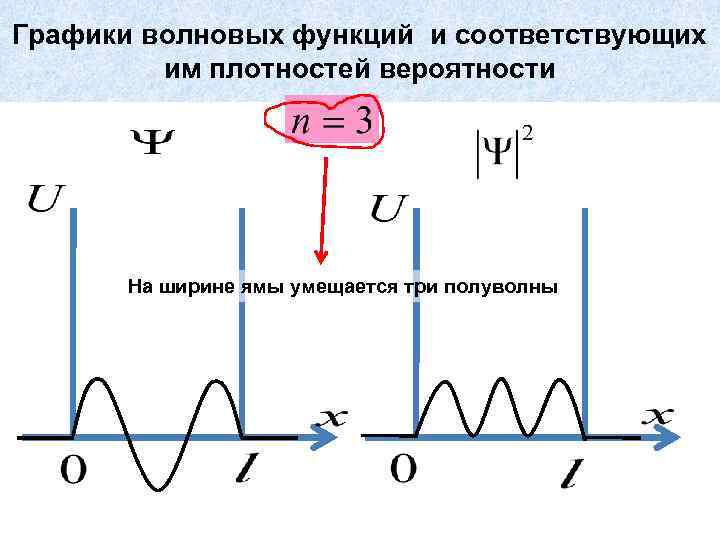
Графики волновых функций и соответствующих им плотностей вероятности На ширине ямы умещается три полуволны

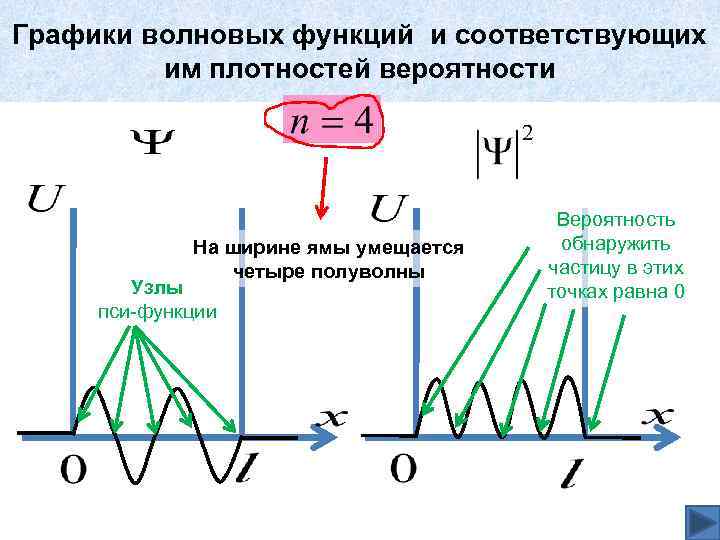
Графики волновых функций и соответствующих им плотностей вероятности На ширине ямы умещается четыре полуволны Узлы пси-функции Вероятность обнаружить частицу в этих точках равна 0

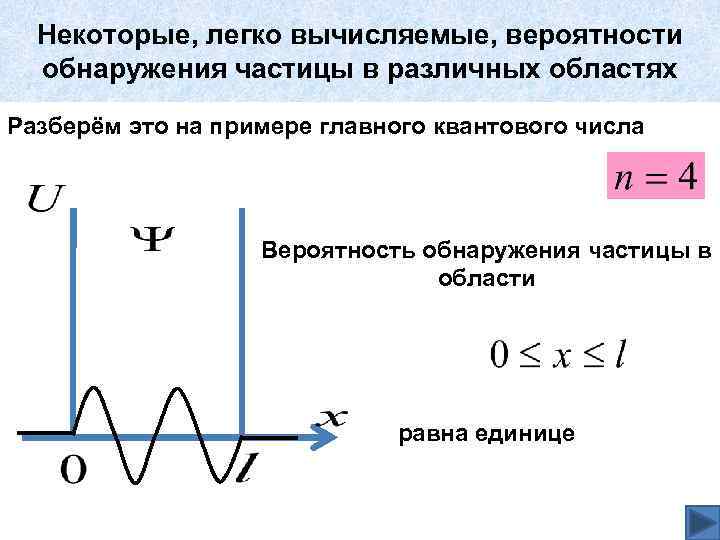
Некоторые, легко вычисляемые, вероятности обнаружения частицы в различных областях Разберём это на примере главного квантового числа Вероятность обнаружения частицы в области равна единице

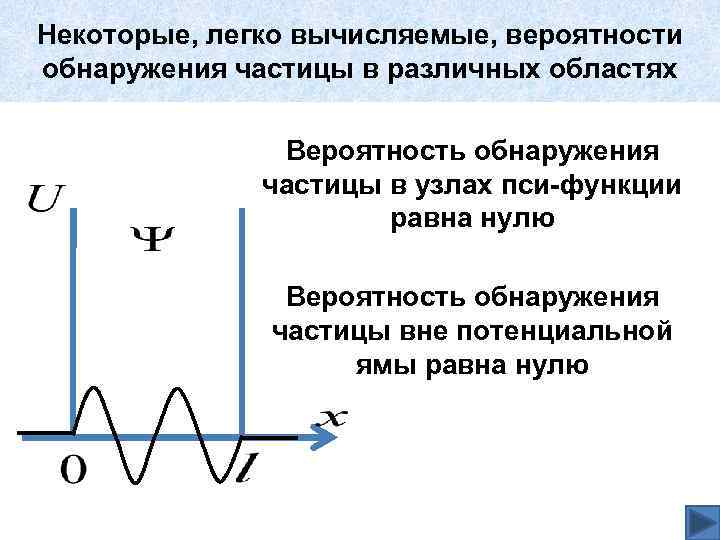
Некоторые, легко вычисляемые, вероятности обнаружения частицы в различных областях Вероятность обнаружения частицы в узлах пси-функции равна нулю Вероятность обнаружения частицы вне потенциальной ямы равна нулю

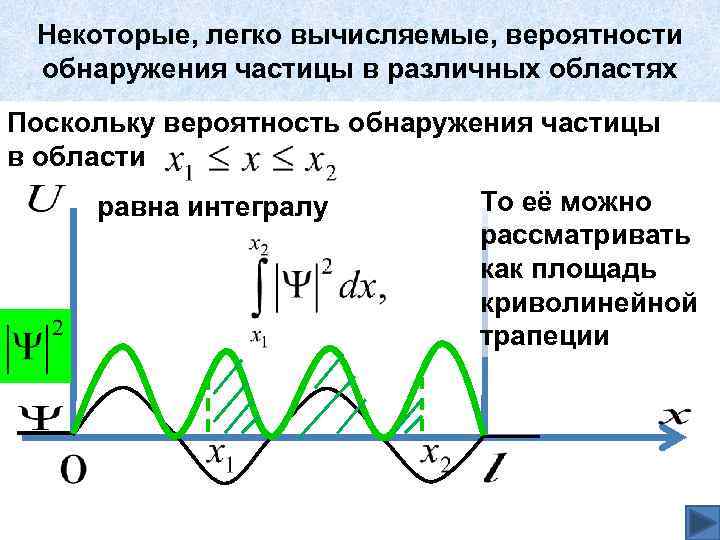
Некоторые, легко вычисляемые, вероятности обнаружения частицы в различных областях Поскольку вероятность обнаружения частицы в области равна интегралу То её можно рассматривать как площадь криволинейной трапеции

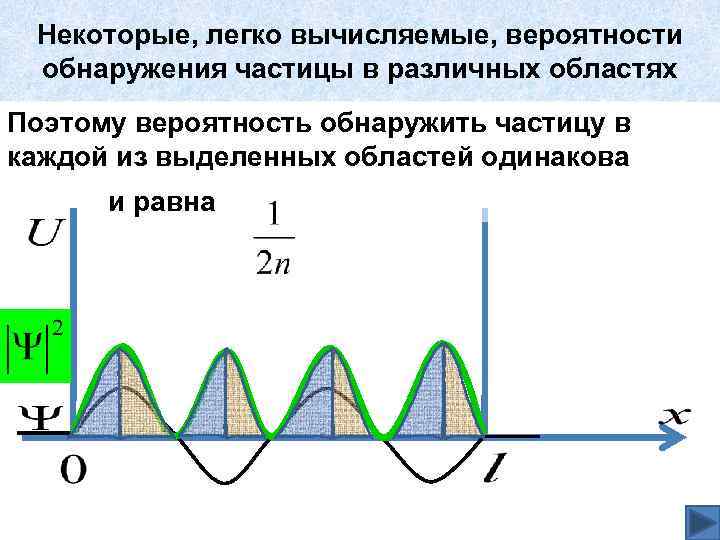
Некоторые, легко вычисляемые, вероятности обнаружения частицы в различных областях Поэтому вероятность обнаружить частицу в каждой из выделенных областей одинакова и равна

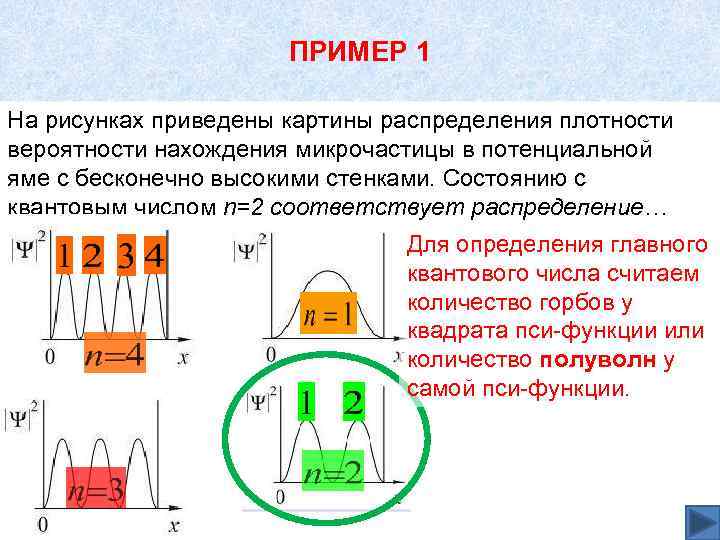
ПРИМЕР 1 На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n=2 соответствует распределение… Для определения главного квантового числа считаем количество горбов у квадрата пси-функции или количество полуволн у самой пси-функции.

ПРИМЕР 2 Волновая функция частицы в потенциальной яме с бесконечно высокими стенками шириной L имеет вид: В яме укладывается одна волна де. Бройля, длина которой равна L Величина импульса частицы в первом возбужденном состоянии (n=2) равна. . . Варианты ответов:

ПРИМЕР 3 Вероятность обнаружить электрон на участке (a, b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле где ω – плотность вероятности, определяемая ψ – функцией. Если ψ – функция имеет вид, указанный на рисунке, то вероятность обнаружить электрон на участке равна Варианты ответов: 1) 2/3; 2) 5/6 3) 1/2; 4) 1/3

УРАВНЕНИЕ ШРЁДИНГЕРА ДЛЯ НЕКОТОРЫХ, ОСОБЫХ СЛУЧАЕВ 40

Уравнение Шрёдингера для частицы в одномерной потенциальной яме с бесконечно высокими стенками 41

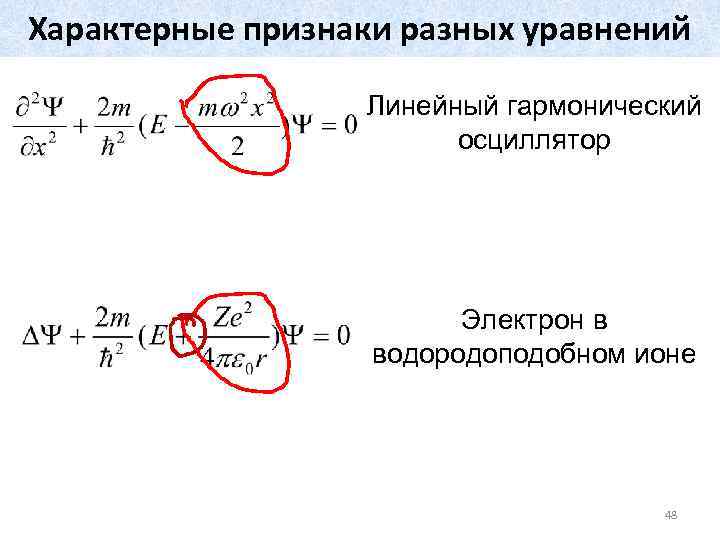
Уравнение Шрёдингера для линейного гармонического осцилятора Если колебания осциллятора происходят под действием некоторой квазиупругой силы то его потенциальная энергия может быть записана в виде 42

Уравнение Шрёдингера для линейного гармонического осцилятора Частота колебаний такого осциллятора аналогична частоте колебаний груза напружине: откуда и, следовательно, 43

Уравнение Шрёдингера для линейного гармонического осциллятора Из стационарного уравнения Шрёдингера и выражения для потенциальной энергии Получаем уравнение Шрёдингера для гармонического осциллятора: 44

Уравнение Шрёдингера для электрона в водородоподобном ионе Водородоподобный ион – ядро и один электрон. Потенциальная энергия электрона в поле ядра определяется произведением заряда электрона на потенциал той точки, где он находится: Подставляя в трехмерное стационарное уравнение Шрёдингера, получаем: 45

Характерные признаки разных уравнений Трёхмерный случай. Стационарное уравнение. Одномерный случай. Стационарное уравнение. Трёхмерный случай. нестационарное уравнение. 46

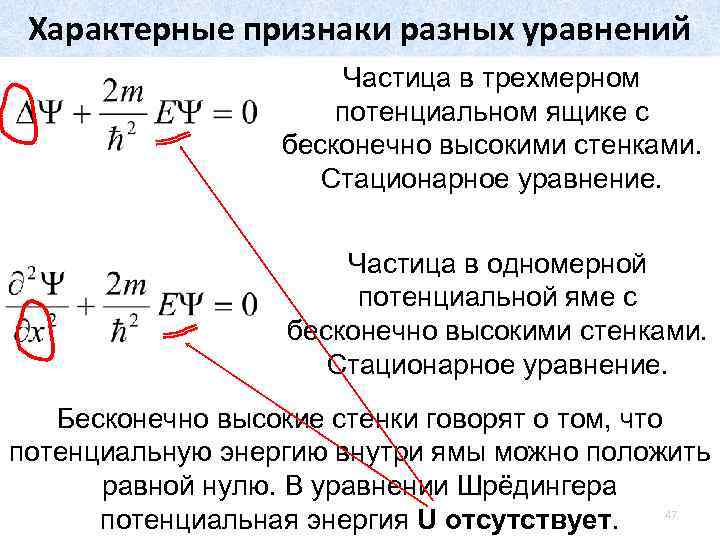
Характерные признаки разных уравнений Частица в трехмерном потенциальном ящике с бесконечно высокими стенками. Стационарное уравнение. Частица в одномерной потенциальной яме с бесконечно высокими стенками. Стационарное уравнение. Бесконечно высокие стенки говорят о том, что потенциальную энергию внутри ямы можно положить равной нулю. В уравнении Шрёдингера 47 потенциальная энергия U отсутствует.

Характерные признаки разных уравнений Линейный гармонический осциллятор Электрон в водородоподобном ионе 48

Ключевые понятия и выводы • Волновая функция (пси-функция) – функция координат и времени, квадрат модуля которой описывает вероятность нахождения частицы в данной точке пространства; • Уравнение Шрёдингера – уравнение, которому должна удовлетворять пси-функция конкретной частицы; 49

Ключевые понятия и выводы свойства пси-функции: • пси функция непрерывная; • пси функция гладкая (то есть её производная тоже непрерывная); • пси-функция нормирована, то есть интеграл квадрата её модуля по всему объёму равен единице 50

Ключевые формулы Формула Название Длина волны де. Бройля Стационарное уравнение Шрёдингера в декартовых координатах 51

Ключевые формулы Формула Название Уравнение Шрёдингера для электрона Стационарное уравнение Шрёдингера для одномерной потенциальной ямы 52

53