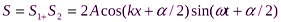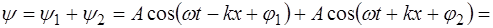Как найти пучности стоячей волны

Частным случаем интерференции волн, являются стоячие волны.

Стоячей волной называется волна, образующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, а в случае поперечных волн еще и одинаковую поляризацию.

Поперечная стоячая волна образуется, например, на натянутой упругой нити, один конец которой закреплен, а другой приводится в колебательное движение.

При наложении двух когерентных бегущих плоских волн вида

и где α-разность фаз волн в точках плоскости x=0, образуется плоская синусоидальная стоячая волна, описываемая уравнением

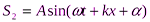
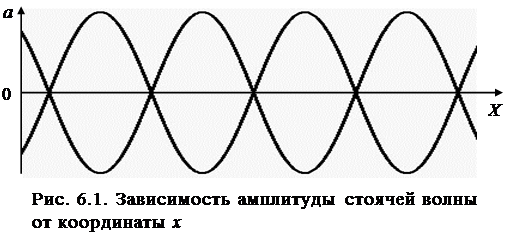
Амплитуда стоячей волны в отличие от амплитуды бегущих волн является периодической функцией координаты x.

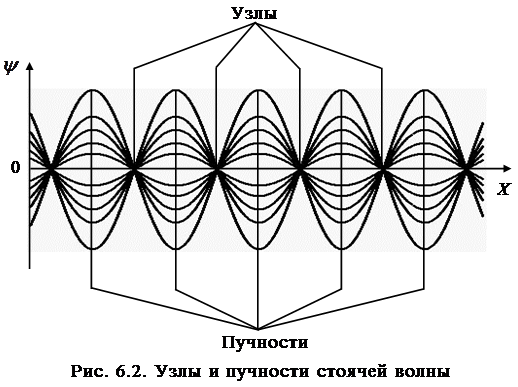
Точки ,в которых амплитуда стоячей волны равна 0, называются узлами, а точки где амплитуда двойная –пучности.

Положение узлов и пучностей находится из условий

k*x+α/2=m*n (пучности) ,где m=0,1,2…

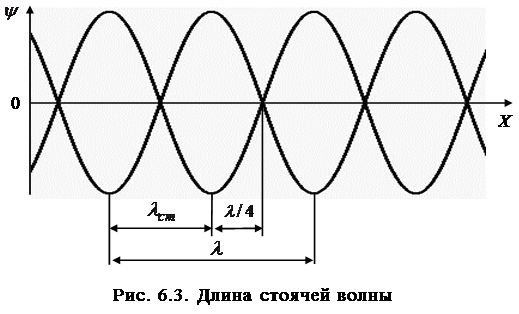
Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины волны λ бегущих волн.

В бегущей волне фаза колебаний зависит от координаты x рассматриваемой точки. В стоячей волне все точки между двумя узлами колеблются с различными амплитудами, но с одинаковыми фазами (синфазно), так как аргумент синуса в уравнении стоячей волны не зависит от координаты x. При переходе через узел фаза колебаний изменяется скачком на π,так как при этом cos(k*x+α/2) изменяет свой знак на противоположный.

Стоячие волны. 6.1 Стоячие волны в упругой среде

6.1 Стоячие волны в упругой среде

Согласно принципу суперпозиции, при распростране-нии в упругой среде одновременно нескольких волн воз-никает их наложение, причем волны не возмущают друг друга: колебания частиц среды являются векторной сум-мой колебаний, которые совершали бы частицы при рас-пространении каждой из волн в отдельности.

Волны, создающие колебания среды, разности фаз меж-ду которыми в каждой точке пространства постоянны, на-зываются когерентными.

При сложении когерентных волн возникает явление интерференции, заключающееся в том, что в одних точ-ках пространства волны усиливают друг друга, а в других точках – ослабляют. Важный случай интерференции наб-людается при наложении двух встречных плоских волн с одинаковой частотой и амплитудой . Возникающие при этом колебания называют стоячей волной. Чаще все-го стоячие волны возникают при отражении бегущей вол-ны от преграды. При этом падающая волна и отраженная навстречу ей волна при сложении дают стоячую волну.

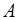
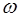
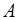
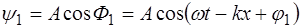
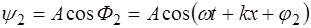
Получим уравнение стоячей волны. Возьмем две плос-кие гармонические волны, распространяющиеся навстечу друг другу вдоль оси X и имеющие одинаковую частоту и амплитуду :

,

,

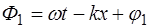
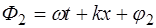
где – фаза колебаний точек среды при про-хождении первой волны;

– фаза колебаний точек среды при про-хождении второй волны.

Разность фаз в каждой точке на оси X не будет зави-сеть от времени, т.е. будет постоянной:

(6.2)

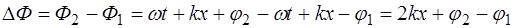
Следовательно, обе волны будут когерентными.

Возникшее в результате сложения рассматриваемых волн колебание частиц среды будет следующим:

. (6.3)

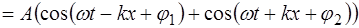
Преобразуем сумму косинусов углов по правилу (4.4) и получим:

(6.4)

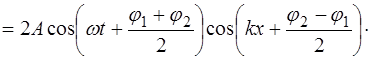
Перегруппировав множители, получим:

(6.5)

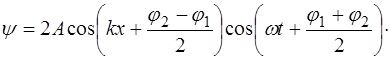
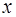
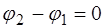
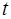
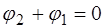
Для упрощения выражения выберем начало отсчета так, чтобы разность фаз и начало отсчета времени , чтобы и сумма фаз была равна нулю: .

Тогда уравнение для суммы волн примет вид:

. (6.6)

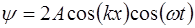
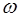
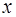
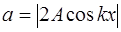
Уравнение (6.6) называется уравнением стоячей вол-ны. Из него видно, что частота стоячей волны равна частоте бегущей волны, а амплитуда, в отличие от бегу-щей волны, зависит от расстояния от начала отсчета :

. (6.7)

С учетом (6.7) уравнение стоячей волны принимает вид:

. (6.8)

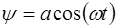
Таким образом, точки среды колеблются с частотой 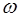, совпадающей с частотой бегущей волны, и амплитудой a, зависящей от положения точки на оси X. Соответственно, амплитуда изменяется по закону косинуса и имеет свои максимумы и минимумы (рис. 6.1).

Для того, чтобы наглядно представить расположение минимумов и максимумов амплитуды заменим, согласно (5.29), волновое число его значением:

. (6.9)

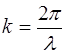
Тогда выражение (6.7) для амплитуды примет вид

(6.10)

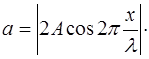
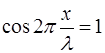
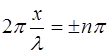
Отсюда становится видно, что амплитуда смещения мак-симальна при , т.е. в точках, координата кото-рых удовлетворяет условию:

, (6.11)

где

Отсюда получаем координаты точек, где амплитуда сме-щения максимальна:

; (6.12)

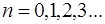
Точки, где амплитуда колебаний среды максимальна, называются пучностями волны.

Амплитуда волны равна нулю в точках, где 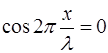. Координата таких точек, называемых узлами волны, удов-летворяет условию:

, (6.13)

где

Из (6.13) видно, что координаты узлов имеют зна-чения:

, (6.14)

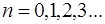
На рис. 6.2 показан примерный вид стоячей волны, от-мечено расположение узлов и пучностей. Видно, что со-седние узлы и пучности смещения отстоят друг от друга на одно и то же расстояние.

Найдем расстояние между соседними пучностями и уз-лами. Из (6.12) получаем расстояние между пучностями:

(6.15)

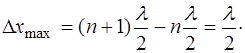
Расстояние между узлами получаем из (6.14):

(6.16)

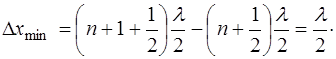
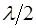
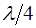
Из полученных соотношений (6.15) и (6.16) видно, что расстояние между соседними узлами, как и между сосед-ними пучностями, постоянно и равно ; узлы и пуч-ности сдвинуты относительно друг друга на (рис. 6.3).

Из определения длины волны можно записать выра-жение для длины стоячей волны: она равна половине дли-ны бегущей волны:

(6.17)

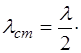
Запишем, с учетом (6.17), выражения для координат уз-лов и пучностей:

, (6.18)

, (6.19)

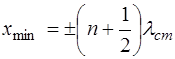
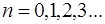
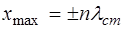
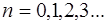
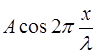
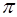
Множитель , определяющий амплитуду стоя-чей волны, меняет свой знак при переходе через нулевое значение, вследствие чего фаза колебаний по разные сто-роны от узла отличается на . Следовательно, все точки, лежащие по разные стороны от узла, колеблются в про-тивофазе. Все точки, находящиеся между соседними уз-лами, колеблются синфазно.

Узлы условно разделяют среду на автономные области, в которых гармонические колебания совершаются незави-симо. Никакой передачи движения между областями нет, и, значит, перетекания энергии между областями нет. То есть нет передачи возмущения вдоль оси 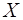. Поэтому волна называется стоячей.

Итак, стоячая волна образуется из двух противополож-но направленных бегущих волн равных частот и амп-литуд. Векторы Умова каждой из этих волн равны по мо-дулю и противоположны при направлению, и при сложе-нии дают ноль. Следовательно, стоячая волна энергии не переносит.

6.2 Примеры стоячих волн

6.2.1 Стоячая волна в струне

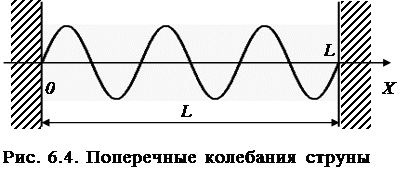
Расмотрим струну длиной L, закрепленную с обоих кон-цов (рис. 6.4).

Расположим вдоль струны ось X таким образом, чтобы левый конец струны имел координату x=0, а правый – x=L. В струне возникают колебания, описываемые урав-нением:

(6.20)

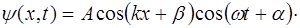
Запишем граничные условия для рассматриваемой стру-ны. Поскольку её концы закреплены, то в точках с коор-динатами x=0 и x=L колебаний нет:

(6.21)

(6.22)

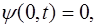
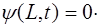
Найдем уравнение колебаний струны исходя из запи-санных граничных условий. Запишем уравнение (6.20) для левого конца струны с учетом (6.21):

(6.23)

Соотношение (6.23) выполняется для любого времени t в двух случаях:

1. . Это возможно в том случае, если коле-бания в струне отсутствуют ( ). Данный случай инте-реса не представляет, и мы его рассматривать не будем.

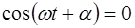
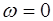
2. . Здесь фаза . Этот случай и позволит нам получить уравнение колебаний струны.

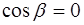
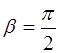
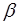
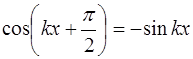
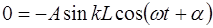
Подставим полученное значение фазы в граничное условие (6.22) для правого конца струны:

. (6.25)

, (6.26)

. (6.27)

Снова возникают два случая, при которых выполняется соотношение (6.27). Случай, когда колебания в струне от-сутствуют ( 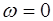), мы рассматривать не будем.

Во втором случае должно выполняться равенство:

, (6.27)

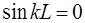
а это возможно, только когда аргумент синуса кратен це-лому числу :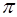

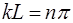
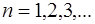
, (6.28)

Значение мы отбрасываем, т.к. при этом , а это означало бы или нулевую длину струны (L=0) или вол-новое число k=0. Учитывая связь (6.9) между волновым числом и длиной волны видно, что для того, чтобы вол-новое число равнялось бы нулю, длина волны должна бы быть бесконечной, а это означало бы отсутствие колебаний.

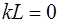
Из (6.28) видно, что волновое число при колебаниях струны, закрепленной с обоих концов, может принимать только определенные дискретные значения:

(6.30)

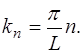
Учитывая (6.9), запишем (6.30) в виде:

(6.31)

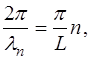
откуда волучаем выражение для возможных длин волн в струне:

(6.31)

Другими словами, на длине струны L должно уклады-ваться целое число n полуволн:

(6.32)

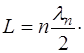
Соответствующие частоты колебаний можно опреде-лить из (5.7):

. (6.33)

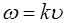
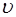
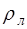
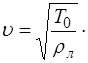
Здесь – фазовая скорость волны, зависящая, соглас-но (5.102), от линейной плотности струны и силы на-тяжения струны :

(6.34)

Подставив (6.34) в (6.33), получим выражение, описы-вающее возможные частоты колебаний струны:

, (6.36)

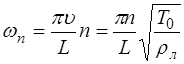
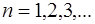
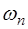
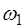
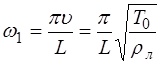
Частоты называют собственными частотами стру-ны. Частоту (при n = 1):

(6.37)

называют основной частотой (или основным тоном) струны. Частоты, определяемые при n>1 называются обертонами или гармониками. Номер гармоники равен n-1. Например, частота :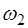

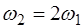
(6.38)

соответствует первой гармонике, а частота :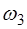

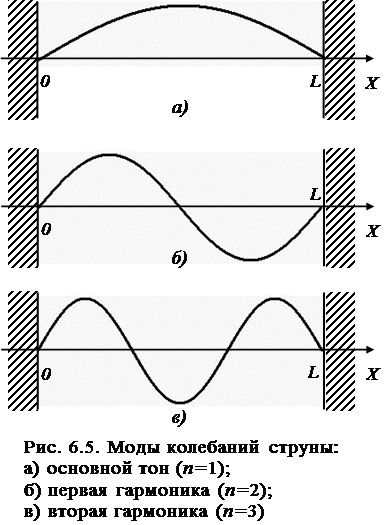
(6.39)

сответствует второй гармонике, и т.д. Поскольку струну можно представить в виде дискретной системы с беско-нечным числом степеней свободы, то каждая гармоника является модой колебаний струны. В общем случае коле-бания струны представляют собой суперпозицию мод.

Каждой гармонике соответствует своя длина волны. Для основного тона (при n=1) длина волны:

, (6.40)

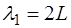
соответственно для первой и второй гармоники (при n=2 и n=3) длины волн будут:

, (6.41)

(6.42)

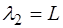
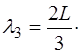
На рис.6.5 показан вид нескольких мод колебаний, осуществляемых струной.

Таким образом, струна с закрепленными концами реа-лизует в рамках классической физики исключительный случай – дискретный спектр частоты колебаний (или длин волн). Таким же образом ведет себя упругий стер-жень с одним или обоими зажатыми концами и колебания воздушного столба в трубах, что и будет рассмотрено в последующих разделах.

6.2.2 Влияние начальных условий на движение

непрерывной струны. Фурье-анализ

Колебания струны с зажатыми концами помимо дис-кретного спектра частот колебаний обладают еще одним важным свойством: конкретная форма колебаний струны зависит от способа возбуждения колебаний, т.е. от на-чальных условий. Рассмотрим подробней.

Уравнение (6.20), описывающее одну моду стоячей вол-ны в струне, является частным решением дифференциаль-ного волнового уравнения (5.61). Поскольку колебание стру-ны складывается из всех возможных мод (для струны – бес-конечное количество), то и общее решение волнового уравнения (5.61) складывается из бесконечного числа частных решений:

, (6.43)

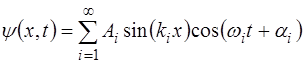
где i – номер моды колебаний. Выражение (6.43) записа-но с учетом того, что концы струны закреплены:

, (6.44)

, (6.45)

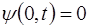
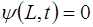
а также с учетом связи частоты i-й моды и ее волнового числа:

(6.46)

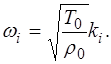
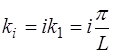
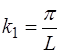
Здесь – волновое число i-й моды;

– волновое число 1-й моды;

Найдем величину начальной фазы для каждой моды колебаний. Для этого в момент времени t=0 придадим струне форму, описываемую функцией f₀(x), выражение для которой получим из (6.43):

. (6.47)

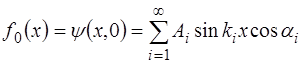
На рис. 6.6 показан пример формы струны, описывае-мой функцией f₀(x).

В момент времени t=0 струна еще покоится, т.е. ско-рость всех ее точек равна нулю. Из (6.43) найдем выраже-ние для скорости точек струны:

, (6.48)

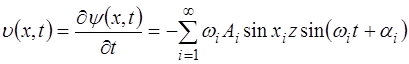
и, подставив в него t=0, получим выражение для скорос-ти точек струны в начальный момент времени:

. (6.49)

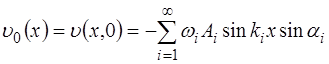
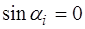
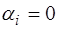
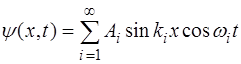
Поскольку в начальный момент времени скорость рав-на нулю, то выражение (6.49) будет равно нулю для всех точек струны, если . Из этого следует, что на-чальная фаза для всех мод тоже равна нулю ( ). С учетом этого выражение (6.43), описывающее движение струны, принимает вид:

, (6.50)

а выражение (6.47), описывающее начальную форму стру-ны, выглядит как:

. (6.51)

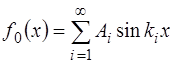
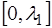
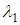
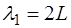
Стоячая волна в струне описывается функцией, перио-дичной на интервале , где равна двум длинам струны (рис. 6.7):

. (6.52)

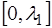
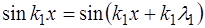
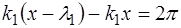
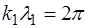
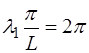
Это видно из того, что периодичность на интервале означает:

. (6.53)

; (6.54)

; (6.55)

, (6.56)

что и приводит нас к выражению (6.52).

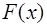
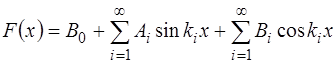
Из математического анализа известно, что любая пе-риодическая функция может быть разложена с высо-кой точностью в ряд Фурье:

, (6.57)

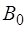
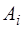
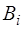
где , , – коэффициенты Фурье.

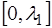
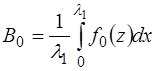
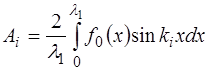
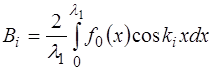
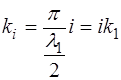
В нашем случае, когда функция является периодичес-кой на интервале , коэффициенты Фурье, согласно [1], рассчитываются как:

, (6.58)

, (6.59)

, (6.60)

. (6.61)

В математике в курсе Фурье-анализа показано, что по-лученные таким образом коэффициенты Фурье для разло-жения периодической функции 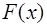фактически и явля-ются коэффициентами разложения функции f₀(x).

Фурье-анализ позволяет разложить колебание, совер-шаемое струной в спектр, т.е. выяснить, какие моды ко-лебаний действительно имеют место при данном способе возбуждения струны.

Рассмотрим два способа возбуждения колебаний струны.

Способ 1. Струне в начальный момент времени прида-ется форма, соответствующая первой моде колебаний и описываемая функцией:

. (6.62)

После того, как струна отпускается, она начинает со-вершать колебания из начального положения. Расчеты по-казывают, что коэффициенты Фурье для этого случая все равны нулю, кроме одного, который равен амплитуде A:

. (6.63)

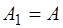
При таком способе возбуждения возникает только одна мода колебаний; никаких обертонов нет.

Способ 2. Струна отводится от положения равновесия посередине, как это происходит в струнных инстру-ментах. Вид начальной формы представлен на рис. 6.8.

Форма струны, изображенная на рис. 6.8, описывается функцией:

при ,

при .

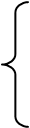
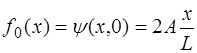
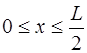
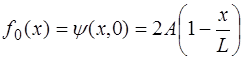
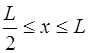
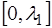
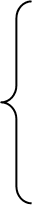
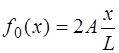
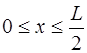
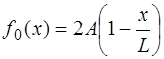
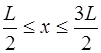
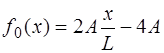
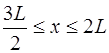
Функция, соответствующая (6.64), и которая является пе-риодической на интервале , записывается следую-щим образом:

при ,

при , (6.65)

при .

Вид периодической функции (6.65) показан на рис.6.9:

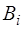
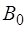
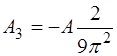
Расчеты показывают, что все коэффициенты Фурье для такой функции равны нулю (включая и коэффициент ). Первые три коэффициента A₁, A₂, A₃ соответственно равны:

, (6.66)

, (6.67)

. (6.68)

Как уже отмечалось, полученные таким образом коэф-фициенты Фурье для разложения периодической функ-ции 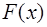фактически и являются коэффициентами разло-жения функции f₀(x).

Тогда, с учетом трех первых слагаемых ряда Фурье, функция (6.64) может быть приближенно представлена следующим образом:

(6.69)

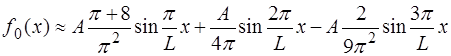
Мы нашли только три первых члена Фурье-разложения функции (6.64). Конечно, полученный нами ряд Фурье (6.69) при конечном количестве членов, в нашем случае равном трём, может воспроизвести исходную функцию лишь при-ближённо. Однако, вычисления коэффициентов Фурье могут быть продолжены. Получится, что при рассматриваемом на-ми случае колебаний в струне возникает много гармоник (теоретически, бесконечный ряд гармоник).

Сравнивая первый и второй рассмотренные случаи, мы видим, что в первом из них была только одна мода, а во втором возникает много гармоник.

Таким образом, рассмотренные случаи показывают, что конкретная форма колебаний струны, зажатой с двух сторон, существенно зависит от способа возбуждения ко-лебаний, т.е., от начальных условий.

|	следующая лекция ==>
Энергия, переносимая упругими волнами	|	Дерматология

Дата добавления: 2015-06-12 ; просмотров: 4173 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Стоячие
волны образуются в результате интерференции
двух встречных плоских волн одинаковой
частоты ω и амплитуды А.

Представим себе,
что в точке S
(рис.7.4) находится вибратор, от которого
вдоль луча SO
распространяется плоская волна. Достигнув
преграды в точке О, волна отразится и
пойдёт в обратном направлении, т.е. вдоль
луча распространяются две бегущие
плоские волны: прямая и обратная. Эти
две волны когерентны, так как рождены
одним и тем же источником и, накладываясь
друг на друга, будут интерферировать
между собой.

Возникающее в
результате интерференции колебательное
состояние среды и называется стоячей
волной.

Запишем уравнение
прямой и обратной бегущей волны:

прямая —
;обратная
—

где S₁
и S₂
– смещение произвольной точки на луче
SO.
С учётом формулы для синуса суммы
результирующее смещение равно

Таким образом,
уравнение стоячей волны имеет вид

(7.17)

Множитель cosωt
показывает, что все точки среды на луче
SО совершают простые гармонические
колебания с частотой
.
Выражениеназывается амплитудой стоячей волны.
Как видно, амплитуда определяется
положением точки на лучеSO
(х).

Максимальное
значение
амплитуды будут иметь точки, для которых

или
(n
= 0, 1, 2,….)

откуда
,
или(7.18)

Точки, имеющие
такие координаты, называют пучностями
стоячей волны.

Минимальное
значение,
равное нулю, будут иметь те точки для
которых

или
(n
= 0, 1, 2,….)

откуда
или(7.19)

Точки, имеющие
такие координаты, называют узлами
стоячей волны.
Сопоставляя выражения (7.18) и (7.19), видим,
что расстояние между соседними пучностями
и соседними узлами равно λ/2.

На
рисунке сплошной линией изображено
смещение колеблющихся точек среды в
некоторый момент времени, пунктирной
кривой – положение этих же точек через
Т/2. Каждая точка совершает колебания с
амплитудой, определяемой её расстоянием
от вибратора (х).

В отличие от
бегущей волны в стоячей волне не
происходит переноса энергии. Энергия
просто переходит из потенциальной (при
максимальном смещении точек среды от
положения равновесия) в кинетическую
(при прохождении точками положения
равновесия)в пределах между узлами,
остающимися неподвижными.

Все точки стоячей
волны в пределах между узлами колеблются
в одинаковой фазе, а по разные стороны
от узла – в противофазе.

Стоячие волны
возникают, например, в закреплённой с
обоих концов натянутой струне при
возбуждении в ней поперечных колебаний.
Причём в местах закреплений располагаются
узлы стоячей волны.

Если стоячая
волна устанавливается в воздушном
столбе, открытом с одного конца (звуковая
волна), то на открытом конце образуется
пучность, а на противоположном – узел.

Примеры решения задач

Пример
. Определите
скорость распространения звука в воде,
если длина волны равна 2м, а частота
колебаний источника ν=725Гц. Определите
также наименьшее расстояние между
точками среды, колеблющимися в одинаковой
фазе.

Дано:
λ=2м; ν=725Гц.

Найти:
υ; х.

Решение.
Длина волны равна расстоянию, на которое
распространяется определённая фаза
волны за период Т, т.е.

,

где υ – скорость
волны; ν — частота колебаний.

Тогда искомая
скорость

υ=λν.

Длина
волны – расстояние между ближайшими
частицами среды, колеблющимися в
одинаковой фазе. Следовательно, искомое
наименьшее расстояние между точками
среды, колеблющимися в одинаковой фазы,
равно длине волны, т.е.

х=λ

Ответ:
υ=1450 м/с; х=2м.

Пример
. Определите,
во сколько раз изменится длина
ультразвуковой волны при переходе её
из меди в сталь, если скорость
распространения ультразвука в меди и
стали соответственно равны υ₁=3,6км/с
и υ₂=5,5
км/с.

Дано:
υ₁=3,6км/с=3,6∙10³м/с.
и υ₂=5,5
км/с =5,5∙10³м/с.

Найти:.

Решение.
При распространении волн частота
колебаний не изменяется при переходе
их одной среды в другую (она зависит
только от свойств источника волн), т.е.
ν₁=
ν₂=
ν.

Связь длины волны
с частотой ν:

,
(1)

где υ – скорость
волны.

Искомое отношение,
согласно (1),

.

Вычисляя,
получаем
(увеличится в 1.53 раза).

Ответ:

Пример
. Один
конец упругого стержня соединён с
источником гармонических колебаний,
подчиняющихся закону
,
а другой конец жёстко закреплён. Учитывая,
то отражение в месте закрепления стержня
происходит от более плотной среды,
определите: 1) уравнение стоячей волны;
2) координаты узлов; 3) координаты
пучностей.

Дано:
.

Найти:
1) ξ (x,
t);
2) х_у;
3) х_n.

Решение.
Уравнение падающей волны

,
(1)

где А – амплитуда
волны; ω — циклическая частота; υ — скорость
волны.

Согласно
условию задачи, отражение в месте
закрепления стержня происходит от более
плотной среды, поэтому волна меняет
фазу на противоположную, и уравнение
отражённой волны

.
(2)

Сложив уравнения
(1) и (2), получим уравнение стоячей волны

откуда

(учли
;
λ=υТ).

В точках среды,
где

(m=0,
1, 2,….) (3)

Амплитуда
колебаний обращается в нуль (наблюдаются
узлы), в точках среды, где

(m=0,
1, 2,….) (4)

Амплитуда
колебаний достигает максимального
значения, равного 2А (наблюдаются
пучности). Искомые координаты узлов и
пучностей находим из выражений (3) и (4):

координаты
узлов
(m=0,
1, 2,….);

координаты
пучностей
(m=0,
1, 2,….).

Ответ:
1)
;(m=0,
1, 2,….);
(m=0,
1, 2,….).

Пример
. Расстояние
между соседними узлами стоячей волны,
создаваемый камертоном в воздухе ℓ
=42см. Принимая скорость звука в воздухе
υ=332 м/с, определите частоту колебаний
ν камертона.

Дано:
ℓ =42см=0,42м; υ=332 м/с.

Найти:
ν.

Решение.
В стоячеё волне расстояние между двумя
соседними узлами равно
.
Следовательно, ℓ=, откуда длина бегущей волны

λ=2ℓ
(1)

Связь
между длиной волны и частотой
.
Подставив в эту формулу значение (1),
получим искомую частоту колебаний
камертона

.

Ответ:
ν=395 Гц.

Пример
. Труба
длиной ℓ = 50см заполнена воздухом и
открыта с одного конца. Принимая скорость
υ звука равной 340 м/с, определите, при
какой наименьшей частоте в трубе будет
возникать стоячая звуковая волна.
Принимая скорость звука в воздухе υ=332
м/с, определите частоту колебаний ν
камертона.

Дано:
ℓ =50см=0,5м; υ=340 м/с.

Найти:
ν₀.

Решение. Частота
будет минимальной при условии, что длина
стоячей волны максимальна.

В
открытой с одного конца трубе на открытой
части будет пучность (отражение от менее
плотной среды), а на закрытой части –
узел (отражение от более плотной среды).
Поэтому в трубе уложится четверть длины
волны:

Учитывая,
что длина волны
,
можем записать

,

Откуда искомая
наименьшая частота

.

Ответ:
ν₀=170
Гц.

Пример
. Два
электропоезда движутся навстречу друг
другу со скоростями υ₁=20
м/с и υ₂=10
м/с. Первый поезд даёт свисток, высота
тона которого соответствует частоте
ν₀=600
Гц. Определите частоту, воспринимаемую
пассажиром второго перед встречей
поездов и после их встречи. Скорость
звука принять равной υ=332 м/с.

Дано:
υ₁=20
м/с; υ₂=10
м/с; ν₀=600
Гц; υ=332 м/с.

Найти:
ν
; ν’.

Решение. Согласно
общей формуле, описывающей эффект
Доплера в акустике, частота звука,
воспринимаемая движущимся приёмником,

,
(1)

где
ν₀—
частота звука, посылаемая источником;
υ_пр
— скорость движения приёмника; υ_ист
— скорость движения источника. Если
источник и приёмник приближаются друг
к другу, то берётся верхний знак, если
удаляются – нижний знак.

Согласно
обозначениями, данным в задаче (υ_пр=υ₂
и υ_ист=υ₁
) и приведённым выше пояснениями, из
формулы (1) искомые частоты, воспринимаемые
пассажиром второго поезда:

Перед встречей
поездов (электропоезда сближаются):

;

После встречи
поездов (поезда удаляются друг от друга):

Ответ:
ν=658
Гц ; ν’ =549 Гц.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Время на прочтение
9 мин

Количество просмотров 81K

Эта статья — перевод. Начало здесь.
Источник.

В программе:
1) Провода болтаются в воздухе, но источник тока/напряжения видит короткое замыкание.
2) На одном конце провода амплитуда равна 0 Вольт, а на другом — 1 Вольт. Как это возможно?
3) Согласование 75 Ом источника сигнала с 300 Ом нагрузкой при помощи правильно подобранного кабеля.

Стоячие волны и резонанс

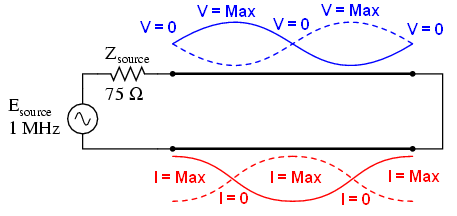
Всегда, когда есть несоотвествие между сопротивлением линии передачи и нагрузкой, происходит отражение. Если падающий сигнал имеет одну частоту, то этот сигнал будет накладываться на отражённые волны, и возникнет стоячая волна.

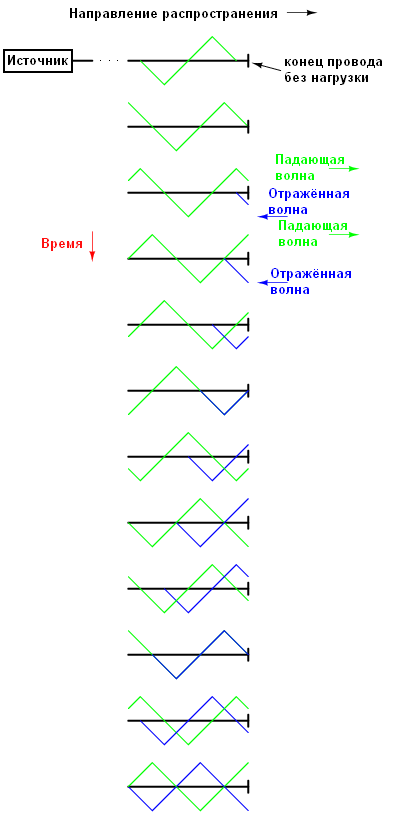
На рисунке показано, как треугольная падающая волна зеркально отражается от открытого конца линии. Для простоты, линия передачи в этом примере показана как единая жирная линия, а не как пара проводов. Падающая волна идёт слева направо, а отражённая – справа налево.

Если мы сложим эти два сигнала, то увидим что третий, стационарный сигнал, создаётся по всей длине линии: красная линия на рисунке ниже – сумма падающей и отражённой волн:

Эта третья волна является суммой падающей и отражённой волны. Она не распространяется по кабелю, как падающая или отражённая волна. Обратите внимание на точки вдоль линии, где падающая и отражённая волна всегда гасят друг друга: эти точки никогда не меняют позицию.

Стоячие волны распространены и в физическом мире. Рассмотрим верёвку, привязанную за один конец, и потрясём её:

Узлы (с точками где нет вибрации) и пучности (точки максимальной вибрации) остаются неизменными по всей длине верёвки. Струнные инструменты также создают стоячую волну, с узлами максимальной и минимальной вибрации вдоль их длины. Основное отличие между верёвкой и струнным инструментом в том, что инструмент уже настроен на правильную частоту вибрации:

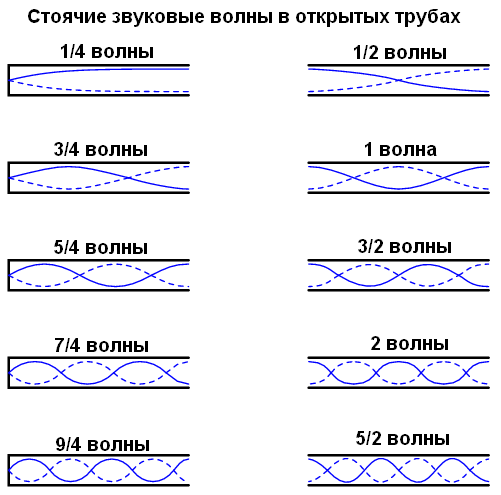
Ветер, дующий через открытые трубы, также производит стоячие волны. В этом случае, колеблются молекулы воздуха в трубе, а не твёрдое тело. Стоячая волна может заканчиваться в узле (минимальная амплитуда) или в пучности(максимальная амплитуда) и это зависит от того, открыт или закрыт другой конец трубки:

Закрытый конец трубы создаёт узел, а открытый – пучность. По аналогии, якорь струны – это узел, а свободный конец (если он есть) – пучность.

Обратите внимание, что внутри трубы могут возникать стоячие волны разных частот. Есть несколько резонансных частот для любой системы, поддерживающей стоячие волны.

Более высокие частоты должны быть кратны базовой частоте.

Фактические частоты для любой из этих гармоник (обертонов) зависят от физического размера трубы и скорости распространения волн (в данном случае — скорости распространения звука).

В линиях связи также возможно создать стоячие волны, и их частота будет зависеть от типа нагрузки на конце линии, от скорости распространения и физической длины. Резонанс в линиях передачи более сложен, чем резонанс струн или воздуха в трубах, потому что мы должны учитывать напряжение и ток волн.

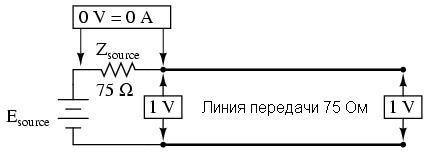
Резонанс в линиях передачи легче понять, используя компьютерное моделирование. Для начала, рассмотрим согласованную линию на 75 Ом:

Используя SPICE для имитации схемы, мы укажем для линии T1 волновое сопротивление 75 Ом(z0 = 75) и задержку распространения 1 мкс. Это удобный способ для выражения физической длины линии передачи – количество времени на распространение сигнала. Для реального кабеля RG-59B/U это будет длина 198 метров. 1 мкс соответствует частоте 1МГц. Я буду выбирать частоты от нуля до этой частоты, чтобы показать, как система реагирует на разные частоты.
Вот SPICE модель:

Transmission line
v1 1 0 ac 1 sin
rsource 1 2 75
t1 2 0 3 0 z0=75 td=1u
rload 3 0 75
.ac lin 101 1m 1meg
* Using «Nutmeg» program to plot analysis
.end

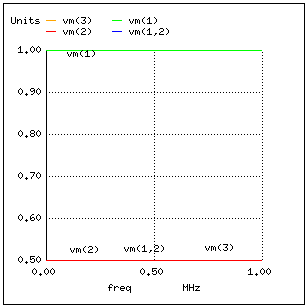
Выполним это моделирование и построим график падения напряжения на сопротивлении источника (Zsource) – это будет индикатор тока, и график напряжения на конце линии (напряжение на нагрузке). Мы увидим, что источник напряжения – на графике показано как vm(1) (величина напряжения между узлом 1 и точкой заземления 0) ровно 1 Вольт. Напряжения в точке 2 и 3 будут 0,5Вольт. Напряжение на резисторе – как индикатор тока – будет 0,5 Вольт:

В системе, где все сопротивления идеально согласованы, не может быть никаких стоячих волн, и нет резонансов на графике Боде.
Теперь давайте изменим сопротивление на 999 МОм, чтобы имитировать открытую линию передачи. Мы определённо должны получить отражённые волны на каких то частотах, от 1мГц до 1МГц:

Transmission line
v1 1 0 ac 1 sin
rsource 1 2 75
t1 2 0 3 0 z0=75 td=1u
rload 3 0 999meg
.ac lin 101 1m 1meg
* Using «Nutmeg» program to plot analysis
.end

Здесь напряжение питания линии vm(1) и напряжение на нагрузке остаются на прежнем уровне – 1Вольт. Другие падения напряжения зависят от частоты(так же от 1мГц до 1 МГц). Есть пять примечательных частот вдоль горизонтальной линии: 0Гц, 250кГц, 500кГц, 750кГц, 1МГц. Изучим каждую точку с учётом напряжения и тока в различных точках схемы.

• 0Гц (на самом деле 1мГц) – сигнал практически постоянного тока, и цепь ведёт себя так же, как если бы было подано 1Вольт постоянного тока. Ток не течёт, так как указано нулевое падение напряжения на резисторе Zsource, график vm(1,2), и напряжение на источнике равно напряжение в конце линии vm(2) (напряжение между точкой 2 и точкой 0).

• На 250кГц мы видим нулевое напряжение в точке 2, максимальный ток от источника и полное напряжение на конце линии.

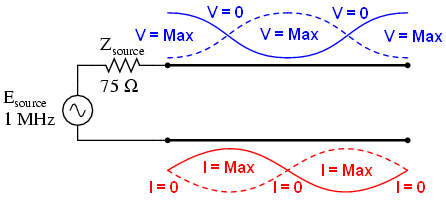
Вы можете быть удивлены, как это может быть? Как мы можем получить полное напряжение на открытом конце линии, если на входе нулевое напряжение? Ответ можно найти в парадоксе стоячей волны. На частоте 250кГц длина линии точно равна ¼ длины волны. Так как конец линии разомкнут, то не может быть никакого тока, но напряжение – будет. Таким образом, на конце провода будет узел для тока (ток равен нулю) и пучность для напряжения(максимальная амплитуда):

• На частоте 500кГц в линию укладывается ровно половина волны, и здесь мы видим ещё одну точку в которой ток равен нулю, а напряжение вновь имеет полную амплитуду:

• На частоте 750 кГц картина похожа на частоту 250кГц: напряжение на источнике равно нулю, и максимальный ток. ¾ волны укладывается в линии, в результате чего источник видит короткое замыкание в точке подключения к линии передачи даже не смотря на то, что на другом конце линии обрыв:

• Когда частота доходит до 1МГц, в линии укладывается один полный период волны. На данный момент, и ток, и напряжение в начале линии равны таковым в конце линии. И если в конце линии ток равен нулю (сопротивление равно 999 МОм), то и в начале линии ток тоже равен нулю. Напряжение на источнике равно напряжению на нагрузке. Фактически, источник видит разомкнутую цепь.

Аналогично короткое замыкание на конце линии генерирует стоячие волны, хотя узлы и пучности по току и напряжению меняются местами: На короткозамкнутом конце линии не будет напряжения (узел), но будет максимальный ток (пучность). Далее идёт моделирование SPICE и иллюстрации того, что происходит на всех интересных частотах: 0Гц, 250 кГц, 500кГц, 750кГц, 1 МГц. Короткое замыкание моделируется сопротивлением нагрузки 0 мкОм.

Transmission line
v1 1 0 ac 1 sin
rsource 1 2 75
t1 2 0 3 0 z0=75 td=1u
rload 3 0 1u
.ac lin 101 1m 1meg
* Using «Nutmeg» program to plot analysis
.end

В обоих примерах(разомкнутая и короткозамкнутая линия) отражается вся энергия. 100 процентов падающей волны достигает конца линии и отражается обратно к источнику. Если, однако, линия передачи нагружена каким-то сопротивлением, будет разница между максимальными и минимальными значениями напряжения и тока вдоль линии.

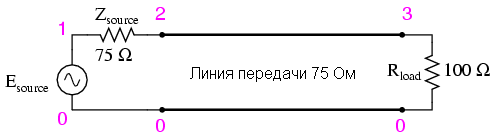
Предположим, что мы нагрузили линию резистором 100 Ом вместо 75:

Построим модель для этого случая:

Transmission line
v1 1 0 ac 1 sin
rsource 1 2 75
t1 2 0 3 0 z0=75 td=1u
rload 3 0 100
.ac lin 101 1m 1meg
* Using «Nutmeg» program to plot analysis
.end

Если мы запустим другой SPICE анализ с выводом текстовых значений вместо графика мы можем обнаружить, что все интересные частоты остались теми же самими (Постоянный ток, 250кГц, 500кГц, 750кГц, и 1МГц):

Transmission line
v1 1 0 ac 1 sin
rsource 1 2 75
t1 2 0 3 0 z0=75 td=1u
rload 3 0 100
.ac lin 5 1m 1meg
.print ac v(1,2) v(1) v(2) v(3)
.end

freq	v(1,2)	v(1)	v(2)	v(3)
1.000E-03	4.286E-01	1.000E+00	5.714E-01	5.714E-01
2.500E+05	5.714E-01	1.000E+00	4.286E-01	5.714E-01
5.000E+05	4.286E-01	1.000E+00	5.714E-01	5.714E-01
7.500E+05	5.714E-01	1.000E+00	4.286E-01	5.714E-01
1.000E+06	4.286E-01	1.000E+00	5.714E-01	5.714E-01

На всех частотах напряжение на источнике в точке 1 равно 1Вольт, как и положено. Напряжение на нагрузке также остаётся постоянным, но имеет меньшую амплитуду (0,5714 Вольт). Однако, напряжение питания линии (точка 2, график v(2)) и ток (график v(1,2)) указывает, что ток от источника меняется в зависимости от частоты.

На нечётных гармониках основной частоты(250кГц и 750кГц) мы видим разные уровни напряжения в начале и конце линии, поскольку на этих частотах стоячие волны создают узел с одной стороны линии и пучность – с другой. В отличие от разомкнутой и короткозамкнутой линии, максимальные значения не достигают ни нуля, ни 100% от исходного сигнала. Но мы всё так же имеем точки с минимумом и максимумом напряжения. То же самое справедливо и для тока. Если нагрузочное сопротивление линии не соответствует волновому сопротивлению линии, мы будем иметь точки максимального и минимального тока на некоторых фиксированных точках линии передачи, соответствующие узлам и пучностям.

Один из способов выражения уровня стоячих волн – отношение максимальной амплитуды (в точке пучности) к минимальной амплитуде для напряжения или тока. Это отношение называется КСВ – коэффициент стоячей волны. Если на линии обрыв или короткое замыкание, то КСВ равен бесконечности, так как минимальная амплитуда будет равна нулю. В примере 75 Ом линии с нагрузкой 100 Ом КСВ будет равен 1,333: максимальное напряжение линии на 250 или 750кГц(0,5714 В) делённое на минимальное напряжение линии (0,4286 В).

КСВ также можно рассчитать, зная нагрузочное сопротивление и волновое сопротивление линии, делением большего значения на меньшее. В нашем примере 100Ω /75Ω = 1,333.

Линия с идеально согласованной нагрузкой будет иметь КСВ равный 1. Это считается идеалом не только из-за того, что отражённые волны – это энергия не достигшая нагрузки, но из-за высоких значений напряжения и тока: высокое напряжение может создать пробой в изоляции, а высокий ток повредить проводники.

Также, линия с плохим КСВ выступает в качестве антенны. Это нежелательно: такая антенна может навести помехи на близлежащие провода. Интересно, что антенны – это открытые линии передач, и работают они при КСВ как можно ближе к 1. Это значит, что вся энергия излучается.

Следующая фотография показывает точку соединения в линии связи радиопередатчика. Большие медные трубы с керамическим изолятором представляют из себя жёсткую коаксиальную линию с волновым сопротивлением 50 Ом.

Гибкий коаксиальный кабель с волновым сопротивлением 50 Ом. Белая пластиковая труба соединяет газ внутри труб: они запечатаны для защиты от влаги. Обратите внимание на плоские провода для соединения линий. Почему они не круглые? Это сделано из-за скин-эффекта, который делает бесполезной большую площадь поперечного сечения на больших частотах.

Как и многие линии связи, они работают на низком КСВ. Как мы увидим в следующем разделе, явление стоячих волн в линиях связи не всегда вредны, так как они могут быть использованы для полезной функции: преобразования импеданса.

Преобразование импеданса

Стоячие волны в резонансных точках короткозамкнутых или открытых линиях могут производить необычные эффекты. При длине линии ½ длины волны (и в кратное число раз больше) источник видит нагрузку как есть. На следующих иллюстрациях это показано:

В обоих случаях на концах линии пучность для напряжения и узел для тока. Линия имитирует нагрузку – бесконечное сопротивление, источник видит обрыв.
То же верно, если на линии короткое замыкание: в точке подключения источника будет минимум напряжения и максимум тока.

Однако, если длина линии равна четверти длины волны, источник при коротком замыкании на конце линии увидит обрыв, а оборванную линию будет видеть как короткозамкнутую.

Линия разомкнута, а источник видит короткое замыкание:

Линия замкнута, а источник видит обрыв:

На этих частотах линия передачи ведёт себя как трансформатор сопротивления, превращая бесконечное сопротивление в нуль и наоборот. Это происходит только в резонансных точках, когда в линию укладывается четверть волны и кратно больше(3/4, 5/4, 7/4, 9/4 …), но если частота известна и неизменна, то это явление может быть использовано для согласования разных волновых сопротивлений друг с другом.
Возьмём в качестве примера линию передачи 75Ω с нагрузкой 100Ω. Из численного моделирования SPICE определим какое сопротивление видит источник:

Простое уравнение связывает волновое сопротивление линии(Z0), импеданс нагрузки(Zload) и входной импеданс(Zinput) для несогласованной линии на нечётной гармоники:

Рассмотрим практический пример, когда надо согласовать нагрузку 300Ω и источник 75Ω. Всё, что нам нужно сделать, так это вычислить правильное волновое сопротивление линии и длину для четверти длины волны на 50МГц.
Во-первых, рассчитаем сопротивление линии. Z0 = Sqrt(75*300) = 150Ω.

Во-вторых, надо рассчитать длину линии. Предположим, коэффициент укорочения 0,85, скорость света 300 тысяч км/сек, скорость сигнала будет 255 тысяч км/сек. Делим эту скорость на частоту сигнала и получаем длину волны 5,1 метр. Нам нужно четверть длину волны – это будет 1,275м.

Вот схема для SPICE анализа:

Мы можем указать длину линии по задержке сигнала. При частоте 50МГц период будет 20нс. Время задержки на четверть длины волны будет 5нс.

Transmission line
v1 1 0 ac 1 sin
rsource 1 2 75
t1 2 0 3 0 z0=150 td=5n
rload 3 0 300
.ac lin 1 50meg 50meg
.print ac v(1,2) v(1) v(2) v(3)
.end

freq	v(1,2)	v(1)	v(2)	v(3)
5.000E+07	5.000E-01	1.000E+00	5.000E-01	1.000E+00

На частоте 50МГц в точке 1-2 падает ровно половина – 0,5В, а вторая половина напряжения падает на линии связи в цепи 2-0. Это означает, что источник видит в нагрузке 75Ω. Нагрузка, однако, получает не половину, а 1 Вольт (напряжение v(3)). На сопротивлении 75Ω падает 0,5В или 3,333мВт – столько же, сколько и на нагрузке 300 Ом при напряжении 1В. В соответствии с теоремой максимальной мощности (теоремой Якоби) на нагрузке рассеивается максимальная возможная мощность. Линия передачи длиной в четверть волны, волновым сопротивлением 150Ω и нагрузкой 300Ω ведёт себя как 75Ωнагрузка.

Конечно, это всё будет работать лишь на 50МГц и нечётных гармониках. Для других частот линию передачи придётся удлинять или укорачивать.

Как ни странно, линия той же длины будет согласовывать 300Ω источник и 75Ω нагрузку. Это показывает, что явление преобразования импеданса в корне отличается от принципа работы трансформатора с двумя обмотками.

Transmission line
v1 1 0 ac 1 sin
rsource 1 2 300
t1 2 0 3 0 z0=150 td=5n
rload 3 0 75
.ac lin 1 50meg 50meg
.print ac v(1,2) v(1) v(2) v(3)
.end

freq	v(1,2)	v(1)	v(2)	v(3)
5.000E+07	5.000E-01	1.000E+00	5.000E-01	2.500E-01

В этом случае на внутреннем сопротивлении источника упадёт 0,5В, или 833мкВт. На нагрузке будет 0,25В – те же 833мкВт.

Этот метод часто используется для согласования линий передачи и антенны в радиопередачиках, так как там частота часто известна и неизменна. Минимальная длина преобразователь импеданса соответствует ¼ длины волны.

Introduction

Standing waves are created when two waves that are travelling in the opposite directions, interfere with each other and are of identical frequency and amplitude.

This whole thing happens when those waves are superimposed and because of it either the energy of those two waves is added together or gets cancelled at all. A vibration rope that is tied at one end will produce the standing wave or normal mode.

What is a Standing Wave?

A standing wave is called the stationary wave. The standing wave simply defines the wave formed on a string that is formed with the superimposition of two waves of the same frequency and amplitude and travels in the opposite direction from each other (Wang et al. 2021).

A mass on a spring has a natural frequency that helps it to swing back and forth freely. However, a stretched string, which is fixed from one end will swing with a whole spectrum of frequency and has its own pattern of vibration. This kind of pattern in vibration is known as the standing wave or normal mode.

If an extended string is fixed from both ends and a continuous wave is tended towards the x-direction, the wave reaches the specific fixed end it reflects and comes back to the left ends (Ong, W & Zainulabidin, 2020).

As the left proceeding wave reflects and starts travelling to the right part, the same cycle continues. It starts overlapping each other, and the ultimate result is in this process, there are too many overlapping waves that never stop overlapping each other (Muchomas, 2022). It forms two types of waves, longitudinal waves and transverse waves and together it creates the Standing waves.

Figure 1: Standing Wave

Equation of a standing wave

If it is considered as at any point that is u and time, and two waves are moving towards left and right, means the opposite direction on a string, and they have the same amplitude, frequency and wavelength (Ong, W & Zainulabidin, 2020). Using the trigonometric identities of sin (a + b) = sin (a) cos (b) + cos(a)sin(b) it can be written and the result can form a equation, that is — y(u,t) = A sin(ku — ωt) + A sin(ku + ωt) = 2A sin(ku)cos(ωt).

As the position and time dependency have been separated, the wave is no longer a travelling wave (Wang et al. 2021). No energy travels alongside the string and it will show that one section of the string will swing with maximum amplitude while the other section does not even move. Here, it creates the standing wave or normal mode.

Figure 2: Formation of standing wave

What are nodes and antinodes?

The pattern of the Standing wave is characterised by the alternative pattern of nodes and antinodes.

Node

Node is a particular point in a standing wave where the wave has the minimum amplitude. It can be defined as all standing waves that are characterized by their position along with the medium that stands still (Ong, W & Zainulabidin, 2020).

When a crest meets the trough, it results in a node. At nodes, the amplitude is 0.

Antinode

Standing waves are also characterized by the Antinodes. The opposite of a node is an Antinode. Antinode creates when the crest meets a crest and a trough meets a trough (labman, 2022).

Antinode can be defined as the region of maximum amplitude that is situated exactly in between the adjacent nodes in a vibrating body or spring, which means a point that goes through the maximum number of displacements in the time of each vibration cycle of a standing wave.

Figure 3: The nodes and antinodes

Example of Standing Wave or normal mode

The best and simplest example of a standing wave is found in the waves produced by any stringed musical instrument, like a plucked guitar string. This plucked guitar string discharges a particular sound frequency that depends on two things, they are the length of the string and how taut or dense the string is (Ong, W & Zainulabidin, 2020).

As only certain standing waves or normal modes can form on the string, as result, each string only makes a certain note. The effects of the standing wave can be seen in a drum too. If powder can be spread on the drum and then make it vibrate, one can check the appearance of a standing wave.

For a better understanding of Standing Wave or normal mode, it is easier to take the example of two people shaking each end of a jump rope (Ualberta, 2022). It will form a standing wave if they started shaking the rope in proper sync.

Conclusion

In short, generally, when two waves reflected or move from both ends produced an interference patterns that is the most complicated and confusing one. However, an integral number of half of the wavelengths fits into the string’s length because the wavelength of the wave is just appropriate; it forms the Standing wave. The pattern of standing waves can be set up in almost any kind of structuration. However, when it is in 2D or 3D, it becomes away more complicated. If one structure vibrates with all the fundamental frequencies then as a result it is shown that all the particles will swing in phase with the exact same frequency.

FAQs

Q1. Mention two examples of standing waves.

Standing wave can be found for sure in any kind of musical instrument that has strings. For example, in guitar, the easiest example of a standing wave is two people shaking each end of a jump rope.

Q2. What is called a normal mode?

Standing wave is also referred to as normal mode and formed through longitudinal waves and transverse waves.

Q3. How node and antinode does connected to standing waves?

The Standing wave pattern is characterized by the alternative pattern of one nodes and antinodes. The amplitude of a standing wave can increase without limit until the structure face damage.

References

Journals

Wang, Z., Shen, Y., Liu, Q., & Fu, X. (2021). To unify azimuthally traveling-wave and standing-wave structured light by ray-wave duality. Journal of Optics, 23(11), 115604. Retrieved from: https://iopscience.iop.org/article/10.1088/2040-8986/ac160b/pdf

Ong, W. S., & Zainulabidin, M. H. (2020). Vibration Characteristics of Beam Structure Attached with Vibration Absorbers at its Vibrational Node and Antinode by Finite Element Analysis. JSE Journal of Science and Engineering, 1(1), 7-16.Retrived from: https://journals.umkt.ac.id/index.php/jse/article/download/519/447

Websites

Muchomas (2022). About Standing waves/Normal modes, Retrieved from: https://muchomas.lassp.cornell.edu/p214/Notes/IntroWaves/node15.html . [Retrieved on 17th June 2022]

ualberta (2022). About Standing Waves; Normal Modes. Retrieved from: https://sites.ualberta.ca [Retrieved on: 17.06.2022]

labman (2022). About Standing waves. Retrieved from: http://labman.phys.utk.edu [Retrieved on 17th June 2022]

physicskey (2022). About standing wave and normal waves. Retrieved from: https://www.physicskey.com/39/standing-waves-and-normal-modes. [Retrieved on 17th June 2022]