Как найти путь алгебра формула

Время, скорость, расстояние

О чем эта статья:

Расстояние

Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.

Расстояние — это длина от одного пункта до другого.

• Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.

Расстояние обозначается латинской буквой s.

Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).

Формула пути

Чтобы найти расстояние, нужно умножить скорость на время движения:

s = v × t

Скорость

Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.

Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.

Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.

Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.

Формула скорости

Чтобы найти скорость, нужно разделить путь на время:

v = s : t

Показатели скорости чаще всего выражаются в м/сек или км/час.

Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.

Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.

Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.

Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.

Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.

Время

Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.

Время — это продолжительность каких-то действий, событий.

• Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.

Время движения обозначается латинской буквой t.

Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.

Формула времени

Чтобы найти время, нужно разделить расстояние на скорость:

t = s : v

Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750 (м)

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит, скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.

Ответ: первый школьник добежал быстрее.

Если известны скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:

t = s : v = 500 : 100 = 5 (мин)

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Формула пути

Определение и формула пути

Линия, которую описывает материальная точка при своем движении, называется траекторией.

Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени от t₁ до t₂.

В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:

В цилиндрических координатах длина пути может быть выражена как:

В сферических координатах формулу длины пути запишем:

Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t₁ называют начальным положением. Очень часто полагают t₁=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).

Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds, который называют элементарным. При этом:

где $bar$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.

Виды движения и формулы длины пути

Длина пути при равномерном движении (v=const) точки равна:

где t₁ – начало отсчета движения, t₂ – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.

Если движение не является равномерным, то можно длину пути $Delta s$ на отрезке времени от $t$ до $t + Delta t$ находят как:

$$Delta s=langle vrangle Delta t(6)$$

где $langle vrangle$ – средняя путевая скорость. При равномерном движении $langle vrangle = v$ .

Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:

где a – постоянное ускорение, v₀ – начальная скорость движения.

Единицы измерения пути

Основной единицей измерения пути в системе СИ является: [s]=м

Примеры решения задач

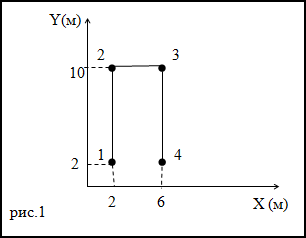
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой, чему равно перемещение, если точка двигалась 1-2-3-4.

Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:

Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:

Ответ. Путь равен 20 м, перемещение равно 4 м.

Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией: x=-0,2t 2 (м) . Какой путь пройдет материальная точка за 5 с?

Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения задачи примем формулу пути в виде:

Подставим в (2.1) функцию x=-0,2t 2 , учтем, что $0 c leq t leq 5 c$ имеем:

Как посчитать путь ускоряющегося тела не используя время

Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.

Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).

Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.

Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.

Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.

Выводим формулу пути без времени

Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.

В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону).

Сонаправленные или противоположно направленные векторы называют коллинеарными векторами. Прочитайте подробнее о коллинеарных векторах.

Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:

( large v_ <0>left( frac<text<м>> right)) – начальная скорость тела;

( large v left( frac<text<м>> right)) – конечная скорость;

( large a left( frac<text<м>>> right)) – ускорение тела;

( large S left( text <м>right)) – путь, пройденный телом;

(large t left( c right)) – время, за которое тело прошло этот путь.

В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.

Что сделать, чтобы получить формулу пути, в которой отсутствует время:

• сначала получить выражение для времени t из уравнения для скорости;
• затем в формулу пути подставить полученное выражение вместо времени t.

Выражаем время из формулы для скорости

Выпишем формулу, связывающую начальную и конечную скорость тела:

[ large v = v_ <0>+ a cdot t ]

Избавимся в правой части от начальной скорости, обозначенной символом ( v_<0>). Для этого из обеих частей уравнения вычтем число ( v_<0>). Получим такую запись:

[ large v — v_ <0>= a cdot t ]

Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». Для этого разделим обе части уравнения на «a»:

Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».

В формулу пути подставим выражение для времени

Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:

В первом уравнении системы будем заменять символ t дробью из второго уравнения. Тогда система из двух уравнений превратится в единственное уравнение. И в этом уравнении не будет символа t времени:

Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.

Упрощаем выражение, расположенное до знака «плюс» в правой части

Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:

Умножим числитель дроби на число (v_<0>).

• сначала числитель обособим скобками;
• затем запишем число (v_<0>) перед скобками;
• а потом внесем это число внутрь скобок.

В числитель дроби, обособленный с помощью скобок помещаем число (v_<0>):

Теперь необходимо умножить скобку на число (v_<0>). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.

Нужно к каждой скорости в скобках дописать число (v_<0>), умножая его на эти скорости. Получим такое выражение:

То есть, вместо первоначальной записи, мы получили такую запись:

Возводим в квадрат дробь

После знака «плюс» в правой части уравнения располагается дробь, которую нужно возвести в квадрат. Обратим внимание на эту дробь:

Правильно возвести дробь в степень поможет рисунок 3.

В результате возведения в квадрат дробь приобретет такой вид:

В числителе этой дроби находится выражение в скобках, которое нужно возвести в квадрат. И нам придется применить одну из формул сокращенного умножения. Запоминать формулы сокращенного умножения удобно в виде, приведенном на рисунке 4.

Используем для этого формулу сокращенного умножения, которая содержит знак «минус». Она называется «Квадрат разности». Тогда числитель дроби превратится в такую запись:

Теперь можем записать полученную дробь:

Упрощаем правую часть, записанную после знака «плюс»

Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:

Мы уже провели некоторые преобразования и можем теперь заменить дробь, возводимую в квадрат более подробной записью:

Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.

Итак, поменяем местами знаменатели дробей:

Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:

А перемножив числители и знаменатели двух дробей, получим такую запись:

Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:

Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».

Теперь, осталось сложить две дроби в правой части – дробь, записанную до знака «плюс» с дробью, записанной после знака «плюс». А чтобы эти дроби можно было сложить, нужно будет привести их к общему знаменателю.

Приводим к общему знаменателю дроби в правой части уравнения

Вернемся еще раз к первоначальному уравнению:

Заменим правую часть этого уравнения выражениями, которые мы получили:

Сравним знаменатели дробей.

Первая дробь обладает знаменателем «a», а вторая – «2a». Выберем число «2a» в качестве общего знаменателя обеих дробей.

Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:

Примечания:

1. Нам известно, что если какое-либо число умножить на единицу, то после умножения это число не изменится. Значит, если какое-либо выражение умножить на единицу, то полученное выражение останется равным самому себе. На единицу можно умножать все, что угодно – дроби, выражения в скобках и т. п.
2. Математики часто применяют прием умножения на единицу. А после этого единицу записывают в виде некоторой дроби. При этом используют правило: Единица – это дробь, у которой числитель и знаменатель равны (одинаковые).

Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:

Получим такую дробь:

Поместим ее в выражение для пути:

Дроби с одинаковыми знаменателями складываем

Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:

Раскроем скобки в числителе полученного выражения:

Примечание: Обратим внимание на то, что в числителе дважды встречается член (2v_ <0>v), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа (2v_<0>v) вычитается такое же число (2vv_<0>). В конце концов, это число покидает нашу запись и, она упрощается:

Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:

Вычтем подобные члены, содержащие ( v^<2>_<0>):

В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:

Примечания:

1. Это формула, с помощью которой можно рассчитать путь тела, когда известны его начальная и конечная скорость, а, так же, ускорение.
2. Видно, что время t в правой части этого выражения отсутствует.
3. Мы выводили эту формулу для случая, когда тело увеличивало скорость.

Как выглядит формула пути без времени, когда скорость тела уменьшается

Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:

Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:

Выводы

Пусть нам известны начальная и конечная скорость тела и его ускорение. Тогда путь, пройденный телом, можно рассчитать так:

Классическим примером текстовой задачи, которая может встретиться вам на ЕГЭ, является задача на движение. Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.

Научиться решать такие задачи довольно легко, для этого нужно знать алгоритм, состоящий всего из 3 шагов.

1. Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
2. Как решать задачи на движение: 3 простых шага
3. Задачи на движение вдогонку: примеры с решением
4. Задачи на движение навстречу: примеры с решением
5. Задачи на движение по течению и против течения: примеры с решением

Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить

Для решения любой задачи на движение вам обязательно нужно знать всего одну формулу, которая вам уже давно известна:И уметь правильно выражать из этой формулы скорость и время:Многие ученики путаются при записи этих формул, допуская ошибки. Чтобы раз и навсегда запомнить формулы нахождения расстояния, скорости и времени, просто нарисуй треугольник. В верхнем углу треугольника напиши S, а внизу — V и t. Проведи горизонтальную черту между ними. Теперь мы можем закрыть рукой ту величину, которую нам нужно найти, и увидим формулу нахождения этой величины. Например, нам нужно найти расстояние. Закрываем рукой S, и на нашем рисунке останется V t – это и есть формула нахождения расстояния. Или нам нужно найти время. Закрываем рукой t, и на нашем рисунке остается  – формула нахождения времени. Нужно найти скорость? Закрываем рукой V, получаем  – формулу нахождения скорости. Главное запомнить, что S должна быть в верхнем углу. Это можно сделать, например, с помощью ассоциации, что S похожа на змею, а змея – хозяйка горы, поэтому она на вершине. Вот как выглядит такой магический треугольник:

Чтобы правильно решить задачу на движение нужно:

1. Определить неизвестное и составить таблицу на основании условия задачи.
2. Составить уравнение на основании таблицы.
3. Вернуться к условиям задачи и записать правильный ответ.

Давайте подробнее разберем каждый шаг:

1. Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
2. На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
3. После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти. Находим неизвестное и записываем ответ.

Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.

Задачи на движение вдогонку: примеры с решением

При решении задачи, по условия которой оба участника движения двигаются в одном направлении, как правило, сравнивается время их движения. Необходимо запомнить правила:

1. Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
2. Если условия задачи содержат общее время, то дроби, выражающее время, складываются.

Давайте разберем, как работают эти правила при решении задач.

Задача 1

Велосипедист и автомобилист одновременно выехали из пункта А в пункт Б, расстояние между которыми равно 50 км. Известно, что скорость автомобилиста на 40 км/ч больше, чем у велосипедиста, в результате чего автомобилист приехал в пункт Б на 4 часа раньше. Найдите скорость велосипедиста.

Решение:

1. Необходимо определить, что взять за переменную Х и составить таблицу. Вспоминаем, что удобнее всего за Х обозначить скорость в том случае, если она прямо не указано в условиях задачи.

В нашем случае скорость в условиях задачи не указана, поэтому скорость велосипедиста обозначаем за Х.

Составляем таблицу, данные для которой берем из условий задачи.

Итак, расстояние (S) нам известно – 50 км, скорость велосипедиста – х, скорость автомобилиста на 40 км/ч больше, значит она равна х + 40. Чтобы определить время вспоминаем формулу t = S / V и подставляем в нее наши значения. Время, затраченное велосипедистом, получится 50 / х, а время, затраченное автомобилистом — 50 / (х + 40).2. На основании таблицы и условий задачи необходимо составить уравнение.

Из условий задачи нам известно, что автомобилист приехал раньше велосипедиста на 4 часа (смотрим наше первое правило). Это значит, что велосипедист затратил на 4 часа больше времени, чем автомобилист. Следовательно,

50 / (х + 40) + 4 = 50 / х

Решаем полученное уравнение, для этого приводим наши дроби к одному знаменателю:

50х + 4х (х + 40) – 50 (х+40) / х (х + 40) = 0

(50х + 4х² + 160х – 50х – 2000) / х (х+40) = 0

(4х² + 160х – 2000) / (х² + 40х) = 0

Умножим обе части уравнение на х² + 40х:

4х² + 160х – 2000 = 0

Разделим обе части уравнения на 4:

х² + 40х – 500 = 0

Находим дискриминант:

D = 40² – 4 * 1 * (-500) = 3600

Далее находим корни уравнения:

х₁ = 10

х₂ = — 50

3. Возвращаемся к условиям задачи и вспоминаем, что же требовалось найти.

Нам нужно было определить скорость велосипедиста, которую мы обозначили за Х.

Скорость велосипедиста должна быть положительна, поэтому х₂ не подходит по смыслу задачи. Следовательно, нас интересует только х₁ и скорость велосипедиста равна 10 км/ч.

Ответ: 10 км/ч.

Задача 2

Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 80 км. На следующий день он поехал обратно, при этом его скорость была на 2 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 2 часа. В итоге на возвращение из города Б в город А у него ушло времени столько же, сколько на путь из города А в город Б. Найдите скорость велосипедиста на пути из города А в город Б.

Решение:

1. Обозначим скорость велосипедиста на пути из города А в город Б как переменную Х.

Составим таблицу.

Из условий задачи: расстояние — 80 км, скорость велосипедиста во второй день – х. Его скорость во второй день была на 2 км/ч больше, чем в первый день, т.е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).2. На основании таблицы и условий задачи составим уравнение.

Из условий задачи нам известно, что во второй день велосипедист останавливался и отдыхал 2 часа, следовательно, в пути он провел на 2 часа меньше (смотрим наше первое правило).  Также нам известно, что общее затраченное велосипедистом время в первый и во второй дни равно. Следовательно:

80 / (х + 2) + 2 =  (80 / х)

Решаем полученное уравнение, для чего приводим дроби к общему знаменателю:

(80х + 160 – 80х – 2х (х+2)) / х (х + 2) = 0

Умножаем обе части уравнения на х (х + 2):

160 – 2х² + 4х = 0

— 2х² — 4х + 160 = 0

Делим обе части уравнения на -2:

х² + 2х – 80 = 0

Находим дискриминант:

D = 2² – 4 * 1 * (-80) = 4 + 320 = 324

Тогда корни уравнения равны:

х₁ = 8

х₂ = — 10

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.

Скорость должна быть положительна, поэтому х₂ = — 10 не подходит по смыслу задачи. Следовательно, скорость велосипедиста равна 8.

Ответ: 8 км/ч.

Задачи на движение навстречу: примеры с решением

Главное, что нужно помнить о движении навстречу: скорости участников движения складываются.

В тех случаях, когда нам неизвестно общее расстояние, то есть мы не можем его определить из условий задачи и из составленных уравнений, данное расстояние следует принимать за единицу.

Примеры решения задач на движение навстречу:

Задача 1

Из города А в город Б выехал автомобилист, через 3 часа навстречу ему выехал мотоциклист со скоростью 60 км/ч. Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Расстояние между городами А и Б равно 470 км. Найдите скорость автомобилиста.

Решение:

1. Обозначим скорость автомобилиста как Х.

Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Следовательно, автомобилист проехал 350 км, а мотоциклист 470 – 350 = 120 км.

Составим таблицу:2. Составим уравнении на основании таблицы и условий задачи.

Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно:

350/х = 120/60 + 3

350/х = 5

Решаем полученное уравнение:

5х = 350

х = 70

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость автомобилиста, которую мы обозначали за Х. Следовательно, скорость автомобилиста равна 70 км/ч.

Ответ: 70 км/ч.

Задача 2

Из городов А и Б одновременно навстречу друг другу выехали автомобилист и велосипедист. Автомобилист приехал в город А на 6 часов раньше, чем велосипедист приехал в город Б. Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?

Решение:

1. Время автомобилиста обозначим как Х.

Примем расстояние между городами А и Б за единицу. Остальные данные берем из условий задачи.

Составим таблицу:2. Составим уравнение на основании таблицы и условий задачи.

Известно, что велосипедист и автомобилист встретились через  4 часа после начала движения  и в сумме преодолели все расстояние от города А до города Б. То есть все расстояние от города А до города Б было преодолено за 4 часа.

Вспоминаем, что при движении навстречу скорости движения участников складываются. Подставим в формулу пути известные нам данные:

((1 / х) +  (1 / (х — 6))) * 4 = 1

Решаем полученное уравнение:

(4 / х) +  (4 / (х — 6)) = 1

Приводим дроби к одному знаменателю:

(4х — 24 + 4х — х² + 6х) / (х (х — 6))  = 0

Делим обе части уравнения на х (х — 6), при условии, что х > 6:

-х² + 14х — 24 = 0

Умножим обе части уравнение на -1:

х² — 14х + 24 = 0

Находим дискриминант нашего квадратного уравнения:

D = 14² – 4 * 1 * 24 = 100

Находим корни уравнения:

х₁ = 12

х₂ = 2

х₂ < 6, следовательно, корнем уравнения не является.

3. Возвращаемся к условиям задачи. Нам необходимо было определить, сколько времени затратил автомобилист на путь из города Б в город А. Это время мы обозначали за Х. Следовательно, автомобилист затратил на путь из города Б в город А 12 часов.

Ответ: 12 часов.

Задачи на движение по течению и против течения: примеры с решением

В условиях задач на движение по реке всегда дано две скорости: собственная скорость судна (скорость, с которой он может двигаться в неподвижной воде) и скорость течения.

При этом возможны две ситуации: когда судно движется по течению и когда судно движется против течения.

Когда судно движется по течению, то течение помогает судну двигаться, оно начинает двигаться быстрее, следовательно, собственная скорость судна и скорость течения складываются.

Когда же судно двигается против течения, то оно ощущает сопротивление, плыть ему становится тяжелее. В этом случае скорость течения будет вычитаться из собственной скорости судна.

Давайте рассмотрим примеры решения задач на движение по реке.

Задача 1

Катер прошел против течения реки 160 км/ч и вернулся в пункт отправления, затратив времени на обратный путь на 8 часов меньше. Найдите скорость катера в неподвижной воде, если известно, что скорость течения реки равна 5 км/ч.

Решение:

1. Обозначим собственную скорость катера – х.

Составим таблицу:2. На основании таблицы и условий задачи составим уравнение.

По условиям задачи известно, что время, затраченное на путь по течению реки, на 8 часов меньше, чем время, затраченное на путь против течения реки (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Соответственно:

160 / (х + 5) + 8 = 160 / (х — 5)

Решаем данное уравнение. Для этого приводим дроби к общему знаменателю:

(160 (х – 5) + 8 (х – 5) (х + 5) – 160 (х + 5)) / (х – 5) (х + 5) = 0

(160х – 800 + (8х – 40) (х + 5) – 160х — 800) / (х – 5) (х + 5)  = 0

Умножаем обе части уравнения на (х – 5) (х + 5):

-1600 + 8х² + 40х – 40х – 200 = 0

8х² – 1800 = 0

8х² = 1800

х² = 225

х_1,2 = ±15

3. Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х₁ = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.

Ответ: 15 км/ч.

Задача 2

Моторная лодка вышла в 9:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв в пункте Б 3 часа, моторная лодка повернула назад и вернулась в пункт А в 20:00. Найдите скорость течения реки, если известно, что собственная скорость моторной лодки 8 км/ч.

Решение:

1. Обозначим скорость течения реки за х. Остальные данные берем из условия задачи.

Составим таблицу:2. Составим уравнение.

Нам известно, что моторная лодка начала свое движение в 9:00, а закончила в 20:00, а также в течение этого времени пробыла без движения во время стоянки – 3 часа. Таким образом, общее время движения будет 20 – 9 – 3 = 8 часов. Когда речь идет об общем времени движения, то нам нужно сложить время движения по течению и время движения против течения (пользуемся вторым правилом, которое разбирали при решении задач на движение вдогонку). Получаем:

30 / (8+х) + 30 / (8-х) = 8

Решаем полученное уравнение. Для этого приводим дроби к общему знаменателю:

(30 (8+х) + 30 (8-х) – 8 (8-х) (8+х)) / (8-х) (8+х) = 0

Умножаем обе части уравнения на (8-х) (8+х):

240 + 30х + 240 – 30х – (64 – 8х) (8+х) = 0

480 – 512 – 64х + 64х – 8х² = 0

8х² = 32

х² = 4

х_1,2 = ±2

3. Возвращаемся к условию задачи. Нам необходимо было найти скорость течения, которую мы обозначили за х. Так как скорость не может быть отрицательной, то х₁ = -2 противоречит условию задачи. Следовательно, скорость течения равна 2 км/ч.

Ответ: 2 км/ч.

Итак, мы разобрались, как решать задачи на движения. В ЕГЭ 2023 помимо задач на движение могут содержаться и другие текстовые задачи: на смеси и сплавы, на работу, на проценты. О том, как их решать, вы можете узнать на нашем сайте, а также .

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

v=S/t, где

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N — механическая мощность,

F — сила,

v — скорость,

cos α — косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Пример №1

Допустим, из точки ( displaystyle A) и из точки ( displaystyle B) навстречу друг другу выехали две машины. Скорость одной машины – ( displaystyle 60) км/ч, а скорость ( displaystyle 2) машины – ( displaystyle 40) км/ч. Они встретились через ( displaystyle 1,2) часа.

Какое расстояние между пунктами ( displaystyle A) и ( displaystyle B)?

1 вариант решения

Можно рассуждать так: машины встретились, значит расстояние между городами – это сумма расстояния, которая прошла первая машина, и расстояния, которое прошла вторая.

( displaystyle 60cdot 1,2text{ }=text{ }72) (км) – путь, который проехала первая машина

( displaystyle 40cdot 1,2text{ }=text{ }48) (км) – путь, который проехала вторая машина

( displaystyle 72 + 48 = 120) (км) – расстояние, которое проехали обе машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).

2 вариант решения (более рациональный)

А можно просто воспользоваться очень логичной формулой о сложении скоростей.

Проверим, работает ли она:

( displaystyle 60 + 40 = 100) (км/ч) – скорость сближения машин

( displaystyle 100cdot 1,2text{ }=text{ }120) (км) – расстояние, которые проехали машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).

Оба решения являются верными. Второе просто более рациональное.

Пример №3

Итак, задача:

Из пункта ( displaystyle A) и пункта ( displaystyle B) машины движутся навстречу друг другу со скоростями ( displaystyle 50) км/ч и ( displaystyle 80) км/ч. Расстояние между пунктами – ( displaystyle 195) км.

Через сколько времени машины встретятся?

1 вариант решения

Пусть ( displaystyle x) – время, которое едут машины, тогда путь первой машины – ( displaystyle 50x), а путь второй машины – ( displaystyle 80x).

Их сумма и будет равна расстоянию между пунктами ( A) и ( B) – ( displaystyle 50x+80x=195).

2 вариант решения (более рациональный)

( displaystyle 50 + 80 = 130) (км/ч) – скорость сближения машин;

( displaystyle 195:130 = 1,5) (ч) – время, которое машины были в пути.

Задача решена.

Пример №4

Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями ( displaystyle 60) км/ч и ( displaystyle 40) км/ч. Через сколько минут они встретятся. Если расстояние между пунктами ( displaystyle 100) км?

2 способа решения:

I способ

Относительная скорость автомобилей ( displaystyle 60+40=100) км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью ( displaystyle 100) км/ч. Так как между автомобилями изначально расстояние ( displaystyle 100) км, время, через которое второй автомобиль проедет мимо первого:

( displaystyle t=frac{100}{100}=1 час=60 минут).

II способ

Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его ( displaystyle t). Тогда первый автомобиль проехал путь ( displaystyle 60t), а второй – ( displaystyle 40t).

В сумме они проехали все ( displaystyle 100) км. Значит,

( displaystyle 60t+40t=100Rightarrow t=1 час=60 минут).

Из пункта ( displaystyle A) в пункт ( displaystyle B), расстояние между которыми ( displaystyle 30) км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на ( displaystyle 65) км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт ( displaystyle B) на ( displaystyle 156) минут позже, чем мотоциклист.

Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать – прямая, пункт ( displaystyle A), пункт ( displaystyle B), две стрелочки…

В общем рисуй, и сейчас сравним, что у тебя получилось.

Пустовато как-то, правда? Рисуем таблицу.

Как ты помнишь, все задачи на движения состоят из ( displaystyle 3) компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах.

Правда, мы добавим еще один столбец – имя, про кого мы пишем информацию – мотоциклист и велосипедист.

Так же в шапке укажи размерность, в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?

У тебя получилась вот такая таблица?

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист
мотоциклист

Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.

Первое, что мы имеем – это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен ( displaystyle 30) км. Вносим!

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист			( displaystyle 30)
мотоциклист			( displaystyle 30)

Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на ( displaystyle 65) км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста…

Возьмем скорость велосипедиста за ( displaystyle x), тогда скорость мотоциклиста будет ( displaystyle x+65)…

Если с такой переменной решение задачи не пойдет – ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист	( displaystyle x)		( displaystyle 30)
мотоциклист	( displaystyle x+65)		( displaystyle 30)

Таблица преобразилась. У нас осталась не заполнена только одна графа – время. Как найти время, когда есть путь и скорость?

Правильно, разделить путь на скорость. Вноси это в таблицу.

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист	( displaystyle x)	( displaystyle frac{30}{x})	( displaystyle 30)
мотоциклист	( displaystyle x+65)	( displaystyle frac{30}{65+x})	( displaystyle 30)

Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.

Что мы можем на нем отразить?

Молодец. Скорость передвижения мотоциклиста и велосипедиста.

Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.

Какие данные не отражены ни в таблице, ни на рисунке?

Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени – ( displaystyle 156) минут.

Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.

( displaystyle 156) минут / ( displaystyle 60) минут = ( displaystyle 2,6) часа.

И что дальше, спросишь ты? А дальше числовая магия!

Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?

Правильно. Мы можем составить уравнение, основываясь на разнице во времени!

( displaystyle frac{30}{x}-frac{30}{65+x}=2,6)

Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.

Это уравнение – рациональное. Если не знаешь, что это такое, прочти тему «Рациональные уравнения».

Приводим слагаемые к общему знаменателю:

( displaystyle frac{30cdot left( 65+x right)}{xcdot left( 65+x right)}-frac{30x}{xcdot left( 65+x right)}=2,6)

Раскроем скобки и приведем подобные слагаемые: Уф! Усвоил? Попробуй свои силы на следующей задаче.

( displaystyle frac{1950}{xcdot left( 65+x right)}=2,6)

Из этого уравнения мы получаем следующее:

( displaystyle 2,6cdot xcdot left( 65+x right)=1950)

( displaystyle xcdot left( 65+x right)=frac{1950}{2,6})

( displaystyle xcdot left( 65+x right)=750)

Раскроем скобки и перенесем все в левую часть уравнения:

( displaystyle {{x}^{2}}+65{x}-750=0)

Вуаля! У нас простое квадратное уравнение. Решаем!

( displaystyle {{x}^{2}}+65{x}-750=0)

( displaystyle D={{b}^{2}}-4ac)

( displaystyle D={{65}^{2}}-4cdot 1cdot left( -750 right)=4225+3000=7225)

( displaystyle sqrt{D}=sqrt{7225}=85)

( displaystyle {{x}_{1,2}}=frac{-bpm sqrt{D}}{2a})

( displaystyle {{x}_{1}}=frac{-65+85}{2}=10)

( displaystyle {{x}_{2}}=frac{-65-85}{2}=-75)

Мы получили два варианта ответа. Смотрим, что мы взяли за ( displaystyle x)? Правильно, скорость велосипедиста.

Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь, о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ – ( displaystyle 10) км/ч.

Пример №9

Два велосипедиста одновременно отправились в ( displaystyle 165)-километровый пробег. Первый ехал со скоростью, на ( displaystyle 5) км/ч большей, чем скорость второго, и прибыл к финишу на ( displaystyle 5,5) часов раньше второго.

Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

Напоминаю:

• Прочитай задачу пару раз – усвой все-все детали. Усвоил?
• Начинай рисовать рисунок – в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
• Проверь, все ли величины у тебя одинаковой размерности, и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь, какие там графы?).
• Пока все это пишешь, думай, что взять за ( displaystyle x)? Выбрал? Записывай в таблицу!
• Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок – помни о «3Р»!

Все сделал? Молодец! У меня получилось, что скорость велосипедиста – ( displaystyle 10) км/ч.

Пример №10

Из пункта ( displaystyle A) круговой трассы выехал велосипедист. Через ( displaystyle 40) минут он еще не вернулся в пункт ( displaystyle A) и из пункта ( displaystyle A) следом за ним отправился мотоциклист.

Через ( displaystyle 20) минут после отправления он догнал велосипедиста в первый раз, а еще через ( displaystyle 40) минут после этого догнал его во второй раз.

Найдите скорость велосипедиста, если длина трассы равна ( displaystyle 50) км. Ответ дайте в км/ч.

Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:

Пусть скорость велосипедиста будет ( displaystyle x), а мотоциклиста – ( displaystyle y). До момента первой встречи велосипедист был в пути ( displaystyle 60) минут, а мотоциклист – ( displaystyle 20).

При этом они проехали равные расстояния:

( displaystyle 60x=20y (1))

Между встречами велосипедист проехал расстояние ( displaystyle 40x), а мотоциклист – ( displaystyle 40y).

Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:

(Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили – спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.)

Значит,

( displaystyle 40x+50=40y (2))

Полученные уравнения решаем в системе:

( displaystyle left{ begin{array}{l}60x=20y\40x+50=40yend{array} right.Leftrightarrow left{ begin{array}{l}y=3x\4x+5=4yend{array} right.Rightarrow text{4}x+5=12xRightarrow )

( displaystyle Rightarrow x=frac{5}{8}=0,625frac{text{км}}{мин}=0,625cdot 60frac{text{км}}{text{ч}}=37,5frac{text{км}}{text{ч}})

Ответ: ( displaystyle 37,5).

Разобрался? Попробуй решить самостоятельно следующие задачи:

Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, – это стоячая вода.

Скорость течения в озере равна ( displaystyle 0).

Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь – налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести.

Это понятно? Логично же.

А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…

Это происходит потому что у реки есть скорость течения, которая относит твой плот по направлению течения.

Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) – он движется со скоростью течения.

Разобрался? Тогда ответь вот на какой вопрос – «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?

Здесь возможно два случая:

1 случай – ты плывешь по течению, и тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.

2 случай – ты плывешь против течения. Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы ( displaystyle 100) метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость – скорость течения.

Как найти расстояние, зная скорость и время?

Как найти время через скорость и расстояние?

Как найти скорость по времени и расстоянию?

Ответы на эти вопросы следуют из формулы пути.

Формула пути связывает между собой скорость, время и расстояние.

Решение любой задачи на движение основано на  применении формулы пути.

1) Формула пути:

   

Чтобы найти расстояние, нужно скорость умножить на время.

2) Формула нахождения времени через скорость и расстояние:

   

Чтобы найти время, надо расстояние разделить на скорость.

3) Формула для нахождения скорости по времени и расстоянию:

   

Чтобы найти скорость, надо расстояние разделить на время.