Как найти путь пройденный бруском

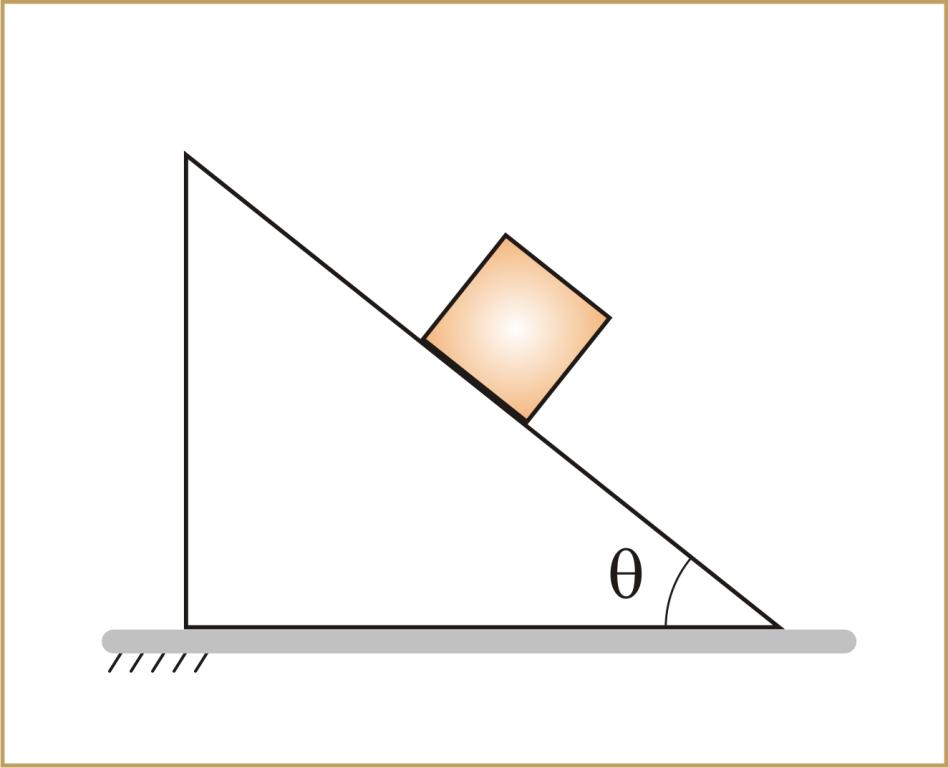
Задача 49. Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол α с горизонтом (рис.36). Коэффициент трения зависит от пройденного пути х по закону μ=kx, где k – постоянная. Найти путь, пройденный бруском до остановки.

Рис.36

Решение.

Применение законов динамики

В данной задаче рассматривается движение под действием переменной результирующей силы.

На брусок действует Земля с силой тяжести mg и наклонная плоскость с силой нормального давления N и силой трения F_тр, величина которой равна

Fтр=μN=kxN.                       (1)

По второму закону Ньютона в векторной форме имеем:

m→a=m→g+→N+→Fтр.

Спроектируем это векторное уравнение на оси координат, указанные на рисунке,

x:      ma=mgsinα−Fтр,                         (2)

y:      0=−mgcosα+N.                             (3)

Разрешая полученную систему уравнений относительно ускорения, получим зависимость ускорения от координаты х:

a=g(sinα−kxcosα).                              (4)

Далее решается кинематическая задача, связанная с преобразованием уравнений (задача третьего класса). Воспользуемся определениями скорости и ускорения

v = dx/dt, a = dv/dt,

и исключим переменные a и dt. В результате получим дифференциальное уравнение с разделяющимися переменными v и х:

vdv=g(sinα−kxcosα)dx.

Интегрируя это уравнение от момента, соответствующего началу движения (v₀=0, x₀=0) до остановки (v_ост=0, x=x_ост), получим

0∫0vdv=xост∫0g(sinα−kxcosα)dx;

0=g⎛⎝sinα∙xост−kcosαx2ост2⎞⎠,

откуда искомая координата остановки равна

xост=2g∙tgαk.

(корень x_ост=0 соответствует началу движения).

Энергетический способ

Значительно чаще эта задача решается с помощью закона изменения энергии.

Рис.37

В состоянии I (рис.37) тело обладает потенциальной энергией

WI=Wp=mgh=mgxостsinα,

в состоянии II (рис.37) — как кинетическая, так и потенциальная энергия равна нулю

WII=0.

Энергия изменяется вследствие работы, совершаемой силой трения:

WII−WI=Aтр.

величина силы трения, как отмечалось раньше, составляет

Fтр=μN=kxmgcosα.

Как видно из формулы, сила трения зависит от пройденного расстояния (координаты х). При перемещении на расстояние dx совершается работа

dA=Fтрdxcosπ=−kxmgcosαdx.

Полная работа до остановки составит

A=−kmgcosαxост∫0xdx=−kmgcosαx2ост2.

Подставим полученные выражения в применяемый закон:

0−mgxостsinα=−kmgcosαx2ост2

и выразим искомую величину — путь, пройденный телом до остановки,

xост=2g∙tgαk.

Видно, что и в этом случае энергетический способ решения задачи оказывается более предпочтительным.

2017-05-20   

Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол $alpha$ с горизонтом. Коэффициент трения зависит от пройденного пути $x$ по закону $k = ax$, где $a$ — постоянная. Найти путь, пройденный бруском до остановки, и максимальную скорость его на этом пути.

Решение:

Из второго закона Ньютона для бруска в проекции х: $F_{x} = mw_{x}$, получаем

$mg sin alpha — kmg cos alpha = mw$

или $v frac{dv}{dx} = g sin alpha — ax g cos alpha$, (as $k= ax$),

или, $vdv = (g sin alpha — ax g cos alpha) dx$

или, $int_{0}^{v} vdv = g int_{0}^{x} ( sin alpha — x cos alpha ) dx$

Итак, $frac{v^{2}}{2} = g ( sin alpha x — frac{x^{2}}{2} a cos alpha) dx$ (1)

Из (1) $v = 0$ либо

$x = 0$, или $x = frac{2}{a} tg alpha$

Поскольку движение бруска является однонаправленным, оно останавливается после прохождения расстояния $frac{2}{a} tg alpha$.

Из (1), при $v_{max}$,

$frac{d}{dx} left ( sin alpha x — frac{x^{2}}{2} a cos alpha right ) = 0$, что дает $x = frac{1}{a} tg alpha$

Следовательно, максимальная скорость будет на расстоянии, $x = frac{1}{a} tg alpha$

Подставляя это значение $x$ в (1) получаем максимальную скорость,

$v_{max} = sqrt{ frac{g sin alpha tg alpha}{a}}$

• Комментировать
• Жалоба
• Ссылка

Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

F¯ = m*a¯

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

M = I*α

Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

a = Δv/Δt;

v = v₀ ± a*t;

S = v₀*t ± a*t²/2

Здесь v₀ — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

α = Δω/Δt;

ω = ω₀ ± α*t;

θ = ω₀*t ± α*t²/2

Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

a = α*r;

v = ω*r

Здесь r — радиус вращения.

Движение по наклонной плоскости: силы

Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

F_f = µ*N

Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

F = m*g*sin(φ) — µ*m*g*cos(φ) = m*g*(sin(φ) — µ*cos(φ)) = m*a

Здесь φ — это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

F = m*g*sin(φ) — F_r = m*a

Где F_r — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

M = F_r*r = I*α

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45^o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

m*g*(sin(φ) — µ*cos(φ)) = m*a =>

a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с²

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

S = a*t²/2

Откуда следует выразить время, и подставить известные значения:

t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

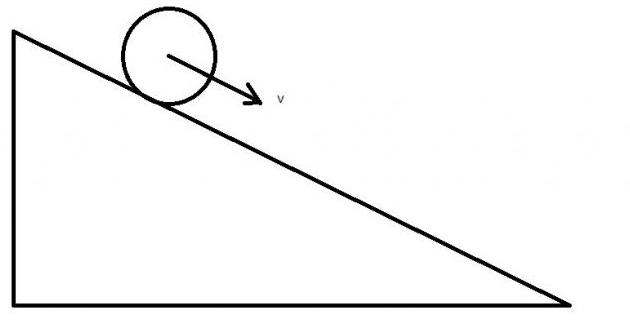
Задача со скатывающимся по плоскости цилиндром

Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30^o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

m*g*sin(φ) — F_r = m*a;

F_r*r = I*α = I*a/r

Момент инерции I цилиндра вычисляется по формуле:

I = 1/2*m*r²

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

F_r*r = 1/2*m*r²*a/r = >

F_r = 1/2*m*a;

m*g*sin(φ) — 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

S = a*t²/2 =>

t = √(2*S/a)

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.