Путь
Пусть частица, двигаясь вдоль некоторой траектории, переместилась из точки 1 в точку 2.
Путь s (или s) равен измеренному вдоль траектории расстоянию, пройденному частицей в процессе движения (длина траектории).
Путь является величиной скалярной, неотрицательной

Связь между путем и модулем скорости частицы
Пусть за малый промежуток времени t частица переместилась из точки 1 в точку 2 траектории. Пройденный частицей путь обозначим s.
Если уменьшать промежуток времени t, точка 2 траектории будет приближаться к точке 1. При этом различие между длиной дуги s и стягивающей ее хордой – модулем перемещения | r| будет уменьшаться.
32

Связь между путем и модулем скорости частицы
В пределе при t 0 отношение длины дуги s к длине хорды | r| равно единице:
lim s 1
t 0 r
Тогда
v dr lim r lim s ds dt t t dtt 0 t 0
Следовательно, модуль вектора скорости равен производной пути по времени

Связь между путем и модулем скорости частицы
Зная зависимость модуля скорости v от времени, можно вычислить пройденный частицей путь:
v dsdt , ds v(t)dt
Интегрируя это равенство, получим:
|
s |
t2 |
t2 |
|
ds v(t)dt, |
s v(t)dt |
|
|
0 |
t1 |
t1 |
34

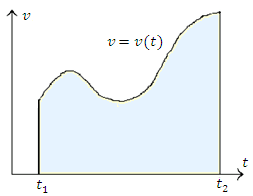
Графическое определение пути
Если задана графическая зависимость модуля скорости частицы от времени t, то путь s, пройденный частицей за промежуток времени от t1 до t2 численно равен площади криволинейной трапеции, ограниченной графиком функции v(t), осью t и вертикальными прямыми t = t1 и t = t2.
t2
s v(t)dt
t1 35

Полное ускорение частицы
Полное ускорение частицы a можно представить в виде суммы двух перпендикулярных друг другу составляющих:
aa an
Модуль полного ускорения:
|
dv 2 |
v4 |
||||||
|
2 |
2 |
||||||
|
a a |
an |
||||||
|
R2 |
|||||||
|
dt |
36

Полное ускорение частицы
37
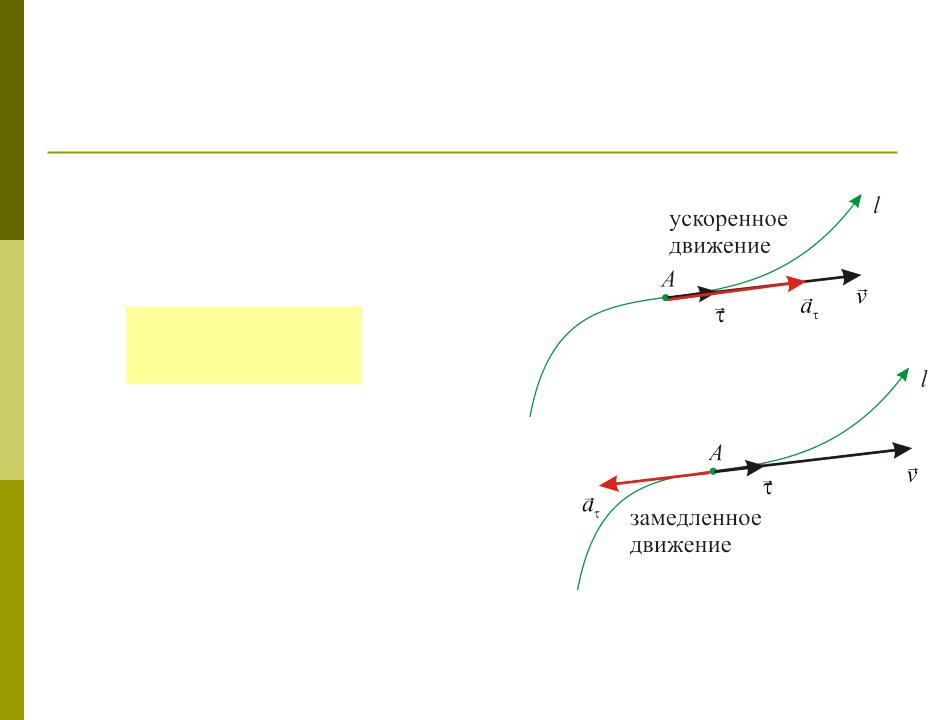
Тангенциальное (касательное) ускорение
Первое слагаемое в этом выражении называется
тангенциальным (касательным) ускорением:
|
dv |
d 2s |
|||||
|
a |
||||||
|
2 |
||||||
|
dt |
dt |
|||||
Вектор a направлен по касательной
к траектории движения частицы; при этом a v, если движение
ускоренное; a v, если движение замедленное.
Тангенциальное ускорение частицы характеризует изменение скорости частицы по модулю (если a = 0,
|
движение является равномерным). |
38 |
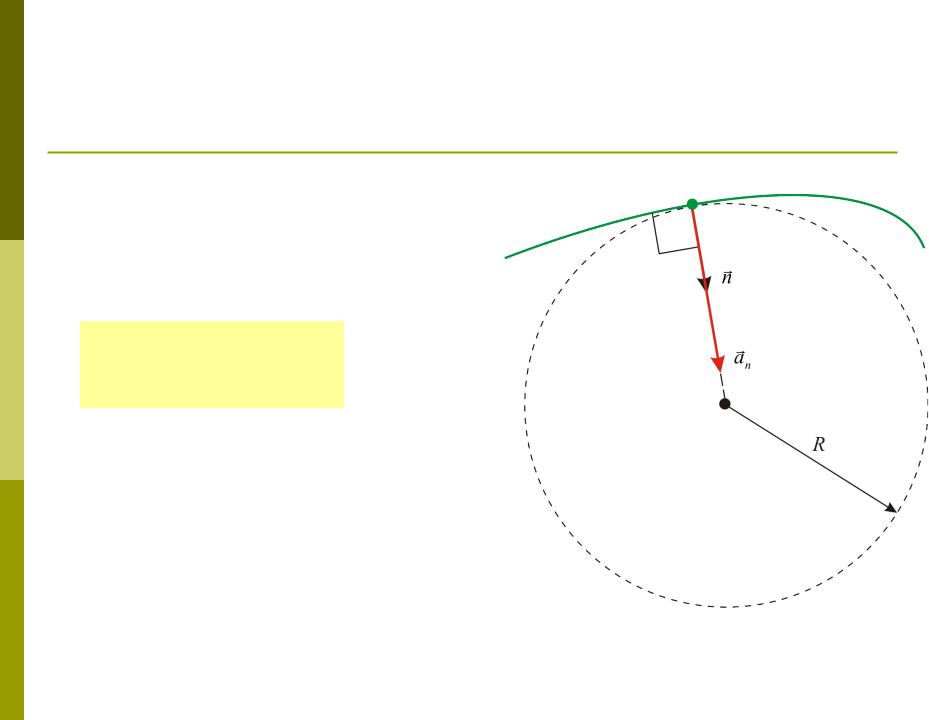
Нормальное
(центростремительное)
ускорениеВторое слагаемое называется
нормальным
(центростремительным) ускорением:
|
v2 |
1 ds |
2 |
||||
|
an |
R |
n |
n |
|||
|
R dt |
Вектор an всегда перпендикулярен касательной к тракетории движения, т.е. an v и an a .
Нормальное ускорение характеризует изменение скорости по направлению (для прямолинейного движения, когда R

ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
1.4 Твердое тело в механике. Виды движения твердого тела
40
Соседние файлы в папке МЕХАН
- #
- #
- #
- #
- #
Конев В.В. Определенные интегралы
Движение частицы с переменной скоростью
| Рассмотрим задачу о вычислении перемещения s частицы за промежуток времени от  до до 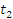 при движении частицы вдоль некоторой прямой с переменной скоростью при движении частицы вдоль некоторой прямой с переменной скоростью 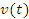 . .
|
Тема: Какой путь проделает частица? (Прочитано 2365 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Частица начала своё движение из начала координат, и её скорость зависит от времени по закону u−(t) = (i−∙A + j−∙B)∙((t/τ))5, где A, B – постоянные величины, i−, j− – единичные орты в декартовой системе координат. Какой путь проделает частица за время t = 1 с, если τ = 1 с. А = 2 м/c, В = 3 м/c. Сделать рисунок.
а) 0,20 м; б) 0,30 м; в) 0,40 м; г) 0,50 м; д) 0,60 м;
Записан
Решение. По условию задачи частица начала своё движение из начала координат, и её скорость зависит от времени по закону
[ begin{align}
& vec{upsilon }(t)=(Acdot vec{i}+Bcdot vec{j})cdot {{((frac{t}{tau }))}^{5}}, \
& vec{upsilon }(t)=Acdot {{(frac{t}{tau })}^{5}}cdot vec{i}+Bcdot {{(frac{t}{tau })}^{5}}cdot vec{j},vec{upsilon }(t)=2cdot {{(frac{t}{1})}^{3}}cdot vec{i}+3cdot {{(frac{t}{1})}^{5}}cdot vec{j}, \
& vec{upsilon }(t)=2cdot {{t}^{5}}cdot vec{i}+3cdot {{t}^{5}}cdot vec{j}(1). \
end{align} ]
Скорость тела меняется и задан закон этого изменения на некотором отрезке от 0 до t с. Тогда путь пройденный телом можно определить через определенный интеграл
[ s={{s}_{0}}+intlimits_{0}^{t}{upsilon (t)dt.} ]
Определим какой путь проделает частица за время t
[ begin{align}
& x={{x}_{0}}+intlimits_{0}^{t}{2cdot {{t}^{5}}dt}={{x}_{0}}+left. 2cdot frac{1}{6}cdot {{t}^{6}} right|_{0}^{t}={{x}_{0}}+frac{2cdot {{t}^{6}}}{6},{{x}_{0}}=0,x=frac{{{t}^{6}}}{3}(2). \
& y={{y}_{0}}+intlimits_{0}^{t}{3cdot {{t}^{5}}dt}={{y}_{0}}+left. 3cdot frac{1}{6}cdot {{t}^{6}} right|_{0}^{t}={{y}_{0}}+frac{3cdot {{t}^{6}}}{6},{{y}_{0}}=0,y=frac{3cdot {{t}^{6}}}{6}=frac{{{t}^{6}}}{2}(3). \
& s=sqrt{{{(frac{{{t}^{6}}}{3})}^{2}}+{{(frac{{{t}^{6}}}{2})}^{2}}}(4). \
& s=sqrt{{{(frac{{{1}^{6}}}{3})}^{2}}+{{(frac{{{1}^{6}}}{2})}^{2}}}=sqrt{frac{1}{9}+frac{1}{4}}=sqrt{frac{4+9}{36}}=frac{sqrt{13}}{6}=0,6. \
end{align} ]
Ответ: д) 0,60 м.
[ begin{align}
& {{v}_{x}}={x}'(t)=2cdot {{t}^{5}};{{v}_{y}}={y}'(t)=3cdot {{t}^{5}}; \
& L=intlimits_{0}^{1}{sqrt{{{(2cdot {{t}^{5}})}^{2}}+{{(3cdot {{t}^{5}})}^{2}}}}dt=intlimits_{0}^{1}{sqrt{4cdot {{t}^{10}}+9cdot {{t}^{10}}}}dt=intlimits_{0}^{1}{sqrt{13cdot {{t}^{10}}}}dt=intlimits_{0}^{1}{{{(13cdot {{t}^{10}})}^{frac{1}{2}}}}dt= \
& =intlimits_{0}^{1}{sqrt{13}cdot {{t}^{5}}}dt=sqrt{13}intlimits_{0}^{1}{{{t}^{5}}}dt=left. sqrt{13}cdot frac{{{t}^{6}}}{6} right|_{0}^{1}=frac{sqrt{13}}{6}=0,6. \
end{align} ]
« Последнее редактирование: 30 Апреля 2018, 06:32 от alsak »
Записан

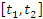 на столь малые интервалы
на столь малые интервалы 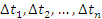 , чтобы изменением скорости частицы в пределах каждого интервала можно было пренебречь.
, чтобы изменением скорости частицы в пределах каждого интервала можно было пренебречь.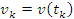 – скорость частицы на промежутке времени
– скорость частицы на промежутке времени 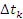 . Тогда перемещение
. Тогда перемещение 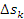 частицы за время
частицы за время 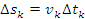 .
.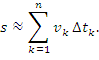
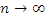 и все
и все 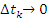 , получаем точную формулу для перемещения частицы за промежуток времени от
, получаем точную формулу для перемещения частицы за промежуток времени от 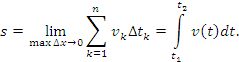
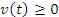 на промежутке
на промежутке 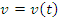 на этом промежутке.
на этом промежутке.