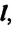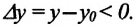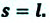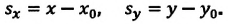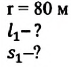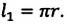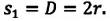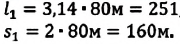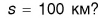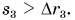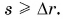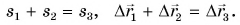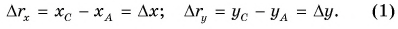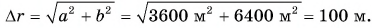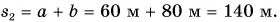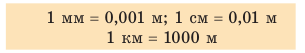Содержание:
Путь и перемещение:
Вы знаете, что любой вид движения совершается по определенной траектории.
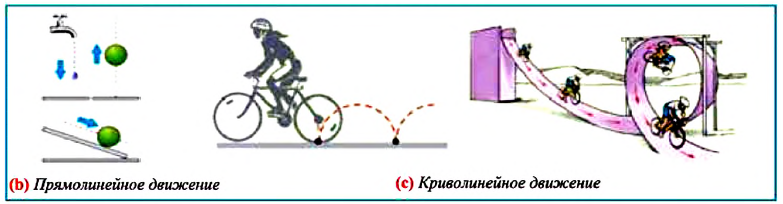
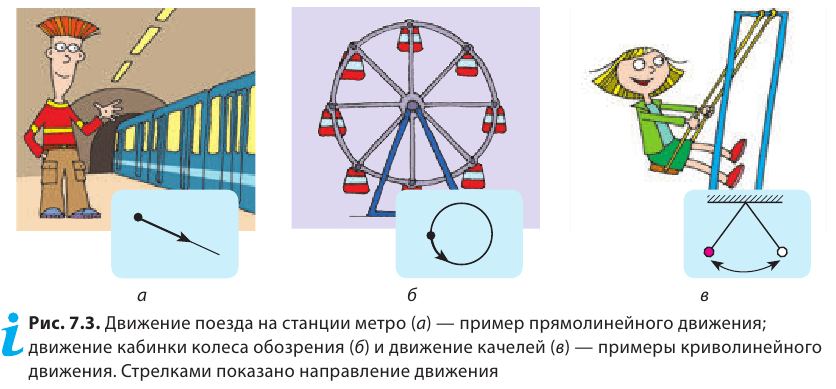
Траектория — это линия, которую описывает материальная точка при своем движении в данной системе отсчета. Эта линия может быть и невидима, например, траектория движения рыбы в воде, самолета в небе, пчелы в воздухе и др., которые можно только вообразить. По форме траектории механическое движение делится на прямолинейное и криволинейное.
Движение, траектория которого представляет собой прямую линию относительно данной системы отсчета, называется прямолинейным движением (b), а движение, траектория которого кривая линия, — криволинейным (с).
Длина траектории движения материальной точки, называется пройденным путем. Пройденный путь является положительной скалярной величиной, обозначается буквой
Для полного описания движения материальной точки необходимо определить изменение его положения в пространстве с течением времени, т.е. определить изменение координат материальной точки, или же изменение его радиус-вектора.
Изменение любой физической величины равно разности его конечного и начального значений и обозначается знаком 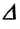
Изменение координат материальной точки во время движения
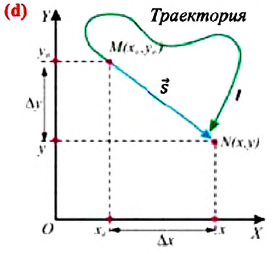
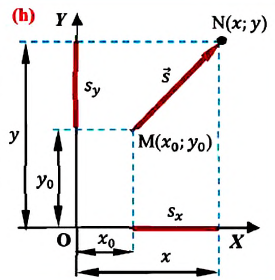
Изменение координат материальной точки во время движения может быть, как положительным, так и отрицательным. Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается 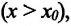
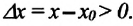
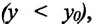
Изменение радиус-вектора материальной точки во время движения
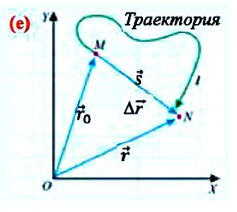
На следующем рисунке представлены радиус-векторы 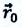
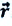
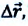
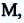
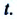

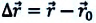
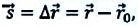
Перемещение — это направленный отрезок прямой, соединяющий начальное положение движущейся материальной точки с ее конечным положением. Перемещение — векторная величина.
Векторная величина — это величина, определяемая, кроме числового значения (модуля), также и направлением.
К вектору перемещения, как векторной величине, можно применить известные действия над векторами — сложение и вычитание векторов, определение результирующего вектора методом треугольника и параллелограмма.
Единицей измерения перемещения, как и пути, в СИ является метр, однако, перемещение имеет отличающийся физический смысл: перемещение показывает, на какое расстояние и в каком направлении изменилось начальное положение материальной точки за данный промежуток времени.
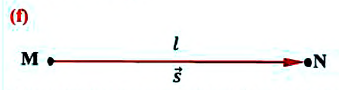
Внимание! Только при прямолинейном движении без изменения направлении, модуль перемещения равен пройденному пути, во всех остальных случаях (при изменении направления прямолинейного движения, криволинейном движении) пройденный путь больше модуля перемещения (е).
Материальная точка прошла расстояние 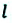
Материальная точка прошла расстояние 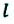
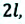
Если при движении материальной точки на плоскости известны его начальные координаты и вектор перемещения, то можно определить координаты конечного положения точки. Например, предположим, что материальная точка совершила перемещение 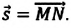
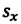
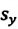
Одинаковы ли путь и перемещение
Задача:
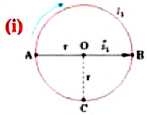
Велосипедист движется по круговому велотреку радиусом 80 м. Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).
Дано:
Решение:
Пройденный путь 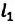
Модуль перемещения же равен диаметру окружности:
Вычисление:
Что такое путь и перемещение
Автобус отправился из Москвы в 9 часов утра. Можно ли определить, где находился автобус в 11 часов, если известно, что он проделал путь
Конечно, нет. Ясно лишь, что в 11 часов он находился в месте, удаленном от Минска не более чем на 100 км (т. е. внутри окружности, изображенной на рисунке 37). Не исключено, что к 11 часам автобус вернулся в Москву.
Значит, для определения конечного положения тела недостаточно знать его начальное положение и пройденный им путь.
Мы нашли бы местонахождение автобуса в 11 часов, если бы знали траекторию его движения (зеленая линия на рисунке 38). Отсчитав 100 км от начальной точки маршрута вдоль траектории, найдем, что в 11 часов автобус прибыл в Борисов.
А можно поступить иначе. Конечное положение автобуса можно определить, зная его начальное положение и всего одну векторную величину, называемую перемещением.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
Обозначим перемещение символом 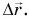
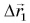
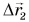
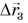
Теперь, даже не зная траектории, по начальной точке и перемещению мы можем найти конечную точку для каждого из участков движения автобуса и для всего маршрута в целом.
Можно ли сравнивать путь S, пройденный телом, с его перемещением 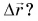
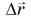
Сравнивать путь S можно с модулем перемещения 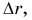
В рассматриваемом примере путь, пройденный автобусом за два часа, 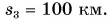
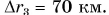
Пройденный путь был бы равен модулю перемещения, если бы автобус все время двигался по прямой, не изменяя направления движения.
Следовательно, путь всегда не меньше модуля перемещения:
Как складывают между собой пути и как — перемещения? Из рисунка 38 находим:
Пройденные пути складывают арифметически, а перемещения — по правилам сложения векторов.
Равен ли при этом модуль 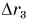
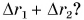
Мы выяснили, что путь и траектория относительны. Покажите на примерах, что перемещение тоже относительно, т. е. зависит от выбора системы отсчета.
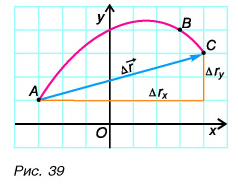
При решении задач важно уметь находить проекции перемещения. Построим вектор перемещения куска мела по школьной доске из точки А в точку С (рис. 39). Из рисунка видно, что проекции вектора 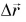
Главные выводы:
- Путь — это длина участка траектории, пройденного телом за данный промежуток времени. Путь — положительная скалярная величина.
- Перемещение тела — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
- Путь не меньше модуля перемещения тела за то же время.
- Пройденные пути складываются арифметически, а перемещения — по правилам сложения векторов.
Пример:
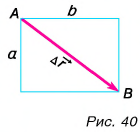
Конькобежец пересек прямоугольную ледовую площадку по диагонали АВ, а пешеход прошел из точки А в точку В по краю площадки (рис. 40). Размеры площадки 60 х 80 м. Определите модули перемещения конькобежца и пешехода и пути, пройденные ими.
Решение
Из рисунка 40 видно, что перемещения пешехода и конькобежца одинаковы. Модуль перемещения:
Путь конькобежца:
Путь пешехода:
Ответ:
- Заказать решение задач по физике
Траектория движения
Возьмите лист бумаги и карандаш. Поставьте на листе точки А и В и соедините их кривой линией (рис. 7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.
Траектория движения — это воображаемая линия, которую описывает в пространстве движущаяся точка. Обычно мы не видим траектории движения тел, но иногда бывают исключения.
Так, в безоблачную погоду высоко в небе можно увидеть белый след, который во время своего движения оставляет самолет*. По этому следу можно определить траекторию движения самолета. Траектории движения каких тел можно восстановить по следам, изображенным на рис. 7.2? В каких случаях траекторию движения «заготавливают» заранее? Форма траектории может быть разной: прямая, окружность, дуга, ломаная и т. д. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел (рис. 7.3).
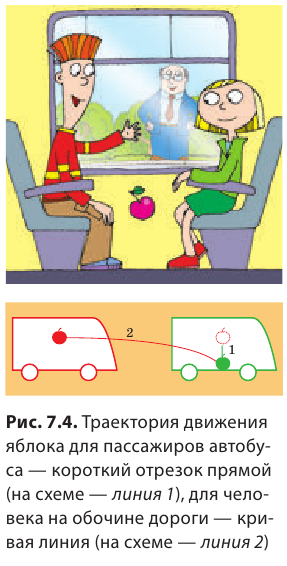
Форма траектории движения тела зависит от того, относительно какой системы отсчета рассматривают движение. Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.
Чем путь отличается от перемещения
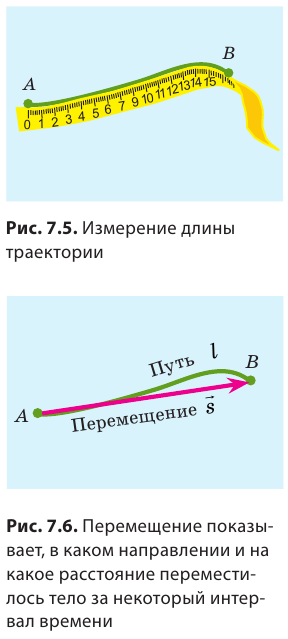
Вернемся к началу (см. рис. 7.1). Чтобы найти путь, который прошел конец карандаша, рисуя кривую линию, необходимо измерить длину этой линии, то есть найти длину траектории (рис. 7.5). Путь — это физическая величина, равная длине траектории. Путь обозначают символом l. Единица пути в СИ — метр: [l]= м. Используют также дольные и кратные единицы пути, например миллиметр (мм), сантиметр (см), километр (км):
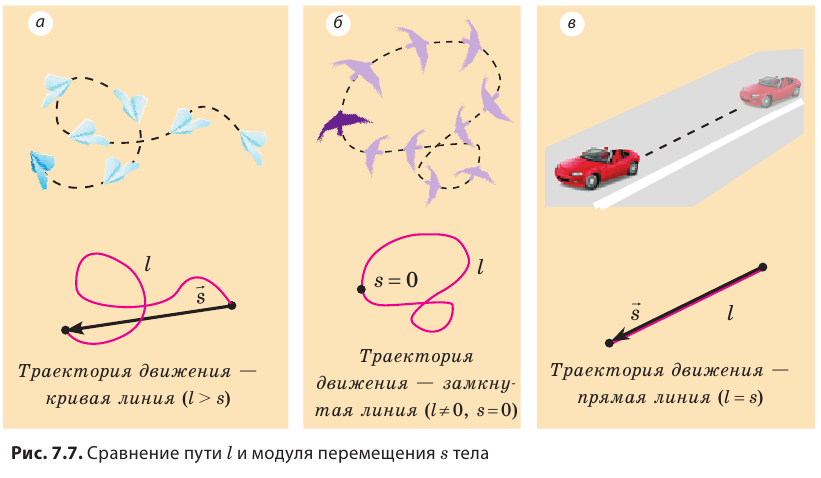
Путь, пройденный телом, будет разным относительно разных систем отсчета. Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).
Направленный отрезок прямой, соединяющий начальное и конечное положения тела, называют перемещением. Перемещение обозначают символом 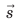
Модуль перемещения, то есть расстояние, на которое переместилось тело в определенном направлении, также обозначают символом s, но без стрелки. Единица перемещения в СИ такая же, как и единица пути, — метр: [s]= м. В общем случае перемещение не совпадает с траекторией движения тела (рис. 7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).
Итоги:
Воображаемая линия, которую описывает в пространстве движущаяся точка, называется траекторией. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел. Путь l — это физическая величина, равная длине траектории. Перемещение 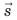
Физические величины, имеющие значение и направление, называется векторными а имеющие только значение — скалярными.
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
На прошлых уроках мы познакомились с определением механического движения, узнали, каким бывает движение, изучили его свойства и характеристики. Теперь нам известны формулы для расчета скорости при равномерном движении ($upsilon = frac{S}{t}$) и средней скорости при неравномерном ($upsilon_{ср} = frac{S}{t}$).
На данном уроке мы посмотрим на эти формулы с другой стороны — научимся использовать их для расчета пути и времени движения, а также рассмотрим графики скорости и пути для равномерного движения.
Формулы для расчета пути и времени движения при равномерном движении тела
Скорость тела при равномерном движении вычисляется по формуле $upsilon = frac{S}{t}$. Отсюда, если мы знаем скорость и время, то можем найти пройденный путь:
$S = upsilon t$.
Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время его движения.
Выразим время:
$t = frac{S}{upsilon}$.
Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле:
$upsilon_{ср} = frac{S}{t}$.
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$large S = upsilon_{ср} t$.
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$t = frac{s}{upsilon_{ср}}$.
График скорости равномерного движения
Так как скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.
Если динозавр начнет двигаться к дому, то его скорость будет положительной, так как направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, так как направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.
Из графика видно, что скорости с течением времени не изменяется – они постоянны в любой выбранный момент времени. Если мы посмотрим на график положительной скорости, то увидим, что $upsilon = 6 frac{м}{с}$, на график отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 space с$.
$S = upsilon t = 6 frac{м}{с} cdot space 4 c = 24 space м$.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 space с$, $S = 2 space м$. Тогда,
$upsilon = frac{S}{t} = frac{2 space м}{1 space с} = 2 frac{м}{с}$.
Задачи
Задача №1
Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 space м}{3600 space с} approx 33 frac{м}{с}$.
Дано:
$upsilon = 120 frac{км}{ч}$
$t = 3 space c$
СИ:
$upsilon = 33 frac{м}{с}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t$,
$S = 33 frac{м}{с} cdot 3 с approx 100 space м$
Ответ: $S = 100 space м$.
Задача №2
Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$,
$900 space км = 900 space 000 м$.
Дано:
$upsilon_{ср} = 40 frac{км}{ч}$
$S = 900 space км$
CИ:
$upsilon_{ср} = 11 frac{м}{с}$
$S = 900 space 000 space м$
$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}}$,
$t = frac{900 space 000 space м}{11 frac{м}{с}} approx 82 space 000 space с$.
Переведем время в часы:
$1 space ч = 60 space мин = 60 cdot 60 space c = 3600 space c$.
Тогда:
$t = frac{82 space 000 space c}{3600 space c} approx 23 space ч$.
Ответ: $t = 23 space ч$.
Больше задач на расчет пути и времени движения с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Пользуясь таблицей 1 из прошлого урока, найдите скорости страуса, автомобиля, искусственного спутника Земли. Определите пути, пройденные ими за $5 space с$.
Дано:
$upsilon_1 = 22 frac{м}{с}$
$upsilon_2 = 20 frac{м}{с}$
$upsilon_3 = 8000 frac{м}{с}$
$t = 5 space с$
$S_1 — ?$
$S_2 — ?$
$S_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь, пройденный страусом:
$S_1 = upsilon_1 t$,
$S_1 = 22 frac{м}{с} cdot 5 space с = 110 space м$.
Путь, пройденный автомобилем:
$S_2 = upsilon_2 t$,
$S_2 = 20 frac{м}{с} cdot 5 space с = 100 space м$.
Путь, пройденный искусственным спутником Земли:
$S_3 = upsilon_3 t$,
$S_3 = 8000 frac{м}{с} cdot 5 space с = 40 space 000 space м = 40 space км$.
Ответ: $S_1 = 110 space м$, $S_2 = 100 space м$, $S_3 = 40 space км$.
Упражнение №2
На велосипеде можно без особого напряжения ехать со скоростью $3 frac{м}{с}$. На какое расстояние можно уехать за $1.5 space ч$?
Дано:
$t = 1.5 space ч$
$upsilon = 3 frac{м}{с}$
СИ:
$t = 5400 space с$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем путь, который можно проехать на велосипеде с указанной скоростью:
$S = upsilon t$,
$S = 3 frac{м}{с} cdot 5400 space с = 16 space 200 space м = 16.2 space км$.
Ответ: $S = 16.2 space км$.
Упражнение №3
На рисунке 4 показан график зависимости пути равномерного движения тела от времени ($S$ — ось пройденного пути, $t$ — ось времени). По этому графику найдите, чему равен путь, пройденный телом за $2 space ч$. Затем рассчитайте скорость тела.
Определим из графика путь, пройденный телом за $2 space ч$. Этому времени на графике соответствует значение пути, равное $200 space км$. Запишем условие задачи и решим ее.
Дано:
$S = 200 space км$
$t = 2 space ч$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитываем по формуле:
$upsilon = frac{S}{t}$.
$upsilon = frac{200 space км}{2 space ч} = 100 frac{км}{ч}$.
Ответ: $upsilon = 100 frac{км}{ч}$.
Упражнение №4
График зависимости скорости равномерного движения тела от времени представлен на рисунке 5. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за $2 space ч$, $4 space ч$.
Из графика видно, что скорость тела равна $8 frac{м}{с}$. Этот график представляет собой прямую, параллельную оси времени, потому что движение равномерное, и скорость тела не изменяется с течением времени. Запишем условие задачи и решим ее.
Дано:
$t_1 = 2 space ч$
$t_2 = 4 space ч$
$upsilon = 8 frac{м}{с}$
СИ:
$t_1 = 7200 space с$
$t_2 = 14 space 400 space с$
$S_1 — ?$
$S_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь рассчитаем по формуле: $S = upsilon t$.
За $2 space ч$ тело пройдет путь:
$S_1 = upsilon t_1$,
$S_1 = 8 frac{м}{с} cdot 7200 space с = 57 space 600 space м = 57.6 space км$.
За $4 space ч$ тело пройдет путь:
$S_2 = upsilon t_2$,
$S_2 = 8 frac{м}{с} cdot 14 space 400 space с = 115 space 200 space м = 115.2 space км$.
Ответ: $S_1 = 57.6 space км$, $S_2 = 115.2 space км$.
Упражнения №5
По графикам зависимости путей от времени (рисунок 6) двух тел, движущихся равномерно, определите скорости этих тел. Скорость какого тела больше?
Для того, чтобы рассчитать скорость тела, нам нужно знать путь и время, за которое этот путь был пройден. Возьмем эти значения для двух тел из их графиков. Первое тело (I) проходит путь, равный $4 space м$, за $2 space с$. Второе тело (II) проходит путь, равный $4 space м$, за $4 space с$. Запишем условие задачи и решим ее.
Дано:
$S = 4 space м$
$t_1 = 2 space с$
$t_2 = 4 space с$
$upsilon_1 — ?$
$upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем скорость первого тела:
$upsilon_1 = frac{S}{t_1}$,
$upsilon_1 = frac{4 space м}{2 space с} = 2 frac{м}{с}$.
Рассчитаем скорость второго тела:
$upsilon_2 = frac{S}{t_2}$,
$upsilon_2 = frac{4 space м}{4 space с} = 1 frac{м}{с}$.
Получается, что скорость первого тела больше скорости второго.
Ответ: $upsilon_1 = 2 frac{м}{с}$, $upsilon_2 = 1 frac{м}{с}$, $upsilon_1 > upsilon_2$.
Путь при неравномерном движении.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Сейчас мы будем рассматривать неравномерное движение — то есть движение, при котором абсолютная величина скорости меняется со временем. Оказывается, существует простая геометрическая интерпретация пути, пройденного телом при произвольном движении.
Начнём с равномерного движения. Пусть скорость тела постоянна и равна . Возьмём два момента времени: начальный момент
и конечный момент
. Длительность рассматриваемого промежутка времени равна
.
Очевидно, что за промежуток времени тело проходит путь:
(1)
Давайте построим график зависимости скорости от времени. В данном случае это будет прямая, параллельная оси абсцисс (рис. 1).
 |
| Рис. 1. Путь при равномерном движении |
Нетрудно видеть, что пройденный путь равен площади прямоугольника, расположенного под графиком скорости. В самом деле, первый множитель в формуле (1) есть вертикальная сторона этого прямоугольника, а второй множитель
— его горизонтальная сторона.
Теперь нам предстоит обобщить эту геометрическую интерпретацию на случай неравномерного движения.
Пусть скорость тела зависит от времени, и на рассматриваемом промежутке
график скорости выглядит, например, так (рис. 2):
 |
| Рис. 2. Неравномерное движение |
Дальше мы рассуждаем следующим образом.
1. Разобьём наш промежуток времени на небольшие отрезки величиной
.
2. Предположим, что на каждом таком отрезке тело движется с постоянной скоростью
. То есть, плавное изменение скорости заменим ступенчатой аппроксимацией*: в течение каждого небольшого отрезка времени тело движется равномерно, а затем скорость тела мгновенно и cкачком меняется.
На рис. 3 показаны две ступенчатые аппроксимации. Ширина ступенек на правом рисунке вдвое меньше, чем на левом.
 |
| Рис. 3. Ступенчатая аппроксимация |
Путь, пройденный за время равномерного движения — это площадь прямоугольника, расположенного под ступенькой. Поэтому путь, пройденный за всё время такого «ступенчатого» движения — это сумма площадей всех прямоугольников на графике.
3. Теперь устремляем к нулю. Ясно, что в пределе наша ступенчатая аппроксимация перейдёт в исходный график скорости на рис. 2. Сумма площадей прямоугольников перейдёт в площадь под графиком скорости; следовательно, эта площадь и есть путь, пройденный телом за время от
до
. (рис. 4
 |
| Рис. 4. Путь при неравномерном движении |
В итоге мы приходим к нужному нам обобщению геометрической интерпретации пути, полученной выше для случая равномерного движения.
| Аппроксимация — это приближённая замена достаточно сложного объекта более простой моделью, которую удобнее изучать. |
Геометрическая интерпретация пути.Путь, пройденный телом при любом движении, равен площади под графиком скорости на заданном промежутке времени.
Посмотрим, как работает эта геометрическая интерпретация в важном частном случае равноускоренного движения.
Задача. Тело, имеющее скорость в начальный момент
, разгоняется с постоянным ускорением
. Найти путь, пройденный телом к моменту времени
.
Решение. Зависимость скорости от времени в данном случае имеет вид:
(2)
График скорости — прямая, изображённая на рис. 5. Искомый путь есть площадь трапеции, расположенной под графиком скорости.
 |
| Рис. 5. Путь при равноускоренном движении |
Меньшее основание трапеции равно . Большее основание равно
. Высота трапеции равна
. Поскольку площадь трапеции есть произведение полусуммы оснований на высоту, имеем:
Эту формулу можно переписать в более привычном виде:
Она, разумеется, вам хорошо известна из темы «Равноускоренное движение».
Задача. График скорости тела является полуокружностью диаметра (рис. 6). Максимальная скорость тела равна
. Найти путь, пройденный телом за время
.
Решение. Как вы знаете, площадь круга радиуса равна
. Но в данной задаче необходимо учесть, что радиусы полуокружности имеют разные размерности: горизонтальный радиус есть время
, а вертикальный радиус есть скорость
.
Поэтому пройденный путь, вычисляемый как площадь полукруга, равен половине произведения на горизонтальный радиус и на вертикальный радиус:
 |
| Рис. 6. К задаче |
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Путь при неравномерном движении.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В физике следует различать траекторию, путь и перемещение.
Определение 1
Траектория — форма линии, описываемая телом. Ее длина представляет собой путь и является скалярной величиной. Перемещением же называется вектор, соединяющий точки начала и конца пути, и направленный от начала к концу.
Длина пути измеряется в системе СИ в метрах, в СГС (сантиметр, грамм, секунда) — в сантиметрах. Применяются и другие единицы измерения длины, в том числе внесистемные (дюйм, фут, ярд, миля и т.д.).
При движении без ускорения путь равен произведению скорости на расстояние:
$S = v cdot (t_2 — t_1) = v cdot Delta t$,
где $v_0$ – скорость тела, $t_2$ — момент времени окончания движения, $t_1$ — момент времени начала движения, $Delta t$ — время движения. График зависимости пути от времени на координатной плоскости в случае такого, называемого равномерным, движения является прямой линией.
Замечание 1
Поскольку скорость — векторная величина, равномерным можно считать только движение по прямой, т.к. при изменении направления движения вектор не остается неизменным даже при сохранении его длины.
Если равноускоренное движение начато с нулевой скорости и известно ускорение, то формула пути имеет вид
$S = frac{a cdot t^{2}}{2}$
где $a$ – ускорение тела.
Объединив два условия, получим общую формулу нахождения пути при равноускоренном движении с произвольной начальной скоростью:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$.
Если движение не равномерное и известна средняя скорость движения, то путь можно выразить и другим способом:
$S = v_{ср.} cdot Delta t$,
где $v_{ср.}$ — средняя скорость движения.
На практике движение бывает равномерным или равноускоренным лишь на небольших фрагментах пути, поэтому для вычисления его длины траекторию разбивают на участки, где тело движется по простым закономерностям, вычисляют длину каждого из них и суммируют. Если известна траектория, то ее разбивают на фрагменты, каждый из которых имеет простую геометрическую форму. Сложив их длины, можно найти путь.
Пример 1
Найти путь, пройденный при движении с ускорением 2 $м/с^2$ в течение 20 с, если скорость на момент начала измерения была равна 10 м/с.
Подставим в формулу численные значения:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$
$S = frac{2 cdot 20^2}{2} + 10 cdot 20 = 600 м$.
Ответ: длина пути составила 600 метров.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$
В цилиндрических координатах длина пути может быть выражена как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$
В сферических координатах формулу длины пути запишем:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением.
Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:
$$d s=|d bar{r}|=v d t$$
где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=vleft(t_{2}-t_{1}right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+frac{a t^{2}}{2}(7)$$
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
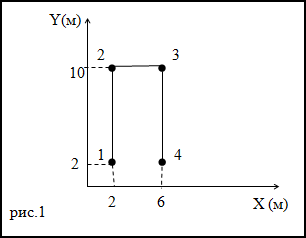
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 — 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:
$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$
Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c leq t leq 5 c$ имеем:
$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.