Парадокс колеса
На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.
В то же время из школьного курса математики известно, что длина окружности равна:
Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.
Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:
C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.
Но на самом деле она проходит фактически путь вдвое больший.
Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.
Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.
Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.
Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.
Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:
V = w*R, где w — угловая скорость вращения колеса.
Фактически линейная скорость внутренних точек колеса должна описываться уравнением:
V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.
Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.
Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.
Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:
dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R
Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.
С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.
Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.
[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.
Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.
Сазонов Сергей 3 сентября 2019 года в 12:54
Писать рецензию на Вашу бредятину «Парадокс колеса» считаю излишним (много чести) — найдите в детском журнале «Квант» за 1975 год статью «ЦИКЛОИДА» . Там — примерно этот круг вопросов. Парадокса нет.
(конец цитаты)
К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.
Задача 1.1 (3)
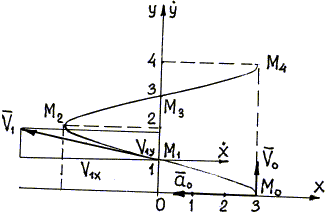
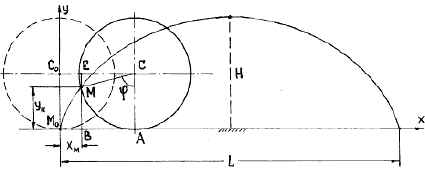
Найти уравнения движения точки М обода колеса радиуса R вагона, который движется по прямолинейному участку пути со скоростью V. Колесо катится без скольжения. Точка М в начальный момент движения соприкасалась с рельсом, т.е. занимала положение М0 (рис. 1.1).
Изобразим на расчетной схеме (рис. 1.1) оси координат х и у, начало координат поместим в начальное положение точки М0.
Рассмотрим два положения колеса: в начальный момент t = 0 и в текущий момент времени t.
Отметим положение точки М на ободе колеса и положение центра С колеса в момент t, координаты точки: xм = М0В, ум = МВ.
Расстояние от центра колеса до рельса остается постоянным и равным R; это значит, что центр C колеса движется по прямой, параллельной оси х. За время t центр колеса переместится на расстояние C0C = Vt (закон равномерного движения точки C), одновременно колесо повернется на угол j .
Чтобы получить уравнения движения точки М, надо координаты этой точки представить как функции времени.
Из расчетной схемы (рис. 1.1) видно, что
Из треугольника МЕС имеем;
МЕ = Rsin (90° – j ) = Rcosj ,
ЕC = Rcos (90° – j ) = Rsinj ,
Тогда хм = Vt – Rsinj , (a)
Найдем зависимость угла j от времени t: так как колесо катится без скольжения, то длина дуги АМ окружности обода колеса (рис.1.1) равна длине отрезка М0А.
но длина дуги АМ равна также произведению радиуса R на центральный угол j ; поэтому Vt = Rj , отсюда 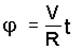
Теперь уравнения (а) будут иметь вид
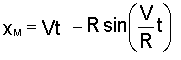
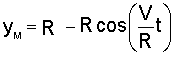
Полученные уравнения представляют собой уравнения движения точки М. В аналитической геометрии показано, что это параметрические уравнения циклоиды (параметром в данном случае является время t). Таким образом, траектория точки обода колеса, движущегося по прямолинейному участку пути без проскальзывания, является циклоидой. Длина одной ветви циклоиды L (рис. 1.1) равна 2p R, высота – H = 2R.
Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи
Основные законы и формулы, применяемые при решении задач
Вращательное движение вокруг неподвижной оси
Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.
Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.
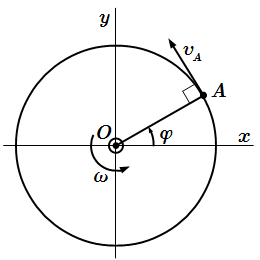
Скорость точки при вращательном движении тела вокруг неподвижной оси
Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .
Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .
Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .
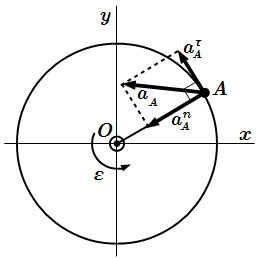
Ускорение точки при вращательном движении тела вокруг неподвижной оси
Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.
Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.
Поступательное прямолинейное движение
Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.
Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.
Соприкосновение тел без проскальзывания
Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.
Пример решения задачи
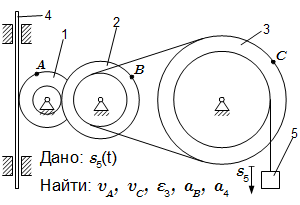
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r1 = 2 см, R1 = 4 см, у колеса 2 – r2 = 6 см, R2 = 8 см, у колеса 3 – r3 = 12 см, R3 = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s5 = t 3 – 6t (см). Положительное направление для s5 – вниз.
Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.
Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.
Дано:
t = 2 с; r1 = 2 см, R1 = 4 см; r2 = 6 см, R2 = 8 см; r3 = 12 см, R3 = 16 см; s5 = t 3 – 6t (см).
Определение скорости и ускорения груза 5
Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.
Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .
Определение угловых скоростей и ускорений колес
Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .
Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .
Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .
Итак, мы нашли:
ω 1 = 5.3333 с –1 , ω 2 = 1.3333 с –1 , ω 3 = 0.5 с –1 , ε 1 = 10.6667 с –2 , ε 2 = 2.6667 с –2 , ε 3 = 1 с –2 .
Определение скоростей точек A и C
Точка A лежит на окружности радиуса R1 с центром в точке O1, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.
Точка C лежит на окружности радиуса R3 с центром O3 на оси вращения. Скорость этой точки:
см/с.
Определение ускорения точки B
Точка B лежит на окружности радиуса R2 с центром O2, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .
Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .
Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .
Определение ускорения рейки 4
Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .
см/с; см/с; с –2 ; см/с 2 ; см/с 2 .
Автор: Олег Одинцов . Опубликовано: 25-10-2019
источники:
http://mydocx.ru/6-108008.html
http://1cov-edu.ru/mehanika/kinematika/opredelenie-skorostej-i-uskorenij-pri-vraschatelnom-dvizhenii/
Равномерное движение тела по окружности
1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ( T ) — время, в течение которого тело совершает один полный оборот. Единица периода — ( [,T,] ) = 1 с.
Частота обращения ( (n) ) — число полных оборотов тела за одну секунду: ( n=N/t ) . Единица частоты обращения — ( [,n,] ) = 1 с -1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: ( n=1/T ) .
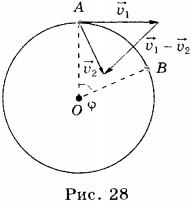
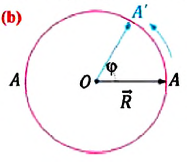
Пусть некоторое тело, движущееся по окружности, за время ( t ) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ( varphi ) .
Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость ( omega ) — физическая величина, равная отношению угла поворота ( varphi ) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ( omega=varphi/t ) . Единица угловой скорости — радиан в секунду, т.е. ( [,omega,] ) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ( 2pi ) . Поэтому ( omega=2pi/T ) .
Линейная скорость тела ( v ) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ( vec=l/t ) . За один оборот точка проходит путь, равный длине окружности. Поэтому ( vec=2pi!R/T ) . Связь между линейной и угловой скоростью выражается формулой: ( v=omega R ) .
Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.
4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ( vec=frac<Deltavec> ) и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.
Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ( a=frac ) . Так как ( v=omega R ) , то ( a=omega^2R ) .
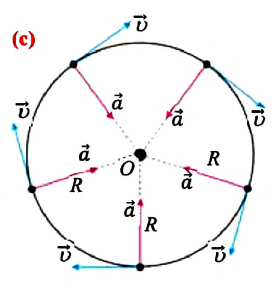
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости
2. Линейная скорость точки 1, находящейся на расстоянии ( R_1 ) от центра вращающегося колеса, равна ( v_1 ) . Чему равна скорость ( v_2 ) точки 2, находящейся от центра на расстоянии ( R_2=4R_1 ) ?
1) ( v_2=v_1 )
2) ( v_2=2v_1 )
3) ( v_2=0,25v_1 )
4) ( v_2=4v_1 )
3. Период обращения точки по окружности можно вычислить по формуле:
1) ( T=2pi!Rv )
2) ( T=2pi!R/v )
3) ( T=2pi v )
4) ( T=2pi/v )
4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:
1) ( omega=a^2R )
2) ( omega=vR^2 )
3) ( omega=vR )
4) ( omega=v/R )
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с
2) 3300 с
3) 3·10 -4 с
4) 5·10 -6 с
9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?
1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц
10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?
1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с
11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения
ФОРМУЛА
1) ( 1/T )
2) ( v^2/R )
3) ( v/R )
4) ( omega R )
5) ( 1/n )
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Равномерное движение по окружности в физике — формулы и определение с примерами
Равномерное движение по окружности:
На предыдущих уроках вы ознакомились с различными видами прямолинейного движения, с величинами, характеризующими эти движения, и определили, как изменяются эти величины со временем.
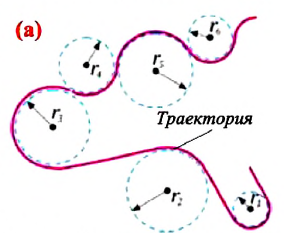
Наиболее простой вид криволинейного движения — это широко распространенное в природе и технике движение по окружности. Вращение точек поверхности Земли вокруг своей оси, точек часовых стрелок, точек автомобильных колес и др. является движением по окружности. Теоретическая и практическая важность изучения движения по окружности заключается в том, что произвольную криволинейную траекторию можно представить как сумму дуг окружностей разных радиусов (а). Самый простой вид движения по окружности — это равномерное движение.
• Равномерное движение по окружности — это движение, при котором модуль скорости материальной точки в каждой точке этой окружности остается неизменным. Такое движение характеризуется следующими величинами:
Период обращения — это время, затраченное на один полный оборот материальной точки по окружности:
Где 
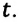
Частота обращения — это число оборотов материальной точки по окружности, совершаемых за единицу времени:
Где 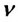
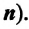
Период и частота обращения обратно пропорциональны друг другу:
Это означает, что во сколько раз уменьшится частота обращения, во столько же раз увеличится период обращения, и наоборот.
Угол поворота — это угол, на который поворачивается радиус-вектор при движении материальной точки по окружности. Угол поворота измеряется отношением длины дуги окружности между начальным и конечным радиус-векторами к радиусу окружности (b):
Где 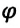
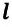
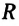
Угол поворота является скалярной величиной, единица его измерения в СИ — радиан:
• 1 рад — это угол поворота радиус-вектора, соответствующий дуге, длина которой равна радиусу окружности
Угловая скорость — это физическая величина, измеряемая отношением угла поворота к промежутку времени, за которое этот поворот совершен:
Угловая скорость материальной точки, равномерно движущейся по окружности, с течением времени остается неизменной 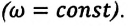
За единицу угловой скорости принята угловая скорость такого равномерного движения по окружности, при котором за 1 секунду радиус-вектор материальной точки поворачивается на угол в 1 радиан.
Материальная точка, движущаяся равномерно по окружности, за время, равное периоду обращения 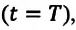
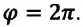
Линейная скорость. Скорость движения материальной точки по окружности называется линейной скоростью. Линейная скорость материальной точки, равномерно движущейся по окружности, оставаясь постоянной по модулю 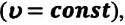
Численное значение линейной скорости при равномерном движении по окружности равно отношению пройденного пути ко времени, затраченному на его прохождение:
Материальная точка, двигаясь равномерно по окружности, за время, равное периоду обращения 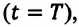
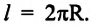
Центростремительное ускорение:
Быстрота изменения направления линейной скорости при равномерном движении по окружности характеризуется физической величиной называемой центростремительным, или нормальным, ускорением. Вектор центростремительного, или нормального, ускорения в любой точке траектории направлен по радиусу к центру окружности (см.: с). Модуль центростремительного ускорения материальной точки при равномерном движении по окружности равен отношению квадрата линейной скорости к радиусу окружности:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Взаимная передача вращательного и поступательного движения
- Движение горизонтально брошенного тела
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея
- Колебательный контур в физике
- Исследовательские методы в физике
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://zaochnik.com/spravochnik/fizika/kinematika/dvizhenie-po-okruzhnosti/
http://www.evkova.org/ravnomernoe-dvizhenie-po-okruzhnosti-v-fizike
Файл «5» внутри архива находится в следующих папках: Лекции по механике, Темы семинарских занятий — 1. Документ из архива «Лекции по механике»,
который расположен в категории «».
Всё это находится в предмете «физика» из 1 семестр, которые можно найти в файловом архиве МГУ им. Ломоносова.
Не смотря на прямую связь этого архива с МГУ им. Ломоносова, его также можно найти и в других разделах. .
1.7. Темы семинарских занятий.
1.7.1.Кинематическое описание механического движения материальной точки
1.7.1.1. Основные величины:
1.Пример. В данный момент времени две частицы, выпущенные из одного источника, имеют следующие координаты (размерности опущены) (рис.66):
первая — x1 = 4, y1 = 3, z1 = 8;
вторая — x2 = 2, y2 = 10, z2 = 5.
Записать радиусы-векторы обеих частиц в данный момент времени и определить расстояние между частицами.

Рис.66
2. Пример. Положение частиц в данный момент времени характеризуется следующими радиус-векторами:

Определить координаты частиц и изобразить положения частиц на чертеже. Определить расстояние между перовой частицей и третьей, и расстояние между второй частице и четвертой.
3. Пример. Точка за время t перешла из положения с радиус-вектором в положение
. Определить: 1) вектор перемещения частицы за время t, 2) модуль вектора перемещения за время t, 3) изобразить радиус-векторы частицы в моменты времени t и t на рисунке и на этом же рисунке изобразить вектор перемещения.
4. Пример. Точка движется в пространстве по закону
а) (t) = (3 — 5t)
+ (4 + 2t2)
+
б) (t) = 5t
— (3 — t2)
-t
.
Как изменяются координаты точки по времени?
5. Пример. Точка движется по закону (t) = 2t
+ 5t
. Определить траекторию движения точки. Закон движения точки задан. В проекциях на оси он имеет вид x(t) = 2t y(t) = 5t. Исключив время, получим y = 5/2 х — траектория движения точки — прямая линия.
6. Пример. Точка движется по закону (t) = 2t
+ 3t2
.
Определить траекторию движения точки.
7. Пример. Определить среднюю и мгновенную скорости точки и
и модуль средней скорости, если она движется по закону
(t) = 3t
+ 5t
.
По определению

8.Пример. Начальная скорость частицы , а конечная
. Найти приращение скорости
и модуль приращения скорости |
|
; |V| =
.
9. Пример. На рис.67 изображен график V = f(t) для частицы. Найти путь, пройденный частицей за 100 секунд.

Рис.67
S = |Vi| t = (70-50) сек 10м/сек = 600 м
10. Пример. В момент t1 = 0 автомобиль движется на восток со скоростью
V= 48 км/час. Через одну минуту автомобиль движется на север с той же скоростью. Чему равно среднее ускорение?
, где
(рис.68)
.

Рис.68
11. Пример. Точка движется по закону Чему равно мгновенное ускорение точки?
По определению
.
1.7.1.2. Кинематические принципы суперпозиций
1.Пример. За время t1 точка переместилась на , а за время t2 = t1 + t3 точка переместилась на
Найти перемещение точки
за время t3 Показать
на риc.69.

Рис.69
По условию . Следовательно,
(рис.69)
.
2. Пример. Собака бежит за велосипедом и лает. За время t велосипедист переместился на величину , а собака — на
а) показать перемещение велосипедиста относительно собаки
б) показать перемещение собаки относительно велосипедиста
собаки

Рис.70 а Рис.70 б
a) =
+
б)
=
+
откуда
а) =
—
б)
=
—
3. Пример. Скорость катера А — , скорость катера В —
. Катера движутся по озеру. 1) Найти скорость катера А относительно катера В (
).
2) Найти скорость катера В относительно катера А ( )
1) =
+
2)
=
+
=
—
=
—

Рис.71 а Рис.71 б
4. Пример: По вагону поезда, идущего со скоростью идет человек. Радиус-вектор, характеризующий положение человека относительно станции
, а относительно вагона
. Как связаны координаты человека в этих двух системах отсчета.
Y


1.7.1.3. Законы движения
1
(Vx, Vy). Записать закон движения тела, если в момент времени t = 0 радиус-вектор
(0, y0). Определить траекторию
=
+
t
x(t) = Vx t
y(t) = y0 + Vy t
Рис.73
Траектория y = y0 + (рис.73)
2. Пример. Камень брошен вверх с начальной скоростью V0 из точки, находящейся на высоте Н от поверхности Земли. Определить скорость камня в момент падения на Землю и максимальную высоту камня.
при h = hmax V(t|h=max ) = 0
t=
h(t = ) = hmax = H + V0(
) +
hmax = H +
В момент падения на землю h(tK) = 0

V(tK) = V — gtK = — .
3. Пример. С башни высотой Н брошен камень с начальной скоростью , направленной под углом к горизонту. Определить дальность полета камня и скорость его в момент падения на землю

Рис.74
В соответствии с выбранной системой координат
Vx = V0 cos
Vy = V0 sin — gt
Искомая дальность S равна координате х в момент падения, т.е. S = xn при t = tn где tn — время полета камня. Тогда S = V0n cos
-H = V0 tn sin —
Решение дает для t

4. Пример. Лодка, имеющая скорость V0 спускает парус в момент времени t0, но продолжает двигаться. Во время этого движения произведены измерения скорости лодки, которые показали гиперболическую зависимость скорости от времени (1/t). Показать, что ускорение лодки было пропорционально квадрату ее скорости.
Пользуясь этими условиями, найти зависимость:
1) пути S, пройденного лодкой от времени,
2) скорости лодки от пути, после того, как на лодке был спущен парус.
По условию , при этом V0 =
, т.е.

S = V0 t0 ln ( ) = V0 t0 ln (
); V = V0 exp (-
); S > 0
1.7.4.Вращательное движение материальной точки
1. Пример. Частица движется равномерно по часовой стрелке по окружности радиуса R, делая за время один оборот. Окружность лежит в плоскости xy, причем центр окружности совпадает с началом координат. В момент t = 0 частица находится в точке с координатами х = 0, y = R. найти среднее значение скорости точки за промежуток времени
а) от 0 до /4; = 4/ R (
—
)
б) от 0 до /2; = -4/ R
в) от 0 до 3/4; = -4/3 R (
+
)
г) от 0 до ; = 0
д) от /4 до 3/4. = -4/ R
2.Пример. Обруч катится по горизонтальной плоскости со скоростью 0 без проскальзывания. Определить мгновенные скорости точек обода А, В, С, Д

Рис.75
Согласно принципу суперпозиции скоростей cкорость любой точки обода
. При отсутствии проскальзывания нижняя точка А обруча, касаясь плоскости, неподвижна относительно ее, потому
A = 0, т.е.
для проекции на ОХ: 0 = V0 – VA, т.е. = V0.
Таким образом, VA = 0, VB = 2 V0,, VD = VC = V0.
3.Пример. Диск радиуса R катится по горизонтальной поверхности без проскальзывания. В некоторый момент известны скорость и ускорение
его центра. Показать на рисунке в этот момент ускорение
верхней точки диска.

Рис.76
4.Пример. Колесо радиуса R катится без скольжения по горизонтальной дороге со скоростью V0. Найти горизонтальную компоненту Vx линейной скорости движения произвольной точки на ободе колеса, вертикальную компоненту Vy этой скорости и модуль полной скорости для этой же точки. Найти значение угла между вектором полной скорости точек на ободе колеса и направлением поступательного движения его оси.

Рис.77
Vx = V0 (1 + cos ) = 2V0 cos /2
Vy = -V0 sin
Vполн = 2V0 cos /2
= -arctg (tg /2) = -/2/
5.Пример. Колесо радиуса R равномерно катится без скольжения по горизонтальному пути со скоростью Найти координаты х и y произвольной точки А на ободе колеса, выразив их как функции времени t или угла поворота колеса полагая, что при t = 0 = 0 x = 0 y = 0
x = R ( — sin ) = R ( t — sin t), y = R(1 — cos ) = R(1 — cos t)
где = t и = V/R.

Рис.78
6. Пример. Найти длину полного пути каждой точки колеса между двумя ее последовательными касаниями полотна дороги.
В примере 4 найдено, что Vполн = 2 V0 cos /2, т.е.
Vполн = 2 R cos /2
dS = Vполн dt = 2 R cos /2 dt = 2 R cos /2 d.
Так как угол между двумя последовательными касаниями одной точкой дороги изменяется от 0 до 2, то
S = 2 2R = 8R.
7. Пример. Найти горизонтальную и вертикальную компоненты вектора ускорения произвольной точки на ободе колеса. Указать величину и направление вектора полного ускорения точек, лежащих на ободе колеса. Колесо катится равномерно и без проскальзывания.
aгориз = sin ; aверт =
cos
При равномерном вращении полное ускорение всегда направлено к центру.
1.7.1.5 Кинематическое описание колебательного движения точки
1.Пример. Построить графики зависимости от времени (х) смещения, (V) скорости и (а) ускорения при простом гармоническом колебании. Найти соотношение между амплитудами смещения скорости и ускорения.

х0 — амплитуда смещение
V0 — амплитуда скорости
а0 — амплитуда ускорения
V0 = х0
а0 = 2 х0 = V0
2.Пример. Горизонтальная платформа совершает в вертикальном направлении гармоническое колебание x = a cos t. На платформе лежит шайба из абсолютно неупругого материала.
а) При каком условии шайба будет отдаляться от платформы, если 2 > g
б) В каком положении находится и в каком направлении движется платформа в момент отрыва от нее шайбы:
В момент отрыва шайбы платформа движется вверх от среднего положения (x > 0 V > 0)
в) На какую высоту h будет подниматься шайба над ее положением, отвечающем среднему положению платформы, в случае, если а = 20 см и
= 10 гц.
h = = 25 см.
1.Вопрос. Зависимость координаты от времени t имеет вид:
а) х = a1 cos t + a2 sin t; б) x = a sin2 t в) x = at sin t;
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,984 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
В
задачах данного раздела определяются
координаты, скорость, ускорение точки
в любой назначенный момент времени при
различных способах задания движения.
Из всех способов задания движения точки
наибольшее распространение получили
координатный и естественный способы.
Рассмотрим
вначале координатный способ задания
движения точки. Положение в пространстве
движущейся точки определяется тремя
координатами в декартовой системе
координат. Эти координаты задаются как
функции времени:
(1.1)
Зависимости
(1.1) называются уравнениями движения
точки в декартовых координатах.
Если
движение точки происходит в плоскости
ху, то задаются только два уравнения
движения:
x
= x(t);
y = y (t).
При
прямолинейном движении точки достаточно
задать одно уравнение движения:
x
= x(t),
если
принять, что ось х совпадает с прямой,
по которой движется точка.
Скорость
точки представляет собой вектор,
характеризующий быстроту и направление
движения точки в данный момент времени.
При
задании движения точки уравнениями
(1.1) проекции скорости на оси декартовых
координат равны:
Модуль
скорости
.
(1.2)
Направление
скорости определяется направляющими
косинусами:

Если
движение точки задается в плоскости
ху, то
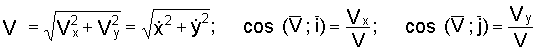
При
прямолинейном движении по оси х:
.
Характеристикой
быстроты изменения скорости является
ускорение
а.
Ускорение точки равно производной от
вектора скорости по времени:

При
задании движения точки уравнениями
(1.1) проекции ускорения на координатные
оси равны:
Модуль
ускорения:
.
(1.3)
Направление
ускорения определяется направляющими
косинусами



Если
движение точки задается в плоскости
ху, то
;
;


При
прямолинейном движении по оси х
;
.
Далее
рассмотрим естественный способ задания
движения точки.
Считается,
что движение точки задано естественным
способом, если указаны ее траектория и
закон изменения криволинейной координаты
s = s(t). Уравнение s = s(t) называется
законом движения точки по траектории.
При этом на траектории указывается
начало отсчета, а также положительное
направление отсчета координаты s в виде
стрелки
.
Модуль
скорости точки определяется по формуле

(1.4)
Вектор
скорости
V направлен по касательной к траектории
в сторону стрелки
,
если,
и в противоположную сторону, если.
Ускорение
точки определяется как векторная сумма
касательного и нормального ускорений
точки:
а
=
а
+
аn
.
Модуль
касательного ускорения определяется
по формуле
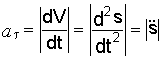
(1.5)
Вектор
касательного ускорения
а
направлен
по касательной к траектории в сторону
стрелки
,
если,
и в противоположную, если.
Модуль
нормального ускорения определяется по
формуле
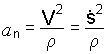
(1.6)
где
– радиус кривизны траектории в данной
точке.
Вектор
нормального ускорения
аn
всегда направлен по главной нормали в
сторону центра кривизны траектории.
Модуль
полного ускорения
.
(1.7)
Если
движение точки задано координатным
способом, то можно определить параметры
движения, характерные для естественного
способа задания движения.
Так
можно, например, по уравнениям движения
точки (1.1) найти уравнение ее траектории
в форме зависимости между координатами.
Для этого надо из уравнений движения
исключить время t. Затем можно найти
закон движения точки по траектории s =
s(t), используя формулу (1.4). Из этой формулы
следует, что ds = V dt; с учетом формулы
(1.2) имеем
и

(1.8)
В
законе движения (1.8) за начало отсчета
координаты s принимается начальное
положение точки, когда t = 0. Знак “плюс”
или “минус” перед интегралом ставится
в зависимости от выбора положительного
направления отсчета координаты s: если
движение точки начинается в сторону
стрелки
,
то следует брать знак “плюс”, в противном
случае – знак “минус”.
Рассмотрим
вначале методику решения задач, в которых
движение точки задано координатным
способом. Уравнения (1.1) определяются
либо из геометрических условий, либо в
результате интегрирования дифференциальных
уравнений движения точки. Интегрирование
дифференциальных уравнений движения
точки рассматривается в разделе “Динамика
точки”, который не входит в данное
пособие. Получение уравнений (1.1) с
использованием геометрии движения
рассмотрим на примере исследования
движения точки обода колеса.
Задача
1.1 (3)
Задача
1.2 (1)
Задача
1.3 (2)
Задача
1.4 (4)
Задача
1.5 (4)
Задача
1.6 (5)
Задача
1.7 (6)
Задача
1.8 (7)
Задача
1.1 (3)
Найти
уравнения движения точки М обода колеса
радиуса R вагона, который движется по
прямолинейному участку пути со скоростью
V. Колесо катится без скольжения. Точка
М в начальный момент движения соприкасалась
с рельсом, т.е. занимала положение М0
(рис. 1.1).
Рис.
1.1
Решение
Изобразим
на расчетной схеме (рис. 1.1) оси координат
х и у, начало координат поместим в
начальное положение точки М0.
Рассмотрим
два положения колеса: в начальный момент
t = 0 и в текущий момент времени t.
Отметим
положение точки М на ободе колеса и
положение центра С колеса в момент t,
координаты точки: xм
= М0В,
ум
= МВ.
Расстояние
от центра колеса до рельса остается
постоянным и равным R; это значит, что
центр C колеса движется по прямой,
параллельной оси х. За время t центр
колеса переместится на расстояние C0C
= Vt (закон равномерного движения точки
C), одновременно колесо повернется на
угол
.
Чтобы
получить уравнения движения точки М,
надо координаты этой точки представить
как функции времени.
Из
расчетной схемы (рис. 1.1) видно, что
хм
= C0C
– ЕС, ум
= ВЕ – МЕ;
или
хм
= Vt – ЕС, ум
= R – МЕ.
Из
треугольника МЕС имеем;
МЕ
= Rsin (90
–
) = Rcos
,
ЕC
= Rcos (90
–
) = Rsin
,
Тогда
хм
= Vt – Rsin
, (a)
ум
= R – Rcos
.
Найдем
зависимость угла
от времени t: так как колесо катится без
скольжения, то длина дуги АМ окружности
обода колеса (рис.1.1) равна длине отрезка
М0А.
При
этом
М0А
= С0С
= Vt ,
но
длина дуги АМ равна также произведению
радиуса R на центральный угол
; поэтому Vt = R
, отсюда
.
Теперь
уравнения (а) будут иметь вид


Полученные
уравнения представляют собой уравнения
движения точки М. В аналитической
геометрии показано, что это параметрические
уравнения циклоиды (параметром в данном
случае является время t). Таким образом,
траектория точки обода колеса, движущегося
по прямолинейному участку пути без
проскальзывания, является циклоидой.
Длина одной ветви циклоиды L (рис. 1.1)
равна 2
R, высота – H = 2R.
Задача
1.2 (1)
Даны
уравнения движения точки:


у – м; t – с).
(б)
-
Определить
уравнение траектории и построить ее. -
Определить
начальное положение точки на траектории. -
Указать
моменты времени, когда точка пересекает
оси координат. -
Найти
закон движения точки по траектории s =
s(t), принимая за начало отсчета расстояний
начальное положение точки. -
Построить
график движения точки.
Решение
1.
Для получения уравнения траектории
вида F(x, y) = 0 исключим из уравнений
движения (б) время t: из первого уравнения
системы (б) найдем
,
подставляя
это выражение во второе уравнение той
же системы, получим уравнение траектории
y
= x + 5.
|
Рис. |
Это
где а– отрезок, отсекаемый прямой на оси |
2.
Для определения положения точки в
начальный момент времени необходимо
подставить значение t = 0 в уравнения
движения (б)
м;
м.
Точка
при t = 0 занимает положение М0
(-1;4).
3.
В момент пересечения точкой оси у
координата х равна нулю, а первое
уравнение системы (б) примет вид:

Отсюда
где
n = 0, 1, 2 …
В
момент пересечения точкой оси х координата
у равна нулю, а второе уравнение системы
(б) примет вид:
или
.
Но
косинус не может быть больше 1.
Следовательно, точка не пересекает ось
х (см. об этом также п. 4 решения задачи).
4.
Для определения закона движения точки
по траектории воспользуемся формулой
(1.8). За начало отсчета координаты s примем
начальное положение точки М0.
Подставляя в уравнения (б) значения t >
0, видим, что с выходом из начального
положения М0
координаты точки х и у увеличиваются.
Это направление движения точки примем
за положительное направление отсчета
координаты s (см. стрелку
на
рис. 1.2), а в формуле (1.8) оставим знак
“плюс”:

Учитывая,
что
получим
или

(в)
Из
закона (в) следует, что координата s не
может быть отрицательной, т.е. точка
движется по полупрямой М0М
(рис.1.2) и ось х не пересекает (см. по этому
поводу п. 3 решения задачи).
5.
График движения точки – это графическое
представление зависимости расстояния
s от времени t. Для построения такого
графика по оси абсцисс откладывают
последовательные значения времени t, а
по оси ординат – соответствующие им
значения расстояния s. Построенные точки
соединяют плавной линией. График
зависимости (в) можно построить быстрее,
если воспользоваться известным графиком
косинуса. Для этого вначале построим
график функции

линия на рис. 1.3), затем этот график
сместим вдоль оси s на величинум.
Рис.
1.3.
Задача
1.3 (2)
Даны
уравнения движения точки:
;

у – см; t – с ).
(г)
-
Определить
уравнение траектории и построить ее. -
Определить
начальное положение точки на ее
траектории. -
Найти
закон движения точки по траектории s =
s(t), принимая за начало отсчета расстояний
начальное положение точки. -
Определить
время T прохождения точкой полной
окружности.
Решение
|
Рис. |
1. Чтобы найти уравнение траектории
|
сложим
эти уравнения и после преобразования
получим
.
Это
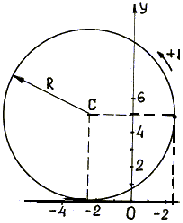
уравнение окружности радиуса R = 5 см,
центр окружности расположен в точке
С (-2,5; 5) (рис. 1.4).
2.
Для определения начального положения
точки подставим значение времени t = 0 в
уравнения (г)
х0
= 5 соs0 – 2,5 = 2,5 см; у0
= 5 sin0 – 5 = 5 см;
Точка
при t = 0 занимает положение М0
(2,5; 5).
3.
Для определения закона движения точки
по траектории воспользуемся формулой
(1.8). За начало отсчета координаты s примем
точку M0.
Из системы уравнений (г) видно, что с
увеличением времени t от нуля x уменьшается,
а y увеличивается.
Такое
возможно, если после выхода из начального
положения точка будет двигаться по
окружности против часовой стрелки. Это
направление движения точки примем за
положительное направление отсчета
координаты s (см. стрелку
на
рис. 1.4), а в формуле (1.8) перед интегралом
оставим знак “плюс”:
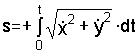
где


Отсюда

.
(д)
4.
Определим время Т прохождения точкой
полной окружности.
Т – время, по
истечении которого s в формуле (д) станет
равным длине окружности 2
R:

Отсюда
с.
Задача
1.4 (4)
Даны
уравнения движения точки:

y = t (x, y – м; t – с ).
(е)
-
Определить
уравнение траектории точки. -
Определить
скорость и ускорение точки при t = 0 и t
= 1 с. -
Построить
траекторию и указать полученные векторы
скорости и ускорения на чертеже.
Решение
1.
Уравнение траектории получается
подстановкой в первое уравнение системы
(е) величины t = y, полученной из второго
уравнения этой системы:
.
(ж)
2.
Модуль скорости точки определяется по
формуле
,
где–
проекции вектора скорости на координатные
оси. Для заданного движения (е) имеем
,
м/c.
При
t = 0

м/c.
Модуль
скорости V0
= 1 м/c.
При
t = 1 с,

м/c.
Модуль
скорости V1
= 4,82 м/с.
Модуль
ускорения точки определяется по формуле
,
где,
–
проекции вектора ускорения на координатные
оси. Для заданного движения (е) имеем
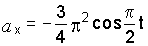
.
При
t = 0
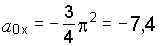
,
.
Модуль
ускорения a0
= 7,4 м/с2.
При
t = 1 с

.
Модуль
ускорения a1
= 0.
3.
Траектория точки (ж) представляет собой
косинусоиду.
|
Рис.1.5 |
Для |
При
t = 1 с x1
= 0, y1 =
1 м, точка занимает положение М1(0;
1). Для этих положений точки построим
векторы скорости и ускорения. От точки
M0
отложим проекции скорости V0x = 0
и V0y = 1
м/с (см. п.2); направление вектора
V0
показано на рис. 1.5. Вектор скорости
V1
построим следующим образом: через точку
M1
проведем оси
и
,
осьпараллельна
оси x, а осьсовпадает
с осью y. Вдоль этих осей от точки M1
отложим отрезки, равные проекциям V1x
и V1y
(с
учетом их знаков); затем построим
прямоугольник, диагональ которого есть
вектор
V1.
Модуль вектора ускорения
a0
равен модулю проекции a0x
(см. п. 2),
a0
направлен от точки M0
в сторону, противоположную положительному
направлению оси x (cкорости
V0,
V1
должны совпадать с касательными к
траектории соответственно в точках M0
и M1.
Вектор
a0
должен быть направлен от точки M0
внутрь кривой).
Задача
1.5 (4)
Даны
уравнения движения точки:
;
(х,
у – м; t – с ).
(з)
-
Определить
уравнение траектории точки. -
Определить
скорость и ускорение точки при t = 1 с. -
Построить
траекторию и указать полученные векторы
скорости и ускорения на чертеже.
Решение
1.
Для того чтобы получить уравнение
траектории, необходимо из уравнений
движения (з) исключить время. Запишем
эти уравнения в виде


Возведем
оба уравнения в квадрат, вычтем второе
из первого и получим уравнение траектории:
x2
– y2
= 42.
(и)
Это
уравнение равнобочной гиперболы, полуось
которой b = 4 м.
2.
Определим проекции скорости
В
заданный момент времени t = 1с, V1x
= 4,68 м/с, V1у
=
6,16 м/с
модуль скорости
м/с.
Определим
проекции ускорения
м/с2,
м/с2
.
В
момент времени t = 1с, а1x
= 6,16 м/с2,
а1у
=
4,68 м/с2
модуль
ускорения
м/с2.
3.
Построим траекторию точки по уравнению
(и). Действительной осью гиперболы
является ось х (рис. 1.6). На траектории
найдем точку М1,
соответствующую моменту времени t = 1 с.
Координаты этой точки: x1 = 2(e +
e-1)
= 6,16 м; y1 = 2(e –
e-1)
= 4,68 м; M1
(6,16; 4,68).
Рис.
1.6
Вектор
скорости построим следующим образом:
через точку М1
проведем оси
и
,
параллельные соответствующим осям x и
y; вдоль этих осей от точки М1
отложим отрезки, равные проекциям V1x
и V1y
(с учетом их знаков). Диагональ
прямоугольника, построенного на этих
отрезках, есть вектор
V1.
Вектор ускорения
a1
строим подобным образом: от точки М1
вдоль оси
отложим
отрезок, равный проекцииa1x,
а вдоль оси
отложим
отрезокa1y.
Затем на этих отрезках строим прямоугольник,
диагональ которого есть вектор
a1.
Вектор скорости
V1
должен быть направлен по касательной
к траектории в точке M1,
а вектор ускорения
a1
должен быть направлен от точки M1
внутрь кривой.
Задача 1.6 (5)
|
Рис. |
Даны уравнения
|
Решение
1.
Чтобы определить уравнение траектории,
следует исключить время из уравнений
движения (к). Учитывая, что
,
получим

Траектория
представляет собой эллипс с полуосями
20 см и 40 см.
2.
Определим время Т, когда точка пересечет
прямую у = 20 см, первое уравнение системы
(к) в этот момент примет вид:
20 = 40 sin2
t, отсюда следует
с.
Найдем
величины скорости и ускорения по
значениям их проекций в момент времени

см/с;
см/с.
Модуль
скорости
см/с.
Проекции
ускорения


Модуль
ускорения
см/с2.
Задача
1.7 (6)
Дан
закон движения точки по окружности
радиуса R = 5 м:
(s
– см; t –с ).
(л)
-
Определить
скорость и ускорение точки при t = 0 и t1
= 10 с. -
Определить
моменты остановки точки. -
Определить
путь, пройденный точкой за 10 с.
Решение
|
Рис. 1.8 |
1. На траектории |
Определим
проекцию скорости на касательную
,
учитывая (л),
.
(м)
При
t = 0,
V
o
= 162 см/с
и t1
= 10 c
V
1
= 12 см/с.
Теперь
отложим найденные проекции скорости
из точек M0
и M1
по соответствующим касательным: V
o
– по касательной
o,
V
1
– по касательной
1.
Векторы
Vo
и
V1
совпадают со своими проекциями V
o
и V1.
Определим
проекции ускорения на естественные оси
координат, учитывая (л),
см/с2;

Ускорение
точки
.
При
t = 0
см/с2;

см/с2.
При
t1
= 10 с
см/с2;
см/с2;
см/с2.
Отложим
из точек M0
и M1
по естественным осям проекции аo,
аno,
а
1,
аn1.
Векторы
a0,
a1
изображаются диагоналями прямоугольников,
построенных на проекциях ускорений.
2.
Чтобы найти моменты остановки, необходимо
найти время t*, когда скорость точки
равна нулю. Из уравнения (м) получим
3(t*)2
– 45t* + 162 = 0.
Решив
это уравнение, будем иметь t1*
= 6 с, t2*
= 9 с.
3.
Поскольку за 10 с точка сделала две
остановки (см. п. 2), пройденный ею путь
за 10 с можно найти как сумму пути,
пройденного точкой от начального
положения до первой остановки, пути,
пройденного точкой от первой до второй
остановки, и пути, пройденного точкой
от второй остановки до момента времени
t1
= 10 с, т.е.
,
где
s0
= -15 см;
см;
см;
см.
Путь,
пройденный точкой за 10 с, равен
см.
Задача
1.8 (7)
По
заданным уравнениям движения точки:
;
(х,
у – м; t – с)
(н)
найти
ее касательное и нормальное ускорение,
а также радиус кривизны траектории для
заданного момента времени t1
= 0,5
с.
Решение
Заданные
уравнения движения точки (н) позволяют
найти проекции скорости точки, м/с,
;
.
Модуль
скорости, м/с,
.
(о)
В
момент времени t1
= 0,5
с V1
= 2 м/с.
Проекции
ускорения точки, м/с2:
.
Модуль
полного ускорения, м/с2
.
(п)
В
момент времени t1
= 0,5
са
= 2 м/с2.
Зная
выражение скорости, как функции времени
t (о), определим модуль касательного
ускорения точки, м/с2,
по формуле (1.5)

(р)
В
момент
с
м/с2.
По
полному ускорению (п) и касательному
ускорению (р) найдем модуль нормального
ускорения точки для
с,
учитывая формулу (1.7)
м/с2.
Нормальное
ускорение аn1
и радиус кривизны траектории
1
связаны зависимостью (1.6), из которой
следует, что при
с






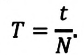
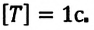
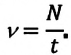
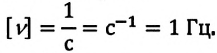
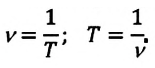
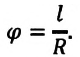
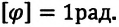
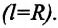
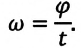
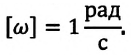
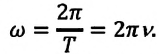
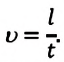
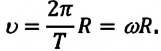
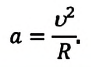



 ,
,




 и
и ;
; ,
,