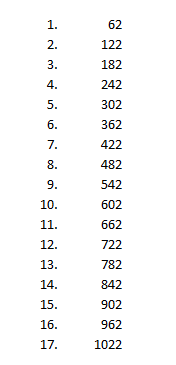Читаю вопрос автора, постепенно вникаю в суть, с одной стороны. А с другой проникаюсь всё большим непониманием сложившейся ситуации, когда на самом деле верного ответа за два года так и не поступило. При этом «ЛО» автором определён, но в нём ответ совсем на другой вопрос — там определяется сумма пятнадцати членов арифметической прогрессии, но не само пятнадцатое число в последовательности. Почему так? Лично мне не понятно.
Попробую абстрагироваться, закрыть глаза на всё до меня написанное, начать всё с нуля и попытаться отыскать верное решение. Для этого первым делом ещё раз перечитываю условия и обязательно (!) комментарий автора к нему. Согласно замечанию следует начать с числа «6», к которому на первом этапе необходимо прибавить «4». Вторым шагом та же самая «четвёрка» добавится к полученной сумме, потом ещё раз к полученной и так четырнадцать раз подряд. то есть примерно так:
- 6 (первое число)
- 6 + 4 = 10
- 10 + 4 = 14
- 14 + 4 = 18 и так далее
Можно продолжать осуществлять расчёты с помощью примитивного калькулятора или производить их в уме, загибая пальцы. Но лично мне привычнее открыть в другом окне электронную таблицу Excel и уже в ней по-скорому состряпать табличку. Поскольку у нас присутствует всего две последовательности из пятнадцати чисел — порядковые номера от 1 до 15 и соответствующие суммы, удобнее сделать горизонтальный вариант таблицы с двумя строчками и пятнадцатью рядами. Так нагляднее:
Итак, первая строка — порядковые номера. Во второй первую ячейку занимает число «6», а каждую следующую формула = (предыдущая ячейка + 4). Компьютер редко ошибается и у меня нет сомнений в правильности вычислений для данного случая. Наверное, вы тоже давно бросили свой взгляд на самую правую колонку, которая является пятнадцатой и в ней сверху порядковый номер «15», а внизу искомое 15-е число арифметической прогрессии. И это число = 62.
Тем же, кто берётся за решение подобного рода задач я хотел бы дать не то, чтобы большой совет, а маленькую рекомендацию. Проверяйте полученные ответы и это избавит вас от ошибок. В данном случае это можно сделать следующим образом. Если первое число «6», а потом мы 14 раз прибавляем к нему по «4», то можно просто прибавить к «шести» произведение «14*4». Кто-то так и сделал, но почему-то получил «60», хотя на самом деле будет на два больше.
- 6 + 4 * 14 = 6 + 56 = 62 — сходится.
Решение:
Т.к. последовательность чисел в задаче постоянно увеличивается на одно и то же число, то не трудно догадаться, что здесь речь идет об арифметической прогрессии, в которой первый член а1 равен 6, а разность d равна 4.
Формула n-ого члена арифметической прогрессии выглядит так:
А нам нужен 15-й, т.е. формула примет вид
Подставляем известные из условия величины и считаем.
Ответ: 62.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#505
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
2
Задание#T8411. В последовательности чисел первое число равно 6,6,6, а каждое следующее больше предыдущего на 4.4.4.
Найдите пятнадцатое число.
4 ответа:
2
0
Данная последовательность есть арифметическая прогрессия с коэффициентом прогрессии 4. Формула суммы арифметической прогрессии Sn=(a1+an)*n/2, где а1 -первый член, an — последний член, n — количество членов. В данном случае S=(1+15)*15/2=8*15=1<wbr />20.
2
0
Аn = 6+4(15n – 1),
где n – порядковый номер каждого последующего пятнадцатого числа.
1
0
если первое число 666 а следующее на 444 больше то можно вычислить число номер 15
- 666 + 444 = 1110
- 1110 + 444 = 1554
- 1554 + 444 = 1998
- 1998 + 444 = 2442
- 2442 + 444 = 2886
- 2886 + 444 = 3330
- 3330 + 444 = 3774
- 3774 + 444 = 4218
- 4218 + 444 = 4662
- 4662 + 444 = 5106
- 5106 + 444 = 5550
- 5550 + 444 = 5994
- 5994 + 444 = 6438
- 6438 + 444 = 6882
- 6882
ответ число под номером 15 равно 6882
последовательность такая:
666 ; 1110 ; 1554 ; 1998 ; 2442 ; 2886 ; 3330 ; 3774 ; 4218 ; 4662 ; 5106 ; 5550 ; 5994 ; 6438 ; 6882
1
0
Здесь имеем арифметическуюю прогрессии. Формула п-ного члена арифметической прогрессии: ап=а1+d(n-1).
В нашем случае а1=6, п=15, d=4
Тогда а15==6+4(15-1)=60.
Ответ: Пятнадцатый член данной последовательности равен 60.
Вот как-то так.
Читайте также
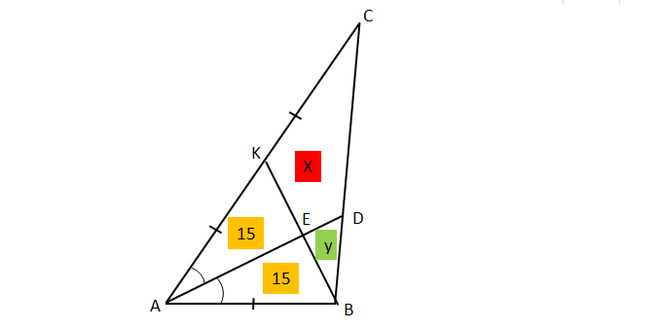
На рисунке, предоставленном автором вопроса, треугольник искаженный и не соответствует условию. По этой причине предлагаю свой вариант рисунка.
Биссектриса угла треугольника делит противоположную сторону на части пропорциональные к прилежащим к ней сторонам. Следовательно согласно условия АВ : АС = 1 :2. Тогда АК = АВ, а треугольник АКВ равносторонний и биссектриса АD делит его на равные части. В свою очередь медиана ВК делит треугольник АСВ на два равновеликих треугольника. Откуда площади треугольников АКЕ и АЕВ составляют по 15 кв. см.
Биссектриса треугольника делит так же площадь треугольника пропорционально прилежащим к ней сторонам. Тогда площади треугольников АDВ и АСD относятся друг к другу как 1 : 2.
На основании сказанного составим систему уравнений, обозначив неизвестные площади треугольников за х и у,
{х + у = 15
{15 + х = 2(15 + У).
Решая систему относительно х, получаем — площадь 4-угольника EDCK равна 25 кв. см.
<h2>Основной государственный экзамен по математике 2015.</h2>
ОГЭ по математике это экзамен который сдают девятиклассники, по сути это подготовка к сдаче экзамена ЕГЭ. Еще в прошлом году ОГЭ назывался ГИА (государственная итоговая аттестация), но в этом году изменили название (по аналогии с ЕГЭ), по сути изменилось только название, порядок проведения и правила остались такие же как и раньше. В 2015 году ОГЭ по математике состоится 27 мая. Минимальное количество баллов которое необходимо набрать чтобы продолжить обучение или получить аттестат — 8 баллов.
Если Вы сдали остальные предметы лучше чем математику, то снова пересдать Вы, естественно, можете в этом году через месяц — в сентябре. Но лучше хорошенько подготовиться, решать побольше КИМов в течении августа и, наконец, сдать математику, не завалив алгебру. ОГЭ в 9 классе очень важно для дальнейшей учебы в целом, так что постарайтесь сделать это как можно лучше.
Насколько мне известно, если Вы не сдадите этот экзамен в сентябре, то передавать будете уже в следующем году вместо с будущими девятиклассниками.
Желаю Вам сдать как можно лучше уже через месяц 
Был убран раздел «Реальная математика». Теперь вопросы из этой секции переехали в первый раздел «Алгебра» и во второй «Геометрия». Все остальное осталось прежним, то есть для получения аттестата или для продолжения обучения в школе, надо набрать не менее 8 баллов. Раньше 3 из них в модуле «Алгебра», 2 в модуле «Геометрия» и 2 в модуле «Реальная математика». Пока что нет точной информации об оценивании в 2018.
Допустим, третий велосипедист догнал второго через х часов, второй велосипедист к этому времени находился в пути уже (х + 1) час, значит, второй и третий спортсмен встретились в 12(х + 1) км от старта, а скорость третьего в этом случае составляет 12(х + 1)/х км/ч.
С момента старта первого велосипедиста до момента встречи его с третьим прошло (х + 10) часов, а значит, их встреча произошла в 22(х + 10) км от старта. Это расстояние третий спортсмен преодолел за 22х(х + 10)/12(х + 1) или (11х² + 110)/(6х + 6) часов, что по условию на 2 часа меньше, чем потребовалось первому спортсмену. Таким образом,
х + 10 — (11х² + 110х)/(6х + 6) = 2, или
5х² + 56х — 48 = 0.
Единственным положительным корнем данного уравнения явл-ся х = 0,8. В этом случае скорость третьего спортсмена 12*(0,8 + 1)/0,8 = 27 км/ч.
Найдите правильный ответ на вопрос ✅ «В последовательности чисел первое число 4, а каждое следующее больше предыдущего на 5. Найдите пятнадцатое число. …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Главная » Математика » В последовательности чисел первое число 4, а каждое следующее больше предыдущего на 5. Найдите пятнадцатое число.
- Учебники
- 6 класс
- Математика 👍
- Никольский
- №112
авторы: Никольский , Потапов, Решетников, Шевкин.
издательство: Просвещение 2015 год
а) Найдите 15% числа 36;
б) Найдите число, 15% которого равны 36.
reshalka.com
Математика 6 класс Никольский. Номер №112
Решение
Решение:
а) 15 *
1
100
* 36 =
15
100
* 36 =
3
20
* 36 =
3
∗
9
5
=
27
5
= 5
2
5
;
б) 15% числа Х = 36.
Найдем чему равен 1% числа Х. 1% числа Х =
36
15
;
Само число Х = 100%, тогда число Х =
36
15
* 100 =
3600
15
= 240.
Ответ: 240.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом