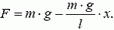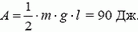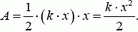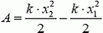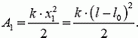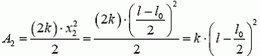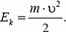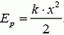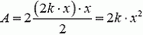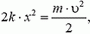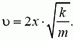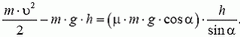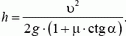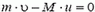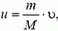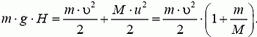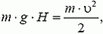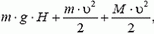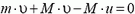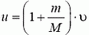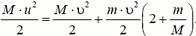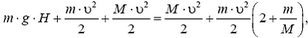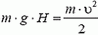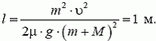Перейти к контенту
Условие задачи:
Какую работу надо совершить, чтобы растянуть пружину с жесткостью 40 кН/м на 0,5 см?
Задача №2.7.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(k=40) кН/м, (x=0,5) см, (A-?)
Решение задачи:
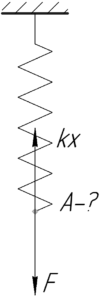
[A = frac{{k{x^2}}}{2}]
Переведем величину деформации (x) в систему СИ:
[0,5;см = frac{{0,5}}{{100}};м = 0,005;м]
[A = frac{{40 cdot {{10}^3} cdot {{0,005}^2}}}{2} = 0,5;Дж = 500;мДж]
Ответ: 500 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.6.15 Деревянный брусок массы 2 кг тянут равномерно по горизонтальной доске с помощью
2.7.2 Какую работу совершает постоянная сила по перемещению на 5 м тела массой 3 кг
2.7.3 Определить работу, необходимую для поднятия груза массой 3 кг на высоту 10 м
( 8 оценок, среднее 4.5 из 5 )
Овчинников О.Ю. Механическая работа и механическая энергия // Квант. — 1985. — № 5. — С. 46-50.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
§ 1. В механике работа, совершаемая постоянной силой 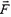
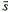
A = F·s·cos α.
Такое понятие не всегда соответствует обыденному представлению о работе. Например, штангист, удерживающий груз на поднятых руках, или носильщик, несущий тяжелый чемодан, механической работы не совершают (объясните — почему?).
Когда действующая на тело сила не постоянна (меняется ее модуль или направление), работу такой силы можно найти следующим образом. Разобьем все перемещение тела на такие малые участки 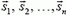
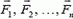
A1 = F1·s1·cos α1,
A2 = F2·s2·cos α2, …
An = Fn·sn·cos αn,
a полная работа будет равна сумме работ на отдельных участках:
A = A1 + A2 + … + An.
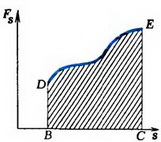
В тех случаях, когда известно, как изменяется от точки к точке проекция силы на направление перемещения Fs = F·cos α, работу можно найти графически (рис. 1). Полная работа на участке ВС численно равна площади фигуры BDEC.
Рис. 1
Задача 1. Чему равна работа по равномерному подъему однородной гладкой цепочки на гладкий горизонтальный стол? Первоначальное положение цепочки указано на рисунке 2, а; ее длина l = 6 м; масса m = 3 кг.
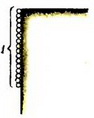

а б в
Рис. 2
В начальный момент на цепочку действует сила тяжести m·g, и для ее удержания требуется сила
F = m·g.
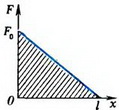
По мере поднятия цепочки на стол сила, необходимая для поднятия, будет уменьшаться. Обозначим длину части цепочки, уже лежащей на столе, через x (рис. 2, б). В этот момент к цепочке надо приложить силу
Построим график зависимости F = F(x) (рис. 2, в). Тогда работа, которую совершит эта сила при равномерном подъеме всей цепочки, будет численно равна площади заштрихованного треугольника:
Заметим, что совершенная работа равна работе по подъему центра тяжести цепочки. Поскольку в начальный момент он находится на расстоянии l/2 от поверхности стола, потребуется работа 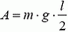
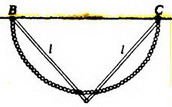
Задача 2. К точкам В и С, находящимся на одной горизонтали, подвешены однородная цепочка длиной 2l и система из двух стержней, соединенных шарниром, каждый из которых имеет длину l (рис. 3, а). Масса цепочки равна массе обоих стержней. Какой из центров тяжести — цепочки или системы стержней — находится ниже?
а
б
Рис. 3.
Подействуем на цепочку таким образом, чтобы ее положение совпало с положением системы стержней (рис. 3, б). Очевидно, что в этом случае центры тяжести цепочки и стержней тоже совпадают. Поскольку для того чтобы перевести цепочку в новое положение потребовалось над ней совершить некоторую работу, можно утверждать, что ее новое положение центра тяжести выше прежнего.
Следовательно, первоначально центр тяжести цепочки находился ниже центра тяжести системы стержней.
Задача 3. В первом опыте пружину, имеющую жесткость k и длину в недеформированном состоянии l0, растягивают до длины l. Во втором опыте эту пружину сначала разрезают на две равные части, затем берут одну из них и растягивают ее тоже до длины l. Определите работу, которую надо совершить в первом и во втором опытах.
Согласно закону Гука, при растяжении пружины на величину x возникает сила упругости Fyпр = –k·x (знак «минус» говорит о том, что сила упругости стремится вернуть пружину в исходное состояние). Для того чтобы растянуть пружину, к ней надо приложить внешнюю силу 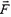
F = –Fyпр = k·x.
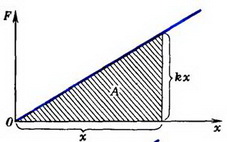
Построим график зависимости F = F(x) (рис. 4, а) и по нему найдем работу, которую должна совершить внешняя сила для растяжения недеформированной пружины на величину x:
а
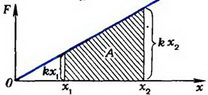
б
Рис. 4.
В случае, когда пружина уже была растянута на величину x1, а теперь ее надо растянуть до x2, работа внешней силы будет равна (рис. 4, б)
Теперь вернемся к нашей задаче. В первом опыте для растяжения целой пружины с жесткостью k из недеформированного состояния до длины l необходимо совершить работу
Во втором опыте до той же длины l растягивают лишь половину пружины так, что удлинение 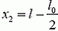
§ 2. В механике принято различать кинетическую энергию, обусловленную движением, и потенциальную, определяемую взаимным расположением тел системы или частей одного и того же тела.
Кинетическая энергия тела массой m, движущегося со скоростью υ, равна
Потенциальная энергия тела, находящегося в поле тяжести на высоте h над нулевым уровнем, равна
Ep= m·g·h,
а потенциальная энергия упруго деформированного тела равна
Между понятиями «механическая работа» и «механическая энергия» есть тесная связь. Работа равнодействующей сил, приложенных к системе, равна изменению кинетической энергии системы:
A= Ek2 – Еk1.
Работа сил тяжести или упругости, действующих в системе, равна взятому с противоположным знаком изменению потенциальной энергии системы:
А = –(Еp2 – Еp1).
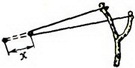
Задача 4. На рогатке закреплена длинная (по сравнению с размерами рогатки) резина с жесткостью k. Найдите максимальную скорость камня массой m, выпущенного из рогатки, если предварительно его оттянули на расстояние x(рис. 5).
Рис. 5
Поскольку резина длинная, можно считать, что на камень действуют две параллельные силы упругости резины 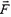
При возвращении в исходное недеформированное состояние резины силы упругости, действующие на камень, совершат работу
За счет этой работы камень приобретет кинетическую энергию
Таким образом,
откуда
Задача 5. Какая работа будет совершена силой F = 30 H при подъеме тела массой m = 2 кг на высоту h = 20 м?
Согласно определению, работа приложенной к телу силы равна
A = F·h = 600 Дж.
С другой стороны, при подъеме тела на высоту h против силы тяжести m·g совершается работа
A‘ = m·g·h = 400 Дж.
Конечно же, ничего странного в расхождении полученных результатов нет. Дело в том, что А‘ — это минимальная работа, которую нужно совершить для поднятия тела. За счет этой работы увеличивается его потенциальная энергия в поле тяжести Земли:
ΔEp= m·g·h = 400 Дж.
Остальная же часть работы идет на увеличение кинетической энергии тела (тело движется с ускорением, а почему?):
ΔEk = A – A‘ = 200 Дж.
Задача 6. На невесомой конструкции из стержней, соединенных шарнирно, подвешен груз массой m (рис. 6). Чему равно натяжение нити?
Рис. 6
Мысленно уменьшим длину нити на величину x, настолько малую, чтобы изменением силы натяжения нити можно было пренебречь. Тогда груз поднимется на высоту 2x (покажите это).
Работа силы натяжения нити при этом будет равна
A = Fн·x,
а потенциальная энергия груза в поле тяжести Земли изменится на
ΔEp = m·g·(2x) = 2m·g·x.
Таким образом,
Fн·x = 2m·g·x,
откуда
Fн = 2m·g.
§ 3. Энергия принадлежит к тем немногим физическим величинам, для которых выполняются законы сохранения.
В частности, если система тел замкнута и тела взаимодействуют друг с другом только силами тяготения и упругости, то полная механическая энергия системы (то есть сумма кинетической и потенциальной энергий) остается постоянной. Действие же силы, трения приводит к тому, что часть механической энергии превращается во внутреннюю энергию системы. Но и в этом случае сумма всех видов энергии системы сохраняется неизменной.
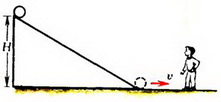
Задача 7. Мальчик на коньках разгоняется до скорости υ и вкатывается на горку, покрытую льдом. До какой высоты, считая от основания горки, он сможет подняться, если коэффициент трения μ, а угол наклона горки к горизонту α?
В начальный момент мальчик обладает кинетической энергией 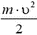
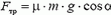
Отсюда находим искомую высоту h:
Задача 8. Камень массой m соскальзывает с гладкой горки высотой Н. Рассмотрим этот процесс в двух различных инерциальных системах отсчета. С точки зрения наблюдателя в неподвижной системе потенциальная энергия камня m·g·H переходит в кинетическую энергию 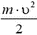
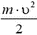
(Аналогичные вопросы подробно разбираются в статье В.А. Орлова «Парадокс «большого» тела», опубликованной в третьем номере журнала за 1978 год. (Примеч. ред.))
Рис. 7
Сразу же скажем, что закон сохранения энергии выполняется и в этом случае. Причина сформулированного в условии парадокса в том, что рассуждения проводились для незамкнутой системы — одного камня, а Земля, с которой камень взаимодействует, не учитывалась. Исправим эту ошибку.
а) В неподвижной системе отсчета (связанной с центром масс системы камень — Земля) в начальный момент камень и Земля покоятся, и вся энергия равна потенциальной энергии системы. В конечный момент камень приобретает скорость 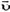
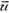
откуда
где М — масса Земли.
Согласно закону сохранения энергии,
Поскольку масса камня ничтожно мала по сравнению с массой Земли, величиной m/М по сравнению с единицей можно пренебречь. Тогда получим
что целиком соответствует условию задачи.
б) В движущейся системе отсчета в начальный момент общая энергия системы равна
а в конечный она равна 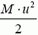
получаем
и
Тогда из закона сохранения энергии имеем
или, пренебрегая величиной m/M по сравнению с двойкой,
— тот же самый результат, что и с точки зрения неподвижного наблюдателя!
Упражнения
1. Тело массой M = 990 г лежит на горизонтальной плоскости. В него попадает пуля массой m = 10 г, летящая горизонтально со скоростью υ = 100 м/с, и застревает в нем. Какой путь пройдет тело до остановки, если коэффициент трения между ним и плоскостью μ = 0,05?
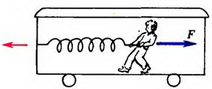
2. В вагоне равномерно идущего поезда стоит человек, натягивающий пружину с силой 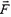
Рис. 8
Ответы
1.
2. В обеих системах отсчета A = 0.
Сила упругости, как и
сила тяжести, является консервативной. Напомним, что консервативная сила —
это такая сила, работа которой при движении тела по замкнутому контуру, равна
нулю. В одном из уроков мы уже убедились, что работу силы упругости нельзя
вычислить, пользуясь общей формулой для работы силы. Дело в том, что сила
упругости изменяется с изменением растяжения или сжатия пружины. Поэтому нам
необходимо будет воспользоваться графиком зависимости силы упругости от
удлинения.
Поскольку сила упругости
линейно зависит от удлинения, нам не составит труда найти площадь под графиком
функции силы упругости. Эта площадь и будет являться работой. На графике
зависимости силы упругости от удлинения обозначим два произвольных значения
силы: F1
и F2.
Этим значениям будут соответствовать значения удлинения х1 и х2.
Как видно из графика, чтобы найти работу, нам нужно вычислить площадь трапеции.
Площадь трапеции равна произведению полусуммы оснований и высоты. Очевидно, что
основания — это F1
и F2,
а высота равна х1 − х2. Тогда,
используя формулу для силы упругости, мы можем вывести окончательное выражение
для работы силы упругости:
Напомним, что изучая
работу силы, мы пришли к выводу, что работа равна изменению кинетической
энергии. В данном случае мы видим, что работа силы упругости равна изменению
потенциальной энергии пружины. Но о потенциальной энергии мы поговорим
немного позже.
Итак, мы выяснили, что работа
силы упругости, так же, как и работа силы тяжести, не зависит от траектории
движения.
Пример решения задачи.
Задача.
Когда пружину, изначально находящуюся в расслабленном состоянии, растянули на 2
см, сила упругости составила 5 Н. Найдите работу силы упругости при растяжении этой
пружины на 8 см.
- Авторы
- Резюме
- Файлы
Иванов Е.М.
Показано, что работа растяжения пружины A>kxm2 , где k — жесткость пружины, xm — максимальное растяжение. При вычислении работы надо использовать значения x и dx, полученные из решения уравнения движения.
Показано, что работа растяжения пружины A>kxm2 , где k — жесткость пружины, xm — максимальное растяжение. При вычислении работы надо использовать значения x и dx, полученные из решения уравнения движения.
It is shown, that work of a stretching of a spring A>kxm2 , where k — rigidity of a spring, xm — the maximal stretching. At calculation of work it is necessary to use values x and dx, the equations of movement received from the decision.
Рассмотрим спиральную пружину, один конец которой закреплен (рис. 1а), а к другому прикреплен груз массой m. Если пружину растянуть или сжать, то возникает сила F, стремящаяся вернуть тело в положение равновесия. При небольших растяжениях x справедлив закон Гука — сила пропорциональна растяжению пружины: F = -kx. Постоянная k называется коэффициентом упругости, или жесткостью пружины. Знак минус означает, что сила F направлена в сторону, противоположную смещению x, т.е. к положению равновесия x = 0. Геометрически (рис. 1b) , k = tgβ, xm — максимальное (амплитудное) растяжение пружины.
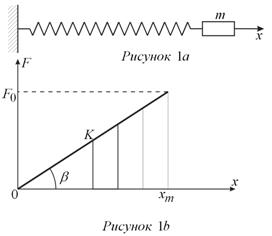
В курсах физики утверждается, что работа при растяжении от x = 0 до xm будет равна
(1)
и эта работа равна потенциальной энергии пружины, растянутой (или сжатой) на величину xm и обладающей жесткостью k. Однако это одно из заблуждений классической механики. Растягивающей силой, равной F = kx, нельзя растянуть пружину даже на долю микрона. Чтобы растянуть пружину, надо приложить растягивающую силу в виде (F1 + k1x ), где F1 >0 (рис. 2а). Уравнение движения (II закон Ньютона) запишем в следующем виде:
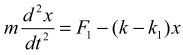
Решение при нулевых начальных условиях (при t = 0, x =0 и V =0) имеет вид
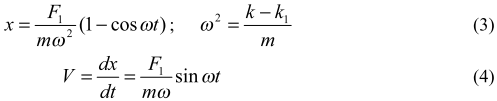
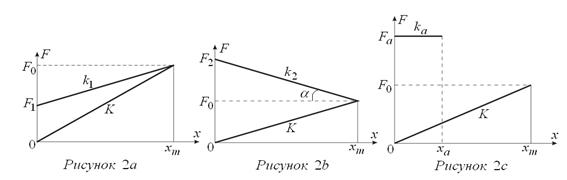
Из решения следует, что если F1 =0, то растяжения пружины не происходит. Амплитудные значения (при x = xm):
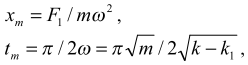
Работу вычисляем по формуле , где F = F1 — (k — k1)x, а x и dx определяются из выражений (3) и (4). Работа, совершаемая растягивающей силой
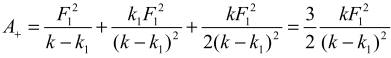
Работа, совершаемая силой упругости пружины
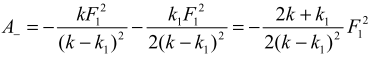
Из соотношения (5) следует, что работа, совершаемая растягивающей силой, не зависит от величин F1 и k1 и равна работе
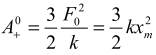
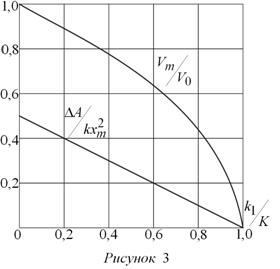
совершаемой постоянной силой F0, при этом работа, совершаемая силой упругости пружины A—0 = -kxm2 разность работ ΔA0 = kxm2 / 2 , конечная скорость при x = xm На рис. 3 даны графики зависимостей Vm / V0 и ΔA = kxm2 от величины отношения K1 / K. ΔA — кинетическая энергия груза.
Рассмотрим случай растягивающей силы FP > F0 (рис.2b) FP = F2 + k2x = F2 — b2x , где b2 = -k2 = tgα. Дифференциальное уравнение движения имеет вид:
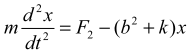
Его решение при нулевых начальных условиях имеет вид:
;
(8)
(9)
Амплитудные значения (при x = xm): xm = F2 / mω2; ;
.
Работа, совершаемая растягивающей силой
(10)
Работа, совершаемая силой упругости пружины
(11)
Кинетическая энергия груза при x = xm
(12)
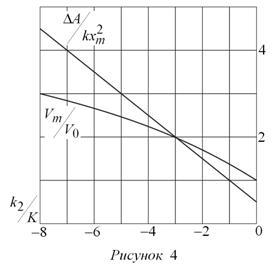
На рис. 4 даны графики изменения безразмерных комплексов ΔA / kxm2 и Vm / V0 в зависимости от величины отношения k2 / k.
Рассмотрим третий способ растяжения пружины с грузом (рис. 2с). Прикладываем растягивающую силу Fa >>F0 для растяжения пружины на некоторое расстояние xa, затем сила Fa отключается, а оставшийся отрезок пути, равный xm — xa, груз проходит по инерции, используя запас кинетической энергии Ka, приобретенный в точке xa. Для первого участка пути дифференциальное уравнение имеет вид
(13)
Его решение при нулевых начальных условиях:
;
(14)
(15)
Время движения до x = xa
(16)
Работу вычисляем по формуле , где F(x) = Fa — kx, а x и dx определяются выражениями (14) и (15). Работа растяжения на участке до x = x0
(17)
Работа, совершаемая силой упругости пружины на этом же участке
(18)
Кинетическая энергия, приобретенная грузом:
(19)
Для второго участка уравнение движения имеет вид
(20)
Начальные условия для этого уравнения примем в виде: при t = 0 координата x = xa, скорость Va определяется выражением (15) при t = ta. Решение будет иметь вид:
(21)
(21a)
Работа силы упругости пружины на участке от x = xa до xm определится интегралом , где x и dx определяются выражениями (21) и (21а):
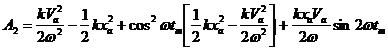
где tm ─ время движения груза от x=xa до x = xm. Условием достижения этой точки является равенство начальной кинетической энергии Ka работе силы упругости пружины A2. Это равенство сводится к трансцендентному уравнению
(23)
где a = kxa2 / 2; b = Ka — a; c = kxaVa / 2ω; φ = ωtm.
Приведем численный пример. Груз массой m = 1 кг, прикрепленный к пружине с жесткостью k = 400 Н/м, растягивается силой F0 = 80 Н на расстояние xm = 0,2. Работа силы растяжения Дж, работа силы упругости пружины
Дж, время t = 0,0785 с.
Проведем растяжение силой Fa по схеме, показанной на рис. 2с. Расчет сведем в таблицу 1.
Таблица 1.
|
Fa [H] |
Ka [Дж] |
ta [c] |
xa [м] |
A+ [Дж] |
A— [Дж] |
tm [c] |
|
8000 |
8 |
0,0005 |
0,001 |
16 |
-8 |
0,078 |
|
800 |
7 |
0,00468 |
0,00876 |
14,015 |
-7,015 |
0,0762 |
|
200 |
6 |
0,0176 |
0,0309 |
12,19 |
-6,19 |
0,0696 |
|
80 |
3,75 |
0,0377 |
0,054 |
8,088 |
-4,338 |
0,0597 |
Таким образом, только в случае растяжения пружины с грузом по схеме, показанной на рис.2с, можно затратить работу на растяжение A+, близкую к потенциальной энергии растянутой пружины П = kxm2 / 2.
Библиографическая ссылка
Иванов Е.М. РАБОТА ДЕФОРМАЦИИ ПРУЖИННОГО МАЯТНИКА // Современные наукоемкие технологии. – 2007. – № 3.
– С. 15-19;
URL: https://top-technologies.ru/ru/article/view?id=24676 (дата обращения: 29.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Пусть
материальная точка перемещается вдоль
оси ох под действием переменной силы

направленной параллельно оси. Тогда
работа, произведённая силойF
при перемещении точки из положения



Пример
5.1. Найти
работу, которую нужно затратить, чтобы
растянуть пружину на 0,05 м, если сила 100
Н растягивает пружину на 0,01 м
По
закону Гука упругая сила F,
растягивающая пружину, пропорциональна
этому растяжению х, т.е.

гдеk
– коэффициент пропорциональности. По
условию сила

растягивает пружину на
т.е.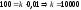
Тогда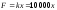
Вычислим
работу:

(Дж)
Определённый
интеграл применяют для вычисления пути
S
прямолинейного движения.
Путь
S,
пройденный материальной точкой за
промежуток времени от
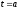
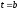
равен определённому интегралу от
скорости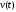
Пример
5.2. Вычислить
путь, пройденный точкой за 4 секунды от
начала движения, если скорость точки

По
условию:

Тогда

Задания для самостоятельного решения
1.
Найти работу производимую при сжатии
пружины на 0,03 м, если для сжатия её на
0,005 м нужно приложить силу в 10 Н.
Ответ:
0,9 Дж.
2.
Сила упругости пружины, растянутой на
0,05 м, равна 3 Н. Найти работу, которую
надо произвести, чтобы растянуть эту
пружину на 0,05 м
Ответ:
0,075 Дж.
3.
Найти работу, которую нужно затратить,
чтобы растянуть пружину на 0,05 м, если
сила 100 Н растягивает пружину на 0,01 м
Ответ:
125 Дж.
4.
Вычислить работу, совершаемую при сжатии
пружины на 15 см, если известно, что для
сжатия пружины на 1 см необходима сила
в 30 Н.
Ответ:
33,75 Дж.
5.
Вычислить работу, совершаемую при сжатии
пружины а 0,08 м, если для сжатия её на
0,01 м нужна Сида в 25 Н.
Ответ:
8 Дж.
6.
Тело движется прямолинейно со скоростью
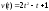
3 с.
Ответ:
16,5 м.
7.
Тело движется прямолинейно со скоростью

найти значение параметра
если известно, что за промежуток времени
от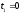

тело прошло путь длиной 40 м.
Ответ:

8.
Тело движется прямолинейно со скоростью
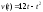
Найти длину пути, пройденного телом от
начала пути, до его остановки.
Указание:
в моменты начала и остановки скорость
тела равна нулю.
Ответ:
288 м.
9.
Найти путь, пройденный точкой за третью
секунду, зная скорость её прямолинейного
движения

Ответ:
11 м.
10.
Два тела начали двигаться по прямой в
один и тот же момент из одной точки в
одном направлении. одно тело двигалось
со скоростью


через 2 секунды.
Ответ:
8м.
Вопросы для самопроверки
1.
Запишите определение определённого
интеграла через предел интегральных
сумм.
2.
Сформулируйте основные свойства
определённого интеграла.
3.
Запишите формулу Ньютона-Лейбница.
4.
Запишите формулу интегрирования по
частям для определённого интеграла.
5.
Запишите формулы для вычисления площадей
плоских фигур.
6.
Запишите формулы для вычисления объёмов
тел вращения.
7.
Запишите формулу для вычисления работы
переменной силы.
8.
Запишите формулу для вычисления пути
прямолинейного движения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #